Probing structural heterogeneities and fluctuations of nucleic acids and denatured proteins

Abstract

We study protein and nucleic acid structure and dynamics using single-molecule FRET and alternating-laser excitation. Freely diffusing molecules are sorted into subpopulations based on single-molecule signals detected within 100 μs to 1 ms. Distance distributions caused by fluctuations faster than 100 μs are studied within these subpopulations by using time-correlated single-photon counting. Measured distance distributions for dsDNA can be accounted for by considering fluorophore linkers and fluorophore rotational diffusion, except that we find smaller fluctuations for internally labeled dsDNA than DNA with one of the fluorophores positioned at a terminal site. We find that the electrostatic portion of the persistence length of short single-stranded poly(dT) varies approximately as the ionic strength (I) to the –1/2 power (I^–1/2), and that the average contribution to the contour length per base is 0.40–0.45 nm. We study unfolded chymotrypsin inhibitor 2 (CI2) and unfolded acyl-CoA binding protein (ACBP) even under conditions where folded and unfolded subpopulations coexist (contributions from folded proteins are excluded by using alternating-laser excitation). At lower denaturant concentrations, unfolded CI2 and ACBP are more compact and display larger fluctuations than at higher denaturant concentrations where only unfolded proteins are present. The experimentally measured fluctuations are larger than the fluctuations predicted from a Gaussian chain model or a wormlike chain model. We propose that the larger fluctuations may indicate transient residual structure in the unfolded state.

In contrast to neutral homopolymers (1), biopolymers such as proteins and nucleic acids have long-range Coulomb interactions (2) and specific, intrachain interactions that strongly affect their structure and dynamics. Protein folding is the most spectacular manifestation of these interactions (3). Understanding biopolymer energy landscapes requires measurements of fluctuating distance distributions occurring over short distances (0.1–100 nm) and many time scales (picoseconds to minutes) (4). The structure and dynamics of charged polymer chains (polyelectrolytes), including dsDNA and ssDNA, are strongly affected by long-range, electrostatic repulsion (2). Because simulations and theory have focused on dilute, single-chain properties, a regime difficult to access by conventional methods, experimental validation of many predictions has been lacking (5). In protein folding studies, folded, unfolded, and partially folded species may be simultaneously present and rapidly interconverting, obscuring the properties of individual species. An experimental method that unravels distance distributions and fast conformational fluctuations is therefore much-needed.

Previous protein folding studies with single-molecule FRET (6–8) measured distance distributions with time resolutions of ≈100 μs. Using nanosecond alternating-laser excitation (nsALEX; see Materials and Methods), we combine the strengths of single-molecule and ensemble FRET methods to provide information on faster fluctuations within individual subpopulations.

Energy transfer efficiency, E, varies with distance between donor (D) and acceptor (A) fluorophores, E = [1 + (R/R₀)⁶]^–1. A polymer's distance distribution, P(R), causes a distribution in E(P(E)) and, hence, multiexponential donor fluorescence life-time decays (9). We analyze time-resolved decays for individual subpopulations, extracting the first two moments, 〈E 〉 and ΔE, of the distribution P(E). These are interpreted in terms of biopolymer contour length, L, and persistence length, l_P (Fig. 1).

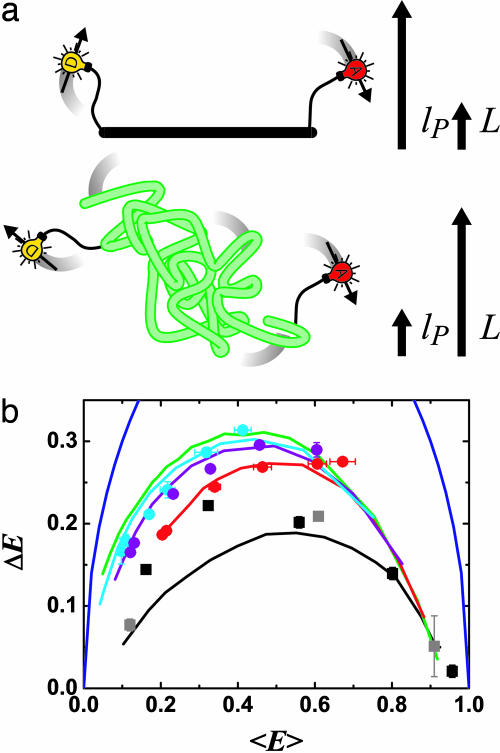
Fig. 1.

FRET reveals distance distributions related to polymer flexibility. (a) Distance distributions in polymers are probed by using FRET from a donor fluorophore (D; yellow bulb) to an acceptor fluorophore (A; red bulb). A rigid rod (Upper, black; with contour length, L, much smaller than persistence length, l_P) is distinguished from a flexible Gaussian chain (Lower, green; L » l_P) and intermediate cases (L ∼ l_P; not shown) by differences in the distributions of energy transfer efficiency, E, caused by distributions in D–A distances. Flexible fluorophore linkers and rotational diffusion of the fluorophores on similar time scales to fluorescence also affect the measurements. (b) Experimental data and simulations of E distributions [P(E)] of D–A-labeled polymers summarized as plots of standard deviation ΔE vs. mean efficiency 〈E 〉. Simulations (with R₀ = 6.9 nm): (i) a rigid rod with linkers and fluorophore rotational diffusion lifetime τ_r similar to the donor fluorescence lifetime τ_f (τ_r ≈ τ_f) (solid black); (ii) wormlike chains with L = 12 nm (solid red), L = 16 nm (solid purple), and L = 20 nm (solid cyan), each with varying l_P, τ_r ≈ τ_f, and linkers; (iii) a Gaussian chain with varying L × l_P, τ_r ≈ τ_f, and linkers (solid green); and (iv) a hypothetical polymer with the largest possible fluctuations 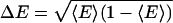(solid blue). Data: dsDNA with 7-, 12-, 17-, 22-, and 27-bp D–A separations (black squares); dsDNA with 5-, 15-, and 25-bp D–A separations (gray squares, internally labeled); ssDNA at varying salt concentration [(dT)₃₀, red circles; (dT)₄₀, purple circles; (dT)₅₀, cyan circles]. For all figures, the data points are averages of two or three independent experiments, and error bars are standard errors of the mean.

We studied three types of biopolymers using nsALEX: (i) dsDNA, portraying a rigid rod; (ii) poly(dT) ssDNA, portraying a flexible homopolymer; and (iii) denatured chymotrypsin inhibitor 2 (CI2) and acyl-CoA binding protein (ACBP), portraying flexible heteropolymers, where ACBP has been shown to exhibit residual structure in the unfolded state (10, 11).

Materials and Methods

nsALEX. We use time division multiplexing of interlaced, picosecond pulses from two synchronized mode-locked lasers to perform ALEX (12) experiments on single molecules in conjunction with time-resolved FRET and time-resolved fluorescence anisotropy measurements (see Nanosecond ALEX in Supporting Appendix, which is published as supporting information on the PNAS web site). Individual molecules are identified by using the photon bursts emitted as they diffuse through a focused-laser excitation volume (burst search algorithm from ref. 13). Detected photons are timed with 50-ns resolution (“macrotiming”) and classified by spectrum [D (yellow) or A (red)] and polarization. Interlacing pulses from two lasers, D_exc (excites D) and A_exc (excites A), with a fixed delay provides a 14.7-ns alternation period for nsALEX. The time delay between the detected photons and the D_exc laser pulse is measured with 17-ps nominal resolution (“microtiming”); the actual resolution of ≈500 ps depends on laser pulse width and the avalanche photodiode time resolution. The microtime provides fluorescence lifetime and the ability to classify photons as due to D_exc or A_exc (whether time delay τ is before or after the A_exc pulse).

Analysis of multiexponential fluorescence lifetime decays is not possible for single diffusing molecules because only up to ≈100 photons are detected per photon burst. However, on a subpopulation basis (14), such analysis is possible, probing distance distributions that fluctuate on time scales down to the fluorescence lifetime (typically the nanosecond time scale).

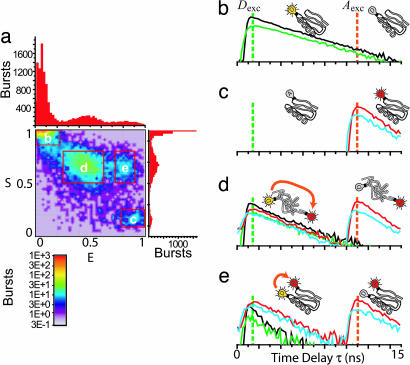
Single-molecule bursts are sorted into different species based on specific ranges E_min ≤ E ≤ E_max and S_min ≤ S ≤ S_max in the 2D E–S histogram; E is the FRET efficiency, and S is the stoichiometric ratio that depends on the presence or absence of D and A for a single molecule (12) (see Nanosecond ALEX in Supporting Appendix). An example of such a histogram for the CI2 C1–C53 mutant at 4 M GdnCl is shown in Fig. 2a. Fluorescence-lifetime histograms are formed by using the photons from all bursts of each selected range for each channel (Fig. 2 b–e). The fluorescence-lifetime decays of subpopulations with D only, A only, and high and low FRET are clearly distinguished. There are two lifetime decays in the A channels arising from D_exc and A_exc, giving a total of six lifetime decays over all channels.

Fig. 2.

Time-resolved FRET curves for subpopulations extracted by using nsALEX. (a) Photon burst histogram resulting from single molecules of D–A-labeled C1–C53 CI2 mutant diffusing through laser spot in 4 M GdnCl. E and S are calculated for each burst and placed in the histogram. Four species are detected, and their corresponding time-resolved fluorescence decay curves are extracted (shown in b–e): parallel D decay (black); perpendicular D decay (green); parallel A decay (red); and perpendicular A decay (cyan). (b) Proteins with D only emit only after D_exc (leakage of D into A channel removed for clarity). (c) Proteins with A only emit only after A_exc (direct excitation of A by D_exc removed for clarity). (d) Unfolded proteins labeled with D and A emit D and A fluorescence after D_exc pulse (ratio of intensities and lifetimes depend on FRET efficiency) and emit A fluorescence after A_exc. (e) Folded proteins labeled with D and A emit similarly to case d, except with a higher relative intensity of A compared with D after the D_exc pulse, and with a shorter D lifetime, indicating a higher E due to shorter average distance.

In principle, the measurements on dsDNA and ssDNA are possible by using bulk time-resolved FRET measurements; however, single-molecule sorting eliminates D-only and A-only species resulting from photobleaching (species labeled with a single D or A or double-D- and double-A-labeled molecules were chromatographically removed; see Sample Preparation and Characterization in Supporting Appendix) and allows the study of polyelectrolytes at very low concentrations. Beyond these technical improvements, nsALEX also affords the detailed study of samples where multiple subpopulations are intrinsic to the system, such as with CI2 and ACBP. Without nsALEX, the properties of unfolded CI2 and ACBP would be obscured by the presence of folded CI2 and ACBP.

Simulations of FRET. We use simulations to obtain expected lifetime decays in the presence of distance distributions and dynamics expected for biopolymers (see Simulations of Fluorescence Lifetime Decays in Supporting Appendix). P(R) and P(E) for biopolymers are described by contour length, L, and persistence length, l_P (15). For L « l_P, R is fixed (rigid rod; black polymer, Fig. 1a). For L » l_P (green polymer, Fig. 1a), a Gaussian chain describes P(R) (15):

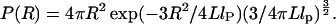For l_P ≈ L, a wormlike chain model is required. We use a series of simulations with varying ratios L/l_P (16, 17). The polymer chain is divided into segments of length l_P/20. Possible configurations are simulated by randomly selecting polar angles (θ, φ), where φ is uniformly distributed over [0,2π], and θ is distributed as P(θ) ∝ θexp[–(θ/Δθ)²] (for segments of length l_P/20, Δθ = 0.102). We performed 1,000,000 simulations with a total length of 1,000 segments, obtaining good approximations to P(R) for 1,000 values of the ratio L/l_P between 0.1 and 50.

Our simulations account for other properties that affect P(E). First, E depends on the relative orientation of the excitation and emission dipoles of D and A through the factor κ²(R₀ ∝ κ²). For a rigid rod with rapid fluorophore rotational diffusion, κ² is replaced by 〈κ² 〉 = 2/3 and E is constant. Dipole orientation restrictions and rotational diffusion on time scales near the fluorescence lifetime shift and widen P(E) (18, 19). Time-resolved fluorescence anisotropy partially characterizes κ² by using rotational diffusion time scales and 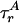for D and A. We model κ effects using dipoles with complete orientational freedom but with incomplete orientational averaging during the fluorescence lifetime (6), an appropriate model for disordered systems and systems using long, flexible fluorophore linkers (19).

Second, fluorophore linkers (length of two or six carbon bonds) widen distance distributions, which we model as one effective Gaussian chain with the parameter, .

Third, fluctuations in distance within the fluorescence lifetime increase 〈E 〉 and lower ΔE. We simulate these effects using Brownian dynamics in a 1D effective potential as well as using Rouse chain dynamics simulations.

“Phase Diagram” for Polymer Fluctuations. A global fit of all six lifetime decays by using a two-state model [approximating P(E) by its first two moments, 〈E 〉 and ΔE], accounting for the rotational diffusion time scales 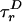(for D) and 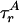(for A) and the temporal response of the photodetectors (see Model Including Anisotropy and Instrument Response in Supporting Appendix), extracts information about a selected subpopulation. Corrections for photons from background and from other diffusing species that “leak” into these histograms are described under Accuracy of Subpopulation Analysis in Supporting Appendix. The global fit allows information from the donor and acceptor decays to constrain lifetimes, donor leakage, and direct excitation of A while extracting information on FRET and FA, greatly improving confidence in the fitted parameters. In this subpopulation analysis, we are not able to distinguish between dynamically changing distance distributions and static distributions not well resolved with E and S (we lose some single-molecule information). However, we are able to eliminate contributions from well resolved species, allowing a very robust analysis of FRET and hence providing novel information on P(E), and therefore on P(R), i.e., polymer fluctuations.

To extract information on P(E), we approximate multiexponential fluorescence lifetime decays using a model with two states of constant FRET efficiencies E₁ and E₂, spending a fraction of time β in state 1 (for complete model, see Model Including Anisotropy and Instrument Response in Supporting Appendix). More sophisticated fitting and deconvolution methods are possible (9, 20–22), but these methods would need to be extended to include polarization effects important in our case; we point out that although we use a simple fitting model, our analysis also uses comparisons with sophisticated simulations to validate results (see Simulations of Fluorescence Lifetime Decays in Supporting Appendix). The D decay is

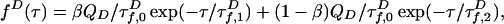[1]

where Q_D is the quantum efficiency. D lifetime 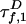is reduced by FRET from its value 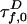in the absence of A: 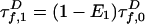. Likewise, 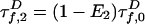. The A decay due to FRET is

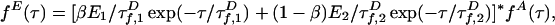[2]

where * denotes convolution. 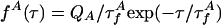is the intrinsic fluorescence decay of A, where 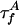and Q_A are defined as for D. The FRET rates 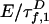and 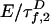in Eq. 2 replace the fluorescence rates 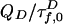in Eq. 1. Hence, the contributions of states 1 and 2 to f^D(τ) and f^E(τ) differ. The most robust analysis uses both decays (as done here), mitigating difficulties in extracting lifetime distributions from multiexponential data (20, 22).

The two-state model defines a discrete probability distribution with moments 〈E 〉 = βE₁ + (1 – β)E₂ and 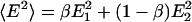. The standard deviation is 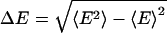. In Fig. 1b, we plot ΔE vs. 〈E 〉 for a series of polymer simulations. This representation has not, to our knowledge, been used to present time-resolved FRET data, which are usually plotted as full, recovered probability distributions in R space. The models used to obtain these distributions typically have two to three free parameters or significant restrictions on smoothness of the results and, hence, do not contain much more information than the two parameters we use. Reducing each distribution to a single point allows more data to be displayed simultaneously, revealing patterns otherwise unseen. The use of E = [1 + (R/R₀)⁶]^–1 rather than R confines all data points to a finite area and focuses on the range of higher sensitivity for FRET.

The values of 〈E 〉 and ΔE for different polymer regimes occupy different regions of Fig. 1b, giving it the “flavor” of a “phase diagram.” Predictions from simulations (see “Phase Diagram” for Polymer Fluctuations and Simulations of Fluorescence Lifetime Decays in Supporting Appendix) are shown for (i) rigid rods (black), (ii) wormlike chains (red, purple, and cyan), (iii) Gaussian chains (green), and (iv) a hypothetical polymer that switches instantaneously between E = 0 and E = 1 states (largest possible fluctuations, blue).

The Gaussian chain model (iii) provides an upper limit on the width of distance distributions described in terms of contour length and persistence length. This upper limit does not depend on R₀ or linker fluctuations, but does depend weakly on the rotational diffusion of the fluorophores (see “Phase Diagram” for Polymer Fluctuations in Supporting Appendix). End-to-end diffusion within the fluorescence lifetime decreases this limit (see Simulations of Fluorescence Lifetime Decays in Supporting Appendix). Experimental data (Fig. 1) lie between the rigid rod regime (solid black) and the largest possible fluctuations (solid blue). Data points above the Gaussian chain regime (solid green) do not describe simple polymer behavior. Instead, they may indicate fluctuations between two states, involving crossing an energy barrier.

Results and Discussion

Rigid Rod (dsDNA). Two series of 40-bp dsDNA fragments were synthesized. In the first series (from ref. 23), each fragment was labeled with tetramethylrhodamine as D on the 5′ end of DNA and internally labeled with Alexa Fluor 647 as A at five positions, with 7-, 12-, 17-, 22-, and 27-bp separations (see Sample Preparation and Characterization in Supporting Appendix). In the second series (from ref. 12), each fragment was internally labeled with tetramethylrhodamine as D at position 5, and internally labeled with Alexa Fluor 647 as A at 3 positions, with 5-, 15-, and 25-bp separations. The nsALEX data for dsDNA is presented in Fig. 1b by plotting ΔE vs. 〈E 〉 (black and gray squares). For rigid rod simulations accounting for fluorophore linkers and rotational diffusion of the fluorophores (solid black line), the effective linker length of 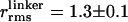nm best matched the ΔE for the dsDNA samples [see Simulating R(t) by Using Static Polymer Models and Calibration of Linker Contribution in Supporting Appendix]. Previously measured 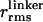on short dsDNA are between 0.7 and 1.3 nm (values converted to 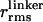) (24, 25). For the end-labeled samples with 0.0 E 0.5 < E < 0.5 (22- and 27-bp separations), the measured ΔE is significantly higher than the simulations.

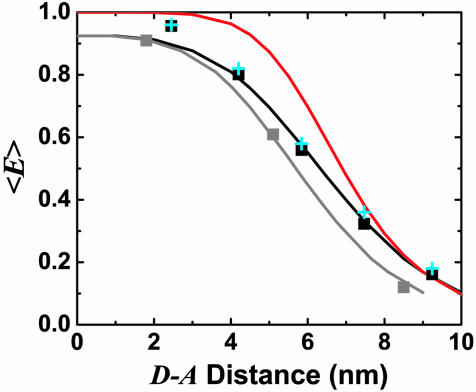
Fig. 3 shows the distance dependence of 〈E 〉 as a function of distance between D and A fluorophore attachment points for both dsDNA series (black and gray squares). Previous calibrated measurements of 〈E 〉 using ALEX intensity ratios rather than fluorescence lifetime are shown for comparison (cyan crosses) (23). There is excellent agreement between these independent determinations of 〈E 〉. The measurements deviate from Förster theory when ignoring linkers and using 〈κ² 〉 = 2/3 (red line). Accounting for linker fluctuations and rotational diffusion (black line) improves agreement between theory and experiment. The red line is a calculation using independent spectroscopic data with R₀ = 6.9 ± 0.1 nm (23). The black line is from simulations using R₀ = 6.9 nm and the linker contributions determined above. The gray line is for simulations with R₀ = 6.2 nm, adjusted to match the gray squares. The change in R₀ is likely related to changes in the environment of D (internal labeling vs. end-labeling); there is a change in the lifetime of D in the absence of A from 4.0 ± 0.1 ns to 3.1 ± 0.1 ns that accounts for roughly half of the change.

Fig. 3.

〈E 〉 vs. distance between attachment points for D and A for dsDNA with 7-, 12-, 17-, 22-, and 27-bp separations (black squares) and dsDNA with 5-, 15-, and 25-bp separations (gray squares). 〈E 〉 calculated from calibrated single-molecule intensity ratios rather than fluorescence lifetime information are shown as cyan crosses (23). FRET model [E = 1/1 + (R/R₀)⁶] with measured R₀ = 69 Å and 〈κ² 〉= 2/3 (solid red) and simulation accounting for linkers and the measured slower rotational diffusion (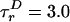 ns and 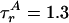ns; solid black) are shown. Simulations were adjusted to R₀ = 62 Å to match gray squares.

The small deviations of the data points for 7-, 12-, and 17-bp separations (high E range) from the simulations in Figs. 1 and 3 may be explained by the use of only one rotational diffusion time scale in the simulation, overestimating κ² effects. The larger deviations of the 22- and 27-bp separations data points (low E range, Fig. 1b) from the simulations are more problematic and cannot be explained by the wormlike chain model. For the 27-bp D–A distance, comparison with wormlike chain simulations gives contour length L = 12 ± 1 nm and persistence length l_P = 9 ± 1 nm. This l_P is five times smaller than the value of 50 nm found at longer distances. Possible explanations for increased ΔE for the 22- and 27-bp separations include dsDNA end fraying, bending of dsDNA for short length scales, and dynamically changing interactions between the fluorophores and DNA. For dsDNA with terminal A-T base pairs, some end fraying is expected (26); at least two frayed base pairs are needed to explain our results [see Simulating R(t) by Using Static Polymer Models and Calibration of Linker Contribution in Supporting Appendix]. In support of this explanation, internally labeled dsDNA (gray squares) shows no such large ΔE, and MD simulations using the sequence show significant fraying of the ends (E. Lau and M. Colvin, personal communication). On the other hand, fraying (and dynamically changing fluorophore–DNA interactions) should also be detected for shorter D–A separations. Internal bends at specific points may also explain these results, but no propensity for such bends or more general flexibility was found in the MD simulations.

Flexible Homopolymer (ssDNA). Because of its charge density and flexibility, ssDNA is strongly affected by ionic strength. nsALEX is well suited to the study of polyelectrolytes in very dilute conditions, a regime inaccessible by using standard methods (2). We studied three lengths of poly(dT) ssDNA labeled at the 3′ end with tetramethylrhodamine and at the 5′ end with Alexa 647 [(dT)30, red circles; (dT)40, purple circles; (dT)50, cyan circles; Figs. 1 and 4; see Sample Preparation and Characterization in Supporting Appendix] as a function of ionic strength. [NaCl] was varied over three orders of magnitude in a 20 mM Tris buffer. As [NaCl] increases, increasingly compact conformations and larger fluctuations are observed. The grid of wormlike chain simulations converts 〈E 〉 and ΔE into L and l_P (see Simulations of Fluorescence Lifetime Decays in Supporting Appendix). For short chains the shape of the distribution function and hence the ratio ΔE/ 〈E 〉 is strongly dependent on l_P/L.

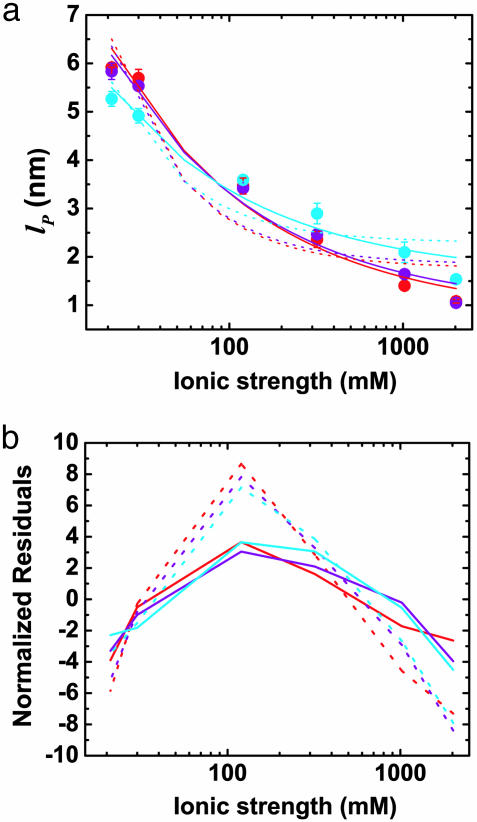
Fig. 4.

Effects of ionic strength on ssDNA flexibility. (a) Extracted persistence length, l_P, vs. ionic strength ([NaCl] + [Tris buffer]) for (dT)₃₀ (red circles), (dT)₄₀ (purple circles), and (dT)₅₀ (cyan circles). Solid red, purple, and cyan lines: respective fits to model, 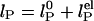with constant, intrinsic persistence length 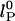and electrostatic contribution 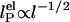. Dotted lines: respective fits to model, 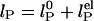, where the electrostatic contribution varies as 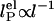. (b) Residuals plotted for fits in a. Fits were weighted by using error value averaged over all data points.

The properties of (dT)₃₀, (dT)₄₀, and (dT)₅₀ match static wormlike chains below [NaCl] = 1 M, with L = 12 ± 1, 15 ± 1, and 18 ± 2 nm, respectively (Fig. 1) and l_P varying from 6 to 2.4 nm (Fig. 4). Accounting for conformational dynamics within the fluorescence lifetime, the average base-to-base distance extracted is between h = 0.40 and 0.45 nm [see Simulating R(t) by Using Dynamic Polymer Models in Supporting Appendix; L = N_monomersh, where N_monomers is the number of monomers]. Our simulations simultaneously and independently match the data for (dT)₃₀, (dT)₄₀, and (dT)₅₀ for almost all salt concentrations, providing high confidence in the extracted h values. At 1–2 M NaCl, ΔE rises above the wormlike chain models with constant L, approaching the Gaussian chain regime. This may be related to calculations showing that the wormlike chain model is not always appropriate for polyelectrolytes (27).

For poly(dT), literature values for h are generally in the 0.5- to 0.7-nm range, with most near 0.6 nm (28, 29). For poly(dT)₃₀, this gives a value for L between 15 and 21 nm. However, our result of h between 0.4 and 0.45 nm is consistent with a model based on NMR measurements of the UpU dimer and light scattering measurements of poly(rU), where h = 0.44 nm (30). Although large-scale stacking was not found, the shortened h was attributed to “residual stacking” conformers interspersed with extended, unstacked conformers.

The dependence of the persistence length l_P on ionic strength is shown in Fig. 4. The values for (dT)₃₀, (dT)₄₀, and (dT)₅₀ match each other and are larger than previous results between 0.75 and 4 nm (28, 29, 31–33) (variations primarily due to differences in buffers and sequence). In theoretical models, l_P is divided into intrinsic 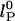and electrostatic 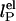components, 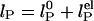. In Odijk–Skolnick–Fixman theory for charged wormlike chains (2) and some extensions to flexible polymers (34, 35), 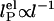, where I is the ionic strength (dotted lines). Others predict 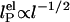(solid lines) (36, 37). Our measurements are better fitted with the 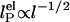dependence ( 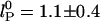nm). The residuals are significant, suggesting that neither of the predicted dependences may be entirely appropriate. If the exponent α for 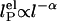is allowed to vary, a better fit is obtained with α = 0.2 ± 0.05 (data not shown), but the extracted 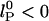. It is possible that this dependence would be different for much longer chains because the ends of ssDNA “see” less charge from neighboring bases than does the center of the chain.

Flexible Heteropolymers (Denatured Proteins). In protein folding, distances fluctuate over many time scales, including those of the overall folding and unfolding processes and of the faster fluctuations within the unfolded state. Using nsALEX, we studied unfolded CI2 and ACBP mutants with the following amino acid positions for D and A: 1–53 (Δ = 53 aa) for CI2, and 17–86 (Δ = 60 aa) for ACBP, each with Alexa Fluor 532 as D and Alexa Fluor 647 as A (literature value R₀ = 6.2 nm; see Sample Preparation and Characterization in Supporting Appendix).

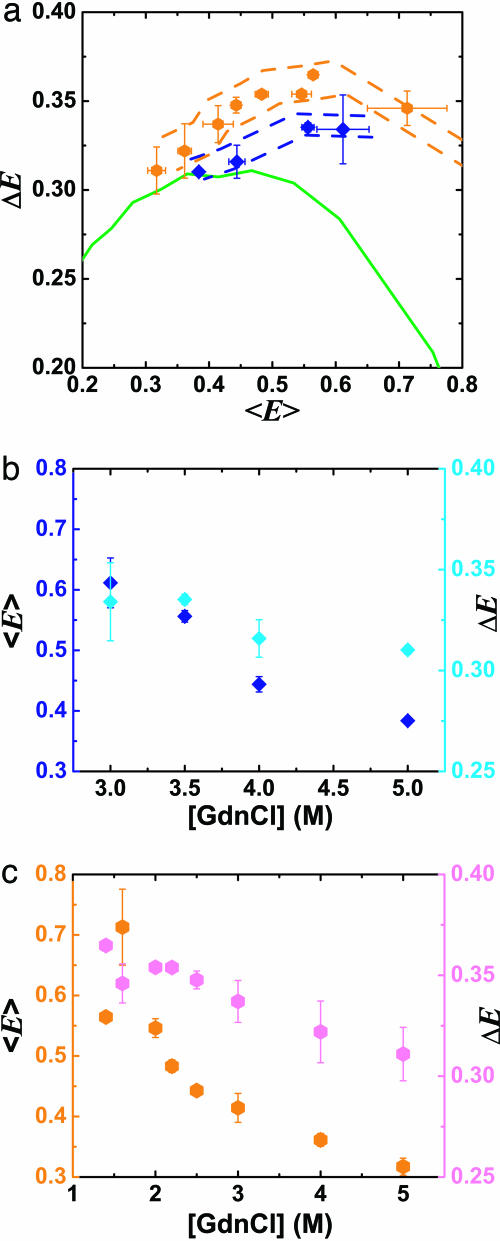
Fig. 5 shows ΔE vs. 〈E 〉 and ΔE, 〈E 〉 vs. [GdnCl] for the unfolded subpopulations of CI2 (blue diamonds) and ACBP (orange hexagons). As seen in other single-molecule studies (6–8), 〈E 〉 of the denatured subpopulation increases with decreasing denaturant concentration (concurrent with the folded state being populated). This increase in 〈E 〉 has been attributed to a hydrophobic collapse of the polypeptide chain (7, 8). Simulations assuming that the denatured state follows a Gaussian chain model predict that as the unfolded CI2 and ACBP become more compact, ΔE should decrease (green line in Fig. 5b). We observe that ΔE increases above this Gaussian chain limit for both proteins (Fig. 5b; Accuracy of Subpopulation Analysis in Supporting Appendix describes corrections for multimolecular events; Assessment of Photophysical Artifacts in Supporting Appendix assesses potential photophysical artifacts). In fact, for ACBP, ΔE is higher than the Gaussian limit even at high denaturant concentrations (5 M GdnCl).

Fig. 5.

Effects of denaturant concentration on distance distributions of unfolded CI2 and ACBP. (a) ΔE vs. 〈E 〉 for the unfolded subpopulation of 1–53 CI2 mutant ([GdnCl] = 3, 3.5, 4, and 5 M; blue diamonds) and 17–86 ACBP mutant ([GdnCl] = 1.4, 1.6, 2, 2.2, 2.5, 3, 4, and 5 M; orange hexagons) at varying denaturant concentrations. Using single-molecule burst analysis, nsALEX excludes contributions from the folded subpopulations of CI2 and ACBP. Simulations for the Gaussian chain with varying L × l_P dye linkers are shown in solid green. Dashed blue and orange lines: outliers denoting maximum possible errors due to photophysical artifacts (see Assessment of Photophysical Artifacts in Supporting Appendix). (b) Same data as in a, plotted as 〈E 〉 (blue diamonds) and ΔE (cyan diamonds) vs. [GdnCl] for unfolded CI2. (c) Same data as in a, plotted as 〈E 〉 (orange hexagons) and ΔE (magenta hexagons) vs. [GdnCl] for unfolded ACBP.

The increase of ΔE above the Gaussian chain limit cannot be explained in terms of the wormlike chain model; it is not simply a change in contour length and/or persistence length. Several studies point to residual structure in denatured states of ACBP (10, 11), whereas CI2 has very little residual structure at high denaturant concentrations (38). Static residual structure in unfolded proteins cannot explain the large ΔE; in an extreme example, a “rigid segment” model of an unfolded protein with segments of native structure interspersed with flexible chains reproduces Gaussian statistics (39). However, transient residual structure would cause dynamic changes in the effective contour and persistence lengths of the protein and widen the distributions beyond simple Gaussian chain or wormlike chain statistics. We propose that the observed large ΔE is due to transient residual structure. This hypothesis is bolstered by two observations. First, the deviation of ΔE from Gaussian statistics tends to increase with lower denaturant, where residual structure is likely more common. Second, ΔE for ACBP is higher than for CI2, in line with observations that ACBP has significantly more residual structure than CI2 (10, 11, 38). This hypothesis may be tested by measuring the dependence of ΔE on the D–A position along the protein chain and on side chain truncations (e.g., hydrophobic core truncations). This would help determine whether the increase in ΔE is due to specific transient structure, or other, yet to be determined deviations from the wormlike chain model.

Our understanding of biopolymers in general, and polyelectrolytes and protein folding in particular, stands to benefit from the ability demonstrated here to sort molecules into subpopulations and probe their distance distributions. The combination of single-molecule sorting with subensemble averaging provides benefits greater than the individual advantages of each approach alone.