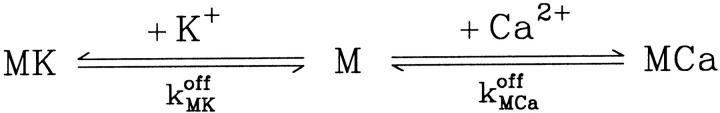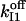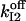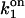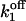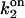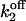Abstract
We propose here a unitary approach to the luminal and cytosolic control of calcium release. A minimal number of model elements that realistically describe different data sets are combined and adapted to correctly respond to various physiological constraints. We couple the kinetic properties of the inositol 1,4,5 trisphosphate receptor/calcium channel with the dynamics of Ca2+ and K+ in both the lumen and cytosol, and by using a detailed simulation approach, we propose that local (on a radial distance ∼2 μm) calcium oscillations in permeabilized cells are driven by the slow inactivation of channels organized in discrete clusters composed of between six and 15 channels. Moreover, the character of these oscillations is found to be extremely sensitive to K+, so that the cytosolic and luminal calcium variations are in or out of phase if the store at equilibrium has tens or hundreds μM Ca2+, respectively, depending on the K+ gradient across the reticulum membrane. Different patterns of calcium signals can be reproduced through variation of only a few parameters.
INTRODUCTION
Release of calcium ions from specialized compartments is a key process in numerous cellular events (Berridge, 1993; Clapham, 1995). The complex nature of intracellular calcium dynamics relies on the interplay between specifically induced calcium fluxes, such as release from the endo- or sarcoplasmic reticulum through the inositol 1,4,5 trisphosphate (IP3) receptor or the ryanodine receptor (RyR), uptake by the endoplasmic reticulum (ER) through the smooth ER Ca2+ pump, or calcium influx from the outside through Ca2+ channels on the plasma membrane, among which store-operated calcium channels are thought to directly sense the ER calcium content. Exchange with mitochondria plays also a significant role in preventing prolonged increases in cytosolic Ca2+ (Hajnóczky et al., 1999).
Nevertheless, the coupled control on both channel gating and store filling plays the key role in shaping cytosolic calcium signals. Studies on the IP3 receptor/Ca2+ channel in its native environment or reconstituted into lipid bilayers have revealed a biphasic effect of Ca2+ on the channel, given by ion binding to antagonist—activating/inhibitory—classes of sites, whereas IP3's binding properties and effects have received various interpretation. The global picture is even more complexed by parallel variations of the intraluminal source of calcium during release. The ER is known to have a high buffering capacity for Ca2+, but little is known about the exact dynamics and role, either direct or indirect, of store filling in calcium signaling. Recently an important feature of calcium release regulation has been characterized (Nguyen et al., 1998) through direct involvement of potassium ions toward mobilization of Ca2+ from the luminal matrix. Moreover, besides the dynamic Ca2+/K+ exchange during release, there exists the additional possibility of a direct effect of luminal calcium at the receptor level. Although this mechanism gained convincing evidence (Györke and Györke, 1998) in the case of the RyR, the corresponding effect on the IP3 receptor (IP3R) still awaits clarification (Taylor and Traynor, 1995).
The many facets of intracellular calcium signaling (Berridge et al., 2000) have proved to be rather difficult to incorporate into a consistent, unitary description. Different proposed models (see Dupont, 1999, for review) involving calcium release properties are able to explain quantal release or incremental detection when applied to permeabilized cell-like conditions, but cannot reproduce IP3-induced oscillations unless applied to intact cell-like conditions, where a conservation rule is generally used for intracellular calcium. The few current quantitative models (De Young and Keizer, 1992; Bezprozvanny and Erlich, 1994; Kaftan et al., 1997; Swillens et al., 1998; Moraru et al., 1999; Swillens et al., 1999) on regulation of IP3R activity have been mainly used to explain the Ca2+ and IP3 dependence of the steady-state open probability, or to simulate Ca2+ release at discrete sites, at constant luminal or cytosolic Ca2+. Moreover, these models are based on data obtained with channels incorporated into reconstituted bilayers, which are quantitatively largely different from data on the outer nuclear membrane.
The present study explores a new dimension of the calcium release dynamics and intends to answer two main questions: 1), to what extent can calcium signals depend on K+, and 2), how can in- or out-of-phase local calcium oscillations be explained in permeabilized cells? To this end we construct a basis for quantifying the dynamical relation between store and cytosolic calcium by coupling it to the IP3R/Ca2+ channel kinetics and to the control of the luminal calcium content by potassium. The model we propose here is based on the derivation of basic parameters that define both Ca2+/K+ exchange inside the store and gating properties of the ER calcium channel in nuclear membranes. With these parameters in hand, we simulate Ca2+ release through a cluster of channels in cylindrical geometry, taking into consideration ion diffusion and binding to endo- and exogenous buffers within the lumen and cytosol, in conditions that reproduce the main features of the physiologic subcellular environment. The model accurately describes a series of disparate experimental data that have not been theoretically considered to the moment and gives a more complete and detailed simulation approach to the calcium release process than previously done. Various approximations currently used (such as buffering approximations, spherical symmetry, constant luminal Ca2+, constant channel current, and neglect of intraluminal ion diffusion) are replaced here by direct approach to the underlying phenomena.
We discuss two possible scenarios for the K+ role in calcium release and show that the previously proposed (Nguyen et al., 1998) K+-dependent release cycle leads to parallel, not antiparallel, local calcium oscillations. Interestingly, we find that local calcium oscillations observed on a seconds scale in permeabilized cells might be driven by the slow inactivation of channels organized in discrete clusters composed of between 6 and 15 channels, and out-of-phase calcium variations appear at rather constant luminal K+. Contrary to the expectation, active implication of K+ actually appears as a key factor in inducing parallel oscillations.
INTRALUMINAL CALCIUM DYNAMICS
In the following we consider the observation (Nguyen et al., 1998) that the glycoprotein matrix inside calcium stores functions as a continuous Ca2+/K+ exchanger. We have used a simple model for describing this commerce, whereby Ca2+ and K+ compete in binding to a common matrix domain M, as shown in Fig. 1. Ion binding kinetics is assumed to be first-order for calcium and hK-order for potassium. All over the paper h denotes Hill coefficients; k, rate constants, K, apparent dissociation constants, and [X], concentration of the X specie. Then the equations governing the dynamical changes in the luminal concentrations read:
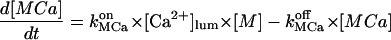 |
(1) |
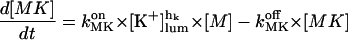 |
(2) |
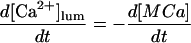 |
(3) |
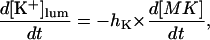 |
(4) |
where [M] + [MCa] + [MK] = Mmax is the total common Ca2+/K+ binding domains concentration.
FIGURE 1.
Reactions assumed in Ca2+ and K+ competing binding to the same luminal matrix domain M.
Assuming that all luminal calcium in resting cells does not leak from the store during the experimental procedure (Nguyen et al., 1998) with blockage of IP3Rs (by heparin) and of Ca2+-ATPase (in absence of ATP), the stationary state of the system obtained when clamping the intraluminal [K+] (with nigericin) is readily obtained as:
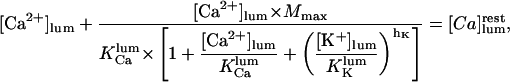 |
(5) |
where 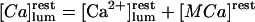 is the total luminal calcium (free + bound) content of resting (unstimulated) permeabilized cells in 140 mM K+ incubating medium. Here the apparent dissociation constants are defined as
is the total luminal calcium (free + bound) content of resting (unstimulated) permeabilized cells in 140 mM K+ incubating medium. Here the apparent dissociation constants are defined as 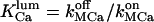 and
and 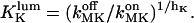
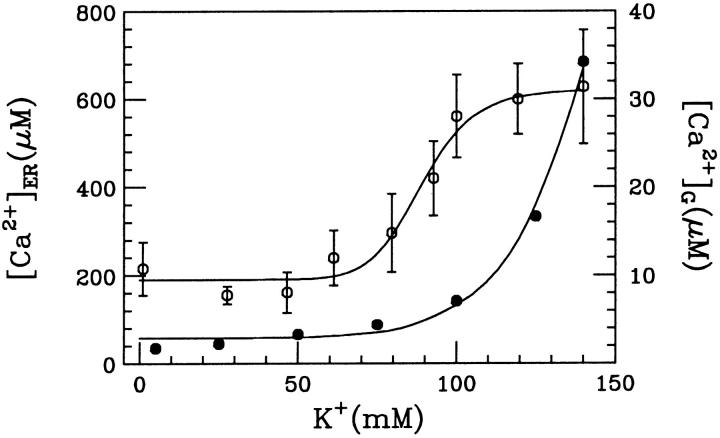
The best fit (shown in Fig. 2) of the data (Nguyen et al., 1998) to Eq. 5 was obtained with the following parameter values:
1). For the endoplasmic reticulum:
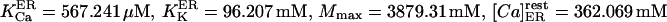 and
and 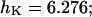 and
and2). For isolated secretory vesicles:
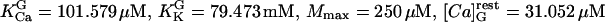 , and
, and 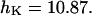
FIGURE 2.
Derivation of intraluminal Ca2+-K+ exchange parameters. Fit of data (Nguyen et al., 1998) to Eq. 5 is obtained by least-square method. Either plot (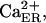 filled circles, or
filled circles, or 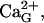 open circles) is drawn by using the corresponding parameters specified in the text.
open circles) is drawn by using the corresponding parameters specified in the text.
The obtained constant of Ca2+ dissociation from the ER protein matrix comes in agreement with generally accepted 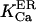 values. However, the model suggests the existence of a huge Ca2+ binding sites pool in the ER, of which the major part is masked by K+, and Ca2+ appears to compete with six K+ ions inside the endoplasmic reticulum of cilliated cell or with 11 K+ ions inside the mucin granules of goblet cells. To the moment there is no proof for such high cooperativity. Obviously, a better analysis would be possible if other data were available, so the model remains open to improvement. Let us see now how it does integrate with the present experimental evidence.
values. However, the model suggests the existence of a huge Ca2+ binding sites pool in the ER, of which the major part is masked by K+, and Ca2+ appears to compete with six K+ ions inside the endoplasmic reticulum of cilliated cell or with 11 K+ ions inside the mucin granules of goblet cells. To the moment there is no proof for such high cooperativity. Obviously, a better analysis would be possible if other data were available, so the model remains open to improvement. Let us see now how it does integrate with the present experimental evidence.
Regulation of the steady free calcium level (100 μM–300 mM) inside the ER is thought to be achieved through binding of Ca2+ ions to luminal glycoproteins as calsequestrin or calreticulin (Nguyen et al., 1998). Purified calsequestrin (with 109 acidic amino acids) binds ∼40 mol Ca2+/mol of calsequestrin with KD = 0.4–1 mM at 150 mM KCl (Mitchell et al., 1988), and 1 mol of calreticulin binds ∼20 mol Ca2+. A quick inspection of our results shows that a mean buffer protein concentration of ∼360 mM/40 ∼ 10 mM would rely inside the ER of cilliated cells. Biochemical analysis should reveal the value of Mmax in the absence of K+. In favor of this, a decrease in the K+ concentration from 150 mM to 20 mM was shown to induce a 6- to 10-fold increase in Ca2+ binding, meaning that a single protein molecule can bind ∼400 Ca2+ ions at 20 mM K+, thus supplying a large number of Ca2+ binding sites of the order 400 × 10 mM = 4 M. The 6- to 10-fold increase in calcium binding also agrees with our result 
In the mucin granules of goblet cells, the resting Ca2+ level is ∼20 μM (Nguyen et al., 1998). The same calculation as above yields a quantity of ∼500 nM luminal binding protein. The different KCa and hK obtained with the two organelles suggest differences in intraluminal conditions (pH, chemical composition, or homogeneity degree) between different calcium stores. Nevertheless further diversity may be due to the cell type (cardiac/cilliated/goblet) or environmental (in vitro/in vivo) conditions (pH, ionic strength) of analysis. This, and the small amount of data, could explain why such a large capacity of intraluminal proteins to bind Ca2+ has not been detected yet. Quantitative measure of the K+ binding capacity of ER buffers would be extremely valuable in determining the exact mechanisms involved in the luminal Ca2+/K+ ion exchange.
Two other points are to be stressed here. One, it is possible that at very low calcium concentration, the ER membrane gets very leaky, similarly to the plasma membrane (Hille, 1992), so we preferred removing the low calcium data, which otherwise alter the fit. Second, the above parameters constrain a minimal free resting 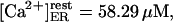 which seems to disagree with the 25–35 μM values observed (Nguyen et al., 1998). We distinguish between two possible explanations for this apparent discrepancy. First, the data on steady-state Ca2+/K+ ion exchange in both the ER and secretory vesicles are obtained with pH 5.5, whereas pHER = 7.1 has been determined in vivo in HeLa cells (Kim et al., 1998). The most reasonable assumption is that a higher, physiological pH might change the Ca2+ and K+ affinities for the luminal matrix. Indeed, a steady
which seems to disagree with the 25–35 μM values observed (Nguyen et al., 1998). We distinguish between two possible explanations for this apparent discrepancy. First, the data on steady-state Ca2+/K+ ion exchange in both the ER and secretory vesicles are obtained with pH 5.5, whereas pHER = 7.1 has been determined in vivo in HeLa cells (Kim et al., 1998). The most reasonable assumption is that a higher, physiological pH might change the Ca2+ and K+ affinities for the luminal matrix. Indeed, a steady 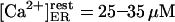 can be readily obtained with calculation based on the assumption that
can be readily obtained with calculation based on the assumption that 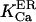 and
and 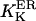 are reduced by the increased pH through a factor fdis > 1 (discussed later on). As a second possibility, we assume fdis = 1 (the pH has no effect on
are reduced by the increased pH through a factor fdis > 1 (discussed later on). As a second possibility, we assume fdis = 1 (the pH has no effect on  and
and 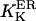 ) and consider calcium outflow at rest. Inasmuch as a steady state is reached in the Ca2+/K+ exchange experiments, we infer that the corresponding flux is flowing through the IP3Rs; otherwise the lumen eventually gets empty. This scenario works if IP3Rs have nonzero open probability in resting cells, which implies a basal, endogenous [IP3] > 0. In the absence of any other data that could clarify these aspects, we shall consider both alternatives in our simulations on calcium release.
) and consider calcium outflow at rest. Inasmuch as a steady state is reached in the Ca2+/K+ exchange experiments, we infer that the corresponding flux is flowing through the IP3Rs; otherwise the lumen eventually gets empty. This scenario works if IP3Rs have nonzero open probability in resting cells, which implies a basal, endogenous [IP3] > 0. In the absence of any other data that could clarify these aspects, we shall consider both alternatives in our simulations on calcium release.
MODEL FOR FAST GATING OF THE IP3R/Ca2+ CHANNEL
IP3 binds to a specific protein complex—the IP3R/Ca2+ channel, located on intracellular Ca2+ stores where it promotes and regulates release of Ca2+ into the cytosol. Each IP3R is a tetramer having a well-defined IP3 binding site per subunit 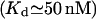 near its NH2-terminus (Marshall and Taylor, 1993; Taylor and Traynor, 1995). Two additional sites, with low
near its NH2-terminus (Marshall and Taylor, 1993; Taylor and Traynor, 1995). Two additional sites, with low 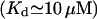 and high
and high 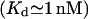 Ca2+ affinity have been described (Kaftan et al., 1997; Moraru et al., 1999), but their location is uncertain. Among all IP3 binding sites, the 1-nM site is the least (≤1%) frequent.
Ca2+ affinity have been described (Kaftan et al., 1997; Moraru et al., 1999), but their location is uncertain. Among all IP3 binding sites, the 1-nM site is the least (≤1%) frequent.
Biochemical studies indicated that Ca2+ binds to the same receptor at up to eight sites per monomer (Mignery et al., 1992; Sienaert et al., 1996, 1997), with seven sites residing on the cytosolic region of the receptor (Sienaert et al., 1997). The Ca2+ affinity has been determined for only one of these sites (Kd = 0.8 μM, Hill coefficient 1). The luminal Ca2+ binding site (Sienaert et al., 1996) could modulate the channel activity as in the case of the homologous Ca2+ release channel of skeletal and cardiac muscle, the RyR, where the existence of such site has clearly been evidenced (Györke and Györke, 1998). The IP3R is currently considered to be regulated by two functional classes of cytosolic calcium binding sites, of which one is activating (we denote it Sa) and one inhibitory (Si). With the channel in its ER membrane environment, the open probability (Po) data in the presence of 10 μM IP3 are well described by a biphasic Hill formula (see Eq. 1 in Mak et al., 1998), whereby Ca2+ binds to Sa with activation constant Ka = 210 ± 20 nM and Hill coefficient ha = 1.9 ± 0.3, and to Si with Ki = 54 ± 3 μM and Hill coefficient ha = 3.9 ± 0.7. As for bilayer experiments, with 2 μM IP3 applied, the channel's activity is maximal in the presence of 0.25 μM cytosolic Ca2+ (Bezprozvanny et al., 1991; Kaftan et al., 1997) and completely inhibited at 5 μM Ca2+, showing both positive and negative feedback of Ca2+ in a bell-shaped Po([Ca2+]) curve, whereas with 180 μM IP3 there is maximal activity at 1 μM Ca2+, with a shallow decline at Ca2+ up to 40 μM. The predictions here (Bezprozvanny et al., 1991; Kaftan et al., 1997) for the Kd's are in the range 0.03–0.2 μM for the activating site and 0.2–1 μM for the inhibitory site, with two or three Ca2+ ions required to bind to the channel for each class of sites.
The regulatory domain of the receptor also includes two–three putative adenine nucleotide-binding sites (Marshall and Taylor, 1993; Taylor and Traynor, 1995). ATP bound to these sites stimulates the receptor, but the way it does so has to be clarified. Direct and systematic investigations (Mak et al., 1999) of the mechanism involved in this regulation showed that ATP allosterically regulates the Ca2+ sensitivity of the Ca2+ activating sites with a functional dissociation constant KATP = 0.27 mM and Hill coefficient of 1, meaning that only one ATP molecule binds to the receptor to stimulate it. The same study suggest that ATP is also involved in the regulation of the Ca2+ affinity of the inhibitory sites, but the data are not sufficient to draw a firm conclusion.
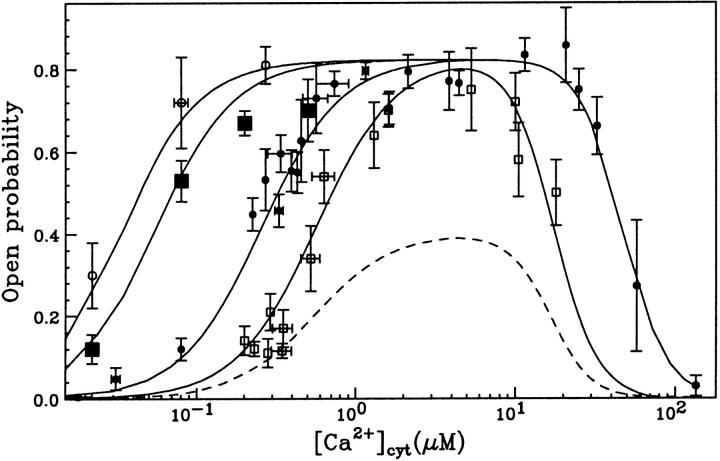
The type I IP3 receptor has been shown to have a high open probability, 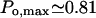 (Mak et al., 1998, 1999), in its native membrane environment, at the physiologic IP3 (∼1 μM) and cytosolic Ca2+ concentration ([Ca2+]cyt ∼0.1 μM), although displaying a greatly reduced activity when incorporated into lipid bilayers,
(Mak et al., 1998, 1999), in its native membrane environment, at the physiologic IP3 (∼1 μM) and cytosolic Ca2+ concentration ([Ca2+]cyt ∼0.1 μM), although displaying a greatly reduced activity when incorporated into lipid bilayers, 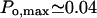 (Kaftan et al.,1997), respectively. In either case the Po dependence on calcium (Bezprozvanny et al., 1991) is bell-shaped, as has been shown also for IP3-induced calcium-45 release in brain synaptosoms (Finch et al., 1991). The data used and analyzed so far in various theoretical models are those obtained with the channel incorporated in artificial membranes. To describe its activity, 8- (De Young and Keizer, 1992), 16- (Kaftan et al., 1997), 18- (Swillens et al., 1999) and recently more complex, 125-state (Moraru et al., 1999) models have been proposed, out of which only the last one describes features of both Po and open-time distributions.
(Kaftan et al.,1997), respectively. In either case the Po dependence on calcium (Bezprozvanny et al., 1991) is bell-shaped, as has been shown also for IP3-induced calcium-45 release in brain synaptosoms (Finch et al., 1991). The data used and analyzed so far in various theoretical models are those obtained with the channel incorporated in artificial membranes. To describe its activity, 8- (De Young and Keizer, 1992), 16- (Kaftan et al., 1997), 18- (Swillens et al., 1999) and recently more complex, 125-state (Moraru et al., 1999) models have been proposed, out of which only the last one describes features of both Po and open-time distributions.
Here we use and analyze data exclusively obtained with channels in their native environment and construct a simple operational model to accurately describe not only Po but also τo (open time) and τc (close time), which is quite a difficult task. Our first steps were to consider first a two-site (four-state) and then three-site (eight-state) model. However, the quantitative results were unsatisfactory, for the models in no way could simultaneously fit the three data sets (Mak et al., 1998). We then added a fourth regulatory site and obtained good agreement to the data.
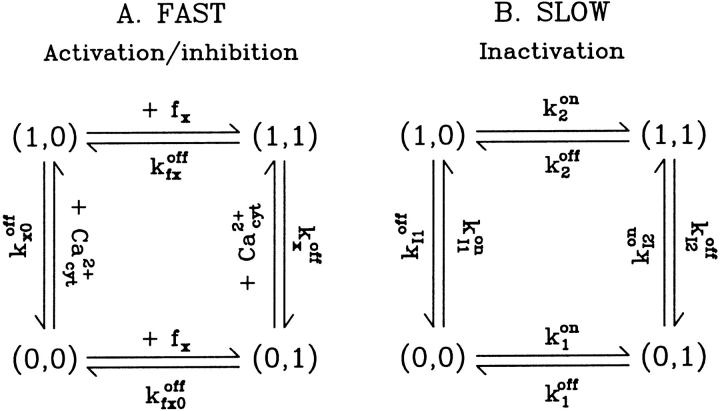
So, our minimal model treats the tetramer receptor as a complex unit, equivalent to a 16-state system at thermal equilibrium. Kinetics of calcium binding at either site are independent of each other, but dependent on binding to the receptor of a specific factor, fa or fi, respectively, as shown in Fig. 3 A. Hence, we are introducing two other regulatory sites, Sfa and Sfi. Because the open dwell time histograms of this channel generally show two distinct components, we assume there are two open states, characterized by bound Sa and both Si and Sfi unbound.
FIGURE 3.
Four-state channel representation and transitions within basic regulatory modules of IP3R fast and slow gating, as assumed in the model. In A, x = a or i and X = A or I characterize the activating and inhibitory module, respectively.
Consequently, our model considers two main independent gating components, described by a reaction scheme of the form depicted in Fig. 3 A. From a structural point of view, each gating module represents a channel domain that includes two regulatory sites: Sa, Sfa for the activating gate, and Si, Sfi for the inhibiting gate. The steady-state open channel probability Po can be easily derived (as shown in Appendix 1) by considering first-order kinetics for the (un)binding reactions, mass balance equations, and the thermodynamical equilibrium constraints (Hille, 1992)
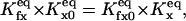 |
(6) |
where 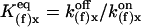 (x = a, i) is the equilibrium constant of the transition q(f)x = 0 to q(f)x = 1. Here q(f)x is the site S(f)x occupancy (0 or 1) and
(x = a, i) is the equilibrium constant of the transition q(f)x = 0 to q(f)x = 1. Here q(f)x is the site S(f)x occupancy (0 or 1) and 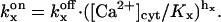
Based on estimation (see Appendix 2) of errors introduced by events undetected during recording of single-channel activity, the data obtained with the Xenopus oocyte type I IP3R/calcium channel in patches of the outer nuclear membrane are well (least-square method) fitted with the parameter values given in Table 1, with arbitrary 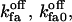 and
and 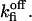 Mean values of the parameters are obtained by best fit with τd = 0.3 ms, the approximate experimental value (Mak et al., 1998; Mak, personal communication). Parameter deviations from mean values are determined such that theoretical curves obtained with 0.2 ms ≤ τd ≤ 0.4 ms remain within experimental error bars. The model simultaneously comes in good agreement (shown in Figs. 4 and 5) with the measured open/close time and Po for the specific conditions of the electrophysiological experiments (Mak et al., 1998), namely: 1.5-μM trans Ca2+, 10-μM IP3, and 500-μM ATP on the cytosolic IP3R side. We have to mention that we obtained a good agreement with the triplet data, i.e.,
Mean values of the parameters are obtained by best fit with τd = 0.3 ms, the approximate experimental value (Mak et al., 1998; Mak, personal communication). Parameter deviations from mean values are determined such that theoretical curves obtained with 0.2 ms ≤ τd ≤ 0.4 ms remain within experimental error bars. The model simultaneously comes in good agreement (shown in Figs. 4 and 5) with the measured open/close time and Po for the specific conditions of the electrophysiological experiments (Mak et al., 1998), namely: 1.5-μM trans Ca2+, 10-μM IP3, and 500-μM ATP on the cytosolic IP3R side. We have to mention that we obtained a good agreement with the triplet data, i.e., 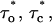 and
and 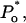 only when a high affinity calcium binding site (Ka = 12 nM) was afforded for. The 500-μM ATP data could be fitted as well with Ka0 = 0.3 μM and ha0 = 2, with essentially the same results.
only when a high affinity calcium binding site (Ka = 12 nM) was afforded for. The 500-μM ATP data could be fitted as well with Ka0 = 0.3 μM and ha0 = 2, with essentially the same results.
TABLE 1.
Parameters of the fast-gating kinetics of the IP3R
| Gating process | Specific conditions | Parameter symbol | Description | Value |
|---|---|---|---|---|
| Ca2+ binding to its cytosolic activating site Sa | fa unbound to Sfa | 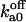 |
Off-rate constant | 65 ± 35 s−1 |
| Ka0 | Dissociation constant | 550 ± 20 nM | ||
| ha0 | Hill coefficient | 1.8 ± 0.1 | ||
| fa bound to Sfa | 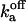 |
Off-rate constant | 270 ± 70 s−1 | |
| Ka | Dissociation constant | 12 nM | ||
| ha | Hill coefficient | 2.1 ± 0.1 | ||
| fa binding to Sfa | Ca2+ bound to Sa | 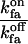 |
On-rate constant to off-rate constant ratio | 3 |
| Ca2+ binding to its cytosolic inhibitory site Si | fi unbound to Sfi | 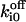 |
Off-rate constant | 40 ± 15 s−1 |
| Ki0 | Dissociation constant | 45 ± 1 μM | ||
| hi0 | Hill coefficient | 3.2 | ||
| fi bound to Sfi | 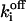 |
Off-rate constant | 3 ± 2.5 s−1 | |
| Ki | Dissociation constant | 18 μM | ||
| hi | Hill coefficient | 3.2 | ||
| fi binding to Sfi | Ca2+ bound to Si | 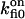 |
On-rate constant | 210 ± 30 s−1 |
 |
Off-rate constant to on-rate constant ratio | 4.5 ± 0.25 |
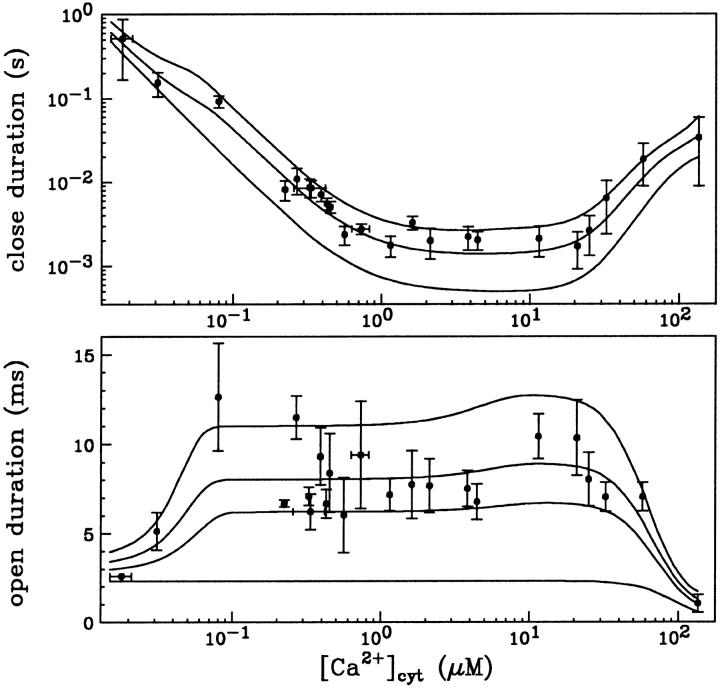
FIGURE 4.
[Ca2+]cyt dependence of the mean open- and closed-channel duration at 10 μM IP3 and 500 μM free ATP. Data are from Mak et al. (1998) and Mak (personal communication). Continuous lines are drawn according to Eqs. 17–19 with parameter values given in the text. The curves in each panel correspond respectively, from the lowest to the upper, to different values of τd: 0, 0.2, 0.3, and 0.4 ms in the lower panel and 0, 0.2, and 0.4 ms in the upper panel.
FIGURE 5.
Open probability of IP3R at 10 μM IP3 and different cytosolic ATP concentrations: 0–12 μM (small squares), 500 μM (filled circles), 4.8 mM (large squares), and 9.5 mM (open circles). Data are from Mak et al. (1998, 1999). Curves represent calculated 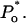 Actual Po differs by <5% (not shown). Dashed line corresponds to predicted Po at 1 mM [Ca2+]lum in the absence of ATP, assuming
Actual Po differs by <5% (not shown). Dashed line corresponds to predicted Po at 1 mM [Ca2+]lum in the absence of ATP, assuming 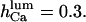
However, the extreme case (Ka = 12 nM and Ka0 = 0.55 μM) offers a more realistic view on channel gating mechanisms, as it can be directly correlated to the stimulatory effect of free ATP on activation of the IP3R by cytosolic calcium. As one can note, the two Ca2+ dissociation constants discussed here are about the same as the activating constants (17 ± 3 nM and 480 ± 20 nM) obtained (Mak et al., 1999) at high and zero ATP, respectively. The interpretation of the allosteric factor fa as free ATP can account for many of the features of ATP dependence of channel activity. So, binding of free ATP at the cytosolic site of the channel can be characterized by a Hill coefficient hATP = 1.3 ± 0.1, and dissociation constant KATP = 215 ± 15 μM in the presence and KATP0 = 90 ± 30 mM in the absence of cytosolic calcium, yielding good theoretical fit (shown in Fig. 5) to the activation data of Mak at different ATP concentrations. Our interpretation is that Ca2+ has either a high or a 50 times lower affinity for its activating cytosolic site Sa, depending on whether free ATP is bound to the regulatory site Sfa or not. ATP binding to IP3R shifts Ka to its low value and thus facilitates channel activation. With Ki0 = 18 μM, the model yields also good agreement (not shown) to the τo and τc data (Mak et al., 1999) obtained with 0–12 μM ATP.
Our calculation (not shown) based on the procedure described (Appendices 1 and 2) proves that simpler gating models (with two or three regulatory sites) cannot adequately fit into the experimental data. We want to stress that the two gating modules discussed here have been developed from the two standard calcium sites. The hypothesis is made that kinetics of Ca2+ binding at each of these two sites are regulated by a distinct factor. At first we had devoted a lot of work to the identification of the ligand fa as IP3 but this resulted (not shown) in a marked dependence of the activation domain of the 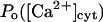 curve on the concentration of IP3, contrary to the data (Mak et al., 1998). Another good candidate, namely ATP, for the same factor fa has been suggested before (Mak et al., 1999) and we have proved here that interpreting ATP as the factor implicated in the activation module regulation very well can explain the related features of channel activity.
curve on the concentration of IP3, contrary to the data (Mak et al., 1998). Another good candidate, namely ATP, for the same factor fa has been suggested before (Mak et al., 1999) and we have proved here that interpreting ATP as the factor implicated in the activation module regulation very well can explain the related features of channel activity.
As for the inhibiting module, evidence is less conclusive. A good choice initially seemed to be IP3, as in the model of De Young and Keizer (1992), with the IP3 binding transition adapted to the present situation, but the results (not shown) came in disagreement with the IP3 effects on Po (Mak et al., 1998), mainly because Po,max greatly depended on IP3 concentration, and the activation domain of the 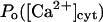 curve was shifted to the right by decreasing [IP3], which is not the case. Neither could ATP provide good explanation for this behavior (from our investigations, not shown). Consequently, we hypothesize here that the factor fi might be luminal Ca2+. In this way the model can explain key features of channel kinetical behavior, such as inhibitory effects of high (0.6–1 mM) [Ca2+]lum in the absence of ATP (Thrower et al., 2000); apparent invariability of Po at low [Ca2+]lum (Mak et al., 1998); decreased open channel duration observed in the presence of calcium in the trans chamber (Bezprozvanny and Erlich, 1994); or the shallow decrease (Thrower et al., 2000) of the longest open time (here τo1) with increasing [Ca2+]lum. The implicated mechanism considered here is closing of the IP3R by luminal Ca2+, whereas for the RyR the opposite effect, namely opening of the luminal gate by calcium, can account for the data obtained (Györke and Györke, 1998). More precisely, for the IP3R, the transition from the (0,0) to the (0,1) state of the inhibition module is assumed to be driven by calcium binding to the luminal site, thus closing the channel (if open). It is quite difficult to make an exact correspondence between data obtained in different experimental conditions. Channel inactivation by 0.6–1 mM [Ca2+]lum in absence of ATP agrees well with
curve was shifted to the right by decreasing [IP3], which is not the case. Neither could ATP provide good explanation for this behavior (from our investigations, not shown). Consequently, we hypothesize here that the factor fi might be luminal Ca2+. In this way the model can explain key features of channel kinetical behavior, such as inhibitory effects of high (0.6–1 mM) [Ca2+]lum in the absence of ATP (Thrower et al., 2000); apparent invariability of Po at low [Ca2+]lum (Mak et al., 1998); decreased open channel duration observed in the presence of calcium in the trans chamber (Bezprozvanny and Erlich, 1994); or the shallow decrease (Thrower et al., 2000) of the longest open time (here τo1) with increasing [Ca2+]lum. The implicated mechanism considered here is closing of the IP3R by luminal Ca2+, whereas for the RyR the opposite effect, namely opening of the luminal gate by calcium, can account for the data obtained (Györke and Györke, 1998). More precisely, for the IP3R, the transition from the (0,0) to the (0,1) state of the inhibition module is assumed to be driven by calcium binding to the luminal site, thus closing the channel (if open). It is quite difficult to make an exact correspondence between data obtained in different experimental conditions. Channel inactivation by 0.6–1 mM [Ca2+]lum in absence of ATP agrees well with 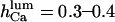 (our model predicts—not shown—that this inactivation is only apparent, with all open channel events being too short for detection with 0.5-ms time resolution (Thrower et al., 2000); in addition, removal of 1 mM [Ca2+]lum inhibition by ATP would agree with an increase of
(our model predicts—not shown—that this inactivation is only apparent, with all open channel events being too short for detection with 0.5-ms time resolution (Thrower et al., 2000); in addition, removal of 1 mM [Ca2+]lum inhibition by ATP would agree with an increase of 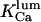 with ATP, which pushes τo above the detection limit). Instead, for specific experimental conditions (Mak and Foskett, 1997), the value
with ATP, which pushes τo above the detection limit). Instead, for specific experimental conditions (Mak and Foskett, 1997), the value 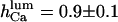 gives
gives 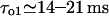 and
and 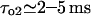 values, close to those obtained by experiment (
values, close to those obtained by experiment (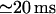 and <5 ms, respectively), but implies a lower threshold for the inhibitory [Ca2+]lum (∼50 μM). The calculated subunitary Hill coefficient could result from negative cooperativity in calcium binding at the luminal site. It yields a dissociation constant
and <5 ms, respectively), but implies a lower threshold for the inhibitory [Ca2+]lum (∼50 μM). The calculated subunitary Hill coefficient could result from negative cooperativity in calcium binding at the luminal site. It yields a dissociation constant 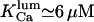 for
for 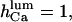 and
and 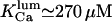 for
for 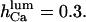
The analysis here does not uniquely declare 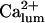 as the factor fi, but provides a series of arguments in favor of this equivalence. In further simulations we shall consider three possible alternatives on this matter (see below). As a final point here, it is worth mentioning that the IP3 dependence of the
as the factor fi, but provides a series of arguments in favor of this equivalence. In further simulations we shall consider three possible alternatives on this matter (see below). As a final point here, it is worth mentioning that the IP3 dependence of the 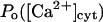 curve can be well reproduced (not shown) by considering the proposed allosteric regulation of the calcium affinity for the Si site by IP3 binding to its 50-nM site with a Hill coefficient of 4 (see Eq. 2, Mak et al., 1998), where Kmax = 54 μM is replaced by the 45 μM obtained here. This dependence will be used in all our simulations (see below).
curve can be well reproduced (not shown) by considering the proposed allosteric regulation of the calcium affinity for the Si site by IP3 binding to its 50-nM site with a Hill coefficient of 4 (see Eq. 2, Mak et al., 1998), where Kmax = 54 μM is replaced by the 45 μM obtained here. This dependence will be used in all our simulations (see below).
SIMULATION OF CALCIUM SIGNALS IN PERMEABILIZED CELLS
Because the calcium release apparatus seems to behave differently in various cell types, generating different patterns of Ca2+ signals, a better understanding of the molecular and cellular mechanisms involved is of great interest. Given the large differences between the channel's properties considered here as compared to previous theoretical studies, we have been looking for defining their effects and determining how the 16-state model could integrate into an operational model of calcium release. We expected largely different features of release kinetics because the channel is inhibited now at higher [Ca2+]cyt (∼100 μM vs. ∼1 μM). Furthermore, calcium release regulation by K+ appears to be crucial in the oscillatory Ca2+ response to agonist stimulation, inasmuch as the calcium signal disappears (Nguyen et al., 1998) in the presence of apamin, a blocker of the small conductance calcium-activated potassium (ASK) channels (see below).
To quantitatively study the effects of potassium ions in calcium release regulation, we coupled the IP3 gating model analyzed above to the dynamics of calcium and potassium in both the lumen and cytosol. Numerical and biophysical aspects of our simulation procedure are detailed in the Appendix 3. The model was tested first on a documented scenario (Nguyen et al., 1998) and improved to come in agreement with two basic processes: 1); calcium oscillations are triggered locally in permeabilized cells; and 2), K+ is implicated in the (in- or out-of-phase) character of these oscillations. It is worth mentioning that a rise of such oscillations in permeabilized cells has not been theoretically explained yet. We have examined the system's behavior under various physiological constraints and inspected the sensitivity of the calcium signals to several parameters. To remain in agreement with the experimental evidence, further improvement of the model has emerged and critical ranges of the free parameters in the model have been determined.
Slow kinetics of calcium release
Simulations based on the 16-state model
At first we strictly used the scenario proposed (Nguyen et al., 1998) and considered (Scenario I) that the equilibrium resting state has low (∼25–35 μM) [Ca2+]ER. Accordingly, we had to consider a potassium extrusion term, which could be due to the K+-H+ exchanger across the reticulum membrane (Nguyen et al., 1998), to restore the chemical equilibrium (see Eq. 5) inside the store. As mentioned before, we were led to lower the dissociation constants 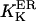 and
and 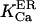 by a factor fdis. After IP3 stimulation, the IP3R/calcium channels open and the resulting increase in [Ca2+]cyt activates the ASK channels on the ER membrane (Nguyen et al., 1998). Consequently, K+ inflow liberates Ca2+ from the luminal matrix. In all our simulations, the system first displayed a pronounced but transient increase in local [Ca2+]cyt (∼3 μM) and ran thereafter into a quasi steady state with high [Ca2+]ER (between 2 and 5 mM) and slightly elevated [Ca2+]cyt (∼0.6 μM). Calcium release is silenced by the inhibitory effect of the high microdomain (Naraghi and Neher, 1997) calcium concentration built up by a current as high as 0.4–1 pA flowing through the channel from the submembrane [Ca2+]ER of ∼2–5 mM.
by a factor fdis. After IP3 stimulation, the IP3R/calcium channels open and the resulting increase in [Ca2+]cyt activates the ASK channels on the ER membrane (Nguyen et al., 1998). Consequently, K+ inflow liberates Ca2+ from the luminal matrix. In all our simulations, the system first displayed a pronounced but transient increase in local [Ca2+]cyt (∼3 μM) and ran thereafter into a quasi steady state with high [Ca2+]ER (between 2 and 5 mM) and slightly elevated [Ca2+]cyt (∼0.6 μM). Calcium release is silenced by the inhibitory effect of the high microdomain (Naraghi and Neher, 1997) calcium concentration built up by a current as high as 0.4–1 pA flowing through the channel from the submembrane [Ca2+]ER of ∼2–5 mM.
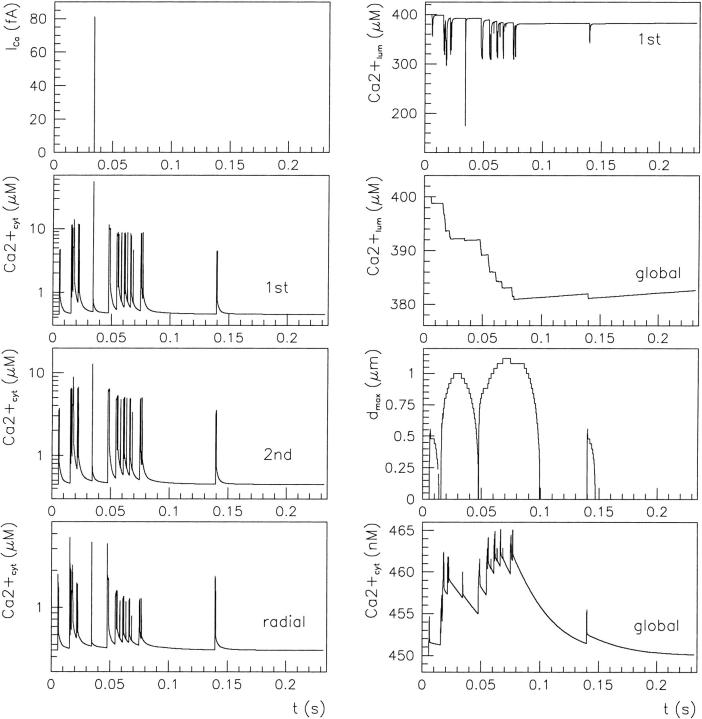
We then undertook the possibility that gating kinetics is modified in vivo (Mak and Foskett, 1997), and assumed 100 times slower channel gating. An example, obtained with NCa = 2, is shown in Fig. 6 A. Increasing NCa produces a similar first spike, followed by more frequent, smaller spikes. However, in all the cases we have investigated (for large variation of the free parameters (not shown)), the resulting variations in intra- and extraluminal free calcium concentrations were not out of phase as expected, but always parallel. In addition, these variations are irregular, not oscillatory-type.
FIGURE 6.
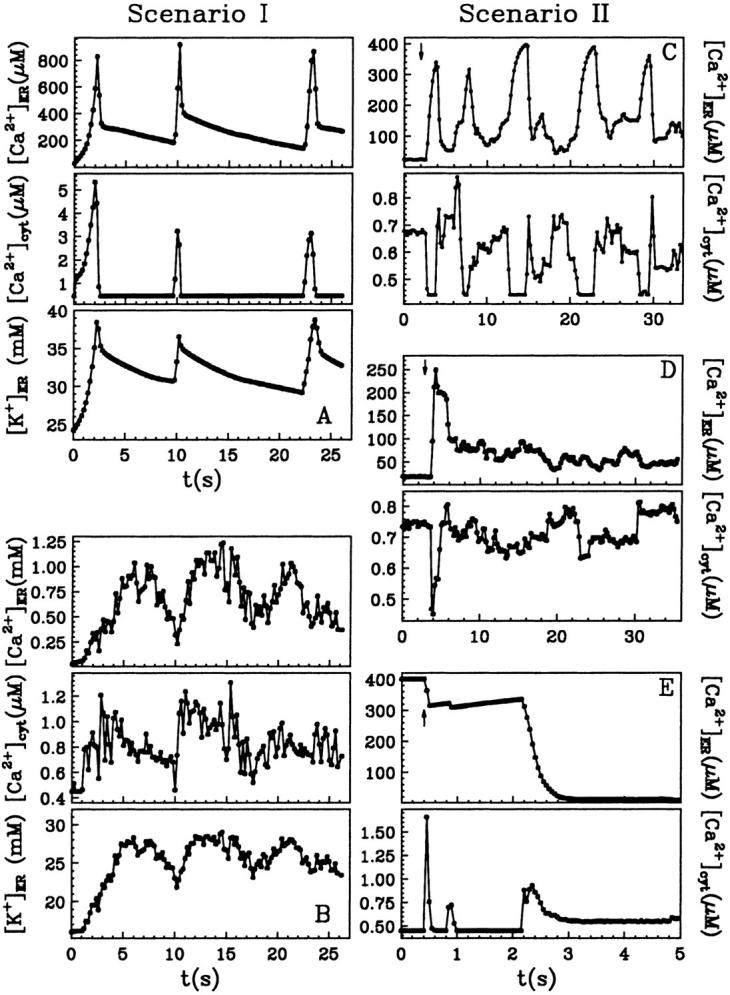
Simulated responses after stimulation of permeabilized cells with 3 μM IP3 at t = 0 in A and B and at moments indicated by arrows in C, D, and E. In C and D, a basal [IP3]b = 30 nM and 100 μM EGTA are considered; otherwise EGTA is present with 40 μM.
Therefore, we have approached another strategy (Scenario II): we assumed that with all IP3Rs closed, the store at equilibrium has 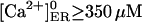 with a calculated
with a calculated 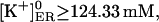 assuming fdis = 1. Then, we considered a basal [IP3]b = 30 nM, which drove [Ca2+]ER to the rest value. However, within large parameter ranges, increasing IP3 to 3 μM has no effect (not shown), which was not unexpected, inasmuch as the Ca2+ channel current is too small and the IP3R Po remains high.
assuming fdis = 1. Then, we considered a basal [IP3]b = 30 nM, which drove [Ca2+]ER to the rest value. However, within large parameter ranges, increasing IP3 to 3 μM has no effect (not shown), which was not unexpected, inasmuch as the Ca2+ channel current is too small and the IP3R Po remains high.
A slow gating component is required
From the results obtained so far, we conclude that the simple model for IP3R gating is not sufficient to explain the observed patterns of calcium signals. So, we suspected that a slow kinetic component of the Xenopus oocyte IP3R has not manifested in vitro (Mak et al., 1998), or was too slow to be detected (see the case of the RyR that adapts 100 times slower in vitro than in vivo (Sachs et al., 1995). Recordings of the type I IP3R activity in its native environment show indeed that an additional, slow kinetic component is active in vivo. However, analysis of inactivation at the receptor level is rendered extremely difficult by its slow kinetics, which reduces the number of events below a reasonable limit appropriate for a standard statistical analysis. When analyzed in the “on-nucleus” configuration (Mak and Foskett, 1997), the channel preserved its fast kinetics features (discussed above), but displayed an additional, slow kinetic component.
All these, along with observations that Ca2+ and IP3 inactivate IP3R and IP3-mediated calcium release on a seconds scale (Parker and Ivorra, 1990; Finch et al., 1991; Hajnóczky and Thomas, 1994; Oancea and Meyer, 1996), have determined us to introduce a Ca2+- and IP3-dependent slow regulatory module. The reaction scheme, shown in Fig. 3 B, was first proposed to explain adaptive behavior and can account for channel inactivation after ligand binding (Sachs et al., 1995). The current active substates in Fig. 3 B are (1,0) and (0,1), so the channel has now four open states, which may correspond to the four different subconductance states observed experimentally (Bezprozvanny et al., 1991, Mak and Foskett, 1997; Thrower et al., 2000). We have chosen the functional dependence  consistent with the interpretation (Hajnóczky and Thomas, 1994) that IP3 may aid Ca2+ to access its inhibitory site (here by fastening Ca2+-binding kinetics), and with three other observations: 1), the initial release rate increases (Hajnóczky and Thomas, 1994) with IP3 in the range 1.5–7.5 μM, so we assume that the IP3 site involved is the low affinity one, i.e.,
consistent with the interpretation (Hajnóczky and Thomas, 1994) that IP3 may aid Ca2+ to access its inhibitory site (here by fastening Ca2+-binding kinetics), and with three other observations: 1), the initial release rate increases (Hajnóczky and Thomas, 1994) with IP3 in the range 1.5–7.5 μM, so we assume that the IP3 site involved is the low affinity one, i.e., 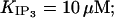 2), the channel recovers from inactivation after IP3 removal or chelation of calcium in the presence of saturating IP3 (Hajnóczky and Thomas, 1994); and 3), half-maximal channel inactivation appears at ∼0.2 or 0.6 μM [Ca2+]cyt (Finch et al., 1991; Hajnóczky and Thomas, 1994); we use then KI = 0.2 μM and hI = 2, as proposed for channels in reconstituted bilayers (Bezprozvanny et al., 1991). The thermodynamical condition was used as before to derive
2), the channel recovers from inactivation after IP3 removal or chelation of calcium in the presence of saturating IP3 (Hajnóczky and Thomas, 1994); and 3), half-maximal channel inactivation appears at ∼0.2 or 0.6 μM [Ca2+]cyt (Finch et al., 1991; Hajnóczky and Thomas, 1994); we use then KI = 0.2 μM and hI = 2, as proposed for channels in reconstituted bilayers (Bezprozvanny et al., 1991). The thermodynamical condition was used as before to derive 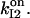 Other parameters were chosen to yield two inactivation components that differ by at least one order (Hajnóczky and Thomas, 1994) and to match as possible the results of Mak and Foskett (1997). For the conditions therein (10 μM IP3, 1 mM ATP, 200 nM [Ca2+]cyt, and 200 nM [Ca2+]lum), event distributions generated by the full 64-state model satisfactorily agree (not shown) with both Po and the mean open and closed time histograms for two sets of kinetic parameters, as specified in Table 3. Analytical and simulated activity of the 64-state, but not 16-state, channel shows inactivation (not shown) of biexponential time course with rate constants of the order of those determined by experiment (Hajnóczky and Thomas, 1994).
Other parameters were chosen to yield two inactivation components that differ by at least one order (Hajnóczky and Thomas, 1994) and to match as possible the results of Mak and Foskett (1997). For the conditions therein (10 μM IP3, 1 mM ATP, 200 nM [Ca2+]cyt, and 200 nM [Ca2+]lum), event distributions generated by the full 64-state model satisfactorily agree (not shown) with both Po and the mean open and closed time histograms for two sets of kinetic parameters, as specified in Table 3. Analytical and simulated activity of the 64-state, but not 16-state, channel shows inactivation (not shown) of biexponential time course with rate constants of the order of those determined by experiment (Hajnóczky and Thomas, 1994).
TABLE 3.
Parameters of slow-gating kinetics of the IP3 receptor
Simulations based on the 64-state model
With the new code applied to Scenario II and using the Set 1 of parameters in Table 3, out-of-phase oscillations were obtained similar to those observed (Nguyen et al., 1998). A typical result is shown in Fig. 6 C. The Ca2+ response strongly depends on 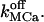 Sharp [Ca2+]ER variations were routinely obtained with
Sharp [Ca2+]ER variations were routinely obtained with 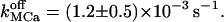 Higher
Higher 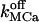 induce rapid Ca2+ mobilization and [Ca2+]ER remains high. Slow Ca2+ dissociation induces rapid store depletion and return of [Ca2+]cyt to a near-basal level after a transient increase (Fig. 6 E, obtained with NCa = 6 and
induce rapid Ca2+ mobilization and [Ca2+]ER remains high. Slow Ca2+ dissociation induces rapid store depletion and return of [Ca2+]cyt to a near-basal level after a transient increase (Fig. 6 E, obtained with NCa = 6 and 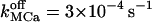 ). Another determining factor shaping the calcium response has been found as the receptor density (Swillens et al., 1999). At low density (NCa < 9), the nonconducting channel periods are generally longer and become highly irregular as NCa → 1. We typically obtained oscillatory-like behavior with NCa = 9–12 (the simulation in Fig. 6 C was obtained with 12 channels per cluster and 1.3 μm lateral spacing between clusters). Increasing NCa reduces the chance that all channels in the cluster are not simultaneously conducting and the interval between inactivity periods becomes longer. In three simulations with NCa = 25 (one shown in Fig. 6 D), we did not obtain a second complete cluster inactivation within 40 s.
). Another determining factor shaping the calcium response has been found as the receptor density (Swillens et al., 1999). At low density (NCa < 9), the nonconducting channel periods are generally longer and become highly irregular as NCa → 1. We typically obtained oscillatory-like behavior with NCa = 9–12 (the simulation in Fig. 6 C was obtained with 12 channels per cluster and 1.3 μm lateral spacing between clusters). Increasing NCa reduces the chance that all channels in the cluster are not simultaneously conducting and the interval between inactivity periods becomes longer. In three simulations with NCa = 25 (one shown in Fig. 6 D), we did not obtain a second complete cluster inactivation within 40 s.
Because the present data on the dependence of IP3R gating on luminal calcium are not conclusive, we relaxed the assumption (see above) that 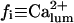 by considering either a weak dependence
by considering either a weak dependence 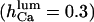 or independence (i.e.,
or independence (i.e., 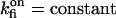 ) of the inhibitory module on
) of the inhibitory module on 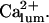 Both choices were not critical to the results. On the contrary, in several simulations (not shown) with the same conditions but
Both choices were not critical to the results. On the contrary, in several simulations (not shown) with the same conditions but  the channels' Po decreases considerably at
the channels' Po decreases considerably at 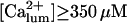 so that the system remained in a quasi steady state with high
so that the system remained in a quasi steady state with high 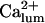 and low
and low 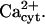 We have not followed this line of investigation, inasmuch as it would be only speculative at the moment. In numerous simulations we have varied the EGTA concentration as specified in Table 2, but its effect on the slow timescale was not critical, as it mainly operates on the signal's amplitude, which remains in the noninhibitory [Ca2+]cyt domain (not shown).
We have not followed this line of investigation, inasmuch as it would be only speculative at the moment. In numerous simulations we have varied the EGTA concentration as specified in Table 2, but its effect on the slow timescale was not critical, as it mainly operates on the signal's amplitude, which remains in the noninhibitory [Ca2+]cyt domain (not shown).
TABLE 2.
Standard parameters in calcium release simulations
| Symbol | Description | Value | References/comments |
|---|---|---|---|
| rT | ER tubule radius | 190–300 nm | Limited by computational time |
| rC | Cytosolic depth from the ER tubule membrane | 2 μm | Swillens et al., 1998 |
| zT | Length of the ER tubule segment ≡ distance between two release sites | 0.75–1.5 μm | Horne and Meyer, 1997;Callamaras and Parker, 1999 |
| BT,fix | Total concentration of the stationary buffer | 120–300 μM | Clapham, 1995; Swillens et al., 1998; Haddock et al., 1999 |
| KB,fix | Dissociation constant of the stationary buffer | 10 μM | Swillens et al., 1998 |
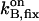 |
On-rate constant of the stationary buffer | 108 M−1 s−1 | Clapham, 1995 |
| BT,mob | Total concentration of the mobile buffer (EGTA) | 40–100 μM | Relatively low level, to minimize the slowing down effects on calcium release (Horne and Meyer, 1997) |
| KB,mob | Dissociation constant of the mobile buffer (EGTA) | 170–670 nM | Pape et al., 1995; Naraghi and Neher, 1997 |
 |
On-rate constant of the mobile buffer (EGTA) | 1.5–2.5 μM−1 s−1 | Pape et al., 1995; Naraghi and Neher, 1997 |
| [K+]ext | Constant cytosolic [K+] at r > rC | 140 mM | Nguyen et al., 1998 |
| [Ca2+]ext | Constant cytosolic [Ca2+] at r > rC | 450 nM | Nguyen et al., 1998 |
| [ATP] | Constant cytosolic [ATP] | 3 mM | Nguyen et al., 1998 |
| [IP3] | Constant cytosolic [IP3] | 3 μM | Nguyen et al., 1998 |
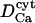 |
Diffusion coefficient of Ca2+ ions in the cytosol | 200–220 μm2 s−1 | Clapham, 1995; Naraghi and Neher, 1997 |
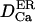 |
Diffusion coefficient of Ca2+ ions in the lumen | 20–50 μm2 s−1 | Kargacin, 1994; Clapham, 1995. One order lower than 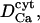 to correct for buffers and extremely tortuous ion pathway to correct for buffers and extremely tortuous ion pathway |
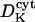 |
Diffusion coefficient of K+ ions in the cytosol | 1500–2000 μm2 s−1 | Hille, 1992 |
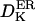 |
Diffusion coefficient of K+ ions in the lumen | 50–160 μm2 s−1 | One order lower than 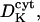 as for Ca2+ as for Ca2+
|
 |
Diffusion coefficient of EGTA in the cytosol | 170–220 μm2 s−1 | Pape et al., 1995; Naraghi and Neher, 1997 |
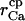 |
Capture radius of the Ca2+ channel | 4–12 nm | Chosen to yield a saturating Ca2+ current ≅0.1 pA at 500 μM [Ca2+]ER (Bezprozvanny and Erlich, 1994; Swillens et al., 1998); corresponds roughly to the dimen sion of the square-shaped mouth of the channel (Swillens et al., 1998) |
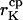 |
Capture radius of the K+ channel | 0.3–4 nm | Hille, 1992 |
| gCa | Single-channel conductance of the Ca2+ channel | 113 pS | Mak and Foskett, 1997 |
| gK | Single-channel conductance of the K+ channel | 15–20 pS | Vergara et al., 1998 |
| KP | Smooth ER Ca2+ pump's activation constant | 0.1–1 μM | De Young and Keizer, 1992; Dupont and Goldbeter, 1994 |
| T | Temperature | 298 K |
Efficiency of interchannel communication was shown (Swillens et al., 1999) to decrease with the distance between receptors (d), and a compact (d = 12 nm) cluster of ∼20–30 channels could explain the currently observed distributions of puffs and blips. Due to the high complexity of the system, our spatial grid was always d ≥ 35 nm. As an alternative (Swillens et al., 1999) we also performed several simulations where a highly compact cluster of 25 channels was comprised in a unique volume element, with 50-nm gridding. The open probabilities were independently simulated for all channels, which are facing now the same microdomain [Ca2+]cyt. The results obtained with this procedure are not qualitatively different from those shown in Fig. 6 D.
Extremely high density of IP3Rs corroborated by rapid Ca2+ mobilization inside the ER can produce sustained, high global [Ca2+]cyt after stimulation, without requiring external calcium influx as currently invoked for explaining a high Ca2+ level in some cells after stimulation (Dupont, 1999). For example, a formation of six clusters, 50-nm interspaced, each consisting of 20, highly packed IP3Rs, yields (not shown) an elevated global [Ca2+]cyt fluctuating between 0.83 and 0.94 μM, whereas the radial average varies between 29–38 μM and [Ca2+]ER remains at 100–113 μM, for 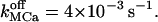
Use of the full model according to Scenario I generates parallel variations in local intra- and extraluminal calcium (an example is shown in Fig. 6 B, obtained with NCa = 9 and the Set 2 of inactivation parameters). Differences between simulations using either of the two sets of inactivation parameters were not crucial for the dynamical behavior of the system. We also have checked that with KI = 0.66 or 0.8 μM (Finch et al., 1991; Moraru et al., 1999) and hI = 1 or 2, oscillatory evolution can as well be reproduced within both scenarios, in conditions mentioned above.
From a careful inspection by simulation (not shown) we conclude that variation of the standard parameters within ranges given in Table 2 do not result in qualitative changes in the shape of calcium signals on the seconds timescale. Instead, the completely free parameters left (namely NCa, NK, fdis, 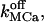 and
and 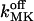 ) appear to be crucial in their modulation. Generally we used NCa = 1–25 (Swillens et al., 1999) and NK = 50–250. We have examined the system's response to large variations in these parameters (not shown). Depending on the scenario, Table 4 indicates parameter values constrained by the requirement to obtain realistic results. For example, within Scenario I, the values therein give fast Ca2+ mobilization and results relevant to the situation. Lower values greatly enlarge the dynamic profiles (not shown). In summary, the system's behavior was found to be extremely sensitive to three factors:
) appear to be crucial in their modulation. Generally we used NCa = 1–25 (Swillens et al., 1999) and NK = 50–250. We have examined the system's response to large variations in these parameters (not shown). Depending on the scenario, Table 4 indicates parameter values constrained by the requirement to obtain realistic results. For example, within Scenario I, the values therein give fast Ca2+ mobilization and results relevant to the situation. Lower values greatly enlarge the dynamic profiles (not shown). In summary, the system's behavior was found to be extremely sensitive to three factors:
The rapidity of Ca2+ and K+ ions in dissociating from the luminal glycoprotein matrix.
The number of Ca2+ channels in the cluster.
The difference between the luminal and cytosolic K+ concentration.
TABLE 4.
Parameters used in simulations using Scenario I or II
| Value
|
|||
|---|---|---|---|
| Symbol | Description | Scenario I | Scenario II |
| NK | Number of ER K+ channels | 100–250 | 50–100 |
| fdis | Factor of increasing Ca2+ and K+ affinity for the luminal matrix | 5–8 | 1 |
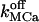 |
Off-rate constant for dissociation of Ca2+ from the luminal matrix | 10–50 s−1 | (0.3–3) × 10−3 s−1 |
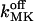 |
Off-rate constant for dissociation of K+ from the luminal matrix | 10–50 s−1 | (3–100) × 10−3 s−1 |
Fast kinetics of calcium release
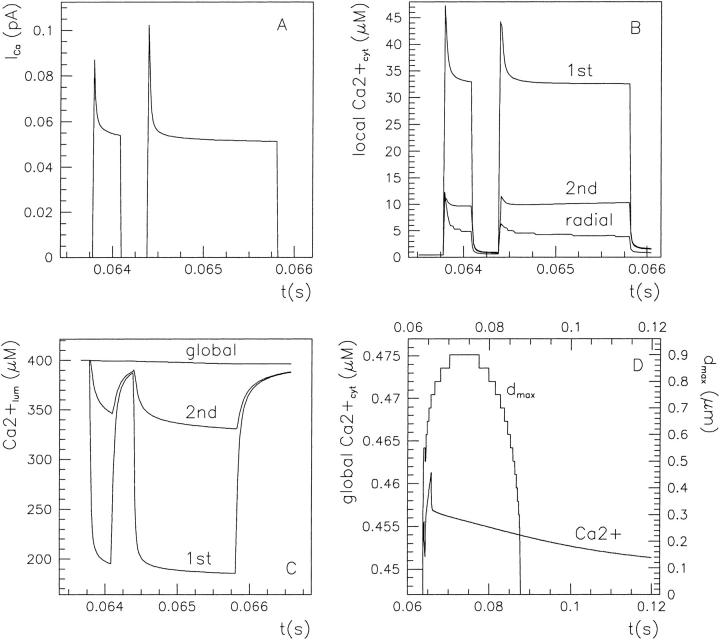
An example of stochastical simulation (based on the 64-state model of the IP3R/Ca2+ channel gating) of subseconds calcium release at a single channel release site according to Scenario II is presented in Fig. 7. Here the luminal equilibrium is determined by the level of 400 μM [Ca2+]lum and that of 127.5 mM [K+]lum (calculated from Eq. 5). During short openings of the IP3R, an initial current of ∼0.1 pA rapidly (<1.5 μs) elevates the average calcium concentration to ∼50 μM in the spatial element (denoted 1st in Fig. 7 B) facing the cytosolic mouth of the channel. The 50-μM value comes in agreement with the calculated Ca2+ profile near (∼50-nm distance) the mouth of the channel in a hemispherical space (Naraghi and Neher, 1997). A steady state is reached within ∼160 μs by equilibration of store calcium outflow with cytosolic Ca2+ buffering, diffusion, and pumping back into the store, provided calcium stabilizes also in the luminal submembrane element (denoted 1st in Fig. 7 C; this requirement can be met if 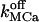 is not too low). At the plateau phase, the channel current is reduced to half-maximal value as a consequence of reduction in the local ER-cytosol Ca2+ gradient. Channel closure is followed by rapid dissipation in the cytosol, so that complete recovery follows channel shut within ∼24 ms. During the whole period of calcium release and consequent dissipation through the cytosol, a corresponding local Ca2+ wave spreads over a maximal radial distance of ∼1 μm (dmax in Fig. 7 D), with a total duration of ∼24 ms. The resulting variations in local calcium concentrations are parallel on the ms scale of channel activity. Global [Ca2+]cyt display a rapid rise immediately after channel opening and a biphasic decrease after channel closure (see Fig. 7 D) with decay constants of the order 1 ms and 40 ms, respectively. The rise phase duration is correlated with the channel open time and not with luminal calcium.
is not too low). At the plateau phase, the channel current is reduced to half-maximal value as a consequence of reduction in the local ER-cytosol Ca2+ gradient. Channel closure is followed by rapid dissipation in the cytosol, so that complete recovery follows channel shut within ∼24 ms. During the whole period of calcium release and consequent dissipation through the cytosol, a corresponding local Ca2+ wave spreads over a maximal radial distance of ∼1 μm (dmax in Fig. 7 D), with a total duration of ∼24 ms. The resulting variations in local calcium concentrations are parallel on the ms scale of channel activity. Global [Ca2+]cyt display a rapid rise immediately after channel opening and a biphasic decrease after channel closure (see Fig. 7 D) with decay constants of the order 1 ms and 40 ms, respectively. The rise phase duration is correlated with the channel open time and not with luminal calcium.
FIGURE 7.
Subseconds calcium release at a single channel site, according to Scenario II. During the 120 s lapsed after 3 μM IP3 stimulation, the channel displays two openings and the corresponding effects are visualized as evolutions of the ionic current (A), local cytosolic (B), or luminal (C) Ca2+ concentration, as well as the global cytosolic calcium signal and wave propagation within the cytosol (D). The buffering level is given by 200 μM endogenous fix buffer and 40 μM EGTA.
The corresponding pattern displayed by a multichannel release site is presented in Fig. 8, where the cluster comprises nine receptors 40-nm interspaced. Local concentrations are calculated with respect to the central channel, which in this simulation performs a single, short opening where the channel current comes to ∼81 fA. As expected, the region (denoted 1st) facing the cytosolic side of the central IP3 receptor senses transient elevations (4–14 μM) induced by openings of channels. During sustained activity of the cluster, the free calcium concentration initially increases in the overall cytosolic volume, then (after ∼50 ms) saturates during a relatively steady release and eventually decays (time constants as above) to the basal level at the end of longer (of the order 100 ms) nonconducting periods.
FIGURE 8.
Fast calcium release dynamics simulated with nine-channel release site. Other conditions as in Fig. 7.
A second possibility for modulation of calcium release by luminal calcium corresponds to the mechanism proposed (Nguyen et al., 1998) (here Scenario I). In Fig. 9 we show the time course followed by calcium released from the ER with low equilibrium level: 30 μM [Ca2+]lum and 16 mM [K+]lum, obtained with fdis = 7. The calcium channel current is now lower than in the previous situation (see Figs. 7 and 8), but increases during release as the submembrane luminal calcium raises. The resulting variations in local luminal calcium and potassium are parallel, being driven by openings of the nearest potassium channel(s) that follow, on a longer timescale, the cytosolic colocalized Ca2+ accumulation. After the initial increase, the obtained cytosolic Ca2+ signal displays saturation again, followed by biphasic decay (time constants ∼1 ms and ∼40 ms) to the basal level within 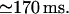
FIGURE 9.
Fast calcium release at six-channel release site in conditions specified by Scenario I. The current through both Ca2+ and K+ channel in the central element on the ER membrane are shown in the upper panels (ICa and IK, respectively). Other notations as in Fig. 7. Over the simulated 250-ms period after IP3 stimulation, calcium is released through the IP3Rs cluster during the first 26 ms only. The stationary buffer level is 120 μM.
DISCUSSION
This study was motivated by the newly unveiled implication of K+ ions in intraluminal calcium handling, and one of its goals was to investigate its concrete effects on the complex process of calcium release from the ER. To this end we construct a simple model to describe the ER Ca2+ channel activity in its native membrane environment and approach various, realistic alternatives to obtain best fits to the data. It is inconveniently true that the high number of factors involved in the dynamic regulation of this channel activity as well as the limited data, which not rarely give rise to discrepancies, imprint a rather speculative character to any theoretical analysis of the calcium release process. However, even simple models that are able to explain most general features of the process have proved valuable tools in the study of the detailed mechanisms of intracellular calcium signaling.
Initially, most models (De Young and Keizer, 1992; Atri et al., 1993; Bezprozvanny and Erlich, 1994) considered three sites responsible for channel activity regulation: one site for IP3 and two sites for Ca2+, one activating and one inhibitory. Within this scheme, the IP3 effect on Po could partially be described by the De Young and Keizer model only. More recently, a low affinity IP3 binding site was included (Kaftan et al., 1997) to explain how the Po([Ca2+]) curve is rightward-shifted by increasing IP3 and inhibition by up to 50 μM Ca2+ relieved. Later, this model has been reformulated (Moraru et al., 1999) to give better fits to the Po and τo data in dependence on both Ca2+ and IP3. To this end, it was assumed that each receptor monomer contains one Ca2+ regulatory site and two IP3 sites, of medium and low affinity, respectively. Another combination has been used in agreement to the Po data at 2 μM IP3 (Bezprozvanny et al., 1991), by considering one IP3 site, two Ca2+ activating sites, and two Ca2+ desensitizing sites, but the model (Swillens et al., 1998) is based on a limited set of data. Essentially, the various outcomes of these models point out to the need for continuous refinement in modeling the complex IP3 regulation as more data are provided and the specific regulatory binding sites identified.
In addition, the different behavior of the channel in different membranes makes the results more confusing. It is possible that reconstitution of the receptor into lipid bilayers alters the protein-protein and protein-lipid interactions and basically reduces by one order the magnitude of Po. It would be interesting to know whether Po at [Ca2+]cyt ≥ 50 μM show inactivation at high IP3 levels in bilayer experiments (see Fig. 6 in Moraru et al., 1999). If this would be the case, the dependence of Po on Ca2+ and IP3 could be explained by the same mechanism as proposed for the channel studied in the ER membrane. Here the data (Mak et al., 1998) indicate that two antagonist classes of Ca2+ binding sites exist and that Ca2+ binds to two monomers to open and to four monomers to close the channel. Moreover, IP3 binding to the medium affinity site only seems to be implicated in regulation of channel activity, and it does so by attenuating the inhibitory effect of Ca2+. Channel activity resumes to fast kinetics in excised membrane patches but spreads on a slow timescale in integral nuclear membrane, clearly showing loss of the slow component in the former case.
To describe the fast gating component of the ER Ca2+ channel, we assume it to be controlled by Ca2+ binding to an activating site, with a calculated Hill coefficient 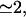 by Ca2+ binding to an inhibitory site, with a calculated Hill coefficient
by Ca2+ binding to an inhibitory site, with a calculated Hill coefficient 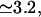 and by a hypothetical ligand (fi) to account for the subunitary Po,max at the plateau domain of the Po(Ca2+) curve (Mak et al., 1998). We show that our model supports the ATP effect on channel activation by allosteric regulation with Kd = 215 μM and h = 1.3, similar to those deduced from a nonstandard Hill formula (Mak et al., 1999). It would be worth seeing whether the ATP binding site could have such low affinity for free ATP in the absence of Ca2+ as calculated here
and by a hypothetical ligand (fi) to account for the subunitary Po,max at the plateau domain of the Po(Ca2+) curve (Mak et al., 1998). We show that our model supports the ATP effect on channel activation by allosteric regulation with Kd = 215 μM and h = 1.3, similar to those deduced from a nonstandard Hill formula (Mak et al., 1999). It would be worth seeing whether the ATP binding site could have such low affinity for free ATP in the absence of Ca2+ as calculated here 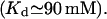 Among the possible candidates as fi ligands, only
Among the possible candidates as fi ligands, only 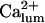 comes in agreement with various data as analyzed with our model, but certainly more data are needed to define the exact mechanism of regulation.
comes in agreement with various data as analyzed with our model, but certainly more data are needed to define the exact mechanism of regulation.
Based on the results obtained here, we propose a number of possible mechanisms involved in calcium release regulation that fairly well describes many experimental data and observations, as follows:
The ER of cilliated cells is a huge reservoir of 4 M Ca2+ binding sites, most of which
 are masked by K+, and a Ca2+ ion must compete with six K+ ions inside the ER and with 11 K+ ions inside the mucin granules of goblet cells.
are masked by K+, and a Ca2+ ion must compete with six K+ ions inside the ER and with 11 K+ ions inside the mucin granules of goblet cells.Ca2+ has a high (Kdis = 12 nM) or a 50 times lower affinity for its activating site on the cytosolic side of the IP3R, depending on whether ATP is bound or not.
Luminal Ca2+ might inhibit IP3R activity with a low, possibly subunitary Hill coefficient.
Both comparison of data on IP3R in excised versus intact nuclear membrane and calcium release simulations lend support for a three-module decomposition of channel gating, as follows: one fast, activating, controlled by cytosolic Ca2+ and ATP; one fast, inhibitory, controlled by cytosolic and luminal Ca2+; and one slow, inactivating, controlled by cytosolic Ca2+ and IP3.
Local calcium oscillations observed on a seconds scale in permeabilized cells might be driven by the slow inactivation of channels organized in discrete clusters composed of between six and 15 channels.
Out-of-phase calcium variations appear at rather constant luminal K+ whereas sustained K+ uptake by the lumen appears as a key factor in inducing parallel oscillations.
Different patterns of calcium signals, as seen in many experiments, can be induced depending on: Ca2+ and K+ fluxes between ER and cytosol, intrinsic rapidity of Ca2+ and K+ dissociation from the luminal matrix, and differences in channel distribution between cell types.
The model we propose here is the first to our knowledge that integrates in a quantitative manner the kinetic properties of the IP3R with both the cytosolic and luminal calcium/potassium dynamics. On this basis we are able to reproduce various and puzzling aspects of calcium signaling observed in many experiments, as, for example, modest or large decreases (Barrero et al., 1997; Golovina and Blaustein, 1997) or increases (Golovina and Blaustein, 1997; Nguyen et al., 1998) in store filling after stimulation. So far, models for electrically excitable cells only could predict enhancement of calcium load during release.
Most important, our model can explain local calcium oscillations even in permeabilized cells, where intracellular calcium is not conserved. The nature of the allosteric transitions involved in the slow inactivation of the IP3R (see Fig. 3 B) remains undefined, but may involve calmodulin (Patel et al., 1997; Missiaen et al., 1999) or IP3 binding to its high affinity site (Kaftan et al., 1997; Moraru et al., 1999). An important prediction of the model is that [Ca2+]cyt and [Ca2+]lum variations result in- or out-of-phase if the ER transmembrane K+ gradient is high or low, respectively (here if the chemical equilibrium in the store is attained at tens or hundreds of μM calcium, respectively). This could have interesting implications in producing distinct local calcium signals arising from distinct ER compartments (Golovina and Blaustein, 1997) or in calcium signaling in electrically excitable cells, where parallel evolutions are generally thought to develop as, for example, in pancreatic β-cells (Gilon et al., 1999). Nevertheless, many aspects of in vivo calcium release need further investigation. At present the data are not abundant and differences between cell types may lead to apparent discrepancies between various experimental results. However, the analysis here offers a more detailed description of the complex interplay between cytosolic and luminal control of calcium release, which undoubtedly has important effects on diverse calcium dependent processes, such as trigger of calcium influx through store-operated calcium channels (Hofer et al., 1998; Huang and Putney, 1998) birth and propagation of calcium waves (Dupont and Goldbeter, 1994; Lukyanenko et al., 1999), excitation-contraction coupling (Stern et al., 1997; Haddock et al., 1999), gene expression (Negulescu et al., 1994), or cell cycle progression (Baran, 1996).
APPENDIX 1: STEADY-STATE OPEN PROBABILITY
The four substates, denoted as X1 = (0,0), X2 = (0,1), X3 = (1,1), and X4 = (1,0), of each X-type gating module (X = A, activating, or X = I, inhibiting) are occupied at steady state with the probabilities:
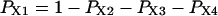 |
(7) |
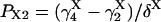 |
(8) |
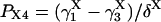 |
(9) |
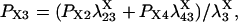 |
(10) |
where
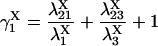 |
(11) |
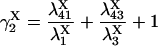 |
(12) |
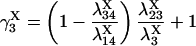 |
(13) |
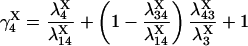 |
(14) |
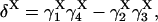 |
(15) |
provided δX ≠ 0. Here 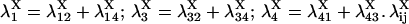 is the rate constant of the transition Xi → Xj, (i,j = 1, 4).
is the rate constant of the transition Xi → Xj, (i,j = 1, 4).
The “A” gate within the activating module is assumed open in both A3 and A4, whereas for the inhibitory module, the “I” gate is open in I1 only. Each macrostate probability is obtained as the product of the partial probabilities of each of the two independent subsystems: P(qa,qfa,qi,qfi) = P(qa,qfa) × P(qi,qfi). The resulting steady-state open channel probability is then
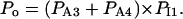 |
(16) |
APPENDIX 2. DWELL-TIME DISTRIBUTIONS AND MISSED EVENTS
A representation of the possible state transitions is shown in Fig. 10. The open/close dwell-time histogram results from transitions from each of the open/closed states to a complementary state. The probability of the channel to leave any s state (s = o, open; s = c, closed) toward a certain state is constant (given by the rate constant of the respective transition), so:
The total number of events with duration τ is
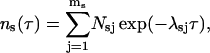 with Nsj = αsjN being the total number of events originating from the state sj and N the total number of openings or, equivalently, closures of the channel during the recording time.
with Nsj = αsjN being the total number of events originating from the state sj and N the total number of openings or, equivalently, closures of the channel during the recording time.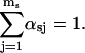
The mean time spent in the s state
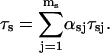
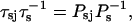 where
where 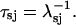
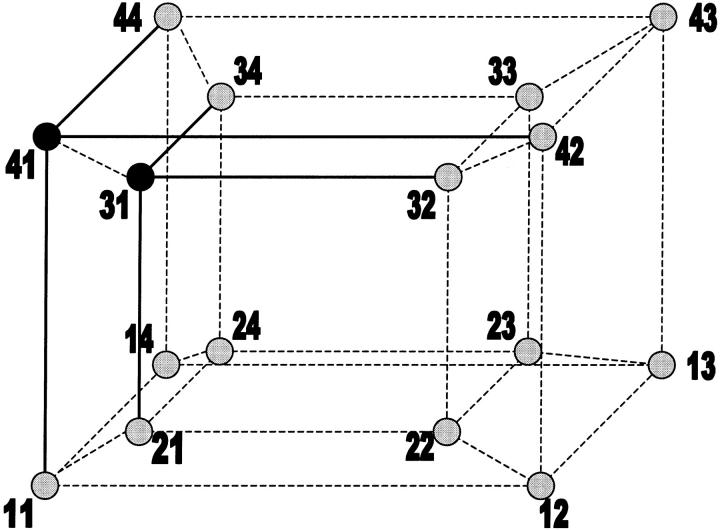
FIGURE 10.
Sixteen-state representation of the IP3R's fast kinetics. Each 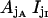 state is labeled by the pair jAjI, with jX representing the current of the four possible substates within the X module. Open and closed states are marked by black and gray circles, respectively. Possible transitions between open states and their neighbor closed states are highlighted.
state is labeled by the pair jAjI, with jX representing the current of the four possible substates within the X module. Open and closed states are marked by black and gray circles, respectively. Possible transitions between open states and their neighbor closed states are highlighted.
λsj is the probability of leaving the sj state toward a complementary s′ state (s′ = c if s = o and s′ = o if s = c) within 1 s; mo = 2 the number of open states; and mc = 6 the number of closed states that can switch directly to an open state. The weighting factors are:
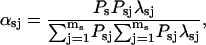 |
(17) |
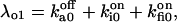 and
and 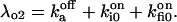 The six components of the closed-state histogram are determined by the transitions: C1 (≡ A2I1) → O1 (≡ A3I1); C2 (≡ A3I2) → O1; C3 (≡ A3I4) → O1; C4 (≡ A1I1) → O2 (≡ A4I1); C5 (≡ A4I2) → O2; and C6 (≡ A4I4) → O2. The corresponding transition rates are:
The six components of the closed-state histogram are determined by the transitions: C1 (≡ A2I1) → O1 (≡ A3I1); C2 (≡ A3I2) → O1; C3 (≡ A3I4) → O1; C4 (≡ A1I1) → O2 (≡ A4I1); C5 (≡ A4I2) → O2; and C6 (≡ A4I4) → O2. The corresponding transition rates are: 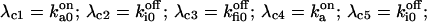 and
and 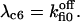 The
The 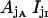 state probability equals
state probability equals 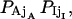 calculated with the aid of Eqs. 7–15.
calculated with the aid of Eqs. 7–15.
To calculate the errors introduced by missed events during channel recording (see also Colquhoun et al., 1996), we estimate the distortion of Po, τo, and τc caused by successions of up to four undetectable events. An event with duration lower than the time detection limit τd is assumed to appear with the same probability all over the recording. The number of detected events reduces to N* = N(ɛo + ɛc − 1), provided ɛo + ɛc > 1. Here 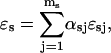 with ɛsj = exp(−λsjτd). Part of the s-type missed events contribute to the apparent s′ state total time, so that the measured mean open/close time can be approximated as:
with ɛsj = exp(−λsjτd). Part of the s-type missed events contribute to the apparent s′ state total time, so that the measured mean open/close time can be approximated as:
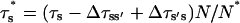 |
(18) |
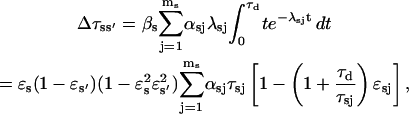 |
(19) |
where 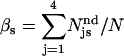 is the fraction of s undetectable events recorded as prolongation of an s′ regular event, and
is the fraction of s undetectable events recorded as prolongation of an s′ regular event, and 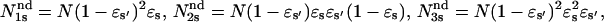 and
and 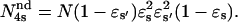 Then the measured
Then the measured 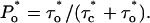 The reliability of this approach was tested with stochastic simulations of each regulatory site occupancy and count of specific events over a period ≥500 s. Average values from 10 different simulations were in good agreement with the theoretical ones for all quantities (N, N*, τo,
The reliability of this approach was tested with stochastic simulations of each regulatory site occupancy and count of specific events over a period ≥500 s. Average values from 10 different simulations were in good agreement with the theoretical ones for all quantities (N, N*, τo, 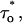 τc,
τc, 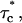 Po, and
Po, and 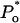 ) with any set of parameters used.
) with any set of parameters used.
APPENDIX 3: SIMULATION PROCEDURE
We discretized the Laplacian operator in cylindrical geometry. The equations for the mobile species evolution were numerically solved according to an explicit finite difference formula, accurate to order (Δr)2, (Δz)2, (Δφ)2, and Δt. We have checked that for the immobile species, the diffusion constrained time step is sufficiently small to yield virtually the same results if using either a first-order or fourth-order solving method. From the geometrical point of view, we consider an ER tubule segment as a cylinder of radius rT, symmetrically surrounded by a cytosolic volume of depth rC. The total simulated volume is then a cylinder of radius rT + rC and length zT, divided into 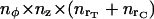 elements, where nx = xmax/Δx for each cylindrical coordinate x (i.e., r, φ, or z). At the ER-cytosol boundary (ECB), we consider a cluster of NCa calcium, and other of NK potassium, equally spaced channels, positioned symmetrically against the planes z = zT/2 and φ = 0. The interchannel distance is assumed to be d. Then, for space discretization, the angular increment is taken as Δφ = d/rT, whereas the radial and longitudinal steps are Δr = Δz = d. The running code was implemented in Fortran language on either UNIX or VAX workstations. It routinely solves a number of
elements, where nx = xmax/Δx for each cylindrical coordinate x (i.e., r, φ, or z). At the ER-cytosol boundary (ECB), we consider a cluster of NCa calcium, and other of NK potassium, equally spaced channels, positioned symmetrically against the planes z = zT/2 and φ = 0. The interchannel distance is assumed to be d. Then, for space discretization, the angular increment is taken as Δφ = d/rT, whereas the radial and longitudinal steps are Δr = Δz = d. The running code was implemented in Fortran language on either UNIX or VAX workstations. It routinely solves a number of 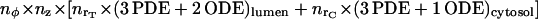 partial (PDE) and ordinary (ODE) differential equations by updating all variables at every instant.
partial (PDE) and ordinary (ODE) differential equations by updating all variables at every instant.
Single channel ionic currents are considered of the form
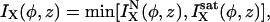 |
(20) |
where
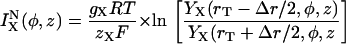 |
(21) |
is the local Nernst potential-driven current and
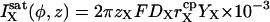 |
(22) |
is the diffusion-limited saturating channel current (Hille, 1992). Here the symbols are: X, ion type (Ca2+ or K+); DX, diffusion coefficient; gX, single channel conductance; zX, ion valence; R, gas constant; T, temperature; F, Faraday constant; YX, local concentration of X ions; and  the capture radius of the pore (nevertheless it may depend also on nongeometric factors involving ion diffusion at the channel mouth). In taking IX of the form given in Eq. 20, we assumed the ER membrane potential is zero, as electroneutrality is currently considered both at rest and during calcium release. We also used a nonequilibrium formula for IX, given by ion binding to a single site inside the channel during permeation (Hille, 1992), with qualitatively similar results. This, however, requires the introduction of several arbitrary kinetic parameters.
the capture radius of the pore (nevertheless it may depend also on nongeometric factors involving ion diffusion at the channel mouth). In taking IX of the form given in Eq. 20, we assumed the ER membrane potential is zero, as electroneutrality is currently considered both at rest and during calcium release. We also used a nonequilibrium formula for IX, given by ion binding to a single site inside the channel during permeation (Hille, 1992), with qualitatively similar results. This, however, requires the introduction of several arbitrary kinetic parameters.
Gating of each apamin-sensitive ASK channel is assumed to be driven by opening of one single gate by calcium binding to one site, with Hill coefficient hASK = 4, apparent dissociation constant KASK = 1 μM (Vergara et al., 1998), and off-rate constant 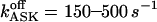 in agreement with specific experimental data (Marrion and Tavalin, 1998). For both calcium and potassium channels, stochastic simulations of each regulatory site occupancy are performed by generating, at every time step, a random number and comparing it to the product between the corresponding transition rate and the time step Δt.
in agreement with specific experimental data (Marrion and Tavalin, 1998). For both calcium and potassium channels, stochastic simulations of each regulatory site occupancy are performed by generating, at every time step, a random number and comparing it to the product between the corresponding transition rate and the time step Δt.
Neumann conditions are introduced at the ECB according to the fluxes crossing each elementary ER membrane patch, among which the Ca2+-ATPase driven flux, 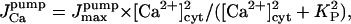 is supposed to be permanent and uniformly distributed on the tubule surface. At r = rC + rT, Dirichlet (constant concentration) conditions were used as specified, whereas at z = 0, zT, and φ = 0, 2π, periodic, and at r = 0, no-flux, boundary conditions were assumed. Periodicity at the z edges is equivalent to considering a uniform distribution of identical, synchronized (Horne and Meyer, 1997) release sites (clusters) along a continuous ER tubule spanning the cytosol over a distance ≫zT and assumed in no vicinity to other tubules over a distance 2rC, as experimentally shown (Callamaras and Parker, 1999) for ∼25% of puffs evoked by subthreshold stimuli, if the tubule orientation is considered here parallel to the plasma membrane. Local concentrations are determined by calculating the radial average at z = zT/2 and φ = 0 (the radial direction through the center of the cluster), over the distance where [Ca2+]cyt(r, φ, z, t) exceeds by a measurable difference (Swillens et al., 1998) of 20 nM the basal level (which is fixed by the concentration in the medium). Global concentrations were calculated over the luminal and cytosolic simulated volume. In all our simulations, ER concentrations resulted practically uniform along the tubule over 0.2 s, and variations in global cytosolic Ca2+ followed exactly the variations in the local concentration, about one order of magnitude lower. All concentrations are averaged every 0.2 s (Nguyen et al., 1998).
is supposed to be permanent and uniformly distributed on the tubule surface. At r = rC + rT, Dirichlet (constant concentration) conditions were used as specified, whereas at z = 0, zT, and φ = 0, 2π, periodic, and at r = 0, no-flux, boundary conditions were assumed. Periodicity at the z edges is equivalent to considering a uniform distribution of identical, synchronized (Horne and Meyer, 1997) release sites (clusters) along a continuous ER tubule spanning the cytosol over a distance ≫zT and assumed in no vicinity to other tubules over a distance 2rC, as experimentally shown (Callamaras and Parker, 1999) for ∼25% of puffs evoked by subthreshold stimuli, if the tubule orientation is considered here parallel to the plasma membrane. Local concentrations are determined by calculating the radial average at z = zT/2 and φ = 0 (the radial direction through the center of the cluster), over the distance where [Ca2+]cyt(r, φ, z, t) exceeds by a measurable difference (Swillens et al., 1998) of 20 nM the basal level (which is fixed by the concentration in the medium). Global concentrations were calculated over the luminal and cytosolic simulated volume. In all our simulations, ER concentrations resulted practically uniform along the tubule over 0.2 s, and variations in global cytosolic Ca2+ followed exactly the variations in the local concentration, about one order of magnitude lower. All concentrations are averaged every 0.2 s (Nguyen et al., 1998). 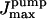 was calculated at every simulation from the condition of equilibrium between total calcium outflow and pump flux at rest.
was calculated at every simulation from the condition of equilibrium between total calcium outflow and pump flux at rest.
The spatio-temporal evolution of each mobile specie concentration (Ym) is calculated according to the reaction-diffusion equation:
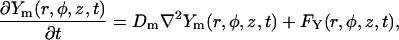 |
(23) |
where FY(r, φ, z, t) is the buffer exchange term. Sources and removal terms are only considered at the ECB and introduced explicitly in the flux boundary conditions. Inside the store, the two mobile species considered are Ca2+ and K+, and the buffering terms are given by Eqs. 3 and 4, respectively. In the cytosol, we determine the evolution of three mobile species, namely Ca2+, K+, and the exogenous calcium mobile buffer EGTA (the endogenous mobile buffer is lost by permeabilization). Cytosolic calcium buffering is calculated with a stoichiometry 1:1 for all buffers, for a total concentration of fix endogenous buffer sites BT,fix or mobile, exogenous BT,mob, without making any buffering approximation. For the mobile buffer and free cytosolic calcium the buffer exchange term is
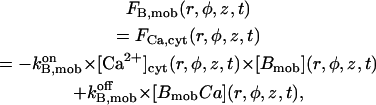 |
(24) |
with 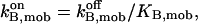 where KB,mob is the respective dissociation constant. The evolution of fix species is determined within the lumen from Eqs. 1 and 2 and within the cytosol from
where KB,mob is the respective dissociation constant. The evolution of fix species is determined within the lumen from Eqs. 1 and 2 and within the cytosol from
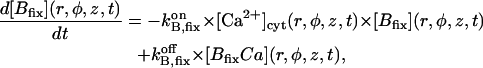 |
(25) |
with 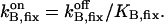 Here again, KB,fix is the dissociation constant of the complex BfixCa. If spatial uniformity is assumed at the initial moment, the conservation rule
Here again, KB,fix is the dissociation constant of the complex BfixCa. If spatial uniformity is assumed at the initial moment, the conservation rule
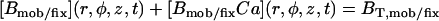 |
(26) |
holds at every instant (Naraghi and Neher, 1997), which reduces the number of equations by two in each spatial element.
The time step Δt = 0.75–1 μs was optimized separately before every simulation and numerically tested on a 0.5-s interval to detect instabilities. The highest sensitivity to Δt was met by [K+] at the “center” of the ER tubule (the first radial iteration). During all simulations, K+ in all central elements was continuously checked to remain below 160 mM. The spatial increment was kept in the range Δr = 35–50 nm. Simulation standard parameter values are given in Table 2.
References
- Atri, A., J. Amundson, D. Clapham, and J. Sneyd. 1993. A single-pool model for intracellular calcium oscillations and waves in the Xenopus laevis oocyte. Biophys. J. 65:1727–1739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baran, I. 1996. Calcium and cell cycle progression: possible effects of external perturbation on cell proliferation. Biophys. J. 70:1198–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrero, M. J., M. Montero, and J. Alvarez. 1997. Dynamics of [Ca2+] in the endoplasmic reticulum and cytoplasm in intact HeLa cells. J. Biol. Chem. 272:27694–27699. [DOI] [PubMed] [Google Scholar]
- Berridge, M. J. 1993. Inositol trisphosphate and calcium signaling. Nature. 361:315–325. [DOI] [PubMed] [Google Scholar]
- Berridge, M. J., P. Lipp, and M. D. Bootman. 2000. The versatility and universality of calcium signalling. Nature Rev. Mol. Cell Biol. 1:11–21. [DOI] [PubMed] [Google Scholar]
- Bezprozvanny, I., and B. E. Erlich. 1994. Inositol (1,4,5)-trisphosphate (InsP3)-gated Ca channels from cerebellum: conduction properties for divalent cations and regulation by intraluminal calcium. J. Gen. Physiol. 104:821–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezprozvanny, I., J. Watras, and B. E. Erlich. 1991. Bell-shaped calcium response curves of Ins(1,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature. 351:751–754. [DOI] [PubMed] [Google Scholar]
- Callamaras, N., and I. Parker. 1999. Radial localization of inositol 1,4,5-trisphosphate-sensitive Ca2+ release sites in Xenopus oocytes resolved by axial confocal linescan imaging. J. Gen. Physiol. 113:199–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clapham, D. E. 1995. Calcium signaling. Cell. 80:259–268. [DOI] [PubMed] [Google Scholar]
- Colquhoun, D., A. G. Hawkes, and K. Srodzinski. 1996. Joint distributions of apparent open and shut times of single-ion channels and maximum likelihood fitting of mechanisms. Philos. Trans. R. Soc. Lond. A354:2555–2590. [Google Scholar]
- De Young, G. W., and J. Keizer. 1992. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. USA. 89:9895–9899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupont, G. 1999. Spatio-temporal organization of cytosolic Ca2+ signals: from experimental to theoretical aspects. Comments Theor. Biol. 5:305–340. [Google Scholar]
- Dupont, G., and A. Goldbeter. 1994. Properties of intracellular Ca2+ waves generated by a model based on Ca(2+)-induced Ca2+ release. Biophys. J. 67:2191–2204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finch, E. A., T. J. Turner, and S. M. Goldin. 1991. Calcium as a coagonist of inositol 1,4,5-trisphosphate-induced calcium release. Science. 252:443–446. [DOI] [PubMed] [Google Scholar]
- Gilon, P., A. Arredouani, P. Gailly, J. Gromada, and J. C. Henquin. 1999. Uptake and release of Ca2+ by the endoplasmic reticulum contribute to the oscillations of the cytosolic Ca2+ concentration triggered by Ca2+ influx in the electrically excitable pancreatic B-cells. J. Biol. Chem. 274:20197–20205. [DOI] [PubMed] [Google Scholar]
- Golovina, V. A., and M. P. Blaustein. 1997. Spatially and functionally distinct Ca2+ stores in sarcoplasmic and endoplasmic reticulum. Science. 275:1643–1648. [DOI] [PubMed] [Google Scholar]
- Györke, I., and S. Györke. 1998. Regulation of the cardiac ryanodine receptor channel by luminal Ca2+ involves luminal Ca2+ sensing sites. Biophys. J. 75:2801–2810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haddock, P. S., W. A. Coetzee, E. Cho, L. Porter, H. Katoh, D. M. Bers, M. S. Jafri, and M. Artman. 1999. Subcellular [Ca2+]i gradients during excitation-contraction coupling in newborn rabbit ventricular myocytes. Circ. Res. 85:415–427. [DOI] [PubMed] [Google Scholar]
- Hajnóczky, G., R. Hager, and A. P. Thomas. 1999. Mitochondria suppress local feedback activation of inositol 1,4,5-trisphosphate receptors by Ca2+. J. Biol. Chem. 274:14157–14162. [DOI] [PubMed] [Google Scholar]
- Hajnóczky, G., and A. P. Thomas. 1994. The inositol trisphosphate calcium channel is inactivated by inositol trisphosphate. Nature. 370:474–477. [DOI] [PubMed] [Google Scholar]
- Hille, B. 1992. Ionic Channels of Excitable Membranes. Sinauer Associates, Sunderland, MA.
- Hofer, A. M., C. Fasolato, and T. Pozzan. 1998. Capacitive Ca2+ entry is closely linked to the filling state of internal Ca2+ stores: a study using simultaneous measurements of ICRAC and intraluminal Ca2+. J. Cell Biol. 140:325–334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horne, J. H., and T. Meyer. 1997. Elementary calcium release units induced by inositol trisphosphate. Science. 276:1690–1693. [DOI] [PubMed] [Google Scholar]
- Huang, Y., and J. W. Putney, Jr. 1998. Relationship between intracellular calcium store depletion and calcium release-activated calcium current in a mast cell line (RBL-1). J. Biol. Chem. 273:19554–19559. [DOI] [PubMed] [Google Scholar]
- Kaftan, E. J., B. E. Ehrlich, and J. Watras. 1997. Inositol 1,4,5-trisphosphate and calcium interact to increase the dynamic range of InsP3 receptor-dependent calcium signaling. J. Gen. Physiol. 110:529–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, J. H., L. Johannes, B. Goud, C. Antony, C. A. Lingwood, R. Daneman, and S. Grinstein. 1998. Noninvasive measurement of the pH of the endoplasmic reticulum at rest and during calcium release. Proc. Natl. Acad. Sci. USA. 95:2997–3002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukyanenko, V., S. Subramanian, I. Györke, T. F. Wiesner, and S. Györke. 1999. The role of luminal Ca2+ in the generation of Ca2+ waves in rat ventricular myocytes. J. Physiol. 518:173–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak, D. O., and J. K. Foskett. 1997. Single-channel kinetics, inactivation, and spatial distribution of inositol (1,4,5) trisphosphate (IP3) receptor in Xenopus oocyte nucleus. J. Gen. Physiol. 109:571–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak, D. O., S. McBride, and J. K. Foskett. 1998. Inositol 1,4,5-tris-phosphate activation of inositol 1,4,5-trisphosphate receptor Ca2+ channel by ligand tuning of Ca2+ inhibition. Proc. Natl. Acad. Sci. USA. 95:15821–15825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak, D. O., S. McBride, and J. K. Foskett. 1999. ATP regulation of type 1 inositol 1,4,5-trisphosphate receptor channel gating by allosteric tuning of Ca2+ activation. J. Biol. Chem. 274:22231–22237. [DOI] [PubMed] [Google Scholar]
- Marrion, N. V., and S. J. Tavalin. 1998. Selective activation of Ca2+-activated K+ channels by co-localized Ca2+ channels in hippocampal neurons. Nature. 395:900–905. [DOI] [PubMed] [Google Scholar]
- Marshall, I. C. B., and C. W. Taylor. 1993. Regulation of inositol 1,4,5-trisphosphate receptors. J. Exp. Biol. 184:161–182. [DOI] [PubMed] [Google Scholar]
- Mignery, G. A., P. A. Johnston, and T. C. Sudhof. 1992. Mechanism of Ca2+ inhibition of inositol 1,4,5-trisphosphate (InsP3) binding to the cerebellar InsP3 receptor. J. Biol. Chem. 267:7450–7455. [PubMed] [Google Scholar]
- Missiaen, L., J. B. Parys, A. F. Weidema, H. Sipma, S. Vanlingen, P. De Smet, G. Callewaert, and H. De Smedt. 1999. The bell-shaped Ca2+ dependence of the inositol 1,4,5-trisphosphate-induced Ca2+ release is modulated by Ca2+/calmodulin. J. Biol. Chem. 274:13748–13751. [DOI] [PubMed] [Google Scholar]
- Mitchell, R. D., H. K. B. Simmerman, and L. R. Jones. 1988. Ca2+ binding effects on protein conformation and protein interactions of canine cardiac calsequestrin, J. Biol. Chem. 263:1376–1381. [PubMed] [Google Scholar]
- Moraru, I. I., E. J. Kaftan, B. E. Ehrlich, and J. Watras. 1999. Regulation of type 1 inositol 1,4,5-trisphosphate-gated calcium channels by InsP3 and calcium. J. Gen. Physiol. 113:837–849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naraghi, M., and E. Neher. 1997. Linearized buffered Ca2+ diffusion in microdomains and its implication for calculation of [Ca2+] at the mouth of a calcium channel. J. Neurosci. 17:6961–6973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Negulescu, P. A., N. Shastri, and M. D. Cahalan. 1994. Intracellular calcium dependence of gene expression in single T lymphocytes. Proc. Natl. Acad. Sci. USA. 91:2873–2877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen, T., W. C. Chin, and P. Verdugo. 1998. Role of Ca2+/K+ ion exchange in intracellular storage and release of Ca2+. Nature. 395:908–912. [DOI] [PubMed] [Google Scholar]
- Oancea, E., and T. Meyer. 1996. Reversible desensitization of inositol trisphosphate-induced calcium release provides a mechanism for repetitive calcium spikes. J. Biol. Chem. 271:17253–17260. [DOI] [PubMed] [Google Scholar]
- Parker, I., and I. Ivorra. 1990. Inhibition by Ca2+ of inositol trisphosphate-mediated Ca2+ liberation: a possible mechanism for oscillatory release of Ca2+. Proc. Natl. Acad. Sci. USA. 87:260–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pape, P. C., D. S. Jong, and W. K. Chandler. 1995. Calcium release and its voltage dependence in frog cut muscle fibers equilibrated with 20 mM EGTA. J. Gen. Physiol. 106:259–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel, S., S. A. Morris, C. E. Adkins, G. O'Beirne, and C. W. Taylor. 1997. Ca2+-independent inhibition of inositol trisphosphate receptors by calmodulin: as a possible means of regulating Ca2+ mobilization. Proc. Natl. Acad. Sci. USA. 94:11627–11632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachs, F., F. Qin, and P. Palade. 1995. Models of Ca2+ release channel adaptation. Science. 267:2010–2011. [DOI] [PubMed] [Google Scholar]
- Sienaert, I., H. De Smedt, J. B. Parys, L. Missiaen, S. Vanlingen, H. Sipma, and R. Casteels. 1996. Characterization of a cytosolic and a luminal Ca2+ binding site in the type I inositol 1,4,5-trisphosphate receptor. J. Biol. Chem. 271:27005–27012. [DOI] [PubMed] [Google Scholar]
- Sienaert, I., L. Missiaen, H. De Smedt, J. B. Parys, H. Sipma, and R. Casteels. 1997. Molecular and functional evidence for multiple Ca2+-binding domains in the type 1 inositol 1,4,5-trisphosphate receptor. J. Biol. Chem. 272:25899–25906. [DOI] [PubMed] [Google Scholar]
- Stern, M. D., G. Pizzaro, and E. Rios. 1997. Local control model of excitation-contraction coupling in skeletal muscle. J. Gen. Physiol. 110:415–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swillens, S., P. Champeil, L. Combettes, and G. Dupont. 1998. Stochastic simulation of a single inositol 1,4,5-trisphosphate-sensitive Ca2+ channel reveals repetitive openings during 'blip-like' Ca2+ transients. Cell Calcium. 23:291–302. [DOI] [PubMed] [Google Scholar]
- Swillens, S., G. Dupont, L. Combettes, and P. Champeil. 1999. From calcium blips to calcium puffs: theoretical analysis of the requirements for interchannel communication. Proc. Natl. Acad. Sci. USA. 96:13750–13755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor, C. W., and D. Traynor. 1995. Calcium and inositol trisphosphate receptors. J. Membr. Biol. 145:109–118. [DOI] [PubMed] [Google Scholar]
- Thrower, E. C., H. Mobasheri, S. Dargan, P. Marius, E. J. A. Lea, and A. P. Dawson. 2000. Interaction of luminal calcium and cytosolic ATP in the control of type 1 inositol (1,4,5) trisphosphate receptor channels. J. Biol. Chem. 275:36049–36055. [DOI] [PubMed] [Google Scholar]
- Vergara, C., R. Latorre, N. V. Marrion, and J. P. Adelman. 1998. Calcium-activated potassium channels. Curr. Opin. Neurobiol. 8:321–329. [DOI] [PubMed] [Google Scholar]