Analyzing Intracellular Binding and Diffusion with Continuous Fluorescence Photobleaching

Abstract

Transport and binding of molecules to specific sites are necessary for the assembly and function of ordered supramolecular structures in cells. For analyzing these processes in vivo, we have developed a confocal fluorescence fluctuation microscope that allows both imaging of the spatial distribution of fluorescent molecules with confocal laser scanning microscopy and probing their mobility at specific positions in the cell with fluorescence correlation spectroscopy and continuous fluorescence photobleaching (CP). Because fluorescence correlation spectroscopy is restricted to rapidly diffusing particles and CP to slower processes, these two methods complement each other. For the analysis of binding-related contributions to mobility we have derived analytical expressions for the temporal behavior of CP curves from which the bound fraction and/or the dissociation rate or residence time at binding sites, respectively, can be obtained. In experiments, we investigated HeLa cells expressing different fluorescent proteins: Although enhanced green fluorescent protein (EGFP) shows high mobility, fusions of histone H2B with the yellow fluorescent protein are incorporated into chromatin, and these nuclei exhibit the presence of a stably bound and a freely diffusing species. Nonpermanent binding was found for mTTF-I, a transcription termination factor for RNA polymerase I, fused with EGFP. The cells show fluorescent nucleoli, and binding is transient. CP yields residence times for mTTF-I-EGFP of ∼13 s.

INTRODUCTION

Many biological processes depend on efficient intracellular transport of molecules. Concentration gradients between cellular compartments (e.g., at membranes) are often established by directed transport processes conducted at pores, at channels, or by motor proteins. On the other hand, within cellular compartments transport is frequently driven by diffusion, which tends to balance concentration gradients. From this point of view, Brownian motion can be considered as a fast, nondirected transport mechanism that depends on the hydrodynamic properties of the molecules, i.e., the translational and the rotational diffusion coefficients. Deviations from simple random walk behavior can occur by additional collisions with structures of much lower mobility, resulting in a geometrically obstructed or a spatially confined motion (anomalous diffusion). Furthermore, proteins face a diverse landscape of binding energies, ranging from specific binding sites to weak nonspecific interactions. Although specific binding is typically characterized by distinct association and dissociation rates and characteristic residence times, leading to a reduced apparent diffusion coefficient, nonspecific interactions often show a broad distribution of residence times and cause anomalous diffusion. For many proteins, transient immobilization is closely connected with their enzymatic or structural function (e.g., in linear diffusion of proteins on DNA), and an inhomogeneous spatial distribution seems to be a common pattern rather than an exception.

Intracellular mobility has been studied during the last decades by different experimental approaches, mainly based on fluorescence techniques with confocal or wide-field optics. i), Fluorescence photobleaching, the photoinduced irreversible transition of fluorophores into a nonfluorescent state, is used in fluorescence recovery or redistribution after photobleaching (FRAP), fluorescence loss in photobleaching (FLIP), and continuous fluorescence microphotolysis experiments. These methods are based on nonequilibrium distributions of fluorescent molecules and their relaxation generated by instantaneous or continuous bleaching of microscopic areas (Axelrod et al., 1976; Cole et al., 1996; Peters et al., 1974, 1981). Typical results are intracellular diffusion coefficients (Houtsmuller et al., 1999; Kao et al., 1993; Seksek et al., 1997; Swaminathan et al., 1997), transport rates (Dahm et al., 2001; Peters, 1983, 1984), or relative mobilities (Lever et al., 2000; Misteli et al., 2000). ii), In fluorescence correlation spectroscopy (FCS), (Schwille, 2001; Webb, 2001), the amplitude and the time course of steady-state concentration fluctuations in a microscopic observation volume are analyzed, resulting in the concentration and the diffusion coefficient of fluorescent molecules in vivo (Berland et al., 1995; Brock et al., 1998; Politz et al., 1998; Schwille et al., 1999a; Wachsmuth et al., 2000). iii), With time-resolved fluorescence imaging, the mobility of nucleic acids tagged with ultraviolet-activated (uncaged) fluorophores (Politz et al., 1999) and even the trajectories of single fluorescent particles can be observed (Kues et al., 2001; Seisenberger et al., 2001). For many of these methods, the green fluorescent protein (GFP) and its spectral relatives are particularly well suited in the intracellular environment due to their high-fluorescence yield, their photobleaching properties (Harms et al., 2001), and because they can be fused to proteins in vivo (White and Stelzer, 1999).

In the above-mentioned studies, it was found that in most cellular compartments inert molecules of the size of typical proteins sense a 2- to 10-fold higher viscosity than in water, whereas various biologically active proteins show a 40- to 100-fold reduced diffusion rate. This can be interpreted as transient binding of otherwise freely diffusing molecules to immobilized structures as one can derive from numerical modeling of FRAP data (Phair and Misteli, 2001; Siggia et al., 2000) or single particle tracking (Kues et al., 2001). From these results the view of the cellular interior has emerged as a crowded but aqueous compartment rather than a viscous gel (Ellis, 2001; Verkman, 2002). Molecules roam the available space statistically and bind transiently to appropriate sites, and seemingly static structures are in a permanent flux of their constituents (Misteli, 2001).

Photobleaching methods provide only indirect evidence for the interplay of diffusion, steric hindrance, and binding-related immobilization. FCS, on the other hand, mainly yields the diffusion properties but is conceptually blind to immobilized molecules. Therefore, we have developed a combination of continuous fluorescence photobleaching (CP) at a spot, FCS, and confocal laser scanning microscopy (CLSM), called fluorescence fluctuation microscopy (FFM), for intracellular applications. With one confocal illumination and detection setup, all three methods can be applied with diffraction-limited resolution. Here we present an approximated analytical treatment of CP curves taking into account diffusion, transient immobilization, and flux between cellular compartments. Comparison with numerical solutions of the underlying differential equations shows that the analytical expressions are equivalent but much more suited to fitting of experimental data. These are then applied to experimental observations of different proteins in vivo: i), Unmodified enhanced green fluorescent protein (EGFP) molecules seem to be freely mobile everywhere in the cell and only obstructed sterically by membranes, filaments, etc. ii), Cells expressing histone H2B, one of the constituents of the chromatin-forming nucleosomes, tagged with enhanced yellow fluorescent protein (EYFP) show a fluorescence intensity pattern that maps the chromatin density. The core histones are known to be immobilized without exchange for more than an hour (Kimura and Cook, 2001; Lever et al., 2000). iii), For the mammalian transcription termination factor mTTF-I, there are binding sites downstream as well as upstream of ribosomal genes. This factor is involved in transcription termination, chromatin remodeling, and replication fork arrest (Grummt, 1999). Cells expressing a mTTF-I-EGFP fusion protein show a nearly exclusive nucleolar staining due to a transient immobilization of the factor. In all three cases, we are able to distinguish between diffusion and binding-related contributions to molecular mobilities and to characterize them in a quantitative manner.

THEORETICAL BACKGROUND

Continuous fluorescence photobleaching

Diffusion, photobleaching, and exchange between a free and a bound fraction of fluorescently labeled molecules result in a characteristic time course of the confocally excited and detected fluorescence. In the following, we present the theoretical CP curves for several cases: a mobile and an immobile fraction with association and dissociation rates smaller than, similar to, and larger than the bleaching rate but always smaller than or similar to the diffusion rate. This covers a wide range of biologically relevant values because in most cases, the binding-related residence time in the microscope focus exceeds the diffusion-related one.

The interaction considered is the binding equilibrium of a freely diffusing fluorescently labeled ligand A to an immobilized receptor B according to

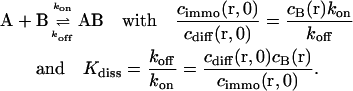(1)

The concentrations c_diff and c_immo describe the distribution of unbleached free and bound ligands, respectively, whereas c_B is the concentration of available binding sites. The ratio of the dissociation and the association rate k_off and k_on yields the dissociation constant K_diss. We assume that the fluorescence is not affected by binding and that ligand binding is in equilibrium throughout the bleaching process so that the concentration of unoccupied binding sites, c_B, is constant.

We further assume that photobleaching of the fluorophore is a simple irreversible first-order reaction with a position-dependent rate constant 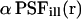(Axelrod et al., 1976). The illumination point spread function 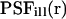is the illumination profile normalized to unity at maximum, whereas α is proportional to the maximum intensity in the sample and a fluorophore-specific bleaching probability, .

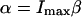We introduce the molecular detection efficiency (MDE) 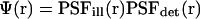of a confocal optical system, which is the product of the illumination and the detection PSF and which we take as a three-dimensional (3D) Gaussian function 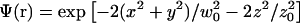as shown for FCS and photobleaching applications in various setups (Qian and Elson, 1991; Rigler et al., 1993; Wedekind et al., 1996). In addition, neglecting chromatic and pinhole size effects, we approximate 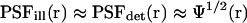also as 3D Gaussian functions (Fig. 1 A). The MDE is used to turn a spatio-temporal concentration distribution 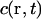of fluorescent molecules into a time-dependent fluorescence signal according to

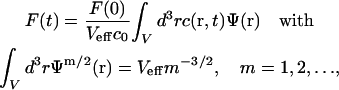(2)

where V_eff is the effective focal volume and c₀ the weighted average concentration in the focus. The sample volume V, significantly larger than V_eff, is the volume in which the molecules can move around rapidly by diffusion (e.g., a nucleus or a whole cell).

FIGURE 1.

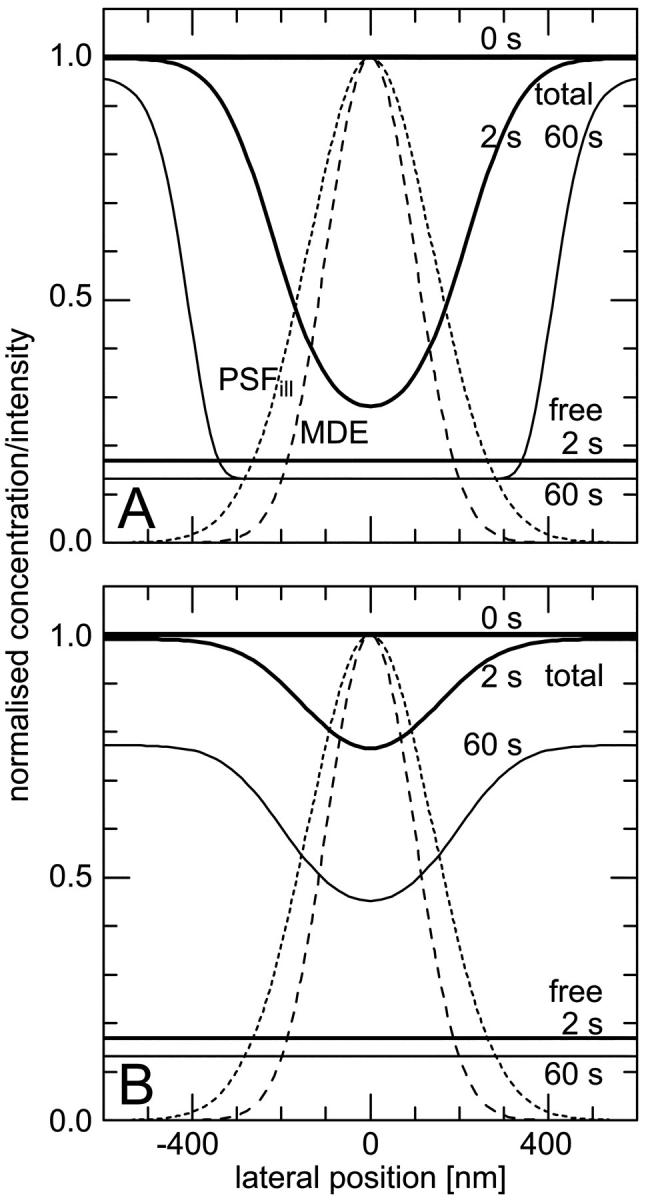
Lateral profiles of the illumination PSF, of the MDE, and of the concentrations of fluorescent molecules in the focal plane during CP experiments. 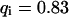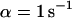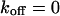(Dotted lines) Gaussian PSF_ill with a 1/e²-radius of 280 nm; (dashed lines) Gaussian MDE with a 1/e²-radius of 200 nm; (solid lines) concentration of the total amount and of the freely mobile fraction of fluorescent molecules directly before (0 s), shortly after starting (2 s), and after bleaching (60 s) for different sets of parameters: (A) , , and , i.e., without exchange, (B) 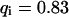, , 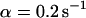and 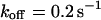, i.e., with a medium dissociation rate.

Then we get the differential equation for the concentration c_diff of the free ligand fraction

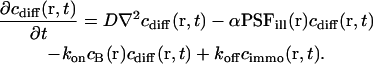(3)

The first term represents diffusion with the diffusion coefficient D, the second accounts for the photobleaching process (Axelrod et al., 1976), and the rest covers the binding-related exchange. The dissociation constants of typical biological interactions as well as the bleaching rates (when applying dim laser intensities as they are used in FCS experiments) are much smaller than the diffusion rate of the free ligand A, i.e., the inverse of the mean dwell time τ_diff in the focus in a typical confocal setup. Therefore, concentration gradients are always balanced rapidly and Eq. 3 simplifies to

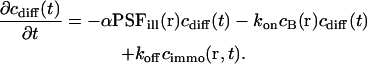(4)

(For the diffusion limit, i.e., when diffusion and association/dissociation rates are similar, see “Large dissociation rates—diffusion limit”) Outside the focus, where k_onc_B and k_off are much larger than αPSF_ill, the interaction terms are dominant and vanish due to the equilibrium. Inside the focus, the concentration of binding sites is assumed constant, 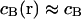, and only the association term contributes because nearly all bound molecules are bleached before dissociation. Integrating Eq. 4 over the sample volume V and then using Eq. 2 we find an exponential decay

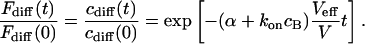(5)

For precisely computing the bleaching rate, one would have to take into account that bleaching takes place everywhere in the illumination cone. The effective size of the bleaching volume is that of a cylinder with the diameter of the focus and the height of the sample volume along the optical axis, i.e., the nucleus or the cell. However, this still results in an exponential decay, albeit with a different decay constant also depending on k_off. Because the bleaching rate constant α is generally not known but depends on the laser intensity, the approach taken in Eq. 5 is sufficient in most cases.

If there is a diffusive equlibrium between two compartments (like the nucleus and the cytoplasm) with a boundary of low permeability (like the nuclear membrane), which can be characterized by a transport rate, a double rather than a single exponential decay is found (Peters, 1983):

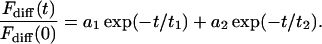(6)

In analogy to Eq. 3, the rate equation of the bound fraction is given by

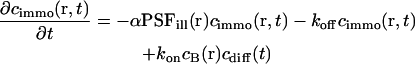(7)

Because the immobilized molecules are bleached much faster, the mobile concentration can be considered approximately constant and we obtain the solution

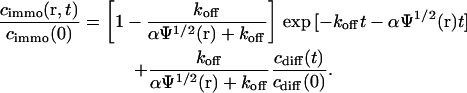(8)

Here we have also used that a homogeneous receptor distribution within the focus leads to an equivalent steady-state distribution of bound ligands, 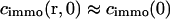. Eq. 8 can be transformed into the corresponding fluorescence signal for the different regimes using Eq.2.

Small dissociation rates

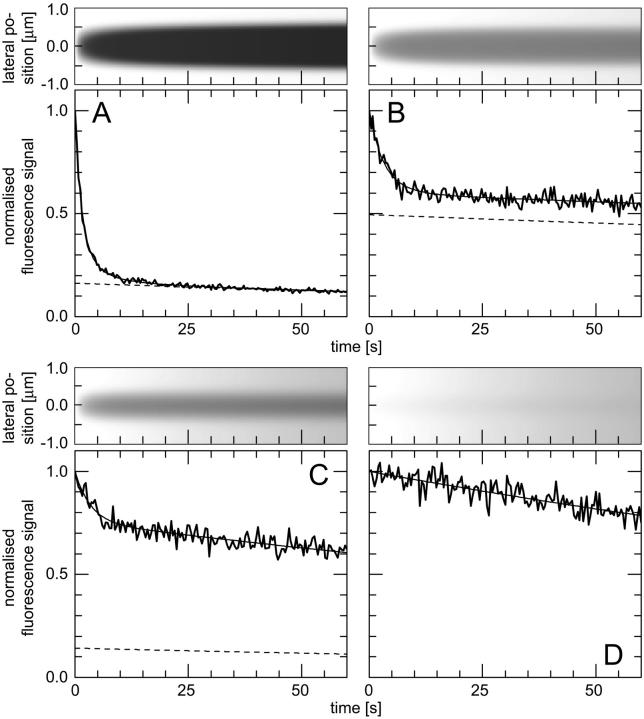
The one-dimensional spatial concentration distribution at different times for 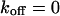and 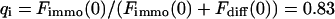as governed by Eqs. 5 and 8 is shown in Figs. 1 A and 2 A together with the bleaching and the detection profile. For small dissociation rates, 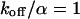, we have calculated numerically the time evolution as well as the dependence on 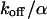in the vicinity of zero for all three terms in Eq. 8 and have then applied a suitable approximation, resulting in

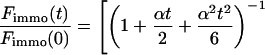(9)

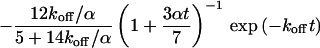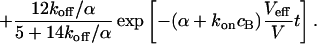FIGURE 2.

(Top) Time course of the lateral concentration profile in the focal plane, calculated with a Gaussian PSF_ill with a 1/e²-radius of 280 nm and Eqs. 5 and 8; (bottom) time course of the fluorescence signal, (thick solid lines) calculated numerically as described in the text, (thin solid lines) from the fit, (dashed lines) contribution of the freely mobile fraction to the fit. 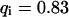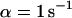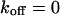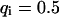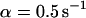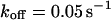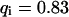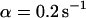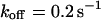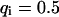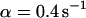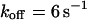Different sets of parameters were applied: (A) , , and , i.e., without exchange, (B) , , and , i.e., with a small dissociation rate, (C) , , and , i.e., with a medium dissociation rate, and (D) , , and , i.e., with a large dissociation rate.

This holds true even in the limit of no exchange. The total fluorescence signal is given by the sum 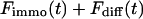and shows a rapid decrease for short times turning into an exponential decay, see Fig. 2, A and B.

Medium dissociation rates

The same procedure is followed, but now in the vicinity of 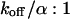(see Figs. 1 B and 2 C for the concentration profile at different times):

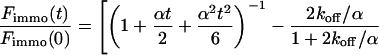(10)

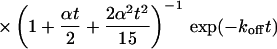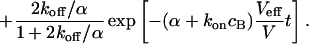Again, the total fluorescence signal is given by the sum 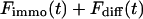. Fig. 2 C shows that in this case as well, a rapid decrease is followed by an exponential decay. Eqs. 9 and 10 are equal for .

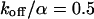Large dissociation rates—diffusion limit

For a fast interaction, 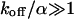, it is not useful to distinguish between a bound and a free fraction of ligands. Rather, the ligands are considered as a freely mobile species with a dwell time in the focus increased by the product of the binding probability and the residence time at the binding site, 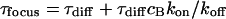. This results in a reduced diffusion coefficient 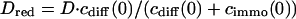. Then, the last two terms in Eq. 4 can be neglected but the bleaching rate is enhanced to 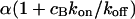, leading again to a single exponential decay

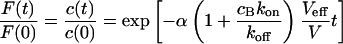(11)

for the total concentration and the fluorescence signal (Fig. 2 D). It should be noted that in this case, which is probably more relevant in membranes, careful FCS measurements might be more helpful than CP to resolve the influence of binding on diffusion.

Numerically calculated CP curves

Except for the size of the focus, the approximated analytical decay functions do not depend on the actual illumination and detection profile. To check their validity, we calculated numerically the spatial distribution and temporal evolution of the ligand concentration (bound and free) using the rate Eqs. 4 and 7 and the corresponding fluorescence signal by means of Eq. 2. However, we applied more precise expressions for the point spread functions, appropriate for an overilluminated back aperture of the objective lens (Born and Wolf, 1980):

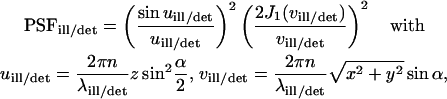(12)

with the first-order Bessel function J₁. The required parameters are the illumination and the detection wavelengths and the numerical aperture of the objective lens 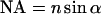with the refractive index n of the immersion liquid.

Fluorescence correlation spectroscopy

The conceptual and theoretical basis of FCS has been well established for years and was reviewed recently (Schwille, 2001; Webb, 2001). Like in this study, most intracellular applications are done with high-resolution microscopes where the above-mentioned Gaussian approximation for the molecular detection efficiency holds (Qian and Elson, 1991; Rigler and Widengren, 1993). Diffusional concentration fluctuations of fluorescently labeled molecules in solution in the diffraction-limited observation volume can be characterized by the normalized autocorrelation function 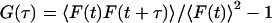of the fluorescence signal. Apart from binding, many geometrical constraints on molecular mobility can be covered phenomenologically with the concept of anomalous diffusion (Feder et al., 1996; Gennerich and Schild, 2000; Schwille et al., 1999b; Wachsmuth et al., 2000), including even spatially confined motions of fluorescent molecules attached to a dynamic polymer system. Autofluorescent proteins, such as EGFP and EYFP used here, show additional signal variations due to conformational fluctuations between fluorescent and dark states (Haupts et al., 1998; Heikal et al., 2000; Schwille et al., 2000). This results in the autocorrelation function (Wachsmuth et al., 2000; Widengren and Rigler, 1998)

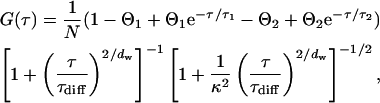(13)

where N denotes the mean number of molecules and 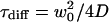their mean dwell time in the focal volume. The latter is related to the diffusion coefficient D and the lateral focus radius w₀ and κ is the ratio of the axial and the lateral radius. The anomaly parameter d_w quantifies the deviation from free diffusion and is larger than two (subdiffusion) for obstructed and sometimes smaller than two (superdiffusion) for confined motion. The probabilities and relaxation times of the occupation of the dark states are given by Θ_1,2 and τ_1,2, respectively. For a mixture of independent species, we use a sum of such equations with the respective parameters.

MATERIALS AND METHODS

Numerical calculations

The parameters of the experimental setup necessary for the numerical calculations are the wavelengths, set to 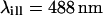(the Ar laser line used) and 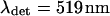(the spectral median of the detection setup for GFP), and the numerical aperture 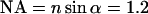of the objective lens in the experimental setup with a refractive index 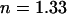for water. The equilibrium concentrations, association and dissociation rates, and the bleaching rate were varied as appropriate.

Maple 5 Release 5.0 (Waterloo Maple, Waterloo, Canada) on a Linux workstation was used for the calculations. Time steps were set to 0.2 s and the focal volume was divided into a stack of concentric rings of 30 nm along the optical axis and 10 nm laterally. Smaller temporal and spatial steps did not change the results. Finally, Gaussian noise with a standard deviation of 5% was added to the curves, which were then fitted as described below.

Experimental setup

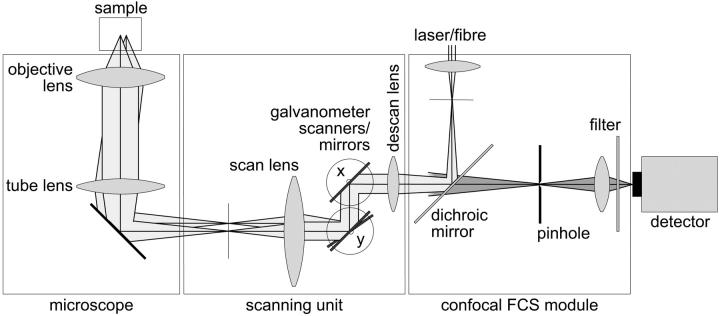
For FCS, CP, and confocal imaging we used a setup of our own construction, the fluorescence fluctuation microscope (FFM). A schematic overview of the optics is given in Fig. 3. The device combines a confocal FCS module (Langowski et al., 2000; Wachsmuth et al., 2000) and a beam-scanning unit attached to the video port of an inverted microscope (IX-70, Olympus Optical, Hamburg, Germany). The 488-nm line of a low noise Ar-Kr laser (643-YB-A01, Melles Griot, Bensheim, Germany) is coupled into the module through a monomode fiber (Laser2000, Wessling, Germany) and illuminates the back aperture of the objective lens UplanApo 60×/1.2NA (Olympus), resulting in a diffraction-limited focus with intensities of the order of 1 kW cm⁻². The excited EGFP and EYFP fluorescence is detected in the range of 515–545 nm with an avalanche photodiode (SPCM-AQR-13, Perkin-Elmer Optoelectronics, Vaudreuil, Canada) in photon-counting mode behind a pinhole with a diameter of 50 μm. Appropriate dichroic mirrors and filters (Omega Optical, Brattleboro, VT) are used for spectral separation and selection. The beam is scanned and positioned using rotating mirrors driven by closed-loop galvanometer scanners M2 (GSI Lumonics, Unterschleißheim, Germany) and a scan lens FVX-IR-PL (Olympus), while a stepping motor moves the objective along the z axis. The control software written in our laboratory allows us to acquire confocal fluorescence and transmission images, and to position the laser with 25 nm precision for CP and FCS. The detector signal is fed into an ALV-5000/E correlator card (ALV, Langen, Germany), which records the signal and calculates its autocorrelation function simultaneously for FCS and CP, and into a PCI-6602 counter/timer card (National Instruments, Munich, Germany) for imaging.

FIGURE 3.

Schematic overview of the optical setup. For simplification, the detection beam path is drawn only behind the dichroic mirror and the scanning mirrors for x and y with parallel pivot axes. The setup benefits from the fact that the beam can be parked at an arbitrary position in the sample and that all operational modes are carried out with avalanche photodiodes in the photon-counting mode so that the signals in CLSM, FCS, and CP can be compared directly.

The CP model functions were fitted to the measured photobleaching curves with the Marquardt-Levenberg algorithm (Press et al., 1992) using the nonlinear least squares fitting tool of Origin 6.1 (OriginLab, Northampton, MA). The theoretical autocorrelation functions were fitted to the FCS data with a program written in our laboratory based on the same algorithm.

Cells

HeLa cells were transfected with vectors expressing the respective protein, i.e., the GFP mutant EGFP, which is optimized for mammalian cell lines (BD Biosciences Clontech, Heidelberg, Germany; see Wachsmuth et al. (2000)), histone H2B fused to the yellow-shifted mutant EYFP (Knoch et al., 2000; T. Weidemann, M. Wachsmuth, T. A. Knoch, G. Müller, W. Waldeck, and J. Langowski, unpublished data), and the mouse transcription termination factor mTTF-I fused to EGFP. Except for mTTF-I, we used stably transfected clones. Transfections were carried out with Lipofectamin as proposed by the manufacturer, and cells were grown in 5% CO₂ atmosphere at 37°C in RPMI medium (Gibco Invitrogen, Karlsruhe, Germany) without phenol red and supplemented with 10% fetal calf serum. For the experiments, cells were cultivated subconfluently on chambered coverglasses (Nunc, Wiesbaden, Germany) and mounted on the microscope stage.

RESULTS

Calculated CP curves

We computed theoretical photobleaching curves using various sets of values for the equilibrium concentrations, the association and dissociation rates, and the bleaching rate, corresponding to the different cases described in the theory section.

The first example, Fig. 2 A, shows the calculated spatio-temporal concentration distribution and fluorescence decay due to bleaching with a rate of 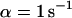for an immobilized fraction 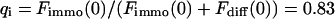that does not exchange with the remaining 17% of freely diffusing molecules. One can clearly see that the concentration drops quickly only in the vicinity of the bleach spot. The rapid fluorescence decrease corresponds to the immobile molecules and is followed by the exponential decay of the free fraction. Fitting a sum of Eqs. 5 and 9 to the calculated curve is only possible for 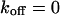and yields an immobilized fraction of 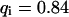very similar to the initially employed value whereas the bleaching rate of 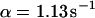is somewhat larger. If both populations exchange slowly, as shown in Fig. 2 B with 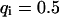, , 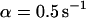and 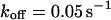, a similar behavior is obtained, and the initial parameters can be recovered with Eqs. 5 and 9 (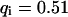, , 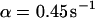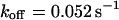). However, although the exponential decay time constant of the total fluorescence signal for longer times is the same as for the contribution of the free fraction, its amplitude increases with 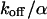, resulting in an “offset” as shown in Fig. 2, B and C. This corresponds to a concentration loss detectable even far away from the bleach spot. In the case of a faster exchange (Fig. 2 C with 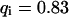, , 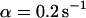and 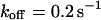), these effects are even more pronounced. Again, the parameters can be recovered from the fit (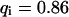, , 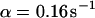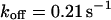) now using Eqs. 5 and 10. For a very fast exchange, (Fig. 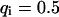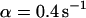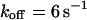2 D with , , and ), the fluorescence decay reduces to a single exponential and the concentration drops homogeneously.

Reshuffling the noise and then fitting again shows that in general, the parameters used for the calculations can be recaptured from the fit with a standard deviation of the order of 10%. This also characterizes the quality of the approximated analytical functions and shows that the analytical expressions and the numerical calculations are equivalent except for an uncertainty of the order of 10%. The great advantage of the analytical expressions is that they are much more convenient for fitting experimental data. Because the parameters are not entirely independent from each other, it is however useful and sometimes necessary to obtain one parameter independently.

Experimental CP curves

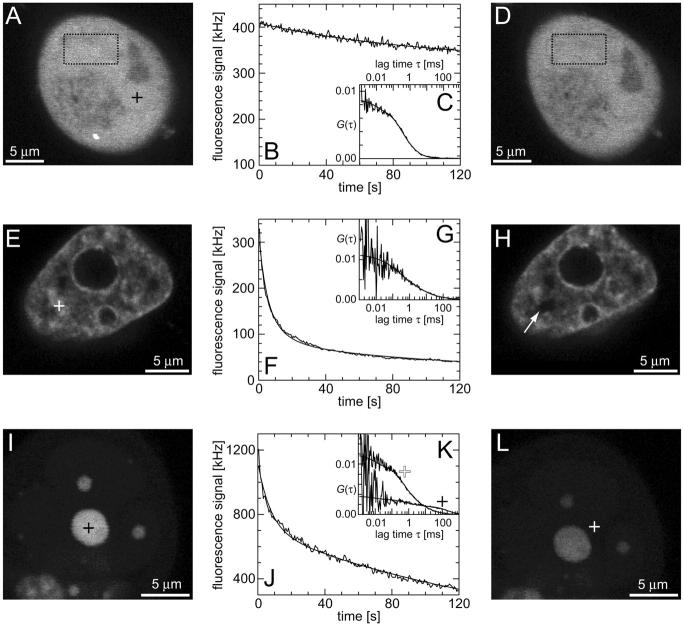
Freely mobile EGFP molecules in HeLa cells

First, the continuous fluorescence photobleaching of intracellular EGFP was studied. Fig. 4 A is a confocal image of an EGFP-expressing HeLa cell, showing a rather homogeneous EGFP distribution. At the position in the nucleus marked with a cross, the fluorescence was continuously bleached and recorded (Fig. 4 B). The resulting decay can be fitted with Eq. 6 as a single exponential decay and a constant offset (i.e., a second exponential decay with infinite time constant) with 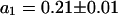, , 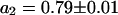and 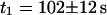and leads to a fluorescence loss of 15% during bleaching. The same confocal section after photobleaching, Fig. 4 D, again shows a homogenous fluorescence distribution with a globally reduced intensity. The average intensity at the bleach spot as well as within the box away from the cross has dropped by 10% about a minute after bleaching. This loss is smaller than directly after bleaching at the cross, i.e., the signal has recovered slightly. Finally, we recorded an FCS measurement of EGFP at the cross (Fig. 4 C) with a reduced illumination intensity to avoid photobleaching. The correlation function can be fitted in the framework of anomalous diffusion with Eq. 13, giving 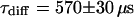and 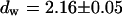. For the parameters of the nonfluorescent states, the values obtained for EGFP in solution from a previous study are applied: 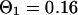, , 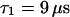, 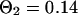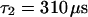(Wachsmuth et al., 2000).

FIGURE 4.

Confocal images, CP, and FCS curves taken from three HeLa cells expressing EGFP (A–D), H2B-EYFP (E–H), and mTTF-I-EGFP (I–L). (A) Confocal section of a cell expressing EGFP; at the marked position in the nucleus (cross) first a CP curve (B) and then a fluorescence autocorrelation (C) were recorded; thereafter, the confocal section was acquired again (D). (E) Confocal section of a cell expressing H2B-EYFP; at the marked position in the nucleus (cross) first a CP curve (F) and then a fluorescence autocorrelation (G) were recorded; thereafter, the confocal section was acquired again (H). (I) Confocal section of a cell expressing mTTF-I-EGFP; at the marked position in the large nucleolus (black cross) first a CP curve (J) and then a fluorescence autocorrelation (K) were recorded; thereafter, the confocal section was acquired again (L); finally, at the marked position between the nucleoli (white cross) a fluorescence autocorrelation (K) was recorded.

These observations agree with the following model, as sketched in Fig. 5 A: The EGFP molecules are inert and freely mobile and only experience steric obstructions by cellular structures. They are found in (at least) two spatially separated and slowly exchanging pools, a nuclear and a cytoplasmic fraction with virtually the same concentration. Although mainly the spot is bleached, the entire nuclear concentration decreases, leading to a flux of molecules into the nucleus slower than diffusion. After bleaching, the gradient to the cytoplasm is gradually equilibrated, leading to a slight recovery of the nuclear EGFP concentration.

FIGURE 5.

Schematic sketches of the models used for the interpretation of the results in cells containing inert molecules like EGFP (A), expressing stably incorporated proteins like histone H2B (B), and expressing transiently binding molecules like mTTF-I (C). For more details see Results.

HeLa cells expressing H2B-EYFP

The behavior of the histone H2B tagged with EYFP is very different from free EGFP. As an example, the confocal section of the nucleus of a HeLa cell expressing H2B-EYFP in Fig. 4 E shows an inhomogeneous fluorescence distribution that can be assigned to chromatin (Kanda et al., 1998). CP at a bright position (marked with a cross) leads to a fast decay for short times, turning into an exponential decay (Fig. 4 F). In the image recorded afterwards, Fig. 4 H, the bleach spot (marked with an arrow) remains dark for a long time, confirming that H2B-EYFP incorporated into chromatin exchanges only very slowly with the free pool. Therefore, a sum of Eqs. 5 and 9 is fitted to the CP curve with 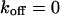. An immobilized fraction of 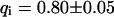and a bleaching rate 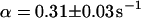are found. To check whether the remaining fluorescence actually belongs to freely mobile molecules, an FCS measurement was recorded at the same position after bleaching. Again, the autocorrelation function (Fig. 4 G), can be analyzed with Eq. 13 with 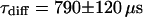, 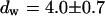(the nonfluorescent correlation times 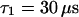, 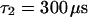are taken from FCS of nucleosomes in solution, T. Weidemann, N. Wachsmuth, T. A. Knoch, G. Müller, W. Waldeck, and J. Langowski, unpublished data), allowing to deduce that the motion of the remaining fluorescent molecules is governed by free but anomalous diffusion.

In this case, the following model can be established (Fig. 5 B): the density of binding sites (nucleosomes) is directly mapped by the concentration of bound (incorporated) molecules, superimposed by a virtually homogeneous mobile fraction. Spot bleaching decimates the bound fraction only locally but strongly and the mobile fraction globally but only weakly. After bleaching at one spot, the bound fraction can be calculated at each pixel, and in combination with FCS, the histone and nucleosome density are obtained (Weidemann et al., submitted for publication).

HeLa cells expressing mTTF-I-EGFP

As a third example, we have investigated the dynamics of the rRNA transcription termination factor mTTF-I tagged with EGFP. Fig. 4 I shows a confocal image of the nucleus of a HeLa cell expressing mTTF-I-EGFP, where the fluorescence is mainly found in the nucleoli. A CP curve obtained at the cross in Fig. 4 I in the largest nucleolus is shown in Fig. 4 J: again, the fast initial decrease turns into a slower decay. The same confocal section after photobleaching, Fig. 4 L, shows that in contrast to the histone, the fluorescence is reduced not only in the bleach spot but in all nucleoli. Assuming that the fluorescence belongs to both the bound and the free fraction in the nucleoli but only to the free fraction in the remainder of the nucleus, we have derived a bound fraction 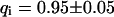directly from the image. Using this, the CP curve can be fitted with a sum of Eqs. 5 and 10, giving a bleaching rate 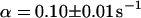as well as a dissociation rate 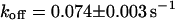or residence time 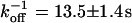at the binding site, respectively. The mean value from five cells amounts to . The autocorrelation function from an additional FCS measurement taken at the bleach spot can be interpreted as a fast component with 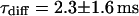and 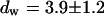and a slow one with 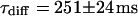and 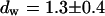. We assign freely yet anomalously diffusing molecules to the fast component, whereas the slow fluctuations probably result from DNA-bound mTTF-I molecules. The Brownian motion of the DNA is much slower than for the free mTTF-I and has a superdiffusive contribution due to its spatial confinement. The FCS data taken between the nucleoli at the marked position in Fig. 4 L show that there, the molecules are unbound and diffusive (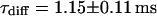, 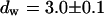; for the other parameters see Freely mobile EGFP molecules in HeLa cells).

The behavior of mTTF-I can be explained as follows, (Fig. 5 C): the bound molecules map the spatial distribution of binding sites and are superimposed by an approximately constant free fraction. This enables us to directly derive the immobilized fraction. The bound molecules are rapidly released from their binding sites and can move within and between nucleoli until they bind to another site. Thus, spot bleaching reduces both the bound and the free concentration proportionally.

DISCUSSION

The present study shows that a combination of CP, FCS, and CLSM, called fluorescence fluctuation microscopy (FFM), can be used for a quantitative characterization of molecular mobilities in living cells. The use of confocal optics provides a diffraction limited resolution. The high sensitivity of the setup allows the use of small illumination intensities and low concentrations of fluorescently labeled molecules. The imaging mode yields spatial distributions, whereas with continuous fluorescence photobleaching, mobility properties on a timescale of seconds (mainly due to transient binding-related immobilization or to flux through membranes) can be investigated. In contrast, fluctuation analysis yields diffusion properties on a millisecond timescale. We show that with an approximated analytical treatment of CP curves taking into account diffusion, transient immobilization, and flux between cellular compartments, binding properties like dissociation rates, residence times, or the ratio of bound and free molecules are easily accessible. This approach is successfully applied to numerically generated data as well as to qualitatively different examples: a freely diffusing, a stably incorporated, and a transiently immobilized protein.

Continuous fluorescence photobleaching benefits from a much simpler experimental setup compared to instantaneous photobleaching (FRAP, FLIP) although it is anticipated that a short deposition of light with high intensities causes less damage in cells than smaller but continuous dose rates (Pawley, 1995; Peters, 1981). However, dim illumination intensities are useful because they are compatible to FCS-adapted setups. Photobleaching is the chemical transition of a molecule into a nonfluorescent conformation upon illumination with excitation light. Proposed mechanisms are the irreversible oxidation and reduction when the molecules are in electronically excited singlet or triplet states (Pawley, 1995; Peters, 1981; Song et al., 1995), thus, the photobleaching yield is proportional to the excitation intensity, as assumed above. A deviation from this linearity can result from triplet quenching due to fluorophore-fluorophore interactions (Song et al., 1996; Song et al., 1997). However, the packaging of the GFP chromophore (Ormö et al., 1996; Yang et al., 1996) may avoid this, making GFP and its spectral relatives particularly suitable for CP. The bleaching rates in the experiments, of the order of 0.2 s⁻¹, agree well with the results from Harms and co-workers (Harms et al., 2001) for excitation intensities of the order of 1 kW cm⁻².

The derivation of the analytical CP curves includes some apparently rough approximations; therefore, we have calculated the time course of the concentrations and the fluorescence signal using the underlying differential equations and more appropriate expressions for the PSFs. Fitting the numerically calculated CP curves with Eqs. 6, 9, and 10 allows us to recover the initially employed parameters with a standard deviation of the order of 10%. This justifies use of the analytical expressions, which are more feasible for data fitting than numerical calculations. However, in some cases, it is necessary to determine one of the parameters independently, because the main effect of transient compared to permanent binding is an additional offset in the long time regime, mimicking a smaller immobilized fraction. Eqs. 9 and 10 are similar enough to give an estimate for the ratio 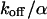independent from the range, and with this estimate the appropriate fit function for the respective range, Eq. 9 or 10, can be selected.

The relatively homogeneous fluorescence distribution in confocal images of EGFP expressing cells as well as FCS of EGFP in these cells indicates that these molecules can diffuse freely within the cell, except for obstructions by intracellular structures as already shown (Partikian et al., 1998; Swaminathan et al., 1997; Wachsmuth et al., 2000). The slow double-exponential decay of the CP data and the slight recovery of the concentration after bleaching can be assigned to limitations of free diffusion by membranes between cellular compartments. This is in a good qualitative agreement with previous studies (Peters, 1983, 1984) where the density and size of nuclear pores could be estimated.

The intensity pattern of fluorescently labeled H2B histones in cells observed in confocal images and their stable incorporation into chromatin as seen with CP reproduce the results from other studies (Kanda et al., 1998; Kimura and Cook, 2001; Lever et al., 2000; Misteli et al., 2000). FCS after bleaching indicates that the remaining fluorescence comes from freely diffusing molecules amounting to less than 20%.

In cells expressing mTTF-I-EGFP, this factor is mainly found in the nucleoli. Nevertheless, FCS shows that a small diffusive fraction is found everywhere in the nucleoplasm, which is accompanied by a larger nucleolar fraction probably bound to DNA and undergoing spatially confined diffusion. From CP, a residence time of ∼13 s for mTTF-I molecules at their binding sites upstream and downstream of rDNA genes is established. There, it plays a role in transcription termination, replication fork arrest and chromatin remodeling (Grummt, 1999). Whether the different functions (Grummt et al., 1986; Längst et al., 1997; Pütter and Grummt, 2002) result in different residence times is still beyond the resolution limit of this method but is the subject of a more detailed investigation.

Similar results have been obtained with particle tracking and FRAP experiments (Kues et al., 2001; Phair and Misteli, 2000). These and our own findings corroborate the proposed model of a dynamic nucleus where biologically active molecules roam or scan the nucleus and bind statistically to specific sites for a characteristic time until they are released again (Misteli, 2001). Some apparently static structures are very stable (like chromatin) but others (like the nucleolus) seem to be much more dynamically organized. CP assisted by CLSM and FCS is a suitable tool to quantify the stability of cellular structures, the mobility of biomolecules, and binding properties in living cells.