Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Aug;85(2):679–685. doi: 10.1016/S0006-3495(03)74511-1

Molecular Dynamics Decomposition of Temperature-Dependent Elastic Neutron Scattering by a Protein Solution

Jennifer A Hayward *, John L Finney †, Roy M Daniel ‡, Jeremy C Smith *
PMCID: PMC1303193  PMID: 12885619

Abstract

Molecular dynamics simulations are performed of bovine pancreatic trypsin inhibitor in a cryosolution over a range of temperatures from 80 to 300 K and the origins identified of elastic dynamic neutron scattering from the solution. The elastic scattering and mean-square displacement calculated from the molecular dynamics trajectories are in reasonable agreement with experiments on a larger protein in the same solvent. The solvent and protein contributions to the scattering from the simulation model are determined. At lower temperatures (<∼200 K) or on shorter timescales (∼10 ps) the scattering contributions are proportional to the isotopic nuclear scattering cross-sections of each component. However, for T > 200 K marked deviations from these cross-sections are seen due to differences in the dynamics of the components of the solution. Rapid activation of solvent diffusion leads to the variation with temperature of the total elastic intensity being determined largely by that of the solvent. At higher temperatures (>240 K) and longer times (∼100 ps) the protein makes the only significant contribution to the scattering, the solvent scattering having moved out of the accessible time-space window. Decomposition of the protein mean-square displacement shows that the observed dynamical transition in the solution at 200–220 K involves activation of both internal motions and external whole-molecule rotational and translational diffusion. The proportion that the external dynamics contributes to the protein mean-square displacement increases to ∼30 and 60% at 300 K on the 10- and 100-ps timescales, respectively.

INTRODUCTION

Neutron scattering is a major technique for the examination of picosecond dynamics in biological systems. However, due to the complexity of the motions present and the large number of disparate scattering nuclei, direct interpretation of experimental results with analytical models can be fraught with difficulty. Molecular dynamics (MD) simulation can be used to overcome this problem. The dynamic structure factor can be calculated from the simulation trajectories, compared with experiment, and used to decompose the contributions to the measured scattering (Smith, 1991, 2000; Kneller and Smith, 1994; Souaille et al., 1996; Morelon et al., 1998; Tarek and Tobias, 2000; Hayward and Smith, 2002).

In recent years neutron scattering and other techniques have been used extensively in research stimulated by the finding that the temperature-dependence of the average mean-square displacement of protein internal motion exhibits a change in gradient at temperatures ranging from ∼170–240 K (Knapp et al., 1982; Parak and Knapp, 1984; Doster et al., 1989; Smith, 1991, 2000; Smith et al., 1990; Rasmussen et al., 1992; Demmel et al., 1997; Fitter et al., 1997; Cordone et al., 1998; Ostermann et al., 2000). Below the transition temperature vibrational motions dominate. Above the transition temperature, the motions may involve continuous and/or jump diffusion and thus allow sampling of different conformational substates existing in different energy wells (Elber and Karplus, 1987; Karplus and Petsko, 1990; Frauenfelder et al., 1991; Kneller and Smith, 1994). It has also been observed that solvent, when present, has an important controlling effect on the dynamical transition (Ferrand et al., 1993; Demmel et al., 1997; Fitter, 1999; Fitter et al., 1997, 1998a,b; Cordone et al., 1998; Vitkup et al., 2000; Réat et al., 2000). Strong timescale dependence has also been found both theoretically (Hayward and Smith, 2002), and in elastic neutron scattering experiments of an enzyme, glutamate dehydrogenase (GDH) in CD3OD/D2O, 70:30, v/v cryosolvent (Daniel et al., 1998, 1999). Some studies have found a relationship between the onset of anharmonic motion and activity of proteins (Parak et al., 1980; Rasmussen et al., 1992; Ferrand et al., 1993; Ding et al., 1994; Ostermann et al., 2000).

Much of the dynamical transition research has involved the use of elastic neutron scattering to derive the average mean-square displacement of the system. In a previous article, MD simulations of an isolated protein, bovine pancreatic trypsin inhibitor (BPTI), were performed as a function of temperature and the simulation data were used to evaluate approximations used in deriving mean-square displacements from experiment (Hayward and Smith, 2002). Here we extend the MD analysis to BPTI in solution. The solvent chosen is CD3OD/D2O, 70:30, v/v, the same as was used in the experiments reported in Daniel et al. (1998, 1999) and Réat et al. (2000). The primary aim of this work is to decompose the contributions to the temperature-dependent elastic scattering.

An important question concerns under what conditions the isotopic coherent and incoherent cross-sections of the sample can be used as a guide to determine the proportions of scattering from each component. Isotopic cross-sections, which are commonly used to estimate the proportions of scattering from the components of a sample, are determined by nuclear properties that are independent of the nuclear dynamics. Formally, they give the cross-section for energy-integrated scattering. They also give an approximate estimate of the relative scattering intensities for components of a system in which the dynamics of the components are similar. However, in cases where the dynamics are significantly different, deviation from this approximation is expected.

Following the previous study of elastic neutron scattering (Hayward and Smith, 2002), here mean-square displacements suitable for comparison with experiment are derived by taking the atomic trajectories, calculating the dynamic structure factor, and subjecting this to the same data treatment process as was used experimentally. A comparison with experiment is made, and the components of the elastic scattering are examined. The scattering is decomposed into solvent and protein contributions, and the protein is further decomposed into external (whole-molecule rotation and translation) diffusion and internal dynamics. The simulation analysis permits the identification of dynamical signals responsible for elastic neutron scattering intensities from a small protein in solution as the timescale and temperature probed vary.

METHODS

Molecular dynamics simulations

The model system consists of one BPTI molecule in CD3OD/D2O, 70:30, v/v in an orthorhombic box of size 41.0 × 37.5 × 46.5 Å3 (on average at 300 K) with periodic boundary conditions. BPTI has 892 atoms and four internal water molecules. There are 658 CD3OD and 661 D2O molecules in the solvent, providing at least three solvent shells around the protein. This is adequate for simulating a protein in a bulk solvent environment.

As in typical neutron scattering experiments, the exchangeable BPTI hydrogen atoms were replaced by deuterium, leaving 324 hydrogen atoms. This system models a solution of a protein in CD3OD/D2O, 70:30 v/v cryosolvent, as has been used in several neutron experiments (Daniel et al., 1998, 1999; Réat et al., 2000). However, the protein used in the above experiments is GDH. The reason for choosing BPTI for the simulations and not GDH is that due to computational limitations, only a small protein could be simulated for a time long enough to cover the experimental timescale and at the required temperatures. Therefore, the assumption is made that the difference between the scattering from GDH and BPTI in the same solvent can be neglected. That this is reasonable is suggested from comparisons of the scattering of different proteins in the same CD3OD/D2O, 70:30 v/v solution, which was the same to within experimental error (Daniel et al., 1998, 1999; Réat et al., 2000). Moreover, the focus of the present work is on decomposing contributions to elastic scattering, a quantity that depends largely on the average mean-square displacement and is relatively insensitive to dynamical details.

The system was simulated using CHARMM (Brooks et al., 1983) version 27 with all-atom parameter set 22 for the protein and methanol (Mackerell et al., 1998). All water molecules were represented by the TIP3P potential (Jorgensen et al., 1983). The simulations were performed in the NPT ensemble. A timestep of 0.001 ps was used with SHAKE (Ryckaert et al., 1977) applied to constrain bonds containing hydrogen or deuterium atoms. Nonbonded and electrostatic interactions were truncated using a shifting function (Steinbach and Brooks, 1994) at 13.0 Å. The pressure of the system was set to be 1 atm.

Simulations were performed at 18 different temperatures: 80 K, 100 K, 120 K, 140 K, and 160 K, then in steps of 10–280 K, and finally 300 K. The starting structure for the first temperature simulated, 80 K, was the energy-minimized BPTI crystal structure (Parkin et al., 1996), Protein Data Bank reference (1BPI) (Berman et al., 2000), equilibrated for 500 ps in a fully equilibrated box of solvent. The starting structures for the rest of the simulations at increasing temperatures were the final structures from the preceding temperature. The systems at each temperature were equilibrated for 150 ps and then data collected every 0.1 ps for 520 ps; i.e., a total simulation time of 670 ps per temperature. The total simulation time was 12.060 ns requiring 597 CPU h running in parallel on 64 processors on an IBM SP2 computer; i.e., 38,208 CPU h. After the final simulation at 300 K the RMS deviation of the backbone heavy atoms from the energy-minimized crystal structure was 1.3 Å and that calculated using only the secondary structural elements was 1.0 Å. Therefore the protein structure remained stable.

Neutron scattering properties

We used the nMOLDYN program (Kneller et al., 1995) to calculate neutron scattering properties from the atomic trajectories.

Dynamic structure factor

The quantity 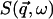Inline graphic is the dynamic structure factor, where 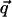Inline graphic is the scattering vector and 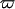Inline graphic is the energy transfer. Here, the self-correlation part of 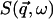Inline graphic is calculated, using

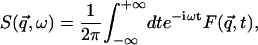graphic file with name M5.gif (1)
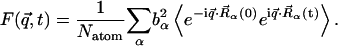graphic file with name M6.gif (2)

Equation 1 shows that the dynamic structure factor is a time Fourier transform of the intermediate scattering function, 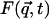Inline graphic. α labels individual atoms whose positions are specified by their time-dependent position vector operators 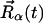Inline graphic. Each atom has a coherent scattering length bα,coh and an incoherent scattering length bα,inc that define the strength of the interaction between the nucleus of the atom and the neutron. These quantities depend only on the isotope involved and when squared are proportional to the corresponding scattering cross-section. The total scattering cross-section 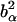Inline graphic is the sum of the incoherent and coherent contributions i.e., 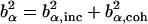Inline graphic, and the sums in Eqs. 1 and 2 run over all atoms (protein + solvent) in the simulated system. In the present calculations the coherent scattering is approximated by the self-coherent (autocorrelation) term, and cross-correlations are neglected—this approximation should be reasonable for the q- and ω-ranges examined here.

The intermediate scattering function is a quantum-mechanical time-correlation function that is replaced by a classical time-correlation function if it is calculated from MD simulations. The detailed balance condition,

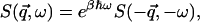graphic file with name M11.gif (3)

does not hold in the classical limit 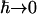Inline graphic. To take account of this we assume the semiclassical correction (Lovesey, 1984), given here for isotropic systems, such as the system under consideration, is

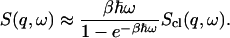graphic file with name M13.gif (4)

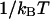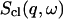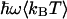The shorthand β stands for Inline graphic and Inline graphic is the classical dynamic structure factor. The semiclassical correction, Eq. 4, is an approximation valid only in the linear response regime Inline graphic.

To mimic experimental conditions in the present work, 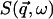Inline graphic, computed using Eqs. 1–3, was convoluted with the Gaussian-shaped instrumental energy resolution function of the instrument IN6 at the Institut Laue-Langevin, Grenoble, France, with a full-width at half-maximum (FWHM) of 100 μeV.

The concentration of BPTI in the simulation is 156 mg/ml, whereas in the experiments we compare with, i.e., Daniel et al. (1998, 1999), and Réat et al. (2000), the protein concentration was ∼100 mg/ml. Therefore, in what follows, when comparison is made with experiment (Fig. 1), the simulation scattering intensities of the solvent and protein are scaled to mimic the experimental concentration. The scaling was performed as follows:

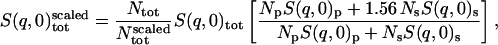graphic file with name M18.gif (5)

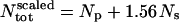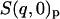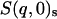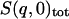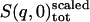where Np and Ns are the number of protein and solvent atoms, respectively, Ntot = Np + Ns and Inline graphic; i.e., the total number of atoms in the system after scaling, Inline graphic, Inline graphic, Inline graphic, and Inline graphicare the single-atom elastic intensities of the protein, solvent, total system, and total system after scaling, respectively.

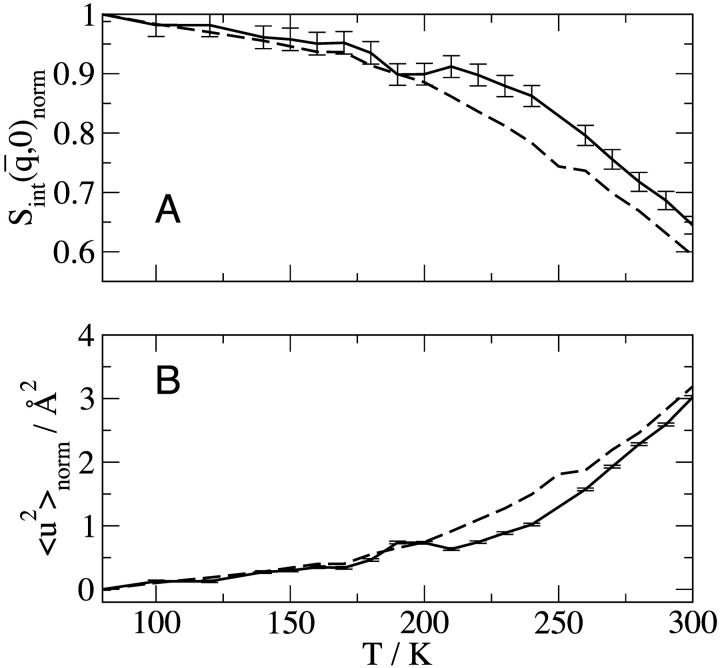
FIGURE 1.

FIGURE 1

Open in a new tab

Temperature-dependence of elastic scattering and mean-square displacement: (——) neutron scattering experiments on the time-of-flight instrument IN6 at the Institut Laue-Langevin, Grenoble, France, for GDH in CD3OD/D2O 70:30 v/v and (- - -) BPTI in CD3OD/D2O, 70:30 v/v calculated from the MD simulations using the IN6 energy resolution function. (A) Normalized integrated elastic intensity with an integrated q-range of: 0.35 < q < 1.03 Å−1 and 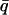Inline graphic = 0.66 Å−1 for GDH; and 0.35 < q < 1.05 Å−1 and 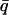Inline graphic = 0.70 Å−1 for BPTI. Results are normalized to one at 80 K. (B) Mean-square displacement, normalized to 0 Å2 at 80 K.

GDH is a functional hexamer. This association will influence its whole-molecule rotational and diffusional properties, which would be expected to be significantly slower than BPTI. This difference should be kept in mind when comparing simulation with experiment in the present study.

Elastic scattering analysis

In this work we perform an analysis and decomposition of the elastic scattering 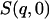Inline graphic.

This quantity is of central importance in analysis of dynamical transition behavior in protein systems. To obtain the elastic scattering 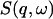Inline graphic was calculated as described in Dynamic Structure Factor, and integrated over the instrumental FWHM energy resolution.

To obtain the mean-square displacement of the system from 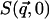Inline graphic, the Gaussian approximation was made. This makes use of the following cumulant expansion (Rahman et al., 1962):

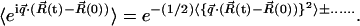graphic file with name M27.gif (6)

Neglecting terms in the exponent of Eq. 6 of order higher than q2, the intermediate scattering function can be written, with the exponent averaged over all directions of 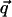Inline graphic, as

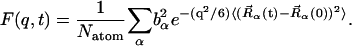graphic file with name M29.gif (7)

The elastic scattering is determined by the t → ∞ limit of 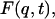Inline graphic i.e., from Eq. 7:

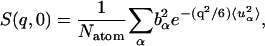graphic file with name M31.gif (8)

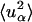where Inline graphic is the t → ∞ mean-square displacement of atom α. The range of applicability of the Gaussian approximation for single atoms in a protein has been examined (Hayward and Smith, 2002). It was found to be valid at values of q < 1. 2 Å−1.

Equation 8 involves a sum of Gaussians. Therefore, even when the Gaussian approximation is valid for individual atoms at low q, because of the fact that a sum of Gaussians is itself not Gaussian, 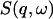Inline graphic will not have a Gaussian form. There will, therefore, be a non-Gaussian contribution to the measured scattering due to motional heterogeneity, i.e., due to the fact that a distribution of mean-square displacements exists in the protein. Neglect of this non-Gaussian contribution corresponds to the following approximation,

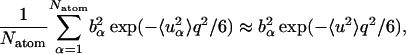graphic file with name M34.gif (9)

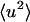where Inline graphic is the mean-square displacement averaged over the atoms in the protein. The approximation in Eq. 9 is valid for q → 0. It has been estimated from MD simulation that for a protein motional heterogeneity reduces the value of the average 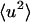Inline graphic calculated using the above approaches by ∼30% (Hayward and Smith, 2002). However, in the present simulation-experiment comparison this error cancels out as we compare experimental results and computer simulation results for which the approximations made in analyzing the data are the same.

A standard way of obtaining 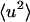Inline graphic from experiment is to take the limiting q → 0 slope of 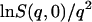Inline graphic vs. q2. This was performed, for example, in Daniel et al. (1998, 1999) and Réat et al. (2000). Although this procedure was found to be useful in identifying dynamical transition points, the required gradient suffered from statistical inaccuracy at low temperatures, leading to poor representation of the linear, harmonic part of 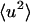Inline graphic vs. T that runs below the dynamical transition. To overcome this problem the “integrated elastic intensity,” 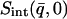Inline graphic, introduced in Réat et al. (2000), can be used. To obtain 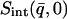Inline graphic (where 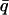Inline graphic stands for the mean of the integration range) 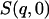Inline graphic is integrated over a range of low q-values. 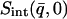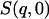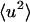Here, Inline graphic was calculated from both the experimental and from the model system Inline graphic and Inline graphic was determined from both the experimental and theoretical 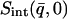Inline graphic, using Eqs. 8 and 9 to derive

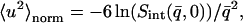graphic file with name M48.gif (10)

where 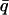Inline graphic is the mean value from the q range used to calculate 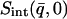Inline graphic and all values are normalized to those at 80 K.

Timescale dependence

We also examine here the timescale dependence of the scattering. This is of particular interest because it was demonstrated, using elastic neutron scattering from instruments of different energy resolutions, that dynamical transition behavior of two enzyme/cryosolvent solutions is strongly time-dependent (Daniel et al., 1999). The time-dependent mean-square displacements, 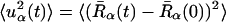Inline graphic, were calculated from the molecular dynamics configurations as follows,

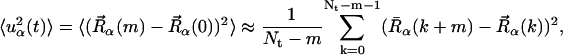graphic file with name M52.gif (11)

where the steps in the trajectory are denoted by k = 0, … , Nt − 1, and Nt is the total number of timesteps. To derive the appropriate neutron-derived quantity the mean-square displacements are weighted by the scattering cross-sections,

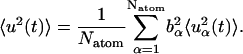graphic file with name M53.gif (12)

External and internal dynamics

The protein trajectory was decomposed into external (whole-molecule diffusion) and internal components. The internal motions were extracted by superimposing every frame from the atomic trajectory with an RMS coordinate fit onto the first frame. The result is a new atomic trajectory of internal motions. The translational mean-square displacement was calculated by creating a new trajectory of the center-of-mass of the protein. The center-of-mass was weighted by the scattering cross-sections. The mean-square displacement for the internal protein motion was subtracted from that of the total protein dynamics. The rotational and translational components of the protein motion were separated by subtraction of the translational mean-square displacement from the external mean-square displacement.

RESULTS

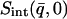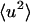Inline graphic and Inline graphic are shown in Fig. 1 from experiments on GDH in CD3OD/D2O, 70:30 v/v and from the model system of BPTI in the same cryosolvent. As described in Methods, for the purposes of comparison the simulation-derived dynamic structure factor has been calculated at the experimental protein concentration and processed in exactly the same way as the experimental quantity. Experiment and simulation are in close agreement up to temperatures of ∼200 K. The small peak in the experimental 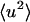Inline graphic at ∼190 K is of unknown origin—it may be due to contamination by diffraction at this temperature. Above ∼220 K deviation from linearity, i.e., dynamical transition behavior, is seen.

This occurs somewhat lower in temperature and more gradually in the simulation than in the experiment. The differences between experiment and simulation at these temperatures are small but significant and may be due to errors in the simulation (e.g., force field, sampling) or in the experiment (e.g., contamination from small-angle or multiple scattering) as well as differences expected between GDH and BPTI (for example, in the whole-molecule diffusional properties). At 300 K the simulation-derived and experimental 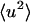Inline graphic agree closely.

We now undertake a decomposition of the dynamical contributions to the scattering from the simulation model. The scattering cross-sections for the protein, solvent, and total system are shown for the simulation model in Table 1. Based on these values, ∼60% of the total scattering originates from the solvent.

TABLE 1.

Incoherent, coherent, and combined scattering cross-sections for the solvent and protein

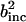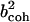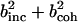Inline graphic Inline graphic Inline graphic
Total 2.7 2.8 5.5
Protein 2.1 0.32 2.4
Solvent 0.64 2.5 3.1
Open in a new tab

All units are 1 × 10−5 Å2.

The relationship between the dynamic structure factor and the isotopic cross-section is characterized by the zeroth-order sum rule

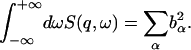graphic file with name M58.gif (13)

Thus the energy-integrated scattering is given by the scattering cross-sections. However, the proportions of scattering in any given subspace of (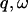Inline graphic) also depend on the microscopic dynamics of the components. To estimate this effect, the relative contributions of solvent and protein to the elastic scattering intensity were calculated. This was performed using the Gaussian approximation in the limit q → 0 with Eq. 8. Equation 8 requires the input of 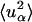Inline graphic, calculated here using Eq. 11 with t = 10 ps or 200 ps. Thus, the scattering contributions on two different timescales are evaluated. The 10-ps timescale approximates an instrumental energy resolution of 100 μeV (FWHM) whereas the 200-ps timescale approximates 5 μeV.

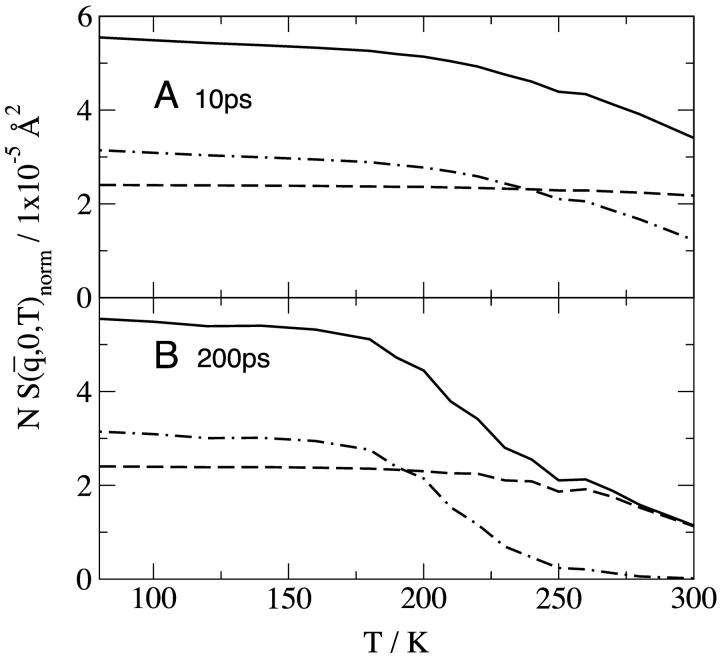
The results for 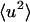Inline graphic calculated at 10 ps are shown in Fig. 2 A. At each temperature, the sum of the protein and solvent contributions gives the intensity for the whole system. At 80 K the proportions of the scattering are given by the ratio of the isotopic cross-sections in Table 1. This remains true up to ∼180 K and reflects the fact that at low temperatures the solvent and protein both vibrate approximately harmonically with roughly similar dynamics. Above 180 K one observes the interesting effect that the variation of the solvent intensity with temperature is much stronger than that of the protein, the consequence of which is that that of the solvent largely determines the change with temperature of the scattering from the solution.

FIGURE 2.

FIGURE 2

Open in a new tab

Normalized elastic intensity calculated using the Gaussian approximation with atomic mean-square displacements at 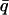Inline graphic = 0.7 Å−1 and as a function of temperature for timescales of (A) 10 ps and (B) 200 ps for (——), whole system; (- - -), protein; and (-.-.-), solvent. The product, NSinc (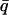Inline graphic = 0.7 Å−1, 0), was determined at each temperature for the whole system, protein, and solvent, where N is the number of atoms in the whole system, protein, or solvent, depending on the component under investigation. The trajectories used to calculate Sinc (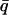Inline graphic = 0.7 Å−1, 0) were normalized such that the atomic 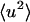Inline graphic are equal to zero at 80 K. The normalization was made so that, for each profile at 80 K, the appropriate scattering cross-section, Inline graphic, shown in Table 1, is recovered.

The long-time results (200 ps) are shown in Fig. 2 B. Once again, the shape of the profile for the whole system is largely determined by that of the solvent. The relative contributions for T < 180 K are similar to those of Fig. 2 A and are again given by the proportions of the isotopic cross-sections. At higher temperatures diffusive motion in the solvent is quickly activated, such that at T > 270 K the solvent scattering is outside the 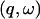Inline graphic window examined, and the solvent intensity is zero. Diffusive motion of the protein is also activated but is more confined, remaining within the accessible 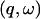Inline graphic window at high temperatures. Thus, at T > 270 K only the protein motion is seen.

To decompose the various contributions to the protein 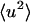Inline graphic, the internal and external (whole-molecule diffusive) dynamics were determined, the latter being further subdivided into rotational and translational components. The protein 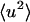Inline graphic were calculated directly from the atomic trajectories, on timescales of 10 and 100 ps.

The results at 10 and 100 ps are shown in Fig. 3. On both timescales, at T < 200 K the internal motions make the only significant contribution to the protein 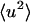Inline graphic. Deviation in linearity is seen in the internal dynamics in Fig. 3 B at a relatively low temperature (∼150 K), a phenomenon that was also seen in simulations of isolated BPTI (Hayward and Smith, 2002). There is a further change in slope of the total protein 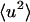Inline graphic at ∼200–220 K on both timescales which involves a change in the internal 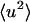Inline graphic together with activation of the external motions. At 10 ps and above ∼200 K the global diffusive and internal 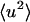Inline graphic increase with temperature at similar rates, and the external motion contributes ∼30% of 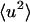Inline graphic for T > 280 K. However, at 100 ps and above ∼200 K the external 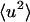Inline graphic increases at a much faster rate than the internal 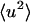Inline graphic. Both 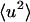Inline graphic are equal in value at ∼260 K. At 300 K the external motions contribute ∼60% to the overall displacement. Rotational and translational motions contribute about equally on both timescales. Self-diffusion coefficients were estimated from the slope of the mean-square displacement curves over 40–120 ps according to the Einstein relation 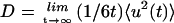Inline graphic. The 300 K rotational and translational diffusion coefficients are ∼3–4 × 10−7 cm2 s−1 and are in the range of experimental values for small proteins in solution.

FIGURE 3.

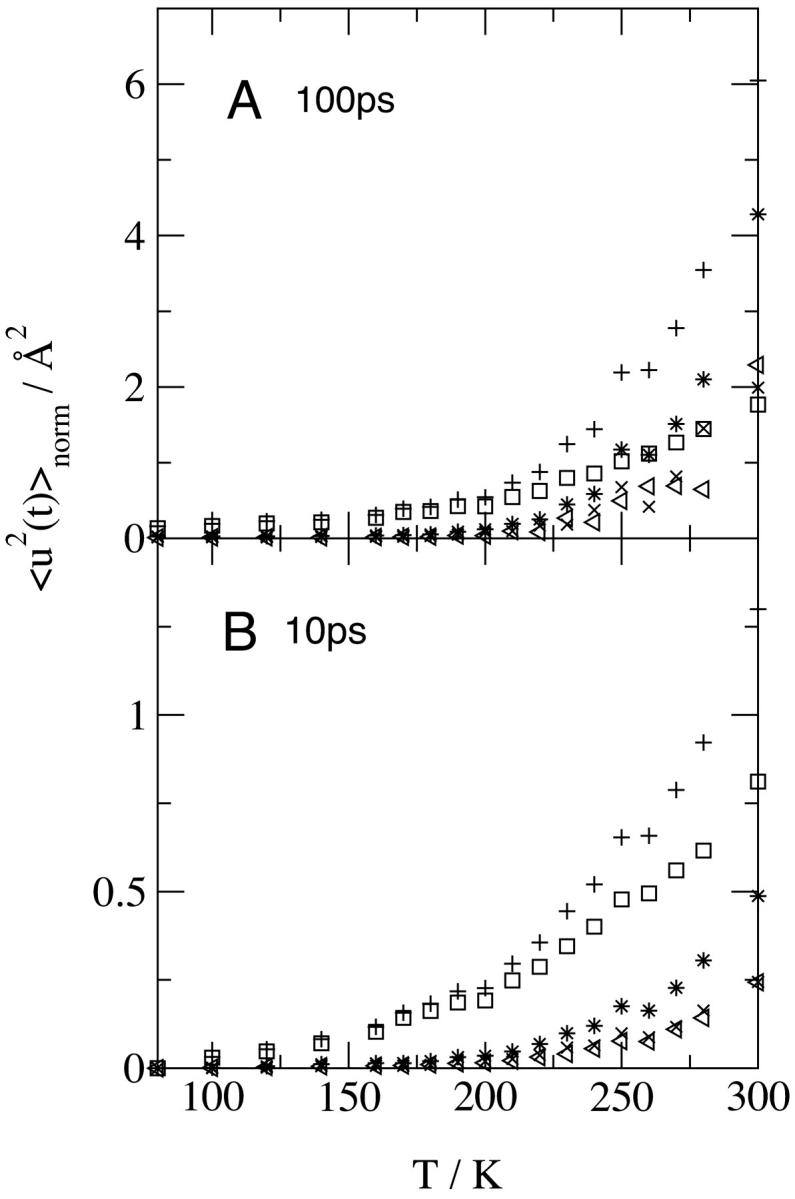
FIGURE 3

Open in a new tab

Temperature-dependence of the mean-square displacement for various components of the protein dynamics calculated directly from the atomic trajectories at a timescale of (A) 100 ps and (B) 10 ps using Eqs. 11 and 12 as described in Timescale Dependence: (+), all of the protein motions; (□), the internal motions; (*), the external motions; (×), the rotational external motion; and (◃), the translational external motion. Results are normalized to 0 Å2 at 80 K.

CONCLUSIONS

This work demonstrates the usefulness of MD simulation in understanding dynamical contributions to neutron scattering from condensed-phase biological systems. When comparing experimental with simulation-derived elastic scattering intensities it must be realized that both contain errors. For example, the simulation will contain force field and sampling errors whereas the experiment may contain inaccuracies originating from counting statistics, multiple scattering, and small-angle scattering. Moreover, the fact that in the present case the simulation and experiment were performed on different proteins may also affect the scattering, particularly as concerns the rotational and translation diffusive component. In a previous article it was shown that both the use of the Gaussian approximation and the existence of a distribution of mean-square displacements lead to quantified errors in the mean-square displacement derived from an experiment on a protein (Hayward and Smith, 2002). However, in the present comparison in Fig. 1, as the same method was used to derive the mean-square displacements from the simulation as from experiment these two sources of error will largely cancel. Nevertheless, given the various remaining potential sources of experimental and simulation error, the temperature-dependence of the experimental and simulation-derived mean-square displacement and integrated elastic intensity in Fig. 1 are in reasonable agreement.

The MD simulations here are decomposed so as to identify the dynamical components of the scattering from the simulation model. At lower temperatures (<∼200 K) or on shorter timescales (∼10 ps) the scattering contributions are given by the isotopic scattering cross-sections. This is probably due to the fact that diffusive motion is absent and the whole system vibrates approximately harmonically. In this case the mean-square displacements of the protein and solvent, and thus the elastic scattering, will be approximately the same. However, for T > 200 K, marked deviations are seen due to differences in the dynamics of the components of the solution. Above 200 K, three classes of dynamics are activated: diffusive solvent motion, external protein diffusion (rotational and translational), and internal protein anharmonic motions. The solvent diffusion rapidly increases with temperature, such that the reduction with temperature of the total elastic intensity is largely dominated by the reduction in solvent self-coherent scattering. The solvent diffusion is such that at higher temperatures (>240 K) and longer times (∼100 ps) the protein makes the only significant contribution to the scattering. This result provides some theoretical support for the recent intriguing report that protein dynamics can be measured using neutron scattering even in H2O solution if an instrument of appropriate energy resolution is used (Tehei et al., 2001).

Decomposition of the protein mean-square displacement shows that internal motion dominates below the dynamical transition at ∼200 K, whereas above it, both anharmonic internal dynamics and external rotational whole-molecule diffusion are activated at ∼180–210 K. The finding that external motion contributes a significant proportion of the picosecond scattering of a protein solution even with deuterated solvent is in harmony with the results of Pérez et al. (1999) in which a careful decomposition of the external and internal contributions to scattering from lysozyme in aqueous solution was performed and was checked with classical measurements of diffusion constants. In the present work it is found that the proportion that the external dynamics contributes to the mean-square displacement depends on the timescale observed, with a correspondingly higher external contribution on longer timescales. This contribution will clearly also be modified by the size of the protein treated, with BPTI, which is relatively small, diffusing relatively quickly. However, a useful experimental strategy for the future would be the development of techniques to reduce the contribution of protein external diffusion (e.g., by tethering on a solid support) such that the “time-space” window in which internal protein motions dominate observed scattering can be fully utilized to observe internal, possibly functional, protein fluctuations.

Acknowledgments

We acknowledge the High-Performance Computing Center in Karlsruhe for time on their IBM RS/6000 SP-256. We thank Valerie Réat and Erika Balog for assistance with the experimental data and Torsten Becker and Alex Tournier for useful discussions.

References

  1. Berman, H. M., J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov, and P. E. Bourne. 2000. The protein data bank. Nucl. Acids Res. 28:235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM. J. Comp. Chem. 4:187–217. [Google Scholar]
  3. Cordone, L., P. Galajda, E. Vitrano, A. Gassmann, A. Ostermann, and F. Parak. 1998. A reduction of protein specific motions in co-ligated myoglobin embedded in a trehalose glass. Eur. Biophys. J. 27:173–176. [DOI] [PubMed] [Google Scholar]
  4. Daniel, R. M., J. C. Smith, M. Ferrand, S. Héry, R. Dunn, and J. L. Finney. 1998. Enzyme activity below the dynamical transition at 220K. Biophys. J. 75:2504–2507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Daniel, R. M., J. L. Finney, V. Réat, R. Dunn, M. Ferrand, and J. C. Smith. 1999. Enzyme dynamics and activity: time-scale dependence of dynamical transitions in glutamate dehydrogenase solution. Biophys. J. 77:2184–2190. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Demmel, F., W. Doster, W. Petry, and A. Schulte. 1997. Vibrational frequency shifts as a probe of hydrogen bonds: thermal expansion and glass transition of myoglobin in mixed solvents. Eur. Biophys. J. 26:327–335. [DOI] [PubMed] [Google Scholar]
  7. Ding, X., B. Rasmussen, G. A. Petesko, and D. Ringe. 1994. Direct structural observation of an acyl-enzyme intermediate in the hydrolysis of an ester substrate by elastase. Biochemistry. 33:9285–9293. [PubMed] [Google Scholar]
  8. Doster, W., S. Cusack, and W. Petry. 1989. Dynamical transition of myoglobin revealed by inelastic neutron scattering. Nature. 337:754–756. [DOI] [PubMed] [Google Scholar]
  9. Elber, R., and M. Karplus. 1987. Multiple conformation states of proteins: a molecular dynamics analysis of myoglobin. Science. 235:318–321. [DOI] [PubMed] [Google Scholar]
  10. Ferrand, M., A. J. Dianoux, W. Petry, and G. Zaccai. 1993. Thermal motions and function of bacteriorhodopsin in purple membranes: effects of temperature and hydration studied by neutron scattering. Proc. Natl. Acad. Sci. USA. 90:9668–9672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fitter, J., R. E. Lechner, and N. A. Dencher. 1997. Picosecond molecular motions in bacteriorhodopsin from neutron scattering. Biophys. J. 73:2126–2137. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fitter, J., O. P. Ernst, T. Hauß, R. E. Lechner, K. P. Hoffmann, and N. A. Dencher. 1998a. Molecular motions and hydration of purple membranes and disk membranes studied by neutron scattering. Eur. Biophys. J. 27:638–645. [DOI] [PubMed] [Google Scholar]
  13. Fitter, J., S. A. W. Verclas, R. E. Lechner, H. Seelert, and N. A. Dencher. 1998b. Function and picosecond dynamics of bacteriorhodopsin in purple membrane at different lipidation and hydration. FEBS Lett. 433:321–325. [DOI] [PubMed] [Google Scholar]
  14. Fitter, J. 1999. The temperature dependence of internal molecular motions in hydrated and dry α-amylase: the role of hydration water in the dynamical transition of proteins. Biophys. J. 76:1034–1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Frauenfelder, H., S. G. Sligar, and P. G. Wolynes. 1991. The energy landscapes and motions of proteins. Science. 254:1598–1603. [DOI] [PubMed] [Google Scholar]
  16. Hayward, J. A., and J. C. Smith. 2002. Temperature dependence of protein dynamics: computer simulation analysis of neutron scattering properties. Biophys. J. 82:1216–1225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
  18. Karplus, M., and G. A. Petsko. 1990. Molecular dynamics simulations in biology. Nature. 347:631–639. [DOI] [PubMed] [Google Scholar]
  19. Knapp, E. W., S. F. Fischer, and F. Parak. 1982. Protein dynamics from Mössbauer. J. Phys. Chem. 86:5042–5047. [Google Scholar]
  20. Kneller, G. R., and J. C. Smith. 1994. Liquid-like side-chain dynamics in myoglobin. J. Mol. Biol. 242:181–185. [DOI] [PubMed] [Google Scholar]
  21. Kneller, G. R., V. Keiner, M. Kneller, and M. Schiller. 1995. nMOLDYN: a program package for a neutron scattering oriented analysis of molecular dynamics simulations. Comp. Phys. Comm. 91:191–214. [DOI] [PubMed] [Google Scholar]
  22. Lovesey, S. W. 1984. Theory of Neutron Scattering from Condensed Matter. Clarendon Press, Oxford.
  23. Mackerell, A. D., D. Bashford, M. Bellot, J. R. Dunbrack, R. L. Evenseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, I. W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, J. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
  24. Morelon, N.-D., G. Kneller, M. Ferrand, A. Grand, J. C. Smith, and M. Bee. 1998. Dynamics of an alkane chain included in an organic matrix. J. Chem. Phys. 109:2883–2904. [Google Scholar]
  25. Ostermann, A., R. Waschipky, F. G. Parak, and G. U. Nienhaus. 2000. Ligand binding and conformational motions in myoglobin. Nature. 404:205–208. [DOI] [PubMed] [Google Scholar]
  26. Parak, F., and E. W. Knapp. 1984. A consistent picture of protein dynamics. Proc. Natl. Acad. Sci. USA. 81:7088–7092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Parak, F., E. N. Frolov, A. A. Kononenko, R. L. Mössbauer, V. I. Goldanskii, and A. B. Rubin. 1980. Evidence for a correlation between the photoinduced electron transfer and dynamic properties of the chromatophore membranes from Rhodospirillum rubrum. FEBS Lett. 117:368–372. [DOI] [PubMed] [Google Scholar]
  28. Parkin, S., B. Rupp, and H. Hope. 1996. Structure of bovine pancreatic trypsin inhibitor at 125K definition of carboxyl-terminal residues Gly-57 and Ala-58. Crystallogr. D. Biol. Crystallogr. 52:18–29. [DOI] [PubMed] [Google Scholar]
  29. Pérez, J., J.-M. Zanotti, and D. Durand. 1999. Evolution of the internal dynamics of two globular proteins from dry powder to solution. Biophys. J. 77:454–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Rahman, A., K. S. Singwi, and A. Sjölander. 1962. Theory of slow neutron scattering by liquids. I. Phys. Rev. 126:986–996. [Google Scholar]
  31. Rasmussen, B. F., A. M. Stock, D. Ringe, and G. A. Petsko. 1992. Crystalline ribonuclease A loses function below the dynamical transition at 220K. Nature. 357:423–424. [DOI] [PubMed] [Google Scholar]
  32. Réat, V., R. Dunn, M. Ferrand, J. L. Finney, R. M. Daniel, and J. C. Smith. 2000. Solvent dependence of dynamic transitions in protein solutions. Proc. Natl. Acad. Sci. USA. 97:9961–9966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes (SHAKE). J. Comp. Phys. 23:327–341. [Google Scholar]
  34. Smith, J. C., K. Kuczera, and M. Karplus. 1990. Temperature-dependence of myoglobin dynamics: neutron spectra calculated from molecular dynamics simulations of myoglobin. Proc. Natl. Acad. Sci. USA. 87:1601–1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Smith, J. C. 1991. Protein dynamics: comparison of simulations with inelastic neutron scattering experiments. Q. Rev. Biophys. 24:227–291. [DOI] [PubMed] [Google Scholar]
  36. Smith, J. C. 2000. Inelastic and quasielastic neutron scattering: complementarity with biomolecular simulation. In Structure and Dynamics of Biomolecules: Neutron Synchroton Radiation for Condensed Matter Studies. Oxford University Press, Oxford. pp.161–180.
  37. Souaille, M., F. Guillaume, and J. C. Smith. 1996. Dynamics of an alkane in a urea host. J. Chem. Phys. 105:1529–1546. [Google Scholar]
  38. Steinbach, P. J., and B. R. Brooks. 1994. New spherical-cutoff methods for long-range forces in macromolecular simulation. J. Comp. Chem. 15:667–683. [Google Scholar]
  39. Tarek, M., and D. J. Tobias. 2000. Enzyme dynamics and activity: time-scale dependence of dynamical transitions in glutamate dehydrogenase solution. Biophys. J. 79:3244–3257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Tehei, M., D. Madern, C. Pfister, and G. Zaccai. 2001. Fast dynamics of malate dehydrogenase and bovine serum albumin measured by neutron scattering under various solvent conditions influencing protein stability. Proc. Natl. Acad. Sci. USA. 98:14356–14361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Vitkup, D., D. Ringe, G. A. Petsko, and M. Karplus. 2000. Solvent mobility and the protein glass transition. Nat. Struct. Biol. 7:34–38. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES