Kinetics of the Micelle-to-Vesicle Transition: Aqueous Lecithin-Bile Salt Mixtures

Abstract

Important routes to lipid vesicles (liposomes) are detergent removal techniques, such as dialysis or dilution. Although they are widely applied, there has been only limited understanding about the structural evolution during the formation of vesicles and the parameters that determine their properties. We use time-resolved static and dynamic light scattering to study vesicle formation in aqueous lecithin-bile salt mixtures. The kinetic rates and vesicle sizes are found to strongly depend on total amphiphile concentration and, even more pronounced, on ionic strength. The observed trends contradict equilibrium calculations, but are in agreement with a kinetic model that we present. This model identifies the key kinetic steps during vesicle formation: rapid formation of disklike intermediate micelles, growth of these metastable micelles, and their closure to form vesicles once line tension dominates bending energy. A comparison of the rates of growth and closure provides a kinetic criterion for the critical size at which disks close and thus for the vesicle size. The model suggests that liposomes are nonequilibrium, kinetically trapped structures of very long lifetime. Their properties are hence controlled by kinetics rather than thermodynamics.

INTRODUCTION

Vesicles, in particular lipid vesicles (liposomes), have an impact on a variety of areas, which range from fundamental science to biotechnology. Vesicles serve as models for cell membranes and allow the study of the basic mechanisms of membrane function, such as fusion (Lichtenberg, 1995; Lasic and Barenholz, 1996). Furthermore, liposomes of controllable size are used as biocompatible and protective structures to encapsulate labile molecules, such as proteins, nucleic acids or drugs, for pharmaceutical, cosmetic or chemical applications; they are also vital to the study of membrane proteins, including determining their structure via two-dimensional crystallization (Lasic, 1993; Lasch, 1995; Lasic, 1997; Rosoff, 1996; Ollivon et al., 2000).

Different methods are used to prepare lipid vesicles using detergent removal techniques: dilution, dialysis, gel exclusion chromatography, adsorption onto polymeric materials, temperature changes, or biochemical reactions (Ollivon et al., 2000). All these methods rely on the very high solubility of detergents compared to lipids. A reduction of the monomeric detergent concentration, for example by dialysis, removes detergent from the aggregates that are present initially, typically spherical or elongated micelles. This change in composition may then induce vesicle formation. Although techniques based on detergent removal are widely used, only limited information is available on the mechanism by which mixed micelles transform into vesicles. A better knowledge of the nonequilibrium behavior could help to optimize the detergents, conditions, and procedures used for vesicle formation.

More generally, little is known about the nonequilibrium behavior of surfactant aggregates, whereas their equilibrium properties are well studied (Evans and Wennerström, 1994). From a physicochemical point of view, particularly interesting are transformations between different monolayer and bilayer topologies (Lipowsky, 1991; Hyde et al., 1997), with the micelle-to-vesicle transition being a classic example. The properties of vesicles are extensively studied theoretically and experimentally in a number of different systems (Schurtenberger et al., 1985; Kaler et al., 1989; Hjelm et al., 1990; Long et al., 1994; Schönfelder and Hoffmann, 1994; Lin et al., 1994; Egelhaaf and Schurtenberger, 1994; Pedersen et al., 1995; Oberdisse et al., 1996; Danino et al., 1997; Cantu et al., 1997; Safran et al., 1990, 1991; Andelman et al., 1994; Fattal et al., 1995). Nevertheless, there has been only limited understanding of their formation and of the sequence of any intermediate structures (Almog et al., 1986, 1990; Edwards and Almgren, 1990, 1991; Walter et al., 1991; Edwards et al., 1993; Silvander et al., 1996; O'Connor et al., 1997; Campbell et al., 1998; Brinkmann et al., 1998; Egelhaaf and Schurtenberger, 1999; Chen et al., 1999; Xia et al., 2002; Schmölzer et al., 2002). It is still not conclusively decided what determines the final (“end-state”) properties of vesicles formed by detergent removal; equilibrium calculations (Safran et al., 1990, 1991) give the wrong trends for the dependence of liposome size on bilayer composition (Schurtenberger et al., 1985; Hjelm et al., 1990; Long et al., 1994; Egelhaaf and Schurtenberger, 1994; Kozlov and Andelman, 1996), although they are in agreement with experiments on catanionic surfactant vesicles (for example Kaler et al. (1989)). This suggests that the end-state liposomes are metastable structures that cannot achieve thermal equilibrium on observable timescales. There is, however, no clear consensus yet on whether liposomes represent a true equilibrium state or a metastable state of very long lifetime.

Here we study the nonequilibrium behavior of aqueous lecithin-bile salt mixtures, which are prime examples of mixed amphiphile solutions that exhibit a spontaneous micelle-to-vesicle transition (Schurtenberger et al., 1985; Hjelm et al., 1990; Long et al., 1994; Egelhaaf and Schurtenberger, 1994; Pedersen et al., 1995). They are of direct importance in biochemistry, physiology, and pharmacy, with the micelle-to-vesicle transition exploited in studies as mentioned above, and implicated in gallstone formation and digestion (Lichtenberg, 1995). In addition, they are well-controlled model systems, and we use them as such in this study of liposome reconstitution.

In aqueous lecithin-bile salt mixtures, different structures are observed with decreasing total concentration: spherical micelles—elongated, polymerlike micelles—vesicles. This sequence can be rationalized based on the concept of spontaneous curvature. The average spontaneous curvature of a monolayer comprising lecithin and bile salt depends on its composition: lecithin alone forms aggregates of low spontaneous curvature whereas bile salt alone forms highly curved (spherical) micelles. At high bile salt content, therefore, spherical or elongated mixed micelles form. Because bile salt is far more soluble than lecithin, a subsequent dilution causes the composition of the aggregates to change, so that the bile salt content is reduced and the spontaneous monolayer curvature decreased. With increasing dilution factor progressively longer, flexible cylindrical micelles are observed, until at higher dilution factors the end state comprises near-monodisperse, unilamellar vesicles whose size decreases with dilution factor (Schurtenberger et al., 1985; Hjelm et al., 1990; Long et al., 1994; Egelhaaf and Schurtenberger, 1994; Pedersen et al., 1995; Arleth et al., 2003).

Time-resolved light and neutron scattering experiments suggest that on a sudden dilution spherical or elongated micelles very quickly change into disklike micelles (within 1 s), which then transform into vesicles in a much slower process, typically 1 h (Egelhaaf and Schurtenberger, 1999). In this system, vesicle formation seems thus to occur along the following path: spherical or elongated micelles—disklike micelles—vesicles. Disklike intermediates have also been suggested under different conditions and for different systems (Walter et al., 1991; Edwards and Almgren, 1991; Luk et al., 1997; O'Connor et al., 1997; Schmölzer et al., 2002).

Note that when a series of samples of varying composition is prepared by dilution, different end-state structures can arise. Each end state might either represent a true equilibrium state, whose structure forms reversibly and does not depend on the preparation method, or a nonequilibrium metastable state, whose structure is generally path dependent and might have a very long life time. (Note that full equilibration is not guaranteed merely by the fact that a structure forms spontaneously.) As mentioned above, the end states observed in the present system range from spherical micelles via progressively longer cylindrical micelles to vesicles. The cylindrical micelles therefore represent compositional intermediates between spherical micelles and vesicles; such intermediates have been extensively studied. This paper mainly addresses kinetic intermediates that form dynamically during the process between an initial state of micelles and an end state comprising vesicles. For the system described here, disklike micelles have been found to arise as kinetic intermediates in this process (Egelhaaf and Schurtenberger, 1999). However, because they remain reactive (with a lifetime of hours), they are not seen as compositional intermediates in the sequence of end states created by varying composition.

We have performed new time-resolved static and dynamic light scattering experiments to elucidate the pathway of vesicle formation and the role of kinetics in determining the end-state properties of the liposomes. Crucially, we not only varied the final total amphiphile concentration c, but also investigated the dependence on salt (NaCl) concentration c_s. (Note that all “global” parameters are collected in Table 1.) We expect c_s to control the electrostatic interactions between negatively charged bile salt molecules and to influence bile salt solubility (Small, 1973), while having only marginal effects on the properties of the neutral lecithin within the range of c_s studied here (Meyuhas et al., 1997). We use a bile salt (taurochenodeoxycholate) with a very low solubility, which shifts the vesicular region to very low lipid concentrations. Under these conditions, interactions between aggregates have a negligible effect on the light scattering results.

TABLE 1.

All “global” parameters used across different sections

A	Rim area of disklike micelle
At	Total rim area density
aD, aL	Headgroup area of detergent and lipid, respectively
c	Concentration
cs	Salt concentration
cmcD, cmcL	Critical micellar concentration of detergent and lipid, respectively
D	Diffusion coefficient
d	Dilution factor
Ed	dlvo interaction energy
Et	Topological energy barrier
e	Electronic charge
f	Attempt frequency
H	Hamaker constant
h	Surface-to-surface distance
hf	Distance at which fusion occurs
I	Scattering intensity
𝒦ij	Rate coefficient (kernel) of the Smoluchowski equation
k	Boltzmann's constant
L	Rim length of disklike micelle
NA	Avogadro's constant
n, nv	Number density of disklike micelles and vesicles, respectively
q	Scattering vector
R	Vesicle radius
Rh	Hydrodynamic radius
r	Radius of the central part of a disklike micelle
S	Reaction surface
T	Temperature
t	Time
Va	van der Waals interaction potential
Vd	dlvo interaction potential
Ve	Electrostatic interaction potential
Vf	Vesiculation index
vD, vL	Molecular volume of detergent and lipid, respectively
αb	Energy gain upon binding of one detergent molecule to the rim
αm	Micellization energy
ɛ	Dielectric constant of water
η	Viscosity
	Mean, Gaussian and effective bending modulus, respectively
κD	Debye length
Λ	Line tension
ρ	Thickness of surfactant layer
σ	Surface (rim) charge density
σΓ	Polydispersity index
τc	Closure time
τg, τG	Growth time and total growth time, respectively
τz	Zimm time
φb	Bulk volume fraction of detergent
φD, φL	Volume fraction of detergent and lipid, respectively
φr	Rim surface fraction covered by detergent
ψ0	Electrostatic potential
Ωd, Ωt	Effective dlvo and topological Boltzmann factor, respectively

Note that subscripts i and j refer to parameters of disks formed from i and j initial disklike micelles, respectively.

Although there have been several attempts at qualitative descriptions, thermodynamic models or simulations of the formation of vesicles (Lasic, 1982, 1987, 1988; Thompson, 1990; Lasic, 1991; Goltsov and Barsukov, 2000; Yamamoto et al., 2002), here we develop a kinetic model, which we test by making a quantitative comparison between our calculations and measurements. (A brief description of our model can be found in Leng et al. (2002).) The important steps in vesicle formation are assumed to be those between the rapidly formed, disklike intermediate micelles and the end-state vesicles. First the disklike micelles grow by coalescence, which is described using a set of Smoluchowski rate equations. They are based on interactions between disks comprising the standard dlvo potential with, in addition, a local packing contribution to describe the formation of a “neck” between two disks. We then describe how large disks become unstable and close to form vesicles. This is due to incomplete coverage of their perimeter by bile salt, which yields a significant line tension. A comparison of growth time and closure time leads to a kinetic criterion for disk closure to form vesicles. Based on this kinetic criterion, vesicle size can be predicted and is in good agreement with our experimental results. This composition-dependent kinetic criterion, and not thermodynamics, is thus thought to control the end-state vesicle size.

MATERIALS AND METHODS

Sample preparation

Lecithin (egg yolk lecithin (grade 1), Lipid Products, South Nutfield, Surrey, UK) and bile salt (taurochenodeoxycholic acid sodium salt, Fluka, Gillingham, Dorset, UK) were dissolved in ethanol in a lecithin-to-bile salt molar ratio of 0.9 and dried under low pressure (Small et al., 1969; Egelhaaf and Schurtenberger, 1994). Then buffer (50 mM Tris, pH 8.0) was added to obtain a stock solution with a total lipid concentration of 50 mg/ml, which corresponds to lecithin and detergent (bile salt) volume fractions 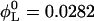and 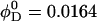, respectively. The stock solution was flushed with nitrogen and equilibrated for a few days at a temperature T = 23°C.

To obtain samples with the desired dilution factor d (defined as the concentration of the stock solution divided by the sample concentration) and salt concentration c_s, the stock solution was diluted with buffer that also contained sodium chloride (NaCl). The samples were flushed with nitrogen, sealed, and kept at 23°C for at least two weeks. In the following we include the ionic strength originating from the buffer, 28.2 mM “effective” salt concentration, in the total salt concentration c_s. We neglect, however, the contribution from counterions of bile salt (Na⁺), because their concentration, less than ∼1 mM, is much smaller than the concentration of added salt (c_s ≥ 50 mM).

Before the light scattering measurements, ∼1 ml of sample is transferred into cylindrical scattering cells (10 mm inner diameter) and centrifuged at 5000 rpm and 23°C for 1 h to remove dust particles from the scattering volume. Samples for time-resolved experiments were prepared as follows: a small amount of the initial solution (d = 2, prepared as described above) is transferred into a scattering cell and centrifuged at 5000 rpm and 23°C for 30 min. It is then rapidly diluted with buffer of a given ionic strength, which has been repeatedly filtered using a Millipore filter (pore size 0.1 μm) to remove dust particles. Subsequently the sample is gently shaken and put into the light scattering instrument. The time from mixing until the first measurement is accurately determined and is typically 30 s.

Light scattering

Static (SLS) and dynamic (DLS) light scattering experiments were performed with an ALV goniometer modified to use fiber-optical detection (Gisler et al., 1995) and equipped with an ALV-5000 correlator and an argon ion laser (Coherent, Innova 90, λ = 514.8 nm). Measurements were made at 23°C and five different scattering angles θ (30°, 50°, 70°, 90°, and 110°). For the DLS measurements, several individual autocorrelation functions were determined at each angle. They were individually analyzed using a second-order cumulant analysis (Koppel, 1972), which yields the average decay rate 〈Γ(q)〉 and a polydispersity index 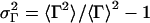where q = (4πn_ref/λ) sin (θ/2) is the scattering vector and n_ref the refractive index of water. The average decay rate is then converted to the collective diffusion coefficient D = 〈Γ(q)〉/q² and hydrodynamic radius R_h = kT/6πηD where k is Boltzmann's constant and η = 10⁻³ Pa s the solvent viscosity. The results were subsequently averaged for each angle. SLS was used to determine the average scattered intensity as a function of scattering vector I(q). The extrapolation to zero scattering vector, I(q → 0), was based on the form factor for a suspension of polydisperse shells with average radius R = R_h, thickness 2ρ = 50 Å (Small, 1967; Pedersen et al., 1995) and a Gaussian size distribution; the radius and its polydispersity were deduced from DLS. In the kinetic measurements, the time dependences of the average scattering intensity I(t) and intensity autocorrelation function, from which D(t) and R_h(t) are obtained, were monitored at one scattering angle (θ = 90°) with an individual measurement time of 5 s.

EXPERIMENTAL RESULTS

General phase behavior

First we examine a range of salt concentrations c_s and dilutions d to determine the conditions that lead to vesicles only. Samples were kept at T = 23°C for at least two weeks before they were visually inspected and investigated by static and dynamic light scattering. These measurements yield the hydrodynamic radius R_h, polydispersity index σ_Γ, and the scattered intensity extrapolated to zero scattering vector I(q → 0), which is proportional to the average molar mass of the aggregates and the concentration (or 1/d).

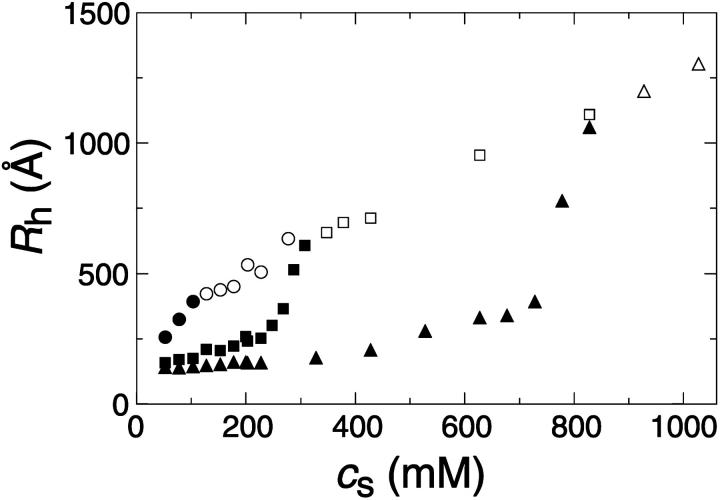
Fig. 1 shows the c_s-dependences for samples with d = 50, which is also typical for other dilutions. At low c_s, R_h, and I(q → 0) show a pronounced increase whereas σ_Γ is approximately constant with σ_Γ ≈ 0.1. The data is consistent with the formation of near-monodisperse vesicles, which has, under similar conditions, already been reported (Schurtenberger et al., 1985; Egelhaaf and Schurtenberger, 1994; Cohen et al., 1998; Degovics et al., 2000). In the range c_s ≈ 200–700 mM a modest, approximately linear increase in the detected average hydrodynamic radius R_h is observed (see also open symbols in Fig. 6) with a concomitant, significant rise in polydispersity. At the same time a dramatic drop in the scattered intensity is detected. This indicates the existence of another type of aggregate of lower scattering power, probably micelles that might coexist with vesicles (Long et al., 1994; Egelhaaf and Schurtenberger, 1994; Pedersen et al., 1995). This is expected for vesicular bile salt-to-lecithin ratios exceeding the maximal amount of bile salt that can be accommodated by vesicles (the “saturation concentration”) (Lichtenberg, 1995; Roth et al., 2000). At even higher c_s ≳ 700 mM, both, R_h and I(q → 0) suddenly drop, indicating that only a small fraction of small aggregates are present in the scattering volume. Consistent with these results, the onset of bulk phase separation can be detected. By polarized light microscopy, this can be identified as lamellar phase coexisting with excess buffer. Here we are interested in the range of salt concentrations c_s and dilutions d where only vesicles are present (Fig. 2, hatched area), which is determined from the dramatic change in I(q → 0) and the change in slope of R_h (solid line, Fig. 1).

FIGURE 1.

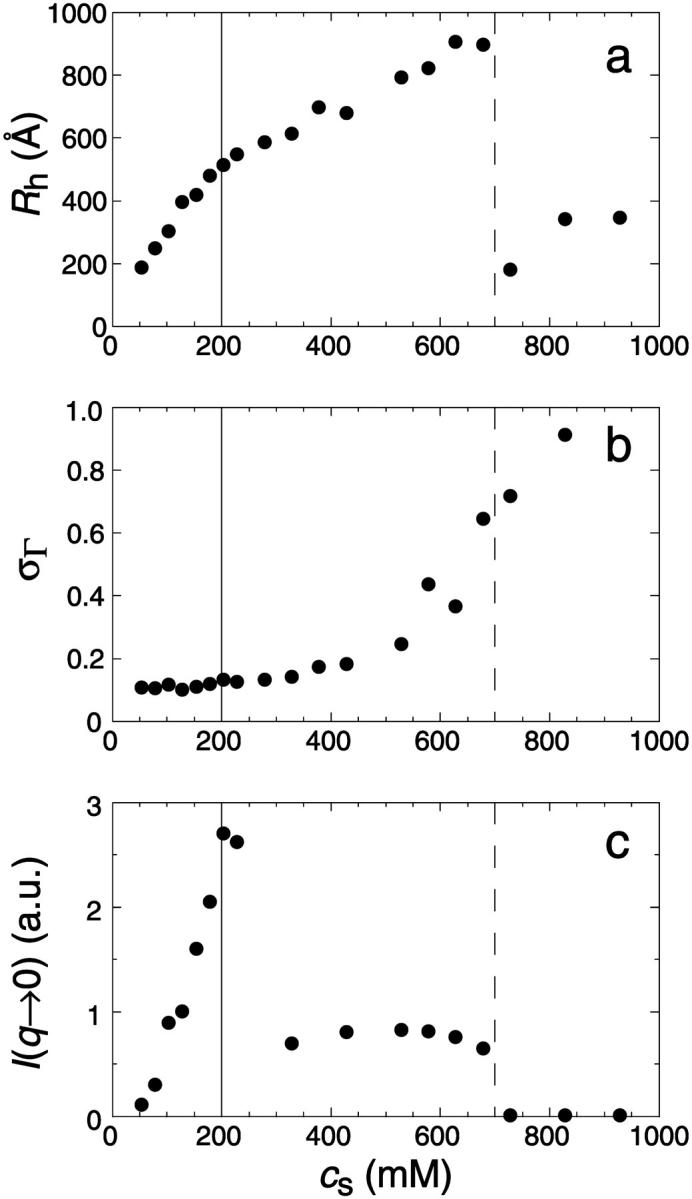
(a) Average hydrodynamic radius R_h, (b) polydispersity index σ_Γ, and (c) average scattered intensity I(q → 0) as a function of salt concentration c_s for samples diluted to d = 50 and left at 23°C for at least two weeks. The different regimes are separated by vertical lines.

FIGURE 6.

Hydrodynamic radius R_h measured in the end state as a function of salt concentration c_s for different final dilutions d (•: 40, ▪: 80, ▴: 120). Solid symbols correspond to vesicular samples and open symbols to samples beyond the vesicular region.

FIGURE 2.

Diagram indicating the range of salt concentrations c_s and dilutions d for which only vesicles are observed (hatched area). The data points refer to changes in the light scattering behavior (Fig. 1, solid lines), while the line is a guide to the eye.

Relaxation after a dilution step

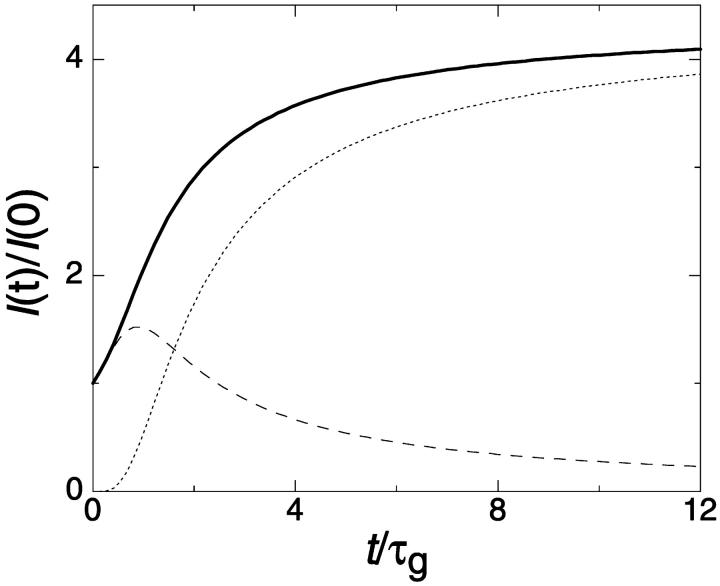
The relaxation after a rapid dilution step from an initial dilution d = 2 to different final dilutions was followed by time-resolved static and dynamic light scattering. The time dependences of the average scattering intensity I(t) and average collective diffusion coefficient D(t) were monitored with a time resolution of 5 s. Two typical examples are shown in Fig. 3. The normalized average scattering intensity I(t)/I(0) increases with time. For low c_s, a slow increase is followed by a faster rise and a slow leveling off (solid line, 180 mM), whereas for higher c_s only a steep increase with saturation is observed (dashed line, 230 mM). On the other hand, the diffusion coefficient D(t) decreases with time, indicating an increase in aggregate size. The timescale and final value depend strongly on c_s and, to a lesser extent, on the final dilution d. The kinetics proceeds faster as c_s is increased or d decreased. Because the time dependences are nontrivial, it is difficult to fully describe them without an appropriate model. We therefore focus for a quantitative characterization on four measures that can be obtained model independently: the hydrodynamic radius immediately after the dilution step R_h(t → 0); the end-state hydrodynamic radius R_h(t → ∞); the normalized initial slope of the intensity, (1/I)(dI/dt)(t → 0), and the normalized initial slope of the diffusion coefficient, (1/D)(dD/dt)(t → 0), which both provide a characteristic timescale of the kinetics.

FIGURE 3.

Time evolution of (a) relative scattered intensity I(t)/I(0) and (b) diffusion coefficient D(t) after a rapid dilution step from an initial dilution d = 2 to a final dilution d = 60 for two salt concentrations c_s (solid line: 180 mM, dashed line: 230 mM). The individual measurement time was 5 s.

Size of the intermediate aggregates

In agreement with previous time-resolved light and neutron scattering experiments (Egelhaaf and Schurtenberger, 1999), the measurements indicate that upon a sudden dilution, intermediate aggregates form rapidly (in less than a second) compared to the timescale of the experiments. This suggests that an extrapolation of R_h to t = 0 yields the hydrodynamic radius of the intermediate aggregates. R_h(t → 0) is found to be ∼60 Å and hardly depends on c_s or d.

Initial rate

The initial slopes of the time dependences of the scattered intensity I(t) and diffusion coefficient D(t) were determined as a function of salt concentration c_s and final dilution d. The slopes were obtained by a second order polynomial fit and are converted into rates 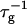according to:

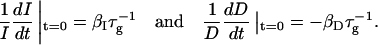(1)

Theoretically, the rate can be related to the rate at which initial, intermediate aggregates coalesce to form aggregates of twice the mass (see “Growth”). Based on intermediate disklike aggregates (Egelhaaf and Schurtenberger, 1999) with a hydrodynamic radius of R_h ≈ 60 Å (see “Size of the intermediate aggregates”), we obtain the theoretical values β_I = 1 and β_D = 0.38 (Appendix A), which are used to convert the experimentally determined slopes to experimental rates 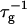(Eq. 1). Consistent values for the initial rate 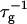(Figs. 4 and 5) are obtained. On increasing c_s, 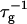shows a steep increase spanning about two decades, which is more pronounced for lower final dilutions d (Fig. 4). This concurs with the increased screening of electrostatic interactions at higher c_s, and also with the presence of higher charge on the disk, i.e., higher bile salt content, at lower d. In contrast, a much weaker dependence of 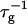on d is observed, whose absolute level, however, heavily depends on c_s (Fig. 5), consistent with the strong dependence of 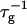on c_s.

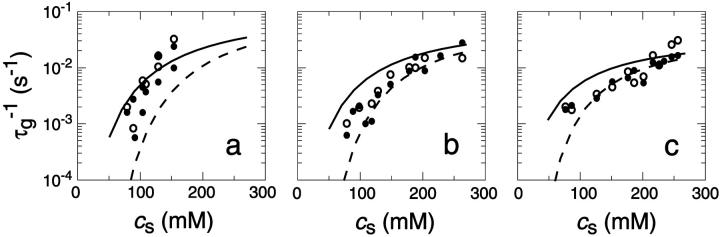
FIGURE 4.

Rate 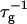obtained from the normalized initial slopes of the scattered intensity (•) and diffusion coefficient (○) as a function of salt concentration c_s for different final dilutions d (a: 40, b: 60, c: 100). Model predictions are shown as lines with electrostatic interactions based on constant potential (solid line) and constant charge (dashed line), respectively. Parameters for calculations: a_D = 200 Ų, α_m = 10 kT and .

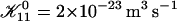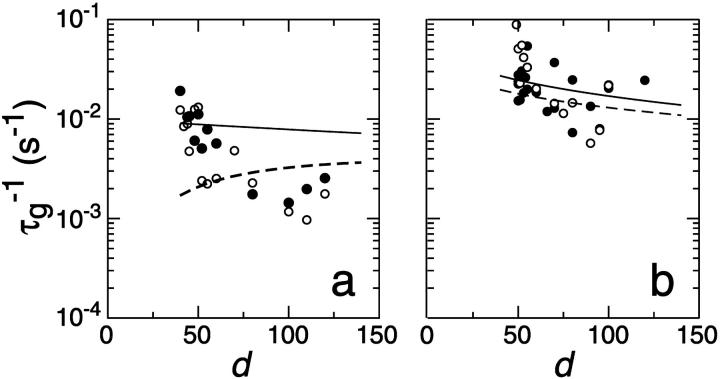
FIGURE 5.

Rate 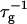obtained from the normalized initial slopes of the scattered intensity (•) and diffusion coefficient (○) as a function of final dilution d for different salt concentrations c_s (a: 130 mM, b: 230 mM). Model predictions are shown as lines with electrostatic interactions based on constant potential (solid line) and constant charge (dashed line), respectively. Parameters for calculations: a_D = 200 Ų, α_m = 10 kT, and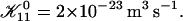

End-state vesicle size

In addition to the time-resolved experiments, the end-state size was determined after the samples were left for at least two weeks at constant temperature (T = 23°C). In the vesicular region (for a larger range of parameters, see “General phase behavior”), the general dependence of R_h on c_s is similar for all dilutions d studied, with typical dilution series shown in Fig. 6 (solid symbols). With increasing c_s, R_h first moderately increases before a pronounced growth is observed, whose onset depends on d.

MODEL

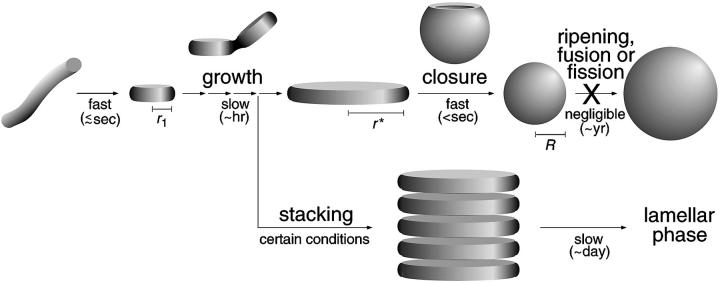
We now examine theoretically the transition from micelles to vesicles and develop a simple model that describes the kinetic pathway, including the properties of the end-state vesicles. Our kinetic model (Fig. 7) assumes that the key kinetic steps during vesicle formation are those leading from the rapidly formed, intermediate disklike micelles to vesicles. First the disklike micelles grow by coalescence and then in a second stage the enlarged disklike micelles close to form vesicles. We also consider stacking of large disklike micelles, which competes with closure and could lead to a lamellar phase. For each step the theoretical predictions will be compared to our experimental data.

FIGURE 7.

Schematic representation of our kinetic model of the micelle-to-vesicle transition. The fundamental steps and their typical timescales are shown: rapid formation of disklike intermediate micelles, successive growth of these micelles up to the critical radius r^* followed by their closure to form vesicles. Ripening of these vesicles to their equilibrium size was not observed, but might occur on a very long timescale. Under certain conditions growth and closure might become slower than stacking, which could lead to the formation of lamellar phase as the end state.

Intermediate disklike micelles

Time-resolved light and neutron scattering experiments suggest that upon rapid dilution, which removes bile salt from the aggregates and thus decreases the average spontaneous curvature, spherical, or elongated micelles very quickly transform into metastable disklike micelles (Egelhaaf and Schurtenberger, 1999).

Geometry

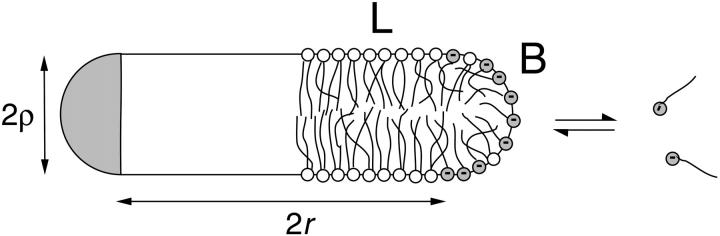
The disklike micelles are composed of lecithin and bile salt. These two amphiphiles have very different properties. Lecithin tends to form aggregates of low spontaneous curvature, typically flat bilayers. In contrast, bile salt has a positive spontaneous curvature and self-assembles into highly curved (spherical) micelles when alone in solution. This suggests that the central part of the disk, which is similar to a flat bilayer, is mainly composed of lipids, whereas the bile salt is sequestered at the rim where the curvature is high (Fig. 8).

FIGURE 8.

Schematic cross section of a disklike micelle. The central bilayer part (radius r, thickness 2ρ) is formed by lipid (L), while the rim also contains bile salt (B). Micellar bile salt is in equilibrium with monomeric bile salt in solution. In contrast, the monomer solubility of lipid is low enough to be neglected.

We thus model the intermediate micelles as consisting of a central, flat part with radius r and thickness 2ρ surrounded by a semitoroidal rim that matches the central part and thus has a radius ρ (Fig. 8). The surface area A of the rim is

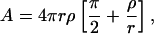(2)

and its outer length L is

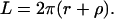(3)

As the central part resembles a bilayer fragment, we take for its thickness a typical bilayer thickness, 2ρ = 50 Å (Small, 1967; Pedersen et al., 1995).

We will argue below (see “Reaction-limited growth of disklike micelles”) that the disks grow by coalescence and thus assume that disk radii only exist in discrete steps: r_i = i^1/2r₁ with the radius of the initial disklike micelles r₁ ≈ 80 Å as determined based on a hydrodynamic radius R_h(t → 0) ≈ 60 Å (see “Size of the intermediate aggregates”). The subscript i refers to a disk formed from i initial disklike micelles with radius r₁; we distinguish parameters referring to disks of different radii by subscripts, but suppress them for brevity if only one size of disk or a disk in general is considered.

Composition

The samples are prepared by diluting a stock solution with lecithin and bile salt volume fractions 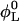and 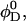respectively. For a sample with dilution factor d, this implies a lecithin volume fraction 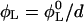and bile salt volume fraction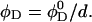

As mentioned above, we assume that the central, flat part is formed by lipids with bile salt sequestered at the highly curved rim (Fig. 8). The solubility of lecithin is very small (cmc_L ≈ 10⁻¹⁰ M (Tanford, 1980)) and monomeric lipid in solution is thus neglected. The total area of the central parts of disks and of the vesicles is related to the total amount of lipid φ_L and assumed constant throughout the kinetic pathway (for these purposes we neglect lipid in the rim):

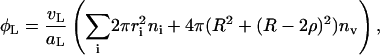(4)

where v_L = 1266 ų and a_L = 72 Ų are the volume and headgroup area of a lecithin molecule, respectively (Small, 1967; Huang and Mason, 1978; Cornell et al., 1980), and n_i and n_v are the number densities of disks of radii r_i and vesicles of radius R, respectively. (Because experiments suggest that the vesicles are near monodisperse, we only consider one size of vesicles R.)

Bile salt is much more soluble and we must take bile salt in bulk solution into account (volume fraction φ_b). Its solubility depends on the ionic strength and lipid concentration, but is for the bile salt we used (taurochenodeoxycholic acid) typically cmc_D ≈ 1 mM (Small, 1973; Duane, 1977). In principle, bile salt also enters into the central part of the disk (volume fraction φ_c). This is driven by the entropy of mixing, but opposed by the curvature elasticity of the mixed bilayer (Kozlov et al., 1997). Based on an estimated equilibrium constant K = φ_c/(φ_bφ_L) = 330 for the partitioning of bile salt between bulk and a bilayer (vesicles) (Schurtenberger et al., 1985; Schubert, 1992; Lasch, 1995; Heerklotz and Seelig, 2000), we estimate that for all conditions investigated only a small fraction (≲0.06) of micellar bile salt is located in the central part. We thus neglect bile salt in the flat, central part of the disks (φ_c ≈ 0). Bile salt is therefore assumed to be partitioned between bulk solution and rims of disks (area fraction φ_r). Conservation of the total amount of bile salt φ_D, partitioned between bulk and rims, thus reads:

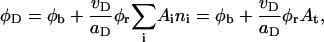(5)

where A_t is the total rim area density, v_D the volume of a bile salt molecule with v_D = 660 ų (Matsuoka et al., 1987), and a_D the rim area covered by one bile salt molecule at complete coverage of the rim. Depending on the conditions, a range of values 150 Ų ≲ a_D ≲ 250 Ų can be found in the literature (Small, 1973; Schurtenberger et al., 1983; Janich et al., 1998); we will use it as an adjustable parameter. Equation 5 considers the most general case of a distribution of disks of different radii r_i. For the initial system, where only disks with radius r₁ are present, it reduces to φ_D = φ_b + (v_D/a_D)φ_rA₁n₁.

The exchange of bile salt between bulk and rim occurs on a timescale of the order of 1 μs (Diamant and Andelman, 1996; Telgmann and Kaatze, 1997). It is thus very fast compared to the processes we aim to describe, which have characteristic times of at least a few seconds (Figs. 3, 4, and 5). We therefore assume local equilibrium. The area fraction φ_r of bile salt on the rim can then be related to the bulk volume fraction φ_b through Davies' isotherm, which describes the adsorption of ionic surfactant (Davies, 1958a, 1958b; Diamant and Andelman, 1996):

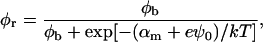(6)

where e is the electronic charge, ψ₀ the electrostatic potential at the interface and the micellization energy α_m accounts for the energy gain when one bile salt molecule is added to a disklike micelle. To our knowledge, there is no value for α_m available and we thus use it as an adjustable parameter. In using this isotherm, we neglect lateral interactions between bile salt molecules within a monolayer and between different disks, and assume that it remains valid for curved monolayers. We furthermore assume that bile salt in bulk only exists in monomeric form.

At the present pH (pH 8.0), lecithin is zwitterionic and thus overall neutral. Bile salt, however, is fully dissociated (Small, 1973) and carries a negative charge. We assume that it is also fully dissociated in the micelles. This leads to a surface charge density σ = eφ_r/a_D and thus creates the electrostatic potential ψ₀ at the interface. For a 1:1 electrolyte, such as NaCl, of molar concentration c_s the surface charge density is related to the potential ψ₀ of a single micelle by the Gouy-Chapman theory (Russel et al., 1991):

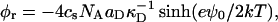(7)

where 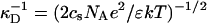is the Debye length and ɛ the dielectric constant of water. (Note that c_s accounts for the added NaCl and the ionic strength originating from the buffer, see “Sample preparation”). We assume that the curvature of the interface does not significantly alter the above equation, because for our samples the (smallest) radius of curvature ρ is larger than the Debye length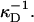

Solving Eqs. 5, 6, and 7 simultaneously yields the composition of the disklike micelles. This depends on solution conditions, such as salt concentration c_s and dilution factor d, as well as molecular parameters, namely a_D, v_D, and α_m. There is no analytical solution of this set of equations, but the general trends are as follows (Fig. 9): For given d, increasing salt concentration c_s progressively screens the electrostatic interactions between bile salt molecules. This favors adsorption of bile salt molecules onto the rim and thus φ_r is increased (Fig. 9 a) and φ_b is decreased (Fig. 9 b). On the other hand, for given c_s, upon dilution bile salt molecules leave the aggregates to maintain the monomer concentration and thus φ_r decreases (Fig. 9 a, inset). Due to the decrease in total concentration, also φ_b decreases (Fig. 9 b, inset). An increase in c_s also affects the electrostatic potential ψ₀, whereas dilution has only a weak effect on ψ₀ (Fig. 9 c).

FIGURE 9.

Effect of salt concentration c_s and dilution d on the composition and properties of disks. (a) Rim area fraction φ_r covered by bile salt and number of bile salt molecules per initial disk φ_rA₁/a_D (right axis); (b) bulk volume fraction φ_b of bile salt and molar concentration of monomeric bile salt φ_b/v_DN_A (right axis); (c) electrostatic energy eψ₀; (d) relative line tension Λ/Λ₀ and relative vesiculation index V_f/V₀ as a function of salt concentration c_s for different dilution factors d (solid line: d = 40, dashed line: d = 80, dotted line: d = 120). The dependences on dilution d are shown in the insets (solid line: c_s = 50 mM; dashed line: c_s = 150 mM; dotted line: c_s = 500 mM). The insets have the same y axes as the main figures. Eqs. 5, 6, and 7 were solved simultaneously for the initial system, i.e., monodisperse disks with i = 1, and Eqs. 9 and 21 were used for panel d. Parameters: r₁ = 80 Å, ρ = 25 Å, a_D = 200 Ų, α_m = 10 kT, and Λ₀ = 0.3 kT/Å. These parameters imply V₀ = 0.6 (Eq. 21).

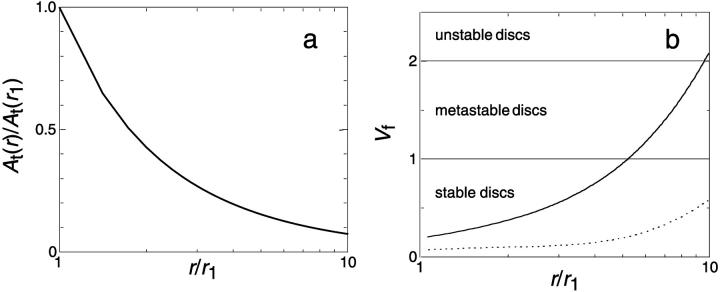
The composition and properties of the disklike micelles also depend on their size r. This is illustrated in Fig. 10, which is based on a monodisperse population of disks of size r. With increasing r and fixed overall composition, the total rim area density A_t decreases (Fig. 10 a), because the total amount of lipid φ_L, and thus of bilayer, is constant (Eq. 4). This decrease in A_t results in an increasing rim coverage φ_r and bulk volume fraction φ_b with increasing radius r. In contrast, the electrostatic potential ψ₀ is hardly affected by an increase in disk size.

FIGURE 10.

Effect of disk radius r on the properties of disks for a constant sample composition. (a) Relative total rim area density A_t(r)/A_t(r₁) and (b) vesiculation index V_f as a function of normalized disk radius r/r₁ for dilution d = 80 and different salt concentrations c_s (solid line: c_s = 50 mM, dotted line: c_s = 500 mM). Eqs. 5, 6, and 7 were solved simultaneously to obtain the composition, and then Eqs. 2, 4, 9, and 21 were used. Disks are assumed to be monodisperse. Parameters: ρ = 25 Å, a_D = 200 Ų, α_m = 10 kT, and Λ₀ = 0.3 kT/Å.

Mechanical properties

The mechanical properties of the disks are determined by the elasticity of the bilayer, which is characterized by the mean bending modulus κ and the Gaussian modulus 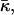as well as a line tension Λ. Under all conditions investigated, φ_r is significantly smaller than 1, typically ∼0.5 (Fig. 9 a). This leads either to the exposure of hydrophobic chains on the perimeter of the central part or local stress on the lecithin monolayer when it bends around the rim to shield the hydrophobic chains. Both cause an excess energy per unit length of rim, which can be expressed as a line tension Λ.

Fromherz (1983) proposed a thermodynamic analogy between surfactant molecules that decrease surface tension and “edge-actant” molecules that decrease line tension. The decrease of Λ upon adsorption of edge-actant molecules is modeled using Gibbs relation for adsorption of bile salt on the rim (which is assumed to reproduce the correct trend also for curved monolayers):

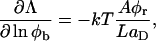(8)

where Aφ_r/La_D is the number of adsorbed bile salt molecules per unit length of rim. This relation links the change of Λ to the adsorption isotherm, which is harmonious with our description of bile salt partitioning between bulk and rim (Eq. 6). Using the Gibbs relation (Eq. 8) together with the Davies' isotherm (Eq. 6), we obtain:

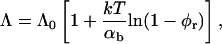(9)

where Λ₀ is the line tension without bile salt (with experimental values Λ₀ = 0.2–0.8 kT/Å, (Moroz and Nelson, 1997) and references therein). We will use Λ₀ as an adjustable parameter. The parameter α_b = Λ₀La_D/A is the size-dependent energy gain upon binding of one bile salt molecule to the rim. It characterizes the ability of an edge actant to lower the line tension by providing a cover with high curvature, but also depends on the nature of the adsorbing surface (the rim). In contrast, the micellization energy α_m (see “Composition”) is related to the energy gain when one bile salt molecule is added to a disklike micelle, which reflects the hydrophobic nature of the molecule. We will see (see “Dependence on salt concentration and dilution”) that the interplay between the (surfactant) hydrophobic effect and the (edge actant) ability to cover a highly curved surface determines the capability of a molecule to stabilize disks. Fig. 9 d illustrates how the line tension Λ is controlled by the salt concentration c_s and dilution factor d: Increasing c_s screens electrostatic interactions and thus favors adsorption of bile salt, i.e., increases φ_r (Fig. 9 a), which relieves packing stress at the rim and hence results in a decrease of the line tension Λ (Eq. 9). On the other hand, increasing dilution d, reduces the bile salt concentration and hence its adsorption (Fig. 9 a, inset), which leads to an increase in line tension Λ (Fig. 9 d, inset). The line tension Λ also depends on the size r of disks through the total rim area density A_t (Fig. 10).

Growth

Reaction-limited growth of disklike micelles

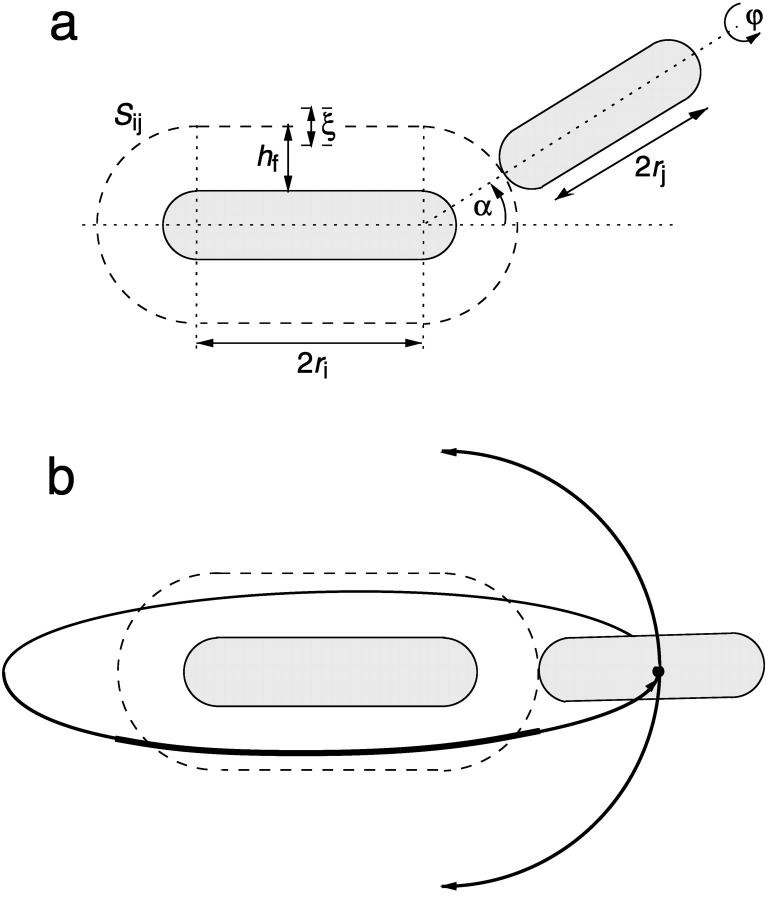
We assume a first stage in which disklike micelles, initially monodisperse, grow. The low solubility of lecithin precludes growth by molecular diffusion or Ostwald ripening. Growth is thus likely to proceed by coalescence (or “aggregation”). When aggregation of two particles occurs immediately at contact, the process is limited by diffusion and in general is fast. Under these conditions, the characteristic aggregation time for a suspension of spheres of number density n₁ is τ ∼ 3η/4kTn₁ (Russel et al., 1991). For the densities of our solutions (n₁ = 10²⁰–10²² m⁻³) and the viscosity of water η = 10⁻³ Pa s, we obtain τ ∼ 10⁻⁵–10⁻³ s. This is much faster than our experimentally observed timescales, which are tens of seconds (Figs. 4 and 5). This rules out a diffusion-limited mechanism and indicates that growth is slowed down by repulsive interactions between disks, which lead to an activation barrier and prevent immediate coalescence. In the limit of a very large repulsive potential (compared to kT), the aggregation is reaction limited and in general the aggregation probability is so small that particles explore all possible mutual configurations before aggregation proceeds (Ball et al., 1987). In principle, we thus have to take into account all possible relative orientations of disks with edge-to-edge, edge-to-face, and face-to-face representing the main classes. However, the experimentally determined initial growth rate 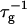strongly depends on salt concentration c_s (Fig. 4) suggesting that electrostatic interactions play a significant role. Because there is little charged bile salt in the flat, central part of the disk (in our model it is in fact neglected), the only configuration involving significant electrostatic interactions is edge-to-edge (Fig. 11). This indicates that this configuration is the dominant one for coalescence. This is corroborated by estimates of the activation barrier (see “Interactions between disklike micelles”) which are lower in the edge-to-edge geometry despite the electrostatic contribution.

FIGURE 11.

Schematic representation of the coalescence of two disklike micelles in a edge-to-edge configuration. (a) Integration over the coordinates of all configurations at separation h ≈ h_f gives the reaction volume S_ijξ with S_ij the reaction surface and ξ the distance over which coalescence can typically occur. (b) The scaling for the reaction surface, S_ij ∼ r_j(r_i + r_j), is obtained by considering a disk of radius r_j sampling all possible edge-to-edge configurations with a disk of radius r_i.

Growth by coalescence is modeled using a set of Smoluchowski rate equations (Russel et al., 1991; Hänggi et al., 1990), which provide the relation between number densities n_k of disks of radii r_k:

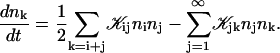(10)

The first term on the right-hand side describes the creation of a k-aggregate by binary collisions of i- and j-aggregates (i + j = k) whereas the second term represents the disappearance of k-aggregates by binary collisions with any other aggregate. Three-body collisions are thus not taken into account and the equation is hence only valid for dilute systems, a condition well satisfied in our experiments. The productive collisions, i.e., those collisions leading to coalescence, between i- and j-aggregates occur with rate coefficients 𝒦_ij, the kernels of the Smoluchowski equations. They contain all the information on the reaction. Before we can calculate the kernels 𝒦_ij and examine the growth of disks, a description of the interactions between disklike micelles is required.

Interactions between disklike micelles

For coalescence to occur, two disks must first approach each other. This is controlled by the interactions between disks, which depend on their distance and relative orientation. Then a topological connection between the disks, a “neck,” has to be formed before coalescence can be completed. In the following we try to estimate the topological barrier to coalescence (the “bare fusion barrier”), which is related to formation of a neck and is expected to be relatively high, and the dlvo interactions, which comprise electrostatic and van der Waals interactions. We will call the sum of topological barrier and dlvo potential at the fusion distance, which represents the overall barrier, the “fusion barrier.”

Topological barrier

Estimating the topological barrier E_t involved in forming a “neck” between two disklike micelles is very difficult. It is, however, similar to the fusion of bilayers, for which several models exist (Leikin et al., 1987; Israelachvili, 1992; Siegel, 1993; Lentz, 1994; Chernomordik et al., 1995; Lee and Lentz, 1997, 1998; Markin and Albanesi, 2002; Kozlovsky and Kozlov, 2002). They suggest that the topological barrier in the face-to-face orientation is ∼25 kT. Above we argued that the strong c_s-dependence of indicates that the edge-to-edge orientation dominates. Compared to the face-to-face (and also face-to-edge) orientation, less surface of similar curvature is involved in the edge-to-edge orientation and we thus expect a significantly lower energy barrier, which nevertheless amounts to several kT. (The actual height of the topological barrier E_t is contained in the adjustable parameter 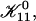see “Initial growth”.) In the presence of bile salt, the spontaneous curvature will become positive. Because the topological barrier depends on the membrane curvature, with negatively curved intermediates involved in the transition, the energy cost of the deformation and hence E_t will increase. We neglect this composition dependence and we also neglect possible compositional inhomogeneities, such as bile salt-depleted, “sticky” patches on the rim, which might lower E_t.

Overcoming the bare fusion barrier of several kT is thus a strongly limiting step and leads to coalescence being reaction limited under all conditions investigated, even for high salt concentrations where electrostatic repulsion is negligible. Fusion occurs at a distance h_f, which is of the order of a molecular length, typically two hydration layers and thus h_f ≈ 10 Å (Leikin et al., 1987).

DLVO interactions

We will first examine dlvo interactions between flat monolayers and then use the Deryaguin approximation to account for the curvature of the monolayers (Israelachvili, 1992; White, 1983). dlvo interactions comprise van der Waals attraction and electrostatic repulsion. The van der Waals interaction energy per unit area is taken as (Israelachvili, 1992)

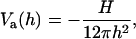(11)

where h is the distance between the monolayers, and H the Hamaker constant of the lipid-water-lipid system (H ≈ 5 × 10⁻²¹ J (Israelachvili, 1992)). We neglect retardation effects.

The negatively charged bile salt molecules lead to a surface charge density σ = eφ_r/a_D and thus control the electrostatic potential ψ₀ at the monolayer (Eq. 7; Fig. 9 c). This results in an electrostatic repulsion between two monolayers. However, the calculation of the electrostatic interaction is complicated by the fact that the bile salt molecules (and thus the charges) are mobile. When exposed to an electric field, for instance caused by another monolayer, bile salt molecules could either move to a more distant point on the monolayer or leave the monolayer. Furthermore, the degree of bile salt dissociation could change. An exact determination of the electrostatic interaction thus requires knowledge on how the charge on each of two approaching monolayers is regulated in response to their growing electrostatic interaction. Whatever the charge regulation mechanism (Russel et al., 1991; Yaminsky et al., 1996; Dean and Sentenac, 1997; Tsao and Sheng, 2001), we expect it to be bracketed by the two limiting cases of constant surface charge and constant surface potential. A crossover between the two regimes might occur and can depend on the charge density of the monolayer; for higher charge densities σ and/or lower salt concentration c_s the constant potential limit should provide a better description, whereas for lower σ and/or higher c_s the constant charge regime should be more appropriate.

We only investigate conditions implying relatively low surface charge densities σ and/or high salt concentrations c_s. Under these conditions, the electrostatic interaction energy per unit area based on constant charge, and constant potential, 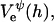respectively, can be approximated by (Russel et al., 1991):

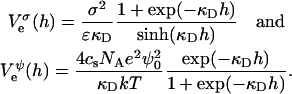(12)

The above Eqs. 11 and 12 describe dlvo interactions between flat monolayers at a distance h. We now use the Deryaguin approximation to take the curvature of the monolayers into account. Based on the total interaction energy per area V_d(h) = V_a(h) + V_e(h), which can either be based on constant charge, 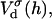or constant potential, 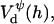the interaction energy E_d(h) of approaching monolayers with arbitrary curvature and orientation can be calculated using (White, 1983):

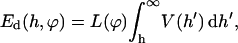(13)

with

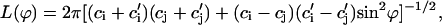(14)

where c_i, 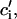c_j, and 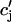are the two principal curvatures of the two monolayers and ϕ is the angle between the principal axes of the two monolayers (Fig. 11 a). Note that the angle α (Fig. 11 a) is an implicit parameter in the curvatures. The Deryaguin approximation is only valid for radii of curvature large compared to the length scale of the interactions. The smallest radius of curvature ρ = 25 Å thus has to be larger than the largest Debye length 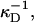which is satisfied for salt concentrations c_s ≳ 20 mM and thus for all conditions investigated.

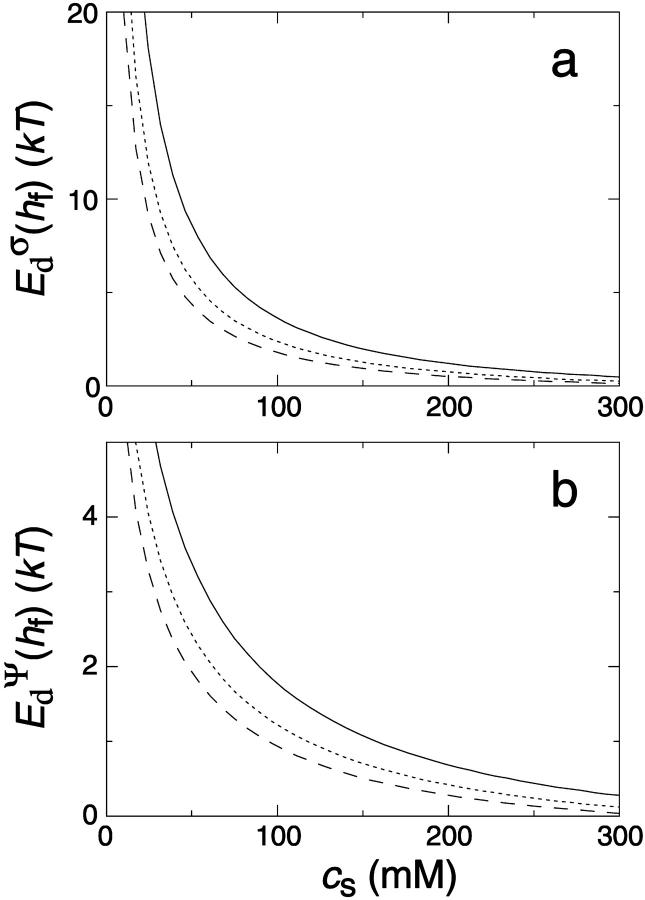
The interaction energy E_d(h) as a function of distance h exhibits a typical behavior with a primary maximum due to the electrostatic repulsion that vanishes at high salt concentration c_s and/or low charge, i.e., small φ_r. More relevant is the interaction energy at the typical fusion distance E_d(h_f). Fig. 12 shows its dependence on c_s for the electrostatic interaction based on constant charge (a) and constant potential (b) respectively. In the case of constant charge, 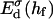is in the range 0–10 kT, whereas a constant potential results in lower values for 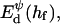0–3 kT, for the salt concentrations c_s ≳ 50 mM studied here. Above ∼300 mM, electrostatic interactions are essentially screened and the contribution of dlvo interactions to the growth rate is expected to be negligible. (There is, however, still an effect of the salt concentration on the line tension Λ due to the salt-dependent bile salt partitioning between rim and bulk; see Fig. 9.)

FIGURE 12.

The dlvo interaction energy E_d(h_f) between two initial disks in edge-to-edge configuration (with ϕ = 0) and for a typical fusion distance h_f = 10 Å as a function of salt concentration c_s for three dilution factors d (solid line: d = 40, dotted line: d = 80, dashed line: d = 120). The electrostatic interactions are based on (a) constant charge, 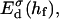and (b) constant potential, 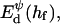respectively.

Rate coefficients

The total fusion barrier E = E_t + E_d depends on the topological barrier E_t as well as the dlvo contribution E_d(h_f). Its maximum is located near the typical fusion distance h_f and is in the order of 10–30 kT (see “Interactions between disklike micelles”). It thus represents a significant barrier to coalescence. This leads to a very small coalescence probability and forces particles to explore all possible configurations before coalescence occurs (reaction-limited regime). This justifies use of classical transition-state theory (Hänggi et al., 1990) for the calculation of fusion rates. Here we only outline the calculation of the rate coefficients, whose details can be found in Appendix B.

The rate coefficients, or kernels, 𝒦_ij of the Smoluchowski rate equations are (Appendix B):

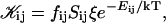(15)

where 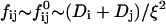is the attempt frequency for coalescence (Eq. 45) with D_i the diffusion coefficient, ξ the distance over which coalescence can typically occur (Figs. 11 a and 17 in Appendix B) and S_ijξ the corresponding reaction volume. (S_ij ≈ 4πr_j(r_j + r_i) is the reaction surface for the edge-to-edge orientation, Fig. 11 and Eq. 38 in Appendix B; although i and j are not interchangeable in S_ij, Eq. 10 ensures symmetry between i and j.) This relation suggests that the reaction surface can be partitioned according to the (strength of) interactions E_ij, i.e., the weight given to a reaction subsurface by the Boltzmann factor. The kernel then consists of a sum of reaction subsurfaces weighted by their Boltzmann factors and interaction-dependent attempt frequencies. If a configuration involves a relatively large barrier and thus a small Boltzmann factor (and small weight), it may be disregarded in a first approximation. This is particularly interesting in the case of anisotropic objects, like disks, with strongly orientation-dependent interactions. In our case, the energy barrier for the edge-to-edge configuration is much smaller than for all other configurations. Using appropriate approximations, it turns out that the contributions from the bare fusion potential and from the dlvo interactions can be decoupled (Appendix B). This renders manipulations relatively simple and we obtain:

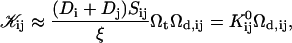(16)

where Ω_t is the effective Boltzmann factor related to the topological barrier and Ω_d,ij an average dlvo Boltzmann factor. A value for Ω_d,ij can be calculated and depends on the dilution factor d, salt concentration c_s and sizes r_i and r_j. The bare fusion rate coefficient 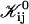contains several unknown constants, but also the dependence on the size of disks, i.e., r_i and r_j. Based on Eq. 16 all 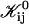can be calculated according to

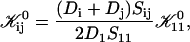(17)

with 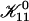remaining the only adjustable parameter. Subsequently all kernels 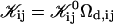can be obtained through Eq. 16.

Initial growth

We can now calculate the rate of initial growth (dimerization) 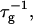which corresponds to the coalescence of two initial disks:

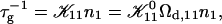(18)

where we used Eq. 16. Because 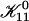does not depend on c_s or d, it represents only a scale factor for 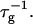We use as an adjustable parameter. The dependence of on c_s and d is contained in Ω_d,11n₁ and is controlled by several parameters, among them the two fit parameters a_D and α_m, which determine the composition of the disklike micelles.

At constant dilution d, the dependence of 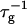on salt concentration c_s is controlled by two effects. Increasing c_s screens the electrostatic interactions and thus tend to increase the rate 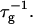At the same time the screened electrostatic interactions favor adsorption of bile salt (φ_r is increased) with a concomitant increase in charge, which then tends to decrease 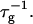In general the first effect, the increase of 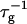with c_s due to the screening of the electrostatic interactions, clearly dominates. The dependence of 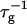on dilution d is also governed by a delicate balance: First, dilution slows down coalescence, because the probability that two disks meet is reduced (n₁ ∼ 1/d). Second, dilution reduces the amount of bile salt φ_r on the rim to maintain the level of monomeric bile salt φ_b, which due to the decreased charge of the disks reduces the electrostatic repulsion and thus speeds up coalescence. Which effect dominates is determined by the level of rim coverage φ_r. This is controlled, among other parameters, by the micellization energy α_m and the rim area covered by one bile salt molecule a_D, which are used as fit parameters. Depending on the value of α_m the rate 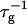can either decrease or increase with d, or its behavior can depend on whether the electrostatic interactions are governed by constant potential or constant charge conditions. A very similar dependence is observed for a_D.

Subsequent growth

Once 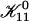is determined all 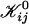and thus all kernels 𝒦_ij can be calculated (Eqs. 16 and 17). The Smoluchowski rate equations (Eq. 10) are thus completely determined and could in principle be solved (numerically) to obtain the time dependence of all densities {n_i(t)}. One complication is that, as the disks grow, the total rim area density A_t decreases (Fig. 10 a). This leads to an increase of rim coverage φ_r (Eq. 5), which in turn results in time-dependent electrostatic interactions and thus ultimately Ω_d,ij(t) and 𝒦_ij(t). The Smoluchowski rate equations thus have to be solved numerically while updating all kernels 𝒦_ij(t) after each time step.

We examine two limiting cases, which will provide bounds for the actual kinetics. Initially, the total rim area density A_t is maximum and will only decrease as the disks grow with time (Fig. 10 a), which results in an increase of φ_r. The initial area fraction 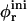thus represents a lower bound to φ_r(t). An upper bound to φ_r is obtained by assuming an evolving, but always monodisperse size distribution of disks, i.e., only one size of disk is present at any given time; a monodisperse size distribution leads to the minimal total rim area. Based on a (hypothetical) monodisperse growth, we thus obtain an upper bound 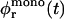for φ_r(t). Hence, the time-dependent rim area fraction φ_r(t) is bracketed by

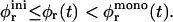(19)

Initially 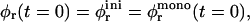but then the area fraction φ_r(t) increases; yet it will never reach 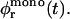For these two limits, all kernels 𝒦_ij can be calculated (Eqs. 16 and 17) and the Smoluchowski rate equations solved numerically (using an adaptive time-step Runge-Kutta scheme). This yields the temporal evolution of densities 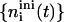and 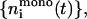which then provide bounds for the actual kinetics.

Comparison with experimental data: rate of initial growth

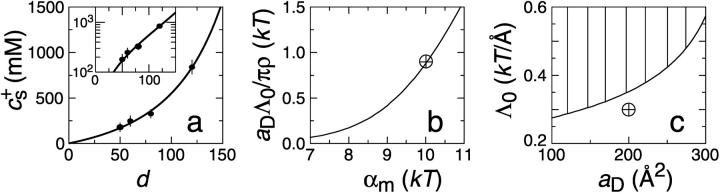
As mentioned above (see “Interactions between disklike micelles” and “Subsequent growth”), a quantitative comparison between our kinetic model and time-resolved experiments (Figs. 4 and 5) is complicated by two factors: First, as the disklike micelles grow, the total rim area density A_t decreases with time and leads to a steady redistribution of bile salt (see “Subsequent growth”). We avoid this complication here, by concentrating on the initial rates 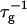(see “Initial growth”). Second, calculation of the electrostatic interactions requires knowledge of how the bile salt on each of two approaching micellar rims is regulated in response to their growing electrostatic interaction. For the present geometry the details are intractable, but we can calculate lower and upper bounds of the rates by assuming constant charge and constant potential, respectively (see “Interactions between disklike micelles”). We thus compare the experimentally determined 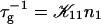(Figs. 4 and 5) with these two bounds. Despite the uncertainty, these data sets contain sufficient information to constrain the free parameters; we obtain a_D = (200 ± 50) Ų, α_m = (10 ± 1.5) kT and 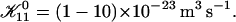In the next section, we will use the experimentally determined end-state vesicle size to further constrain the ranges of these values (see “Comparison with experimental data: vesicle size”).

Fits (obtained by visual inspection) are displayed in Figs. 4 and 5. The bounding estimates of 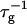for constant potential (solid line) and constant charge (dashed line) are found to reproduce the experimental trends on variation of c_s and d and bracket the experimental data under most conditions. They tend to agree better with the constant potential limit for strong electrostatic interactions, i.e., low c_s and low d, and with the constant charge limit for weak electrostatic interactions, i.e., high c_s and high d (Fig. 4). In general, the results for the dependence on salt concentration c_s are better than on dilution d. This could be because, in our model, bile salt in the central part of the disks is neglected instead of introducing another isotherm (Heerklotz and Seelig, 2000); for varying dilution and thus changing bile salt concentration, this approximation should be more severe. Furthermore, we also neglected the formation of pure bile salt micelles, which would lead to a bile salt activity different from the bile salt concentration and the isotherm (Eq. 6) would no longer be valid; the consequence is expected to be similar to an additional partitioning of bile salt in the central part and the effect on the d-dependence should be stronger than on the c_s-dependence.

Closure

After the coalescence period, the disklike micelles close to form vesicles. Bending and closure decrease the length of the rim and are thus driven by line tension Λ. This is, however, opposed by the bending modulus κ and Gaussian modulus 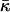of the lecithin bilayer in the central part of the disk. Closure is also resisted by electrostatic repulsion in the closing rim (Betterton and Brenner, 1999) and the need to squeeze internal solvent through an increasingly smaller opening; we neglect both these effects. The balance between line tension and rigidity depends on the size of the disk; with increasing size the energy gained by eliminating the (growing) rim increases. Closure will thus become more favorable as the disk grows and the characteristic closure time τ_c is expected to decrease with increasing disk size. Comparing τ_c to the coalescence time defines a kinetic closure criterion that allows us to calculate the disk radius r^* for which closure is faster than growth. This in turn determines the radius of the formed vesicles R = r^*/2. At this point the end state is reached. The low solubility of lipid precludes ripening, and fusion of vesicles is also extremely slow in the absence of edges due to the large topological barriers involved (see “Ripening”). Within our model, the vesicle size is thus determined by kinetics rather than thermodynamics.

Closure mechanism

The elastic and line energy associated with the spherical deformation of a disk of radius r at constant area can be written as a function of the shape parameter p that ranges from 0 for a planar disk to 1 for a vesicle (p is defined as the ratio between the vesicle radius and the radius of curvature of the corresponding open vesicle or bent disk) (Fromherz, 1983):

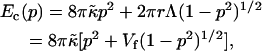(20)

where 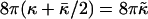is the elastic energy of a (closed) vesicle and 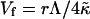a “vesiculation index,” which essentially is the ratio of line energy to bending energy. V_f hence characterizes the relative stability of disks and vesicles: for 0 < V_f < 1 disks are more stable than vesicles, for V_f = 1 they coexist with E_c(0) = E_c(1), for 1 < V_f < 2 disks are metastable, and for V_f > 2 disks are unstable and can close rapidly without the need to overcome any energy barrier.

The stability of disks is controlled by the vesiculation index V_f and hence three parameters: r, Λ, and 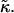The role of 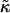for vesiculation has already been the subject of several studies (Helfrich, 1986; Safran et al., 1990; Porte and Ligoure, 1995). We assume that 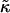is independent of the composition of the sample and thus constant, with 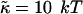(Israelachvili, 1992). (This is consistent with our approximation that the central bilayer part consists of lipids only and does not contain bile salt.) We therefore concentrate in this study on the roles of r and Λ.

Using the dependence of Λ on the rim area fraction φ_r of bile salt (Eq. 9), V_f can directly be related to the adsorption of edge actant:

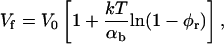(21)

where 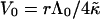is the vesiculation index of detergent-free disks. For the initial disks (r₁ = 80 Å, 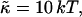and Λ₀ = 0.3 kT/Å) we obtain V₀ = 0.6 and an energy barrier E_c ≈ 120 kT, indicating that the initial disks are kinetically stable toward closure. Presence of bile salt on the rim will decrease Λ and thus stabilize the disks further. The initial disklike micelles are stable toward closure mainly due to their (small) size. They will, however, grow (see “Growth”) and once the disk size r reaches V_f = 2, they will spontaneously transform to vesicles (Fig. 10 b).

Although vesicles form spontaneously for V_f > 2, a thermally induced shape transformation from disks to vesicles can already occur for V_f ≥ 1, which represents a transition between two states with an activation barrier. The characteristic time τ_c for the transformation from disks to vesicles depends on the height of the energy barrier (Eq. 20):

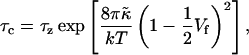(22)

where τ_z = 6πηr³/kT is a “Zimm time” related to the rotational relaxation time of a disk (Doi and Edwards, 1988) and thus involves viscous dissipation in the liquid surrounding the disk as it closes. This dominates dissipation within the bilayer under the present conditions (Seifert and Langer, 1993). Growth of the disklike micelles results in a drop of the energy barrier that corresponds to the energy of a transition state made of an incomplete sphere with a circular rim (Fig. 7). This leads to a very rapid decrease in closure time τ_c beyond a certain disk radius, which depends on c_s and d. A stability diagram for disks (Fig. 13) illustrates the interplay between size r and rim area fraction φ_r covered by bile salt (which controls Λ); τ_c decreases with increasing r and decreasing φ_r. It also shows that the closure time τ_c strongly changes within a very narrow range. This is due to the drastic effect of the exponential factor, whereas the prefactor has a rather weak influence. The values of φ_r and in particular r for which closure occurs, thus hardly depend on the time allowed for closure, and are very robust to the details of the closure criterion.

FIGURE 13.

Stability diagram of disks toward closure to form vesicles as a function of rim area fraction φ_r covered by bile salt and disk radius r. Bold lines correspond to V_f = 0, 1, and 2, which delimit regions of stable, metastable, and unstable disks. Shown are also lines of constant closure time τ_c = 10⁻³ s (solid line), 1 s (dashed line), and 10³ s (dotted line), respectively. Parameters: a_D = 200 Ų, Λ₀ = 0.3 kT/Å, and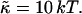

Growth, closure, and end-state vesicle size

Because the initial disklike micelles are stable toward closure, they first grow (see “Growth”) until their radius reaches a threshold r^* and closure becomes faster than growth. While the disks grow, the total rim surface A_t decreases and the rim area fraction φ_r covered by bile salt increases and stabilizes the disks by lowering the line tension Λ (Fig. 10). Therefore, r^* and hence the vesicle size R, depend on the actual value of φ_r(t). This results in a time-dependent threshold r^*(t). The mechanism of the growth process, which determines φ_r(t) and hence r^*(t), is thus crucial for the determination of the vesicle size and polydispersity. To our knowledge, this connection, which demonstrates the importance of kinetics for the final vesicle size (or strictly, size distribution), has not been clearly identified before.

The threshold radius r^* leads to a “sink” for disks with radius r ≥ r^* because they form vesicles that are inert. The feedback of the changing disk composition on r^* and hence the vesicle radius R, requires a numerical solution of the Smoluchowski rate equations with a continuous update of 𝒦_ij(t) and r^*(t). We can nevertheless qualitatively rationalize the trend of the end-state vesicle size R as a function of salt concentration c_s and dilution d (Fig. 6). For constant dilution d, electrostatic repulsion between bile salt molecules is progressively screened upon increasing c_s leading to faster growth, but also a higher tendency of the bile salt to cover the rim and thus a reduced line tension Λ with a resulting increase in closure time τ_c. Disks will thus grow further before they close. The dramatic increase of vesicle size R over a rather narrow range of c_s (Fig. 6, d = 80 and 120) corresponds to the sharp drop in line tension Λ arising from a salt-induced increase of rim coverage φ_r (Fig. 9). On the other hand, for constant c_s, increasing the dilution has a relatively small effect on the growth time (see “Initial growth”), but τ_c significantly drops in response to the decrease in φ_r and resulting increase in Λ (Fig. 9). With increasing dilution disks will thus close earlier, and smaller vesicles will form.

For a quantitative examination, we use the two previously described limits: 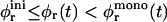(Eq. 19). Equating φ_r(t) to its initial value 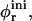the underestimated rim coverage leads to an overestimation of Λ and thus favors closure resulting in an underestimated vesicle size. An underestimated rim coverage also results in an underestimated electrostatic interaction and hence in an overestimated growth rate and an overestimated vesicle size. Due to the strong dependence of τ_c on φ_r and r (Fig. 13), the effect on Λ clearly dominates. For the same reason, monodisperse growth overestimates the vesicle size, so that Rⁱⁿⁱ ≤ R < R^mono. We expect the lower bound to provide a better estimate for small final vesicles, when only limited growth occurred before closure, whereas the upper bound is more appropriate for large vesicles (but even in this case represents only a hypothetical limit). In these two limits we can calculate the total growth time τ_G, which we approximate by τ_G ≈ τ_G(i) = (𝒦_iin_i)⁻¹. (Because the growth time increases with disk size (see “Growth”), a better approximation would be τ_G = (𝒦_1in_i)⁻¹, but this is not consistent with a monodisperse growth scheme.) The growth time τ_G is then compared to the closure time τ_c. Closure is expected to occur for τ_G ≥ τ_c (the “closure criterion” discussed previously). This defines the threshold disk radius r^* and thus the end-state vesicle radius R = r^*/2. The rate coefficients 𝒦_ij (Eq. 16) and thus the growth time τ_G depend on the disk size r by a power law, whereas the closure time τ_c is related to r by an exponential factor (Eq. 22) and thus shows a much stronger dependence on r.

In practice, to determine the threshold disk radius r^* as a function of salt concentration c_s and dilution d we use the following algorithm: τ_G and τ_c are calculated for r_i with i incremented until the closure criterion, τ_G ≥ τ_c, is met. In the limiting case of fixed disk composition, 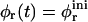is constant, whereas in the limit of monodisperse growth the equations determining the composition of the disks (Eqs. 5, 6, and 7) have to be solved at each step. Before a quantitative comparison of the final vesicle size with experimental data is presented (see “Comparison with experimental data: vesicle size”), we first examine the entire kinetics and the connection between the c_s- and d-dependences.

In the limit 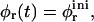the rim coverage is known and kept constant. This allows us to calculate all rate coefficients 𝒦_ij and to solve the Smoluchowski rate equations numerically. Vesicle formation is modeled by introducing a “sink” value r^* above which disks close spontaneously and are removed from the process described by Eq. 10. The temporal evolution of densities {n_i(t)} can then be determined and the time evolution of the total scattering intensity I(t) as well as the contributions by disks and vesicles can be calculated. A typical example is shown in Fig. 14. The initial increase of I(t) is caused by the growth of disks, whose contribution, however, soon decreases due to the closure of large disks to form vesicles. At the same time, the contribution of vesicles increases from zero intensity until the final scattered intensity is reached when all disks have been transformed to vesicles. The time dependence of the total scattered intensity I(t) is qualitatively very similar to the measured scattering intensity (Fig. 3). Both show an inflection point at early times that is related to the interplay between the disappearance of disks and the formation of vesicles. This implies a nonexponential time dependence and suggests that the kinetics of the transition is not well described by a simple first order kinetics or half-life.

FIGURE 14.

Calculated time evolution of the total normalized scattering intensity (solid line) and the contributions of disks (dashed line) and vesicles (dotted line). Calculations are based on the approximation of constant (initial) composition, electrostatic interactions with constant potential, and closure occurring at r^* = r₅. The other parameters are chosen to match our experimental conditions.

Dependence on salt concentration and dilution

As previously discussed, φ_r is a crucial parameter, which not only affects the electrostatic interactions and thus growth and τ_G, but, more importantly, line tension Λ and thus τ_c (Eqs. 9 and 22). This suggests that any combination of c_s and d that produces the same φ_r, not only corresponds to the same aggregate composition, but, crucially, should result in similar kinetics and thus final vesicle size R. We now derive such a relation between c_s and d for the special case of large disks (and thus large vesicles).

The disk size as a function of rim coverage φ_r diverges for a rim coverage 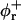(Fig. 13), which corresponds to a vanishingly small line tension Λ. For Λ = 0, Eq. 9 yields

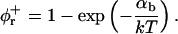(23)

Furthermore, in the limit of large disks, the relative total rim area density A_t(r)/A_t(r₁) vanishes and almost all bile salt is in bulk (Eq. 5):

(24)

Eqs. 6 and 7 now provide the relation between 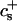and d for combinations, which produces the same :

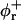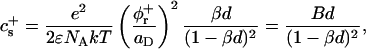(25)

with 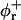given by Eq. 23 and

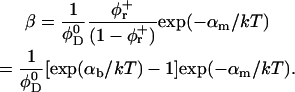(26)

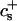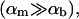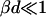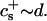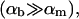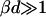Here α_b = a_DΛ₀L/A → a_DΛ₀/πρ for large disks with (Eq. 9). The dependence of on d is governed by βd, which in turn is controlled by the balance between the micellization energy α_m and the binding energy α_b (see “Mechanical properties”). If the hydrophobic nature of the molecule dominates then and On the other hand, if the edge activity dominates then and 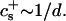In the intermediate regime, 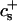shows a strong dependence on d and diverges for d = 1/β.

Fig. 15 a shows agreement of the experimental trend in 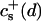with Eq. 25, producing the fit values β = 3.91 × 10⁻³ and B = 1.98 mM (see “Comparison with experimental data: vesicle size”). Furthermore, if we use these fitted values to normalize c_s by the dilution-dependent 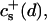we expect the vesicle radius to diverge for 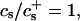so that the data sets for different dilutions should lie on top of each other for large vesicle radii, i.e., close to 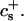This is observed (Fig. 16 b); in fact, the data collapse extends to very low 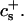This suggests that the above equivalence between c_s and d (Eq. 25) not only holds for large vesicles, but is more generally valid.

FIGURE 15.

(a) Salt concentration 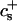for which the disk radius diverges as a function of dilution d. The line is a fit based on Eq. 25 and yields β = 3.91 × 10⁻³ and B = 1.98 mM. The insert shows a semilogarithmic plot of the same data. (b) Binding energy a_DΛ₀/πρ as a function of micellization energy α_m. The line corresponds to combinations satisfying β = 3.91 × 10⁻³. (c) Line tension in the absence of bile salt, Λ₀, as a function of rim area a_D covered by one bile salt molecule. The line corresponds to combinations satisfying B = 1.98 mM. Combinations in the hatched area are excluded because the calculation is based on the monodisperse growth regime (see text for details). The set of parameters that fits all our data best is represented by ⊕.

FIGURE 16.

End-state vesicle radius R as a function of (a) salt concentration c_s for dilutions d = 80 (○) and d = 120 (•) and (b) normalized salt concentration 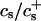for different dilutions d (▴: 40, ⋄: 50, ▪: 60, ○: 80, •: 120) with 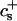calculated according to Eq. 25. Lines are calculated based on the monodisperse growth (solid line) and fixed composition (dashed line) approximations, respectively, using a_D = 200 Ų, α_m = 10 kT, and Λ₀ = 0.3 kT/Å. The lines in panel b are calculated for d = 120.

Comparison with experimental data: vesicle size

The predictions of our model are now compared to the end-state vesicle size, which we determined by light scattering for different salt concentrations c_s and dilutions d (Fig. 6). The data should be bracketed by the two limits of constant composition and monodisperse growth (Eq. 19). The fact that the model predicts only bounds rather than actual values complicates the fit procedure. Fit parameters are Λ₀, a_D, α_m, and 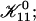note that preliminary estimates for the latter two parameters were already determined by fitting our kinetic data (see “Comparison with experimental data: rate of initial growth”). Their determination is based on Eq. 25, which is used to fit the experimentally determined dependence on dilution d of the salt concentration 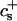for which the vesicle radius diverges (Figs. 6 and 15 a). The effect of d on 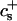is found to be strong and we obtain β = (3.91 ± 0.01) × 10⁻³ and B = (1.98 ± 0.01) mM. The value of β depends on the binding energy a_DΛ₀/πρ and the micellization energy α_m (Eq. 26) with the solid line in Fig. 15 b indicating all combinations consistent with β = 3.91 × 10⁻³. Because the binding energy depends on a_DΛ₀, fits for a_D and Λ₀ are coupled. They can, however, be determined using B (Eq. 25), which provides a relation between a_D and Λ₀ (solid line in Fig. 15 c). Because Eq. 25 is only strictly valid for the limit of monodisperse growth and large vesicles, B is an upper bound and thus values above the solid line in Fig. 15 c (hatched area) have to be excluded. These arguments can only guide the determination of the fit parameters. The values were refined by considering both limiting approximations for φ_r(t) (fixed composition and monodisperse growth; see “Growth, closure, and end-state vesicle size”), and both limits for the electrostatic interactions (constant charge and constant potential; see “Interactions between disklike micelles”). A comparison with all our data for the end-state vesicle size and initial growth rate, yields Λ₀ = 0.3 kT/Å, a_D = 200 Ų, α_m = 10 kT, and 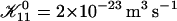as best values (⊕ in Fig. 15, b and c). These values lead to a consistent description of all our experimental data; the limits calculated based on our model bracket most of the kinetic data on the initial growth rate (Figs. 4 and 5) and the end-state vesicle size as a function of salt concentration c_s and dilution d (Fig. 16). They also lead to a good collapse of the different dilution series (see “Dependence on salt concentration and dilution”; Fig. 16 b), which is very sensitive to the choice of parameters.

These values of the fit parameters agree well with literature values and other estimates where available. The value Λ₀ = 0.3 kT/Å lies in the range of values, 0.2–0.8 kT/Å, cited in the literature (see “Mechanical properties”) (Moroz and Nelson, 1997). No value of a_D exists for the adsorption on a rim. However, at the (flat) air-water interface a_D ≈ 150 Ų was found (Small, 1973), whereas the size and aggregation number of pure (spherical) bile salt micelles imply a_D ≲ 250 Ų (Schurtenberger et al., 1983; Janich et al., 1998). These values thus bracket our value of a_D = 200 Ų. To our knowledge, α_m has not been determined. It, however, controls the monomer concentration of bile salt, which has been determined (Small, 1973; Duane, 1977). According to our model, the partitioning constant of the isotherm reads:

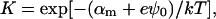(27)

which depends on composition, i.e., c_s and d. It provides an estimate for the order of magnitude of the monomer concentration c_b = K/v_DN_A. For α_m = 10 kT, c_s = 150 mM, and 50 ≤ d ≤ 150, we obtain 0.37 ≤ c_b ≤ 0.55 mM (see also Fig. 9 b). This value is comparable to the bulk bile salt concentration in solutions containing lipid-bile salt mixed micelles (∼0.5 mM, (Small, 1973; Duane, 1977)).

Ripening

Ripening of our vesicles to their equilibrium size was not observed, but might occur on a very long timescale. The observed near-indefinite lifetime of the end-state liposomes, despite the fact that they are kinetic in origin, shows that both monomeric diffusion (Ostwald ripening) (Somoza et al., 1996; Zhdanov and Kasemo, 2000; Olsson and Wennerström, 2002) and vesicle fusion or fission (Golubovic and Golubovic, 1997) are ineffective in bringing these liposomes to thermal equilibrium. The first observation is consistent with the very low solubility of lecithin and the second with our finding that, among the disklike intermediates, coalescence is edge-to-edge and not face-to-face. In contrast, relaxation to equilibrium may occur more rapidly for vesicles more prone to fusion or fission and/or formed by more soluble amphiphiles, such as some mixtures of anionic and cationic surfactants (Kaler et al., 1989; Madani and Kaler, 1990; O'Connor et al., 1997; Marques, 2000; Schmölzer et al., 2002). The ability to ripen or fuse thus plays an important role in determining whether vesicles reach equilibrium or represent kinetically trapped, metastable states of very long lifetime and may give a new physicochemical basis for their classification (Marques, 2000). Moreover, there are indications (Edwards and Almgren, 1992; Lopez et al., 2001) that a coarsening mechanism leading to partial equilibration could be mediated by coexisting mixed micelles or simple bile salt micelles, if present.

Stacking

It is possible that under certain conditions disks cannot only grow and close, but also stack. This would prevent vesicle formation and could result in the development of lamellar (smectic A) phase as the end state. Stacking is driven by the van der Waals attraction between parallel disks, which for distances of ∼20 Å dominates for high enough salt concentrations c_s over electrostatic repulsion and steric effects, such as hydration and protrusion. Although this is known to stabilize lamellar phases (Israelachvili, 1992), we have to consider the particular properties of disks, especially their finite size, the effect of a displacement of their centers and a tilt of the disk normals. The interaction energy shows a well, but this is significant only for a small fraction of configurations (nearly parallel, hardly displaced or tilted disks at an optimum distance) and for disks that have grown already. Stacking is thus a rare event leading to an “entropy barrier” and a reaction-limited mechanism rather than a diffusion-controlled process, although there might be no energy barrier to overcome. The characteristic stacking time τ_s depends on salt concentration c_s, dilution d, and disk radius r and, for negligible electrostatic interactions (i.e., high c_s), is estimated to be of a similar order of magnitude as the other timescales, the growth time τ_G and closure time τ_c. Stacking could therefore represent a possible path at high salt concentrations (Fig. 7). An accurate estimate of τ_s is, however, needed before a meaningful kinetic criterion can be developed for stacking to occur before vesiculation, leading to a smectic end state.

CONCLUSION AND OUTLOOK

Our semiquantitative kinetic model describes the fundamental kinetic steps during vesicle formation: rapid formation of disklike intermediate micelles, growth of these micelles, and closure to form vesicles (Fig. 7). It also identifies the important control parameters (d, c_s, Λ, α_m), which determine the kinetics as well as the end-state vesicle size. The vesicle size results from the competition between growth and closure and thus a kinetic criterion. The fact that our model reproduces the experimental trends (including the kinetic rates as well as the end-state size of the vesicles) indicates that liposomes in our system, despite their spontaneous formation, are nonequilibrium metastable structures with a size controlled by kinetics, not thermodynamics. This explains why calculations based on thermodynamic equilibrium (Safran et al., 1990, 1991) fail to predict the experimentally observed dependence of vesicle size on composition (Schurtenberger et al., 1985; Hjelm et al., 1990; Long et al., 1994; Egelhaaf and Schurtenberger, 1994; Kozlov and Andelman, 1996).

Our model was developed and tested for aqueous mixtures of lecithin and bile salt. In particular the very low solubility of lipid molecules and the large energy barrier toward fusion or fission are key factors that prevent any significant equilibration of the vesicles once they are formed. This is in contrast to most surfactant systems, where self-assembly is fully reversible and the entire system reaches thermodynamic equilibrium in a relatively short time. A physicochemical classification of vesicles (Marques, 2000) may thus be based on the ability of vesicles to ripen or fuse. A complete picture should, however, also include stacking of (large) disklike micelles. A comparison of growth, closure, and stacking rates is expected to provide a kinetic criterion to decide whether vesicles are formed, as we have assumed, without creation of lamellar (smectic A) phase intervening. Although we suggest that vesicles are nonequilibrium, kinetically trapped structures with a very long lifetime, the lamellar (smectic A) phase could well be the real equilibrium state of the system. The proposed model therefore suggests a possible need to reconsider the phase behavior of lipid-detergent systems in the dilute regime.

Although our model is based on lecithin-bile salt mixtures, variants of the model could perhaps be applied to other systems, in particular other lipid-detergent mixtures (Jiskoot et al., 1986; Kaler et al., 1989; Edwards and Almgren, 1991; Silvander et al., 1996; O'Connor et al., 1997; Campbell et al., 1998; Brinkmann et al., 1998; Chen et al., 1999; Marques, 2000; Ollivon et al., 2000; Almgren, 2000; Xia et al., 2002; Schmölzer et al., 2002) or lipid-peptide mixtures (Dufourc et al., 1986; Saitoh et al., 1998; Suezaki et al., 1999), which undergo a similar micelle-to-vesicle transition. Because the parameters Λ, and α_m are independently accessible for various other systems, it should be possible to predict and understand their behavior based on the model we present here; we are currently investigating this. It might also be possible to control the vesicle formation and end-state vesicle size by choosing appropriate amphiphiles or amphiphile mixtures as well as favorable solution conditions. This offers the possibility, for mankind and nature, to prepare kinetically trapped structures, which can be less sensitive to environmental changes than equilibrium ones. This might be particularly interesting for the preparation of functional vesicles with encapsulated or incorporated molecules (Lasch, 1995; Rosoff, 1996); for the reconstitution of membrane proteins (Ollivon et al., 2000); or for the creation of two-dimensional crystals of membrane proteins (Rigaud et al., 2000). These studies should profit from an improved understanding of the micelle-to-vesicle transition, in particular the evolution of intermediate structures and the parameters controlling this sequence. Although our experiments used dilution to remove detergent (bile salt) from the aggregates, it should also be applicable to other detergent removal techniques, such as dialysis, temperature jumps, or biochemical reactions (Ollivon et al., 2000). The introduction of a kinetic criterion will also permit a comparison with other experimental timescales, such as the rate of detergent removal during dialysis. The influence of these rates on the properties of the end-state vesicles (Seras-Cansell et al., 1996; Ollivon et al., 2000) could then possibly be rationalized.

Particularly striking is the strong dependence of the end-state vesicle size on NaCl concentration which, through its effect on the (charged) bile salt, modulates the kinetics although there is little bile salt left in the end-state vesicles (at least for the higher dilutions). This illustrates that the kinetic pathways that arise under physiological conditions can sometimes best be studied by applying controlled deviations from these conditions. In many applications of liposomes, as mentioned previously, a large range of solution parameters must be searched to find the best conditions to ensure the desired end-state properties. It is hoped that knowledge about the dependence of the kinetic pathway on important control parameters, such as salt concentration, may help to reduce this effort. It is also interesting that under physiological conditions and using a physiological detergent (bile salt), vesicles form on a physiologically significant timescale of minutes.

APPENDIX A

Rate of initial growth

In our simultaneous static and dynamic light scattering experiments we determined the time dependence of the total scattered intensity I(t) and average diffusion coefficient D(t) (see “Relaxation after a dilution step”). Their normalized initial slopes were converted to rates (Eq. 1). In this appendix we quantitatively link the experimentally determined initial slopes to our model, in particular the growth time (Eq. 18) and kernel 𝒦₁₁ of the Smoluchowski rate equations (Eq. 10).

The total scattered intensity I(t) is the sum of the individual scattered intensities of all species present, because the concentrations of our samples are low enough (below ∼1 mg/ml) to neglect interactions between aggregates. During the very early stage, we only consider contributions from the initial disklike micelles and disklike micelles created by coalescence of two initial micelles (number densities n_i, radii r_i, thickness ρ):

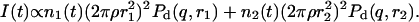(28)

Due to the small size of the disks, the form factor P_d(q, r_i) ≈ 1 for our q-range. Using the first-order expansion of the Smoluchowski rate equations (Eq. 10) at t → 0,

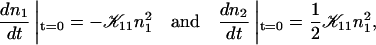(29)

we obtain for the initial slope of I(t)

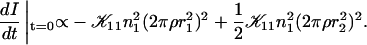(30)

With 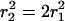and Eq. 18, the normalized initial slope hence is

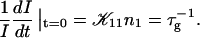(31)

The parameter β_I in Eq. 1 is thus β_I = 1.

To calculate the average diffusion coefficient D(t), the individual diffusion coefficients D_i have to be weighted by the corresponding scattered intensities I_i(t). We again only take the two smallest disks into account and obtain

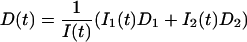(32)

and

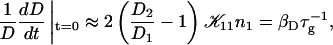(33)

using Eqs. 29 and 31 and considering that D(0) = D₁. The proportionality constant β_D depends on the size of the disks. For disks with radii r₁ = 80 Å and r₂ = 2^1/2r₁ and thickness 2ρ = 50 Å, as observed in our experiments, we obtain β_D = 0.38.

APPENDIX B

Kernels

In this appendix we estimate the rate coefficients or kernels 𝒦_ij of the Smoluchowski rate equations (Eq. 10). In our system the topological barrier dominates over the dlvo interactions (see “Interactions between disklike micelles”). They represent a significant barrier to coalescence with a height of typically 10–30 kT. The system is thus reaction limited and the kernels read (Ball et al., 1987):

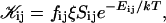(34)

where f_ij is the attempt frequency for coalescence, ξ the distance over which coalescence can occur, S_ij the reaction surface (and thus ξS_ij the reaction volume, Fig. 11), and E_ij the potential of the transition state (the “fusion barrier”). In a reaction limited regime, the reaction (i.e., coalescence) has a very low probability and many attempts to cross the high energy barrier are required until coalescence occurs. Phase space at the transition state is hence fully explored. We can thus use a statistical approach that is based on the calculation of the partition function restricted to the conditions where disks can coalesce, i.e., the transition state portion of phase space (Hänggi et al., 1990). As will be shown below, this provides an estimate of the reaction surface S_ij and a decoupling approximation for the potential of the transition state E_ij. This statistical approach does, however, not consider the characteristic timescale and will therefore not provide an estimate for the attempt frequency. The attempt frequency f_ij depends on the motion (diffusion) of the disks and their interaction potential. It can be estimated using a deterministic approach solving the “equations of motion” (Hänggi et al., 1990), which is often rather involved, particularly for anisotropic objects with orientation-dependent interactions. In the following we will combine these two approaches to obtain an estimate of the kernel 𝒦_ij and its dependence on disk radii r_i and r_j and solution conditions, such as salt concentration c_s and dilution d.

Reaction surface and fusion barrier

We first use the statistical approach to estimate the reaction surface S_ij and to investigate the role of the fusion barrier E_ij. The reaction surface is essentially the surface that two disks may sample before coalescence. For a disk of radius r_j, which samples all configurations at the transition state near a disk of radius r_i, the reaction surface scales as S_ij ∼ r_j(r_i + r_j) (Fig. 11 b) if we assume that all configurations have the same fusion barrier. This estimate does not take into account that different regions of the reaction surface, and thus different configurations 𝒞, have to be weighted by their (different) transition energies through their Boltzmann factors. To determine the Boltzmann-weighted reaction surface Z_ij = S_ij exp(−E_ij/kT), we calculate the partition function of the system Z_ij restricted to the transition state configurations 𝒞:

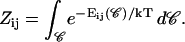(35)

The fusion barrier E_ij(𝒞) = E_t(α) + E_d,ij (h_f, ϕ, α) involves the bare edge-to-edge fusion energy E_t(α) and the dlvo part E_d,ij (h_f, ϕ, α) (see “Interactions between disklike micelles”). The orientations, i.e., ϕ and α, are illustrated in Fig. 11 a. The dlvo part shows a weak dependence on α (through the Deryaguin approximation, Eq. 14), which we neglect here. As a result of this approximation, the dlvo and bare fusion contribution become decoupled:

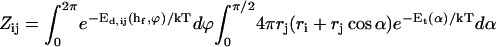(36)

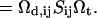(37)

The first integral is essentially the average dlvo Boltzmann factor Ω_d,ij. The second integral can be written as the product of the reaction surface S_ij and topological Boltzmann factor Ω_t. Both depend on the angular dependence of the bare fusion barrier E_t(α), which, however, only affects the prefactors. We will use:

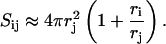(38)

and

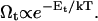(39)

Little is known about the bare fusion barrier and we thus use Ω_t as a fit parameter; it is, together with further unknown parameters, included in the fit parameter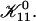

Attempt frequency

Now the motion of the aggregates is examined to obtain an estimate of the attempt frequency f_ij and length ξ. This involves solving a mutual diffusion equation. For the sake of simplicity, we examine two approaching spheres, which we expect to show the same trends as two disks. The diffusion equation gives the number N_j of spheres j undergoing diffusion toward a sphere i and subsequent aggregation per unit time (Russel et al., 1991):

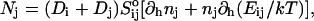(40)

where E_ij(h) is the interaction potential and 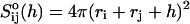the reaction surface with h the surface-to-surface distance between interacting spheres. With the boundary conditions n_j(h → ∞) = n_j and n_j(h = h_f) = 0, one obtains (Hänggi et al., 1990)

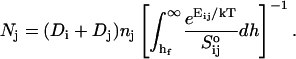(41)

To solve this equation, we have to estimate the functional form of the fusion potential E_ij(h). (Note that for the statistical approach above, we only considered the height of the barrier E_ij(h_f).) Based on earlier considerations, it is reasonable to assume that the fusion potential is peaked around h_f and large, i.e., 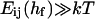(Fig. 17). The exponential in Eq. 41 thus contributes mainly around h = h_f. We hence expand E_ij(h) around h_f:

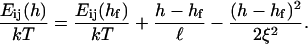(42)

The penetration length of the potential ℓ is defined as

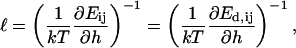(43)

using the fact that we expand E_ij around the maximum of E_t. This expansion reduces the dlvo potential to a driving force (−kT/ℓ). The radius of curvature of the topological potential −ξ is given by

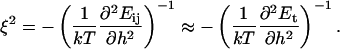(44)

Although the following results and conclusions depend on this expansion, the trends are general (Hänggi et al., 1990). To calculate the integral in Eq. 41, we limit the integral to the range where we expect the major contribution: h_f ≤ h ≤ h_F with E_ij(h_F) = E_ij(h_f) − kT (Fig. 17). Using 𝒦_ij = N_j/n_j and Eq. 34, we obtain

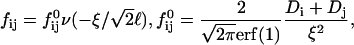(45)

and

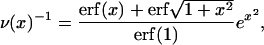(46)

with erf(x) the error function and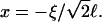

FIGURE 17.

Schematic representation of the interaction potential between two disklike micelles as a function of their surface separation h. The total potential E(h) (“fusion potential,” solid line) consists of the topological barrier E_t (“bare fusion potential,” dotted line) and dlvo interactions E_d(h) (dashed line). Fusion typically occurs at a separation h_f, while disks may fuse over a distance ξ. An expansion of E around h = h_f defines a “penetration length” ℓ and a “radius of curvature” ξ.

In the absence of any interaction other than the bare fusion potential, the penetration length diverges (ℓ → ∞ and thus x → 0) and 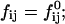the process is governed by diffusion across the bare fusion barrier only. However, ℓ takes finite values if further interactions are present, which might either be repulsive (x > 0) or attractive (x < 0). Depending on whether the driving force introduced by the additional potential hinders (repulsive) or aids (attractive) crossing of the bare fusion barrier, ν(x) either decreases or increases. Therefore, 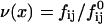reflects the modification of the attempt frequency by the additional (dlvo) potential. If the bare fusion potential is sharply peaked at h_f relative to the length scale of changes in the additional potential, i.e., then ν(x) ≈ 1 and 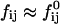independent of the nature of the additional potential. We assume that this is the case.

The combination of the attempt frequency f_ij and distance ξ, over which coalescence can occur, with the estimates from the statistical approach for the weighted reaction surface S_ij (Eq. 38) and its Boltzmann factors (Eqs. 36, 37, and 39) yields the rate coefficients 𝒦_ij (Eq. 34).