Dynamics of Pinned Membranes with Application to Protein Diffusion on the Surface of Red Blood Cells

Abstract

We present a theoretical treatment and simulation algorithm for the dynamics of Helfrich elastic membrane surfaces in the presence of general harmonic perturbations and hydrodynamic coupling to the surrounding solvent. In the limit of localized and strong interactions, this harmonic model can be used to pin the membrane to intracellular/intercellular structures. We consider the case of pinning to the cytoskeleton and use such a model to estimate the macroscopic diffusion constant for band 3 protein on the surface of human erythrocytes. Comparison to experimental results suggests that thermal undulations of the membrane surface should play a significant role in protein mobility on the red blood cell.

INTRODUCTION

Biological membranes are essential for life as we know it (Gennis, 1989; Lipowsky, 1991; Lodish et al., 1995). The central role played by membranes and membrane dynamics in biological processes has generated strong interest in simulation algorithms for lipid bilayers in recent years. Perhaps the most prevalent studies to date have involved molecular dynamics (MD) simulation on atomically detailed lipid/water models (Feller, 2000; Pastor, 1994; Tobias et al., 1997; Tieleman et al., 1997; Marrink et al., 2001). Unfortunately, the usual computational limits inherent to fully atomic models preclude MD from simulating processes that occur on length scales significantly larger than several nanometers and/or timescales significantly longer than tens of nanoseconds. Many membrane-dependent biological processes cannot be studied with MD for this reason. Representative examples of processes inaccessible to direct MD simulation include lateral diffusion of lipids/proteins in complex environments (Jacobson et al., 1995; Koppel et al., 1981), cellular motility (Pollard et al., 2000; Stossel, 1993; Theriot and Mitchison, 1991; Howard, 2001), lipid raft dynamics (Sheets et al., 1995; Simons and Ikonen, 2000), long-ranged membrane-mediated protein-protein interactions (Marcelja, 1976; Owicki et al., 1978; Lague et al., 1998; Dan et al., 1993; Goulian et al., 1993; Kim et al., 1998; Weikl, 2002), and budding in multicomponent membranes (Kumar and Rao, 1998; Kumar et al., 2001).

Various simulation methodologies have emerged in attempts to bridge the gap between slow biological processes and the limitations of MD. A number of models represent each lipid molecule by one or more simple shapes (spheres, ellipsoids, or rods) in flexible or rigid configurations. The majority of such models include explicit solvent in the form of hydrophilic spheres (Shillcock and Lipowsky, 2002; Yamamoto et al., 2002; Lopez et al., 2002; Smit et al., 1993; Groot and Rabone, 2001; Goetz and Lipowsky, 1998; Soddemann et al., 2001; Ayton et al., 2001), whereas a few have succeeded in capturing fluid membrane behavior without solvent (Drouffe et al., 1991; Noguchi and Takasu, 2001; Farago, 2003; Brannigan and Brown, 2003). Hybrids of particle-based and continuous methods, such as tethered membranes, are able to investigate macroscopic properties while retaining some mesoscopic resolution (Kantor et al., 1987; Ho and Baumgartner, 1990; Baumgartner and Ho, 1990; Lipowsky and Zielenska, 1989; Kumar and Rao, 1998; Ayton and Voth, 2002). Although many of these models hold promise for illuminating various biological processes, simulations of simplified membranes have so far been conducted primarily for model testing and the measurement of material properties.

Historically, theoretical studies of membrane biophysics predate simulations. The work of Helfrich (1973) established an elastic model for membrane energetics that has since seen use in diverse studies ranging from the “flicker” effect in red blood cells (Brochard and Lennon, 1975) to the interaction between membrane-bound proteins (Dan et al., 1993; Goulian et al., 1993; Kim et al., 1998; Golestanian et al., 1996; Weikl, 2002) and the formation of the immunological synapse (Qi et al., 2001). When combined with stochastic low-Reynolds-number hydrodynamic coupling to the surrounding solvent (Milner and Safran, 1987; Schneider et al., 1984; Brochard and Lennon, 1975; Granek, 1997; Brown, 2003) the Helfrich picture provides a means to study bilayer dynamics as well as thermodynamics/energetics.

Although simulations involving dynamic elastic sheets have seen some recent use in biophysics (Laradji, 1999; Qi et al., 2001; Brown, 2003) the main use of such models has been in analytical theory. In this article, we describe a normal mode decomposition for elastic membrane sheets in quasiplanar geometries. When interactions with the membrane can be treated harmonically, the transformation to normal modes allows for exact time evolution analogous to such transformations in crystals (Ashcroft and Mermin, 1976) and molecules (Atkins, 1990). The power of this approach is that it enables the study of membrane dynamics in situations involving interaction with external perturbations, but with the flexibility to choose long time steps, thus making simulation of slow biological processes feasible.

In this work, we apply this simulation methodology to the mobility of membrane-bound proteins on the surface of the red blood cell. The motion of proteins on the erythrocyte surface (Cherry, 1979; Koppel et al., 1981; Schindler et al., 1980; Sheetz et al., 1980; Sheetz, 1983) is known to exhibit deviations from the purely diffusive behavior predicted by the fluid mosaic model (Singer and Nicolson, 1972; Saffman and Delbruck, 1975). Although such deviations are certainly not unique to red blood cells (Jacobson et al., 1995; Saxton and Jacobson, 1997; Fleming, 1987; Winckler et al., 1999; Saxton, 1990b), band 3 protein on the surface of erythrocytes has been particularly well studied in this context. It is now generally accepted that transmembrane proteins with significant intracellular domains exhibit two diffusion constants on the erythrocyte surface: a microscopic diffusion constant over short length scales and a smaller macroscopic diffusion constant over length scales longer than tens of nanometers (Tsuji and Ohnishi, 1986; Tsuji et al., 1988; Edidin et al., 1991; Corbett et al., 1994; Kusumi and Sako, 1996; Tomishige, 1997; Tomishige et al., 1998). This behavior is attributed to interactions between mobile proteins and the underlying spectrin network of corrals as proposed in the matrix (Sheetz, 1983) or skeleton fence (Kusumi et al., 1993) model (see Fig. 1).

FIGURE 1.

Schematic illustration of the behavior of transmembrane proteins in the red blood cell (the matrix or skeleton fence model). The cytoskeleton immediately below the membrane hinders protein transport by confining the protein temporarily to a localized corral (a). Jumps from one corral to another occur slowly and have previously been postulated to result from dynamic reorganization of the cytoskeletal matrix, by (b) dissociation of spectrin tetramers, (c) thermal fluctuations in the shape of the cytoskeleton, or (d) infrequent crossing events where the protein is thermally kicked hard enough to force its way over a relatively static cytoskeleton. This study considers a different possibility—that shape fluctuations of the lipid bilayer may allow for corral hopping (e).

Although the skeleton fence model appears consistent with experiment (at least in the case of red blood cells), the mechanism by which the protein escapes from corrals has not been definitively established. Previous theoretical studies have either used very general models to fit the experimental data (Saxton, 1995) or have assumed that rearrangements of the spectrin network are necessary for a protein to escape confinement (Saxton, 1989, 1990a,b; Boal, 1994; Boal and Boey, 1995; Leitner et al., 2000; Brown et al., 2000). In recent work (Brown, 2003), we considered the possibility that fluctuations of the lipid bilayer could assist proteins in escaping localized corrals. Although our study provided qualitative support for this hypothesis, the modeling did not allow for explicit coupling between spectrin and the lipid bilayer. The present work extends our earlier model to include pinning between the lipid bilayer and underlying spectrin network via the harmonic pinning interactions discussed above. Our models again indicate support for the theory that thermal bilayer fluctuations are involved in protein mobility over the cell surface.

The organization of this article is as follows. In the next section, we introduce the equations that govern the dynamics of our pinned membrane and are the basis of our Fourier space Brownian dynamics method. We then show that the Fourier representation provides us with a convenient way of performing simulations by evolving membrane configurations stochastically in time. Analytical results for our model are presented and subsequently used to study the importance of membrane fluctuations in protein mobility over the surface of the red blood cell. In the last section, we discuss the results and conclude.

A PINNED MEMBRANE MODEL

We begin by specifying the Hamiltonian for a lipid bilayer as the Helfrich bending energy (Helfrich, 1973) at zero surface tension plus a harmonic potential,

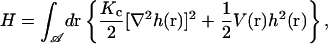(1)

where K_c is the bending modulus, 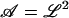is the projected area of the membrane, r = (x, y) is the position in the xy plane, and h(r) specifies the local displacement of the membrane away from the flat configuration defined by h(r) = 0. In general, Eq. 1 may be supplemented with a term to account for nonvanishing surface tension (Safran, 1994). We assume a negligible surface tension in this study for simplicity and because this condition is appropriate to the application we consider later. The function V(r) is at this point arbitrary, but will later be chosen to represent localized pinning to the cytoskeleton.

Although in some cases we study subportions of the membrane embedded within a larger system, we always consider the total system to be periodic over a square with sides of length ℒ. This geometry allows us to express the Hamiltonian in its Fourier representation,

(2)

where the Fourier transform pairs are

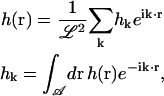(3)

and the k vectors are given by (2πm/ℒ, 2πn/ℒ) where m and n are integers. The Fourier representation allows us to find a set of decoupled eigenmodes, which we can evolve separately in time. For V(r) = 0, the modes are completely decoupled in the Fourier representation, whereas for nonzero V(r), decoupling is accomplished by further transformation (see Appendix A). It is important to note that for most of our applications, the amplitude of the k = 0 mode is set equal to zero so that the center of mass for the entire membrane does not move. Motion of the center of mass of the membrane corresponds to simple diffusion and is not typically of interest. It is possible to allow for diffusion of the center of mass as described in Appendix B.

Dynamics are described by the Langevin equation for a set of hydrodynamically interacting Brownian particles (Doi and Edwards, 1986) in the continuum limit. Inertia is neglected as is appropriate for the low-Reynolds-number environment of the cell (Purcell, 1977) and the assumption of linear response gives (Granek, 1997)

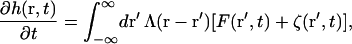(4)

where Λ(r − r′) is the hydrodynamic interaction specified by the Oseen tensor (Doi and Edwards, 1986),

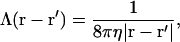(5)

F(r, t) is the force per area given by the functional derivative of the Hamiltonian,

(6)

and ζ(r, t) is a Gaussian white random force (van Kampen, 1992) that satisfies the fluctuation-dissipation theorem

(7)

and where the inverse of Λ(r − r′) is defined by

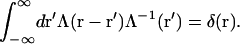(8)

Points on the membrane surface hydrodynamically interact with the rest of the membrane (including periodic copies) over the entire xy plane. Using the Fourier-transformed Oseen interaction

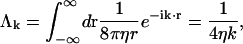(9)

we may rewrite the Langevin equation in its Fourier representation as

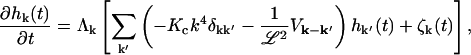(10)

where ζ_k(t) are the Fourier space components of ζ(r, t) (defined in the same way as in Eq. 3) that obey

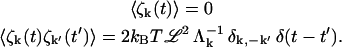(11)

The thermodynamics and stochastic time evolution of the membrane in Fourier space are completely specified by Eqs. 2, 10, and 11. Evolution in real space is realized by inverse Fourier transforming via Eq. 3.

Time propagation

The Fourier space equations of the previous section are suitable for developing a simple and efficient algorithm for studying membrane dynamics through simulations. In a previous article (Brown, 2003) we described such an algorithm for a free membrane sheet, but here we generalize to allow harmonic interactions such as pinning (very strong and very localized harmonic interactions). To proceed, we express the Hamiltonian and the Langevin equations in terms of appropriately decoupled eigenmodes indexed by i with amplitudes d_i and eigenvalues ω_i (see Appendix A for details),

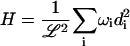(12)

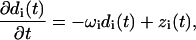(13)

where z_i(t) are random forces that satisfy

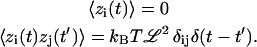(14)

The above equations represent a set of independent Ornstein-Uhlenbeck processes characterized by (van Kampen, 1992):

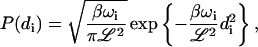(15)

(16)

where β = 1/k_BT, P(d_i) is the equilibrium probability distribution for the amplitude d_i and 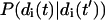is the conditional probability for mode i to have amplitude d_i(t) at time t given that it had the amplitude d_i(t′) at earlier time t′. The equilibrium probability distribution follows immediately from the Hamiltonian and the canonical distribution (Chandler, 1987) whereas the conditional probability follows from the solution to the Fokker-Planck formulation of the Langevin equation (van Kampen, 1992).

A complete discussion of the independent modes used in Eqs. 12–16 may be found in Appendix A. We do note here that these equations reduce to the results of our prior work (Brown, 2003) in the limit that V(r) = 0. In this case, the general transformations described in Appendix A imply that the eigenmodes d_i are given by the real and imaginary parts of the rescaled Fourier modes in the upper half-k plane. Furthermore, the eigenvalues for these modes are given by (real and imaginary parts share the same eigenvalue)

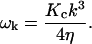(17)

Equations 12 and 13 then yield

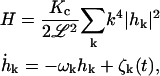(18)

which are identical to Eqs. 1 and 2 in our previous publication (Brown, 2003). Similarly, Eq. 4 of our earlier article follows immediately from Eqs. 15 and 16, provided the rules for transforming probability distributions are followed (van Kampen, 1992) and the fact that h_k contains independent real and imaginary contributions is taken into account.

Returning to the general problem, we now specify a method of simulation that allows us to evolve membrane configurations. First, we pick amplitudes from the equilibrium distribution in Eq. 15 by drawing from a normal distribution (Press et al., 1994). Real-space configurations are obtained by inverting the diagonalization transformation in Appendix A, and inverse Fourier transforming to get the position space heights at each point. To evolve forward in time from t′ to t, we again draw normally distributed amplitudes d_i(t) conditional on the value of d_i(t′) from Eq. 16. Inversion to real space through the same procedure as before leads to the membrane configuration at time t.

Because the Ornstein-Uhlenbeck process is Markovian and therefore depends only on time differences, we can take time steps that are as large or small as we desire; taking many small steps up to time t gives a final result that is statistically identical to one large step. The membrane can therefore be evolved arbitrarily far into the future with complete accuracy. Averages, correlation functions, and other statistical properties are calculated by sampling from sufficiently large ensembles of membranes generated by this technique. The procedure described here is analogous to Brownian dynamics with hydrodynamic interactions (Ermak and McCammon, 1978) with the distinction that eigenmodes are being evolved rather than positions. We have chosen a harmonic model to allow for arbitrarily large time steps. Although the mathematical derivation is tedious, it should be stressed that the eigenmode picture described above and in Appendix A is simply a normal mode decomposition for membrane surfaces evolving under overdamped stochastic dynamics.

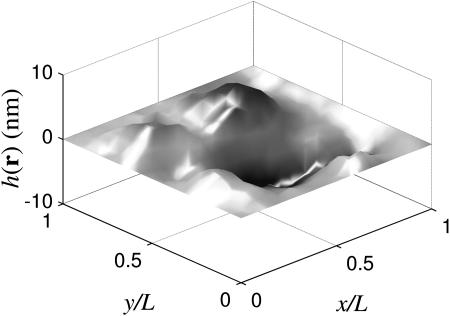
As an illustration of our method, we present several examples that demonstrate pinning of the membrane with harmonic potentials. In this section and in following sections, we choose physical parameters appropriate to the membrane of the red blood cell as listed in Table 1. As a first example, we pin the membrane around the border of a square corral by using V(r) = γ[δ(x) + δ(y)], where γ is sufficiently large to keep the membrane pinned along the two edges (the other two sides are automatically pinned by the periodic boundary conditions). In practice, we have used γ = 5 × 10⁶ ergs cm⁻² throughout this work. This value was chosen to be large enough to ensure that the sheet is effectively pinned. Increasing γ leads to no changes in any results reported in this or subsequent sections. One realization of the membrane generated using our simulation technique is shown in Fig. 2. Although thermal fluctuations are apparent in the middle of the sheet, all motion at the edges has been quenched by the pinning interaction.

TABLE 1.

Parameters for band 3 on the erythrocyte membrane

Parameter	Description	Value	Reference
Kc	Bending modulus	2 × 10−13 ergs	*
η	Cytoplasm viscosity	0.06 poise	*
T	Temperature	37°C	Body temp.
γ	Pinning constant	5 × 106 ergs cm−2
h0	Depth of cytoplasmic domain of band 3	6 nm	†
D	Band 3 diffusion constant	0.53 μm2 s−1	‡
λ	Lattice spacing	7 nm	§
tD	Random walk time step	23 μs	§

^*Brochard and Lennon (1975) and Zilker et al. (1992).

^†Zhang et al. (2000).

^‡Tomishige et al. (1998).

^§Brown (2003).

FIGURE 2.

Membrane configuration for a square sheet pinned along the border of the simulation box (ℒ = 112 nm) and using physical parameters (K_c,η,T,γ) from Table 1. Notice that half of the membrane is above the plane and half is below, as expected for h_k=0 = 0.

As a second example, we demonstrate pinning above the xy plane in Fig. 3. We have used

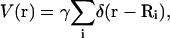(19)

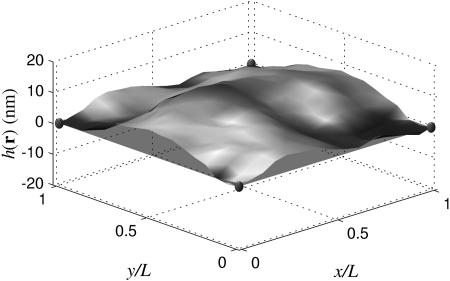
where the pinning sites are located at discrete R_i points in the plane with an additional term for pinning above the plane as in Eq. A19. Pinning the membrane over points distributed in three dimensions is mathematically possible, but forcing large amplitude, high curvature geometries results in structures inconsistent with the assumptions of our model. We will concentrate only on planar pinning geometries in this work with the exception of this particular example. We introduce at this point a new length scale L ≤ ℒ, which represents the size of the membrane that has been sampled from a possibly larger periodic box of linear dimension ℒ. These subregions have no restriction on the height of the center of mass. In Fig. 3 we see that over dimensions of L, the membrane is free to lie entirely above the z = 0 plane. A similar simulation, but with L = ℒ, results in a steeper cone-shaped protrusion in the center of the square to enable the sheet to attain negative displacements around the periphery.

FIGURE 3.

Membrane configuration with L = 112 nm embedded in a larger system of size ℒ = 3L (the rest of the system outside of the corral is not shown). The pinning occurs at the corners at z = 0, and at the center of the corral at a height of z = 40 nm (small spheres indicate pinning sites). Note that the entire system must have its center of mass at zero, but within this corral, the center of mass is clearly above zero.

We now use Eq. 19 to examine distributions of pinning sites that are more relevant to the applications discussed later in this article. We start by using the simplest geometry of a square membrane pinned at the corners. Typical membrane configurations and their time evolutions generated by our Fourier space Brownian dynamics method are shown in Fig. 4 for both pinned and free membranes. The longer wavelength modes are seen to persist longer than the shorter wavelength modes which are evolving on this timescale. This behavior is to be expected based on the form of Eq. 17.

FIGURE 4.

Time evolution of both a free (top) and pinned membrane (bottom) of corral length ℒ = L = 112 nm using the physical parameters for a red blood cell listed in Table 1. The membrane configuration is constructed by sampling from Eqs. 15 and 16, reconstructing the Fourier modes, and inverse transforming. The red spheres are located at points where the membrane has been explicitly pinned. The long wavelength modes relax at a slower rate compared to the short wavelength modes as expected from the free membrane results in Eq. 17. The center of mass of each configuration is forced to be zero because we have set the k = 0 mode equal to zero. For this geometry, pinning quenches undulations.

As noted in Figs. 2 and 4, the center of mass is restricted to be zero because we have explicitly set the h_k=0 = 0. All configurations are therefore forced to have regions both above and below the plane defined by h(r) = 0. In a more realistic membrane, we expect, in general, a nonzero center of mass for individual corrals and the possibility of dome-shaped configurations where the membrane is mostly above the plane. These configurations would be dominated by wavelengths ∼2L that are not present in the system with a single corral where the longest wavelength mode is L. To allow these longer wavelength modes, we make the system size larger while placing pinning sites spaced by L. Within individual corrals, the center of mass need not be zero, although the total center of mass of the whole membrane must still lie in the xy plane. Increasing the system size has a large effect on undulations in the membrane as can be seen in Figs. 5 and 6. The average amplitudes are higher, indicating the dominance of the modes with wavelength 2L, and the center of mass of the membrane in a single corral is no longer constrained to be at zero. These pinning configurations are expected to be more closely related to the actual situation on the surface of the red blood cell than those of Fig. 4.

FIGURE 5.

Comparison of the free membrane and a larger membrane with square pinning. The pinning sites are located at every multiple of L = 112 nm in both the x and y directions as indicated by the red spheres and dots. The transparent green plane indicates h(r) = 0. (a) Membrane configuration drawn from Eq. 15 for a system periodic with ℒ = 3L. (b) The y = 0 edge of the configuration. (c) Magnified view of one corner of the configuration from the large system. Note that the center of mass of this single corral is above zero. (d) A free membrane which has the restriction that half of the membrane be above zero and the other half below zero.

FIGURE 6.

The same comparison as in Fig. 5 except with triangular pinning relevant for the red blood cell membrane. The pinning sites are located at (1/2,0), (3/2,0), (1,0), (1,1), (1,2), (2,1/2), and (2,3/2) in units of L.

One might expect that allowing the k = 0 mode to evolve in time via diffusive dynamics within a simulation box of size L would capture the dominant features obtained by sampling from a larger geometry. We can (with some ambiguity) indeed treat the k = 0 mode dynamically (see Appendix B). This generalization allows configurations where the center of mass is nonzero, thus recovering in a rough sense what was gained by including the ∼2L wavelength modes for the larger systems. One configuration of the membrane which includes the k = 0 mode is shown in Fig. 7. We note, however, that the method shown in Appendix B is crude. We cannot capture all of the features of the larger systems because of the requirement that the membrane be periodic at opposite edges of the corral. In other words, the wavelength ∼2L modes that we expect to be in the red blood cell membrane are not actually present here. We have found that including the k = 0 mode does not lead to good agreement with larger simulations.

FIGURE 7.

One realization of the membrane with L = ℒ = 112 nm including the k = 0 mode. The presence of this mode allows the center of mass to be nonzero, but still requires periodicity over L.

Height autocorrelation function

Although the simulation technique described in the previous section is useful and efficient, analytical results are preferable when they are available. The most fundamental quantity that characterizes dynamic membrane fluctuations is the autocorrelation function for the height h(r,t). This quantity is directly measurable by light scattering and other experimental techniques. Past studies of membrane dynamics have used height autocorrelation functions in unconstrained geometries (Milner and Safran, 1987; Schneider et al., 1984; Brochard and Lennon, 1975; Zilman and Granek, 1996) to explain, for example, the flicker effect in erythrocytes (Brochard and Lennon, 1975) and relaxation dynamics in membrane sponge phases (Zilman and Granek, 1996). Starting with Eqs. 12–14, the time correlation function of the eigenmodes d_i(t) is

(20)

Expanding the height h(r, t) in terms of these eigenmodes (see Appendix A),

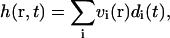(21)

with coefficients v_i(r) defined in Eq. A17, we arrive at an expression for the autocorrelation function

(22)

An important related quantity, the mean-square height 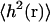, is given by setting t = 0.

To gain intuition about the relative importance of each of the modes, we again examine a free membrane with V(r) = 0 and ℒ = L. The results in this case are particularly simple and amenable to interpretation. The autocorrelation is a sum over exponentials

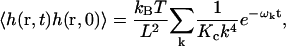(23)

where the relaxation frequency is defined in Eq. 17. In this simple case it is possible to approximate the sum over modes by an integral (Granek, 1997). However, this approximation is not appropriate for the cases we consider because ℒ is not sufficiently large. In the above expression for the autocorrelation function, we see that the terms with frequencies ω_k ≳ t⁻¹ are exponentially suppressed. Essentially, the short wavelength modes relax quickly enough that they are uncorrelated on the timescale of t. In addition, large k modes are also energetically unfavorable due the large amount of bending required to produce such modes. The short wavelength modes are further suppressed by the k⁻⁴ dependence. Therefore, for both 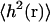and the autocorrelation function, we can cut off our sums at some sufficiently large value of k. In contrast, the long wavelength modes dominate both the autocorrelation function and the mean-square displacement. The above observations were visually apparent from the membrane configurations generated by our simulation algorithm in the previous section.

Application to protein mobility

Our motivation for studying a pinned membrane surface is understanding protein mobility on the surface of red blood cells. Although the fluid mosaic model would predict purely diffusive behavior for membrane components and this behavior is in fact often observed for lipids (Lee et al., 1993), the skeleton fence model best describes the motion of band 3 protein on the surface of red blood cells where there exist both microscopic and macroscopic diffusion constants (Tsuji and Ohnishi, 1986; Tsuji et al., 1988; Edidin et al., 1991; Corbett et al., 1994; Kusumi and Sako, 1996; Tomishige, 1997; Tomishige et al., 1998). Single particle tracking experiments have shown that proteins do indeed freely diffuse in a confined region with occasional hops to similar neighboring regions (Tomishige et al., 1998). Electron microscopy of the red blood cell membrane shows a network of roughly triangular corrals formed by spectrin filaments (Byers and Branton, 1985; Liu et al., 1987) connected to the membrane by anchoring proteins band 4.1, ankyrin, and band 3 (Luna and Hitt, 1992; Steck, 1989; Janmey, 1995; Sackmann, 1995). These corrals hinder the motion of proteins over length scales larger than tens of nanometers, whereas the motion is freely diffusive within the corral. Our goal is to study the possible role of membrane fluctuations in the global diffusivity of band 3 on the erythrocyte surface.

The model for membrane dynamics presented in the previous sections is suitable for the study of protein mobility. We will use the measured microscopic diffusion constant along with a gating mechanism regulated by thermal membrane fluctuations to derive a macroscopic diffusion constant that can be compared with the experimental value D_macro = 6.6 × 10⁻³ μm² s⁻¹ (Tomishige et al., 1998). Our treatment closely follows Brown (2003). To begin, we note that the microscopic diffusion constant D = 0.53 μm² s⁻¹ (Tomishige et al., 1998) is two orders of magnitude greater than the macroscopic diffusion constant. It is assumed that this discrepancy is explained by frequent steric clashes between band 3 dimers and spectrin filaments, which reduce macroscopic diffusivity (see Fig. 1). Crystallography indicates that band 3 protrudes a distance of h₀ ∼ 6 nm into the red blood cell (Zhang et al., 2000). We assume in our model that band 3 cannot escape the confines of a corral unless the height of the membrane at the edge of the corral is greater than h₀. We neglect the dynamics of the cytoskeleton in creating such a gap, so the criteria for band 3 to meet an “open door” when it approaches the corral boundary is simply h(r, t) > h₀. The possibility of spectrin dynamics contributing to global diffusivity of band 3 has been studied elsewhere (Saxton, 1989, 1990a,b; Boal, 1994; Boal and Boey, 1995; Leitner et al., 2000; Brown et al., 2000).

The requirement that the membrane height be greater than h₀ is not quite sufficient to allow passage because band 3 cannot instantaneously move over the cytoskeletal barrier. The protein must diffuse over spectrin a distance approximately one-half the total sum of the diameter of the band 3 dimer and the thickness of a spectrin dimer. This distance is ∼ℓ = 7 nm (Leitner et al., 2000) from which we estimate that the time to diffuse a distance equal to ℓ is t_D = ℓ²/4D = 23 μs. Hopping from one corral to the next should not be permitted unless the height of the membrane is greater than h₀ for an interval of t_D (or some significant fraction of that time interval; see Discussion in Brown, 2003).

The above conditions specify a dynamic gating mechanism which we now quantify. We use the statistics of membrane fluctuations to formulate an approximate transmission probability (Saxton, 1995) at the edge of corral regions. With these probabilities, it is straightforward to estimate escape rates from an individual corral and hence a macroscopic diffusion constant reflecting infrequent hops between corrals.

As a first step toward the determination of a macroscopic diffusion constant, we require the equilibrium probability that the membrane height is greater than h₀ (see Appendix C)

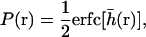(24)

where the dimensionless variable is defined as

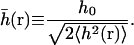(25)

We also need the correlated probability that the height is greater than h₀ at time t, given that the height was greater than h₀ at time 0 (see Appendix C),

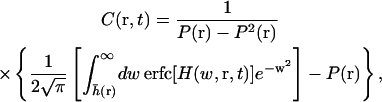(26)

where

(27)

and A(r, t) is the normalized autocorrelation function

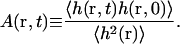(28)

C(r, t) approximately reflects the probability that a gap of size h₀ will persist for time t (Brown, 2003). Note that both of these quantities depend only on the autocorrelation function for which we have the analytical solutions (to within a single matrix diagonalization).

Results for both P(r) and C(r, t) for the free membrane case were computed in a previous article (Brown, 2003) using the simulation method described earlier. Here we present results based on our analytical expressions (Eqs. 23, 24, and 26). Although our general equations are exact, the autocorrelation function is given in terms of a complicated sum over modes, even for the free membrane case where Fourier modes are already diagonal. It is most meaningful to study these solutions graphically. The parameters for the red blood cell in Table 1 are used in all of the following. In Fig. 8, we show both the analytical results and the results from the simulation technique described earlier. In the limit of large statistical sampling the simulations reproduce analytical theory as expected. The discrepancy between data shown here and in previous work (Brown, 2003) is attributable to two sources. In prior simulations, a programming error in the determination of C(r, t) led to slight inaccuracies (compare Fig. 8 with Fig. 5 of Brown, 2003). In addition, an integral approximation for the sum over modes was previously used (Brown, 2003) to estimate P(h₀). The system size in this case is not large enough for this approximation to be reasonably accurate (compare Fig. 8 with Fig. 4 of Brown, 2003).

FIGURE 8.

Analytical and simulation results for statistical quantities related to thermal membrane undulations discussed in the text. The upper plot shows the probability that the height is greater than h₀ as a function of h₀ for a free membrane with ℒ = L = 140 nm. The lower plot shows the number correlation function as a function of time for the same system, but with h₀ = 6 nm (the size of band 3). Analytical results are based on Eqs. 23, 24, and 26 with physical parameters taken from Table 1. Simulation data based on Eqs. 15 and 16 is plotted for different sample sizes. At 10⁵ samples, the data is indistinguishable from the analytical results on the scale of this figure. The value of ℒ = 140 nm is chosen for comparison with our previous results (Brown, 2003).

We now consider cases where the membrane surface is explicitly pinned to the underlying spectrin skeleton to more accurately reflect geometries expected in the red blood cell. Plots of P(r) as a function of h₀ and C(r, t) as a function of t for pinned membranes are shown in Fig. 9 for both square and triangular corral geometries (see Figs. 5 and 6 for the precise locations of the pinning sites). Note that there is a significant difference when the system size ℒ increases to include more corrals even though we only consider statistics over a single corral. This behavior is expected because larger simulation boxes allow for inclusion of ∼2L wavelength modes as discussed previously, and net translation of the membrane center of mass over a single corral.

FIGURE 9.

Statistical quantities that characterize protein mobility for L = 112 nm. Each column represents a particular geometry and system size (ℒ) shown in parenthesis. The upper plots show the probability that the height is greater than h₀ as a function of h₀. The lower plots show the number correlation function as a function of time using h₀ = 6 nm. We plot at several values of x using constant y = 0 for the square geometry and y = L for the triangular geometry so that the x coordinate always moves along the edge of the corral (refer to Figs. 5 and 6 for the location of the pinning sites). For all plots, the case of the free membrane with ℒ = L is shown for reference. In the case of a pinned system with ℒ = L, the plot at the midpoint of the corral edge (x = 0.5L) is essentially indistinguishable from the plot for the free membrane. The same is not true for the larger systems, where P(r) and C(r, t) at x = 0.25L are already larger than the free membrane values. The square and triangular systems saturate at 4L so that the plots are the same as for ℒ = ∞.

In contrast, we find little difference between the large systems (ℒ > L) with different geometries. The net effect of this insensitivity to geometry translates into small effects on the macroscopic diffusion coefficient with changes in corral shape, in agreement with previous models for the same system (Saxton, 1995).

The presence of pinning sites slightly complicates matters relative to the free membrane case. For a free membrane, every point on the sheet is equivalent and hence P(r) and C(r, t) actually display no dependence on r. The multiple lines in the frames of Fig. 9 reflect different distances along the boundary between pinning sites. As expected, P(r) and C(r, t) tend to zero as the pinning sites are approached. Pinned geometries favor escape of proteins from points furthest removed from pinning sites. We note that at ∼4L for both geometries, the results no longer change with increases in the system size so that, effectively, ℒ is infinite for these cases.

The product C(r, t_D)P(r) gives the approximate probability that the membrane displacement is greater than h₀ between times 0 and t_D at position r. Fig. 10 shows plots of this quantity for various system sizes and geometries. Using the dynamic gating interpretation, the probability that a protein will encounter an opening in the cytoskeletal barrier averaged over the length of one edge of the corral is given by

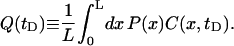(29)

Inside the corral, we assume that that the protein executes a random walk. In the square geometry, the corral is broken into squares with sides length ℓ = 7 nm (the approximate distance that band 3 needs to diffuse to get over the cytoskeleton). The protein has a probability Q(t_D) of escaping if it is both adjacent to the boundary and moving toward the fence. The probability of being on a boundary square is f_sq = (4N − 4)/N², where N = L/ℓ, and the probability of moving in the right direction is 1/4. The total rate of escape from the corral is then k_sq = f_sqQ_sq(t_D)/(4t_D). For the triangular geometry, we use equilateral triangles for the corrals even though the geometry in Fig. 6 is slightly different. The lack of sensitivity to geometry allows us to make these changes without affecting the results significantly. The equilateral triangular corral is broken up into a set of smaller equilateral triangles with sides 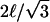. Assuming that the protein sits in the center of these triangles, we have diffusion on a hexagonal lattice with steps length ℓ. The fraction of the triangles on the boundary is f_tr = (3N − 3)/N², where , and the probability of moving in the right direction is 1/3. The total escape rate for this geometry is k_tr = f_trQ_tr(t_D)/(3t_D).

FIGURE 10.

Plot of the opening probability P(x)C(x, t_D) as a function of x/L with L = 112 nm and h₀ = 6 nm for different geometries and system sizes (ℒ) shown in parentheses. The systems used here are the same as those used in Fig. 9. We use constant y = 0 for the square geometry and y = L for the triangular geometry (refer to Figs. 5 and 6 for the location of the pinning sites). For reference, the value of the escape probability for the free membrane is 0.12 × 10⁻³. The larger systems have average probabilities that are more than an order of magnitude larger than the smaller systems. The geometry, however, makes little difference. Notice the slight drop near x = 0.5L for the case ℒ = L. The longest wavelength mode in this case goes through zero at the midpoint, causing a dip that is an artifact of periodicity over the length scale of the corral. In the larger systems, the dominant modes have longer wavelengths and this behavior is not observed.

We now model the global diffusion of proteins as a random walk between corrals with escape rate k. For the square geometry, the diffusion occurs on a square lattice with spacing L and the macroscopic diffusion constant is (see Appendix C)

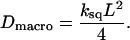(30)

For the triangular geometry, the diffusion occurs on a hexagonal lattice with sides length and (see Appendix C)

(31)

The values of the macroscopic diffusion constants for various geometries, system sizes, and corral lengths are listed in Table 2. Again, we note that increasing the corral size significantly affects the results, whereas the geometry does not. For this reason, we will restrict our focus to the results for the square geometry. To make contact with experiment, we note that measurements done by single particle tracking have found distributions of corral sizes from 50 to 200 nm and distributions of macroscopic diffusion constants ranging from 10⁻¹ to 10⁻³ μm²s⁻¹ with median values L ∼110 nm and D_macro ∼6.6 × 10⁻³ μm² s⁻¹ (Tomishige et al., 1998). In comparison to the large system sizes where boundary condition artifacts are absent, we see that for L = 112 nm, the predicted diffusion constant is approximately an order of magnitude larger than the median experimental value. A corral size of 84 nm, however, approximately reproduces the median macroscopic diffusion constant.

TABLE 2.

Table of calculated macroscopic diffusion constants

L (nm)	Geometry	System size	Pinning	Escape probability	Dmacro (μm2 s−1)
70	Square	L	Free	1.2 × 10−11	5.7 × 10−11
	Square	L	Pinned	5.3 × 10−12	2.5 × 10−11
	Square	∞	Pinned	1.0 × 10−4	5.0 × 10−4
73	Triangle	∞	Pinned	1.2 × 10−4	5.6 × 10−4
84	Square	L	Free	6.7 × 10−8	3.9 × 10−7
	Square	L	Pinned	3.2 × 10−8	1.9 × 10−7
	Square	∞	Pinned	9.5 × 10−4	5.6 × 10−3
89	Triangle	∞	Pinned	1.3 × 10−3	8.0 × 10−3
112	Square	L	Free	1.2 × 10−4	9.2 × 10−4
	Square	L	Pinned	6.1 × 10−5	4.8 × 10−4
	Square	∞	Pinned	8.7 × 10−3	7.0 × 10−2
113	Triangle	∞	Pinned	8.3 × 10−3	6.6 × 10−2
140	Square	L	Free	2.4 × 10−3	2.5 × 10−2
	Square	L	Pinned	1.4 × 10−3	1.4 × 10−2
	Square	∞	Pinned	2.6 × 10−2	2.6 × 10−1
137	Triangle	∞	Pinned	2.2 × 10−2	2.2 × 10−1

The pinning geometries are as shown in Figs. 5 and 6. The notation ℒ = ∞ indicates that we have used a system size such that the results no longer change with increases in ℒ, which in practice occurs at ∼4L. For the square geometry, L is a multiple of ℓ = 7 nm. For the triangular geometry, L is a multiple of 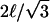as required for diffusion on a hexagonal lattice of sides ℓ. The diffusion constant for L = 12ℓ = 84 nm large square pinned system (D_macro = 5.6 × 10⁻³ μm² s⁻¹) and ∼89 nm large triangular pinned system (D_macro = 8.0 × 10⁻³ μm² s⁻¹) give the best agreement with the experimental value D_macro = 6.6 × 10⁻³ μm² s⁻¹ (Tomishige et al., 1998).

The simplifications and approximations in our model prevent us from making detailed quantitative predictions. Indeed, the significant spread in experimental data makes comparison to theory difficult even for a more refined model. However, the fact that membrane undulations within our model lead to global diffusion faster than observed in experiment clearly indicates that bilayer fluctuations cannot be ignored in this system. Membrane undulations likely play an important role in the mobility of band 3 on the surface of the red blood cell.

In the above calculations, we have fixed the value h₀ = 6 nm to agree with the experimentally determined structure of band 3 (Zhang et al., 2000). For completeness, we show that variation of the height required for the passage of the protein can have large effects on the macroscopic diffusion constant. Fig. 11 shows the case for a system ℒ = 4L with square pinning. Increasing h₀ from 6 nm to 10 nm decreases the macroscopic diffusion constant by an order of magnitude. Experimentally, cleaving of the cytoplasmic domain of band 3 by trypsin increases the macroscopic diffusion constant by an order of magnitude while leaving the microscopic diffusion constant the same (Tomishige et al., 1998). This observation is in qualitative agreement with the trend that we predict, although different models involving thermal motions of spectrin would be expected to make similar predictions (Boal and Boey, 1995). To our knowledge, there has been no systematic study that measures the diffusion constants for different sizes of cleaved band 3 or other proteins.

FIGURE 11.

Plot of the macroscopic diffusion constant D_macro as a function of h₀ for a square pinned membrane with L = 112 nm and ℒ = 4L. Global diffusivity shows a strong dependence on the extent of intracellular protrusion of the mobile protein.

Thermal conformational gating has previously been implicated as a mechanism for enzyme specificity (Zhou et al., 1998). Fig. 11 suggests that thermal membrane undulations lead to a similar specificity in the global diffusion of membrane-bound proteins. Proteins with large cytoplasmic domains will diffuse more slowly than proteins with smaller internal domains.

DISCUSSION

We have introduced a dynamic model for pinned membranes that allows for simulations over biologically relevant length and timescales. In addition, the harmonic nature of the model leads to analytically tractable (requiring a single matrix diagonalization) expressions for various statistical quantities, such as the height autocorrelation function, which we have used to characterize protein mobility. We have presented for the first time analytical results for the free membrane model from a previous article (Brown, 2003), and have extended these results by adding a general harmonic interaction. Specifically, this harmonic potential is used to mimic pinning of the membrane to the cytoskeleton. With this pinning interaction, we can increase the size of the membrane although maintaining the size of the corral, creating a more realistic model of the bilayer which includes longer wavelength modes not present in the free sheet model. Inclusion of these modes increases the macroscopic diffusion constant by an order of magnitude or more depending on the corral size.

Our previous success (Brown, 2003) in using free membrane statistics to study the mobility of membrane-bound proteins turns out to be largely fortuitous. Pinning interactions decrease D_macro when ℒ = L relative to the free membrane by quenching undulations. However, increasing the system size in pinned systems so that ℒ > L increases undulation amplitudes by removing artifacts of periodic boundary conditions over the corral dimension. For the length scales studied here, the effect of increasing system size more than compensates for quenching caused by pinning interactions. The free membrane statistics actually do a poor job relative to our pinned simulations at the smaller end of the experimentally determined L distribution. At the higher end the free sheet model performs better, but still underestimates D_macro by an order of magnitude relative to pinned geometries in large systems.

In developing a model that is applicable to long times and large distances, we have ignored many of the detailed interactions between the bilayer, proteins, and cytoskeleton that are present in real cellular systems. In our application to protein mobility, the membrane is approximated as a continuous sheet and all interactions are ignored with the exception of pinning to the underlying spectrin matrix and the interaction between band 3 and the cytoskeleton (modeled approximately by our dynamic gating mechanism). In particular, our harmonic model is not able to account for the short-ranged repulsive interactions between the cytoskeleton and bilayer. Inclusion of such effects may alter the calculated numerical values for D_macro, but should not alter our qualitative conclusions. Even with pinning, thermal membrane undulations have significant amplitudes over the length scale of red blood cell corrals. These undulations must play a role in global mobility of transmembrane proteins.

The physical constants we have used in our study are taken from experimental measurements as discussed previously (Brown, 2003). Although we have neglected certain physical phenomena in our modeling, the use of experimental numbers for D and K_c do take some details of the cellular environment implicitly into account. For instance, although K_c is expected to vary in the vicinity of a pinning site or band 3 protein, we have not explicitly included this effect in our model. The experimental value we have used for K_c takes such inhomogeneity into account in an averaged sense. We do not, however, capture correlations between diffusion and membrane undulations in our model—an effect which can be important in other biophysical phenomena (Kumar and Rao, 1998; Kumar et al., 2001). Similarly, although the experimental value for D does take into account interactions with other diffusive and anchored proteins in the bilayer in an averaged way, we neglect correlations between microscopic mobility and position in the bilayer. Hydrodynamic drag in the two-dimensional sheet may cause slower motion near pinning sites. Because proteins cannot effectively escape near these sites, we do not expect this omission to be a serious shortcoming of our modeling.

In conclusion, we have presented a simulation methodology for lipid bilayers based on Helfrich elastic energetics (Helfrich, 1973) and nonlocal, overdamped Langevin dynamics (Milner and Safran, 1987; Schneider et al., 1984; Brochard and Lennon, 1975; Granek, 1997). In contrast with a related previous study (Brown, 2003), this methodology is applicable to membrane surfaces with external interactions. The present study uses a normal mode decomposition in Fourier space to evolve systems forward in time and is dependent upon the harmonic nature of the interactions we have assumed. For strong pinning, a harmonic potential is adequately effective and we have been able to simulate dynamic pinned membrane surfaces with this algorithm. We note that Fourier space Monte Carlo methods have been used to study equilibrium properties of membrane surfaces (Gouliaev and Nagle, 1998a,b). This report is the first that we are aware of to model dynamic membranes that are explicitly pinned, although there are theories for the partition function of membranes with anchored segments (Weikl and Lipowsky, 2000). A recent letter (Gov et al., 2003) has studied longer wavelength membrane modes (longer than L) in the red blood cell by incorporating a completely delocalized attraction between cytoskeleton and lipid bilayer. Though very interesting in its own context, this study does not seem directly applicable to the question of membrane protein diffusion. Our results are useful for analyzing large membranes with multiple pinning sites and different geometries, and, specifically, have been used to study the mobility of band 3 on the surface of the red blood cell. For this application, we were able to derive our results analytically and verify them by simulation. From the calculated macroscopic diffusion constants we conclude that thermal membrane undulations are likely to play a role in the global diffusion of proteins over the surface of the membrane. Although we have examined the red blood cell because it is widely studied experimentally, steric interaction with the cytoskeletal filaments has been implicated in hindering protein diffusion for other cellular systems (Fleming, 1987; Saxton and Jacobson, 1997; Winckler et al., 1999; Saxton, 1990b). The qualitative findings of our study, that membrane undulations can affect protein mobility, may hold for these more complicated systems as well.

APPENDIX A

Diagonalization of the Hamiltonian and Langevin equations

To find the eigenmodes of the system defined by Eqs. 2 and 10, we make the change of variables,

(A1)

To put our equations in a matrix form,

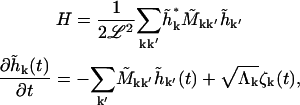(A2)

where

(A3)

is a Hermitian matrix. Because h(r, t) is real, we must have 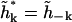so that we do not have the freedom to specify both and 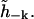Let the real and imaginary parts of the amplitude be 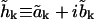so the condition that h(r, t) be real implies 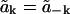and 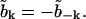We also define the real and imaginary parts 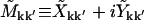, and V_k ≡ T_k + iU_k, giving

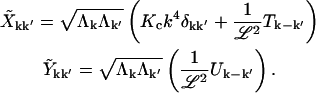(A4)

Because is Hermitian, we must have 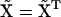and 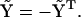Defining 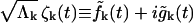and rewriting Eq. 11, the random forces satisfy

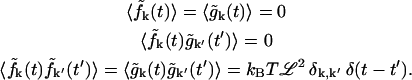(A5)

To simplify the notation, we use bold upper-case letters to signify matrices and bold lower-case letters to signify vectors. With the definitions above, the Hamiltonian and Langevin equations are

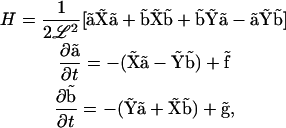(A6)

where matrix multiplication is implied.

For this and the following appendices, let q represent the wave vectors for only those modes that are independent so that only one of k and −k are in the set q. Using 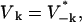which implies that T_k = T_−k and U_k = − U_−k, we define

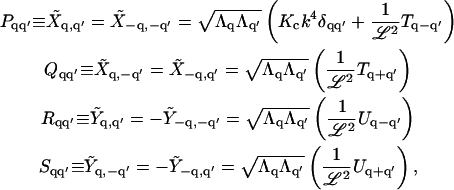(A7)

so that schematically,

(A8)

Let a and b be vectors of only the independent amplitudes a_q and b_q and similarly for f and g. In terms of these definitions,

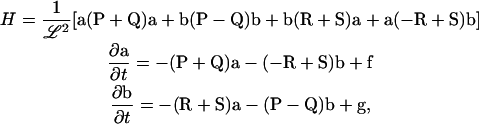(A9)

which is simplified further if we write

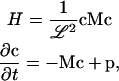(A10)

where we define c ≡ (a, b), p ≡ (f, g), and the matrix

(A11)

The random forces satisfy

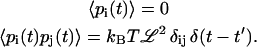(A12)

The fact that P = P^T, Q = Q^T, R = −R^T, and S = S^T implies that M is a symmetric matrix and can be diagonalized with an orthogonal transformation U. Let ω_i be the eigenvalues, d ≡ U⁻¹c, and z ≡ U⁻¹p, so that

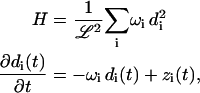(A13)

where z_i are random forces that satisfy

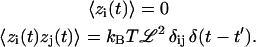(A14)

Finally, we express h(r, t) in terms of the eigenmodes d_i

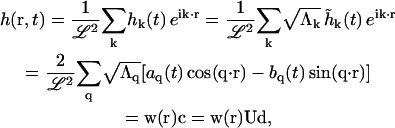(A15)

where the vector w is defined as

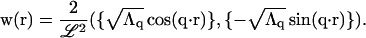(A16)

If we define the vector

(A17)

then in terms of the eigenmodes, the height is given by

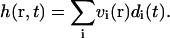(A18)

For completeness, we generalize pinning at sites R_i in two dimensions to pinning at sites (R_i, z_i) in three dimensions by rewriting the harmonic term in the Hamiltonian as

(A19)

The resulting equations in Fourier space analogous to Eq. A10 are

(A20)

where

(A21)

The essential difference is a shift in the variable c. The results previously derived are valid if this modification is made throughout.

APPENDIX B

Addition of the k = 0 mode

For the k = 0 mode, the k and −k mode are the same so that we must modify the transformation in Eq. A1 to be

(B1)

Because 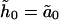is real, there is no 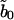mode. Applying the transformation, Eqs. A2 and A3 become

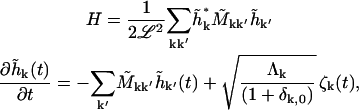(B2)

where

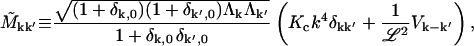(B3)

and the k = 0 mode is included in all sums. We use

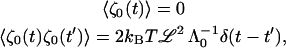(B4)

and the definition 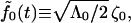to write the fluctuation-dissipation relation

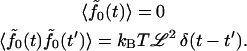(B5)

We keep Eq. A10, but with the definitions c ≡ (a, a₀, b), p ≡ (f, f₀, g), and

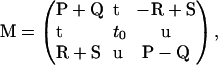(B6)

where

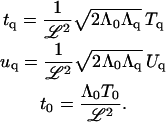(B7)

The rest of Appendix A holds except with

(B8)

The membrane must be pinned for the inclusion of the k = 0 mode to be meaningful. The free membrane with a k = 0 mode has an equal probability of being anywhere in space, forcing the mean-square displacement to become infinite.

According to Eq. 9, the value of Λ₀ diverges in our model where each point on the membrane is hydrodynamically coupled to all other points. For the k = 0 mode only, we replace Eq. 10 with

(B9)

so that we only integrate over the area of the corral. It is not clear how to specify Λ₀ when there is a pinning interaction and all modes are coupled in the force F(r, t), but we can attempt to give a value for a single square of free membrane diffusing by itself. If we assume that there is a constant force per unit area f over the surface, then the center of mass velocity is given by

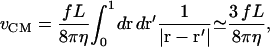(B10)

where the integral has been done numerically. We identify the coefficient in front of the f to be Λ₀ = 3L/8πη which is the value we use in our simulations.

APPENDIX C

Macroscopic diffusion constant

The equilibrium probability that the height is greater than h₀ is

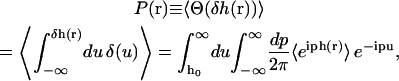(C1)

where δh(r) ≡ h(r) − h₀. We have used the integral representation of the Heaviside step function Θ and the spectral representation of the delta function (Arfken and Weber, 2001). As a consequence of the fact that we can expand h(r) in eigenmodes with Gaussian probability distributions, the cumulant expansion for 〈e^iph(r)〉 is exact at second order (van Kampen, 1992). The equilibrium probability is thus equivalently written

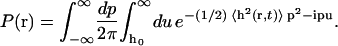(C2)

Performing the Gaussian integrals recovers the results in Eqs. 24 and 25. The probability is completely specified by the mean-square displacement from Eq. 22.

The correlated probability that the height is greater than h₀ at time t given that it was greater than h₀ at time 0 is given by the number correlation function

(C3)

where and δh(r, t) ≡ h(r, t) − h₀. The quantity

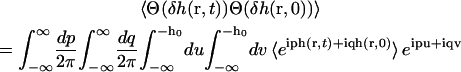(C4)

is calculated in the same way as P(r) noting that

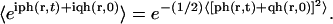(C5)

Performing the Gaussian integrals, we recover the results in Eqs. 26–28. This result is similar to previous results for number correlation functions for a single Gaussian mode diffusing in a harmonic well (Zhou et al., 1998; Brown, 2003).

In the text, we compute an escape rate k from the corral using P(r) and C(r, t). We define a random walk on the lattice created by the centers of the corrals with time step Δt = 1/k. For the square lattice with sides L, the mean-square distance after N steps is

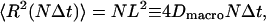(C6)

from which we derive Eq. 30. Similarly, we compute the same quantity for a random walk on a hexagonal lattice with sides which is applicable to the triangular geometry. The correlations between steps at different times all vanish and the result is

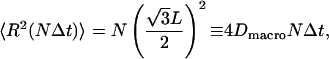(C7)

from which we recover Eq. 31.