Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jun;86(6):3846–3854. doi: 10.1529/biophysj.103.034736

Molecular Mechanism of Domain Swapping in Proteins: An Analysis of Slower Motions

Sibsankar Kundu 1, Robert L Jernigan 1
PMCID: PMC1304286  PMID: 15189881

Abstract

Domain swapping is a structural phenomenon that plays an important role in the mechanism of oligomerization of some proteins. The monomer units in the oligomeric structure become entangled with each other. Here we investigate the mechanism of domain swapping in diphtheria toxin and the structural criteria required for it to occur by analyzing the slower modes of motion with elastic network models, Gaussian network model and anisotropic network model. We take diphtheria toxin as a representative of this class of domain-swapped proteins and show that the domain, which is being swapped in the dimeric state, rotates and twists, in going from the “open” to the “closed” state, about a hinge axis that passes through the middle of the loop extending between two domains. A combination of the intra- and intermolecular contacts of the dimer is almost equivalent to that of the monomer, which shows that the relative orientations of the residues in both forms are almost identical. This is also reflected in the calculated B-factors when compared with the experimentally determined B-factors in x-ray crystal structures. The slowest modes of both the monomer and dimer show a common hinge centered on residue 387. The differences in distances between the monomer and the dimer also shows the hinge at nearly the same location (residue 381). Finally, the first three dominant modes of anisotropic network model together shows a twisting motion about the hinge centered on residue 387. We further identify the location of hinges for a set of another 12 domain swapped proteins and give the quantitative measures of the motions of the swapped domains toward their “closed” state, i.e., the overlap and correlation between vectors.

INTRODUCTION

Domain swapping is a well-known phenomenon in structural biology, which can be described as one sequence having two folds (Murray et al., 1995); it is believed to play an important role in the mechanism of oligomerization in the evolutionary pathway of some proteins (Liu and Eisenberg, 2002; Newcomer, 2002; Xu et al., 1998; Schlunegger et al., 1997). Some proteins remain functional only in the oligomeric state. There are almost 40 domain swapped proteins studied so far by different research groups and described in a systematic way in Liu and Eisenberg (2002). The process of domain swapping is described as the domain of one subunit being replaced by the identical domain of the other subunit (Bennett et al., 1995; Schlunegger et al., 1997). The monomeric units in the dimer or oligomer are always extended to achieve intertwining with the other unit, and this state of the monomer is generally called the “open monomeric state” and the interface is termed the “open interface”. On the other hand, the monomeric state, which is not coupled with the other molecule, is independent and much more compact, and is generally called the “closed monomeric state”, with the interface being called the “closed interface”. The structural criteria to be satisfied for a protein to exhibit the phenomenon of domain swapping have been described in the article by Newcomer (2002).

Even though the phenomenon has been observed in many proteins (Liu and Eisenberg, 2002), the mechanism of domain swapping has been explored by only a few research groups (Hayes et al., 1999; Kuhlman et al., 2001; Rousseau et al., 2001; Schymkowitz et al., 2001; Xu et al., 1998), and there remains much that is unknown. Among them, most of the studies to date were performed by crystallographers, and there have been only a few theoretical studies aimed at understanding the transition mechanism (Gouldson and Reynolds, 1997; Gouldson et al., 1998; Alonso et al., 2000; Xu et al., 1998). The hinge mechanism for this class of proteins is crucial for the manifestation of this phenomenon (Liu and Eisenberg, 2002; Newcomer, 2002) and has been engineered and studied by several groups (Murray et al., 1995; Green et al., 1995; Albright et al., 1996).

Among the various domain swapped dimers and oligomers, diphtheria toxin (DT) is a good representative of this class of proteins, that are sufficiently complete structures for coarse grained analysis, where dimerization occurs through domain swapping in true sense, since in some other cases a segment rather than a domain is swapped and they should, truly, be designated as segment swapped proteins. The physiological relevance of domain swapping and its relation to protein function was described in Liu and Eisenberg (2002). DT is a model protein, which undergoes domain swapping to form dimers. The protein functions through its three distinct domains: catalytic domain (C, shown in red in Fig. 1), translocation domain (T, shown in green in Fig. 1), and the receptor domain (R, shown in blue in Fig. 1) (Bennett et al., 1994a, 1994b; Bennett and Eisenberg, 1994).

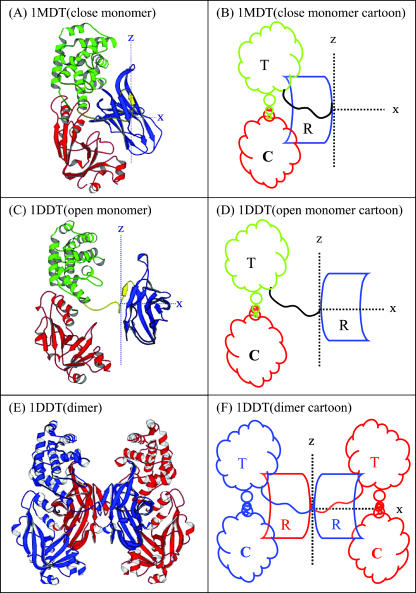
FIGURE 1.

FIGURE 1

Open in a new tab

A shows the monomer in the monomeric state (closed state), B is the corresponding cartoon; C shows the monomer in the dimeric state (open state), D is the corresponding cartoon; E shows the dimer in the dimeric state (two open monomers intertwined), and F is its corresponding cartoon. For these structures there must exist an axis of rotation perpendicular to the linking segment (shown as z axis, the C2 axis) about which a rotation takes place during the transition to the dimer with a slight twist along the x axis.

In this work, we elaborate the mechanism of domain swapping in DT by analyzing the large-scale domain or cluster motions about a hinge. We locate the major hinges using the slower modes in the Gaussian network model (GNM) and determine the direction of the motion of the swapped domain about the hinge by the anisotropic network model (ANM). The structural changes between the two forms are also described in terms of a hinge defined as the structural region having the least local displacements. Apart from DT, we also investigate the application of the approach to identify the locus and direction of domain swapping for a set of a further 12 proteins (Liu and Eisenberg, 2002).

MODEL AND METHODOLOGY

Gaussian network model

The GNM describes a protein as an elastic network of α-carbons connected by harmonic springs where the modes of vibration of this elastic network represent the fluctuations of atoms about their mean positions using a highly cohesive model for proteins. It serves well to confirm the intrinsic flexibility of the structure, represented experimentally by crystallographic B-factors (Bahar et al., 1997; Kundu et al., 2002). GNM has recently been used to account for large-scale conformational motions, cluster and domain motions, low frequency backbone motions (Tirion, 1996; Bahar et al., 1997, 1998; Haliloglu et al., 1997; Higo and Umeyama, 1997; Haliloglu and Bahar, 1999; Hinsen and Kneller, 1999; Doruker et al., 2000) in biomolecular systems and motions in crystals (Kundu et al., 2002). The theory and the concept of the GNM and ANM elastic networks was also used recently in an extremely interesting way by Ming et al. (2002) to describe the motions of a protein from its electron density map where no information of the atomic coordinates are available.

The model assumes an elastic network of harmonic springs, set up between each pair of nodes within a certain cutoff distance. The force constant is identical for all springs. The model provides a uniform elastic medium confined within the shape of the macromolecule. The theory accounts for slow cluster motions, which can aid in establishing functional mechanisms. The construction of the Kirchhoff or valence-adjacency matrix of such a structure is the first step as given in Eq. 1:

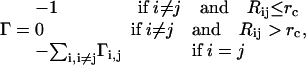graphic file with name M1.gif (1)

where i and j are indices of α-carbons and 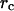Inline graphic is the cutoff distance, an adjustable parameter but not a very sensitive one.

The inverse of this Kirchhoff matrix is related to the magnitude of relative fluctuations of the ith and jth units in the network as shown in Eq. 2 and when i = j, this represents the mean-square fluctuation of each unit. The intrinsic flexibility of the structure, which is reported in the crystallographic B-factors, is also directly related to the mean-square fluctuations by Eq. 3:

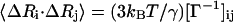graphic file with name M3.gif (2)
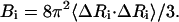graphic file with name M4.gif (3)

The mean-square fluctuations of each unit and the cross-correlation fluctuations between different units are proportional to the diagonal and off-diagonal elements of the inverse of the Kirchhoff matrix, respectively. This inverse can also be expressed as

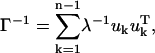graphic file with name M5.gif (4)

where λ are the eigenvalues and 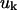Inline graphic are the eigenvectors of 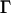Inline graphic and superscript T indicates transpose. The eigenvector with the lowest nonzero eigenvalue represents the slowest motion, which are usually domain or cluster motions. For this symmetric positive semidefinite matrix, the identical pseudo-inverse can be obtained using a singular value decomposition method.

Although GNM provides the magnitudes of the displacements of atoms or chain units from their equilibrium positions for large scale motions, it does not provide any information on the directionality of the motions.

Anisotropic network model

The ANM is an extension of GNM, which adds directionalities to the motions. The directional displacements are essential for generating the specification of changed conformations. Atilgan et al. (2001) gave a detailed theoretical development. Unlike GNM, where there is a single zero eigenvalue, ANM gives rise to six zero eigenvalues corresponding to the three overall translational and three overall rotational degrees of freedom. The eigenvector corresponding to the lowest nonzero eigenvalue corresponds to the largest scale motion (also the largest contribution to the total motion).

Change in internal distances for residues

The above quantities are appropriate for monitoring changes in the displacements that are large, but another measure is required to follow the relatively small-scale motions at hinge sites. The change in the sum of internal distances for each residue is an appropriate parameter for identifying the locations and motions of hinges during transitions (Hinsen, 1998; Hinsen et al., 1999).

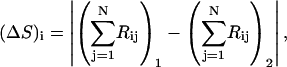graphic file with name M8.gif (5)

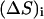where Inline graphic represents the differences in the sum of internal distances of the ith residue to all j residues to which it is directly connected and the subscripts 1 and 2 identify conformation 1 and conformation 2. We call this quantity the “relative displacement” between two structures. This quantity plays an important role in determining the details of hinge motions in the process of transformation. This is a simple and powerful means for locating and studying the hinges in any structural transformation.

Overlap coefficient

The overlap between the conformational change vector and the ANM vector is described by Tama and Sanejouand (2001) and is expressed as

graphic file with name M10.gif (6)

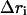where Inline graphic is the conformational displacement of the ith residue and 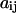Inline graphic is the displacement of the ith residue in the jth ANM mode. The overlap represents a measure of the extent to which a particular mode is in the direction of the displacement of the swapped cluster toward its final “closed” state. The conformational change vector is defined as the difference of the two conformational vectors (Tama and Sanejouand, 2001) after properly aligned over all Cα atoms.

Correlation coefficient

This quantity measures the correlation between the magnitudes of displacements between the conformational change vector and the ANM vector, and indicates whether the less displaced and more displaced Cα atoms are coherent between two vectors:

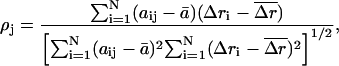graphic file with name M13.gif (7)

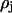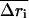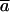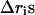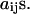
where Inline graphic is the correlation coefficient between the two vectors, Inline graphic and Inline graphic are the means of the corresponding Inline graphic and Inline graphic

Method of calculation

To calculate the slowest modes, the Kirchhoff matrix has first been constructed, according to Eq. 1 by using a cutoff of 7.0 Å, which is then decomposed into eigenmodes by the standard singular value decomposition method given in Eq. 3. The crystal coordinate data of the monomeric (1MDT) and the dimeric (1DDT) DT were obtained from the Protein Data Bank (Berman et al., 2000). The directional motions were obtained by ANM calculations with a cutoff of 15.0 Å, which is described in detail by Atilgan et al. (2001). The dimer in Fig. 1 E was visualized using the CNS system program (Brunger et al., 1998).

RESULTS AND DISCUSSION

Domain swapping in DT is believed to occur in two distinct steps: a), opening of the “closed monomer” into the “open monomeric state” and b), two “open monomers” then becoming entangled or intertwined to form the domain swapped dimer. The monomeric DT is by definition in the “closed” state and the dimeric DT is in the “open” state. The open state (PDB code 1DDT) is shown in Fig. 1 C and the corresponding cartoon in Fig. 1 D, and the closed state (PDB code 1MDT) is shown in Fig. 1, A and B. The receptor domain of DT, shown in blue in Fig. 1, is the domain that is swapped in the dimeric state.

A systematic way to determine the mechanism of domain swapping is to locate the hinges associated with motions for different timescales or modes. The opening of the monomer occurs about a hinge and the R domain rotates almost 180° about this hinge axis (shown as z axis, the C2 axis). There is a slight twist about an axis perpendicular to the previous one (shown in Fig. 1 as x axis). In this work, we mainly stress the closing of the dimer with the GNM and ANM approach. As shown and discussed by Tama and Sanejouand (2001), studying the open state is more effective and logical since the domains and clusters are more separated in that form.

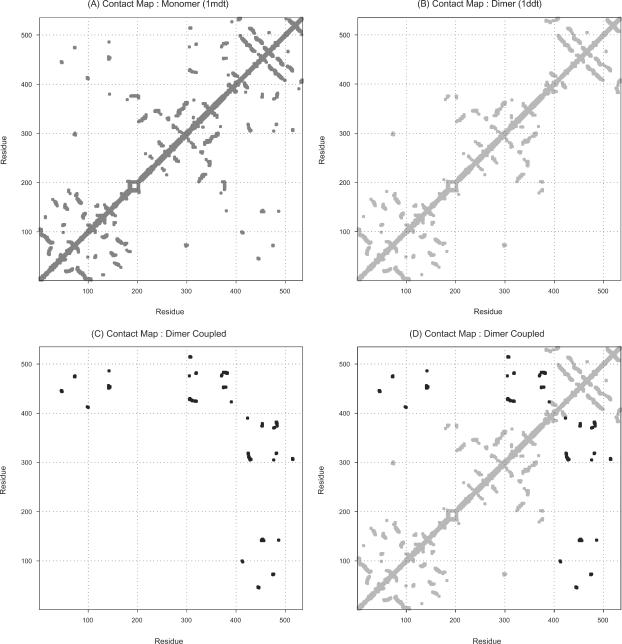
The contact maps of the closed monomeric state, open monomeric state, and coupled dimeric state are shown in Fig. 2. The monomers have, obviously, only intramolecular contacts, whereas the dimers have both intra- and intermolecular contacts. This figure shows how the intra- and intermolecular contacts in the coupled dimeric state are mutually exclusive to each other, and when combined how the contact map actually looks, nearly identical to that of the monomeric state. The contact map of the closed monomeric state is shown in Fig. 2 A. The intramolecular contacts of the open monomer are shown in Fig. 2 B and intermolecular contacts of the open monomer are shown in Fig. 2 C. The combination of intra- and intermolecular contact maps (shown in Fig. 2 D) of the dimer perfectly matches with the contact map of the monomer, which shows that the dimer actually looks like the monomer in the crystal environment.

FIGURE 2.

FIGURE 2

Open in a new tab

(A) Contact map of the monomer in the monomeric DT. (B) Intramolecular contact map of the dimer in the dimeric DT. (C) Intermolecular contact map when two open monomers intertwine in the dimeric DT. (D) Combination of the intramolecular (shown in B) and intermolecular (shown in C) contact map in the dimeric DT is almost completely equivalent to the contact map of the monomeric state. B and C separately show that the inter- and intramolecular contacts in the dimeric DT are mutually exclusive.

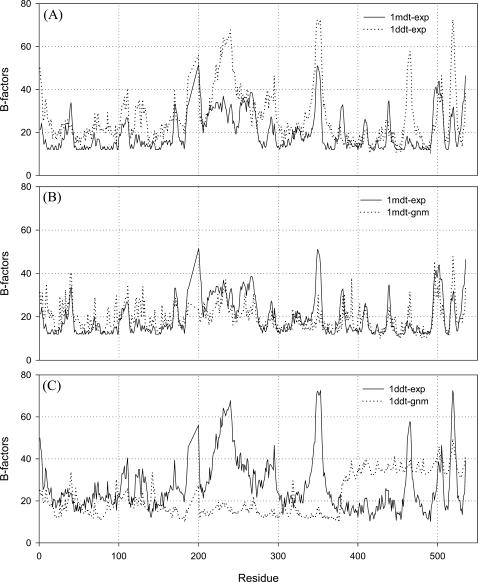
The most notable thing is that the crystallographic B-factors of DT in the monomeric and dimeric states have almost the same shape (Fig. 3 A). The calculated B-factors (using GNM) for each “single protein molecule” are also compared with their corresponding crystallographic B-factors in both states (Fig. 3 B for the monomer and Fig. 3 C for the dimer). This plot shows that the domain-swapped dimer actually looks like a monomer, but in reality part of this originates in one molecule and part is from the other molecule. This strongly indicates that the dimers in the crystal resemble the monomer, which is why this is called domain swapping. The experimental and calculated B-factor values correlate well with the compact monomeric state, but not in the case of the “single molecule” of dimers. The calculated B-factors of the “single molecule” DT in the dimeric state is not similar (Fig. 3 C) to the crystallographic B-factors because of the fact that the R domain goes far away from the other two domains in the open state. The inclusion of the effect of the neighbors, which resembles the crystal environment of the molecule, in the calculation improves the results, and the calculated B-factors correlate well with the crystallographic B-factors (Kundu et al., 2002).

FIGURE 3.

FIGURE 3

Open in a new tab

(A) Experimental B-factors of the monomer (solid line) and the dimer (dotted line). (B) Experimental (solid line) and calculated (dotted line) B-factors of the monomeric DT. (C) Experimental (solid line) and calculated (dotted line) B-factors of the dimeric DT. The deviation between the two curves in the dimeric state (shown in C) was explained in our previous article (Kundu et al., 2002), where the difference disappears when the neighboring molecules are included in the calculation, which resembles the damped motions in the crystal environment of the single protein molecule. For the monomeric compact structure, the GNM calculations reproduce the B-factors more accurately (B). The experimental curves of both the monomer and the dimer have almost the same shapes. This fact shows that the crystalline state of both monomer and dimer have similar packing, equivalent environment, and similar motions. This is because of the fact that in the domain-swapped dimer, the R domain of one molecule sits beside the other molecule so closely (in the crystal) that the two parts of the different molecules seem to be a single monomer. This is another way to show the domain swapping for this protein.

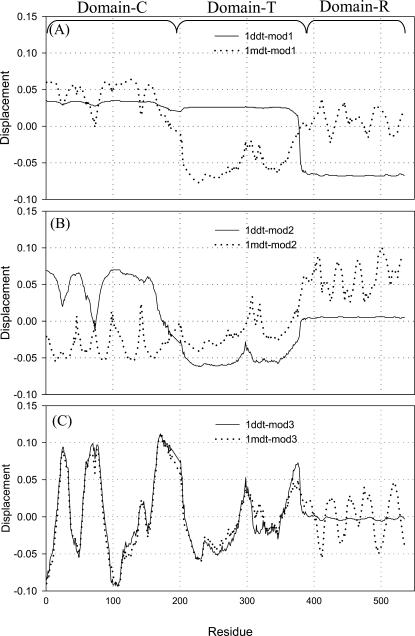
In Fig. 4, we show the first three mode shapes of both monomeric and dimeric forms of DT. These are the most dominant modes in the process of transformation from one state to the other. Fig. 4 A shows the slowest mode of both states (monomer in dotted line and dimer in solid line), where an isolated domain is highly distinguished in the dimeric state. The crossing of the horizontal zero axis in the slower modes determines the separation of the protein into domains insofar as there are sufficient residues to form a stable domain (Fiedler, 1975; Holm and Sander, 1994; Xu et al., 2000). This domain is shown in blue in Fig. 1 C. The same domain in the monomeric state is quite close, which is clear from Fig. 4 A and Fig. 1 A. The point where both vectors (for the slowest mode of both the forms) cross the horizontal axis (x = 0 in Fig. 4 A) is the common and dominant hinge location about which the swapped domain opens and closes. In these modes, both molecules have a common hinge axis, about which the major transformation, from the “open” to the “closed” form occurs, presumably in either direction. Fig. 4 A shows that most dominant hinge that is common to both structures is located around 387. This dominant hinge is also prominent in the second mode (Fig. 4 B). The purpose of analyzing these modes is to find out the dominant hinges about which the major transformation from one state to other takes place. We also determine the hinge locations by this method for another set of 12 proteins and list them in Table 1. The calculated hinge location agrees well with the literature values (Liu and Eisenberg, 2002) except for one protein, CksHs1.

FIGURE 4.

FIGURE 4

Open in a new tab

(A) First mode shape of the dimer (1ddt, solid line) and monomer (1mdt, dotted line). This shows that there is a clear hinge at the middle of the loop, extending from the swapped domain to the other part of the same subunit (residues 390–394). The second mode of 1ddt divides the first two domains separately at residues 170–180. But there is still a hinge in the extending loop region (near 385–395). The slowest motion (corresponding to the first mode) of the molecule has a single hinge located in the connected loop. The next higher mode (second, shown as the dotted line in B) indicates two hinges. One is at the same location as in mode 1 and the other between two other domains. (A) First mode of 1ddt (dimer) and 1mdt (dotted line). (B) Second mode of 1ddt (dimer) and 1mdt (monomer). (C) Third mode of 1ddt (dimer) and 1mdt (monomer).

TABLE 1.

List of domain-swapped proteins and their hinge locations by our method and from the literature (Liu and Eisenberg, 2002)

Number of residues
Hinge location (literature)*
Hinge location (by GNM)†
Hinge location (by Eq. 5)
Mode 1–3
Protein name Monomer Oligomer Overlap Correlation
Barnase 1brn 1yvs 110 37–41 39 39 0.306 −0.326
Calbindin 4icb 1ht9 76 38–47 41 43 0.251 −0.763
Cro 1orc 1cro 71 55 53 56 0.148 −0.763
Cyanovirin-N 2ezm 3ezm 101 50–53 52 52 0.054 0.177
Diphtheria toxin 1mdt 1ddt 535 379–387 387 381 0.335 −0.544
Human prion 1qlx 1i4m 108 188–198 192 195 0.543 −0.393
Protein L B1 domain 1hz5 1jml 62 52–55 47 53 0.178 0.287
RNase A N-terminal 5rsa 1a2w 124 15–22 24 22 0.173 −0.599
RNase A C-terminal 5rsa 1f0v 124 112–115 108 112 0.088 −0.570
Phosphorylated N-Spo0A 1qmp 1dz3 129 103–109 106 105 0.434 −0.398
suc1 1sce 1puc 113 85–91 84 87 0.551 −0.255
CksHs1 1dks 1cks 79 60–65 37 62 0.283 0.567
IFN-β 1rmi 1ilk 160 108–118 116 111 0.016 0.017
Open in a new tab
†

Slowest mode of GNM.

Another feature to be noted is the similarity in the individual modes of the two states, i.e., similarity in a sense of the large-scale domain motions determined by the point of crossing the horizontal axis. In Fig. 4 we see that mode 1 of the monomeric DT (Fig. 4 A) is quite similar in shape with mode 2 of the dimer (Fig. 4 B), and mode 2 of the monomeric DT (Fig. 4 B) is similar to the mode 1 of the dimer (Fig. 4 A) as far as the number of domains is concerned. Mode 1 of the dimer has two domains, and mode 1 of the monomer has three domains (Fig. 4 A) but in Fig. 4 B mode 2 of the dimer shows three distinct domains. This reordering of modes actually accounts for the fact that the transformation from one state to another takes place by swapping of the domains. The third-slowest mode (Fig. 4 C) is very similar for Domain C and Domain T in both states. The small fluctuations of the modes for Domain R in the monomeric state (1MDT) are quite obvious because the R domain comes very close to the other two domains, i.e., C and T domains. On the other hand, the smoothing of modes in dimers (1DDT) occurs because of the small change in the relative distances between the R domain and the other two domains (C and T domains), since the R domain is far away from the other two domains in the dimeric state.

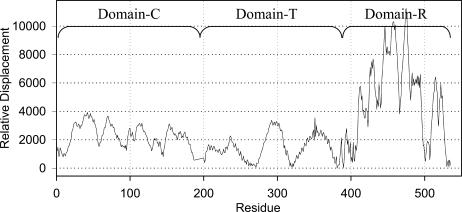
We also explore the local sum of all intramolecular distances centered about each Cα atom and use the differences between the corresponding values for the two forms (according to Eq. 5) to identify the locations of the hinge for the transition. This difference is shown in Fig. 5 for each residue. This shows a clear hinge around residue 381. The global minimum in this curve represents the most dominant hinge for domain swapping between the monomer and the dimer. The next levels of less dominant hinges are located at 265–271, 318–320, and 400–403, which are also obvious from the first and second modes. The other set of less dominant hinges have smaller effects on the transformation and are shown in Fig. 5. The minima are considered to be the hinge points and the maxima are the most mobile regions. This method is also applied to another set of 12 proteins and the hinge locations are given in Table 1. The hinge locations are taken as the minima in the plots of the type of Fig. 5. The hinge locations determined in this method are in full agreement with the literature values (Liu and Eisenberg, 2002).

FIGURE 5.

FIGURE 5

Open in a new tab

Absolute value of the differences of internal distances, which is indicated in the figure as relative displacement, between the monomeric and dimeric states of diphtheria toxin (1ddt and 1mdt) according to Eq. 4. The minimum in this curve represents the major hinge in the molecule. Here it is shown around residue 390.

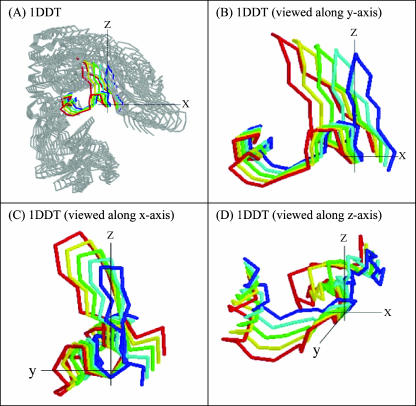
The ANM calculations, with the first three slowest internal modes, show that the receptor domain in the open state, which is far away from the other two domains, rotates about the hinge axis (shown as y axis) toward the other two domains (viz. C and T domains) with a small twist about an axis perpendicular to the y axis (shown as x axis) as shown in Fig. 6. The backbone structures of the different frames in the dynamic transitions are shown in different colors. The dynamics of the whole molecule is shown in Fig. 6 A and the loop region is shown in Fig. 6 B (a view along the y axis), 6 C (a view along the x axis), and 6 D (a view along the z axis). This calculation clearly indicates the contribution of the slowest modes to the rotation of the domains about a C2 axis. This result shows a putative pathway for the closing-opening transition. Here we start with the “open” conformation and show how much it is closing by the three slowest ANM modes. We calculate the overlap coefficients and correlation coefficients (Tama and Sanejouand, 2001) by Eqs. 6 and 7 for another set of 12 proteins given in Table 1. Whereas the expression in Eq. 6 describes the extent to which the three slowest modes are directionally correlated with the conformational change vector, the expression in Eq. 7 describes the magnitude of the correlation between the two vectors. The overlap value shows a maximum of 0.5 for the proteins cyanovirin-N, human prion, and suc1. This means the direction overlaps by half with the conformational change vector, and the three slowest modes play a major role in the transformation. The overlap value goes to a minimum of 0.016 for the protein IFN-β, which indicates that the three slowest modes and the conformational change vector do not agree. It is to be noted that the overlap coefficient ranges from 0.0 to 1.0, but the correlation coefficient values range from −1.0 to 1.0. Thus for most of the proteins in Table 1, the first three modes play an important role in the transformation from the “open” to the “closed” state.

FIGURE 6.

FIGURE 6

Open in a new tab

The first three combined slowest modes of ANM calculation clearly show that there is a large rotation around the z axis (B), viewed along the y axis, and (D), viewed along z axis, the C2 axis) and a small rotation around the x axis (shown in C, viewed along x axis). B–D are the enlarged view of the hinge region shown in color in (A), and the convention of the axes are same with Fig. 1.

CONCLUSION

Transformation from the “closed” monomeric state to “open” monomeric state is the key to the phenomenon of domain swapping, and this type of transformation occurs through a large structural change. In this work, the same principal hinge for the domain swapping transition for diphtheria toxin has been easy to locate in both the open and closed forms. This is a remarkable finding, given the large-scale nature of the transition. Recall that the fluctuations calculated by the GNM and ANM approaches are actually quite small. The implication is that these transitions are so highly “embedded” in the structures that both forms even in their initial fluctuations will tend strongly to move in the direction to effect this particular transition. Consequently, it is justifiable to term this transition extremely robust. However, it must be realized that the contact maps, which are the basis of the computations with the GNM and ANM models, are virtually identical; this is what actually causes both monomeric and dimeric structures to have the same dominant motions. The elastic network models serve to represent appropriately this type of structural transformation with a systematic analysis of the hierarchical hinge location and motions about them. The change in the sum of local internal distances for each residue is a simple measure to aid in locating the hinges for large structural transitions from one state to the other.

References

  1. Albright, R. A., M. C. Mossing, and B. W. Matthews. 1996. High-resolution structure of an engineered Cro monomer shows changes in conformation relative to the native dimer. Biochemistry. 35:735–742. [DOI] [PubMed] [Google Scholar]
  2. Alonso, D. O., E. Alm, and V. Daggett. 2000. Characterization of the unfolding pathway of the cell-cycle protein p13suc1 by molecular dynamics simulations: implications for domain swapping. Struct. Fold. Des. 8:101–110. [DOI] [PubMed] [Google Scholar]
  3. Atilgan, A. R., S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80:505–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bahar, I., A. R. Atilgan, M. C. Demirel, and B. Erman. 1998. Vibrational dynamics of folded proteins: significance of slow and fast motions in relation to function and stability. Phys. Rev. Lett. 80:2733–2736. [Google Scholar]
  5. Bahar, I., A. R. Atilgan, and B. Erman. 1997. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 2:173–181. [DOI] [PubMed] [Google Scholar]
  6. Bennett, M. J., and D. Eisenberg. 1994. Refined structure of monomeric diphtheria toxin at 2.3 Å resolution. Protein Sci. 3:1464–1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bennett, M. J., S. Choe, and D. Eisenberg. 1994a. Domain swapping: entangling alliances between proteins. Proc. Natl. Acad. Sci. USA. 91:3127–3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bennett, M. J., S. Choe, and D. Eisenberg. 1994b. Refined structure of dimeric diphtheria toxin at 2.0 Å resolution. Protein Sci. 3:1444–1463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bennett, M. J., M. P. Schlunegger, and D. Eisenberg. 1995. 3D domain swapping: a mechanism for oligomer assembly. Protein Sci. 4:2455–2468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Berman, H. M., J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov, and P. E. Bourne. 2000. The Protein Data Bank. Nucleic Acids Res. 28:235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Brunger, A. T., P. D. Adams, G. M. Clore, W. L. Delano, P. Gros, R. W. Grosse-Kunstleve, J.-S. Jiang, J. Kuszewski, M. Nilges, N. S. Pannu, R. J. Read, L. M. Rice, T. Simonson, and G. L. Warren. 1998. Crystallography and NMR System (CNS): a new software system for macromolecular structure determination. Acta Crystallogr. D Biol. Crystallogr. 54:905–921. [DOI] [PubMed] [Google Scholar]
  12. Doruker, P., A. R. Atilgan, and I. Bahar. 2000. Dynamics of proteins predicted by molecular dynamics simulations and analytical approaches: application to α-amylase inhibitor. Proteins. 40:512–524. [PubMed] [Google Scholar]
  13. Fiedler, M. 1975. A property of eigenvectors of non-negative symmetric matrices and its application to graph theory. Czechoslovak Math J. 25:619–633. [Google Scholar]
  14. Gouldson, P. R., and C. A. Reynolds. 1997. Simulations on dimeric peptides: evidence for domain swapping in G-protein coupled receptors? Biochem. Soc. Trans. 25:1066–1071. [DOI] [PubMed] [Google Scholar]
  15. Gouldson, P. R., C. R. Snell, R. P. Bywater, C. Higgs, and C. A. Reynolds. 1998. Domain swapping in G-protein coupled receptors. Protein Eng. 11:1181–1193. [DOI] [PubMed] [Google Scholar]
  16. Green, S. M., A. G. Gittis, A. K. Meeker, and E. E. Lattman. 1995. One-step evolution of a dimer from a monomeric protein. Nat. Struct. Biol. 2:746–751. [DOI] [PubMed] [Google Scholar]
  17. Haliloglu, T., and I. Bahar. 1999. Structure-based analysis of protein dynamics: comparison of theoretical results for hen lysozyme with X-ray diffraction and NMR relaxation data. Proteins. 37:654–667. [DOI] [PubMed] [Google Scholar]
  18. Haliloglu, T., I. Bahar, and B. Erman. 1997. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 79:3090–3093. [Google Scholar]
  19. Hayes, M. V., R. B. Sessions, R. L. Brady, and A. R. Clarke. 1999. Engineered assembly of intertwined oligomers of immunoglobulin chain. J. Mol. Biol. 285:1857–1867. [DOI] [PubMed] [Google Scholar]
  20. Higo, J., and H. Umeyama. 1997. Protein dynamics determined by backbone conformation and atom packing. Protein Eng. 10:373–380. [DOI] [PubMed] [Google Scholar]
  21. Hinsen, K. 1998. Analysis of domain motions by approximate normal mode calculations. Proteins. 33:417–429. [DOI] [PubMed] [Google Scholar]
  22. Hinsen, K., and G. R. Kneller. 1999. A simplified force field for describing vibrational protein dynamics over the whole frequency range. J. Chem. Phys. 111:10766–10769. [Google Scholar]
  23. Hinsen, K., A. Thomas, and M. J. Field. 1999. Analysis of domain motions in large proteins. Proteins. 34:369–382. [PubMed] [Google Scholar]
  24. Holm, L., and C. Sander. 1994. Parser for protein folding units. Proteins. 19:256–268. [DOI] [PubMed] [Google Scholar]
  25. Kuhlman, B., J. W. O'Neill, D. E. Kim, K. Y. Zhang, and D. Baker. 2001. Conversion of monomeric protein L to an obligate dimer by computational protein design. Proc. Natl. Acad. Sci. USA. 98:10687–10691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kundu, S., J. S. Melton, D. C. Sorensen, and G. N. Phillips Jr. 2002. Dynamics of proteins in crystals: comparison of experiment with simple models. Biophys. J. 83:723P–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Liu, Y., and D. Eisenberg. 2002. 3D domain swapping: as domains continue to swap. Protein Sci. 11:1285–1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Ming, D., Y. Kong, M. A. Lambert, Z. Huang, and J. Ma. 2002. How to describe protein motion without amino acid sequence and atomic coordinates. Proc. Natl. Acad. Sci. USA. 99:8620–8625. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Murray, A. J., S. J. Lewis, A. N. Barclay, and R. L. Brady. 1995. One sequence, two folds: A metastable structure of CD2. Proc. Natl. Acad. Sci. USA. 92:7337–7341. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Newcomer, M. E. 2002. Protein folding and three dimensional domain swapping: a strained relationship? Curr. Opin. Struct. Biol. 12:48–53. [DOI] [PubMed] [Google Scholar]
  31. Rousseau, F., J. W. Schymkowitz, H. R. Wilkinson, and L. S. Itzhaki. 2001. Three-dimensional domain swapping in p13suc1 occurs in the unfolded state and is controlled by conserved proline residues. Proc. Natl. Acad. Sci. USA. 98:5596–5601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Schlunegger, M. P., M. J. Bennett, and D. Eisenberg. 1997. Oligomer formation by 3D domain swapping: a model for protein assembly and misassembly. Adv. Protein Chem. 50:61–122. [DOI] [PubMed] [Google Scholar]
  33. Schymkowitz, J. W., F. Rousseau, H. R. Wilkinson, A. Friedler, and L. S. Itzhaki. 2001. Observation of signal transduction in three-dimensional domain swapping. Nat. Struct. Biol. 8:888–892. [DOI] [PubMed] [Google Scholar]
  34. Tama, F., and Y. H. Sanejouand. 2001. Conformational change of proteins arising from normal mode calculations. Protein Eng. 14:1–6. [DOI] [PubMed] [Google Scholar]
  35. Tirion, M. M. 1996. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 77:1905–1908. [DOI] [PubMed] [Google Scholar]
  36. Xu, D., C. Tsai, and R. Nussinov. 1998. Mechanism and evolution of protein dimerization. Protein Sci. 7:533–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Xu, Y., D. Xu, and H. N. Gabow. 2000. Protein domain decomposition using a graph-theoretic approach. Bioinformatics. 16:1091–1104. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES