Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jul;87(1):14–22. doi: 10.1529/biophysj.103.024562

Bilayer Conformation of Fusion Peptide of Influenza Virus Hemagglutinin: A Molecular Dynamics Simulation Study

Qiang Huang *,†, Cheng-Lung Chen *, Andreas Herrmann †
PMCID: PMC1304337  PMID: 15240440

Abstract

Unraveling the conformation of membrane-bound viral fusion peptides is essential for understanding how those peptides destabilize the bilayer topology of lipids that is important for virus-cell membrane fusion. Here, molecular dynamics (MD) simulations were performed to investigate the conformation of the 20 amino acids long fusion peptide of influenza hemagglutinin of strain X31 bound to a dimyristoyl phosphatidylcholine (DMPC) bilayer. The simulations revealed that the peptide adopts a kinked conformation, in agreement with the NMR structures of a related peptide in detergent micelles. The peptide is located at the amphipathic interface between the headgroups and hydrocarbon chains of the lipid by an energetically favorable arrangement: The hydrophobic side chains of the peptides are embedded into the hydrophobic region and the hydrophilic side chains are in the headgroup region. The N-terminus of the peptide is localized close to the amphipathic interface. The molecular dynamics simulations also revealed that the peptide affects the surrounding bilayer structure. The average hydrophobic thickness of the lipid phase close to the N-terminus is reduced in comparison with the average hydrophobic thickness of a pure dimyristoyl phosphatidylcholine bilayer.

INTRODUCTION

Membrane fusion between enveloped viruses and host cell membranes is an obligatory process of viral infection mediated by viral glycoproteins, e.g., by influenza virus hemagglutinin (HA) (Wilson et al., 1981) and by gp41 of HIV1 (Chan et al., 1997). HA is one of the best-studied viral proteins mediating fusion (for a review see Skehel and Wiley, 2000). This protein organizes as a homotrimer. Each monomer consists of two subunits (polypeptides): HA1 and the membrane spanning HA2. The potential of HA for mediating fusion is activated by acidic pH (for a review see Wiley and Skehel, 1987). Such an activation is accompanied by a formation of an extended, trimeric coiled-coil structure of the HA2 subunits (Carr and Kim, 1993; Bullough et al., 1994; for a review see Eckert and Kim, 2001). This conformational transition enables the first 20 amino acids of the HA2 N-terminal region, the so-called “fusion peptide”, to bind to and to insert into target cell membrane (Durrer et al., 1996; Harter et al., 1989; Stegmann et al., 1991; Tsurudome et al., 1992). Many studies have shown that the interaction of the HA fusion peptide with the target membrane is an important factor for membrane fusion (for a review see Epand, 2003). To understand the role of this peptide in membrane fusion, it is essential to understand how the fusion peptide organizes in a membrane and how it affects the bilayer structure.

Large efforts have been made to determine the structure of the HA fusion peptide in membranes. A theoretical analysis showed a distinct pattern of hydrophobicity along the peptide, suggesting that the peptide adopts a predominantly α-helical conformation upon its binding to the membrane, with a specific tilted orientation with respect to the horizontal membrane plane (Efremov et al., 1999). This has been experimentally supported for various native and synthetic viral fusion peptides by various approaches including electron paramagnetic resonance (EPR), circular dichroism (CD), attenuated total reflection-Fourier transform infrared (ATR-FTIR), NMR, and neutron diffraction (Bradshaw et al., 2000; Chang et al., 1997, 2000; Dubovskii et al., 2000; Lüneberg et al., 1995; Macosko et al., 1997). Low-resolution studies have suggested that the membrane-bound peptide adopts a rod-like, regular α-helix conformation tilted with respect to the membrane plane by ∼45° (Lüneberg et al., 1995) or 25° (Macosko et al., 1997). However, it is difficult to determine the high-resolution structure of the membrane-bound peptide at the atomic level, due to the strong tendency of the peptide to aggregate in solution as well as in membranes. Recently, Han and Tamm (2000) linked the HA fusion peptide of strain X31 (20 amino acids: GLFGA-IAGFI-ENGWE-GMIDG) to a polar peptide (seven amino acids: -GCGKKKK) to prevent aggregation. Using this synthetic peptide P20H7, Han et al. (2001) successfully determined the structure of the first 20 amino acids (i.e., HA fusion peptide) in detergent micelles of dodecylphosphocholine (DPC) by NMR. They showed that these 20 amino acids fold into a V-shaped structure, forming a hydrophobic pocket on the side of the peptide oriented to the hydrophobic region of micelles. Based on secondary structure measurements by CD, Han et al. (2001) concluded that the conformation of P20H7 bound to a phospholipid bilayer is very similar to that in DPC micelles.

To understand the precise role of the fusion peptide in membrane fusion, it is also necessary to consider the effects of the embedded peptide on the structure of lipid bilayer. For example, the peptide may affect the topology and dynamics of lipids surrounding the peptide. Indeed, a change of the order parameter of lipid acyl chains (Han et al., 1999), an increase of intrinsic negative membrane curvature (Epand, 1998), and phase transitions from lamellar to nonlamellar structures (Colotto and Epand, 1997; Siegel and Epand, 2000) have been reported in the presence of the fusion peptide. It remains a challenge for experimental approaches to provide structural information of the peptide-surrounding lipids. As a complementary approach to experiments, molecular dynamics (MD) simulation may provide such information. MD simulation has been applied recently to study the interaction of peptides with lipid bilayers (e.g., see Belohorcova et al., 2000; Sankararamakrishnan and Weinstein, 2000). Kamath and Wong (2002) have reported a 1.4-ns MD simulation study on the membrane structure of the human immunodeficiency virus gp41 fusion domain in a 1-palmitoyl-2-oleoylphosphatidylethanolamine (POPE) bilayer.

The purpose of this study was to investigate the bilayer-bound conformation of the HA fusion peptide and the impact of the peptide on the structure of the bilayer by MD simulations. We performed simulations for the fusion peptide of HA (strain X31) in a dimyristoyl phosphatidylcholine (DMPC) bilayer. To examine the effect of the protonation state of the N-terminus, we simulated two protonation states of the peptide: one with an unprotonated N-terminus and another with a protonated N-terminus. Important structural features of the peptides and the bilayer were analyzed based on MD simulation trajectories.

METHODS

Sequences of the fusion peptide

We examined the 20 amino acids long fusion peptide of HA X31 strain (GLFGA-IAGFI-ENGWE-GMIDG) in two different protonation states of the N-terminus. The peptide with an unprotonated N-terminus is referred to as peptide I, whereas that with a protonated N-terminus as peptide II. Except for the N-terminus (Zhou et al., 2000), we are not aware of any study presenting definite data about the protonation states of other residues of the peptide (i.e., Glu-11, Glu-15, and Asp-19). Therefore, we assumed that these three residues are unprotonated reflecting the typical protonation state at neutral pH.

Initial structures of the simulated systems

The CHARMM program (Brooks et al., 1983) was used to construct two peptide-bilayer systems for MD simulations (systems I and II). Peptides I and II were placed in systems I and II, respectively. All hydrogen topology and parameter files were taken from MacKerell et al. (1998).

System I was built up with a similar procedure developed by Woolf and Roux (1994, 1996). The initial conformation and orientation of peptide I in the DMPC bilayer (Fig. 1 A) was adopted as a rod-like regular α-helix according to the low-resolution data of CD and electron paramagnetic resonance studies (Lüneberg et al., 1995; Macosko et al., 1997). The central plane of the bilayer system was defined as the xy plane at z = 0 (Fig. 1 A). The helical peptide was placed at a position in which its center of mass (COM) was ∼5 Å above the central plane. The helical axis was tilted by an angle of 35° with respect to the central plane. This angle corresponds to the average of the values of 45° and 25° obtained by Lüneberg et al. (1995) and Macosko et al. (1997), respectively. The projection of the helical axis in the plane was along the x axis. The N-terminus was orientated toward the central plane (Fig. 1 A).

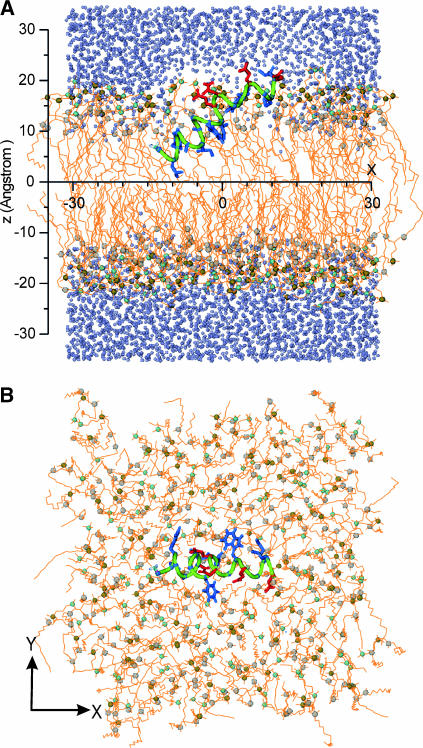
FIGURE 1.

FIGURE 1

Open in a new tab

The initial structure of system I. (A) Side view. (B) Top view. The backbone of the peptide is in green, the hydrophobic side chains in blue, and the hydrophilic side chains in red. The lipids are drawn as orange lines except for the N (cyan sphere), P (tan sphere), and carbonyl C (gray sphere) atoms. Water molecules are indicated as iceblue spheres (not shown in B). For clarity of the peptide, some lipids and water molecule in A are removed.

The initial size of the simulation box was determined by the number of DMPC molecules, the cross section area of DMPC molecule, and the number of hydrated water molecules of the bilayer. The average cross section area of a single DMPC of 59.8 Å2 observed at 30°C (Petrache et al., 1998) was taken. To surround the peptide completely, 60 DMPC molecules were placed in the peptide-harboring leaflet (designated as top leaflet) of the bilayer. The DMPC number of the bottom leaflet was chosen to match the area of the top leaflet. The projection area of the peptide in the xy plane was ∼360 Å2 corresponding to the cross section area of about six DMPCs. Thus, the number of DMPCs in the bottom leaflet was set to 66. As a consequence, all eight sides of the unit cell in x- and y-directions were 62.8 Å in length.

The initial positions of DMPC molecules were determined by the following procedure. Keeping the peptide rigid, van der Waals (vdW) spheres representing DMPC lipids were placed to determine the initial positions of DMPC phosphates in both leaflets. The z coordinates of the phosphate groups of the top and bottom leaflets are +17 and −17 Å, respectively. Subsequently, the vdW spheres were substituted by DMPC molecules. The conformation of each DMPC molecule was selected randomly from a set of 2000 preequilibrated DMPC lipids (Venable et al., 1993; Woolf and Roux, 1994). By systematical rotation and translation, unfavorable contacts between heavy atoms within a distance of 2.6 Å were avoided. To get a fully hydrated bilayer, ∼4800 preequilibrated water molecules were placed on the top and bottom regions of the bilayer. The water molecules were restricted to the DMPC headgroup region forming the hydration layers, and then the height of the unit cell was set to 72 Å. Thus, the dimension of the unit cell was 62.8 Å × 62.8 Å × 72 Å. The whole system contained ∼30,000 atoms.

We constructed the initial configuration of system II from system I. Except for the additional proton at the N-terminus (Gly-1), the initial coordinates of atoms of system II were obtained from system I after a 1-ns NVE simulation (for details see below). To generate peptide II, a proton was added to the nitrogen at the N-terminus of peptide I to form an 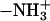Inline graphic group with standard angles and bond lengths.

Initial simulations

To release the starting system, a Langevin dynamics run was first carried out. The system was coupled to a heat bath of 303 K. In a 125-ps run, atomic constraints were employed by using the following procedure: i), First, the backbone of the peptide was fixed, the center of mass of each DMPC was restrained, and the penetration of water was prevented by harmonic forces; ii), next, harmonic forces were used to restrain the peptide, whereas those forces to lipids and water were reduced; and iii), subsequently, the restraints on the peptide were released gradually. Following the Langevin dynamics, NVE (constant number of particles, volume, and energy) simulations were performed for ∼1.5 ns (1.4 ns for system I and 1.5 ns for system II).

The simulations at this stage were carried with CHARMM program using the mentioned all-atom force fields and TIP3 water model (Jorgensen et al., 1983). In the simulations, periodic rectangular boundary conditions were applied, and the time step was 2 fs. The SHAKE algorithm was employed to fix all the lengths of bonds involving hydrogen atoms. Electrostatic and vdW interactions were cut off above 12 Å.

NPT simulations

Starting with the configurations obtained by the initial all-atom NVE simulations at ∼1.5 ns (see above), we switched to united-atom force fields to speed up the simulations. To this end, we used the program package GROMACS (Berendsen et al., 1995; Lindahl et al., 2001). The forced fields for peptide were GROMACS force fields and those for lipids were taken from Berger et al. (1997). The SPC model was used for water molecules (Berendsen et al., 1981).

The simulations were performed employing an NPT ensemble (i.e., constant number of particles, pressure, and temperature) with a time step of 2 fs. The simulated pressure was P = 1 bar, and the temperature T = 303 K. Anisotropic pressure-coupling (Berendsen et al., 1984) in x-, y-, and z-directions was used so that the area per lipid was allowed to adjust during the simulations. The Berendsen temperature coupling was used with a coupling constant of 0.1 ps. All bond lengths were constrained by LINCS algorithm (Hess et al., 1997). The cutoff for vdW interactions was 10 Å. The electrostatic interactions were calculated using the particle mesh Ewald method (Darden et al., 1993; Essmann et al., 1995): The cutoff for real-space interactions was 10 Å, and reciprocal-space interactions were evaluated on a 1.2-Å grid with fourth-order spline interpolation. Atomic coordinates of the simulated systems were saved every 2 ps for analysis. Molecular graphics were produced by the program VMD (Humphrey et al., 1996).

RESULTS AND DISCUSSION

Equilibration properties

In the initial phase of NVE simulations, we observed a significant change in the backbone conformations of peptides I and II adopting a kinked shape structure (see below). However, no further significant changes of the backbone conformations occurred for t > 400 ps. Compared with the conformation at t = 400 ps of the NVE simulations, the mean value of root-mean-square deviations (RMSD) of heavy atoms of the backbone of peptide I was 1.9 ± 0.40 Å (average of the time interval from 0.4 to1.4 ns) and that of peptide II, 2.0 ± 0.49 Å (average of the time interval from 0.4 to 1.5 ns).

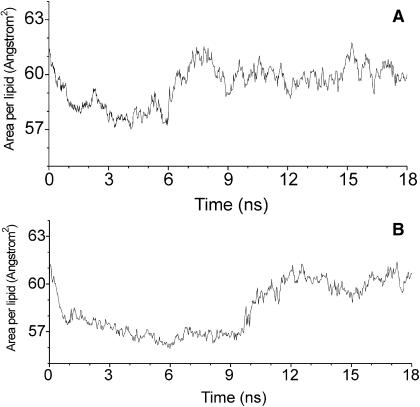
Starting with the configurations obtained by the initial NVE simulations at ∼1.5 ns, we performed NPT simulations for a period of 18 ns for both systems. To illustrate the organization of the peptides in a DMPC bilayer, snapshots of the simulations are shown in Fig. 2. Snapshots at t = 0 ns correspond to those of the initial NVE simulations at ∼1.5 ns (see Methods). In the NPT simulations, the average area per lipid is a characteristic parameter for monitoring the equilibration process of the systems. The time evolution of the area per lipid is shown in Fig. 3. For both systems, the area per lipid fluctuates slightly about the experimental value of 59.8 Å2 (Petrache et al., 1998) for t > 11 ns. The average value of the period from 11 to18 ns is 60.0 ± 0.6 Å2 and 60.1± 0.5 Å2 for systems I and II, respectively. These values are in very good agreement with the experimental value. Therefore, both systems can be considered to be in equilibrium for t > 11 ns. The time evolution of the secondary structure of the bilayer-bound peptide also supports that the systems were equilibrated (see below). Therefore, all related average properties of the systems presented in the following subsections were calculated based on the MD trajectories from 11 to 18 ns.

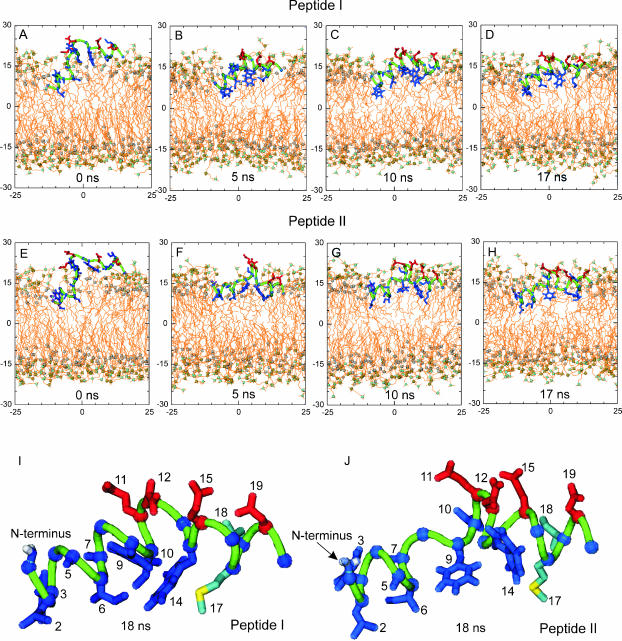
FIGURE 2.

FIGURE 2

Open in a new tab

Snapshots of the conformations of peptides I (A–D) and II (E–H) in NPT simulations. The hydrophobic pocket of peptide I (I) and peptide II (J) at 18 ns. The molecular drawing methods are the same as in Fig. 1. For clarity of the peptide, all water molecules and some lipids are removed.

FIGURE 3.

FIGURE 3

Open in a new tab

Time evolution of the area per lipid for system I (A) and system II (B).

Note that the simulation period needed for equilibrating a peptide-bilayer system depends largely on the choice of the initial conformation of the peptide. Because of limited computational capacity, most of MD studies on peptide-bilayer systems to date usually are simulations covering a period from several to tens of nanoseconds. One may wonder whether this timescale is sufficient for equilibration. As pointed out by Petrache et al. (2000), if the equilibrium conformation of the peptide is close to the initial conformation, MD trajectories may sample an equilibrium population of states in the vicinity of the initial conformation. In our systems, the initial conformation of the peptides was not chosen randomly. The starting α-helical conformation of peptide I was suggested as the bilayer-bound conformation of the fusion peptide by low-resolution experiments (Lüneberg et al., 1995; Macosko et al., 1997). The initial conformation of peptide II was the 1-ns conformation of peptide I of the initial NVE run. This fact may allow the NPT simulations to reach the equilibrated state in a relatively short period. The latter is supported in that the average area per lipid is in good agreement with the experimental value. Therefore, our simulation can be regarded as a refinement of the low-resolution experimental structure (i.e., the α-helical conformation), but not as a simulation of the folding process of the fusion peptide from a randomly chosen conformation.

Conformations of bilayer-bound peptide I and II

Our MD simulations revealed that both peptide I and II adopt a kinked shape conformation that is different from the previously proposed rod-like α-helical structure (Lüneberg et al., 1995; Macosko et al., 1997). The kinked conformation is consistent with the NMR structure of P20H7 (Han et al., 2001). With respect to the low-energy NMR conformer of P20H7 at pH 5, the mean root-mean-square deviation value of all heavy atoms for peptide I is 3.03 ± 0.30 Å and that for peptide II is 5.04 ± 0.17 Å (averaged over the period from 11 to 18 ns). These values indicate that the MD conformation of the fusion peptide in a DMPC bilayer is similar to that found in DPC micelles by NMR (Han et al., 2001).

Experimental studies have shown that helical structures are typical for membrane-bound fusion peptides (e.g., see Chang et al., 2000; Gray et al., 1996; Han et al., 1999). To characterize the secondary structure of peptide I and II, we employed the DSSP program (http://www.cmbi.kun.nl/gv/dssp/) and the do_dssp program from the GROMACS package. Details about the definitions of the secondary structure elements can be seen in Kabsch and Sander (1983). The time evolutions of the secondary structure for peptide I and II are presented in Fig. 4.

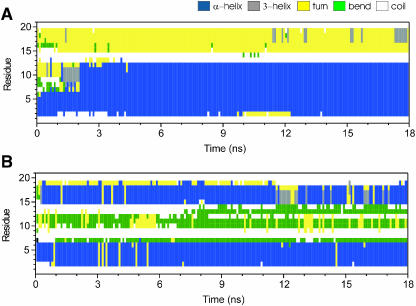
FIGURE 4.

FIGURE 4

Open in a new tab

Time evolution of secondary structures of peptide I (A) and II (B).

For peptide I, Fig. 4 A shows that the residues 2–12 form a stable α-helix for t > ∼2 ns, in good agreement with the NMR structures of the fusion peptide at pH 5 and pH 7.4 (Han et al., 2001). The residues 13 and 14 are always in a coil state, indicating that these two residues have no specific hydrogen bonding with other residues. This feature is also consistent with the experimental structure of the fusion peptide P20H7. Residues 15–19 typically form a hydrogen bonded turn. However, residues 16–19 occasionally adopt a 310-helical conformation (shown in gray in Fig. 4 A). Notably, a short 310-helix in this region is also present in the NMR structure of P20H7 at pH 5. Peptide II harbors two α-helical segments, residues 2–6 and 15–18 (Fig. 4 B). The latter also occasionally forms a 310-helix for t > 11 ns. Residues 10–13 are organized as a bend region with high curvature.

The MD simulation reveals that the helical content (i.e., the number of residues in helical form) of both peptides is ∼50%. This value is in agreement with experiments showing that the helical content of the HA fusion peptide is in the range from 25% to 50% (Chang et al., 2000; Gray et al., 1996; Han et al., 1999).

Location and orientation of peptide side chains in bilayers

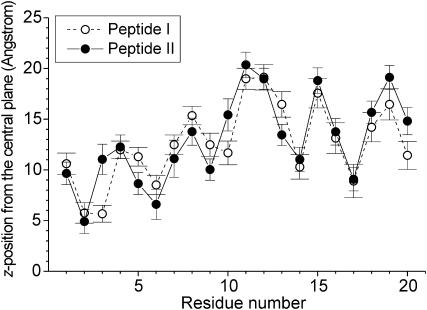
Fig. 2 shows that the fusion peptide is located at the interface between the headgroups and the hydrocarbon chains of the DMPC bilayer. Fig. 5 summarizes the average z-positions of the side chains for peptide I and II (averaged over the MD trajectories from 11 to 18 ns). Here, the center of mass of a side chain is taken to represent the z-position of the whole residue (in case of Gly, the Cα atom is taken). The z coordinates of the residues are found to be similar for peptide I and II. Among all 20 amino acids, the maximal difference of z coordinates for a given residue between peptide I and II is ∼5 Å (i.e., those of Phe-3). As deduced from a comparison of standard deviations, the fluctuations of the z-position of the residues in both peptides are similar (see the error bars in Fig. 5). The polar residues Glu-11 and Asn-12 of the kinked domain locate at the DMPC headgroup region (Fig. 2) and have the largest distance from the central plane with a z coordinate of 19 ∼ 20 Å (Fig. 5). The polar residues Glu-15 and Asp-19, which are oriented to the bulk water, have very similar z-positions. For peptide I, the residues most deeply inserted into the bilayer are Leu-2 and Phe-3, which locate about 5 Å above the center plane of the bilayer. For peptide II, the most deeply immersed residue, Leu-2, has a similar z-position (∼5 Å). Thus, the deepest residues of peptide I and II are rather close to the central plane.

FIGURE 5.

FIGURE 5

Open in a new tab

The average z-positions of peptide side chains in a DMPC bilayer. The standard deviations are shown by error bars.

Recently, Zhou et al. (2000) suggested that the N-terminus of HA fusion peptide (strain X31) is close to the aqueous phase and is protonated at both neutral and low pH conditions. Indeed, our simulations show that the N-terminus, Gly-1, is oriented toward the polar headgroup region (see Fig. 2). As shown in Fig. 5 for the protonated and the unprotonated state, Gly-1 has an average z-position of ∼10 Å in the DMPC bilayer. Therefore, consistent with the conclusion of Zhou et al. (2000), the MD simulations indicate that the protonation state of the N-terminus is not a factor determining the bilayer position of the N-terminal Gly-1.

A pocket-like hydrophobic region is formed on the side of the peptide oriented to the central plane of the bilayer. In Fig. 2 (I and J), a more detailed illustration of the hydrophobic pocket for peptide I and II at 18 ns is shown. The pocket is formed by a cluster of eight hydrophobic residues: Leu-2, Phe-3, Ala-5, Ile-6, Ala-7, Phe-9, Ile-10, and Trp-14 (in blue). On the other side of the peptide, four hydrophilic residues (i.e., Glu-11, Asn-12, Glu-15, and Asp-19 in red in Fig. 2) project to the bulk water. Such an arrangement of hydrophobic and hydrophilic residues is energetically favorable, because the hydrophobic residues have a tendency to partition into the hydrocarbon core of the bilayer, whereas the hydrophilic residues have the opposite tendency orientating toward the water bulk. We surmise that the cluster of the hydrophobic residues is an essential factor for the tight binding of HA to the target membrane. A sequence comparison has shown that these hydrophobic residues are conserved in 13 serotypes of HAs of influenza A viruses (Nobusawa et al., 1991), also implying that such a cluster region is crucial for the fusion activity of HA.

The above results show that the residues from Glu-11 to Gly-20 of peptides form a stable amphipathic segment. Four polar residues (Glu-11, Asn-12, Glu-15, and Asp-19) arrange as a hydrophilic face, whereas three nonpolar residues (Trp-14, Met-17, and Ile-18) form a hydrophobic face. Therefore, the segment is located at the interface between the hydrocarbon chains and polar headgroups of the DMPC bilayer. In contrast, the segment from Gly-1 to Ile-10 is not amphipathic because there is no polar residue in this segment. Compared to the C-terminal segment from Glu-11 to Gly-20, this part inserts more deeply into the hydrophobic core of the bilayer. We suppose that this specific arrangement of hydrophobic and hydrophilic residues is decisive for the formation of the kinked conformation at the bilayer interface. Such a conformation may be essential for membrane fusion. If so, the replacement of a residue by an amino acid of different properties (e.g., a hydrophobic residue by a hydrophilic residue) should abolish fusion. It has been shown that fusion activity was inhibited when Ile-10 (hydrophobic) was replaced by Gly (nonhydrophobic). However, fusion activity was maintained when Ile-10 was replaced by a hydrophobic residue (Ala) (Cross et al., 2001).

Note that the chain length (14 carbon atoms) of the DMPC lipids used in the simulations is shorter than that of lipids usually occurring in biological membranes. Thus, one may wonder whether the conformation of the fusion peptide in biological membranes is somewhat different. To the best of our knowledge, however, so far there is no evidence that the bilayer-bound conformation of the fusion peptide changes with the length of the hydrocarbon chain. Indeed, the experimental results by Han et al. (2001) suggested that the peptide conformation in the DPC micelles (chain length: 12 carbon atoms) is very similar to that in the bilayers composed of 1-palmitoyl-2-oleoylphosphatidylcholine (POPC)/1-palmitoyl-2-oleoylphosphatidylglycerol (POPG) (chain length: 18 carbon atoms). The reason for this is that the fusion peptide is located at the interface between hydrocarbon chains and headgroups, and only the hydrophobic side chains immerse into the hydrophobic core. As we have already discussed, the major factor determining the bilayer-bound conformation of the fusion peptide is the amphipathic interface between headgroups and hydrocarbon chains, but not solely the hydrocarbon core. Because the amphipathic interface is essentially the same for phospholipid bilayers with hydrocarbon chains of different lengths (at least for those with the same headgroups), the conformation of the fusion peptide is similar.

Perturbation of peptide-surrounding lipids

Experimental evidence has already been presented that the insertion of the HA fusion peptide affects the organization of the bilayer (see Introduction). We explored our approach to address which alterations of the lipid phase are induced by the insertion of the hydrophobic side chains of the fusion peptide. We found that the average hydrophobic thickness of the bilayer is affected by the fusion peptide.

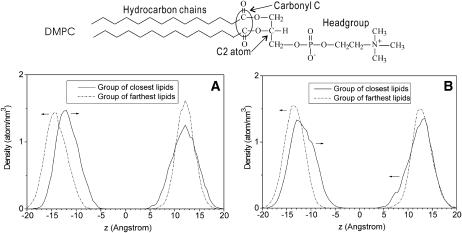
To characterize the influence of the embedded fusion peptide on the thickness of the bilayer, we investigated the average position of the phospholipid carbonyl C atoms (see Fig. 6 for two carbonyl C atoms in DMPC) and its dynamics. These atoms were chosen since they define the interface between polar headgroups and hydrophobic chains. Thus, their z-position provides a reasonable measure for the thickness of the hydrophobic region of the bilayer. In the bulk phase of a pure DMPC bilayer, the average z-position of carbonyl C atoms is ∼14 Å from the central plane, with fluctuations in the range between 8 and 20 Å (Smondyrev and Berkowitz, 1999; Zubrzycki et al., 2000). To examine how the insertion of the peptide affects the z-position of the carbonyl C atoms, we investigated in each leaflet two groups of lipids that have the smallest (closest group) and the greatest (farthest group) distance to the N-terminus of the peptide. To each group, 15 DMPC molecules were assigned according to the distance between the C2 atom and the N atom of the N-terminus (Gly-1) (see Fig. 6 for the C2 atom of DMPC). The assignment was done for each frame of the MD trajectories (t > 11 ns), and then the z-positions of the carbonyl C-atoms of lipids in the assigned groups were taken to calculate the density profile (Fig. 6). For both systems, we found that in the top leaflet harboring the peptide the average z-positions of the carbonyl C atoms of the two groups are very similar. However, the density profile of the closest group is broader with respect to the farthest group. This indicates larger fluctuations of lipids in the neighborhood of the peptide. The latter was also observed for the bottom leaflet, in particular for system II (Fig. 6 B).

FIGURE 6.

FIGURE 6

Open in a new tab

Density profiles along the bilayer normal for the carbonyl C atoms of the lipids closest to and farthest from the N-terminus. (A) System I. (B) System II.

Compared with the average z-positions of carbonyl C atoms in pure DMPC bilayer, in the top leaflet of both systems the carbonyl C atoms of both groups were found to shift toward the central plane by ∼2 Å. In addition, we observed a shift of the average z-position of the carbonyl C atom of the closest group toward the central plane by ∼3 and 4 Å for systems I and II, respectively. As a consequence, the local hydrophobic thickness near the N-terminus is ∼4 Å smaller than that at the larger distance from the N-terminus. Very likely, disordering of the arrangement of the hydrocarbon chains of peptide-surrounding lipids causes the local reduction of the bilayer thickness. This effect may become even more pronounced by a concerted action of several fusion peptides. Indeed, oligomerization of fusogenic peptides has been suggested to promote local membrane destabilization (Lau et al., 2004). Hristova et al. (2001) have shown that dimeric melittin causes larger structural perturbations of the bilayer in comparison with the monomer (Hristova, et al., 2001).

CONCLUSIONS

In this study, we examined the conformation of the HA fusion peptide (strain X31) in a DMPC bilayer by 18-ns NPT simulations. In agreement with the structure of the fusion peptide obtained from an NMR study (Han et al., 2001), the simulations revealed that the bilayer-bound fusion peptide is not a rigid, rod-like helix but adopts a kinked shape conformation. The analysis of the secondary structure indicated that the helical content of the fusion peptide was found to be in the range of experimental data. The simulations showed that the peptide is located at the amphipathic interface between the polar headgroups and hydrocarbon chains. The specific sequence and distribution of hydrophobic and hydrophilic residues along the HA fusion peptide may be crucial for the formation of the kinked conformation at the amphipathic interface.

We found that the local hydrophobic thickness of the bilayer region close to the N-terminus of the peptide is reduced in comparison with the hydrophobic thickness of the bulk lipid phase, indicating that the lipids surrounding the fusion peptide undergo a displacement along the axis normal to the bilayer. The rearrangement of the peptide surrounding lipids and the perturbation of the bilayer thickness might reflect the destabilization of the membrane essential for membrane fusion. Further studies will show how the fusion activity of (mutant) fusion peptides correlates with the kinked shape conformation of the peptide and the local rearrangement of the lipid phase in the vicinity of the peptide.

Finally, we want to emphasize the limitations of the molecular modeling approach. For example, because there is no information available on the protonation state of several residues of the fusion peptide, and no reliable method exists to simulate a peptide-bilayer system at low pH conditions, we cannot adapt exactly all experimental conditions of interest. Also, these simulations did not allow to change the numbers of DMPCs in the top and bottom leaflet that might introduce artifacts (Dolan et al., 2002). In addition, it is still very difficult to simulate systems consisting of a larger number of lipids and/or fusion peptides for periods as long as tens or hundreds of nanoseconds due to limited computational capacity. Such studies may provide more fusion relevant details, e.g., how fusion peptides cause local bilayer rearrangement at a larger length scale and the importance of fusion peptide interactions for bilayer perturbation. However, a huge number of examples including this study have proven that theoretical studies such as MD simulation can provide reasonable results complementing experimental data.

Acknowledgments

Special thanks to Dr. Thomas Korte, Chih-Yu Hua for assistance in using computer hardware, and R. P. Sivaramakrishna and Dr. Kai Ludwig for many valuable discussions.

This work was supported by grants of the National Science Council and by the MOE Program for Promoting Academic Excellence of Universities (to C.-L.C.) and the Deutsche Forschungsgemeinschaft (to A.H.). Part of the work was completed during a stay of Q.H. at Humboldt-University Berlin supported by a scholarship from DAAD (German Academic Exchange Service).

References

  1. Belohorcova, K., J. Qian, and J. H. Davis. 2000. Molecular dynamics and 2H-NMR study of the influence of an amphiphilic peptide on membrane order and dynamics. Biophys. J. 79:3201–3216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
  3. Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction models for water in relation to protein hydration. In Intermolecular Forces. B. Pullman, editor. Reidel, Dordrecht, The Netherlands. 331–342.
  4. Berendsen, H. J. C., D. van der Spoel, and R. van Drunen. 1995. GROMACS: a message-passing parallel molecular-dynamics implementation. Comput. Phys. Commun. 91:43–56. [Google Scholar]
  5. Berger, O., O. Edholm, and F. Jähnig. 1997. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72:2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bradshaw, J. P., M. J. M. Darkes, T. A. Harroun, J. Katsaras, and R. M. Epand. 2000. Oblique membrane insertion of viral fusion peptide probed by neutron diffraction. Biochemistry. 39:6581–6585. [DOI] [PubMed] [Google Scholar]
  7. Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy minimization and dynamics calculations. J. Comp. Chem. 4:187–217. [Google Scholar]
  8. Bullough, P. A., F. M. Hughson, J. J. Skehel, and D. C. Wiley. 1994. Structure of influenza haemagglutinin at the pH of membrane fusion. Nature. 371:37–43. [DOI] [PubMed] [Google Scholar]
  9. Carr, C. M., and P. S. Kim. 1993. A spring-loaded mechanism for the conformational change of influenza hemagglutinin. Cell. 73:823–832. [DOI] [PubMed] [Google Scholar]
  10. Chan, D. C., D. Fass, J. M. Berger, and P. S. Kim. 1997. Core structure of gp41 from the HIV envelope glycoprotein. Cell. 89:263–273. [DOI] [PubMed] [Google Scholar]
  11. Chang, D. K., S. F. Cheng, and W. J. Chien. 1997. The amino-terminal fusion domain peptide of human immunodeficiency virus type 1 gp41 inserts into the sodium dodecylsulfate micelle primarily as a helix with a conserved glycine at the micellewater Interface. J. Virol. 71:6593–6602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chang, D.-K., S.-F. Cheng, V. Deo Trivedi, and S.-H. Yang. 2000. The amino-terminal region of the fusion peptide of influenza virus hemagglutinin HA2 inserts into sodium dodecyl sulfate micelle with residues 16–18 at the aqueous boundary at acidic pH. Oligomerization and the conformational flexibility. J. Biol. Chem. 275:19150–19158. [DOI] [PubMed] [Google Scholar]
  13. Colotto, A., and R. M. Epand. 1997. Structural study of the relationship between the rate of membrane fusion and the ability of the fusion peptide of influenza virus to perturb bilayers. Biochemistry. 36:7644–7651. [DOI] [PubMed] [Google Scholar]
  14. Cross, K. J., S. A. Wharton, J. J. Skehel, D. C. Wiley, and D. A. Steinhauer. 2001. Studies on influenza haemagglutinin fusion peptide mutants generated by reverse genetics. EMBO J. 20:4432–4442. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
  16. Dolan, E. A., R. M. Venable, R. W. Pastor, and B. R. Brooks. 2002. Simulations of membranes and other interfacial system using P21 and Pc periodic boundary conditions. Biophys. J. 82:2317–2325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Dubovskii, P. V., H. Li, S. Takahashi, A. S. Arseniev, and K. Akasaka. 2000. Structure of an analog of fusion peptide from hemagglutinin. Protein Sci. 9:786–798. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Durrer, P., C. Galli, S. Hoenke, C. Corti, R. Gluck, T. Vorherr, and J. Brunner. 1996. H1-induced membrane insertion of influenza virus hemagglutinin involves the HA2 amino-terminal fusion peptide but not the coiled coil region. J. Biol. Chem. 271:13417–13421. [DOI] [PubMed] [Google Scholar]
  19. Eckert, D. M., and P. S. Kim. 2001. Mechanisms of viral membrane fusion and its inhibition. Annu. Rev. Biochem. 70:777–810. [DOI] [PubMed] [Google Scholar]
  20. Efremov, R. G., D. E. Nolde, P. E. Volynsky, A. A. Chernyavsky, P. V. Dubovskii, and A. S. Arseniev. 1999. Factors important for fusogenic activity of peptides: molecular modeling study of analogs of fusion peptide of influenza virus hemagglutinin. FEBS Lett. 462:205–210. [DOI] [PubMed] [Google Scholar]
  21. Epand, R. M. 1998. Lipid polymorphism and protein-lipid interactions. Biochim. Biophys. Acta. 1376:353–368. [DOI] [PubMed] [Google Scholar]
  22. Epand, R. M. 2003. Fusion peptide and the mechanism of viral fusion. Biochem. Biochys. Acta. 1614:116–121. [DOI] [PubMed] [Google Scholar]
  23. Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
  24. Gray, C., S. A. Tatulian, S. A. Wharton, and L. K. Tamm. 1996. Effect of the N-terminal glycine on the secondary structure, orientation, and interaction of the influenza hemagglutinin fusion peptide with lipid bilayers. Biophys. J. 70:2275–2286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Han, X., J. N. Bushweller, D. S. Cafiso, and L. K. Tamm. 2001. Membrane structure and fusiontriggering conformational change of the fusion domain from influenza hemagglutinin. Nat. Struct. Biol. 8:715–720. [DOI] [PubMed] [Google Scholar]
  26. Han, X., D. A. Steinhauer, S. A. Wharton, and L. K. Tamm. 1999. Interaction of mutant influenza virus hemagglutinin fusion peptides with lipid bilayers: probing the role of hydrophobic residue size in the central region of the fusion peptide. Biochemistry. 38:15052–15059. [DOI] [PubMed] [Google Scholar]
  27. Han, X., and L. K. Tamm. 2000. A host-guest system to study structure-function relationships of membrane fusion peptides. Proc. Natl. Acad. Sci. USA. 97:13097–13102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Harter, C., P. James, T. Bachi, G. Semenza, and J. Brunner. 1989. Hydrophobic binding of the ectodomain of influenza hemagglutinin to membranes occurs through the “fusion peptide”. J. Biol. Chem. 264:6459–6464. [PubMed] [Google Scholar]
  29. Hess, B., H. Bekker, H. J. C. Berendsen, and J. Fraaije. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
  30. Hristova, K., C. E. Dempsey, and S. H. White. 2001. Structure, location, and lipid perturbations of melittin at the membrane interface. Biophys. J. 80:801–811. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
  32. Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
  33. Kabsch, W., and C. Sander. 1983. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 22:2577–2637. [DOI] [PubMed] [Google Scholar]
  34. Kamath, S., and T. C. Wong. 2002. Membrane structure of the human immunodeficiency virus gp41 fusion domain by molecular dynamics simulation. Biophys. J. 83:135–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Lau, W. L., D. S. Ege, J. D. Lear, D. A. Hammer, and W. F. DeGrado. 2004. Oligomerization of fusogenic peptides promotes membrane fusion by enhancing membrane destabilization. Biophys. J. 86:272–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Mod. 7:306–317. [Google Scholar]
  37. Lüneberg, J., I. Martin, F. Nussler, J. M. Ruysschaert, and A. Herrmann. 1995. Structure and topology of the influenza virus fusion peptide in lipid bilayers. J. Biol. Chem. 270:27606–27614. [DOI] [PubMed] [Google Scholar]
  38. MacKerell, A. D. J., D. Bashford, M. Bellot, R. L. J. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodholm, W. E. I. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
  39. Macosko, J. C., C. H. Kim, and Y. K. Shin. 1997. The membrane topology of the fusion peptide region of influenza hemagglutinin determined by spin-labeling EPR. J. Mol. Biol. 267:1139–1148. [DOI] [PubMed] [Google Scholar]
  40. Nobusawa, E., T. Aoyama, H. Kato, Y. Suzuki, Y. Tateno, and K. Nakajima. 1991. Comparison of complete amino acid sequences and receptor-binding properties among 13 serotypes of hemagglutinin of influenza A viruses. Virology. 182:475–485. [DOI] [PubMed] [Google Scholar]
  41. Petrache, H. I., A. Grossfield, K. R. MacKenzie, D. M. Engelman, and T. B. Woolf. 2000. Modulation of glycophorin A transmembrane helix interactions by lipid bilayers: molecular dynamics calculations. J. Mol. Biol. 302:727–746. [DOI] [PubMed] [Google Scholar]
  42. Petrache, H. I., S. Tristram-Nagle, and J. F. Nagle. 1998. Fluid phase structure of EPC and DMPC bilayers. Chem. Phys. Lipids. 95:83–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sankararamakrishnan, R., and H. Weinstein. 2000. Molecular dynamics simulations predict a tilted orientation for the helical region of dynorphin A(1–17) in dimyristoylphosphatidylcholine bilayers. Biophys. J. 79:2331–2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Siegel, D. P., and R. M. Epand. 2000. Effect of influenza hemagglutinin fusion peptide on lamellar/inverted phase transitions in dipalmitoleoylphosphatidylethanolamine: implications for membrane fusion mechanisms. Biochim. Biophys. Acta. 1468:87–98. [DOI] [PubMed] [Google Scholar]
  45. Skehel, J. J., and D. C. Wiley. 2000. Receptor binding and membrane fusion in virus entry: the influenza hemagglutinin. Annu. Rev. Biochem. 69:531–569. [DOI] [PubMed] [Google Scholar]
  46. Smondyrev, A. M., and M. L. Berkowitz. 1999. Molecular dynamics simulation of fluorination effects on a phospholipid bilayer. J. Chem. Phys. 111:9864–9870. [Google Scholar]
  47. Stegmann, T., J. M. Delfino, F. M. Richards, and A. Helenius. 1991. The HA2 subunit of influenza hemagglutinin inserts into the target membrane prior to fusion. J. Biol. Chem. 266:18404–18410. [PubMed] [Google Scholar]
  48. Tsurudome, M., R. Gluck, R. Graf, R. Falchetto, V. Schaller, and J. Brunner. 1992. Lipid interactions of the hemagglutinin HA2 NH2-terminal segment during influenza virus-induced membrane fusion. J. Biol. Chem. 267:20225–20232. [PubMed] [Google Scholar]
  49. Venable, R. M., Y. Zhang, B. J. Hardy, and R. W. Pastor. 1993. Molecular dynamics simulations of a lipid bilayer and of hexadecane: an investigation of membrane fluidity. Science. 262:223–226. [DOI] [PubMed] [Google Scholar]
  50. Wiley, D. C., and J. J. Skehel. 1987. The structure and function of the hemagglutinin membrane glyprotein of influenza virus. Annu. Rev. Biochem. 56:365–395. [DOI] [PubMed] [Google Scholar]
  51. Wilson, I. A., J. J. Skehel, and D. C. Wiley. 1981. Structure of the haemagglutinin membrane glycoprotein of influenza virus at 3 Å resolution. Nature. 289:366–373. [DOI] [PubMed] [Google Scholar]
  52. Woolf, T. B., and B. Roux. 1994. Molecular dynamics simulation of the gramicidin channel in a phospholipid bilayer. Proc. Natl. Acad. Sci. USA. 91:11631–11635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Woolf, T. B., and B. Roux. 1996. Structure, energetics and dynamics of lipid-protein interactions: a molecular dynamics study of the gramicidin a channel in a DMPC bilayer. Proteins. 24:92–114. [DOI] [PubMed] [Google Scholar]
  54. Zhou, Z., J. C. Macosko, D. W. Hughes, B. G. Sayer, J. Hawes, and R. M. Epand. 2000. 15N-NMR study of the ionization properties of the influenza virus fusion peptide in zwitterionic phospholipid dispersions. Biophys. J. 78:2418–2425. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Zubrzycki, I. Z., Y. Xu, M. Madrid, and P. Tang. 2000. Molecular dynamics simulations of a fully hydrated dimyristoylphosphatidylcholine membrane in liquid-crystalline phase. J. Chem. Phys. 112:3437–3441. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES