LexA-DNA Bond Strength by Single Molecule Force Spectroscopy

Abstract

The SOS system of Escherichia coli is coordinated by two proteins: LexA, a repressor protein of several unlinked genes, and the coprotease RecA. As known to date LexA controls 31 genes with slightly different DNA binding motifs allowing for a variable degree of repression from one gene to the other. Besides the SOS system LexA plays an important role in the regulation of transcription. The protein regulates transcription by using particular motifs to bind DNA, the helix-turn-helix motif. Here, we employed AFM-based single molecule force spectroscopy to characterize the interaction of LexA protein with two different DNA motifs: recA and yebG. We measured the dissociation rates to be 0.045 s⁻¹ for recA and 0.13 s⁻¹ for yebG, respectively, which is in accordance with the predicted higher affinity between LexA-recA compared to LexA-yebG. The widths of the binding potentials were determined to be 5.4 ± 1 Å and 4.9 ± 0.5 Å, respectively. This short-ranged potential is characteristic for a stiff hydrogen-bonding network between protein and DNA. The unbinding occurs in a breakup rather than a gradual sliding.

INTRODUCTION

Escherichia coli reacts with a complex response to DNA damage or inhibition of DNA replication. This response, termed SOS system, includes phenomena such as enhanced DNA repair and mutagenesis, inhibition of cell division and prophage induction. The SOS system is predominantly controlled by two proteins: LexA, a repressor protein of several unlinked genes and the coprotease RecA (Little and Mount, 1982). Transcription factors and other regulatory proteins require two types of ability, the recognition of specific target sequences located in enhancers, promoters, or other regulatory elements that affect a particular target gene and after having bound to DNA, a transcription factor, or a positive regulatory protein, exercises its function by binding to other components of the transcription apparatus. LexA is a prokaryotic regulatory protein in which DNA recognition is mediated by a variant of the classical helix-turn-helix motif, with an insertion in the turn region (Harrison and Aggarwal, 1990; Holm et al., 1994). The helix-turn-helix motif was originally identified as the DNA-binding domain of phage repressors. One α-helix lies in the wide groove of DNA; the other lies at an angle across DNA. A related form of the motif is present in the homeodomain, a sequence first characterized in several proteins coded by genes concerned with developmental regulation in Drosophila. It is also present in genes for mammalian transcription factors (Lewin, 2000). The structure of LexA repressor from E. coli reveals an unexpected structural similarity to a widespread class of prokaryotic and eukaryotic regulatory CAP proteins (Holm et al., 1994).

LexA is a dimeric protein of 202 amino acids (25 kDa) whose monomers are linked by a flexible “hinge” region. The COOH-terminal domains provide most of the contact for dimerization. The NH₂-terminal domains bind selectively to certain DNA sequences, the so-called operator DNA (Kim and Little, 1992). The three-dimensional structure of the LexA-DNA binding domain has been solved by NMR spectroscopy (Fogh et al., 1994). The crystal structure of the protein-DNA complex reveals that each of the monomers binds one-half of the operator DNA (Pabo and Sauer, 1992; Luisi, 1995). However, since all known SOS operator sequences are highly palindromic (Schnarr et al., 1991), LexA interacts functionally with the operator DNA as a dimer. Recently, it was shown that under ambient conditions — comparable to the ones in the experiments here — the dissociation constant for the LexA-dimer is in the picomolar range (Mohana-Borges et al., 2000).

The operator consensus sequence (so-called SOS box) is a perfect 20 bp palindrome, TACTGTATATATATACAGTA (Berg, 1988; Schnarr et al., 1991). The sequence among different DNA binding motifs varies slightly, allowing for a variable degree of repression from one gene to the other (Wertman and Mount, 1985). A complex superposition of specific hydrogen bonds and van der Waals interactions between protein and DNA explains the pronounced specificity of LexA repressor for the consensus CTGT motif, a conclusion that was corroborated by mutagenesis data (Knegtel et al., 1995).

The DNA binding properties of LexA repressor and the isolated DNA binding domain have been studied extensively using biochemical and biophysical methods such as methylation protection, ethylation interference, hydroxyl-radical footprinting, photocrosslinking, mutagenesis, NMR spectroscopy, and atomic force microscopy (AFM) imaging (Hurstel et al., 1988; Lloubes et al., 1991; Dumoulin et al., 1993, 1996; Fogh et al., 1994; Knegtel et al., 1995; Costa et al., submitted for publication). Together, these data had yielded a wealth of information on the orientation of the recognition helix in the major groove and possible specific contacts between protein and DNA. Based on the measured dissociation constant of K_D = 2 nM between LexA and its operator recA, by DNase footprinting, (Lewis et al., 1994) the dissociation constant between LexA and yebG was predicted based on the calculated Heterology Index to be K_D = 20 nM (Fernandez de Henestrosa et al., 2000). The purpose of this study here was to further characterize the binding mode and to quantify the interaction between LexA and yebG by direct experiments.

In recent years AFM-based force spectroscopy has been established as a powerful tool to measure unbinding forces of individual molecular complexes in the piconewton range (Florin et al.,1994; Viani et al., 1999). This technique was used to study both inter- and intramolecular interactions of complex biological and synthetic macromolecules with extremely high accuracy and force resolution. It has been applied for direct measurements between complementary DNA strands (Lee et al., 1994a; Rief et al., 1997a,b, 1998, 1999; Strunz et al., 1999) and single ligand-receptor pairs (Lee et al., 1994b; Moy et al., 1994; Hinterdorfer et al., 1996; Schwesinger et al., 2000). Recently as a first example a quantitative study of dsDNA-protein interaction (Bartels et al., 2003) was reported (Bockelmann et al., 2002; Koch et al., 2002).

In such experiments one of the binding partners is covalently attached with polymeric spacer molecules to the tip of an AFM cantilever, the other binding partner to a sample surface. The AFM-tip is brought into contact with the surface and a specific bond between these two molecules is allowed to form. Upon retraction the bond between the binding partners is increasingly loaded until it finally ruptures. Both the stretching of the polymeric spacers and the rupture of the molecular complex are recorded by measuring the deflection of the cantilever spring.

Molecular recognition of biomolecules comprises multiple weak noncovalent interactions, which form a complex energy landscape between the binding partners. Because of the finite probability of such complexes to dissociate spontaneously, such bonds will fail at any level of pulling force if this force is applied for a sufficiently long time span. Thus, the strength of such a bond depends on the time derivative of the force, the so-called loading rate. Conceptually this picture is equivalent to a tilting of the energy landscape of the bond by the applied force, which lowers energy barriers, and thus decreases the probability of bond survival (Merkel et al., 1999). Measuring the unbinding force as a function of the loading rate thus reveals information on the energy landscape, which otherwise is not accessible by other techniques. As was shown by Evans and Ritchie (1997), both the dissociation rate (k_off) and the width of the binding potential (Δx) can be determined from such rate-dependent measurements. Alternatively these parameters may also be derived by a rigorous analysis of the unbinding force histograms (Friedsam et al., 2003).

Here, we employed rate-dependent single molecule force spectroscopy by AFM-related techniques to characterize the binding of LexA protein with the DNA binding motifs, recA and yebG. We determined the characteristic width of the energy landscape along a force-driven pathway and derived the dissociation rate (k_off) value for each operator sequence.

MATERIAL AND METHODS

Protein purification

All reagents were of analytical grade. Distilled water was filtered and deionized through a Millipore (Billerica, MA) water purification system. Ultrapure urea was obtained from Sigma (St. Louis, MO). LexA protein was over expressed using E. coli strain BL21 (λDE3) carrying the plasmid pJWL228, in which lexA is fused to a T7 RNA polymerase promoter (kindly supplied by J. W. Little, University of Arizona, Tucson, AZ). Growth of the bacteria, induction of expression, and purification of LexA were performed as described previously (Little et al., 1994). Purified LexA was stored in stock buffer: 50 mM Tris-HCl, 200 mM NaCl, 0.1 mM EDTA, and 5% glycerol, in liquid nitrogen, at final concentration of 34 μM.

DNA binding motifs

The DNA sequences were synthesized by nucleic acids synthesis (IBA, Göttingen, Germany). Both DNA strands are 5′- amino modified. RecA operator: (5-ATA GCT CAC TTG ATA CTG TAT GAG CAT ACA GTA TAA TTG (0.1 nmol/μl); and yebG operator (5-ACT CAA GTT CCT TCG GAG CCT ACT GTA TAA AAT CAC AGT TAG CAA GAT GT-3) (0.1 nmol/μl).

AFM tip and sample surface functionalization

Before functionalization, Si₃N₄ cantilevers (Veeco Microscopes, Model A MLCT-AVHW, Mannheim, Germany) were cleaned by placing them under a mercury UV light (UVP Pen-Ray) for 30 min. The cantilever silanization was carried out by incubating at 90°C for 10 min in N′-[3-(trimethoxysilyl)propyl]diethylene-triamine (Aldrich). After washing in ethanol, followed by deionized water at 90° C for 2 h, they were incubated at room temperature for 10 min with carboxymethylamylose-10 mg (Sigma) + NHS-4 mg (N-hydroxysuccinimide, Aldrich) + EDC-17 mg (1- ethyl-3-[3-(dimethylamino)propyl]carbamide, Sigma) diluted in 200 mL PBS, and finally washed several times in PBS. In the last step, the cantilevers were incubated either with 20 μL recA operator or yebG operator at room temperature for 1 h 30 min.

Aminoslides (Quantifoil Micro tools GmbH, Jena, Germany) were incubated at room temperature for 10 min with carboxymethylamylose-10 mg + NHS-4 mg + EDC-17 mg diluted in 200 mL PBS; followed by several washing steps in PBS. Afterwards, the aminoslides were incubated with 10 μL of LexA protein (34 mM) at room temperature for 1 h 30 min.

Force spectroscopy

Force spectroscopy measurements were performed at room temperature in PBS with a homebuilt instrument described elsewhere in more detail (Benoit, 2002). Cantilevers with different spring constants were employed from 8 mN/m to 18 mN/m (Cantilever C — Veeco), and from 39 to 42 mN/m (Cantilever D — Veeco). The spring constants were measured in each experiment by the thermal fluctuation method (Lévy and Maaloum, 2002).

Data analysis

A detailed description of the data analysis is given elsewhere (Friedsam et al., 2003). Briefly: the measured force-distance curves were analyzed with an algorithm written in Igor (Wavemetrics Inc., Oregon). Each force-distance curve was fitted with an FJC-model, to determine the polymer length. A fixed persistence length of 4.5 Å was used. The force loading rate was determined by the slope of the fit at the rupture point multiplied with the speed and corrected by the bending of the cantilever. The rupture forces, the loading rates, and the spacer lengths of thousands of force curves were plotted in three separate histograms, respectively.

Based on the assumption of a one-barrier binding potential, the bond rupture probability under external force F is given by:

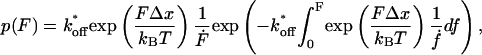(1)

where k_B is the Boltzmann constant and T the absolute temperature (Evans and Ritchie, 1997; Heymann and Grubmüller, 2000; Friedsam et al., 2003). The goal of the fit procedure is to extract the potential width (Δx) and the dissociation rate (k_off). Since in our experiments the spacer lengths vary, the force loading rates dF/dt vary although the pulling speed is kept constant. Therefore the bond rupture probability density p(F) was calculated according to Eq. 1 for every spacer length in the measured histogram. These p(F)-functions were then weighted according to their occurrence in the histogram and added up. The result is a semi- hypothetical rupture force histogram based on the two input parameters k_off and Δx, which were varied to find the best fit to the measured rupture force histogram. In the case of a spacer length distribution, this procedure results in a significantly more accurate determination of both k_off and Δx than the usual method, which uses an average spacer length in combination with equation 2.

RESULTS

LexA-recA operator interaction

To investigate LexA-recA operator binding affinity by single molecule force spectroscopy, both LexA and recA were covalently bound, via a polymer spacer, to the amino glass slide and the AFM tip, respectively (as described in Materials and Methods). The experimental setup is sketched in Fig. 1 a. To corroborate that our immobilization approach does not interfere with the ability of LexA to recognize and bind to the operator DNA specifically, we performed in a separate experiment a fluorescence assay, with Cy5 dye labeled LexA. After immobilizing the LexA-Cy5, we performed several washing steps in stringent conditions. Then the fluorescence was measured to confirm the covalent binding of LexA to the amino glass slide, followed by a test of the DNA-protein complex formation using the operator DNA labeled with Cy3 at the 5′-end. This assay confirmed that the LexA protein kept the ability to bind to the operator DNA after immobilization (data not shown).

FIGURE 1.

(a) Setup of the AFM experiment: the cantilever is aminosilanized and functionalized with carboxymethylamylose to which the DNA-operator is covalently bound to the side groups. The aminoslide is coated with carboxymethylamylose to which the LexA protein is linked. The DNA-Operator and the protein LexA are allowed to form bonds during the experiment. As all other bonds are covalent and therefore much stronger, the LexA-dsDNA bond is ruptured when the cantilever is retracted. (b) Typical single approach-retract cycle. The black curve shows the cantilever approaching to the surface, where it waits (contact time) under a contact force of 80 pN. The gray curve is the retrace with an increasing (stretching of the carboxymethylamylose) force to an unbinding event. (c) Example for a block experiment. Force curves were captured at a constant rate. The graph shows the length of an unbinding event, which occurs in the ongoing performed retract curves. By the time of the black line, free LexA is added to block the dsDNA at the tip. The graph of unbinding distances shows clearly the decrease in the fraction of force curves showing an unbinding event.

Fig. 1 b shows a typical approach-retract cycle recorded under the conditions given above. The tip was approached to the surface while the deflection of the cantilever was monitored. To avoid damage of the immobilized protein the contact force was limited to a value between 50–200 pN. Upon retract the deflection was recorded. A gradual increase of the force followed by a discrete drop, indicating the stretching of the polymer and the bond rupture was observed in about half of the force curves. In the other cases the retract curve followed the approach curve indicating that no bond had formed. By adjusting the time that the tip remains in contact with the surface (0.1–2 s) this 50% chance of bond formation was kept roughly constant throughout the experiment. Under consideration that different unbinding events have different spacer lengths, it is possible to analyze rupture events separately. Accordingly the success rate for a certain single bond formation was kept below 15% (depend from each experiment) to ensure a likelihood for double binding events below 7% (Tees et al., 2001).

To demonstrate that the unbinding event reflects the specific interaction between LexA and recA, we performed blocking experiments. After several hundreds of force curves, free LexA was added to the solution. As a result the adhesion rate decreased by 95% (Fig. 1 c). In addition we performed an experiment where we measured the interaction between the fully functionalized tip and a sample surface, where just the last step, the coupling of LexA to the carboxymethylamylose had been not carried out. No apparent interaction was detected (data not shown). Experiment with carboxymethylamylose on the tip versus carboxymethylamylose on the slide led to <2% interactions.

Thousands of such approach and retract cycles as the one shown in Fig. 1 b were automatically recorded at the same spot with the same pulling speed under the same conditions and analyzed as a data block after the procedure given above. In Fig. 2 the force distribution, loading rate distribution, and spacer length distribution derived from such an experimental block are shown. Fig. 2 a shows the resulting unbinding force histogram together with the best-fit line (black) for the theoretical force distribution according to Eq. 1. The best-fit parameters were found to be 5.8 Å for the potential width and 0.058 s⁻¹ for the dissociation rate. The dotted black curve, representing a fit with deviating parameters (Δx = 6 Å, k_off = 0.01 s⁻¹) is shown for a comparison of the quality of the fit. The spacer length distribution exhibits several peaks ranging from 500 to 5000 monomers, indicating that different molecule were alternatively or sequentially probed in the course of the experiment.

FIGURE 2.

(a) Example for a force distribution of the unbinding events of LexA and the DNA recA operator from one experimental block. The black curve demonstrates the best fit with the fit parameter k_off = 0.058 s⁻¹ and Δx = 5.8 Å for the receptor ligand system. The black dashed curve presents the sensibility of the fit algorithm, with parameters Δx = 6.0 Å and k_off = 0.01 s⁻¹. The gray area in the lower force regime shows the resolution limit of the instrument. (b) The associated loading rate distribution (100–3000 pN/s) to a with the best fit (black) and the two incorrect fits (dashed black) showing the sensibility. The intensity of occurrence is plotted versus the natural logarithm of the loading rate. The gray area in the lower force regime shows the resolution limit of the instrument. (c) Monomer number distribution (4.5 Å for carboxymethylamylose) of the spacer, obtained from the freely jointed chain fit for all rupture events.

Several sets of experiments were performed at different pulling velocities varying between 300 to 3000 nm/s, which equals loading rates from 500 pN/s to 9000 pN/s. The fits to the rupture force and loading rate histograms revealed similar mean values for the potential width (5.4 ± 1.0) Å and the dissociation rate (0.048 ± 0.020)s⁻¹.

LexA-yebG operator interaction

Based on the same approach we determined the affinity of the LexA repressor protein, to an alternative sequence, the yebG operator. Model calculations predict that the yebG operator has a lower affinity (K_d = 20 nM) in comparison to the recA operator (K_d = 2 nM). In analogy to the experiments described above, we measured the interaction between LexA and the yebG operator at a constant pulling velocity of 2830 nm/s. At comparable contact parameters the measured binding likelihood of 21% was lower in these experiments compared to the 50% measured before with the recA sample. The specificity of the interaction was demonstrated by blocking experiments with free LexA as described above. Upon addition the adhesion rate decreased by 22%.

The rupture force histogram of the LexA-yebG bond is plotted in Fig. 3 a. The best fit was found to be 5.0 Å for the potential width and 0.19 s⁻¹ for the dissociation rate. For a comparison the fit with the recA parameters is shown in black. Based on several sets of such experiments carried out at pulling velocities between 1000–3000 nm/s, which equals loading rates from 500 pN/s to 7000 pN/s, the best fits revealed a potential width of (4.9 ± 0.5) Å and a dissociation rate of (0.13 ± 0.08)s⁻¹ for the interaction between LexA and the yebG operator.

FIGURE 3.

(a) Force distribution of the unbinding events of LexA and the DNA yebG operator, which k_off = 0.19 s⁻¹ and Δx = 5.0 Å as fit parameters for the best fit (black) for the receptor ligand system. The dashed black curve represents the fit for the LexA-recA binding system. The gray area in the lower force regime shows the resolution limit of the instrument. (b) The associated loading rate distribution (200–10000 pN/s) to a with the best fit (black) and fit for the LexA-recA system (dashed black). The gray area in the lower force regime shows the resolution limit of the instrument. (c) Monomer number distribution (4.5 Å for carboxymethylamylose) of the spacer, obtained from the freely jointed chain fit for all rupture events.

Loading rate-spacer length dependence

Since the spacer length histograms shown before exhibit multiple peaks, it is very likely that they are the combinatory result of multiple interactions of a small number (<3 on each side) of binding partners, whose spacers differ in length and/or attachment. With such a discrete spacer length distribution, the quality of the fit and the accuracy of the underlying model can be checked by analyzing the different populations independently. At a constant speed of the cantilever, the loading rate ( in Eq. 1) depends on the different spacer lengths. Therefore, even if potential width and dissociation rate are the same, the maximum of the bond rupture probability is shifted to higher forces for shorter spacer lengths since those are causing higher loading rates.

The spacer length histogram given in Fig. 4 a shows a drastic example of two discrete spacer lengths, one at 1000 and the other at 3500 monomer units. Most likely they reflect two individual sample molecules, which were probed randomly in this single experimental block. The corresponding rupture force histograms of the molecular complexes anchored by the short and the long spacer were plotted in different colors and were fitted separately to Eq. 1 (see Fig. 4 b) using the values of 5.6 ± 0.2 Å for the potential width and 2.7 ± 0.15 10⁻² s⁻¹ for the dissociation rate. In both cases we found very good agreement between the measured histograms and the bond rupture probability distribution, which is based on the previously determined parameters for potential width and dissociation rate.

FIGURE 4.

(a) Monomer number distribution of the spacer from one experimental block. Under constant pulling speed, short spacers (black) lead to higher loading rate than long spacers (gray). Higher loading rates affect higher forces, which can be observed in b. (b) Force distribution of the short (black) and long (gray) spacers. Both distributions are fitted with the same fit parameters (k_off = 0.027 s⁻¹ ανδ Δx = 5.75 Å for the gray fit; k_off = 0.025 s⁻¹ and Δx = 5.50 Å for the black fit).

The good agreement between the theoretical curve and the measured histograms in both cases strongly corroborates the robustness of our analysis procedure. It furthermore demonstrates quite convincingly that in the case of variable spacer lengths a rupture force analysis of the individual force curves with implicit length analysis is mandatory.

DISCUSSION

Single molecule force spectroscopy has been successfully employed in many different instances to elucidate the binding mode and the effective width of the interaction potential, which determine the specificity of molecular recognition. The interpretation of these data was based on an extension of Kramers theory (Kramers, 1940; Hänggi et al., 1990) which was first elaborated by Bell (1978) and then applied to molecular bonds by Evans (Evans and Ritchie, 1997) and others (Heymann and Grubmüller, 2000; Seifert, 2000). In this approach the thermal dissociation rate k_off equals ν₀exp(−E/k_BT), where ν₀ is the attempt frequency, E is the activation energy for dissociation, and k_BT (4.1 pN nm at room temperature) is the thermal energy. In a model with a single energy barrier of height E along the separation path, the application of an external force F leads to an exponential increase of the off-rate k_off (F) = k_off exp(FΔx/k_BT), where the separation Δx is a length scale describing the separation of the energy minimum from the maximum barrier. When the load on the complex increases with a loading rate 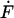, the most probable unbinding force F* depends logarithmically on the loading rate (Evans and Ritchie, 1997):

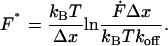(2)

The parameter 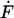is defined by retract velocity times elasticity and is determined from the force-displacement curves corrected by the tip bending and hydrodynamic forces. Although the elasticity is a nonlinear function of the force, related to the nonlinear entropic elasticity of the polymer spacer, Eq. 2 still can be used as a good approach for calculating the most probable unbinding force (Strunz et al., 1999).

However, it has been shown that the length distribution of the polymer spacers leads to a distribution of the loading rates and causes a variation in the force distribution. Dependent on its shape a length distribution of the polymer spacer drastically alters the maximum of the rupture force distribution (Friedsam et al., 2003). Consequently for the most probable rupture force the length distribution was taken into account. The dissociation rate and the potential width were determined directly from a probability density function for the rupture forces and the loading rates. This fit function uses the dissociation rate and the potential width as fit parameters, as described in Eq. 1. Furthermore, by using this method it is possible to separate nonspecific interactions by treating certain peaks with respect to the number of monomers of the polymer spacer (Friedsam et al., 2003).

An analysis of the probability density function (Eq. 1) also shows that multiple peak maxima in the force distribution may be caused by different spacer length and is not necessarily the result of a double potential with two different potential widths (Merkel et al., 1999).

In 1994 the “heterology index” (HI) was introduced by Lewis et al. (1994), describing the degree of divergence of any 20-nucleotide sequence from the consensus LexA box. This was previously described by Berg and Von Hippel (1988), using a mathematical formula. Those sequences with a low HI value are closer to the consensus LexA box and are predicted to bind LexA with greater affinity than those sites with a higher HI score (Fernandez de Henestrosa et al., 2000). On a number of LexA binding sites gel mobility shift assays (Lewis et al., 1994) and Northern analysis (Fernandez de Henestrosa et al., 2000) were performed to prove the approach. Here we present a direct approach to measure the binding factor between LexA and the sequence of the respective LexA box using an AFM-based single molecule force spectroscopy. This provides insights into the linkage between DNA-protein interactions and DNA recognition. The dissociation rate was found to be 0.048 s⁻¹ for the recA operator and 0.13 s⁻¹ for the yebG operator. In a simple two level system the K_D values of 2 nM for recA and 20 nM for yebG (Lewis et al., 1994) would convert into on-rates of 25 × 10⁶/Mol × s and 7 × 10⁶/Mol × s. Both values are slightly above the diffusion limit of the on-reaction, but well within the range that would be expected for a protein-DNA complex, and confirm the predicted higher affinity between LexA-recA compared to LexA-yebG. Steric hindrances as well as Coulomb long-range attraction may contribute to this deviation but need further investigation for clarification.

The potential width Δx was found to be in the range of 4.9 Å for yebG and 5.4 Å for recA. This value is significantly larger than the 3.5–4 Å typically found for receptor ligand interactions like biotin-avidin (Grubmüller et al., 1996; Evans and Ritchie, 1999) or antibody-antigen (Schwesinger et al., 2000). Also the potential width for the unfolding of Ig domains in Titin was found to be in the same range (Rief et al., 1997b; Oberhauser et al., 2001; Li et al., 2002). This short potential width clearly indicates an all or none unbinding mechanism. It is more a breakup of the bond rather than a gradual “unpeeling” or sliding of the protein along the DNA-operator. This kind of bond rupture is characteristic for short-range hydrogen bonds rather than hydrophobic or van der Waals interactions and clearly points toward the high specificity of the interaction.

Based on x-ray data, the interaction length of the LexA-helix that interacts with the major groove of the DNA and which is assumed to block by its tight binding any transcription is between 10 and 15 Å (Pabo and Sauer, 1992; Luisi, 1995). This means that the binding potential for the forced unbinding is much narrower than the geometrical width of the interaction zone.

Another most remarkable and surprising result was the finding that the interaction of the repressor stabilizes the interaction of both halves of the DNA duplex: the measured unbinding force exceeds the force required to shear the bare DNA duplex. Unbinding forces of plain DNA duplexes in shear geometry, which would come closest to the unbinding geometry in the LexA complex, have been measured to be in the range of 35–45 pN at loading rates comparable to the ones in our experiment (Strunz et al., 1999), so that this mechanism would be conceivable in terms of forces. However, this unbinding mechanism would result in a single-stranded DNA at the tip and the other strand free in solution, since the affinity of LexA to single-stranded DNA is expected to be very low. This in turn would mean that no repeated experiments would be possible at the same spot, which is in contradiction to the several hundreds to thousands of experiments carried out in each cycle. This finding in turn means that either the force is not acting on the second half of the duplex or the interaction of the protein with the DNA stabilizes the duplex and prevents it from unbinding at these levels of external force.

An alternative possibility could be that the LexA dimer is forced to dissociate, leaving one monomer at the surface and the other monomer bound to the duplex and so to the tip. Since the binding constant of the monomeric LexA to the DNA duplex is low, this complex would dissociate and again leave the system in a state, which would not allow repeated experiments and, in the same line of argument as used above, would not agree with our findings.

The third possibility would be that the interaction between the LexA dimer and the duplex opens in an all or none event, meaning that as soon as one of the helixes detaches from the groove of the duplex, the other follows within the time resolution of the experiment. This rather nonspectacular but reasonable scenario would leave both dimers intact and would allow an immediate rebinding upon contact formation, which is what we consistently observe in our experiments.

CONCLUSION

DNA-regulation is a hallmark of functional cellular networks. A profound understanding of the modes of interaction between the regulating proteins and certain operator sequences as well as their quantitative evaluation is therefore of utmost importance for modern molecular and cell biology. Where in the past the AFM has proven to be extremely instrumental in mapping the interactions sites and identifying interaction geometries by imaging the samples with unparalleled resolution (Schaper et al., 1993; Hansma, 2001; Costa et al., submitted for publication) modern techniques of single molecule force spectroscopy allow a detailed elucidation of the binding mechanisms. Off-rates may be determined even where only a few molecules are available and, more importantly, for the first time a measure of the width of the interaction potential has become available, which reveals details on the dynamic mode of unbinding.

This study employed a novel data analysis method, which accounts for the poly-disparity of the polymeric anchors employed for coupling the binding partners. This method allowed us to determine for the first time the effective potential width of one of the most important regulatory DNA binders in Bacteria. This system was chosen to be able to compare our values with both crystal data and thermodynamic off-rates. The second block of experiments was then devoted to a system where neither x-ray structure nor off rate was measured yet.

This study shows quite convincingly that a mere docking of two molecular models, even when they are based on crystal data, does not provide the parameter that determines the mechanical stability of a complex, its effective potential widths, and thus an insight into the mechanism of unbinding. This parameter that links binding energy and barrier height, which may alternatively be determined by titration studies or rate measurements, respectively, to the physiologically relevant parameter bond strength can only be determined by force spectroscopy, and may not be inferred from the structure. We are very optimistic that this new quality of information together with the extremely low amounts of material needed for this kind of experiment, may offer striking advantages that open a wider range of applications.