A Semianalytic Model of Leukocyte Rolling

Abstract

Rolling allows leukocytes to maintain adhesion to vascular endothelium and to molecularly coated surfaces in flow chambers. Using insights from adhesive dynamics, a computational method for simulating leukocyte rolling and firm adhesion, we have developed a semianalytic model for the steady-state rolling of a leukocyte. After formation in a force-free region of the contact zone, receptor-ligand bonds are transported into the trailing edge of the contact zone. Rolling velocity results from a balance of the convective flux of bonds and the rate of dissociation at the back edge of the contact zone. We compare the model's results to that of adhesive dynamics and to experimental data on the rolling of leukocytes, with good agreement. We calculate the dependence of rolling velocity on shear rate, intrinsic forward and reverse reaction rates, bond stiffness, and reactive compliance, and use the model to calculate a state diagram relating molecular parameters and the dynamic state of adhesion. A dimensionless form of the analytic model permits exploration of the parameters that control rolling. The chemical affinity of a receptor-ligand pair does not uniquely determine rolling velocity. We elucidate a fundamental relationship between off-rate, ligand density, and reactive compliance at the transition between firm and rolling adhesion. The model provides a rapid method for screening system parameters for the potential to mediate rolling.

INTRODUCTION

In the inflammatory response, neutrophil rolling is prerequisite to neutrophil activation, firm adhesion, extravasation, and migration to the site of inflammation (Springer, 1994). Exposure to inflammatory chemokines activates vascular endothelial cells and drives the up-regulation and presentation of E- and P-selectin to circulating leukocytes. The transient formation and breakage of bonds between selectins and their glycoprotein ligands present on the neutrophil mediate rolling (Lawrence and Springer, 1991, 1993). Similarly, L-selectin-mediated interactions allow lymphocytes to traffic through secondary lymphoid organs (Kansas, 1996). Selectin-ligand interactions also play a key role in the metastatic spread of blood-borne neoplastic cells (Orr et al., 2000) and in recruitment of monocytes to atherosclerotic lesions in model systems (Ley, 2003).

In vitro cell-free systems of ligand- and receptor-coated polystyrene beads and surfaces accurately recreate rolling behavior (Moore et al., 1995; Brunk et al., 1996; Brunk and Hammer, 1997; Goetz et al., 1997; Rodgers et al., 2000; Greenberg et al., 2000; Park et al., 2002). This work further demonstrates that rolling is due to the physical chemistry of receptor-ligand interactions, since rolling could be recreated on an inert particle. Cell-free systems have allowed a systematic study of the effect of selectin-ligand density and shear stress on rolling dynamics.

A progression of theoretical models provides additional insight into the biophysics of rolling. A one-dimensional model of membrane peeling developed by Dembo and co-workers established a quantitative relationship between applied force, adhesion molecule chemical rate constants, and transient and steady-state detachment velocities (Dembo et al., 1988). This peeling model, though applicable to the trailing edge of a rolling leukocyte, does not take into account probabilistic binding within a defined contact zone between membranes. Adhesive dynamics (AD) (Hammer and Apte, 1992), a time-dependent simulation, modeled receptor-mediated adhesion over a three-dimensional contact zone between a flat surface and a rigid, spherical cell with spring-like bonds. AD considered bond formation and breakage as stochastic events while maintaining a relationship between detachment (or rolling), force, and kinetic constants. A balance of hydrodynamic, colloidal, and bonding forces determined the translational and rotational motion of the neutrophil. The results from AD simulations successfully recreated the dynamics of rolling, including transitions between states of nonadhesion, rolling, transient attachment, and firm adhesion (Hammer and Apte, 1992; Chang et al., 2000). A later version of AD employed the Bell model for dissociation rate (Bell, 1978), which has been shown to describe accurately the dissociation of selectin-ligand bonds (Chen and Springer, 2001; Evans et al., 2001). The Bell model expresses the net dissociation rate as a function of the unstressed dissociation rate, the force on the bond, and reactive compliance, a parameter equivalent to binding pocket length that relates reactivity and applied force. The resulting adhesion-state diagrams revealed that the unstressed dissociation rate and reactive compliance are critical properties governing the adhesive state of a particular system (Chang et al., 2000).

Although AD is a useful tool for studying and predicting the dynamics of rolling behavior, it is computationally intensive and does not allow us to explore parameterization easily. A less computationally intensive model that still captures essential details of adhesive behavior may be more accessible and permit more facile investigation of molecular properties governing the biophysics of rolling.

Insights gleaned from AD simulations suggest the simplifying assumptions that drive the development of such a model. Early results established that during rolling, cells do not slip over the surface; the magnitude of the translational velocity equals the product of the angular velocity and particle radius (Hammer and Apte, 1992). Additional AD results demonstrated that only bonds at the trailing edge of the contact zone were under stress and that increases in instantaneous velocity correlated directly with breakage of trailing edge bonds (King and Hammer, 2001). It is therefore reasonable to simplify force and torque balances by restricting the transmission of tension between cell and vessel wall to those bonds at the trailing edge of the contact zone.

Although a simple, semianalytic biophysical model of steady-state leukocyte rolling has been developed previously (Tozeren and Ley, 1992), a number of features distinguish the model presented here from that model. First, Tozeren and Ley included a slip velocity between cell and wall, but as indicated above, such a velocity is not necessary. Second, the previous model considered all bonds to bear tension, whereas we find it is only necessary to restrict the tension to the trailing edge. Disparate methods for defining force and torque balances and for calculating the mass balance of receptors therefore result. Whereas the Tozeren and Ley model performs force and torque balances by integrating bond density over the entire contact zone surface, our model balances the convection of bonds formed in the leading portion of the contact zone with the rate of bond dissociation in the trailing portion. Furthermore, the current analytic model employs the most accurate description of a bond's force-dissociation behavior (Evans et al., 2001). In addition, our ability to parameterize the model fully allows for a thorough and unprecedented exploration of the factors that control leukocyte rolling.

This article develops a semianalytic model of leukocyte rolling driven by insight obtained from detailed simulation. We present results in both dimensional and dimensionless form, show that this model can approximate experimental results, and provide a state diagram of the simplified model for comparison to the AD simulation. Dimensional analysis permits investigation of the biophysical parameters that govern rolling behavior. We demonstrate definitively that rolling velocity is not uniquely determined by chemical affinity and show that at conditions of high affinity, rolling velocity is specified by the rate of bond breakage. We also present a fundamental relationship between intrinsic reverse reaction rate, ligand surface density, and reactive compliance at the detachment point, the transition from firm to rolling adhesion.

MODEL DEVELOPMENT

A schematic diagram of the semianalytic model, with coordinate axes, appears in Fig. 1. We model the leukocyte as a rigid sphere of radius a and the endothelium as a flat wall. The sphere rolls at steady state in a linear shear flow at constant separation distance H₀. We restrict translational and rotational velocities to one direction each (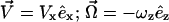), and require that 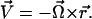We consider one type of receptor-ligand pair and assume an even distribution of receptor and ligand on sphere and wall, respectively. Only those bonds at the trailing edge of the contact zone transmit tension between the two surfaces at an angle θ.

FIGURE 1.

Schematic diagram of the semianalytic model. The contact zone of radius L is at separation distance H₀ from the wall. H_max and H_min are distances at which the reverse reaction rate, k_r, is 100 and 2 times the intrinsic rate, 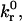respectively. The contact zone is divided into leading and trailing zones where y = H_min, or x = −L + δ. The bonds in the trailing zone, simplified as a homogenous population of “average” bonds, exert tension at the midpoint between the x coordinates corresponding to H_max and H_min.

The definition of the contact zone (see Fig. 1) employs the Bell model for net dissociation rate, k_r,

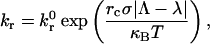(1)

where 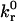is the intrinsic dissociation rate, σ is the bond spring constant, λ is the equilibrium bond length, κ_BT is the thermal energy, Λ is the stressed bond length, and r_c is the reactive compliance, or binding pocket length. We set the radial outer limit of the contact zone to correspond to a separation, y = H_max, between the wall and sphere such that The boundary between the leading and trailing contact zones exists at x = −L + δ, where the wall-sphere separation, y = H_min, yields 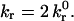This definition of the contact zone constructs a region of stress at the back edge at which a bond's reverse reaction rate is compromised. This should occur once the off-rate is accelerated () and continue to where the dissociation is virtually instantaneous ().

In the leading contact zone, we assume that bonds form in the absence of applied force at the intrinsic forward rate 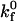and that 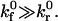We neglect the breakage term in the leading zone conservation equation (since the bonds are not under stress) and assume zero bond density at the leading edge. By approximating the contact zone surfaces as parallel rectangular plates (a reasonable assumption for H₀ ≪ a), we may write

(2)

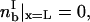(3)

where V_x is the translational velocity, 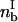is the bond density in the leading zone, n_RT is the receptor density on the cell, and n_LT is the ligand density on the wall.

In the trailing zone, we assume a homogenous population of bonds that exerts tension at x = −L + δ/2 and has length H_mid/sinθ, where H_mid is the separation distance at x = −L + δ/2. The placement of the stress in the center of the trailing zone represents an ensemble average or mean-field description of the stress that is distributed among the entire trailing contact zone. The model's precision does not warrant more precise placement of the stress.

The total force exerted on the cell due to bonding, F^bond, is

(4)

where S_δ and 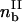are the area and bond density of the trailing zone, respectively. The component forces and torque are written

(5)

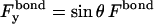(6)

(7)

Bonds break at a rate specified by the Bell model. We further assume k_r ≫ k_f here and neglect formation. Therefore, the rate of breakage in the trailing zone must balance the convection of bonds from the leading zone,

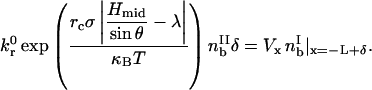(8)

The known functional relationships between rotational and translational velocities and applied forces and torques (Goldman et al., 1967a,b) for this system are

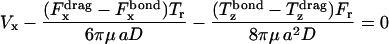(9)

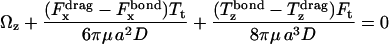(10)

with

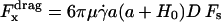(11)

(12)

where 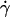is the shear rate, μ is the viscosity, Ω_z is the angular velocity, and D, T_r, T_t, F_r, F_t, F_s, and T_s are functions of a and h₀.

A nonspecific repulsive force, 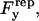opposes a buoyant force and the vertical component of the bond force. We employ a phenomenological expression for repulsive potential, Γ(h), based on steric stabilization and electrostatic repulsion of the glycocalyx (Bell et al., 1984),

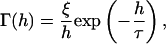(13)

where ξ is a force required for glycocalyx compression, h is a separation distance, and τ is a characteristic length. Differentiating this equation with respect to h and integrating the negative result over the contact area yields 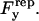The vertical force balance becomes

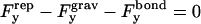(14)

where is the buoyant force.

The solution algorithm employs nested loops to solve for V_x, θ, and H₀. The inner loop solves for the first three variables using a Newton-Raphson method with damping factor and numerical Jacobian; the outer loop conducts a binary search for H₀. This semianalytic algorithm permits the solution of hundreds of different parameter combinations within a time period ranging from several minutes to ∼1 h. A single AD realization, on the other hand, requires computational time ranging anywhere from 30 min to an entire day. Due to its stochastic nature, AD requires multiple realizations to predict adhesive behavior accurately at a single set of system parameters. Therefore, the semianalytic model significantly reduces the computational load.

A cell is considered to be rolling if the resulting velocity satisfies 0.5 V_H > V_x > 0.01 V_H, where V_H is the hydrodynamic velocity of a particle at the given separation distance. Conditions that yield solutions with h* < 0.75 δ_B are excluded, where h* and δ_B are the dimensionless forms of nearest separation between bead and equilibrium bond length, respectively. The Appendix provides the dimensionless variables, equations, and parameters for this system. Table 2 lists all dimensionless parameters that emerge from the model, and their definitions.

TABLE 2.

Dimensionless parameter ranges used in model

Symbol	Definition	Description	Value range
η		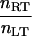Receptor density/ligand density	10−3 – 10°
χ		Forward reaction rate/flow rate	10−4 – 102
β		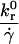Reverse reaction rate/flow rate	10−3 – 101
M0		Bond-spring energy/thermal energy	40 – 90
ν		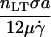Bond spring force/flow force	103 – 107
Zbond		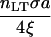Bond force/steric stabilization force	10−3 – 10°
Zgrav		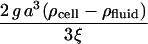Buoyant force/steric stabilization force	10−7 – 10−5
δB		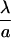Equilibrium bond length	0.01 – 0.014
δSS		Characteristic steric stabilization length	0.01 – 0.014

RESULTS

The values of dimensional parameters used in this model are listed in Table 1. The chosen cell radius is reasonable for a neutrophil (Lawrence and Springer, 1991) and matches that used in used in AD simulations (Hammer and Apte, 1992; Chang and Hammer, 2000; Chang et al., 2000). Equilibrium bond lengths are similar to estimates based on crystal structures determined for E- and P-selectin bound to ligands (Somers et al., 2000). The values of bond spring constant and nonspecific repulsion constant fall within estimated ranges (Bell et al., 1984; Dembo et al., 1988). Chosen shear rates span the physiological range. Receptor and ligand densities are also reasonable values known to support rolling (Rodgers et al., 2000; Brunk and Hammer, 1997; Lawrence and Springer, 1991). Values for the intrinsic reverse reaction rate, are similar to those estimated for selectin-ligand pairs using tether-lifetime data (Alon et al., 1997). Values of the reactive compliance are similar to those used in AD simulations by Chang et al. (2000), which compiled results of reactive compliance from many different experimental studies.

TABLE 1.

Dimensional parameters used in model

Parameter	Definition	Value
a	Cell radius	5 μm
μ	Viscosity	0.01 g/cm/s
T	Temperature	310 K
λ	Equilibrium bond length	20–70 nm
τ	Repulsion characteristic length	20–70 nm
ξ	Nonspecific repulsion constant	5 × 10−4 dyne
	Shear rate	1 – 800 s−1
rC	Reactive compliance	0.1 – 0.55 Å
σ	Bond spring constant	0.5 – 5 dyne/cm
nLT	Ligand surface density	1 – 400 #/μm2
nRT	Receptor surface density	1 – 50 #/μm2
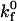	Intrinsic forward reaction rate	10−3 – 101μm2/s
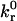	Intrinsic reverse reaction rate	10−1 – 102 s−1

Dimensional results

We first report results in dimensional form for easy comparison to biological rolling data. This model can recreate experimental data (Lawrence and Springer, 1991) for neutrophils rolling in vitro on surfaces coated with P-selectin (Fig. 2). Dimensional parameter values fall within the ranges described above and in Table 1. In particular, for receptor density on the cell, n_RT, we use 48 molecules of PSGL-1/μm² (Rodgers et al., 2000). Both experiment and model demonstrate that rolling velocity increases as a function of shear rate.

FIGURE 2.

Dimensional results comparable to experimental data of Lawrence and Springer (1991) for neutrophils rolling over P-selectin coated surfaces. Solid markers represent model results with PSGL-1 site density on the neutrophil surface (n_RT = 48 #/μm²) taken from Rodgers et al. (2000). Open markers represent experimental data. Parameter values are indicated in legends.

We further plot the dimensional rolling velocity as a function of shear rate and for various values of bond spring constant, σ (Fig. 3 A), and reactive compliance, r_C (Fig. 3 B). We restrict the dimensional rolling velocities to a range of values reasonable for cell-free systems (Brunk and Hammer, 1997) and for neutrophils determined experimentally in vivo and in vitro (Lawrence and Springer, 1991, 1993; Dunne et al., 2002). At larger spring constants (σ), rolling velocity increases more rapidly with shear rate (Fig. 3 A). Similarly, larger values of reactive compliance (r_c) lead to a faster increase in rolling velocity with shear rate (Fig. 3 B). Thus, variations in rolling velocity with shear rate can reflect changes in the molecular properties that determine the bond's response to applied force; concomitantly, lower values of the spring constant and reactive compliance are needed to maintain rolling over a range of shear rates.

FIGURE 3.

Dimensional rolling velocity as a function of shear rate at several values of σ, the bond spring constant (A) and of r_C, the reactive compliance (B). n_RT = 48 #/μm², n_LT = 200 #/μm², ξ = 5 × 10⁻⁴ dyne, and λ = 70 nm.

Fig. 4 illustrates how the rolling velocity's dependence on shear rate changes with intrinsic forward (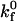) and reverse (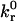) reaction rates. At low 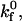rolling velocity increases rapidly over a small range of shear rates (Fig. 4 A). At low 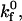lower values of expand the region of shear rates that permit rolling and obviously permit rolling at higher shear rates. At high 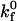(Fig. 4 C), rolling velocity exhibits linear dependence on shear rate from 0 to 500 s⁻¹. At an intermediate 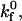rolling velocity is a sharp function of shear rate at high off-rates but a weak function of shear rate at low off-rates (Fig. 4 B).

FIGURE 4.

Dimensional rolling velocity as a function of shear rate at various for (A) (B) 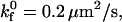and (C) 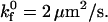n_LT = 100 #/μm², ξ = 5 × 10⁻⁴ dyne, and λ = 70 nm.

State diagram for the semianalytic model

Fig. 5 A presents a dimensional state diagram for our model at reasonable parameter values. Solid lines enclose the combinations of Bell model parameters, 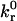and r_C, that support rolling at two different values of bond spring constant (σ = 1 and 2.5 dyne/cm). In the region above the upper boundary, adhesion is not supported, whereas in the region below lower boundary, firm adhesion is supported. The open markers correspond to measured Bell model parameters for selectins and their ligands (Alon et al., 1995, 1997, 1998; Fritz et al., 1998; Smith et al., 1999; Ramachandran et al., 1999). A larger value of σ shifts the rolling region to smaller r_C. This is an expected result, for k_r is exponentially dependent on the product of these parameters.

FIGURE 5.

Adhesion state diagrams. (A) Semianalytic model dimensional state diagram with 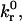intrinsic reverse reaction rate, plotted versus r_C, reactive compliance, for bond spring constant, σ, values of 2.5 and 1 dyne/cm. Solid lines enclose rolling state phase space. Open markers correspond to Bell model parameters for various selectins and their ligands, cataloged in Chang et al. (2000). (B) Adhesive dynamics state diagram. The upper and lower boundaries of the transient adhesion state delimit fractional stop times of 0.01 and 0.7, respectively. A mean velocity of 0.5 V_H parameterizes the upper boundary of the fast adhesion state, and the dotted and dashed lines correspond to 0.3 V_H and 0.1 V_H, respectively. Open markers correspond to Bell model parameters for various selectins and their ligands. (Reproduced with permission; Chang et al., 2000).

Comparison to the adhesive dynamics state diagram (Fig. 5 B; Chang et al., 2000) shows that this model predicts rolling for a narrower range of Bell model parameters. The left and right boundaries result from stringent simplifying assumptions and demarcate the points beyond which a solution for rolling does not exist. Because the size of the contact zone is inversely proportional to r_C, there is a maximum r_C above which the contact area is too small to support rolling for given receptor and ligand densities. This value establishes the right-side border. The left border, or low r_C, marks where the separation distance is <75% of the bond length. Beyond this border, there is significant bond compression within the leading contact zone, thus violating the no-stress assumption. However, the shape of the state diagram is preserved despite these simplifications, and it matches the principal region in which rolling dynamics are seen. Therefore, this analytic model faithfully recreates the rolling regime, and thus is useful for assessing parameters needed to support rolling.

Dimensionless results

As mentioned above, Table 2 and Appendix 1 provide definitions of dimensionless parameters and variables. Dimensionless results for rolling velocity, V*, contact angle, θ*, and trailing zone bond density, BD₂*, appear in Fig. 6. Dimensionless separation distance, h*, is further scaled by dimensionless bond length, δ_B. Results are plotted as a function of η, the ratio of receptor to ligand density, and parameterized by β, the dimensionless reverse reaction rate. For the values of χ used here (where ligand density is high), rolling velocity falls as η increases, and larger values of β suggest that a higher η is required to support rolling (Fig. 6 A). At faster velocities, the contact angle decreases to provide a larger bond force x component needed to balance the higher drag force (Fig. 6 B). However, a smaller contact angle reduces bond torque, and at some small angle, the torque balance no longer supports rolling. Scaling the dimensionless separation distance, h*, by the dimensionless bond length, δ_B, indicates that there is negligible bond compression in the contact zone for these conditions (Fig. 6 C), since h*/δ_B ∼ 1. Higher bond density, BD₂*, corresponds to slower rolling velocity (Fig. 6 D).

FIGURE 6.

Dimensionless steady-state rolling velocity V* (A), contact angle θ* (B), separation distance scaled by dimensionless equilibrium bond length h*/δ_B (C), and trailing zone bond density output BD₂* (D) as a function of η, ratio of receptor to ligand densities. Upper and lower dashed lines in A indicate 0.5 V_H and 0.01 V_H, respectively. The curves are parameterized by β, the dimensionless reverse reaction rate, which increases from left to right. The rolling velocity is anti-correlated with BD₂*. M₀ = 87.6, χ = 0.2, ν = 1.2 × 10⁶, Z_bond = 9.38 × 10³, Z_grav = 4.1 × 10⁻⁵, δ_B = 0.01, and δ_SS = 0.01.

Parameterization of chemical affinity

The dimensionless model permits a further investigation of parameterization. A state diagram constructed using axes of dimensionless reverse (β) and forward (χ) reaction rates appears in Fig. 7. The solid line demarcates the boundary between rolling adhesion (above) and firm adhesion (below) at a standard set of conditions (see figure). The other lines indicate the displacement of the boundary between rolling and firm adhesion for different values of η, ν, and M₀.

FIGURE 7.

State diagram depicting the β-χ boundary between rolling and firm adhesion. (β is the dimensionless reverse reaction rate, and χ is the dimensionless forward reaction rate.) The solid line corresponds to dimensionless parameters in the upper left corner of the figure. Other lines represent boundaries resulting from replacement of an individual parameter with an indicated value. All curves have the same characteristic shape, where β is independent of χ at high χ, but β is proportional to χ at low χ.

Fig. 7 illustrates two distinct regimes in the effect of χ on the value of β required for the onset of rolling. At high χ, the value of β is independent of χ. At high values of χ, the reaction of bonds in the interface reaches steady state, and the dynamic state of adhesion is dictated by dissociation (β). This can be considered a “dissociation-controlled” regime. At low χ (<0.02), the value of log₁₀(β) at which firm adhesion occurs increases linearly with log₁₀(χ). In this region, rolling adhesion results from a more tenuous balance between bond breakage and formation. As the bond formation role increases, more bonds form in the interface, and a higher value of β can be tolerated for rolling adhesion.

Analysis of the systems of equations in dimensionless form allows us to observe additional qualitative trends not immediately observable otherwise. As expected, increasing the relative receptor density, η, allows higher values of β to be permitted for rolling. Decreasing the strength of bonds relative to flow strength (decreasing ν), lowers values of β that can be permitted for rolling. Higher values of the bond energy relative to thermal energy (increasing M₀) also lower the value of β permitted for rolling.

It is often presumed that rolling velocity, or the ability to roll, is a function of the chemical affinity of receptor-ligand bonds. Fig. 8 illustrates how dimensionless rolling velocity depends on chemical affinity. We plot normalized dimensionless rolling velocity as a function of χ/β, a ratio proportional to the equilibrium association constant K_A, at various values of constant χ (Fig. 8 A) and constant β (Fig. 8 B). As is clear from Fig. 8, the value of χ/β does not determine uniquely the rolling velocity: the same value of velocity can be achieved at various χ/β. The converse also holds: a single value of χ/β can yield a range of velocities. We also find that at χ/β > 0.2 (high affinity), rolling velocity becomes a function solely of β. Again, this represents the “dissociation-controlled” regime. At lower affinities, both χ and β contribute. Thus, rolling is not uniquely determined by the chemical affinity of receptor-ligand pairs.

FIGURE 8.

Dependence of rolling velocity on chemical affinity. Rolling velocity, normalized to 50% of the hydrodynamic velocity (V_50%H) as a function of χ/β for several values of constant β (A) and constant χ (B). Upper and lower dashed lines indicate 0.01 V_H and 0.5 V_H, respectively. Chemical affinity does not determine a unique rolling velocity; for one value of χ/β, a range of rolling velocities exists. Conversely, rolling velocity does not require a unique chemical affinity; one value of rolling velocity can be achieved by many χ/β. At high chemical affinity, χ/β, rolling velocity is determined by β.

For any value of χ or β, there exists a lower limit on χ/β below which adhesion cannot be supported. Thus, there is a minimum value of χ/β required for rolling interactions. Fig. 8 A demonstrates that at low χ, the transition from firm adhesion (V*/V*_50%H = 0) to a nonadhesive state (V*/V*_50%H ∼ 1) occurs over a very small range of χ/β. This restriction on χ/β indicates that the tenuous balance between χ and β that establishes the boundary between firm and rolling adhesion, presented in Fig. 5, also exists for the transition from rolling to no adhesion at low χ. The rolling velocity is set by the value of β for high χ/β (Fig. 8 B), again illustrating the dissociation-controlled regime.

Fig. 9 illustrates the dependence of the transition from rolling to firm adhesion on β and the quotient ν/M₀ (the ratio of thermal energy to a combined kinematic/chemical energy, which in dimensional form is 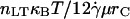). The transition between rolling and firm adhesion occurs along a line with a slope ≈1, whereas the remaining parameters simply determine the specific location in the β-ν/M₀ plane. Thus, one can conclude that β ∝ ν/M₀ at the transition, or 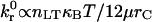, a surprisingly simple relationship that dictates the onset of rolling. At higher relative receptor density (η), rolling is observed at faster reverse rates (β). Increasing bond-spring energy relative to thermal energy (higher M₀) reduces the reverse reaction rate required for rolling. A slower forward reaction rate, χ, also pushes the boundary between rolling and firm adhesion to lower β. Conversely, increasing χ shifts the boundary to higher β, but there is an upper limit at χ ∼ 0.02 beyond which no further shift results because rolling is uniquely determined by β for χ ≥ 0.02 (see previous results). However, for all of these parameter changes, the linear relationship between β and ν/M₀ is maintained, suggesting it is a fundamental controller of the onset of adhesion.

FIGURE 9.

State diagram depicting the β-ν/M₀ boundary between rolling and firm adhesion. The solid line corresponds to dimensionless parameters in the upper left corner of the figure. Other lines represent boundaries resulting from replacement of an individual parameter with an indicated value. Surprisingly, β is proportional to ν/M₀ for all parameter values, leading to a unique scaling for the onset of rolling adhesion.

Given the importance of M₀/ν in controlling the onset of rolling, it is worth considering how M₀/ν controls the dynamics of rolling beyond the transition. In Fig. 10, we plot normalized dimensionless velocity as a function of M₀/ν (the ratio of a combined kinematic/chemical energy to thermal energy: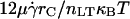) at various values of dimensionless on-rate. The curves in Fig. 10, A–C, are parameterized by M₀, the dimensionless term directly proportional to reactive compliance. For all on-rates depicted, rolling velocity increases with M₀/ν, as expected, since higher values of M₀/ν correspond, in dimensional terms, to larger reactive compliances or to decreased ligand densities. However, the parameterized curves are superimposed on one another at low M₀/ν but separate at high M₀/ν. Thus, rolling velocity itself is not a unique function of M₀/ν, and reactive compliance (M₀) plays a much larger role in determining rolling velocity at low ligand densities (high M₀/ν).

FIGURE 10.

Dimensionless rolling velocity, normalized to 50% V_H, as a function of M₀/ν, for three values of dimensionless forward rate, χ: (A) 0.002, (B) 0.2, and (C) 20. Results for various values of M₀, the ratio of bond-spring energy to thermal energy, appear in each subplot.

The steepness of this transition from firm adhesion to a nonadhesive state increases as the on-rate decreases. At χ = 0.002 (low on-rate; Fig. 10 A), the transition occurs over ∼1 order of magnitude of M₀/ν. At χ = 0.2 (intermediate on-rate; Fig. 10 B) and χ = 20 (high affinity; Fig. 10 C), the transition occurs over ∼1.5 and 2 orders of magnitude, respectively. Thus higher on-rates allow rolling over a greater range of ligand density or reactive compliance.

DISCUSSION

In this article, we employed results from detailed simulation of leukocyte rolling to develop a less computationally intensive analytical model that permits a more thorough analysis of the biophysics of adhesion. The semianalytic, steady-state model presented here describes state transitions between firm adhesion, rolling, and no adhesion and is capable of predicting tunable experimental conditions for which a cell will roll. Such adjustable parameters include flow shear rate and receptor and ligand surface densities as well as the mechanical strength and chemical reactivity of adhesion molecules. The latter two properties can be specified through designer molecular synthesis. Despite its relative simplicity, our model captures the essential biophysics of rolling whereby the receptor-ligand off-rate in the trailing edge of the contact zone governs adhesive behavior. In addition, construction in dimensionless form allows the model to investigate complete parameterization of the system.

Measured values of Bell model parameters fall within the rolling adhesion region of our model's state diagram, and our model can approximate experimental data for neutrophils. We note that, in contrast to biological rolling velocity measurements that demonstrate a concave-downward, plateau response of rolling velocity to increased shear rate (Lawrence and Springer, 1991), our model predicts concave-upward functionality. The rigidity of our modeled cell, or conversely the lack of neutrophil deformability, likely explains this difference. The contact area for a deformable cell would increase with shear rate and facilitate bond formation, thus dampening the effect of shear force on the rolling velocity.

Comparison of our findings with those of the previous analytic model of Tozeren and Ley (1992) is required. Their model allowed for a slip velocity between cell and vessel wall and permitted bonds throughout the contact zone to transmit tension, whereas our model eliminated the slip velocity and restricted bond-mediated tension to the trailing edge of the contact zone. Further, their model employed a simplified bond dissociation relationship that did not explicitly couple the rate constant with molecular response to applied force, whereas we employed the Bell model for dissociation. However, both models are able to approximate the biological rolling velocity measurements of Lawrence and Springer (1991), and both models demonstrate a saturation range for bond formation in which further increases in forward binding rate do not slow rolling. Tozeren and Ley also predict that rolling is possible even for very high affinity (low dissociation constant) receptors when the forward reaction rate is sufficiently large. Our model confirms and enhances this finding through its full parameterization of rolling behavior and direct exploration of the effect of chemical affinity on rolling velocity (Fig. 8, A and B).

A significant discrepancy, however, exists between our model's results and those of Tozeren and Ley. The current model demonstrates an increase in rolling velocity for larger bond spring constant, σ, (Fig. 3 A), whereas the previous model predicts a slower rolling velocity for a stiffer bond (doubling σ from 1 to 2 dyne/cm yielded a decrease in V_roll from 39 to 14 μm/s). This difference is due to the disparate methods for describing the bond dissociation rate. Our model employs the Bell model's explicit coupling of the dissociation rate to the force acting on the bond. Thus, as σ increases, both the force on the bond and the dissociation rate increase, and rolling velocity increases. Tozeren and Ley, on the other hand, employ a fixed dissociation rate for all bonds above the equilibrium length, with no dependence on bond stiffness. In their model, the bond spring constant contributes solely to the force and torque balance such that a larger spring constant yields stronger bonds, more resistance to shear flow, and slower rolling velocities.

Although the simplifying assumptions of our model provide some global benefits, the detailed description of rolling behavior offered by simulation is lost. To be specific, this model cannot recreate the temporal variation in the dynamics of rolling. This may result in an overestimation of the adhesiveness required for rolling. Whereas an AD-simulated cell might experience large fluctuations in motion, including brief detachments, yet still move with some average rolling velocity, the assumptions of the analytic model require sustained attachment and constant rolling velocity. On the other hand, our model disregards the role of initial tethering in establishing an adhesive state. Because the model provides a solution solely for steady-state conditions of rolling, the initial adhesive strength required to capture the cell from the free stream is not required. This effect may counterbalance the lack of dynamic flexibility.

However, ability to perform dimensional analysis, not possible previously, more than amply compensates for these minor inconveniences. Dimensional analysis permitted the mapping of the boundary between firm and rolling adhesion, or detachment point, as a function of dimensionless forward (χ) and reverse (β) reaction rates. Results demonstrated two regimes along this boundary, one at low forward rates where the transition is a function of both rates, and the other at high forward rates where the transition occurs at the same reverse rate regardless of forward rate. In this dissociation-controlled region of fast forward rates, the kinetics of bond breakage limit rolling behavior. Here, increases in intrinsic reaction rate neither enhance bond formation nor alter rolling velocity or adhesive state; all bonds that will ever form already do form. At low dimensionless forward rate, on the other hand, the transition from firm to rolling adhesion requires a distinct pairing of χ and β, and enhancement of χ or reduction in β results in firm adhesion.

Additional dimensional analysis showed that receptor-ligand chemical affinity does not uniquely specify rolling velocity. Instead, at high affinity, rolling velocity is independent of chemical affinity, and the reverse reaction rate alone determines rolling velocity. Here, sufficient bond formation ensures that the cell remains adhered to the wall, so the rate of bond breakage controls the rolling velocity. Thus different receptor-ligand pairs with the same affinity will not necessarily mediate rolling at identical rolling velocities; differences in absolute values of off-rate would account for any observed disparities. However, at low affinity, rolling velocity scales inversely with the chemical affinity, and it is more sensitive to changes in chemical affinity at lower on-rates. This again reflects a tenuous balance between bond formation and breakage required for rolling. At sufficiently slow on-rates, the rolling state has reduced stability in response to perturbations in parameters. Further, our results indicate that the chemical affinity needs to be a minimum value for a system to support rolling. Below this value, the rate of bond dissociation exceeds the rate of formation. These results will be surprising to some biologists since it means high affinity receptor-ligand interactions can lead to all dynamic states of adhesion (not just firm adhesion), and low affinity does not necessarily guarantee rolling interactions.

The linear dependence of β on M₀/ν that describes the boundary between rolling and firm adhesion reveals a fundamental relationship governing system parameters at the point where a cell just begins to roll: 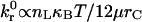. At this critical condition, is directly proportional to ligand density, n_LT, and thermal energy, κ_BT, and is inversely proportional to the viscosity, μ, and reactive compliance, r_C. Thus, for a given receptor ligand pair with a single 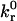and r_C, a stationary particle can be induced to roll by decreasing the ligand density on the wall surface, decreasing the temperature, or increasing the fluid viscosity. In vivo, where blood viscosity and temperature are approximately constant, the critical 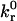for detachment depends only on ligand density and reactive compliance. This provides insight into biological controls that can induce the detachment of firmly bound cells. This result further stresses the importance of the reactive compliance in dictating rolling behavior, and thus the extreme efforts to measure this parameter using the biomembrane force probe (Evans et al., 2001) or atomic force microscopy (Zhang et al., 2002) are justified.

These results are consistent with previous work (Chen et al., 1997) comparing rolling behavior mediated by monoclonal antibodies and their neutrophil cell-surface antigens with rolling behavior mediated by selectins bound to their natural ligands. Differences in Bell model parameters, determined using kinetic data of transient tether detachments, indicated that these molecular properties of the selectin-ligand bond account for the observed disparities. Selectins supported rolling over a wider range of wall shear stresses than did a mAb to CD15, a difference attributed to a measured mAb reactive compliance two-to fourfold higher than that of selectins. Results from the analytic model (Fig. 3 B) concur with this finding. Selectins also supported rolling over a wider range of wall site densities than the CD15 mAb. The analytic model demonstrates that lower selectin 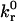, intrinsic off-rate (β in dimensionless form), could explain such results (Fig. 6 A). Indeed, Chen and co-workers report that the mAb intrinsic off-rate is 2–3 times greater than that of selectins. In addition, some species of mAb could support only firm adhesion. Results from the analytic model suggest an explanation that fast on-rate and slow off-rate, specifically high affinity combined with a slow off-rate, yields this all-or-none adhesive behavior (Fig. 8 B). Chemical affinity, or the relationship between on- and off-rates, plays a roll in determining rolling behavior (or firm adhesion) only at low values of chemical affinity. When chemical affinity is high, rolling velocity and/or adhesive state is determined by the off-rate alone.

Leukocyte recruitment to endothelium contributes to a significant number of pathological states of chronic and acute inflammation, including auto-immune diseases, burn injury, ischemia-reperfusion injury, and allergic responses (McMurray, 1996.). We hope next to use this model to assess the effect of pharmaceutical potency on the inhibition of rolling interactions, thus demonstrating how a biophysical understanding of adhesion can contribute practical knowledge to the control of cell biology.

APPENDIX

This section defines the dimensionless variables, parameters, and equations used in the semianalytic model. The four dimensionless variables are

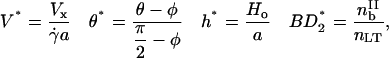(A1)

where

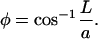(A2)

The appropriate dimensionless groups are

(A3)

The ranges of parameter values appear in Table 1. The equation and boundary condition for bond formation are

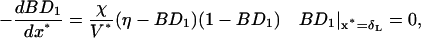(A4, A5)

where

(A6)

The convection-breakage balance is

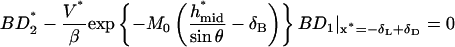(A7)

where

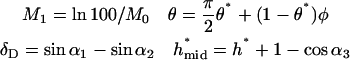(A8)

with

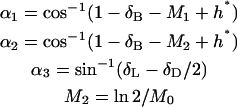(A9)

The functional relationships between rotational and translational velocities and applied forces and torques are

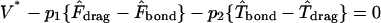(A10)

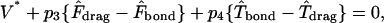(A11)

where dimensional forces and torques are

(A12)

and D, T_r, T_t, F_r, F_t, F_s, and T_s are functions of h* as described in Goldman et al. (1967a,b).

The vertical force balance is

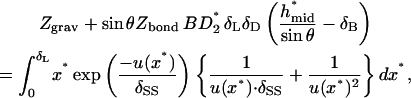(A13)

where

(A14)

The solution algorithm involves an outer loop for finding h* and an inner loop for finding θ*, BD₂*, and V*. Using first-guess solution values, Eq. A4 is integrated using boundary condition Eq. A5. The resulting function for BD₁ is evaluated as needed in Eq. A7, and a modified Newton-Raphson method is used with Eqs. A7, A10, and A11, such that each iteration requires integration of Eq. A4. Upon solution of the inner loop, the vertical force balance (Eq. A13) is evaluated. The value of h* is increased or decreased as needed and the inner loop is solved again until all balances have <2% error.