Comparing Folding Codes in Simple Heteropolymer Models of Protein Evolutionary Landscape: Robustness of the Superfunnel Paradigm

Abstract

Understanding the evolution of biopolymers is a key element in rationalizing their structures and functions. Simple exact models (SEMs) are well-positioned to address general principles of evolution as they permit the exhaustive enumeration of both sequence and structure (conformational) spaces. The physics-based models of the complete mapping between genotypes and phenotypes afforded by SEMs have proven valuable for gaining insight into how adaptation and selection operate among large collections of sequences and structures. This study compares the properties of evolutionary landscapes of a variety of SEMs to delineate robust predictions and possible model-specific artifacts. Among the models studied, the ruggedness of evolutionary landscape is significantly model-dependent; those derived from more proteinlike models appear to be smoother. We found that a common practice of restricting protein structure space to maximally compact lattice conformations results in (i.e., “designs in”) many encodable (designable) structures that are not otherwise encodable in the corresponding unrestrained structure space. This discrepancy is especially severe for model potentials that seek to mimic the major role of hydrophobic interactions in protein folding. In general, restricting conformations to be maximally compact leads to larger changes in the model genotype-phenotype mapping than a moderate shifting of reference state energy of the model potential function to allow for more specific encoding via the “designing out” effects of repulsive interactions. Despite these variations, the superfunnel paradigm applies to all SEMs we have tested: For a majority of neutral nets across different models, there exists a funnel-like organization of native stabilities for the sequences in a neutral net encoding for the same structure, and the thermodynamically most stable sequence is also the most robust against mutation.

INTRODUCTION

Simple exact models (SEMs) are physically motivated caricatures of biopolymers (Dill et al., 1995; Chan and Bornberg-Bauer, 2002). A hallmark of these models is their highly simplified representations of the sequence and conformational spaces. Among the many versatile SEM approaches, a common simplification is to utilize self-avoiding lattice walks to approximately account for conformational variations. For proteins, sequence variations and interaction heterogeneity are often modeled by a reduced alphabet with <20 amino acid types, whereby a set of simple nearest-lattice-neighbor contact energies, designed to capture certain major components of the driving forces for folding, is employed to mimic the intrachain interactions in real proteins. SEMs were originally developed to study principles of protein folding, thermodynamic stability (Lau and Dill, 1989), and mutations (Lau and Dill, 1990). Related but more elaborate lattice representations have also been used for protein structure prediction (Skolnick and Kolinski, 1990; Kolinski and Skolnick, 2004). From a modeling perspective, an important advantage of SEMs is that the ground-state conformation(s), the density of states, and the partition function of a given model sequence can be exactly determined, thereby affording a complete, unambiguous description of the model's thermodynamics.

Rationale for using SEMs to study evolution

SEMs have few adjustable parameters. This is particularly valuable for the formulation and evaluation of general concepts, because the simplicity of SEMs provides for a clear logical link between a set of assumptions and their consequences in the context of an explicit-chain model (Chan et al., 2002). Deductive reasoning using SEMs is transparent. It is not obscured as is sometimes the case in models that entail complex constructions and invoke approximations of unspecified accuracy. In the SEM approach, proposed scenarios for biopolymer behavior can be tested by performing relatively inexpensive simulations to explore how the assumed (input) SEM parameters lead to predictions (output) that may or may not be consistent with the desired (experimental) phenomena. In this way, the SEM methodology can often offer deep insights when it is applied to tackle questions that cannot yet be addressed by experiments or atomistic modeling. (For reviews see Chan and Dill, 1993; Bryngelson et al., 1995; Dill et al., 1995; Karplus and Šali, 1995; Shakhnovich, 1996; Thirumalai and Woodson, 1996; Dill and Chan, 1997; Pande et al., 1997; and Chan et al., 2002, 2004.)

For certain SEMs, an exhaustive mapping between all possible sequences and their ground-state conformations is feasible, as was first demonstrated in a short-chain two-dimensional model (Chan and Dill, 1991). This computational tractability allows for a physics-based, explicit-chain embodiment of key evolutionary concepts from theoretical biology (Lipman and Wilbur, 1991). Prime examples include the idea of neutral evolution, i.e., biopolymers wandering in a space of equally viable mutants, wherein a neutral network of sequences encoding for the same structure is interconnected by single-point mutations; and inspiring imageries of evolutionary processes as walks on a multidimensional fitness landscape (Maynard-Smith, 1970; Kimura, 1983; Wright, 1932). Extensive SEM studies of evolutionary populations under various selection and adaption constraints have become possible since powerful and inexpensive computers started to be available ∼15 years ago. (See, e.g., Irbäck and Sandelin, 2000; Cui et al., 2002; Xia and Levitt, 2002; and Sandelin, 2004, for recent applications to crossovers and the evolution of protein structure and stability; see Blackburne and Hirst, 2001; Williams et al., 2001; and Bloom et al., 2004, for SEM treatments of evolution of function; see Chan and Bornberg-Bauer, 2002, and Xia and Levitt, 2004a, for reviews.) As an example of these advances, a key concept that has emerged from SEM studies is that of the superfunnel, the main subject of this investigation. The superfunnel paradigm stipulates that sequence-space topology of neutral nets tend to adopt funnel-like organizations, and that mutational stability (plasticity) of a sequence is strongly correlated with its native thermodynamic stability. Among other insights it affords, this theoretical framework serves to rationalize the often concomitant thermodynamic and mutational robustness of natural wild-type proteins (Bornberg-Bauer and Chan, 1999).

THEORETICAL PERSPECTIVES AND MOTIVATIONS

Simplifying assumptions in SEMs

Even with the SEMs' drastically simplified representations of intrachain interaction heterogeneity and chain geometry, the protein-folding problem is NP-complete for the simplest of such models (Paterson and Przytycka, 1996; Crescenzi et al., 1998). In this regard, computational studies of proteins are more seriously hampered than those of RNA, for which polynomial folding algorithms exist (Tacker et al., 1996). As a result, in using lattice protein models for evolutionary studies, one often has to resort to restricting the conformational (shape) space by allowing only compact conformations (Hinds and Levitt, 1996) (by restricting model chains to an elliptical bounding volume (Hinds and Levitt, 1992)) or even maximally compact conformations (Taverna and Goldstein, 2000), or to smaller alphabets (Bornberg-Bauer, 1997a), or both (Li et al., 1996; Cejtin et al., 2002).

The “hydrophobic polar” (HP) model (Lau and Dill, 1989; Chan and Dill, 1990, 1991; Dill et al., 1995) is a widely used two-letter alphabet (i.e., with two residue or monomer types, H and P). The model was designed to capture the essential features of hydrophobic interactions, which is a major stabilizing force in protein folding (Kauzmann, 1959; Dill, 1990). Another popular approach employs more heterogeneous interaction schemes with a 20-letter alphabet (Abkevich et al., 1996; Buchler and Goldstein, 1999). In approaches that allow for the variation of individual contact interactions that are not based upon residue types, the effective number of residue types—as a parametrization of interaction heterogeneity—can be much higher than 20 (Chan and Dill, 1996; Buchler and Goldstein, 1999).

By virtue of their simplification, the scope of SEMs is limited. Recent in-depth analyses indicate that many common SEMs are insufficient for the finer thermodynamic and kinetic details of protein folding, especially the high degree of thermodynamic and kinetic cooperativity exhibited by many real, small, single-domain proteins. Therefore, as far as properties of individual proteins are concerned, more complex modeling constructs are preferable (Chan et al., 2004). Nonetheless, for evolutionary applications that require an extended coverage of both the sequence and conformational spaces, SEMs remain a uniquely useful tool: From a practical standpoint, the required extended coverage of sequence and conformational spaces is currently not achievable in more complex models. More importantly, at a physical level, insofar as the consistency principle (Gō, 1983) or principle of minimal frustration (Bryngelson and Wolynes, 1987; Bryngelson et al., 1995) is applicable to natural proteins, and a given SEM's potential function is motivated by a major part of the intrachain interactions in real proteins (e.g., by attempting to capture the hydrophobic interactions as in the HP model), the SEM sequence-to-structure mapping is physically viable, for the following reason: although the SEM potential function may have to be augmented to achieve a better mimicry of protein energetics (Chan, 2000; Salvi and De Los Rios, 2003), for a model sequence that embodies the minimal-frustration principle, by and large the additional terms are expected to consistently favor the same native structure as that encoded by the more rudimentary SEM code (Chan et al., 2002, 2004; Chan and Bornberg-Bauer, 2002; Cui et al., 2002; Sandelin, 2004). This perspective is supported by recent insightful analyses of database structures of real proteins. These studies have demonstrated that the general trends of both the sequential (along-the-chain; Irbäck and Sandelin, 2000) and spatial (core-packing; Sandelin, 2004) distributions of hydrophobic residues in real protein structures are very similar to that predicted by the two-dimensional (2D) HP model. Echoing the latter observation, the less-than-perfect correlation between sequence hydrophobicity and surface exposure patterns in database proteins has been found to resemble that of a three-dimensional (3D) off-lattice hydrophobic-polar model of protein folding as well (Mölbert et al., 2004).

Restricting to maximally compact conformations: potential problems

The most commonly used lattices for chain representations in SEMs are the 2D square lattice and 3D simple cubic lattices. For the HP model, exact enumerations that account for all possible self-avoiding walks have been performed extensively on two-dimensional square lattices to determine the ground-state conformations of all possible sequences (Chan and Dill, 1991; Bornberg-Bauer, 1997b; Bornberg-Bauer and Chan, 1999; Cui et al., 2002; Irbäck and Troein, 2002). In other studies, however, only selected sequences from an enormous sequence space are considered (e.g., those along an evolutionary trajectory). Sometimes, for the sake of computational tractability, the native conformation of a given sequence is defined as the lowest-energy conformation of a highly restricted set of maximally compact structures (conformations) rather than determined exhaustively from the set of all possible conformations. These include restricting to 2D 4 × 4 and 5 × 5 conformations (Buchler and Goldstein, 2000; Govindarajan and Goldstein, 1997) and 3D 3 × 3 × 3 (Li et al., 1996) and more recently 3 × 3 × 4 conformations (Cejtin et al., 2002).

As far as polymer physics is concerned, restricting conformational possibility to maximally compact structures (or maximally compact states, MCSs) represents a drastic step with serious consequences (Chan and Dill, 1996). Artifacts are likely in MCS approaches: Both rigorous lattice computations (Yue et al., 1995; Micheletti et al., 1998; Backofen et al., 1999; Ejtehadi et al., 1999; Irbäck and Troein, 2002) and analyses of real protein structures (Goodsell and Olson, 1993) indicate that true ground-state conformations of model proteins with physically plausible intrachain interactions and real protein native structures are not necessarily maximally compact. Under the MCS restriction, the behavior of a model heteropolymer would no longer be the product of the physical assumption embodied in the model energy function and conformational freedom alone, but rather the result of an altered energy function. Indeed, it has been shown that enforcing MCSs often changes the ground-state conformation(s) of a given sequence; the statistics of the sequence-structure mapping are significantly affected by the MCS restriction as well (Chan and Dill, 1996). Intuitively, it wouldn't be surprising that on average a larger number of sequences would map onto a given structure (i.e., the structure would have a larger convergence; Chan and Dill, 1991) if the structural space is smaller because of the MCS restriction. For the case of 25mer 2D HP sequences (chain length n = 25), exact enumeration data (Irbäck and Troein, 2002) shows that 99.99% of the sequences determined by the MCS approach to have a unique ground-state conformation in fact do not, as these sequences actually have more than one lowest-energy conformation when the full conformational space is considered (Chan and Bornberg-Bauer, 2002).

The superfunnel idea: model dependence?

Several general features of the protein sequence-structure mapping have been rationalized by multiple studies using a wide range of SEMs (Chan et al., 2002). A robust property—which applies to RNA as well (Tacker et al., 1996)—is that some structures (i.e., ground-state conformations) are much more highly represented than others in the sequence space. In other words, many more sequences encode for the over-represented structures (with large convergence sets) than other structures (with smaller convergence sets) (Schuster et al., 1994; Li et al., 1996; Bornberg-Bauer, 1997b; Govindarajan and Goldstein, 1996; Buchler and Goldstein, 2000). Another robust feature of protein SEMs is the topological organization of sequences encoding for the same structure in neutral nets. They tend to form extensive networks connected by small mutational steps, on which an evolutionary trajectory may traverse without changing the structure being encoded (Bornberg-Bauer, 1997b; Govindarajan and Goldstein, 1997; Bornberg-Bauer and Chan, 1999; Trinquier and Sanejouand, 1999).

By comparison, more detailed properties of neutral net organization have thus far been investigated using only a rather limited set of SEMs. A central feature is the superfunnel paradigm: Certain neutral nets have been shown to organize in a funnel-like manner centered around a prototype sequence (Bornberg-Bauer and Chan, 1999). This sequence has the largest number of neutral mutations, the highest thermodynamic stability for the native conformation, and often represents the consensus sequence of the protein family. For the 2D HP model, native stability tends to decrease as one moves away in sequence space from the prototype sequence, thus the sequence-space variation of native stability with respect to the Hamming distance from the prototype sequence resembles that of a funnel (Bornberg-Bauer and Chan, 1999), reminiscent of conformational-space funnels for protein folding (Leopold et al., 1992; Wolynes et al., 1995; Dill and Chan, 1997).

Sequences folding not uniquely but with relatively low degeneracies are enriched in the evolutionary vicinity of these superfunnels. Some of these sequences connect two or more neutral nets, simultaneously encode for more than one structure, and thus can serve as evolutionary switches (Trinquier and Sanejouand, 1999; Bornberg-Bauer, 2002). Moreover, uniquely folding 2D HP sequences (and prototype sequences in particular) have been shown to exhibit a significant degree of modular architecture, sometimes with clearly identifiable “autonomous folding units” acting as building blocks for larger structures (Cui et al., 2002; Chan and Bornberg-Bauer, 2002). Consequently, and consistent with recent experiments (Voigt et al., 2002; Otey et al., 2004), recombinations in conjunction with single-point substitutions are found to be more efficient in exploring novel 2D HP structures than single-point mutations alone (Cui et al., 2002). A subsequent insightful study shows that recombinations can also lead to significantly higher steady-state populations of prototype sequences (Xia and Levitt, 2002) than population dynamics based solely on single-point substitutions (Cui et al., 2002). A more recent investigation of two variants of the 2D HP model confirmed the existence of superfunnels for native stability and found superfunnels for folding rates as well (Xia and Levitt, 2004b), lending credence to the earlier stipulation that funnel-like organization of sequence space should generally apply for “any measure of fitness provided that its variation with respect to mutations is essentially smooth” (Bornberg-Bauer and Chan, 1999). To ascertain the generality and robustness of superfunnel organizations, here we extend our investigation to a wider range of SEMs with different model interaction schemes.

Evaluating and comparing SEMs of evolution

To our knowledge, the most extensive studies to date to evaluate parameter dependencies in SEMs of evolution have been carried out by Buchler and Goldstein (1999, 2000). They considered a collection of 2-, 4-, 20-, and ∞-letter models, restricted conformational enumeration to 2D MCSs that can fit within a 5 × 5 square, and concluded that structures that are highly designable for two-letter alphabets are not necessarily highly designable with larger alphabets.

The focus of this study is different, and is complementary to that of Buchler and Goldstein. In view of potential problems in reaching a proper physical interpretation of MCS models (see above), we employ full conformation enumerations as well as MCS enumerations. To allow for an exhaustive accounting of sequence space, here we consider only two-letter alphabets; but we compare highly diverse two-letter model interaction schemes with different modes of residue-residue interactions and different degrees of repulsive interactions. In this work, we seek to answer three questions:

1. How does an overall shift in contact energies from a mainly attractive potential to one with strong repulsive interactions influence the aforementioned key features of the sequence-structure mapping, particularly the biases in sequence-space structure distribution, the topologies of neutral nets, and the existence of superfunnels?

2. If there are significant differences among the models we evaluate, do the differences hinge upon whether the model potential is proteinlike, i.e., whether the model attempts to capture the main physical driving forces in real proteins?

3. How does restricting conformational possibility to MCSs affect the predicted evolutionary properties?

MODELS AND METHODS

Sequence-structure mappings in this study are constructed using well-described methods from our earlier work (Chan and Dill, 1991, 1996; Dill et al., 1995; Bornberg-Bauer and Chan, 1999). Here we compare six two-letter model interaction schemes, namely the HP, AB, shifted HP, shifted AB, and the perturbed-homopolymer HP and AB models as defined before (Chan and Dill, 1996), for chains with n = 18 monomers configured on 2D square lattices (Fig. 1). For each model, all possible 2¹⁸ sequences are analyzed and each of their density of states (number of conformations as a function of energy) exhaustively enumerated. The physical motivations for studying these models have been provided and their basic sequence-structure statistics explored (Chan and Dill, 1996), but their densities of states and mutational/evolutionary properties have not been systematically compared. To investigate their dependence on modeling parameters, evolutionary statistics of all six models are now computed along the line in previous, more limited studies of the HP and AB models (Bornberg-Bauer and Chan, 1999).

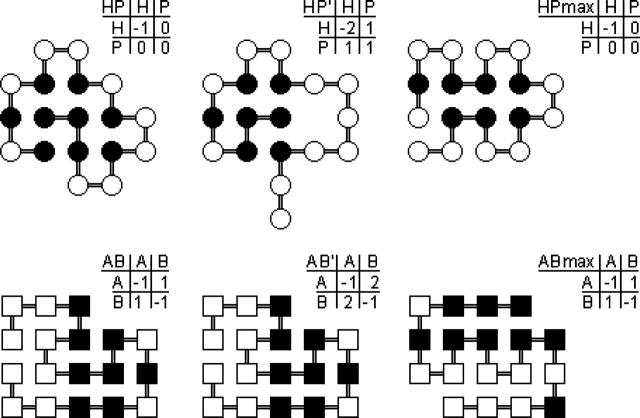
FIGURE 1.

The six heteropolymer models studied in this work. Here the “shifted” and “perturbed-homopolymer” models (Chan and Dill, 1996) are denoted, respectively, by a prime superscript (′) and a “max” notation. The energy matrices (with matrix elements e_ijs) provide the relative interaction energies of pairwise contact between various types of monomers (i, j). Using the energy matrices shown, ground-state conformations are determined by exhaustive enumeration of all possible self-avoiding walks for the HP, HP′, AB, and AB′ models; but enumeration is limited to the maximally compact conformational states (MCSs) for the HPmax and ABmax models. The conformations in this figure are the top-ranking structures, i.e., these ground-state conformations are encoded by the largest number of sequences in their respective models (cf. Table 1). H, P, A, and B monomers (residues) are represented by solid and open circles and solid and open squares, respectively. The sequences shown in this figure are the prototype sequences of their neutral nets.

Briefly, in the HP model, the H and P monomers (beads) represent two classes of amino acids that admit only one type of stabilizing interaction: An attractive energy ɛ (ɛ < 0) is assigned to a pair of nonsequential H monomers if they form a spatial nearest-neighbor contact (termed an HH contact). As discussed above, although the HP model is insufficient for calorimetric cooperativity and its energy landscape is rather rugged (Chan and Dill, 1994), short-chain 2D HP models are well suited for investigating the mapping from sequences onto structures (Irbäck and Sandelin, 2000; Chan et al., 2002, 2004; Chan and Bornberg-Bauer, 2002; Cui et al., 2002; Sandelin, 2004). Indeed, folded structures of short 2D HP sequences have realistic, proteinlike surface/core ratios, and on average have small ground-state degeneracy. A small but nonnegligible fraction of these sequences map uniquely onto only one ground-state conformation and thus may serve as models of globular proteins (Chan and Dill, 1996).

In contrast, in the AB model, like monomers attract and unlike monomers repel (Chan and Dill, 1996). Although this investigation focuses on 2D AB and related models, it is worth noting that variations of the AB model have been studied extensively in 3D applications as well (Shakhnovich and Gutin, 1993; Socci and Onuchic, 1994). The repulsive interactions in the AB model enable more “designing out”; hence the number of sequences having a unique ground-state conformation (g = 1 sequences) is much higher in the AB model than in the HP model (Table 1). However, the AB model is less proteinlike because the A and B monomers tend to segregate in the native structure (see bottom row of Fig. 1), and they do not appear to correspond to any physicochemical classification of amino acid residues. As such, the AB interaction potential is instructive as an example of heteropolymer models that can achieve proteinlike ground-state uniqueness via a manifestly nonproteinlike interaction scheme.

TABLE 1.

Summary of sequence-structure-mapping statistics of the six models studied in this work and their neutral nets and evolutionary superfunnel-related properties

	HP	HP′	HPmax	AB	AB′	ABmax
No. of g = 1 sequences (% of sequence space)	6349 (2.4%)	30196 (11.5%)	32927 (12.6%)	34700 (13.2%)	34706 (13.2%)	37226 (14.2%)
No. of g = 1 sequences with maximally compact ground states	1142	971	32927	26342	25174	37226
% of g = 1 sequences with maximally compact ground states	18.0%	3.2%	100%	75.9%	72.5%	100%
No. of neutral sets (i.e., No. of encodable structures)	1475	6693	1224	4127	4490	1577
No. of encodable structures that are maximally compact	331	310	1224	1493	1493	1577
% of encodable structures that are maximally compact	22.4%	4.6%	100%	36.2%	33.3%	100%
Average neutral set size	4.3	4.5	26.9	8.4	7.7	23.6
No. of neutral nets	1706	7347	2349	16270	17116	12442
Average neutral net size	3.7	4.1	14.0	2.1	2.0	3.0
% of neutral sets that are fragmented (for neutral sets with >2 sequences)	25.3%	14.2%	59.2%	100%	100%	100%
Size of largest neutral net	48	51	267	26	22	72
Longest neutral path in the largest neutral net	7	8	12	6	5	11
% of neutral nets conforming to the superfunnel paradigm (for neutral nets with >2 sequences)	88.8%	88.7%	66.0%	64.2%	64.5%	66.4%

The number of neutral sets is equal to the number of encodable structures. The longest neutral path in a neutral net refers to the maximum Hamming distance separating two sequences within the same neutral net. The percentage of superfunnel-conforming HP neutral nets in this table is identical to that determined before (Bornberg-Bauer and Chan, 1999). For the AB model, the present computation indicates that 1390 (35.8% = 100% − 64.2%) of the 3882 neutral nets with more than two sequences each do not conform to the superfunnel paradigm. They encompass a total of 6548 AB sequences. This result differs slightly from the corresponding 1378 nonsuperfunnel AB neutral nets (35.5% of 3882, encompassing 6484 sequences) we reported previously (Bornberg-Bauer and Chan, 1999). (The number 1348 on page 10692 of this reference is a typographical error.) This discrepancy is insignificant as it arises merely from minute differences in the roundoff of the floating-point values for native stability in the two independent calculations. For all 12 additional neutral nets determined here to be nonsuperfunnels, the native stability of the AB sequence of maximal mutational stability is almost identical to the maximum stability of the given AB neutral net.

For each of the above models we apply two variations: 1), using a shifted energy matrix with stronger repulsive interactions; and 2), restricting conformational variation to MCSs. Building on the HP and AB models, their respective shifted models incorporate stronger repulsive interactions (Fig. 1), which tend to enhance interaction specificity. It is noteworthy that both MCS restriction (see above) and shifting represent significant changes in the physics of intrachain interactions. As has been critically discussed for a class of 3D 20-letter lattice models (Abkevich et al., 1996), a shifted interaction potential may bear little resemblance to the original unshifted interaction scheme (Chan and Dill, 1996; Chan, 1999; Chan et al., 2002).

RESULTS AND DISCUSSION

Sequence statistics

A contrast of the degeneracy, encodability and neutral net/superfunnel statistics of the six models is given in Table 1. A small part of this data, in particular that for the HP and AB models, has been discussed in other contexts (Chan and Dill, 1996; Bornberg-Bauer and Chan, 1999); this information is included here to provide a more comprehensive comparison. In general, repulsive interactions are more conducive to designing out nontarget structures. Hence they tend to decrease sequence degeneracy and enhance structural encodability (Chan and Dill, 1996). Consistent with this expectation, Table 1 shows that shifting does not have too much effect on the statistics for the AB model, which already has its own repulsive interactions. But it has a very prominent effect on the more proteinlike HP model: The number of nondegenerate (encoding) sequences of the shifted HP′ model increases by almost fivefold relative to that of the HP model. This is partly because the HP model has only attractive and neutral interactions and therefore its energetics is quite nonspecific before shifting.

The upper-middle conformation in Fig. 1 provides an example of a structure that is not encodable in the HP model but is encodable in the shifted HP′ model. Indeed, in the HP′ model, this top-ranking structure is not only encodable, but is maximally encodable, with 51 sequences sharing it as their common unique ground-state conformation. This structure is not very compact. It has two monomers at one chain end sticking out. Obviously, such a structure would not be encodable in the HP model because in that case a dangling chain end can bend, either resulting in an increase in the number of favorable contacts (if the chain end is an H that can form contacts with other Hs on the surface of the rest of the protein) or leading to a degenerate ground state. In the HP′ model in our study, however, sequences can be chosen such that any bending of this two-monomer chain end would result in a repulsive interaction and therefore is disfavored. This example illustrates graphically the utility of repulsive interactions in designing out alternate conformations that would otherwise compete with the target ground state.

A similarly large increase (more than fivefold) in the number of uniquely folding (g = 1) sequences results from modifying the HP model to the HPmax model; but not from modifying the AB model to the ABmax model. The increase is so much more prominent for the HP family because most often fewer HH contacts are achievable in MCSs than in more open conformations. Therefore, when open conformations are eliminated in the HPmax model, a much higher fraction of the 1673 MCSs becomes encodable (from 331/1673 = 19.8% to 1224/1673 = 73.2%, cf. Table 1). On the other hand, in the (unrestricted) AB model, most of the 1673 MCSs (1493/1673 = 89.2%) are already encodable. So imposing the MCS restriction only leads to a marginal increase in encodability to 1577/1673 = 94.3% in the ABmax model. In the AB model, the native conformations of a large majority (75.9%) of the 34,700 uniquely folding sequences are MCSs to begin with. Consequently, only marginal increases in the number of g = 1 sequences are effected by shifting (six sequences, 0.017%) and MCS restriction (2526 sequences, 7.3%).

In short, for the more proteinlike HP family, shifting the intrachain interaction energies greatly enhances the designing out capability, whereas enforcing MCSs artificially designs in many more structures. Both effects lead to a very large increase in the number of uniquely folding sequences. In contrast, the corresponding effects are—though not nonexistent—quite insignificant for the AB family of models.

Neutral sets

We next turn to the statistics of neutral sets and neutral nets (Schuster et al., 1994; Renner and Bornberg-Bauer, 1997; Bornberg-Bauer and Chan, 1999). A neutral set of a given structure is the set of all g = 1 sequences that have it as their ground-state conformation. Previously, it has also been referred to as a convergence set (Chan and Dill, 1991). Thus, an encodable structure is one with a nonempty neutral set. Basic encodability statistics of the six models in Table 1 was explored (Chan and Dill, 1996), and aspects of neutral set properties of the HP and AB models were investigated (Bornberg-Bauer and Chan, 1999). But no systematic study has been conducted to compare the sizes of their neutral sets with that of the shifted and MCS-restricted versions of these models.

Table 1 indicates that for the HP family, the number of encodable structures (i.e., the number of neutral sets) undergoes a large increase (≈4.5-fold) when the HP model is modified to the shifted HP′ model, which allows more designing out. Since most of the encodable structures in the HP model are not MCSs, changing the HP model to the HPmax model results in a small decrease in the number of neutral sets, notwithstanding the large increase of neutral sets for MCSs. On the other hand, shifting the AB model to the AB′ model only leads to a small increase in neutral sets (363 more neutral sets, representing a mere 363/4127 = 8.8% increase). Because of the repulsive interactions it contains, the AB model encodes many more structures than the HP model, and much of this enhanced encodability comes from more open structures. Thus, it is not surprising that imposing MCS restriction on the AB model results in a large decrease (from 4127 to 1577) in the number of neutral sets.

As noted above, despite the AB and AB′ models' ability to encode relatively open conformations, they have much stronger preferences for MCSs than the more proteinlike HP and HP′ models. This difference is most strikingly illustrated by the sizes of their neutral sets for MCSs versus those for non-MCSs. For the HP and HP′ models, the average MCS neutral set sizes are, respectively, 1142/331 = 3.5 and 971/310 = 3.1. These are slightly smaller than the average neutral set size of 4.6 for non-MCSs in both the HP and HP′ models, indicating that MCSs are not particularly favored in the HP and HP′ interaction scheme. This situation is drastically different from that in the AB and AB′ models: Average MCS neutral set sizes are 17.6 and 16.9 for the AB and AB′ models, respectively, whereas average non-MCS neutral set size is only 3.2 for these models. In other words, for these models, the average MCS neutral set is more than five times larger than the average non-MCS set, implying that the AB and AB′ interaction scheme is strongly favorable to MCSs. Hence enforcing MCS on the AB model is in some respects redundant in that it produces little change to the sequence-structure statistics (see Table 1 and discussion above).

Despite these important differences, there is one clear trend of neutral set size distribution that is robust across all six different models. Generally, a few large neutral sets dominate over many small neutral sets in a Zipf-like version (detailed data not shown), as was observed previously for several different models of biopolymers (Schuster et al., 1994; Li et al., 1996; Bornberg-Bauer, 1997b). Here we find that distributions of neutral net size also follow a similar pattern (see below).

Neutral nets

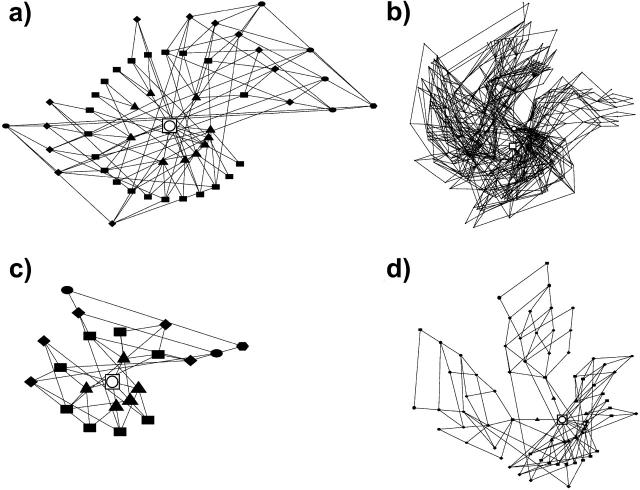
A neutral net is a subset of a neutral set for which all sequences are interconnected with one another via a series of single point mutations. A neutral set can be fragmented into several neutral nets if not all of the sequences in the set are interconnected. These interconnections are depicted in Fig. 2 for neutral nets from four different models. Corresponding drawings for the HP and AB models are available elsewhere (Bornberg-Bauer and Chan, 1999).

FIGURE 2.

Topology of the largest neutral net in the (a) HP′, (b) HPmax, (c) AB′, and (d) ABmax models. Sequences encoding for the same structures (provided in Fig. 1) are represented by solid symbols (dots, circles, triangles, etc.); and mutational connectivity by a single-point substitution between two sequences is depicted by a line joining a pair of symbols. For a given neutral net, the prototype sequence and the sequence with maximum native stability (as defined in Fig. 3 below) are marked, respectively, by an open circle and an open square. A neutral net conforms to the superfunnel paradigm if both conditions are satisfied by the same sequence. In a, c, and d, different symbols denote sequences with different Hamming distances from the prototype sequence (Bornberg-Bauer and Chan, 1999).

Interestingly, most of the HP and HP′ neutral sets are not fragmented (Table 1). Their average neutral net/set size ratios are 3.7/4.3 = 0.86 and 4.1/4.5 = 0.91, respectively. In contrast, all neutral sets in the AB family of models are fragmented. As a result, the corresponding neutral net/set size ratios for the AB (0.25) and AB′ (0.26) models are much smaller. The average neutral set size in the AB and AB′ models are about twice that of the HP and HP′ models. One contributing factor to this phenomenon is the A ↔ B symmetry in these models: Given a structure is encoded by an AB sequence, a sequence obtained by interchanging the A and B monomers in the given sequence will also encode for the same structure. However, for the n = 18 AB and AB′ models presented here, any two sets of neutral sequences connecting to two individual sequences related by A ↔ B interchange are not interconnected to each other (the “longest neutral path” entries in Table 1 for AB and AB′ are less than n/2 = 9), thus all of their neutral sets involve a basic A ↔ B fragmentation. Nonetheless, even after this factor of 2 is taken into account, on average the neutral sets in the AB and AB′ models (≈4 neutral nets per neutral set) are still significantly more fragmented than that in the HP and HP′ models (≈1.1–1.2 neutral nets per neutral set).

Although MCS restriction dramatically increases the average neutral set size for both the HP and AB models, it significantly increases only the average neutral net size of the HP model but not that of the AB model. On average, the HPmax neutral sets (1.9 nets per set, net/set size ratio = 0.52) are more fragmented than the HP and HP′ models, but are less fragmented than the AB family of models (7.9 nets/set for ABmax, corresponding average net/set size ratio = 0.13). MCS restriction induces a large increase in the average net size for the HP model (from 3.7 to 14.0), but leads to only a slight increase for the AB model (from 2.0 to 3.0). MCS restriction allows for the emergence of much larger neutral nets in both the HPmax and ABmax models. But the largest neutral net in the HPmax model is almost four times as large as that in the ABmax model. The largest HPmax neutral net comprises 267 sequences, compared to 48 for the largest HP neutral net. The longest continuous path of neutral mutations in the largest HPmax neutral net is 12, almost twice as long as that for the largest HP neutral net. As conformational space is reduced in the MCS models, sequences that previously encode for different structures or are degenerate are now grouped together to form larger neutral nets. In other words, many sequences that fold to a particular structure in the HPmax scheme would not do so if the conformational space was not restricted. This finding is also consistent with a recent investigation of two n = 24 2D HP-like models (Xia and Levitt, 2004b). Taken together, as for other aspects of the sequence-structure mapping discussed above, MCS restriction appears to have a much more profound impact on the more proteinlike HP model than on the AB model.

Conformity to the superfunnel paradigm and ruggedness of evolutionary landscapes

The prototype sequence of a neutral net has the maximum number of neutral neighbors and thus is mutationally most stable. In other words, the prototype sequence is connected by single-point substitutions to the largest number of other sequences in the neutral net. When there is more than one such sequence in a neutral net, the prototype sequence is taken to be the one that also has the highest native thermodynamic stability (Bornberg-Bauer, 1997a; Bornberg-Bauer and Chan, 1999).

Fig. 2 shows that sequences in a neutral net are topologically organized around the prototype sequence. This applies to the four models shown in the figure as well as HP and AB model neutral nets depicted previously (Bornberg-Bauer, 1997b; Bornberg-Bauer and Chan, 1999; Chan and Bornberg-Bauer, 2002). To ascertain the thermodynamic stability of model native (ground-state) structures, densities of states of all g = 1 sequences of the shifted and MCS models are determined here by exhaustive conformational enumeration, as has been performed for the HP and AB models (Bornberg-Bauer and Chan, 1999). Following the procedure laid out in this reference, the partition function of every g = 1 sequence in all six models is constructed. The strengths of intrachain interactions are controlled by an overall parameter ɛ (ɛ < 0). Using the relative pairwise contact energy e_ij between monomer types i and j in Fig. 1 for the different models, the energy of an i, j contact is assigned to be ɛe_ij with Boltzmann weight exp(−ɛe_ij/k_BT), where k_BT is Boltzmann constant times absolute temperature. Then, native stability of every sequence is quantitated by the −ɛ/k_BT value at the given sequence's thermodynamic folding-denaturation transition midpoint, i.e., when the fractional Boltzmann population of the unique ground-state conformation is 1/2, as we have formulated before. Sequences with thermodynamically more stable native structures have smaller midpoint (−ɛ/k_BT) values.

A neutral net is said to conform to the superfunnel paradigm if its prototype sequence (of maximal mutational stability, a sequence-space property) is also the sequence with the maximum native thermodynamic stability (a conformational-space property) among the sequences in the neutral net (Bornberg-Bauer and Chan, 1999). Table 1 assesses the degree to which neutral nets of different models conform to this paradigm (bottom line of entries). A majority of neutral nets in all six models follow the superfunnel paradigm, but the percentages of superfunnel-conforming neutral nets are significantly higher (≈90%) for the HP and HP′ models than for the other four models (≈65%). In this particular regard, it is noteworthy that the MCS-restricted HPmax model resembles the AB family of models rather than displaying kinship with the HP and HP′ models.

Fig. 3 provides examples of both superfunnel-conforming (a, c, and d) and nonsuperfunnel neutral nets (b). In this figure, the prototype sequence coincides with the sequence with maximum native stability for the HP, AB′, and ABmax neutral nets, but the prototype and maximum-stability sequences are different for the HPmax neutral net shown (cf. Fig. 2). In the graphs in Fig. 3, the single-point substitutions are represented by lines joining pairs of sequences with successive Hamming distances from the prototype sequence. In general, the smoothness of a superfunnel may be characterized by the slopes of these lines. A positive slope implies that the given mutation increases (or decreases) native stability when the sequence moves closer toward (or farther away from) the prototype sequence. On the other hand, a negative slope means that the given mutation would lead to a decrease in native stability when the sequence is moved closer toward the prototype sequence, and vice versa. The HP′ superfunnel in Fig. 3 has no negative slopes; all of its 115 mutational connections have positive slopes (a feature very similar to that of the largest HP model; Bornberg-Bauer and Chan, 1999). We therefore regard this superfunnel as “smooth,” because when the model HP′ protein evolves toward the prototype sequence, its native stability increases monotonically. In contrast, the less proteinlike AB′ and ABmax superfunnels in Fig. 3 are more “rugged”—as is the case for the largest n = 18 AB superfunnel (Bornberg-Bauer and Chan, 1999)—in that they have many negative slopes, some of which are quite steep. This feature means that a mutation that brings an AB-type sequence closer to the prototype sequence can sometimes lead to a significant decrease in native stability. In this respect, it is clear from Fig. 3 that the largest HPmax neutral net (a nonsuperfunnel) also has a high degree of sequence-space ruggedness, further indicating that the evolutionary properties of the MCS-restricted HPmax model are quite dissimilar to that of the more proteinlike HP or HP′ model.

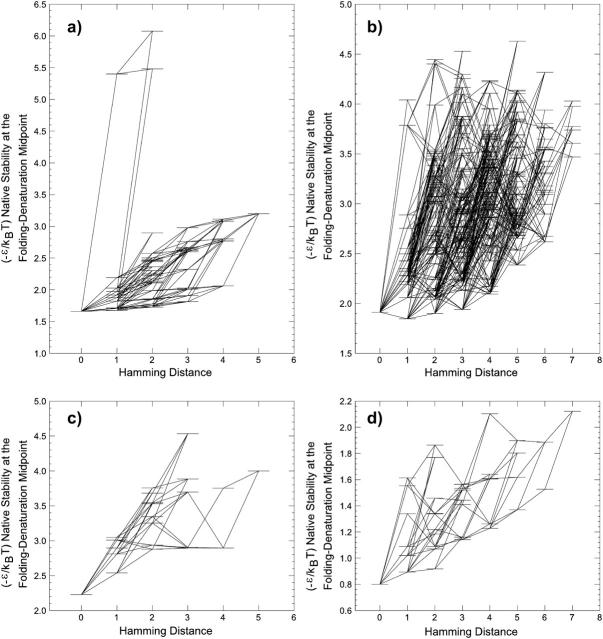
FIGURE 3.

Native stabilities of the (a) HP′, (b) HPmax, (c) AB′, and (d) ABmax sequences in the neutral nets in Fig. 2 are indicated by short horizontal levels. They correspond to the (−ɛ/k_BT) value (vertical scale) at the transition midpoint. Neutral single-point mutations (lines in Fig. 2) are indicated here by lines joining horizontal levels. The horizontal scale provides the Hamming distance from the prototype sequence of the given neutral net. Note that each horizontal level in the ABmax neutral net in d represents a sequence as well as the sequence obtained by performing A ↔ B interchange on it.

Two peculiar features of the smooth HP′ superfunnel in Fig. 3 are readily related to its particular native structure and the HP′ interaction scheme (Fig. 1). First, mutations at some of the sites in the more open parts of this superfunnel's native conformation, namely the two-monomer dangling end and the cavity-encircling loop, lead only to minute decreases in native stability. A case in point would be a P → H mutation of the second-last monomer at the dangling end. This type of mutation results in almost nonexistent stability gaps (Δs; Bornberg-Bauer and Chan, 1999) between the prototype sequence and some of the low-lying (high native stability) nonprototype sequences in this superfunnel. Second, all three mutations on the prototype sequence that lead to a dramatic decrease in native stability (changing the midpoint (−ɛ/k_BT) from 1.66 to >5) involve an H → P mutation of the third monomer from the nondangling end of the native conformation. It is clear that this is an important “anchoring” site of the structure; and it is quite remarkable that changing its interaction from being attractive to repulsive can even be tolerated.

Fig. 4 shows the distribution of neutral net size (insets) and the variation of native stability of the prototype sequence as a function of neutral net size (main plots). As for neutral sets (Schuster et al., 1994; Li et al., 1996; Bornberg-Bauer, 1997b), all six models have many small neutral nets but only a few large neutral nets. On average, native stability of the prototype sequence increases (lower midpoint (−ɛ/k_BT)) with increasing size of the neutral net, although the stability of prototype sequences of some smaller neutral nets can exceed that of larger nets. This observation suggests that structures that have larger neutral nets (which tend also to have larger neutral sets or greater designabilities; Li et al., 1996, 1998; Koehl and Levitt, 2002; Wingreen et al., 2004; see also Govindarajan and Goldstein, 1996; Buchler and Goldstein, 2000) are more capable of being encoded by sequences with higher native thermodynamic stabilities.

FIGURE 4.

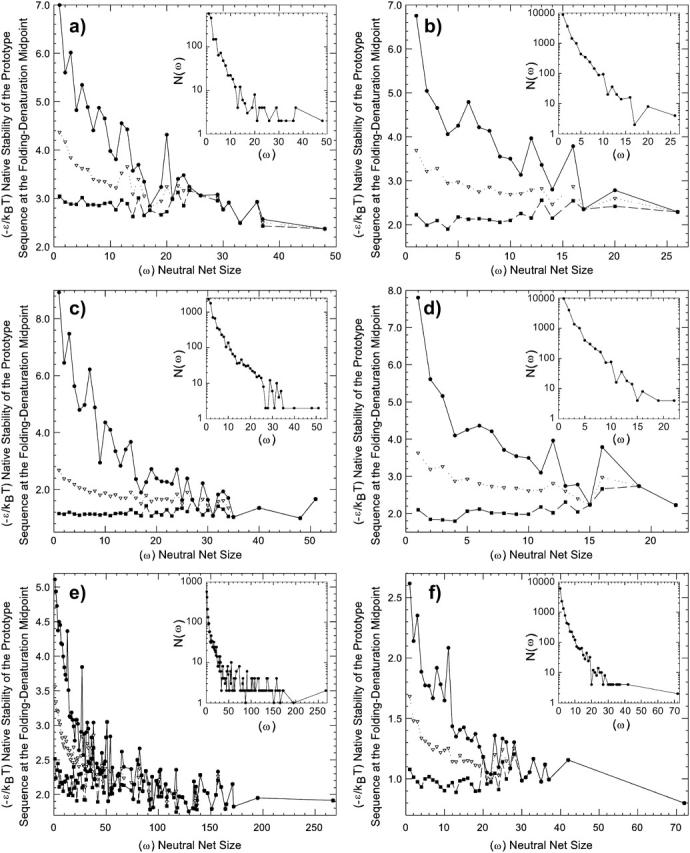
Distribution of neutral net sizes (insets) and native thermodynamic stability of the prototype sequences, for the (a) HP, (b) AB, (c) HP′, (d) AB′, (e) HPmax, and (f) ABmax models. For every model studied, each inverted triangle shows the average native stability (as measured by the (−ɛ/k_BT) at the transition midpoint) among the prototype sequences of neutral nets of a given size; the highest and lowest native stabilities among the same set of prototype sequences are indicated by a square and a dot, respectively. (Note that a higher (−ɛ/k_BT) value here means that the native state is thermodynamically less stable.) Insets show the number of neutral nets 𝒩(ω) as a function of size ω. Solid or dashed lines connecting data points in this figure serve merely as a guide for the eye. We note that panels a and b, for the HP and AB models presented here, are the corrected version of, and should therefore replace, the upper panels of Figs. 3 and 4 in Bornberg-Bauer and Chan (1999). Owing to a technical oversight, instead of recording the thermodynamic stabilities of prototype sequences as they should, the previously published figures erroneously provided the corresponding statistics for the sequences that are most stable in their neutral nets. Despite this error, the discrepancies between the two sets of results are very minor, since a majority of neutral nets are superfunnels with the prototype sequence also being the most stable. Consequently, the general trends exhibited by the two sets of figures are virtually identical, and the conclusions of the previous study remain unchanged.

Structural correlations between different interaction schemes

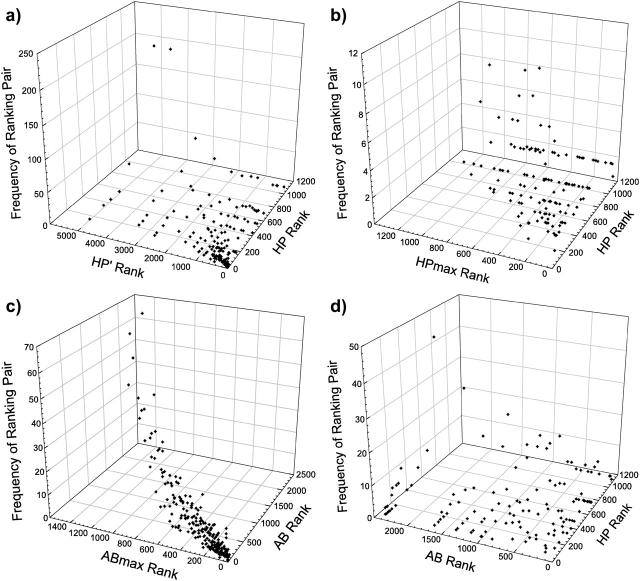
Table 2 and Fig. 5 study the relationship between encodable structures in different models. Different models encode different structures. Some structures are encodable in one model but not encodable (i.e., have designability = 0) in others. Hence, the analysis here applies only to overlapping structures that are encodable in both of the models being compared. In some cases, such as that of HP versus HPmax and HP′ versus ABmax, the numbers and percentages of overlapping structures are small, underscoring that the physics embodied by these models are very different. We rank the encodable structures in a model by their neutral set sizes (Table 2). Here we focus on how well correlated is the rank of a given structure in a model with the rank of the same structure in another model. A high correlation is expected if the physics of the two models are similar. Conversely, a low correlation would imply that the driving forces in the two models favor significantly different sets of chain architectures. Table 2 affords such structural correlation data between every possible pair of different models studied in this work. Example scatter plots are provided in Fig. 5.

TABLE 2.

Correlation of structure rank in different models

	HP′ (6693)	HPmax (1224)	AB (4127)	AB′ (4490)	ABmax(1577)
HP (1475)	0.74 (1317)	0.56 (331)	−0.15 (550)	−0.17 (540)	0.10 (327)
	89.3%	27.0%	37.3%	36.6%	22.2%
HP′ (6693)		0.59 (310)	−0.19 (964)	−0.20 (1004)	0.11 (306)
		25.3%	23.4%	22.4%	19.4%
HPmax (1224)			0.20 (1106)	0.20 (1106)	0.18 (1172)
			90.4%	90.4%	95.8%
AB (4127)				0.98 (4095)	0.92 (1493)
				99.2%	94.7%
AB′ (4490)					0.91 (1493)
					94.7%

Structures are ranked by the sizes of their neutral sets in a given model; the structure with the largest neutral set is ranked 1, and so on. When two or more structures have the same neutral set size, they are assigned the same rank, in a “golf ranking” manner. For example, in the HP model, the three largest neutral set sizes are 48, 37, and 36, and the number of neutral sets with such sizes are, respectively, 2, 4, and 2. Thus, the structures encoded by these eight neutral sets are ranked accordingly as 1, 1, 3, 3, 3, 3, 7, 7. The rank of a structure depends on the model interaction scheme. For every pairing of the six models studied here, the Pearson correlation coefficient for the rank of the (overlapping) structures that are encodable in both models is provided as the first entry in each box of this table. The number of overlapping structures is given in parentheses (second entry in each box). This overlapping number as a percentage of the total number of encodable structures of the less encodable model is also provided (bottom entry in each box). The total number of encodable structures for each of the models (from Table 1) is shown in parentheses with the model names.

FIGURE 5.

Correlation of structure ranking: (a) HP versus HP′; (b) HP versus HPmax; (c) AB versus ABmax; and (d) HP versus AB models. For a given model, encodable structures are ranked by the sizes of their neutral (convergence) sets. For a pair of models being compared here, the ranks of every structure encodable in both models are provided by the two horizontal scales (the rank can be different in the two models), whereas the number of structures sharing a given pair of ranks is indicated by the vertical scale.

Table 2 highlights the fact that the HP and AB families of models share little in common. This is not surprising in view of their very different interaction schemes. The nine correlation coefficients between the two families (the top three rows and the right-hand three columns at the upper right of Table 2) are all small, ranging between +0.2 and −0.2 (Fig. 5 d). On the other hand, the correlation within the AB family is uniformly extremely high (three boxes at the lower right of Table 2; Fig. 5 c). The percentages of overlapping structures are 94% or more, with all three structural correlation coefficients >0.9. As noted above, shifting and MCS-restriction apparently do not have much effect on the sequence-structure mapping of the AB model. The correlation between the HP and HP′ model is also high, though not to the same degree as that among the AB family of models. This suggests that the similarities between the HP and HP′ models are substantial, especially among the structures with large neutral sets (Fig. 5 a). One conspicuous aspect is that the native structures in both models have clearly discernible hydrophobic cores and most of them are not maximally compact (Fig. 1 and Table 1). This finding is also consistent with recent rigorous analyses of one particular class of HP-like models (Ejtehadi et al., 1999; Shahrezaei and Ejtehadi, 2000). In contrast, the present structural correlation between either the HP or the HP′ model with the HPmax model is significantly lower (correlation coefficient <0.6; Fig. 5 b), again suggesting that enforcing MCS on the more proteinlike HP model tends to lead to serious artifacts.

CONCLUDING REMARKS

This comparative study of six two-letter SEMs of protein evolutionary landscape has been based on exact, unrestricted exhaustive enumeration of sequence and conformational spaces. Thus, results in this work partly bridge a gap in theoretical understanding between earlier full-conformation evolutionary studies of one or two two-letter alphabets (Bornberg-Bauer, 1997b, 2002; Bornberg-Bauer and Chan, 1999) and more recent comparative studies of MCS-restricted models with larger alphabets (up to 20 letters for residue-based interactions; Buchler and Goldstein, 2000). As emphasized above, SEMs are uniquely suited for posing and addressing questions of general principles in biomolecular evolution, and for rationalizing patterns in the protein structure database (Irbäck and Sandelin, 2000; Sandelin, 2004) and recent experimental findings (Otey et al., 2004). SEM approaches are complementary to analytical treatments of evolution and modeling techniques that utilize more elaborate but less tractable chain representations (see, e.g., Kauffman and Levin, 1987; Macken and Perelson, 1989; van Nimwegen et al., 1999; Ancel and Fontana, 2000; Bastolla et al., 2003a,b).

A central advantage of SEMs is that they provide explicit-chain models of complete sequence-structure mapping that are built upon polymer physics, albeit only in a rudimentary manner. It is this physical aspect that sets SEMs apart from other forms of model sequence-structure mapping, whose physical plausibility is often uncertain since basic polymer properties such as chain connectivity and excluded volume are not taken into account in some of these approaches. It follows that the physicality of the SEM constructs one uses for studying protein evolution is of overarching importance. One should strive to capture as much essential physics of proteins as possible and reduce arbitrariness in the model sequence-structure mapping, and achieve these goals within the confine of limited computational resources. From this vantage point, any restriction on sequence and conformational variation should be critically examined.

Here we found that several key qualitative features of the evolutionary sequence-structure mapping are fairly robust across the models we have investigated. These include a strong bias in sequence-space structure distribution (some structures have much bigger neutral sets than others), possibility of extensive neutral nets, and to some extent the conformity of neutral nets to the superfunnel paradigm. These similarities suggest that these properties are rather general for explicit-chain models of genotype-phenotype mapping.

However, it is equally important to realize that there are quantitative as well as more subtle differences among the models studied here. Interestingly, the more proteinlike HP and HP′ models appear to have smoother superfunnels, much less fragmented neutral sets (a neutral set may be viewed as a protein family encoding for the same structure), and a significantly higher fraction of their neutral nets conforming to the superfunnel paradigm than the other models. We found that restricting conformational variation to MCSs has a much more drastic effect on the more proteinlike HP model than on the AB interaction scheme. It is clear that such a restriction imposes a significant change in the fundamental physics of the hydrophobicity-like interactions of the HP model. In several respects, such as neutral set fragmentation, neutral net ruggedness, and conformity to the superfunnel paradigm, the MCS-restricted HPmax model deviates substantially from the original HP model, sometimes as much as that of the differences between the AB family of models and the HP model. As a result, the structural correlation between the HP and HPmax models is not high, since many prominent structures in the HP model are not MCSs and thus are precluded in the HPmax scheme. It also appears that because of the MCS-restricted models' severe constraints on the folded shapes, modular protein evolution cannot be readily addressed by these constructs. In contrast, modularity and autonomous folding units arise naturally in the unrestricted HP model (Cui et al., 2002; Irbäck and Troein, 2002; Chan and Bornberg-Bauer, 2002). All in all, we conclude that these facts should always be taken into serious account, and caution should be exercised in the physical interpretation of results from MCS-restricted evolutionary models.

An instructive future extension of this analysis would be to employ full conformational enumeration to evaluate sequence-structure mapping models with larger alphabets, including rigorously addressing the degree to which the physics of their intrachain interactions is proteinlike (Chan, 1999; Chan et al., 2002). In view of the more complex calculations that this would entail, recent developments in constraint-based computational techniques (Backofen et al., 1999) should be of use in this endeavor.