Computational Protein Design Is a Challenge for Implicit Solvation Models

Abstract

Increasingly complex schemes for representing solvent effects in an implicit fashion are being used in computational analyses of biological macromolecules. These schemes speed up the calculations by orders of magnitude and are assumed to compromise little on essential features of the solvation phenomenon. In this work we examine this assumption. Five implicit solvation models, a surface area-based empirical model, two models that approximate the generalized Born treatment and a finite difference Poisson-Boltzmann method are challenged in situations differing from those where these models were calibrated. These situations are encountered in automatic protein design procedures, whose job is to select sequences, which stabilize a given protein 3D structure, from a large number of alternatives. To this end we evaluate the energetic cost of burying amino acids in thousands of environments with different solvent exposures belonging, respectively, to decoys built with random sequences and to native protein crystal structures. In addition we perform actual sequence design calculations. Except for the crudest surface area-based procedure, all the tested models tend to favor the burial of polar amino acids in the protein interior over nonpolar ones, a behavior that leads to poor performance in protein design calculations. We show, on the other hand, that three of the examined models are nonetheless capable of discriminating between the native fold and many nonnative alternatives, a test commonly used to validate force fields. It is concluded that protein design is a particularly challenging test for implicit solvation models because it requires accurate estimates of the solvation contribution of individual residues. This contrasts with native recognition, which depends less on solvation and more on other nonbonded contributions.

INTRODUCTION

Despite recent progress, the treatment of the electrostatic effects due to the surrounding solvent in computer simulations of biological macromolecules remains a challenge (Simonson, 2001, and references therein).

In the most detailed microscopic approach, solvent molecules are treated explicitly, and the electrostatic properties of both solvent and solute are obtained by averaging over a very large number of configurations of the system. However, available computer power usually severely limits the size of configuration space that can be explored, and problems can arise when long-range electrostatic interactions are truncated or summed over an infinite periodic array using Ewald summation techniques (Sagui and Darden, 1999, and references therein).

This prompted interest in models, which incorporate the influence of the solvent in an implicit fashion (see Roux and Simonson, 1999, for review). These are of two main types, empirical models and models based on continuum electrostatics.

Empirical models generally assume that the solvation free energy of the solute is a sum of atom or group contributions. Each group contribution is approximated by a linear function of its solvent-accessible surface area (Eisenberg and McLachlan, 1986; Wesson and Eisenberg, 1992; Ooi et al.,1987; Schiffer et al., 1992) or by the volume it occupies within a defined solvation shell (Gibson and Scheraga, 1967; Kang et al., 1988; Colonna-Cesari and Sander, 1990). The surface area-based models involve deriving group-based solvation parameters by fitting to amino acid transfer (Eisenberg and McLachlan, 1986) and vapor-to-water (Ooi et al.,1987) free energies. Through these empirically adjusted parameters, these models incorporate the hydrophobic and electrostatic components of solvation, but they omit the solvent screening of the interactions between charges, which must be introduced as an additional term.

Solvent models based on continuum electrostatics define the solute interior and the solvent as regions with different dielectric constants, and the electrostatic solvation free energy is computed by solving the Poisson-Boltzmann equations (Kirkwood and Westheimer, 1938). In their most popular applications to biological systems, finite difference algorithms are used to solve these equations for molecular boundaries of arbitrary size (Honig and Nicholls,1995). These methods represent a rigorous treatment of continuum electrostatics, which takes into account self energies (solvation of single charges) as well as screening effects (charge-charge and charge-dipole interactions). Their many successful applications to biological problems (see Bashford and Case, 2000; Simonson, 2001, for review) have established them as a standard in the field.

But numerical continuum electrostatics also have their drawbacks. In most implementations (see Simonson, 2001, and references therein), with the exception of a few (Luo et al., 2002), the calculations are too time-consuming to be performed routinely. Often one also encounters convergence problems, which may depend on the resolution of the solute-solvent boundary, on the partial charge representation, and on the difficulty in mapping forces related to the dielectric boundary onto individual atoms.

In light of these problems semianalytical and analytical treatments of continuum electrostatics models have been proposed (for reviews, see Roux and Simonson, 1999; Lazaridis and Karplus, 1999a; Bashford and Case, 2000; Simonson, 2001; Feig and Brooks, 2004). In these approximations the electrostatic potential is usually a complex but differentiable function of the solute atomic positions, and can therefore be readily updated during energy minimization and molecular dynamics simulations.

Several of these models are now routinely available in modelling packages such as CHARMM, AMBER, and XPLOR, and a number of groups reported good agreement of their performance with the full continuum approach for protein-ligand binding (Zou et al., 1999) pKa shifts (Bashford and Karplus, 1990) and proteins (Jayaram et al., 1998; Onufriev et al., 2002), and in molecular dynamics (MD) simulations of proteins and nucleic acids (Dominy and Brooks, 1999: Schaefer et al., 1998; Williams and Hall, 1999; Tsui and Case, 2000). These models have therefore been gaining appreciation as promising alternatives to their more time-consuming counterparts.

In this article we report a critical appraisal of several implicit solvation models in the framework of a relatively novel application area, that of computational protein design. Computational procedures for protein design aim at solving the so-called “inverse-folding” problem (Drexler, 1981), which consists of starting from a given protein 3D structure—usually a known structure from the Protein Data Bank (PDB)—and searching for the amino acid sequence or sequences that are compatible with this structure.

Protein design procedures work by sampling in discrete steps a very large number of side-chain conformations and amino acid sequences that can be built onto the considered backbone (Kraemer-Pecore et al., 2001; Jaramillo et al., 2001; Lazar et al., 2003). This involves visiting a large number of states, the majority of which are energetically unfavorable. These “frustrated” states (Goldstein et al., 1992) might involve buried charges, exposed hydrophobic groups, or unfavorable charge-charge interactions. The main task of the design procedure is to single out from among all sampled states those with lowest energy. Such low-energy solutions should in principle represent amino acid sequences that are likely to adopt the considered 3D structure.

There has been quite some debate about the force fields appropriate for protein design (Gordon et al., 1999). Most current force fields consist of ad hoc combinations of several terms. These usually include a van der Waals term, as well as additional terms representing hydrogen bonds, residue secondary structure propensities (Dahiyat et al., 1997), and solvation effects. The latter term is commonly represented using empirical models in conjunction with various sets of atomic solvation parameters (Eisenberg and McLachlan, 1986; Ooi et al., 1987). The balancing between the different energy terms is generally obtained through weighting coefficients, which are empirically adjusted to maximize the fit with experimental data such as melting temperatures of the designed proteins, or to reproduce nativelike sequences (Kuhlman and Baker, 2000; Desjarlais and Handel, 1999; Raha et al., 2000). The number and values of these coefficients vary among authors, making it difficult to evaluate and compare the influence of the different terms on the results.

In this work we assess the performance of implicit solvation models by testing their ability to distinguish between favorable and unfavorable sequence-structure combinations. The analyzed models are the empirical atomic solvation model (EAS) of Ooi et al. (1987), the solvation model implemented in the effective energy function (EEF1) of Lazaridis and Karplus (1999a), and two analytical approximations to the generalized Born equation, one by Schaefer and Karplus (1996), analytic continuum electrostatics (ACE), and the other by Lee et al. (2002), termed generalized Born using molecular volume (GBMV). In addition we evaluate the finite difference Poisson-Boltzmann procedure (Honig and Nicholls. 1995), since it is often used as the reference against which implicit solvation models are benchmarked (Tsui and Case, 2000; Onufriev et al., 2002). For all the examined models, we use implementations available in CHARMM (Brooks et al., 1983) and the CHARMM-based protein design software DESIGNER (Wernisch et al., 2000).

First, these models are used to estimate the contributions of individual amino acid residues to the folding free energy of proteinlike decoys, when those residues are placed in thousands of different proteinlike environments similar to those typically encountered in protein design calculations. From these data the cost of transferring the different amino acids from bulk water to the protein interior is estimated and compared between different amino acids positioned in similar environments. As a control the same calculations are repeated on different environments from 362 high-resolution protein crystal structures deposited in the PDB (Berman et al., 2000).

Second, the CHARMM-based protein design procedure implemented in DESIGNER is used to illustrate the performance of a subset of the examined solvation models in actual protein design calculations. DESIGNER is particularly well suited for this task. Its energetic criteria for scoring sequences are entirely based on CHARMM force fields and involve no ad hoc scaling or extensive parameter-fitting, except for adjustments of a few physically meaningful parameters such as the dielectric constant, and corrections for approximations in the calculations of solvent exposure (Wernisch et al., 2000).

Third, three of the analyzed solvation models EAS, ACE, and EEF1, are tested as to their ability in distinguishing between native and nonnative sequence-structure combinations. The EEF1 model was previously reported to perform successfully in similar tests (Lazaridis and Karplus, 1999b), prompting its use in protein-folding simulations (Sali et al., 1994).

The three analyses taken together represent a first instance in which several implicit solvation models are confronted with a range of challenges. This is shown to provide useful insights into the limitations of these models and hints on how these limitations might be overcome.

METHODS

Scoring and selecting sequences with DESIGNER

To score and rank computed sequences for a given backbone structure, or different amino acids in a given environment, we use a quantity akin to the folding free energy as previously described (Wernisch et al., 2000):

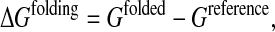(1)

where G^folded is the protein free energy in the folded state and G^reference is the free energy in a reference state, which is used as a model for the protein unfolded state.

In designing sequences compatible with a given backbone structure, the backbone coordinates are kept fixed, and when comparing the free energies of different amino acids in various environments, both the backbone and the surrounding side chains are kept fixed. Therefore the evaluation of ΔG^folding can be restricted to the part of the free energy that arises from pairwise interactions between the side chains of the considered residues and between these side chains and their fixed surroundings.

The side chain-restricted free energy of the folded state is then expressed as an effective energy, which is the sum of the following terms (Wernisch et al., 2000):

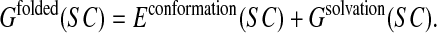(2)

E^conformation(SC) is the classical conformational energy computed using the CHARMM 22 force field (MacKerell et al.,1998) and is expressed as a sum of pairwise contributions. G^solvation(SC) represents the solvation free energy. In this force field, side-chain and backbone conformations are represented in full atomic detail (including all hydrogen atoms).

In the standard protocol of the protein design software DESIGNER, G^solvation(SC) is computed using the empirical atomic solvation model (see below). The electrostatic term is computed using a dielectric constant of 8 and a switching function operating between 6 and 7 Å. Different treatments of the electrostatic term are used with other solvation models (see below). Unless otherwise stated, side-chain conformations are modeled using the backbone-dependent rotamer library of Dunbrack and Karplus (1993).

For all other details of the protein design protocol, the reader is referred to Wernisch et al. (2000).

Free energy of the reference state

The free energy of the reference state, also restricted to contributions from side chains only, G^reference(SC), is calculated as the sum of the free energy contributions of isolated amino acids:

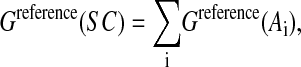(3)

where A_i are the isolated amino acids, modeled by the standard dipeptide unit with the N-acetyl-N′-methylamide backbone, and the sum is performed over the sequence of the protein. As for the folded state, G^reference(A) is expressed as a sum of two terms:

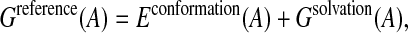(4)

where E^conformation(A) and G^solvation(A) are the contributions from conformational and solvation energies, respectively.

Calculation of the two energy terms in Eq. 4 involves computing the Boltzmann averages of the conformational and solvation energies over all possible side-chain conformations of A. As for the folded state the conformational energy is evaluated using the CHARMM-22 force field, whereas the solvation energy is evaluated using either Eq. 5 (see below) or other implicit solvation models.

Solvation free energy models

In this study, the solvation free energy in Eq. 2 is successively represented by the four different implicit solvation models detailed below.

Empirical atomic solvation model

This is the model implemented in the standard sequence design protocol of the software DESIGNER (Wernisch et al., 2000). In this model G^solvation is expressed as a linear function of the solute-solvent-accessible surface area as follows (Ooi et al., 1987):

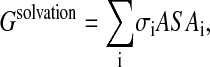(5)

where ASA_i is the accessible surface area of atom i, and σ_i, are the atomic solvation parameters, which are taken here as those for the vacuum-to-water transfer process (Ooi et al.,1987). The ASA_i is computed using the CHARMM22 van der Waals radii and a probe radius of 1.4 Å.

In the folded state, G^solvation is computed as a sum of several contributions. A contribution from the area buried by the interactions between the pairs of variable side chains, which is approximated by the weighted sum of the areas buried by all pairs, and the areas buried by the interactions of each side chain and the template, which are computed exactly. In the standard DESIGNER settings used here, a weight of 0.5 is applied to the pairwise term. This was shown to yield values for G^solvation differing by at most 15% from those computed using exact surface area calculations (Wernisch et al., 2000).

In computing G^solvation in the reference state, where the contributions of individual amino acids are simply summed (see below), the atomic ASA values are scaled down by 20%. This downscaling is justified by the fact that the straightforward summation in Eq. 5 overestimates the solvent accessible surface area in the unfolded state, because it neglects all interactions between side chains (Street and Mayo, 1998). Applying this scaling factor amounts to accounting for such interactions and considering that in the unfolded state residues are on the average ∼20% buried (Khechinashvili et al., 1995).

Effective energy function (EEF1)

This is the solvent-exclusion model with an empirical screening developed by Lazaridis and Karplus (1999a) and implemented in CHARMM. The solvation free energy is written as a sum over atom contributions:

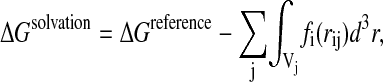(6)

where 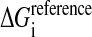is the solvation reference energy of atom i in a reference state, where it is completely accessible to the solvent. In the CHARMM implementation the values for 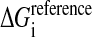are taken as the experimentally determined vacuum-to-water solvation energies of the corresponding groups in small molecules (Privalov and Makhatadze, 1993; Makhatadze and Privalov, 1993), except for the ionic groups which have arbitrary values to prevent the burial of charged residues (see below).

The second term is an integral over the solvation free energy density of group i at point r. It contains contributions from solute-solvent energy, solvent reorganization energy, solute-solvent entropy, and solvent reorganization entropy. The integral is over the volume V_j of group j that displaces solvent molecules around i; the summation is over all groups j surrounding i, and r_ij is the distance between groups i and j. In the discrete approximation, the integral is replaced by the product of the solvation free energy density of atom i times the volume V_j, with the latter being approximated by the volume of a sphere of a given radius.

The solvation free energy density is assumed to be a Gaussian function of the dimensionless distance from the atom:

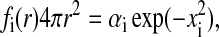(7)

with 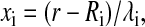where R_i is the van der Waals radius of i, λ_i is the correlation length, and 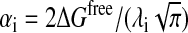is a proportionality coefficient with ΔG^free being the solvation free energy of the isolated atom.

The values of the various parameters (atom types i, their volumes V_i, their correlation lengths L, ΔG^reference and ΔG^free) required to compute the solvation free energy using Eqs. 6 and 7, and various other settings were taken as described in Lazaridis and Karplus (1999a). This includes the use of neutralized ionic side chains and a distance-dependent dielectric function applied to all atoms, including buried ones.

The generalized Born approximations ACE and GBMV

The ACE solvation model, introduced by Schaefer and Karplus (1996), belongs to the models based on the generalized Born equation. This equation gives an approximation to the electrostatic screening interaction energy 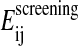between two charged groups in the presence of a continuum dielectric:

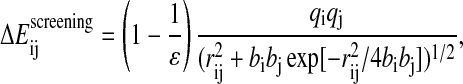(8)

where q_i and q_j are the atomic partial charges, ɛ is the solvent dielectric constant, and b_i and b_j are the effective Born radii, computed as follows:

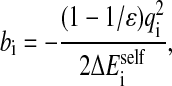(9)

where 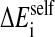is the solvation free energy of group i.

The total solvation free energy is expressed as a sum of three terms:

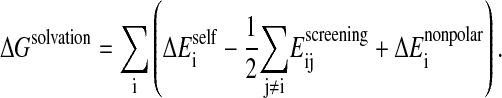(10)

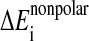is a surface area-dependent approximation to the hydrophobic solvation term. The screening term 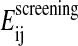depends on the structural environment through the b_i variable of the surrounding groups. 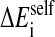is computed using an approximation to the integral of the energy density of the electric field over space.

The more recent generalized Born implementation by Lee et al. (2002), abbreviated GBMV, is a successor of the ACE model, where Eq. 9 is replaced by a higher-order empirical correction term for the Born radii that improves their fit with the radii calculated from Poisson theory. In the calculations performed here we used the GBMV setting recommended by Feig et al. (2004).

Solvation with the finite difference Poisson-Boltzmann procedure

The electrostatic contribution to the solvation free energy is computed using the fullest treatment of continuum electrostatics embodied in the finite difference Poisson-Boltzmann (FDPB) procedure. We use the procedure implemented in the CHARMM package. The van der Waals radii and partial charges are those of the CHARMM22 parameter set. The probe size for water is 1.4 Å, and the values of 4 and 80 are used for the protein and solvent dielectric constants, respectively. The calculations are performed using a dielectric constant of 4 for evaluating the Coulomb term and a box with dimensions equaling twice the maximum diameter of our protein decoys, with 99 grid points in each dimension. A single focusing iteration is performed.

The FDPB calculations, being very computationally demanding, are applied to a smaller subset of 990 decoy structures (see below). The electrostatic component of the solvation free energy is computed by performing the FDPB calculations in vacuum (solvent dielectric = 1) and in water (solvent dielectric = 80) and taking the difference:

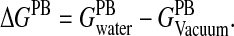(11)

The solvation free energy is then computed as the sum of the electrostatic components and a surface area dependent nonpolar solvation term as follows:

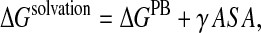(12)

where ASA is the protein solvent-accessible surface area (computed using a probe radius of 1.4 Å) and γ = 6 cal/Ų is the proportionality coefficient for the vapor-to-water transfer free energy versus accessible surface area (Ben Naim and Marcus, 1984).

Generating proteinlike decoys with random sequences

To generate a very large number of different environments for amino acids, where they would experience the entire range of solvent exposures (from completely exposed to completely buried), while being surrounded by residues with various degrees of polarity, structures were built into which random sequences were fitted, as follows.

First, we selected 45 high-resolution protein x-ray structures and 45 structures corresponding to models of minimum energy sequences computed by DESIGNER in full-design calculations performed previously (Jaramillo et al., 2002).

Second, the selected structures were unfolded using the protocol of Elcock for generating nativelike unfolded states of proteins (Elcock, 1999). The unfolding involved gradually increasing the Van der Waals radii to 3.0 Å, in steps of 0.5 Å. At each step, the electrostatic interactions were switched off and the energy of the structure was minimized using 50 steps of steepest descent followed by 250 steps of conjugate gradient minimization. The resulting unfolded structures had a minimal number of interactions while keeping a residual nativelike topology, making it possible to easily thread onto each of them a sequence chosen at random. The resulting structures displayed on average a root-mean-square deviation of 8 Å with the original structures.

Third, the random sequences were built into each of the unfolded structures using the “naïve” rotamer library recently proposed for misfolded structures, which contains only one rotamer per amino acid, thereby avoiding the costly task of side-chain modeling (Samudrala et al., 2000).

In a fourth and last step, each structure was relaxed by first performing 300 steps of Newton-Raphson minimization, followed by a 50-ps (1 ps = 10⁻¹² s) molecular dynamics run with EEF1 and then another 300 Newton-Raphson iterations. This produced structures displaying on average a root-mean-square deviation of 12.3 Å relative to the original structures.

All in all, this yielded 1372 polypeptide structures, displaying some degree of compactness. This ensemble of decoys comprises >80,000 residues, where each of the 20 amino acids appears >4000 times, given that the amino acids in the random sequences were chosen from a uniform probability distribution.

Data on protein crystal structures

In a second set of calculations we considered a set of 362 protein crystal structures deposited in the PDB, having 61–410 residues. These structures were selected using the PQS server (Henrick and Thornton, 1998) by searching for structures that are monomeric, with no disulphide bridges. This yielded 7954 matches, which were pruned, using the PISCES server (Wang and Dunbrack, 2003), to yield a subset with <25% sequence identity and a resolution better than 2.5 Å. Those were “cleaned” further to remove structures with gaps, yielding a final set of 362 structures, whose PDB-RSCB codes are given in the supplementary material.

Computing protein-to-water transfer free energies

Using the structures built as described above, the free energy cost of burying an amino acid residue to various extents in proteinlike environments was computed. This was done by computing for all instances of a given amino acid type the solvent-accessible surface area of the residue and its interaction free energy (including the conformational as well as solvation terms) with the remainder of the protein.

The cost of transferring an amino acid from the bulk solvent, where it is completely accessible, to the protein interior, where it is completely buried, was estimated by computing the difference:

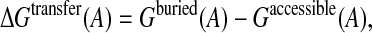(13)

where G^accessible(A) is the average free energy of the amino acid A, when its accessibility is in excess of 80%, and G^buried(A) is the average free energy of the same amino acid when it is completely buried (<1% accessibility to solvent).

RESULTS

Contributions of amino acids to the folding free energy as a function of solvent exposure

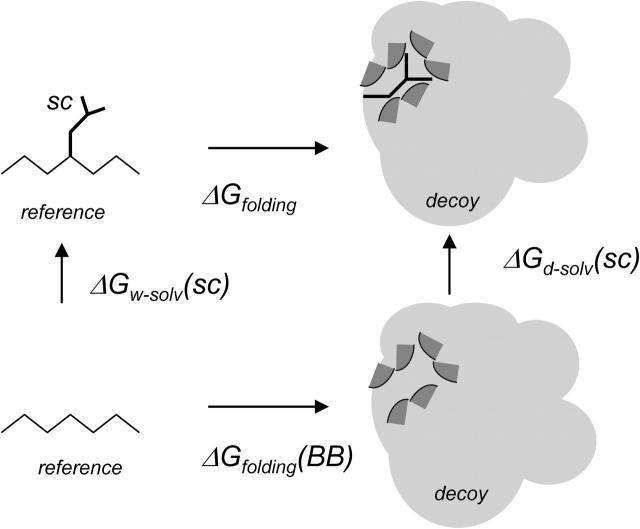
The contribution to the folding free energy of 1372 proteinlike decoy structures is evaluated for individual amino acid side chains positioned in ∼4000 different proteinlike environments, similar to those typically encountered in protein design calculations. The decoy structures are generated as described in Methods. The free energy contribution of an amino acid A is computed as the difference (ΔΔG_i(A)) between the decoy folding free energies in the presence and absence of the considered amino acid in position i, using the thermodynamic cycle shown in Fig. 1. Thus, ΔΔG_i takes into account the total free energy cost of desolvating in part or in whole the amino acid itself, as well as the cost of the partial desolvation of neighboring residues and the vacuum interaction terms of the considered residue with all surrounding atoms.

FIGURE 1.

Thermodynamic cycle for calculating the contribution of an amino acid side chain to the folding free energy of a decoy structure. ΔG folding is the contribution of the considered residue (back bone and side chain) to the free energy of folding of the protein (here the decoy). ΔG (BB) folding is the contribution of the backbone of the considered residue to the folding free energy of the decoy. Δ_Gw-solv(SC) is the free energy cost of introducing the side chain into the water solvent. ΔG_d-solv (SC), is the free energy cost of introducing the same side chain into the decoy structure. This cost includes the interaction energy of the side chain with the surrounding residues in the decoy as well as the cost of burying side-chain atoms and surrounding decoy atoms.

The calculations are carried out with four implicit solvation models. The EAS model of Ooi et al. (1987), the EEF1 model of Lazaridis and Karplus (1999a), and two analytical approximations to the generalized Born equation, ACE (Schaefer and Karplus, 1996) and GBMV (Lee et al., 2002). In addition, calculations are performed with the classical finite difference Poisson-Boltzmann procedure.

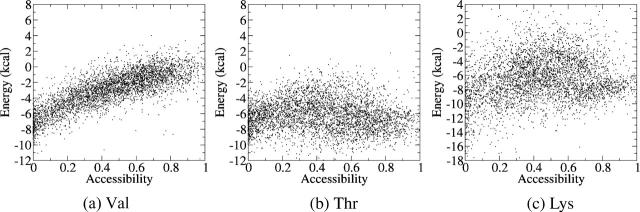
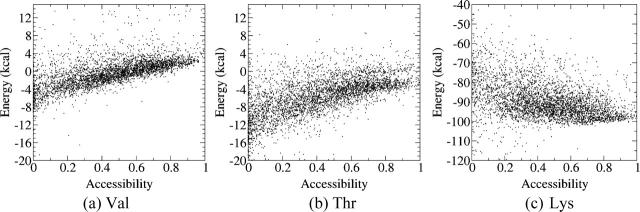
Folding and transfer free energies with the EAS model

Fig. 2 plots the contributions to the folding free energy of Val, Thr, and Lys respectively, as a function of their solvent accessibility (SA) in the decoy structures. The folding free energy was computed using the all-atom CHARMM22 force field in combination with the solvation term of Ooi et al. (1987), parameterized as previously described (Wernisch et al., 2000; see Methods). Each plot was obtained by computing ΔΔG_i for one of the considered amino acids in all structures and all positions within each structure where it was found, totalling ∼4000 different values.

FIGURE 2.

Contributions of individual amino acids to the folding free energy (kcal/mol) of proteinlike decoys, as a function of their solvent accessibility, computed with the EAS solvation model. (a) Energy of the Val side chain versus its SA for 4018 random environments. (b) Energy of the Thr side chain versus its SA for 4174 random environments. (c) Energy of the Lys side chain versus its SA for 4176 random environments. The energy values were computed as indicated in Fig. 1 and described in the text. The SA is defined as the ratio of the side-chain ASA in the decoy over its ASA when it is completely solvated.

We see that the free energy contribution of the hydrophobic side chain Val (Fig. 2 a) is highly favorable (−11 to −3 kcal/mol) when this side chain is nearly completely buried (SA values <0.1) and that it becomes less favorable as the solvent accessibility of the side chain increases. The spread in values is quite large, most likely due to the different environments in which the Val side chains in our decoy structures find themselves, as discussed below.

Fig. 2 b shows the equivalent plot obtained for the isosteric but more polar Thr side chain. The contribution of Thr to the folding free energy is similar to that of Val when this residue is nearly completely buried (SA <0.1). But unlike for Val, this contribution remains roughly constant and favorable as the side chain becomes more solvent exposed. The spread in values is on the whole larger than for Val, given that the Thr side chain can make H-bonds with neighboring groups in some environments and not in others.

The clear differences between the Val and Thr plots are hence consistent with the physical chemical properties of the two side chains, in particular with the fact that Val is less soluble than Thr in bulk solvent.

The equivalent plot for the charged Lys side chain is shown in Fig. 2 c. The spread of free energy values is particularly large, reflecting the great variability in the local environments of this amino acid in our decoys. Some of the completely buried Lys side chains provide very stabilizing contributions (from −18 to −16 kcal/mol), due to the H-bonds they make with other polar residues. The more accessible of these side chains also provide stabilizing contributions, albeit of lower magnitude (from −8 to −6 kcal/mol).

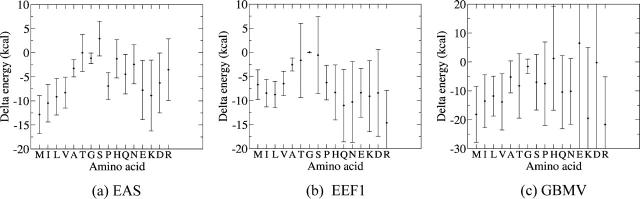
Similar plots are generated for all the amino acid side chains, save for prolines and glycines. Using those plots we then compute for each of the considered amino acids the free energy contribution averaged over slabs of solvent accessibility, when the residue is completely buried (0 < SA ≤ 0.01) and when it is completely accessible (0.80 < SA ≤ 1), respectively. The difference between these two values is defined as ΔG^T, the free energy cost of transferring the side chain from pure water to the protein interior.

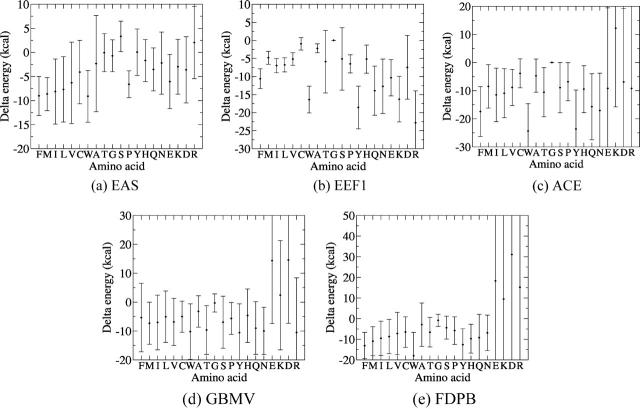
Fig. 7 a plots the ΔG^T values and their associated standard deviations for the different amino acids, ordered according to a commonly used hydrophobicity scale (Engelman and Steitz, 1981). This plot shows, first of all, that the standard deviations of the ΔG^T values are very large, in line with the large spread in the folding free energy values of individual residues. Next it reveals that the ΔG^T values of the nonpolar residues are in general lower than those of polar and charged ones, and that the average ΔG^T values of the nonpolar residues tend to increase with decreasing hydrophobicity. It is particularly noteworthy that the values for polar residues such as Thr or Asn are significantly larger than those of hydrophobics such as Val or Ile(leu), with limited overlap between the distributions of the ΔG^T values for these two types of residue. The highest ΔG^T values are displayed by Arg, Tyr, and His residues, with those for Lys and the negatively charged Asp and Glu residues displaying somewhat lower values.

FIGURE 7.

Transfer free energies of amino acids from water to the protein interior, computed using the five different implicit solvation models analyzed in this study. The transfer free energy was computed as 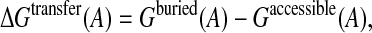where G^accessible(A) is the average free energy of the amino acid A, when its accessibility to solvent is >80%, and G^buried(A), is the average free energy of the same amino acid when it is completely buried (<1% accessibility). Dark circles represent average values, and bars, standard deviations. (a) ΔG^transfer computed with the EAS solvation model. (b) ΔG^transfer computed with the EEF1 solvation model. (c) ΔG^transfer computed with the ACE solvation model. (d) ΔG^transfer computed with the GBMV solvation model. (e) ΔG^transfer computed using FDPB and a surface area-dependent hydrophobic term (see Methods).

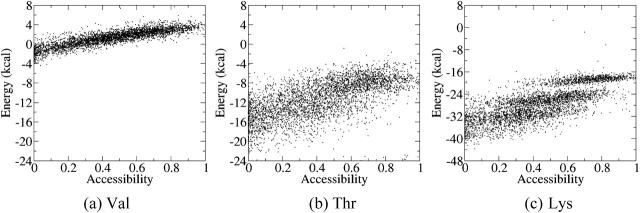
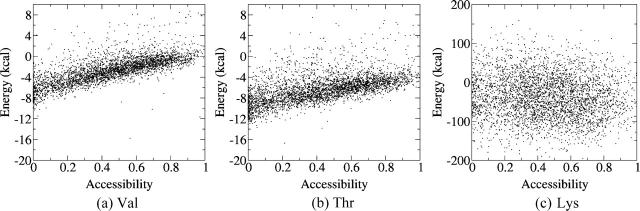
Folding and transfer free energies with EEF1 and the generalized Born solvation models

The calculations described above were repeated using the EEF1 and two generalized Born solvation models, ACE and GBMV, respectively (see Methods). Fig. 3 illustrates the results obtained with EEF1 for the same three residues as those discussed above. Val (Fig. 3 a) displays rather tightly clustered values that start at about −4 kcal/mol for low exposures of <0.1 Ų, increasing slowly and linearly to values of about +5 kcal/mol for completely exposed Val side chain. Thr (Fig. 3 b) displays significantly more negative free energy values in buried positions (from −24 to −22 kcal/mol) than Val. These values remain negative but become progressively less favorable as the Thr side chain becomes more exposed. A roughly similar trend is observed for Lys (Fig. 3 c), but the free energy values of buried Lys residues are now in the −44 to −22 kcal/mol range when the residues are completely buried, and increase to ∼−16 kcal/mol when they are completely exposed.

FIGURE 3.

Contributions of individual amino acids to the folding free energy (kcal/mol) of proteinlike decoys, as a function of their solvent accessibility, computed with the EEF1 solvation model. (a) Energy of the Val side chain versus its SA for 4018 random environments. (b) Energy of the Thr side chain versus its SA for 4174 random environments. (c) Energy of the Lys side chain versus its SA for 4176 random environments. The energy values were computed as indicated in Fig. 1 and described in the text. The SA is defined as the ratio of the side-chain ASA in the decoy over its ASA when it is completely solvated.

The ΔG^T values for the different amino acids computed from these data are shown in Fig. 7 b, together with their standard deviations. These values are plotted in the same order of increasing side-chain polarity as for the plot of Fig. 7 a. It is striking to see that except for Trp, hydrophobic amino acids have, on average, a less favorable water-to-protein ΔG^T values than polar residues, with the lowest value overall being displayed by Arg, representing a rather nonphysical behavior.

Results obtained with the ACE model are illustrated in Figs. 4 and 7 c and those obtained with the GBMV model are shown in Figs. 5 and 7 d. The ACE free energy versus SA plots of Val and Thr (Fig. 4, a and b) display qualitatively the same behavior as in the calculations with EEF1, although the actual values differ somewhat. The Lys plot (Fig. 4 c) is, however, quite different. Unlike with EEF1, in the ACE model the Lys free energy contribution becomes more favorable as the side chain exposure increases with, on average, free energy values of −80 kcal/mol for completely buried Lys side chains to values near −100 kcal/mol when they are completely exposed. Overall, however, this yields average ΔG^T values that are roughly similar for the different amino acids, irrespective of their polarity with, however, extremely large standard deviations for the four charged residues, E, K, D, and R (Fig. 7 c).

FIGURE 4.

Contributions of individual amino acids to the folding free energy (kcal/mol) of proteinlike decoys, as a function of their solvent accessibility, computed with the ACE solvation model. (a) Energy of the Val side chain versus its SA for 4018 random environments. (b) Energy of the Thr side chain versus its SA for 4174 random environments. (c) Energy of the Lys side chain versus its SA for 4176 random environments. The energy values were computed as indicated in Fig. 1 and described in the text. The SA is defined as the ratio of the side-chain ASA in the decoy over its ASA when it is completely solvated.

FIGURE 5.

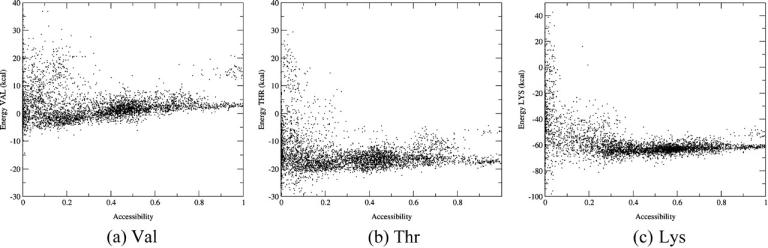
Contributions of individual amino acids to the folding free energy (kcal/mol) of proteinlike decoys, as a function of their solvent accessibility, computed using the generalized Born implementation of Lee et al. (2002). (a) Energy of the Val side chain versus its SA for 4018 random environments. (b) Energy of the Thr side chain versus its SA for 4174 random environments. (c) Energy of the Lys side chain versus its SA for 4176 random environments. The energy values were computed as indicated in Fig. 1 and described in the text. The SA is defined as the ratio of the side-chain ASA in the decoy over its ASA when it is completely solvated.

The behavior of the GBMV folding free energy curves (Fig. 5) is somewhat different. The spread in values is significantly reduced for all three side chains, when their accessibility exceeds ∼20%. We see furthermore that the free energy values change little with residue exposure and more strikingly, that folding free energy values for Thr and Lys, respectively a polar and charged residue, are lower than for the hydrophobic Val residues, representing a rather nonphysical behavior, once again. Fig. 7 d, which displays the GBMV ΔG^T values for all the 20 amino acids, reveals a qualitatively similar behavior to that observed with ACE (Fig. 7 c), but with an even more marked similarity between the average ΔG^T values of polar and nonpolar residues. We see, in particular, that Arg has a tighter distribution of ΔG^T values than with ACE, but features one of the lowest average values of the entire plot, which is even lower than those of most nonpolar residues.

Folding and transfer free energies with Poisson-Boltzmann electrostatics

To complete the analysis, the same calculations as those described above were also performed using the finite difference Poisson-Boltzman approach (Gilson et al.,1993) as described in Methods. Fig. 6 plots the resulting SA-dependent free energy contributions of Val, Thr, and Lys, respectively. The ΔG^T plots are given in Fig. 7 e.

FIGURE 6.

Contributions of individual amino acids to the folding free energy (kcal/mol) of proteinlike decoys, as a function of their solvent accessibility, computed using the FDPB electrostatics and surface area-dependent hydrophobic term. (a) Energy of the Val side chain versus its SA for 4018 random environments. (b) Energy of the Thr side chain versus its SA for 4174 random environments. (c) Energy of the Lys side chain versus its SA for 4176 random environments. The energy values were computed as indicated in Fig. 1 and described in the text. The SA is defined as the ratio of the side chain ASA in the decoy over its ASA when it is completely solvated.

Val and Thr (Fig. 6, a and b) display a similar behavior as in the calculations with the ACE model, although the spread of values for both amino acids, but particularly for Thr, is somewhat narrower in the FDPB plots, but not as narrow as in the GBMV plots of Fig. 5. In contrast, the SA-dependent Lys plot (Fig. 6 c) is different from that with ACE or from any of the other implicit solvation models tested here (Figs. 3 c and 4 c). The side-chain free energy shows little variability with the SA, but displays a very wide spread in values, spanning a record range of ∼180 kcal/mol.

Overall the FDPB method yields average amino acid ΔG^T values that show no clear trend as a function of amino acid polarity (Fig. 7 e). This is partly due to the very large spread of values, resulting in large standard deviations (>30 kcal/mol), particularly for the charged side chains (E, D, R, and K).

Thus, on the whole, the trends observed with the FDPB procedure applied using the standard CHARMM partial charges and atomic radii are similar to those obtained with the generalized Born-based ACE and GBMV models. These trends remain unchanged after making several variations of the FDPB protocol, which include different definitions for the solvent boundary, different partial charge sets, and different procedures for side-chain modeling, as discussed below and presented in the supplementary material.

Amino acid transfer free energies in protein crystal structures

Although our decoys are proteinlike they obviously do not represent thermodynamically stable structures and are clearly more poorly packed than native proteins. To investigate the effect that this might have on the folding and transfer free energy values computed with the different implicit solvation models, we repeated some of the calculations described above on a set of 362 known high-resolution protein crystal structures, representing between 3000 and 6000 different environments for the 20 amino acids. In particular we computed the SA-dependent residue folding free energies and the corresponding transfer free energies using the EAS, EEF1, and GBMV models. Having verified that the values obtained with the GBMV model were highly correlated with those computed with the FDPB method (correlation coefficient = 0.99), we did not perform calculations with the latter method.

The folding free energy versus SA plots for Val, Thr, and Lys computed with all three models are given in the supplementary material (Figs. S3–S5). The average ΔG^T values and corresponding standard deviations are plotted in Fig. 8, for all the amino acids for which the number of observations was sufficient. A first general observation that can be made from this figure is that in the well-packed crystal structures the average amino acid ΔG^T values are often lower than those obtained with the decoys (Fig. 7). This is the case in particular for the ΔG^T values of hydrophobic and charged amino acids computed with the EAS and the GBMV models, but not of the polar ones (Fig. 8 versus Fig. 7). Interestingly, GBMV yields larger standard deviations for the ΔG^T values computed in the crystal structures than in the decoys.

FIGURE 8.

Transfer free energies of amino acids from water to the protein interior, in 362 high-resolution protein crystal structures deposited in the PDB. The energies were computed using three of the implicit solvation models analyzed in this study. The transfer free energies were computed as detailed in the legend of Fig. 7. Shown are the average values (dark circles) and corresponding standard deviations (bars). (a) ΔG^transfer computed with the EAS solvation model. (b) ΔG^transfer computed with the EEF1 solvation model. (c) ΔG^transfer computed with the GBMV solvation model.

The lower transfer free energies for nonpolar residues in the crystal structures are probably a consequence of better packing of the protein core in these structures than in our decoys. The origin of the lower energies of charged residues might reflect the occasional existence in native proteins of buried charged side chains that have evolved to form favorable interactions with the rest of the protein. We could indeed check that in a few of the crystal structures, Lys and Arg side chains had very low interaction energies (∼−30 to −40 kcal/mol, with EAS). Such low energies were rarely if ever detected in the decoys.

Of the three tested models, EAS appears here, too, to produce the best separation between the distributions of the ΔG^T values for nonpolar versus polar amino acids, although this separation is less than in the decoys. On the whole, the standard deviations of the ΔG^T values are also lower than those obtained with the EEF1 and GBMV models and lower than those computed with the EAS model in our decoys.

Protein design with implicit solvation models

Having assessed how the different solvation models fare in evaluating the free energy cost of transferring amino acids from water to the protein interior in our proteinlike decoys, we now proceed to evaluate their effectiveness in selecting amino acid sequences likely to stabilize a nativelike protein structure in actual protein design calculations.

In protein design procedures such as those used here and elsewhere (Dahiyat et al., 1997; Raha et al., 2000; Koehl and Levitt, 1999a,b; Kuhlman and Baker, 2000), energies are computed as a sum of single-residue and residue-pair contributions. Energy terms involving many-body contributions can therefore not be readily included, unless approximated by pairwise terms. Of the different solvation models analyzed here, only two could therefore be evaluated in the context of actual protein design calculations. These are the EAS model, which includes a surface area-dependent term for which pairwise approximations have been derived by some of us (Wernisch et al., 2000) and by other authors (Street and Mayo, 1998), and the EEF1 model, where the solvation free energy density is expressed as a sum of pairwise contributions (Lazaridis and Karplus, 1999a).

Results obtained using these two solvation models in protein design calculations on the structure of the completely helical 54-residue engrailed homeobox domain protein (PDB_RCSB code 1enh) are presented in Figs. 9 and 10.

FIGURE 9.

Profiles of the designed sequences computed by DESIGNER for the homeodomain protein (RSCB-PDB code 1enh), using the EAS model (a) and the EEF1 model (b), respectively. The first row lists the residue number. The second and third rows list the wild-type sequence and the consensus-designed sequence (the most probable amino acid at each position along the polypeptide), respectively, using the one-letter amino acid code. Subsequent rows list the amino acids that occur with a frequency >10%. Buried positions (those with a solvent-accessible surface area of <25% in the native structure) are colored red in the wild-type sequence. Designs with the EAS model produced a total of 104 sequences; those with the EEF1 model produced 186 sequences.

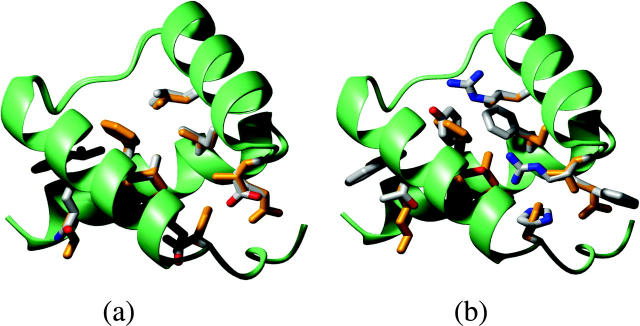
FIGURE 10.

Arrangements of amino acid side chains in the core of the minimum energy-designed protein and the wild-type protein for the homeodomain protein, using the EAS model (a) and the EEF1 model (b), respectively. The side chains in the wild-type structures are colored yellow, those of the designed structures are colored using the CPK convention. It is clearly visible that the sequence and structures designed using the EAS model are more nativelike than the one designed using the EEF1 model. In the latter structure, several buried hydrophobic residues are replaced by polar ones.

Fig. 9 lists, for the design calculation with each solvation model, the minimum energy sequence and a summary of the sequence profiles derived from the entire family of selected low-energy sequences—those within a given energy window above the minimum energy sequence. The calculations performed using the EAS model (Fig. 9 a) yield sequences with, on average, 16.6% identity to the wild-type homeobox domain sequence. This identity is higher for buried residues (38% on average) than for residues on the protein surface (7%), as previously reported (Jaramillo et al., 2002).

A very different result is observed for the sequences designed using the EEF1 model (Fig. 9 b). These sequences differ much more from the wild-type sequence, with, on average, 8.5% identity for all residues and 10% identity for buried residues. Quite strikingly, many of the hydrophobic amino acids in the wild-type are replaced by either polar amino acids or Trp or Phe residues, so that the designed proteins contain a large proportion of polar or aromatic amino acids, even in the protein core.

This result clearly contradicts what we know about proteins and about the role played by the hydrophobic effect in stabilizing the folded state. But it can be readily rationalized on the basis of the amino acid transfer free energies computed with the EEF1 model in our decoys (Fig. 7 b), or in the native crystal structures (Fig. 8 b). We see indeed that, on average, the transfer free energies for hydrophobic side chains such as Leu, Val, and Ala are all several kcal/mol higher than those of polar amino acids such as Thr, Tyr, and Arg, rather than the other way around. These polar amino acids are therefore systematically favored over nonpolar ones in the protein design calculations even in buried positions, leading to physically unsound sequence selections. Likewise, Phe and Trp side chains have lower transfer free energies than the other hydrophobic amino acids, favoring their ready incorporation into the protein core in the design calculations.

Fig. 10 illustrates the arrangement of core side chains in the 3D structures built for the minimum energy sequences obtained using the EAS and EEF1 models, when these are superimposed onto the native homeobox domain structure. Inspection of this arrangement confirms that the protein designed using the EAS model (Fig. 10 a) is nativelike, as the side-chain types and conformations in the designed and native proteins are very similar. This is clearly not the case for the protein designed using the EEF1 model. The core of the latter protein contains buried polar groups (e.g., 2 Arg and 1 His residues), which often form H-bonds to other polar groups (Fig. 10 b).

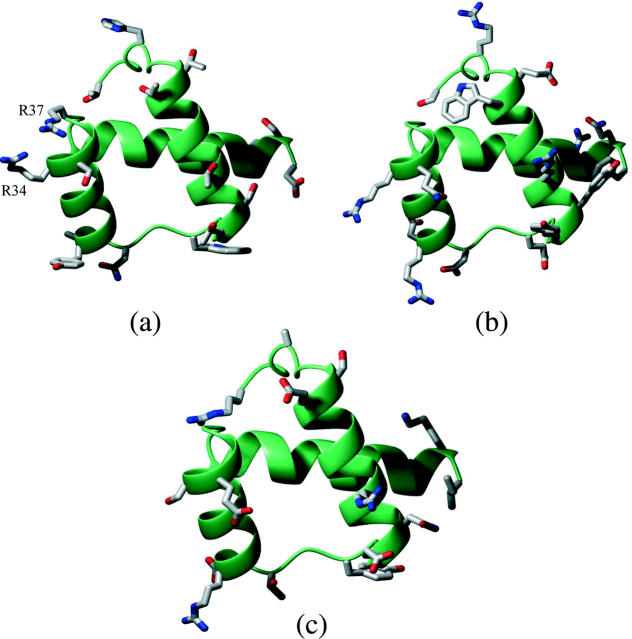
The protein designed using EEF1 also displays some unusual—and possibly physically unsound—constellations of surface residues, as illustrated in Fig. 11 a. It features close interactions between the side chains of Arg 34 and Arg 37 (4.2 Å distance between nitrogen atoms of different arginines), as well as a completely buried Arg 38. Close interactions of this type are not observed in the native homeobox structure (Fig. 11 c), which contains many positively charged side chains on the surface, involved in DNA binding, or in the minimum energy-designed protein with the EAS model (Fig. 11 b), which yields an increased proportion of charged side chains on the protein surface (Jaramillo et al., 2002).

FIGURE 11.

Arrangements of amino acid side chains on the surface of minimum energy-designed and wild-type homeodomain proteins. The minimum energy-designed proteins were computed using the EEF1 and EAS models, respectively. (a) Minimum energy-designed protein using the EEF1 solvation model. (b) Minimum energy-designed protein using the EAS solvation model. (c) Wild-type homeodomain crystal structure (PDB RSCB-code 1enh).

Distinguishing between nativelike and misfolded structures

To evaluate the suitability of a given force field for conformational search procedures or for fold prediction, a simple test is commonly performed (Lazaridis and Karplus, 1999b; Wodak and Rooman, 1993). The amino acid sequence of a protein, whose 3D structure is known, is modeled into a set of decoys, represented by backbones of unrelated proteins retrieved from the Protein Data Bank or by compact proteinlike structures generated computationally. The force field is then used to compute the energies of the modeled nonnative decoys and of the native protein structure. A suitable force field is required to yield a distinctly lower energy for the native sequence-structure combination than for the nonnative ones.

The EEF1 model was previously shown to perform adequately in such tests (Lazaridis and Karplus, 1999b). Here, three of the analyzed solvation models, the EAS, EEF1, and ACE models, are subjected to an analogous test similar in spirit to the classical test of Novotny et al. (1988). We consider two proteins of similar size, that adopt different folds, the all-α homeobox domain and the all-β SH3 domain proteins. For each domain the family of natural sequences is obtained from multiple alignments available in PFAM (Bateman et al., 2002). These alignments are pruned of sequences with unusually large or numerous insertions or deletions, and structural alignments are used to improve the sequence alignment in regions. The final number of considered sequences is 534 for SH3 and 1225 for the homeodomain.

These sequences are successively modeled onto the representative structure of each protein family, using the side-chain modeling procedure implemented in DESIGNER. These structures are the N-terminal SH3 domain from C-crk (PDB-RCSB code 1cka) and the engrailed homeobox domain structure (PDB-RCSB code 1enh). The sequence-structure alignments for the homologs were taken directly from the multiple alignments, and those for the nonhomologs were obtained by simply aligning successive residues in the sequence-structure pair.

Fig. 12 illustrates the results obtained by modeling the 534 sequences of SH3 domains onto the backbones of the SH3 and homeodomain structures, respectively. Very similar results were obtained when performing the symmetrical experiment, whereby the 1225 sequences of the homeodomain family are successively modeled onto the backbones of the C-crk SH3 domain and homeodomain, respectively (see supplementary material, Fig. S6).

FIGURE 12.

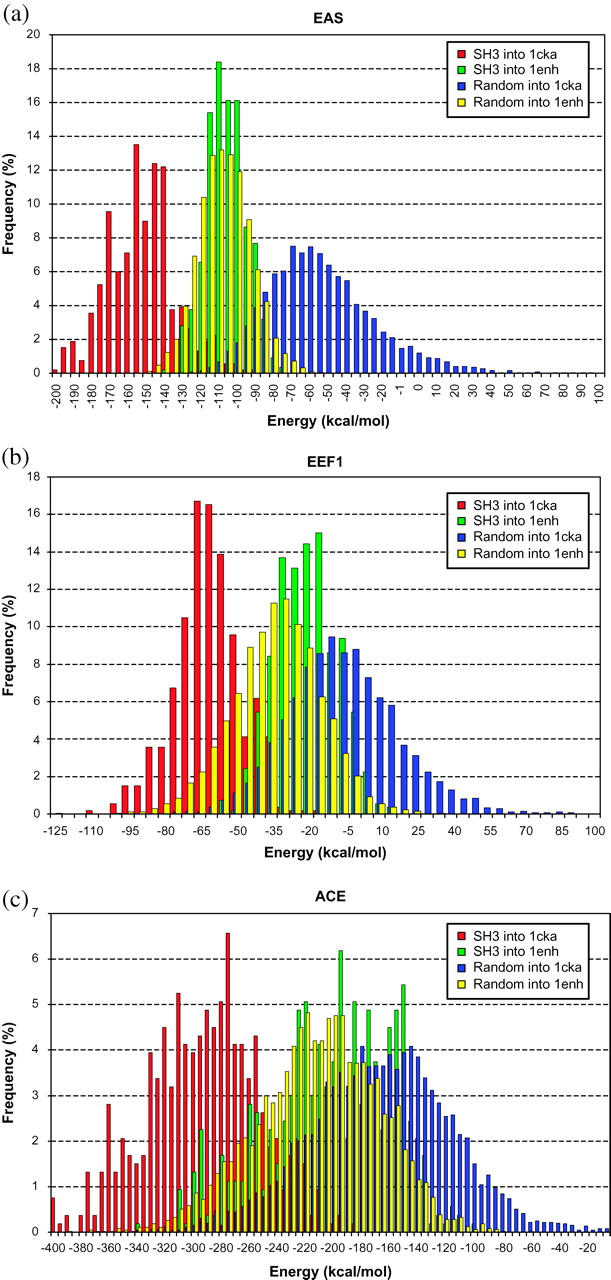
Distinguishing between nativelike and misfolded structures using various implicit solvation models. (a) Distributions of protein energies computed using the EAS solvation model. (b) Distributions of protein energies computed using the EEF1 solvation model. (c) Distributions of protein energies computed using the ACE solvation model. Each of the plots displays four different distributions. The one displayed with red bars represents the energies computed when the natural sequences of the SH3 domain are mounted onto the backbone of the C-crk SH3 domain (PDB-RCSB code 1cka). The green bars represent energies of the natural SH3 domain sequences mounted onto the engrailed homeodomain backbone (PDB-RSCB code 1enh). The blue and yellow bars represent energies of random sequences (see text for details), when those are mounted onto the SH3 (1cka) backbone and homeodomain (1enh) backbone, respectively.

The different panels of Fig. 12 display four distinct distributions of energy values. The first represents the energies computed for the structures representing native sequences of SH3 proteins modeled onto the backbone of their representative structure (red bars). The second represents the energies of the structures in which sequences from the SH3 domains are modeled into the homeodomain backbone (green bars). The third and fourth distributions represent the energies computed for a set of 4978 random sequences built onto the homeodomain and SH3 representative structures, respectively. These sequences were generated considering equal probabilities for the 20 amino acids at each residue position, and using DESIGNER to model the side-chain conformations.

We see that the force fields incorporating all three considered solvation models yield on average lower energies for the native sequence-structure combinations, where the natural sequences of the SH3 domain are mounted onto the backbone of the C-crk SH3 domain, than for the nonnative combinations, where the SH3 sequences are mounted onto the backbone of the unrelated engrailed homeodomain.

Furthermore, the separation between the energy distributions for native and nonnative sequence-structure combinations in the different panels of Fig. 12 is rather good. With energies for the native sequence structure combinations between 77 and 141 kcal/mol lower, on average, than those of the nonnative combinations.

With all three solvation models, the two energy distributions display nevertheless some overlap, indicating that a fraction of the SH3 domain sequences display similar energies when these sequences are mounted onto SH3 and homeodomain backbones. This most likely reflects the wide sequence variability of this family, which is usually also accompanied by some variability in the corresponding structures, thereby blurring the difference between sequences modeled into the backbone of a homolog versus a nonhomolog.

Interestingly, we find that the smallest overlap between energies of nativelike and nonnative structures is obtained with the EAS model in all tests (see Fig. 12 and Fig. S6 in supplementary material), whereas the largest overlap occurs with the ACE model (Fig. 12 c), in line with the large spread of values in the energy versus accessibility plots of individual amino acids (Fig. 4).

It is furthermore noteworthy that the energies computed for the models built by fitting random sequences into either the SH3 or homeobox backbones overlap rather well with those of the nonnative sequence-structure combinations—where the SH3 sequences are mounted onto the homeodomain backbone. Occasionally however, one set of these random structures yields rather low energies, similar to those computed for nativelike structures. This happens mostly with the EEF1 model, as illustrated in Fig. 12 b, and Fig. S6 of the supplementary material.

We thus see that all three tested force fields are capable of distinguishing reasonably effectively between the native and nonnative conformation of a given protein sequence, even when the native conformation is modeled by the backbone of a homolog. This result confirms previous findings on the adequate performance of the EEF1 model in this regard, but contrasts with the findings described above on the rather poor performance of all the considered implicit solvation schemes, save for the EAS model, in both the transfer free energy and protein design calculations.

The ability to discriminate between native and nonnative conformations is hence no guarantee for adequate performance in protein design or transfer free energy estimations. The reason is that the latter two types of calculations directly gauge the solvation contributions of individual residues and residue pairs. In contrast, fold discrimination is much less dependent on solvation and more on other nonbonded terms. This is illustrated in the studies of Novotny et al. (1988) and Lazaridis and Karplus (1999b), which show that adequate native fold recognition can be achieved solely on the basis of the vacuum CHARMM potential. The important role played by van der Waals and Coulomb interactions is also clearly evident from fold discrimination results obtained previously with EEF1 (Lazaridis and Karplus, 1999b).

DISCUSSION

In this work, we assessed the performance of five different implicit solvation models in two large-scale systematic tests. In one, we evaluated the contribution of individual amino acids to the folding free energy of proteinlike decoys by computing the cost of transferring the amino acids from bulk solvent to the protein interior. The main aim of this test was to challenge the different models with situations commonly encountered in protein design calculations, without actually having to perform these calculations with all the models, since some of them did not lend themselves to such calculations.

The results of this test lead to rather unexpected observations. Four of the tested solvation models, the EEF1 effective energy function, two generalized Born approximations (ACE and GBMV), as well as the fullest continuum solvation treatment embodied in the FDPB calculations, display inadequate performance. These models yield higher or similar water-to-protein transfer free energies for nonpolar as for many of the polar residues and as a result, favor the burial of polar amino acid in the protein interior over nonpolar ones, which goes counter to our understanding of the hydrophobic effect.

Actual protein design calculations performed for the engrailed homeobox domain protein, using one of the models—the EEF1 force field—confirm these findings. The lowest energy sequences designed using this force field were very different from the wild-type sequence. They had polar residues buried in the protein interior, and unfavorable electrostatic interactions between side chains on the protein surface. On the other hand, protein design calculations performed on the same template but using the EAS model, yielded more nativelike sequences, having nonpolar residues in the protein core and stabilizing interactions between polar and charged residues on the protein surface. We could show that this favorable behavior was paralleled by a reasonable performance of the EAS solvation model in our systematic decoy-based test.

Clearly, our decoy structures, as well as most of those built during the design calculations represent suboptimally packed systems that are furthermore not in thermodynamic equilibrium with their surroundings. To check the influence that these properties may have on the results, we performed a second large-scale test. In this latter test, the EAS and EEF1 models as well as GBMV, a more recent generalized Born implementation, were used to evaluate the contribution of individual amino acids to the folding free energy as well as their solvent-to-protein transfer free energies in a set of 362 high-resolution crystal structures deposited in the PDB. These are in principle experimentally determined structures representing well-packed equilibrium conformations. The computed energies did however display essentially the same trends as with our decoys. The simple EAS model yielded on average lower solvent-to-protein transfer free energies for nonpolar than for polar amino acids. In contrast, the EEF1 model produced an opposite trend: on average, polar amino acids had lower transfer free energies than nonpolar ones. Transfer free energies computed with the GBMV model showed an intermediate behavior, and displayed a large spread, particularly for charged amino acids.

These observations, taken together, lead us to the following conclusions. One is that the large-scale systematic tests performed either on proteinlike decoys or on high-resolution crystal structures are useful for benchmarking force fields for protein design calculations. Second, we conclude that protein design calculations and our proxy benchmarks constitute far more stringent tests for protein force fields than those most commonly performed. Indeed the tests to which the EEF1, ACE, and many other models were previously subjected involved mainly checking that they did not unfold the protein during standard molecular dynamics simulations and that they adequately represented protein solution conformations (Schaefer et al., 1998), or that they were capable of discriminating between the native fold and many nonnative alternatives (tests performed with EEF1, Lazaridis and Karplus, 1999b).

Analogous native recognition tests performed here for all five solvation models show them to perform roughly equally adequately (data not shown). These tests are hence not a good benchmark for these models. We see indeed that the EEF1 model performs well in native recognition tests but yields the worst results for amino acid transfer free energies in both native crystal structures and decoys, and performs poorly in protein design calculations. This discrepancy arises because solvation effects are not adequately represented in this model. Our calculations clearly reveal this problem because they directly evaluate transfer/folding free energies of individual amino acids and hence their solvation properties. On the other hand, fold discrimination as commonly practiced is primarily driven by nonbonded contributions (often mainly van der Waals), with a smaller influence from solvation, as already evident from previous work (Novotny et al., 1988; Lazaridis and Karplus, 1999b).

This suggests that the EEF1 model can therefore not be trusted for systematic conformational or sequence space explorations such as those in previously reported studies of complete unfolding pathways of proteins (Sali et al., 1994), or those that sample nonnative regions in sequence space (Kuhlman and Baker, 2000). Its use in docking calculations, involving macromolecules or small molecules should also be critically reevaluated.

Of the remaining four models tested here only the EAS model displays acceptable performance both in ranking the solvation energies of different amino acids in our systematic test and in protein design calculations. Ironically, this model is the simplest and the oldest of the four implicit solvation models tested here. It is also the default model currently available in the DESIGNER software (Wernisch et al., 2000; Jaramillo et al., 2002), and was one of the first models to be incorporated into standard molecular dynamics software (Wesson and Eisenberg, 1992).

On the other hand, having found that the more sophisticated generalized Born models, ACE and GBMV, as well as the FDPB treatment, do not perform well in our systematic tests, we predict that they would likewise perform poorly in actual protein design calculations.

The reasons underlying the poor performance of EEF1 and the two generalized Born models are not immediately obvious, given that these models involve many approximations and empirical parameter adjustments. One potential problem with EEF1 and ACE could be that they can yield nonzero solvation energies for deeply buried groups, which in EEF1 can be rather large and stabilizing, especially for ionic groups (Lazaridis and Karplus, 1999a). With ACE, problems can also arise from inadequate modeling of the effective Born radii, which are a very sensitive component of the model.

The poor performance of the FDPB and the GBVM solvation models is much more surprising. The FDPB model is presently considered as the reference against which various more approximate treatments must be compared, and GBMV is one of the more recent implementations of the generalized Born approximation, shown to mimic well the FDPB behavior (Lee et al., 2002). Other generalized Born models were also reported to reproduce well FDPB results (Edinger et al., 1997; Schaefer and Karplus, 1996), but without actually comparing the computed values to any experimental measures.

Such comparisons were, however, reported previously for transfer and hydration free energies of peptides and organic compounds computed with the FDPB, and shown to yield satisfactory results (Sitkoff et al., 1994, 1996), but the latter studies involved fitting the atomic partial charges, the atomic radii, and the solvent probe radius for calculating the molecular boundaries. The FDPB calculations reported here were performed in very much the same manner as in the latter reported works. We used the same proportionality constant for the surface area-dependent hydrophobic terms, but with a unique solvent probe size of 1.4 Å for both solvent and vacuum calculations, and standard CHARMM partial charges and radii. However, using different probe sizes for the vacuum (zero) and solvent (1.4 Å) calculations, as in Sitkoff et al. (1996) but keeping the standard CHARMM charges and radii, or replacing them with the radii of Nina et al. (1999) did not improve the results (see Figs. S1 and S2 of supplementary material).

Explaining these disturbing findings will clearly require further analysis. An important aspect to investigate is the influence that very unusual molecular boundaries, such as those defined by the poorly packed environments generated in our decoys, could have on the FDPB calculations. We see indeed that the GBMV amino acid transfer free energies behave more like we expect them to with regard to the differences between polar and nonpolar amino acids in crystal structures (Fig. 8 c) than in our decoys (Fig. 7 d). Probably parameters of the models could be adjusted to correct some of the problems. For example, in the FDPB solvation, the nonpolar contribution to the solvation free energy is approximated by a surface area-dependent term (see Methods), which could be modified to penalize more the burial of hydrophilic groups (Wagner and Simonson, 1999).

It should be clear, however, that the conclusions reached in this study do not necessarily apply to other proposed approximations to the generalized Born formalism, which have not been tested here (for review, see Feig and Brooks, 2004), since each implementation embodies different approximations.

It must likewise be stressed that several of the criteria whereby we judged a solvation model to perform well in evaluating transfer free energies or in protein design calculations are extremely crude. For the transfer free energies, only a rough ranking of hydrophobic versus polar amino acids was evaluated. The performance in protein design calculations was also evaluated qualitatively. We examined the incorporation of polar versus nonpolar amino acids in the protein interior, and checked for unusual interactions between polar residues on the protein surface.

With the current status of these solvation models, this is sufficient for pointing out their most blatant limitations. Hence, our finding that the EAS model performs better than all the other models tested here by no means certifies it as an accurate solvation model. Such certification will require much finer and more quantitative tests, aimed at reproducing not only solvation energies but also changes in protein stability caused by mutations, which would be evaluated in a realistic situation where adjustments of the protein backbone can also take place.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.