Abstract
Receptor-ligand bonds that mediate cell adhesion are often subjected to forces that regulate their dissociation via modulating off-rates. Off-rates control how long receptor-ligand bonds last and how much force they withstand. One should therefore be able to determine off-rates from either bond lifetime or unbinding force measurements. However, substantial discrepancies exist between the force dependence of off-rates derived from the two types of measurements even for the same interactions, e.g., selectins dissociating from their ligands, which mediate the tethering and rolling of leukocytes on vascular surfaces during inflammation and immune surveillance. We used atomic force microscopy to measure survival times of P-selectin dissociating from P-selectin glycoprotein ligand 1 or from an antibody in both bond lifetime and unbinding force experiments. By a new method of data analysis, we showed that the discrepancies resulted from the assumption that off-rates were functions of force only. The off-rates derived from forced dissociation data depended not only on force but also on the history of force application. This finding provides a new paradigm for understanding how force regulates receptor-ligand interactions.
INTRODUCTION
The selectin family of adhesion molecules are C-type lectins with three known members: L-selectin, expressed on leukocytes, binds to ligands on endothelial cells and on other leukocytes; P-selectin and E-selectin, expressed on activated platelets and/or endothelial cells, recognize ligands on leukocytes or platelets. The major leukocyte ligand for selectins is P-selectin glycoprotein ligand-1 (PSGL-1). Ca2+-dependent interactions of selectins with cell-surface glycoconjugates mediate tethering and rolling of flowing leukocytes on vascular surfaces in response to infection or tissue injury (Vestweber and Blanks, 1999; McEver, 2001, 2002). In this mechanically stressful environment, different forces are applied to selectin-PSGL-1 bonds at various rates. In part, the relationship between off-rate and force determines how efficiently tethers produce rolling and how rapidly and stably cells roll (Yago et al., 2004).
Bell (1978) was the first to suggest that the dissociation of adhesive receptor-ligand complexes, here termed bonds, which provide anchoring between cells or between a cell and the extracellular matrix, could be influenced by force, just as gaseous chemical reactions are affected by pressure. Although not validated, all published work to date has assumed that off-rate depends on the instantaneous force level (Bell, 1978; Dembo et al., 1988; Evans and Ritchie, 1997; Izrailev et al., 1997). This assumption has provided a theoretical framework for conceptualizing how applied force might alter the bond lifetime and how loading rate might affect the unbinding force of a receptor-ligand bond. It has also been the basis for determining the relationship between off-rate koff and force f from two types of measurements. The first type is bond lifetimes measured in a range of constant forces, which was used to obtain the first experimental estimate of koff(f) (Alon et al., 1995). All bond lifetime measurements have been made using a flow chamber (Alon et al., 1995, 1997, 1998; Chen and Springer, 2001; Dwir et al., 2001, 2002, 2003; Smith et al., 1999; Ramachandran et al., 1999, 2001; Yago et al., 2002, 2004) except for our recent work, which used atomic force microscopy (AFM) (Marshall et al., 2003; Sarangapani et al., 2004). The second type of measurement is unbinding forces measured in a range of constant loading rates, which have recently been popularized by the theory of dynamic force spectroscopy (DFS) analysis (Merkel et al., 1999; Evans et al., 2001; Evans, 2001; Evans and Williams, 2002) (see Materials and Methods below). The unbinding force measurements have been made using AFM (Fritz et al., 1998; Yuan et al., 2000; Li et al., 2003; Zhang et al., 2002, 2004; Hanley et al., 2003, 2004); a biointerface force probe (BFP) (Merkel et al., 1999; Simson et al., 1999; Strunz et al., 1999; Evans et al., 2001; Evans and Williams, 2002), or a microcantilever (Tees et al., 2001).
However, the above two measurement methods have often yielded drastically different koff versus f relationships for the same interactions, e.g., selectins dissociating from their ligands (Alon et al., 1995, 1997, 1998; Chen and Springer, 2001; Dwir et al., 2001, 2002, 2003; Smith et al., 1999; Ramachandran et al., 1999, 2001; Yago et al., 2002, 2004; Marshall et al., 2003; Sarangapani et al., 2004; Fritz et al., 1998; Evans et al., 2001; Evans and Williams, 2002; Hanley et al., 2003, 2004; Zhang et al., 2004). This is quite puzzling because it has been a generally accepted notion that off-rates govern both receptor-ligand bond lifetimes and bond strength. As such, one expects to be able to determine off-rates from either bond lifetime or unbinding force measurements. It is difficult to identify the causes for the discrepant results because of the many potential differences involved, as different laboratories obtained their results using different reagents and techniques. Using AFM to measure off-rates of P-selectin dissociating from PSGL-1 or from an antibody, we showed that the discrepancies were results of the two types of measurements—unbinding forces and bond lifetimes—themselves. Analyzing these data with a new method of time-to-dissociation analysis, we showed that the off-rate depended not only on force but also on force history. This finding reconciles previous discrepancies and provides a new paradigm for understanding how force regulates receptor-ligand dissociation.
MATERIALS AND METHODS
AFM experiments
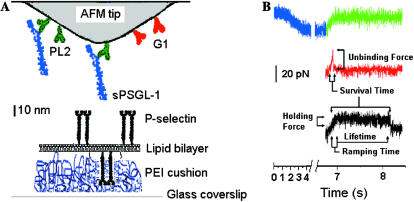
Our AFM system and reagents have been described previously (Marshall et al., 2003; Sarangapani et al., 2004). Briefly, cantilevers (ThermoMicroscopes, Sunnyvale, CA) of spring constants 4–13 pN/nm, each calibrated in situ by thermal fluctuation analysis (Hutter and Bechhoefer, 1993), were functionalized by capturing a monomeric recombinant soluble PSGL-1 (sPSGL-1) (Yago et al., 2002) with a nonblocking monoclonal antibody (mAb) PL2 against PSGL-1 (Moore et al., 1995). PL2 or a blocking anti-P-selectin mAb G1 (Geng et al., 1990) were adsorbed on the cantilever tip (Fig. 1 A) followed by blocking with 1% bovine serum albumin in Hanks' balanced salt solution. Membrane P-selectin purified from human platelets (Moore et al., 1994) was reconstituted into glass-supported, polyethylenimine (PEI)-cushioned lipid bilayers (Fig. 1 A) using the method of vesicle fusion (Wong et al., 1999, McConnell et al., 1986). The P-selectin density was kept low to achieve infrequent binding, which is required to ensure binding to be mediated by a small number of (most likely just one) bond(s) (Zhu et al., 2002). Cantilever tips bearing sPSGL-1 or G1 were repeatedly brought into contact with the P-selectin-bilayer to allow bond formation and retracted to record the rare adhesion events (<20%). Three sets of data—unbinding forces, bond lifetimes, and survival times–were collected along two families of force histories: constant-rate loading, where force increased linearly with time, and constant-force loading, where force initially increased linearly with time and then became constant once a prescribed level was achieved (Fig. 1 B). The unbinding force (or holding force in the bond lifetime experiment) was measured from the force difference at the point of bond failure (Fig. 1 B). The bond lifetime was measured from the instant when the bond was fully loaded to a desired force to the instant of bond dissociation at that force. In both assays, the survival time, or the time to dissociation, was measured from the instant when the bond was first loaded to the instant of bond dissociation, regardless of the history of force application. The loading rate rf was determined as the ratio of unbinding force (or holding force) to survival time (or ramping time) because the f versus t curves during ramping were linear in the force range tested. Force averaging was used to circumvent thermally driven force fluctuations (Marshall et al., 2003; Sarangapani et al., 2004).
FIGURE 1.
AFM experiment. (A) Functionalizing the AFM. The schematic represents a composite of all molecules adsorbed or captured. Adsorbed anti-PSGL-1 mAb PL2 was used to capture sPSGL-1. Anti-P-selectin mAb G1 was adsorbed on a separate tip. P-selectin was reconstituted in a PEI-cushioned lipid bilayer. (B) Force-scan curves. The approach tracing was horizontal (zero mean force) initially but was bent downward when the tip was compressed onto the bilayer. The retraction tracing mirrored the approach tracing until the cantilever returned to the unbent position. After this point, >80% of the retraction tracings leveled off, even though the cantilever continued to retract, indicating the absence of adhesion (top tracing). In <20% of the cases, the retraction tracing was bent upward, indicating a tensile force that was applied to the tip through a molecular bond linked to the bilayer. In the unbinding force experiment, the cantilever was retracted at a constant rate until the tip sprang back to the unbent position (middle tracing). In the bond lifetime experiment, once retracted a predetermined distance, the cantilever was stopped to apply a constant force to the bond (bottom tracing). Unbinding forces were measured along the former loading histories. Bond lifetimes were measured along the constant force portion of the latter loading histories. Survival times were measured along both loading histories (indicated).
Theory and data analysis
Data were analyzed with the kinetic theory for the first-order irreversible unbinding of single bonds along a single thermodynamic pathway for dissociation,
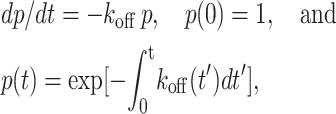 |
(1a–c) |
where p is the probability of having a bond at time 0 to remain intact at time t. Different solutions can be obtained depending on the assumed relationships between the off-rate koff and time t. Existing theories assume off-rate to be a function of force f only, such that koff depends on t only implicitly through f (Bell, 1978; Dembo et al., 1988; Evans and Ritchie, 1997; Izrailev et al., 1997; Evans, 2001; Zhu, 2000; Strunz et al., 2000; Hummer and Szabo, 2003). Along a constant-rate (rf) force history f = rft, the time dependence of p and koff in Eq. 1 can be transformed to their respective force dependence, which yields the respective cumulative probability pc for a bond to unbind at force not exceeding f and the probability density pd for a bond to unbind at force f,
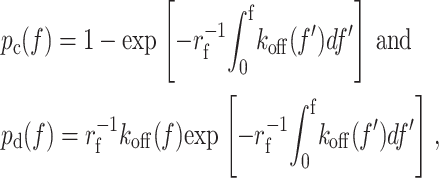 |
(2a, b) |
which correspond to the cumulative frequency and the unbinding force histogram, respectively (cf. Figs. 2 A, 3, and 4).
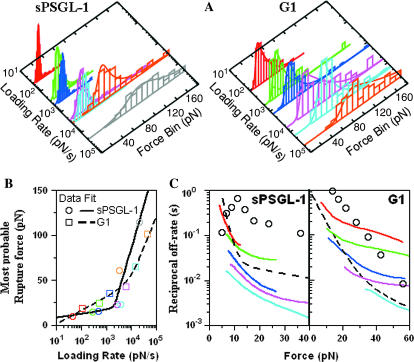
FIGURE 2.
Discrepancies between actually measured bond lifetimes and those predicted from unbinding force analysis. (A) Histograms of unbinding forces (>40 measurements for each loading rate) measured at various loading rates for P-selectin interacting with sPSGL-1 (left panel, ∼600 total measurements) and G1 (right panel, ∼450 total measurements). Equations 2 and 3 were fit to each histogram (curves) to determine the most probable unbinding force, fm, for that loading rate, rf. (B) fm was plotted against rf in the log scale (points with colors match the histogram colors in (A), which were fitted by Eq. 4 (curves) to evaluate the parameters for each interaction. The best-fit parameters for the P-selectin-sPSGL-1 bonds are k1 = 0.0770 s−1, a1 = 2.41 nm, k2 = 33.6 s−1, and a2 = 0.0991 nm. The best-fit parameters for the P-selectin-G1 bonds are: k1 = 1.08 s−1, a1 = 0.664 nm, k2 = 54.7 s−1, and a2 = 0.137 nm. (C) Using these parameters and Eq. 3, 1/koff was plotted against f (black dashed curves) for P-selectin interacting with sPSGL-1 (left panel) and G1 (right panel). Three closely matched lifetime measures, 〈t〉,σ(t), and −1/slope obtained directly from bond lifetime experiments (Marshall et al., 2003; Sarangapani et al., 2004) were averaged and shown for comparison (circles). 1/koff versus f data estimated from individual unbinding force histograms according to Eq. 6 (solid curves, colors match those in the histograms) were shown in the force range where bond lifetime data were available for P-selectin dissociating from sPSGL-1 (left panel) and G1 (right panel).
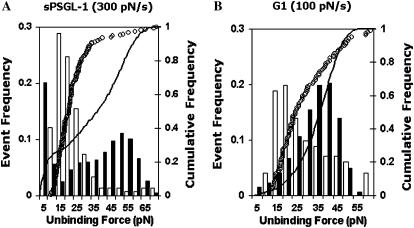
FIGURE 3.
Discrepancies between unbinding force histograms and cumulative frequencies actually measured and predicted. Using Eq. 2 and koff(f) determined from the bond lifetime data, the cumulative probability pc (curves) for a bond (loaded with a constant rate of rf = 300 pN/s) to unbind at force not exceeding f and the probability density pd (solid bars) for a bond (loaded by the same ramp rate) to unbind at force f were predicted for P-selectin interacting with sPSGL-1 (A) and G1 (B). These were compared to the unbinding forces measured along the same constant-rate loading path and analyzed by histogram (open bars) and cumulative frequency (open circles) for the two interactions.
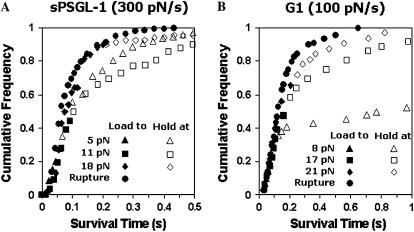
FIGURE 4.
Discrepancies among cumulative frequency versus survival time curves from unbinding force and bond lifetime measurements. Survival times of bonds of P-selectin interacting with sPSGL-1 (A) or G1 (B) were measured from the unbinding force and bond lifetime experiments and analyzed by cumulative frequencies. For the former experiment, bonds were loaded continuously at the indicated constant rates until rupture (solid circles). For the latter experiment, bonds were initially loaded at the same rates to the indicated forces and were then held at those forces. Some of the bonds failed during ramping (solid triangles, squares, and diamonds) whereas others dissociated during holding (open triangles, squares, and diamonds). Only survival times of every third point are shown for clarity. Although two out of three points were skipped to avoid obscuring different symbols, the curve shapes are identical if all data points are included.
The constant-rate loading experiments were analyzed by dynamic force spectroscopy, a method for determining koff(f) from single molecule unbinding/unfolding force data (Merkel et al., 1999; Evans et al., 2001; Evans, 2001; Evans and Williams, 2002; Hummer and Szabo, 2003). The “bond strength” fm, defined as the most probable unbinding force and measured as the peak force from the unbinding force histogram, is plotted against the logarithm of the loading rate rf (cf. Fig. 2 B). This is referred to as a “strength spectrum”, which often appears as a nearly piecewise linear curve. Such strength spectra have been interpreted using an off-rate expressed as multiple Bell (1978) models in a serial arrangement (Merkel et al., 1999; Evans et al., 2001; Evans, 2001; Evans and Williams, 2002):
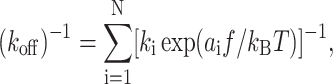 |
(3) |
where kB is the Boltzmann constant, T is the absolute temperature, and ai and ki (i = 1, 2, …, N) are parameters. Differentiating pd in Eq. 2b with respect to f and setting the resulting equation to zero yield an equation for finding the bond strength fm. Substituting Eq. 3 into it yields a relationship between the loading rate rf and fm (Merkel et al., 1999; Evans et al., 2001; Evans, 2001; Evans and Williams, 2002):
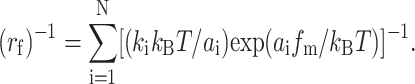 |
(4) |
Fitting Eq. 4 to the strength spectra, i.e., fm versus rf data (cf. Fig. 2 B), allows evaluation of the parameters ai and ki, which are interpreted as related to the locations and differences, respectively, in heights of the ith energy barrier along the force-driven dissociation path (Merkel et al., 1999).
The bond lifetime data were analyzed by Eq. 1c after setting as time 0 the instant when the desired force level had just been achieved along a constant-force force history. It follows from the assumption of off-rate being a function of force only that koff becomes a constant for t > 0 and that Eq. 1c is reduced to p = exp(−kofft). The reciprocal off-rate 1/koff at a given force was then estimated from three lifetime measures: the mean [〈t〉 = −∫0∞t(dp/dt)dt)] and standard deviation {σ(t) = [−∫0∞(t − 〈t〉)2(dp/dt)dt]1/2} of lifetimes and the reciprocal negative slope of the ln(No. of events with a lifetime ≥ t) versus t plot (Marshall et al., 2003; Sarangapani et al., 2004).
The survival time data were analyzed by a new method, which allows determination of the complete function koff(t) from a single distribution of survival times measured along an arbitrary force history. By comparison, to determine koff(f) from the above DFS or lifetime analysis requires, respectively, multiple unbinding force histograms or multiple bond lifetime histograms, which have to be measured along their respective families of force histories. The new method has removed the restrictive assumptions that koff is a single-valued function of f and that it depends on t only through f. The two remaining general assumptions are: a), the dissociation of single molecular bonds obeys Eq. 1 along any force history; and b), once the force history is specified, the off-rate becomes a single-valued but general function of the survival time t, which includes but is not limited to its dependence on t through f. To develop this method, we solved koff from Eq. 1:
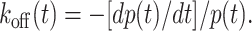 |
(5) |
We noted that the right-hand side of Eq. 5 could be measured as 1 − p, and d(1 − p)/dt corresponded to the respective cumulative frequency and histogram of survival time data. To minimize irregular fluctuations caused by numerical differentiation of finite data points, the measured cumulative frequency data were smoothed by cubic spline fitting, which was then differentiated. The result was substituted along with the fitted cumulative frequency into Eq. 5 to estimate koff(t) without any a priori assumption of its functional form.
For unbinding forces measured at a single loading rate, i.e., along a given constant-rate force history where force and time are related by f = rft, Eq. 5 can be rearranged to obtain an explicit expression for off-rate as a function of force:
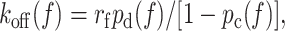 |
(6) |
which can also be derived directly from Eq. 2.
RESULTS
Off-rates derived from unbinding forces fail to predict measured bond lifetimes
Forces at which P-selectin unbound from sPSGL-1 or G1 were measured by retracting the cantilever at constant rates (ranging from 0.03 to 30 μm/s). Binding was specific because adhesion frequencies, bond lifetimes, and unbinding forces were substantially reduced when P-selectin, sPSGL-1, or G1 was absent and when blocking mAb against P-selectin or PSGL-1 or the divalent-cation chelator EDTA was added to the media (data not shown; see Marshall et al., 2003). The unbinding force histograms exhibited typical single peaks and shifted rightward toward larger forces as the loading rate was increased (Fig. 2 A), similar to previously reported histograms (Merkel et al., 1999; Hanley et al., 2003). To apply the DFS analysis (Merkel et al., 1999; Evans et al., 2001; Evans, 2001; Evans and Williams, 2002), the “strength spectra” were generated by plotting the peak force fm against the loading rate rf in a log scale, which displayed two line segments for each of the interactions (Fig. 2 B). The force dependence of off-rate koff was determined by fitting these data to Eq. 4, which was derived based on a double Bell model in series (i.e., N = 2 in Eq. 3) assumed a priori for koff(f).
The bond lifetimes measured at the constant-force loading experiments were exponentially distributed. At each force level, the 1/koff was determined from the mean or standard deviation of lifetimes or from the −1/slope of the ln(No. of events with a lifetime ≥ t) versus t plot, which show good agreement, as predicted from the first-order dissociation kinetics. The directly measured bond lifetime versus force data (points) were compared to the 1/koff versus f relationship (black dashed curves) previously determined from the DFS analysis of the unbinding force measurements (Fig. 2 C).
Unexpectedly, the 1/koff values determined from the two assays differed drastically. For the P-selectin-sPSGL-1 interaction (Fig. 2 C, left panel), the directly measured bond lifetime data behaved as a catch-slip transitional bond, where force first prolonged and then shortened bond lifetimes (Marshall et al., 2003). In sharp contrast, the 1/koff curve obtained from the unbinding force data decreased monotonically with force, exhibiting only slip bond characteristics. For the P-selectin-G1 interaction (Fig. 2 C, right panel), the directly measured bond lifetime data followed a straight line in the semilog plot, indicating a single exponential function for koff(f) that was well described by the Bell (1978) model. By comparison, the 1/koff curve obtained from the unbinding force data included two line segments in the semilog plot (Fig. 2 B), thereby requiring two exponential functions for its description, which was ∼10-fold smaller than that determined from the bond lifetime data in the force range tested (Fig. 2 C, right panel).
In addition to the DFS analysis (Fig. 2 B), the off-rate was estimated (Fig. 2 C, solid curves) directly from the unbinding force data (Fig. 2 A, color-matched histograms) using a new method without a priori assumption as to its functional form (see Materials and Methods, Eq. 6). This method utilized the entire histogram and cumulative frequency data as opposed to only the peak value of the histogram, and it enabled evaluation of koff(f) from unbinding forces measured at a single loading rate as opposed to requiring a range of loading rates.
Two observations can be made from this analysis of the unbinding force data: a), the 1/koff values (Fig. 2 C, colored solid curves) were considerably different from the directly measured bond lifetime data for both P-selectin-sPSGL-1 and P-selectin-G1 interactions; and b), the 1/koff versus f curves estimated from individual unbinding force histograms were qualitatively similar to, but quantitatively different from each other and from the 1/koff versus f curve estimated from the DFS analysis of all histograms (Fig. 2 C). These observations raised questions about the validity of Eq. 3 that was assumed a priori. Additionally, the 1/koff versus f curve was loading-rate sensitive—the larger the rf the smaller the 1/koff, which provided initial evidence for the force history dependence of the off-rate (Fig. 2 C). The loading-rate sensitivity was not a result of a compliant linkage to the adhesive interface, because the loading rates were measured experimentally, which had already accounted for the nearly linear elasticity of the interacting molecules (B. T. Marshall, K. K. Sarangapani, J. Wu, M. B. Lawrence, R. P. McEver, and C. Zhu, unpublished data).
Off-rates derived from bond lifetimes fail to predict measured unbinding forces
Alternatively, we used the force dependence of off-rate determined from the bond lifetime measurements to predict the unbinding forces according to Eq. 2b. The predicted unbinding force distributions differed drastically from those actually measured (Fig. 3 and data not shown for histograms at other loading rates). For the P-selectin-sPSGL-1 interaction, the koff(f) obtained from the bond lifetime data predicted a minimum at ∼15 pN followed by a maximum at ∼50 pN in the unbinding force histogram at a loading rate of 300 pN/s (Fig. 3 A, solid bars). By comparison, the unbinding force histogram directly measured at rf = 300 pN/s had no minimum and peaked at ∼15 pN (Fig. 3 A, open bars). For the P-selectin-G1 interaction, the koff(f) obtained from the bond lifetime data predicted an unbinding force distribution (Fig. 3 B, solid bars) that was shifted rightward toward larger forces relative to the measured distribution (Fig. 3 B, open bars). The peak force moved from ∼20 pN to ∼40 pN in the histogram at rf = 100 pN/s. Thus, although both can be interpreted using the same theoretical framework, which is based on the concept that force modulates the off-rate of receptor-ligand dissociation, the bond lifetime and unbinding force data result in two koff(f) functions that drastically differ not only quantitatively but also qualitatively.
Survival time analysis reveals bond stabilization once ramping stops
One possible explanation for the discrepancy might be that, in the constant-force bond lifetime assay, a weaker, shorter-lived subpopulation of bonds broke during ramping before the desired level of force was achieved. This could select a stronger, longer-lived subpopulation of bonds that survived the force ramping phase for the bond lifetime measurements, resulting in a smaller koff than that estimated from the unbinding force measurements of both subpopulations of bonds. To examine this possibility, we added to the bond lifetime data the previously omitted unbinding events that occurred during the ramping phase and replotted the extended data in survival time histograms. To allow direct comparison, the unbinding force histograms were also converted to survival time histograms.
For P-selectin-sPSGL-1 (Fig. 4 A) or P-selectin-G1 (Fig. 4 B) interactions, the cumulative frequencies from both the bond lifetime and unbinding force assays displayed identical behavior while the bonds were being loaded by a ramp force (solid symbols). Only after the force histories deviated was a difference in the cumulative frequencies evident: curves from the bond lifetime assay (open symbols) increased with survival time less rapidly than that from the unbinding force assay (solid circles). Therefore, the same population of bonds existed in both assays at the point where the force histories diverged. Interestingly, clamping the force at a constant level appeared to stabilize the bonds, resulting in their slower dissociation than that resulted from continuing to ramp up the force at a constant rate. Thus, the differences in the koff(f) obtained from the two assays were caused by the change in force histories, not by the omission of unbinding events during the ramping phase of the bond lifetime assay. Clamping the force at higher and higher levels stabilized the P-selectin-G1 bonds less and less, giving rise to their slip bond characteristic (Fig. 4 B). By contrast, increasing the holding force stabilized the P-selectin-sPSGL-1 bonds initially more and then less, resulting in their catch-slip transitional bond characteristic (Fig. 4 A).
Off-rate as a functional of loading history rather than a function of force
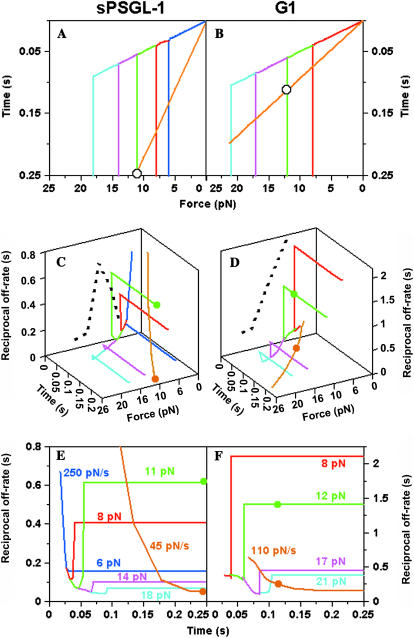
We have established that the history of force application affects the force dependence of off-rate. To directly compare the off-rates determined from different measurements, we calculated koff as a function of survival time along a given force history with our new method (Eq. 5) using the cumulative frequency data without a priori assumptions as to how koff depended on time and/or force. The history of force application was plotted on the f-t (x-y) plane (Fig. 5, A and B), and the reciprocal off-rate (z axis) was shown as a three-dimensional (3D) curve (Fig. 5, C and D). The projection of the koff curve on the f-t plane corresponds to the force history along which the bonds were loaded.
FIGURE 5.
3D 1/koff curves along various loading histories and their projections on the f-t plane and on the t-1/koff plane. (A, C, and E) sPSGL-1 data. (B, D, and F) G1 data. (A and B) Loading paths along which the off-rates were measured are depicted for the constant-rate (straight lines) and constant-force (two-segment lines) histories of force application. Note that the value axes are in reverse order so that they can be easily related to the perspective projections from C and D. (C and D) Reciprocal off-rates (1/koff, z axis) are plotted as 3D curves in space whose projections on the f-t (x-y) plane are the force histories. For the same points on the f-t plane, the 1/koff values could be very different if evaluated along different force histories, as exemplified by the green and orange solid circles in C and D. The dotted lines show the projections on the f-1/koff (x-z) plane of the 3D 1/koff curves measured along the holding portion of the constant-force force histories, which reveal a catch-slip transitional bond in C and a slip bond in D. (E and F) Projections of the 3D 1/koff curves on the t-1/koff (y-z) plane. Only partial data are shown for clarity. For the 1/koff curves determined from the unbinding force data, only those values defined in the same time and force ranges of the bond lifetime data are shown.
In the unbinding force experiment, force histories were represented by straight lines on the f-t plane radiating from the origin, with different slopes representing different loading rates (Fig. 5, A and B). The 1/koff values along different force histories were qualitatively similar in that they decreased monotonically in f and t, displaying typical slip bond characteristics. However, quantitative differences in the 1/koff values among force histories with distinct loading rates were clearly observable for both P-selectin-sPSGL-1 (Fig. 5 C) and P-selectin-G1 (Fig. 5 D) interactions, confirming the results seen in Fig. 2 C. In fact, the f-1/koff (x-z) plane projections of the 3D 1/koff curves along constant-rate force histories (not shown) are identical to the 1/koff versus f curves determined from Eq. 5 (cf. Fig. 2 C), as expected.
In the bond lifetime experiment, force histories were represented by two-line segments on the f-t plane (Fig. 5, A and B): a straight line from the origin (the ramping portion) followed by lines parallel to the t axis (the holding portion). The 1/koff values along the ramping portions were identical to those obtained from an unbinding force experiment performed at the same loading rate. However, the bond lifetime data diverged from the unbinding force data when the force histories turned onto the holding portions. The 1/koff values jumped to higher levels and remained constant, which can be clearly seen from the projections of the 3D 1/koff curves onto the t-1/koff (y-z) plane (Fig. 5, E and F).
By analyzing both unbinding force and bond lifetime experiments in the same framework of survival time, the force dependence of off-rate obtained from the bond lifetime experiment was not biased by exclusion of any data. The different relationships between koff and f were a result of the different force histories. The jumps in the 1/koff values resulted from the corner points in the survival time cumulative frequency curves (cf. Fig. 4), which reflected the stabilization of bonds by stopping the ramping and holding the force constant.
The projection on the f-1/koff (x-z) plane of a 3D 1/koff curve along the holding portion of a constant-force force history was a single point because the off-rate remained the same value for all times when the bonds were held at a constant force. The locus of many such points (dotted curves in Fig. 5, C and D) over a range of forces produced a 1/koff versus f curve. Again, the catch-slip transitional bond was seen for the P-selectin-sPSGL-1 interaction and the slip bond was seen for the P-selectin-G1 interaction, agreeing with the bond lifetime data in Fig. 2 C.
The differences in koff values at the same f (Fig. 2 C) and at the same t (Fig. 5, E and F) indicated that the off-rate was not a function of force or of time only. Closer inspection revealed that koff was not even a single-valued function of the dual variables f and t, but it depended on the entire history of force application to the bond. This force-history dependence was most evident by comparing the 1/koff values at the same endpoint on the f-t plane evaluated along two different histories: a), a constant-rate force history with a low rate (orange lines in Fig. 5, A and B), and b), a high-rate history that ramped until the desired force was reached and then held at a constant force until the desired time was reached (two-segment green lines in Fig. 5, A and B). Even though this endpoint (intersection of the two force histories, indicated by a black open circle in Fig. 5, A and B) was arrived in the same duration of time to the same level of force, the two 1/koff values (orange and green solid circles in Fig. 5, C and D) were clearly very different. The same can be seen in Fig. 5, E and F, where the two distinct pairs of orange and green solid circles are projected on the t-1/koff plane.
DISCUSSION
Substantial discrepancies have been reported in the force dependence of off-rates of selectins dissociating from ligands (Alon et al., 1995, 1997, 1998; Chen and Springer, 2001; Dwir et al., 2001, 2002, 2003; Smith et al., 1999; Ramachandran et al., 1999, 2001; Yago et al., 2002, 2004; Marshall et al., 2003; Sarangapani et al., 2004; Fritz et al., 1998; Evans et al., 2001; Evans and Williams, 2002; Hanley et al., 2003, 2004; Zhang et al., 2004). It has been difficult to identify the causes of these discrepancies because the experiments were performed in different laboratories using different reagents and techniques to measure different quantities that were analyzed differently. Unbinding forces were measured by AFM (Fritz et al., 1998; Hanley et al., 2003, 2004; Zhang et al., 2004) and BFP (Evans et al., 2001; Evans and Williams, 2002) and analyzed by DFS, and bond lifetimes were measured in flow chambers (Alon et al., 1995, 1997, 1998; Chen and Springer, 2001; Dwir et al., 2001, 2002, 2003; Smith et al., 1999; Ramachandran et al., 1999, 2001; Yago et al., 2002, 2004; Marshall et al., 2003; Sarangapani et al., 2004) and by AFM (Marshall et al., 2003; Sarangapani et al., 2004) and analyzed by the ln(No. of events with a lifetime ≥ t) versus t plot. Some authors attributed these discrepancies to the higher force and/or temporal sensitivities of the AFM and BFP techniques than the flow chamber, which might enable the former to detect interactions supported by fewer and/or shorter-lived bonds than the latter (Evans et al., 2001; Hanley et al., 2003). However, our recent bond lifetime measurements with AFM and flow chamber yielded closely matched koff versus f relationships—catch-slip transitional bonds for P- and L-selectins interacting with PSGL-1 and slip bonds for interactions with their respective mAbs (Marshall et al., 2003; Sarangapani et al., 2004)—that reaffirmed the assertion that the intrinsic off-rates for the same molecular interactions should be independent of the experimental techniques used to measure them (Zhu, 2000; Strunz et al., 2000).
In this study, we eliminated most of the potential differences by measuring the unbinding forces and bond lifetimes in the same laboratory with the same reagents and the same AFM instrument; using cantilevers of similar spring constants to contact bilayers prepared the same way with the same approach velocity, contact time, and contact force. The same numbers of bonds must have been formed during the contact phase of the two assays and been detected as such; yet the off-rates estimated from unbinding forces and bond lifetimes were still very different. Although quite surprising at first glance, this unexpected finding, obtained from carefully controlled experiments and analyses, can be rationalized by reexamining the assumptions underlying the analysis by which off-rates are evaluated from the data. It is possible that the kinetic mechanism assumed here—the first-order irreversible unbinding of individual bonds along a single thermodynamic pathway for dissociation as described by Eq. 1—may overly simplify the interactions in question. Were this the case, the koff(f) evaluated from our analysis would have been apparent rather than intrinsic off-rates. Thus, our data suggest that kinetic mechanisms more complex than Eq. 1, which has been assumed in all publications except a recent work (Evans et al., 2004), may be required to describe the dissociation of P-selectin from sPSGL-1 and from G1. Alternatively, the assumption that off-rates were single-valued functions of force only may not be always true. In fact, replacing it with a more general assumption that off-rates can depend on the entire history of force application has reconciled the discrepant koff(f) as reflecting the different types of measurements—bond lifetimes versus unbinding forces—that were made along different force histories.
Since Bell (1978) proposed that force could influence off-rate, koff has only been considered a single-valued function of f (Bell, 1978; Dembo et al., 1988; Evans and Ritchie, 1997; Izrailev et al., 1997). Our data suggest that koff may depend on the entire history of force application rather than the instantaneous value of force, thereby challenging the existing paradigm. The concept of force affecting kinetic rate is based on the idea that work done by the force can be superimposed on the binding potential of the interacting molecules, which tilts the energy landscape, thereby altering the rate of dissociation. Thermodynamically, however, work is a path function rather than a point function—its value depends on the path along which the force is applied rather than on the particular force value at any single point in the path. Although it is valid to add the path-independent conservative work onto the potential energy, this is not the case for the path-dependent dissipative work because it simply represents nonrecoverable losses that are not additive to the potential energy (Izrailev et al., 1997; Balsera et al., 1997). It also seems reasonable that the relative proportions of the conservative and dissipative work should depend on the history of force application, which would then give rise to a force history dependence of the off-rate. Thus, the concept of force-history dependence of off-rate does not contradict but rather generalizes the concept of force dependence of off-rate. Not only is the former more fundamental and realistic than the latter, but the latter can also be reduced from the former as a special case if the force histories are restricted to those of constant-forces only. This generalized concept reconciles the apparent discrepancies in the koff versus f relationships obtained from unbinding force and bond lifetime measurements (this work and Alon et al., 1995, 1997, 1998; Chen and Springer, 2001; Dwir et al., 2001, 2002, 2003; Smith et al., 1999; Ramachandran et al., 1999, 2001; Yago et al., 2002, 2004; Marshall et al., 2003; Sarangapani et al., 2004; Fritz et al., 1998; Evans et al., 2001; Evans and Williams, 2002; Hanley et al., 2003, 2004; Zhang et al., 2004). It further provides a new paradigm for understanding how force regulates biological interactions.
Acknowledgments
We thank V. Moy for providing the AFM design and training.
This work was supported by National Institutes of Health grants AI44902 and HL65631. B.T.M. was a recipient of the Whitaker Foundation Graduate Fellowship.
Bryan T. Marshall's present address is Aderans Research Institute, Atlanta, GA 30332.
References
- Alon, R., D. A. Hammer, and T. A. Springer. 1995. Lifetime of the P-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 374:539–542. [DOI] [PubMed] [Google Scholar]
- Alon, R., S. Chen, R. Fuhlbrigge, K. D. Puri, and T. A. Springer. 1998. The kinetics and shear threshold of transient and rolling interactions of L-selectin with its ligand on leukocytes. Proc. Natl. Acad. Sci. USA. 95:11631–11636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alon, R., S. Chen, K. D. Puri, E. B. Finger, and T. A. Springer. 1997. The kinetics of L-selectin tethers and the mechanics of selectin-mediated rolling. J. Cell Biol. 138:1169–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balsera, M., S. Stepaniants, S. Izrailev, Y. Oono, and K. Schulten. 1997. Reconstructing potential energy functions from simulated force-induced unbinding processes. Biophys. J. 73:1281–1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- Chen, S., and T. A. Springer. 2001. Selectin receptor-ligand bonds: Formation limited by shear rate and dissociation governed by the Bell model. Proc. Natl. Acad. Sci. USA. 98:950–955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dembo, M., D. C. Tourney, K. Saxman, and D. Hammer. 1988. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. Royal Soc. London. 234:55–83. [DOI] [PubMed] [Google Scholar]
- Dwir, O., G. S. Kansas, and R. Alon. 2001. Cytoplasmic anchorage of L-selectin controls leukocyte capture and rolling by increasing the mechanical stability of the selectin tether. J. Cell Biol. 155:145–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dwir, O., A. Solomon, S. Mangan, G. S. Kansas, U. S. Schwarz, and R. Alon. 2003. Avidity enhancement of L-selectin bonds by flow: shear-promoted rotation of leukocytes turn labile bonds into functional tethers. J. Cell Biol. 163:649–659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dwir, O., D. A. Steeber, U. S. Schwarz, R. T. Camphausen, G. S. Kansas, T. F. Tedder, and R. Alon. 2002. L-selectin dimerization enhances tether formation to properly spaced ligand. J. Biol. Chem. 277:21130–21139. [DOI] [PubMed] [Google Scholar]
- Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans, E., A. Leung, D. Hammer, and S. Simon. 2001. Chemically distinct transition states govern rapid dissociation of single L-selectin bonds under force. Proc. Natl. Acad. Sci. USA. 98:3784–3789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans, E. A. 2001. Probing the relation between force-lifetime-and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 30:105–128. [DOI] [PubMed] [Google Scholar]
- Evans, E. A., and P. Williams. 2002. Dynamic force spectroscopy: I. Single bonds. In Physics of Bio-Molecules and Cells. H. Flyvberg, F. Julicher, P. Ormos, and F. David, editors. EDP Sciences, Springer-Verlag, Paris. 145–185.
- Evans, E., A. Leung, V. Heinrich, and C. Zhu. 2004. Mechanical switching and coupling between two pathways for dissociation in the PSGL-1:P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA. 101:11281–11286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz, J., A. G. Katopodis, F. Kolbinger, and D. Anselmetti. 1998. Force-mediated kinetics of single P-selectin/ligand complexes observed by atomic force microscopy. Proc. Natl. Acad. Sci. USA. 95:12283–12288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geng, J.-G., M. P. Bevilacqua, K. L. Moore, T. M. McIntyre, S. M. Prescott, J. M. Kim, G. A. Bliss, G. A. Zimmerman, and R. P. McEver. 1990. Rapid neutrophil adhesion to activated endothelium mediated by GMP-140. Nature. 343:757–760. [DOI] [PubMed] [Google Scholar]
- Hanley, W., O. McCarty, S. Jadhav, Y. Tseng, D. Wirtz, and K. Konstantopoulos. 2003. Single molecule characterization of P-selectin/ligand binding. J. Biol. Chem. 278:10556–10561. [DOI] [PubMed] [Google Scholar]
- Hanley, W., D. Wirtz, and K. Konstantopoulos. 2004. Distinct kinetic and mechanical properties govern selectin-leukocyte interactions. J. Cell Sci. 117:2503–2511. [DOI] [PubMed] [Google Scholar]
- Hummer, G., and A. Szabo. 2003. Kinetics from nonequilibrium single-molecule pulling experiments. Biophys. J. 85:5–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutter, J. L., and J. Bechhoefer. 1993. Calibration of atomic-force microscope tips. Rev. Sci. Instrum. 64:1868–1873. [Google Scholar]
- Izrailev, S., S. Stepaniants, M. Balsera, Y. Oono, and K. Schulten. 1997. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 72:1568–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, F., S. D. Redick, H. P. Erickson, and V. T. Moy. 2003. Force measurements of the α5β1 integrin-fibronectin interaction. Biophys. J. 84:1252–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall, B. T., M. Long, J. W. Piper, T. Yago, R. P. McEver, and C. Zhu. 2003. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 423:190–193. [DOI] [PubMed] [Google Scholar]
- McConnell, H. M., T. H. Watts, R. M. Weis, and A. A. Brian. 1986. Supported planar membranes in studies of cell-cell recognition in the immune system. Biochim. Biophys. Acta. 864:95–106. [DOI] [PubMed] [Google Scholar]
- McEver, R. P. 2001. Adhesive interactions of leukocytes, platelets, and the vessel wall during hemostasis and inflammation. Thromb. Haemost. 86:746–756. [PubMed] [Google Scholar]
- McEver, R. P. 2002. Selectins: lectins that initiate cell adhesion under flow. Curr. Opin. Cell Biol. 14:581–586. [DOI] [PubMed] [Google Scholar]
- Merkel, R., P. Nassoy, A. Leung, K. Ritchie, and E. Evans. 1999. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 397:50–53. [DOI] [PubMed] [Google Scholar]
- Moore, K. L., S. F. Eaton, D. E. Lyons, H. S. Lichenstein, R. D. Cummings, and R. P. McEver. 1994. The P-selectin glycoprotein ligand from human neutrophils displays sialylated, fucosylated, O-linked poly-N-acetyllactosamine. J. Biol. Chem. 269:23318–23327. [PubMed] [Google Scholar]
- Moore, K. L., K. D. Patel, R. E. Bruehl, L. Fugang, D. A. Johnson, H. S. Lichenstein, R. D. Cummings, D. F. Bainton, and R. P. McEver. 1995. P-selectin glycoprotein ligand-1 mediates rolling of human neutrophils on P-selectin. J. Cell Biol. 128:661–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran, V., M. U. Nollert, H. Qiu, W. J. Liu, R. D. Cummings, C. Zhu, and R. P. McEver. 1999. Tyrosine replacement in P-selectin glycoprotein ligand-1 affects distinct kinetic and mechanical properties of bonds with P- and L- selectin. Proc. Natl. Acad. Sci. USA. 96:13771–13776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran, V., T. Yago, T. K. Epperson, M. M. A. Kobzdej, M. U. Nollert, R. D. Cummings, C. Zhu, and R. P. McEver. 2001. Dimerization of a selectin and its ligand stabilizes cell rolling and enhances tether strength in shear flow. Proc. Natl. Acad. Sci. USA. 98:10166–10171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarangapani, K. K., T. Yago, A. G. Klopocki, M. B. Lawrence, C. B. Fieger, S. D. Rosen, R. P. McEver, and C. Zhu. 2004. Low force decelerates L-selectin dissociation from P-selectin glycoprotein ligand-1 and endoglycan. J. Biol. Chem. 279:2291–2298. [DOI] [PubMed] [Google Scholar]
- Simson, D. A., M. Strigl, M. Hohenadel, and R. Merkel. 1999. Statistical breakage of single protein A-IgG bonds reveals crossover from spontaneous to force-induced bond dissociation. Phys. Rev. Lett. 83:652–655. [Google Scholar]
- Smith, M. J., E. L. Berg, and M. B. Lawrence. 1999. A direct comparison of selectin-mediated transient, adhesive events using high temporal resolution. Biophys. J. 77:3371–3383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strunz, T., K. Oroszlan, R. Schafer, and H. J. Guntherodt. 1999. Dynamic force spectroscopy of single DNA molecules. Proc. Natl. Acad. Sci. USA. 96:11277–11282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strunz, T., K. Oroszlan, I. Schumakovitch, H. Guntherodt, and M. Hegner. 2000. Model energy landscapes and the force-induced dissociation of ligand-receptor bonds. Biophys. J. 79:1206–1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tees, D. F., R. E. Waugh, and D. A. Hammer. 2001. A microcantilever device to assess the effect of force on the lifetime of selectin-carbohydrate bonds. Biophys. J. 80:668–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vestweber, D., and J. E. Blanks. 1999. Mechanisms that regulate the function of the selectins and their ligands. Physiol. Rev. 79:181–213. [DOI] [PubMed] [Google Scholar]
- Wong, J. Y., J. Majewski, M. Seitz, C. K. Park, J. N. Israelachvili, and G. S. Smith. 1999. Polymer-cushioned bilayers. I. A structural study of various preparation methods using neutron reflectometry. Biophys. J. 77:1445–1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yago, T., A. Leppänen, H. Qiu, W. D. Marcus, M. U. Nollert, C. Zhu, R. D. Cummings, and R. P. McEver. 2002. Distinct molecular and cellular contributions to stabilizing selectin-mediated rolling under flow. J. Cell Biol. 158:787–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yago, T., J. Wu, C. D. Wey, A. G. Klopocki, C. Zhu, and R. P. McEver. 2004. Catch bonds govern adhesion through L-selectin at threshold shear. J. Cell Biol. 66:913–923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan, C., A. Chen, P. Kolb, and V. T. Moy. 2000. Energy landscape of streptavidin-biotin complexes measured by atomic force microscopy. Biochemistry. 39:10219–10223. [DOI] [PubMed] [Google Scholar]
- Zhang, X., D. F. Bogorin, and V. T. Moy. 2004. Molecular basis of the dynamic strength of the sialyl Lewis X-selectin interaction. Chemphyschem. 5:175–182. [DOI] [PubMed] [Google Scholar]
- Zhang, X., E. Wojcikiewicz, and V. T. Moy. 2002. Force spectroscopy of the leukocyte function-associated antigen-1/intercellular adhesion molecule-1 interaction. Biophys. J. 83:2270–2279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, C. 2000. Kinetics and mechanics of cell adhesion. J. Biomech. 33:23–33. [DOI] [PubMed] [Google Scholar]
- Zhu, C., M. Long, S. E. Chesla, and P. Bongrand. 2002. Measuring receptor/ligand interaction at the single-bond level: experimental and interpretative issues. Ann. Biomed. Eng. 30:305–314. [DOI] [PubMed] [Google Scholar]