Abstract
Given the three-dimensional structure of a protein, its thermodynamic properties are calculated using a recently introduced distance constraint model (DCM) within a mean-field treatment. The DCM is constructed from a free energy decomposition that partitions microscopic interactions into a variety of constraint types, i.e., covalent bonds, salt-bridges, hydrogen-bonds, and torsional-forces, each associated with an enthalpy and entropy contribution. A Gibbs ensemble of accessible microstates is defined by a set of topologically distinct mechanical frameworks generated by perturbing away from the native constraint topology. The total enthalpy of a given framework is calculated as a linear sum of enthalpy components over all constraints present. Total entropy is generally a nonadditive property of free energy decompositions. Here, we calculate total entropy as a linear sum of entropy components over a set of independent constraints determined by a graph algorithm that builds up a mechanical framework one constraint at a time, placing constraints with lower entropy before those with greater entropy. This procedure provides a natural mechanism for enthalpy-entropy compensation. A minimal DCM with five phenomenological parameters is found to capture the essential physics relating thermodynamic response to network rigidity. Moreover, two parameters are fixed by simultaneously fitting to heat capacity curves for histidine binding protein and ubiquitin at five different pH conditions. The three free parameter DCM provides a quantitative characterization of conformational flexibility consistent with thermodynamic stability. It is found that native hydrogen bond topology provides a key signature in governing molecular cooperativity and the folding-unfolding transition.
INTRODUCTION
The stability of a folded protein, its degree of conformational flexibility, and its functional efficiency strongly depend upon thermodynamic environment. The difference in Gibbs free energy between folded and unfolded conformations, ΔG ≡ GF − GU, dictates whether the native fold will be stable. In a two-state model of protein folding, only folded and unfolded states contribute to protein thermodynamics, where ΔG is commonly characterized using three parameters (Kumar and Nussinov, 2001) consisting of the folding-unfolding transition temperature (i.e., melting temperature, Tm), the enthalpy of unfolding, ΔH, and the change in heat capacity upon unfolding, ΔCp. These thermodynamic parameters are obtained by fitting to experimental measurements using differential scanning calorimetry (DSC). The two-state thermodynamic model has the drawback that after parameters are obtained from experiment, prediction of other associated quantities is limited.
Predicting protein thermodynamics is a difficult problem. Multicanonical Monte Carlo (MC) simulations (Okamoto, 1998) and molecular dynamics (MD) simulations in conjunction with replica-exchange sampling (Pitera and Swope, 2003) are among promising all-atom methods. Go-like models can simulate larger proteins (Leonhard et al., 2003) by using phenomenological parameters, but calculations involving 60 residues still require months of massively parallel supercomputing. Ising-like coarse grain statistical mechanical models that account for partial unfolding of the native structure (Hilser and Freire, 1996; Hilser et al., 1998) compromise between computational efficiency and predictive power. These model schemes generate ensembles by perturbing away from the native state topology. Even simpler, are free energy decomposition approaches (Makhatadze and Privalov, 1993) that predict ΔG, ΔH, and ΔS by assuming thermodynamic quantities are additive over component parts, where each part is associated with thermodynamic properties tabulated from model compound transfer measurements (Makhatadze and Privalov, 1993; Hedwig and Hinz, 2003). Although offering virtually instantaneous calculation times, there is a fundamental problem with free energy decompositions. Unlike enthalpies (or energies), component entropies are nonadditive (Mark and van Gunsteren, 1994; Brady and Sharp, 1995; Dill, 1997). Nevertheless, ΔH correlates well with the number of residues and total accessible surface area of the native fold (Robertson and Murphy, 1997).
In this article, protein thermodynamics will be calculated using a distance constraint model (DCM) (Jacobs et al., 2003). The DCM restores the utility of a free energy decomposition by regarding network rigidity as an underlying mechanical interaction. The DCM offers a practical approximation scheme to account for the nonadditivity of component entropies resulting from mechanical correlations between component parts of the decomposition. That is, the forming and breaking of rigid substructures provide an enthalpy-entropy compensation mechanism that governs molecular cooperativity, and gives rise to nucleation effects. These nucleation effects strongly depend on the cross-linking properties of the constraint topology. Exact calculations for the DCM have been successful in predicting thermodynamic properties in polypeptides that exhibit both normal and inverted helix-coil transitions (Jacobs et al., 2003; Jacobs and Wood, 2004). Proteins have rich cross-linking constraint topologies that make exact calculations intractable. Therefore, the DCM is solved here within a mean-field treatment. Heat capacity, stability curves, and a variety of order parameters are calculated. Of particular importance is the global flexibility order parameter, defined as the average number of independent degrees of freedom per residue. Landau free energy functions with respect to the global flexibility order parameter provides a direct means of correlating protein stability to conformational flexibility.
The calculations performed here rely on FIRST (Jacobs et al., 2001) to determine mechanical properties of a given framework. FIRST is an acronym for Floppy Inclusion and Rigid Substructure Topography, which is based on a fast graph algorithm that identifies all rigid clusters, over-constrained regions, flexible regions having correlated motions, and independent constraints. A number of previous reports have used FIRST to understand mechanical stability of protein structure (Jacobs et al., 2001; Hespenheide et al., 2002; Rader et al., 2002; Rader and Bahar, 2004) The main focus of this article is to show how protein stability-flexibility relationships can be quantified by combining free energy decomposition and network rigidity calculations within an ensemble-based approach.
METHODS
Distance constraint model
The DCM is based on two key ingredients. The first is a free energy decomposition where microscopic interactions are partitioned into distinct types. The second, guided by previous work with FIRST (Jacobs et al., 2001), is to represent a variety of short-ranged interaction types as mechanical constraints. The mechanical representation of free energy components is a critical feature in the DCM to overcome the problem of nonadditivity in component entropies. Taken together, a constraint of type t is associated with a partial configuration integral, Qt. When there is no coupling between constraints, the partition function is given by 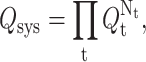 where Nt is the number of constraints of type t present in the system. From the relationship,
where Nt is the number of constraints of type t present in the system. From the relationship, 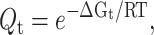 where R is the ideal gas constant and T is absolute temperature, the total free energy with respect to a reference state, is a linear sum given as
where R is the ideal gas constant and T is absolute temperature, the total free energy with respect to a reference state, is a linear sum given as 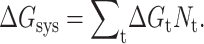 In general, ΔGt will depend on the environment of the constraint, which includes the local conformational state of the protein. In one extreme limit, constraints of the same type are independent of their local surroundings. In the other extreme, variation in local environment breaks all degeneracies, such that each constraint effectively defines a unique type. The labeling of constraint types, with index t, is convenient because it handles all possible model details ranging between these extremes.
In general, ΔGt will depend on the environment of the constraint, which includes the local conformational state of the protein. In one extreme limit, constraints of the same type are independent of their local surroundings. In the other extreme, variation in local environment breaks all degeneracies, such that each constraint effectively defines a unique type. The labeling of constraint types, with index t, is convenient because it handles all possible model details ranging between these extremes.
Constraints of type t are assigned enthalpy and entropy contributions by Gibbs free energy relation ΔGt = ΔHt − TΔSt. Constraints with (large, small) values of ΔSt are said to be (weak, strong) because larger ΔSt implies more phase space is associated with Qt, which is defined through a presumed coarse graining procedure. The DCM accounts for coupling between subsystems (constraints) in terms of generic mechanical properties of a bar-joint framework (constraint topology). The term generic (Jacobs and Thorpe, 1995) implies that all frameworks with the same topological distribution of constraints have the same rigidity properties independent of specific atomic coordinates. Consequently, the DCM is tractable because the rigidity calculations are done using a fast graph algorithm (Jacobs et al., 2001) that scales near linearly with number of atoms. Viewing network rigidity as an underlying mechanical interaction between constraints, total enthalpy and entropy for framework 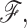 are given by:
are given by:
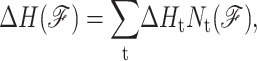 |
(1) |
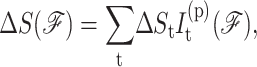 |
(2) |
where 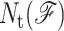 is the number of constraints of type t present in mechanical framework
is the number of constraints of type t present in mechanical framework 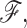 and
and 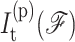 is the corresponding number of independent constraints preferentially determined.
is the corresponding number of independent constraints preferentially determined.
The preferential set of independent constraints is determined by a mathematically well-defined procedure, given by:
Sort all constraints based on entropy assignments in increasing order, thereby ranking them from strongest to weakest.
Add constraints recursively one at a time according to the rank ordering from strongest to weakest, identifying the independent constraints until the entire framework is completely rigid.
Equation 2 gives strong constraints precedence in defining rigid substructures, while regarding weaker constraints within these rigid substructures as fully accommodating. Redundant constraints do not lower conformational entropy. This procedure provides a lowest upper bound estimate for conformational entropy. Taken together, Eqs. 1 and 2 are at the heart of providing an enthalpy-entropy compensation mechanism. Many favorable constraints will lower energy, but their distribution in the network is critical. When many constraints are placed in a local region, then that region becomes overconstrained with redundant constraints. The higher density of favorable constraints lowers energy, but the accompanying decrease in entropy is limited by the loss of conformational freedom associated with the formation of a rigid substructure. Thus, dense pockets of favorable constraints are resistant to thermal fluctuations at low temperatures, but as temperature increases, the entropic penalty drives rigid substructures to spontaneously break apart! Mechanical correlations between constraints give rise to molecular cooperativity, where allostery is associated with the long-range nature of network rigidity (Jacobs and Thorpe, 1995).
The constraint types considered in this work, and their parameterizations are listed in Table 1. The central force and bond-bending forces associated with covalent bonds define the strongest set of distance constraints, and these are considered quenched. Consequently, covalent bond constraints are not explicitly parameterized, because they simply shift the reference free energy while defining a flexible template framework on to which additional weaker constraints are placed. Covalent bonds that remain free to rotate within the template framework are partitioned into nativelike or disordered conformational states. This coarse grain description is analogous to the Lifson-Roig model (Lifson and Roig, 1961) that partitions backbone conformations into helical or coil states. An (energy, entropy) of (v, Rδnat) is assigned when the local conformation is nativelike, otherwise (0, Rδdis). The zero energy is selected for the disordered state without loss of generality.
TABLE 1.
Free energy decomposition scheme
| Type of interaction | ΔH | ΔS |
|---|---|---|
| Covalent bonds | — | — |
| Native torsion | v | Rδnat |
| Disordered torsion | 0 | Rδdis |
| Intramolecular H-bonds | Eenv | 3Rγenv |
| Solvent H-bonds | u | — |
As discussed in the text, covalent bond constraints are not explicitly parameterized, nor is the entropy for the H-bonds between protein and solvent. Parameterization for the intramolecular H-bonds accounts for local environment. All other parameters are assumed independent of local environment.
After prior work (Jacobs et al., 2001), an H-bond is mechanically represented by three distance constraints, while its local environment is taken into account using an empirical energy function (Dahiyat et al., 1997) that gives Eenv depending on atomic geometry of the native three-dimensional structure. Salt bridges are considered special types of H-bonds, where only the radial part of the energy function is used. The maximal entropy of 3Rγenv is assigned to an H-bond when its three distance constraints are independent, each yielding a contribution of Rγenv. Depending on network rigidity, an H-bond can contribute 0, 1, 2, 3 amounts of Rγenv. The entropy parameter, γenv, is specified by assuming γenv is a linear function of Eenv. Over the range between −8 Kcal/mol to 0, the linear relation yields;
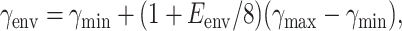 |
(3) |
where γmin and γmax serve as free parameters. Because one entropy parameter can be set arbitrarily, Eq. 3 is simplified by fixing γmin ≡ 0. The justification for Eq. 3 is twofold: i), As energy well depth of an H-bond decreases its curvature is expected to decrease—corresponding to a constraint with greater entropy contribution; and ii), FIRST successfully characterizes H-bond strength in terms of energy; therefore, Eq. 3 is used to preserve relative differences in H-bond strength previously found successful.
The intramolecular hydrogen bond network (HBN) is not static, but consists of many fluctuating cross links within the template framework. In exchange for breaking intramolecular H-bonds, the DCM allows for protein-solvent H-bonding. Protein-solvent H-bonds are parameterized only by energy, u, after prior work on polypeptides (Jacobs et al., 2003; Jacobs and Wood, 2004). The entropy parameter is unspecified because solvent is assumed too mobile to limit conformational flexibility. The minimal DCM has five free-parameters, consisting of two energy parameters {v, u} and three pure entropy parameters {δnat, δdis, γmax}.
Mean-field theory
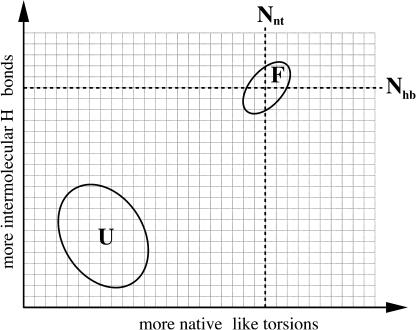
An ensemble based approach similar to that used in COREX (Hilser and Freire, 1996) is employed involving a restricted sample of frameworks that are perturbed away from the known native constraint topology. In COREX the ensemble is generated by partitioning the protein at the residue level into blocks along the sequence where the blocks can be nativelike or unfolded (disordered). Alternate partitions are considered by shifting blocks with an exhaustive enumeration of partially unfolded states. In contrast, the method used here is a hybrid between mean-field Landau theory and MC sampling, which allows free energy landscapes and thermodynamic response functions to be calculated. As shown in Fig. 1, a two-dimensional grid is defined where each node represents a subensemble of frameworks. Each node on the grid specifies an average number of native-torsion constraints and average number of H-bond constraints present. The subensemble of frameworks within a node is characterized by Lagrange multipliers, essentially being chemical potentials that are introduced to control the average number of constraints.
FIGURE 1.
Schematic representation of the free energy landscape in constraint space. Labels (F, U) are for the folded and unfolded free energy basins.
The statistical properties of a subensemble of frameworks within a given node is quantified as a product function of independently distributed probabilities. The mean-field approximation appears through the assumption that the probability for constraint t to be present, given by pt, is independent of all other constraint probabilities. Then the probability for the occurrence of framework, 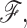 is given by:
is given by:
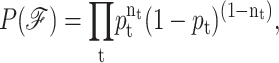 |
(4) |
where nt = (1, 0) when constraint t (is, is not) present, and pt must be determined. The variational function, pt, is selected to model a two-level system defining the situation that the constraint is either present with energy Et, or not present with energy 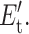 This is mathematically equivalent to a Fermi-Dirac probability distribution given by:
This is mathematically equivalent to a Fermi-Dirac probability distribution given by:
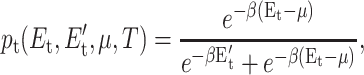 |
(5) |
where chemical potential μ represents either μnt or μhb for native-torsion or H-bond constraints, respectively. The chemical potentials are adjusted to yield average numbers of native-torsion constraints, Nnt, or H-bonds present, Nhb. A node specified by (Nnt, Nhb) defines a macrostate that emerges from a subensemble of frameworks characterized by Eqs. 4 and 5. From Table1, 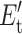 is equal to (0, u) for a (torsion, H-bond) constraint.
is equal to (0, u) for a (torsion, H-bond) constraint.
The next part in carrying out the mean-field approximation involves defining a Landau free energy function for each node, given by:
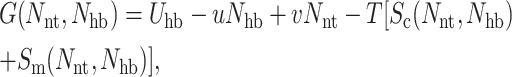 |
(6) |
where Uhb is the average intramolecular H-bond energy, Sc(Nnt, Nhb) is the conformational entropy, and Sm(Nnt, Nhb) is the mixing entropy associated with the number of frameworks in the subensemble consistent with the specified macrostate (Nnt, Nhb). The −uNhb term energetically favors the breaking of intramolecular H-bonds, where u is expected to be a negative energy for protein-solvent interactions. The vNnt term energetically favors the formation of nativelike conformations, as v is expected to be negative. In the extreme case of no native-torsions and no intramolecular H-bonds, the completely disordered template framework defines the zero reference energy. Operationally, Eq. 6 is solved by determining {pt} for specified (Nnt, Nhb) using iterative-numerical methods to find μhb that satisfies 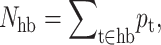 and the probability for a nativelike torsion is simply given as
and the probability for a nativelike torsion is simply given as 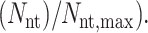 The average intramolecular H-bond energy is calculated as
The average intramolecular H-bond energy is calculated as 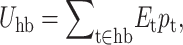 whereas mixing entropy is given by
whereas mixing entropy is given by 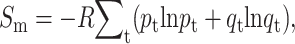 with qt = 1 − pt.
with qt = 1 − pt.
For each framework sampled, the preferential independent constraints are determined via network rigidity calculations as described above. Then at each node
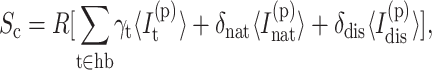 |
(7) |
where 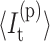 is the average number of independent constraints associated with constraint t. Because of the massive degeneracy in torsion constraint states, they are explicitly labeled as
is the average number of independent constraints associated with constraint t. Because of the massive degeneracy in torsion constraint states, they are explicitly labeled as 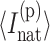 and
and 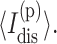 The number of independent constraints self average, requiring as little as 200 realizations (per node) to obtain good estimates. For the entire free energy landscape, a million frameworks are typically sampled per thermodynamic condition to obtain average mechanical properties. For each node the extensive quantity
The number of independent constraints self average, requiring as little as 200 realizations (per node) to obtain good estimates. For the entire free energy landscape, a million frameworks are typically sampled per thermodynamic condition to obtain average mechanical properties. For each node the extensive quantity 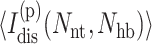 characterizes the global degree of flexibility. To better facilitate comparisons between proteins of different sizes, an intensive measure for the global flexibility of a protein with n residues is defined as
characterizes the global degree of flexibility. To better facilitate comparisons between proteins of different sizes, an intensive measure for the global flexibility of a protein with n residues is defined as
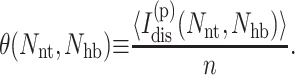 |
(8) |
Many different nodes may have similar degree of flexibility due to trade off between constraint types and their locations. A Landau free energy function is defined as G(θ) = − RT ln Z(θ), where
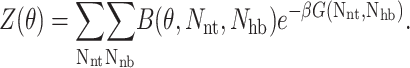 |
(9) |
The binning function B(θ, Nnt, Nhb) is (0,1) if node (Nnt,Nhb) has a degree of flexibility sufficiently close to the specified value θ, where we use 0.01 as a bin size.
Structure preparation and parameter optimization
Ubiquitin (UBQ) (Protein Data Bank (PDB) ID: 1ubq), a common protein that functions as a tag for protein degradation by proteasomes, was selected from the ProTherm Database (Gromiha et al., 1999) because it is small (76 residues), has known x-ray crystal structure (Vijay-Kumar et al., 1987), and DSC measurements (Wintrode et al., 1994) at five different pH conditions ranging between 2 to 4 are available. The histidine binding protein (PDB ID: 1hsl), aiding in periplasmic transport, was selected due to prior experience with it (Huynh, 2002). The histidine binding protein (HBP) is much larger with 238 residues. The x-ray crystal structure for HBP is known (Yao et al., 1994) and DSC measurements give heat capacity curves at pH 8.3 in the apo and bound form (Kreimer et al., 2000). Missing hydrogen atoms within the PDB files are added because the H-bond energy function (Dahiyat et al., 1997) depends on hydrogen atom location. Therefore, single-site titration theory as implemented in UHBD (Madura et al., 1991) is used to calculate the probability for a hydrogen atom to be protonated for specified pH. Hydrogen atoms are (kept, removed) if their probability for protonation is (greater, less) than 50 percent (for technical details, see Livesay et al., 2003; Torrez et al., 2003).
Model parameters are determined by fitting to heat capacity. A baseline is added to account for background contributions and because DSC gives excess heat capacity, making absolute values difficult to ascertain. A common functional form is employed, given by:
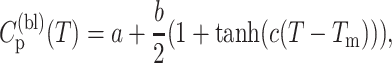 |
(10) |
where Tm is the temperature of maximum heat capacity, and a, b, and c are conditionally optimized. Simulated annealing is used for derivative-free optimization. Generally, when few parameters are used to account for different kinds of interactions (effects), they become nontransferable by compensating each other—leading to multiple good fits. This problem was alleviated by requiring γmax and δdis to be transferable. Six heat capacity curves were fitted to simultaneously (five for UBQ and one for HBP) using ten parameters. Four consisting of {γmax, δdis δnat, v} that were forced to be the same across the dataset, and u was allowed to differ between the six cases. This resulted in γmax = 1.986 and δdis = 2.560 to be determined and fixed. Subsequently {δnat, u, v} are used as free parameters to fit to the heat capacity data of UBQ and HBP. DCM calculations are separately made at different temperatures (with same parameters). Optimization was implemented using LAM-MPI (http://www.lam-mpi.org) on a Beowulf cluster with each CPU running a different temperature.
RESULTS
Heat capacity predictions
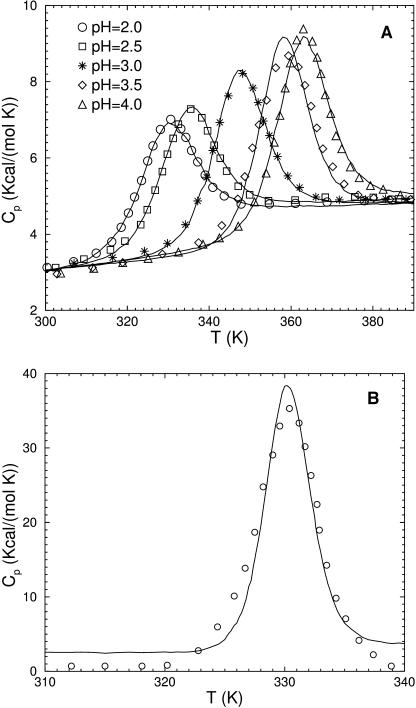
Experimental heat capacity curves with corresponding best fits for UBQ and HBP are shown in Fig. 2. Including baselines the DCM reproduces essential features of heat capacity markedly well. To our knowledge, no other all-atom models, or free energy decomposition schemes have reproduced heat capacity curves to such a degree. It is worth emphasizing that in the minimal DCM, only the HBN provides cross-linking topology that leads to the nonadditivity of entropy during the nucleation of rigid substructures. These results support the suggestion by Cooper (2000) that a major contribution to protein heat capacity appears through an order-disorder phase transition within the HBN. Differences in the transition temperatures defined by the peak in heat capacity are accounted for by the phenomenological DCM parameters that implicitly take into account solvent effects, such as pH conditions. Best fit and corresponding baseline parameters are listed in Table 2 for five different pH values for UBQ, and for four different cases for HBP.
FIGURE 2.
Heat capacity as a function of temperature for (a) UBQ and (b) HBP; solid line, calculated; symbols, measured.
TABLE 2.
Parameters obtained from best-fitting to heat capacity, where Tm locates the peak
| Heat capacity fit | Tm | δnat | u | υ | a | b | c |
|---|---|---|---|---|---|---|---|
| pH 2.0 UBQ | 330.6 | 1.60 | −1.78 | −0.45 | 1.5 | 3.3 | 0.01 |
| pH 2.5 UBQ | 335.5 | 1.60 | −1.78 | −0.48 | 1.6 | 3.4 | 0.01 |
| pH 3.0 UBQ | 348.2 | 1.60 | −1.80 | −0.57 | 1.6 | 3.4 | 0.01 |
| pH 3.5 UBQ | 359.4 | 1.60 | −1.80 | −0.63 | 1.9 | 3.0 | 0.01 |
| pH 4.0 UBQ | 363.0 | 1.60 | −2.02 | −0.83 | 1.5 | 3.9 | 0.01 |
| apo chain A HBP | 330.4 | 1.42 | −2.42 | −0.91 | 0.9 | −1.0 | 0.19 |
| apo chain B HBP | 330.4 | 1.42 | −1.91 | −0.64 | 1.0 | −1.0 | 0.20 |
| HIS bound chain A HBP | 340.3 | 1.24 | −2.49 | −0.94 | 1.0 | 0.0 | 0.0 |
| HIS bound chain B HBP | 340.3 | 1.24 | −2.23 | −0.86 | 1.0 | 0.0 | 0.0 |
The two transferable parameters are: γmax = 1.986 and δdis = 2.560 obtained by simultaneous fitting of five UBQ and chain B-apo form HBP data sets. No interpolating function of pH was found for UBQ.
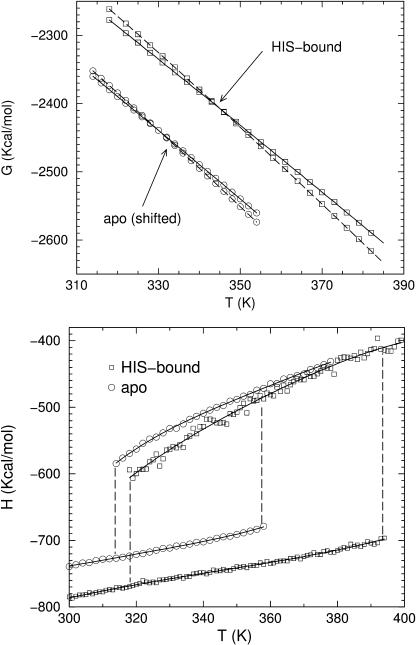
The crystal structure for HBP (Yao et al., 1994) resolved the protein histidine complex as an asymmetric dimer defined by chains A and B. Assuming the biological functioning unit is monomeric (see for example, http://www.rcsb.org/pdb/biounit_tutorial.html) the two chains were processed individually using their respective 3D structures as a native template framework. Although the backbone of each subunit is nearly the same, there are notable differences in the HBN. Chain A has an average H-bond energy of −2.48 Kcal/mol with a total of 342 H-bonds, whereas chain B has an average H-bond energy of −2.27 Kcal/mol with a total of 360 H-bonds. There are 243 H-bonds common to both chains, whereas (99, 117) H-bonds are unique to chain (A, B). Although similar, there are enough differences in the HBN to test the sensitivity of the DCM on input structure. Four cases result by considering each chain in the ligated and apo (achieved by computationally plucking out the histidine) forms. Different δnat values are required to fit to the ligand-bound (holo) and apo forms, and different u, v parameters are required for each case. Except for chain B in apo form (B-apo), fitting was done using the three parameter DCM.
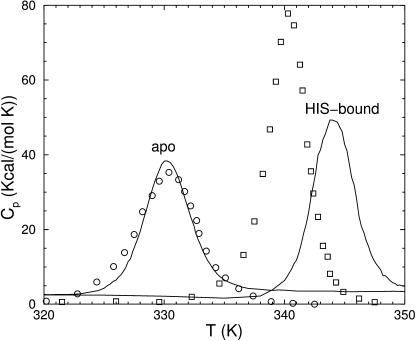
Best fits to heat capacity for all 4 HBP-cases are in acceptable agreement with measurements despite the aforementioned structural variance (see Fig. S1 in supplementary materials). The variance among the four cases of HBP highlights the importance of working with well optimized structures. On the other hand, these results show that the minimal three parameter DCM provides a practical way to directly connect thermodynamic response to structure without being overly dependent on resolution. Notice δnat goes from 1.42 (apo) to 1.24 (ligand-bound) upon the binding of histidine. The smaller δnat indicates a more dramatic nucleation process is taking place, which is consistent with HBP becoming rigidified upon histidine binding. Comparison of measured and predicted heat capacity for HBP in apo and holo forms is shown in Fig. 3, where best-fit parameters for apo-form are used to predict Cp upon substrate binding. The qualitative agreement found with experiment is encouraging, albeit model oversimplifications do reflect in the quantitative results.
FIGURE 3.
Heat capacity for HBP as a function of temperature; circle symbols, measured in apo form; square symbols, measured in holo form; and solid lines, calculated using chain B and best-fit parameters for apo form. Without parameter reoptimization, correct trends are predicted.
Landau free energy and protein stability
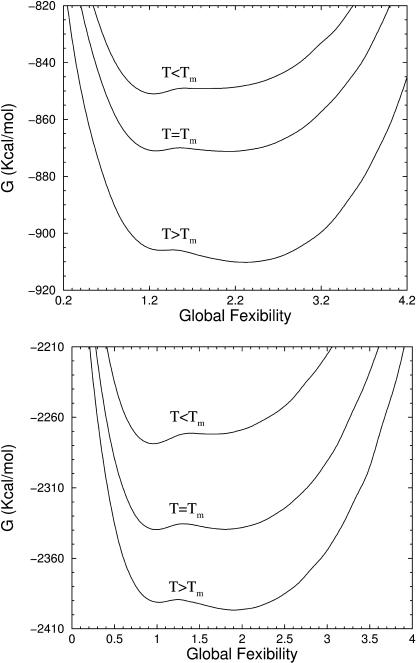
Through the Landau free energy, protein stability and flexibility are directly linked. From the best-fit parameters given in Table 2 the Landau free energy as a function of flexibility order parameter is plotted in Fig. 4 for UBQ and HBP, respectively. The calculated Landau free energies are smoothed with respect to the flexibility order parameter to eliminate extraneous noise appearing from MC sampling. Example of an unsmoothed calculation and its smoothed counterpart is shown in supplemental materials, Fig. S2. The order parameter characterizes global flexibility as the average number of accessible biologically relevant independent degrees of freedom per residue. The shape of the Landau free energy curves is found to be globally stable with two local minimum near the transition temperature. The local minimum of free energy at (low, high) flexibility corresponds to a (native, unfolded) structure. The existence of a double minimum at the transition temperature implies a first order transition (two-state) takes place.
FIGURE 4.
Landau free energy versus flexibility order parameter. (a) UBQ at pH 3.0 for temperatures (339 K, 350 K, 369 K), respectively less than, equal to, and greater than the melting temperature. Near Tm, two minima exist separated by a barrier. At low T, the native state (more rigid) is favored, whereas at high T the flexible disordered state is favored. (b) Landau free energy for HBP versus flexibility order parameter for temperatures (318 K, 330 K, 341 K), respectively less than, equal to, and greater than Tm. Parameters are for chain B apo-form.
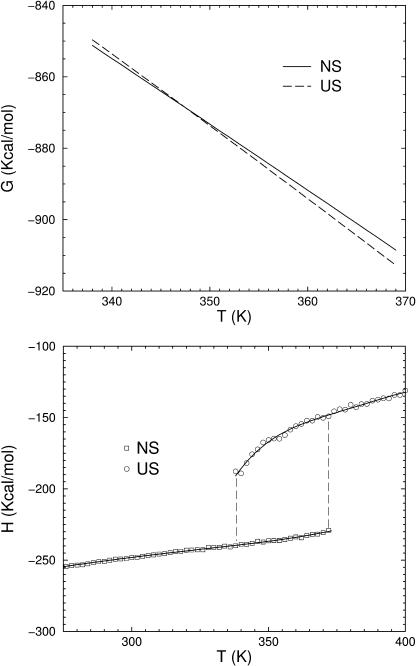
Each minimum in the free energy landscape is a stable (or metastable) phase of constraint topologies that interchange through a structural transition. The free energy basins that encompass the two minimums are labeled as θNS and θUS for the native and unfolded states respectively. Global stability implies protein structure is thermodynamically unstable whenever it becomes extremely rigid or extremely flexible. Thus, the native fold will be intrinsically flexible, whereas the unfolded protein retains some mechanical rigidity. The latter observation implies the unfolded structure is not simply a random coil (i.e., Gaussian chain). Rather, there is less entropic rigidity in exchange for mechanical rigidity associated with a more compact structure. The difference in global flexibility between unfolded and native states at the transition temperature is given by Δθ ≡ θUS − θNS. The flexibility difference was found to be ≈ 3/4 for UBQ implying a release of three degrees of freedom for every four residues upon unfolding. A flexibility difference of ≈ 0.9 for HBP was found. In both proteins these results suggest the unfolded ensemble of conformations retain a substantial number of rigid substructures. Although the ensemble of frameworks is generated by perturbing away from the native state, it is capable of describing the random coil limit. Therefore, it is reasonable to conclude that there are nativelike contacts present in the unfolded ensemble. Furthermore, depending on mechanical stability characterized by the rigidity transition (see below), nativelike substructures may or may not fluctuate via forming and breaking apart.
Small differences of only a few Kcal/mol in free energy are captured on a scale that is typically 8–13 Kcal/(mol residue), as exemplified in the inset of Fig. S2 in supplemental materials. The enthalpy-entropy compensation mechanism provided by network rigidity applies throughout the process of redistributing constraints as conformation changes while maintaining quasistatic thermodynamic equilibrium. The global flexibility order parameter, therefore, characterizes the continuous kinetic path associated with the forming and breaking of constraints. It is natural to assume the free energy barrier reflects folding and unfolding kinetics, where θTS is used to label its location. The barrier height at the transition temperature is found to be sensitive to the parameters. For the best-fit parameters listed in Table 2 the barrier heights for UBQ from pH 2 to pH 4 are respectively calculated to be {0.82, 0.85, 1.07, 1.42, 0.94} Kcal/mol and for HBP chain A the apo and holo forms are found to be 1.64 and 5.87 Kcal/mol. Results for chain B in (apo, holo) form are (4.04, 9.01) Kcal/mol. Furthermore, calculating a flexibility reaction coordinate based on constraint topologies perturbed from the native fold, is consistent with two recent findings: i), Native-state topology is a major determinant for two-state folding rates (Baker, 2000; Gromiha, 2003); and ii), folding pathways have successfully been identified with FIRST by modeling the kinetic process through H-bond dilution starting from the native fold-constraint topology (Hespenheide et al., 2002; Rader et al., 2002). The calculated barrier heights for UBQ (at different pHs) are typically considerably lower than those for HBP, and the barrier for HBP holo form is higher than apo form—all in qualitative agreement with expectations.
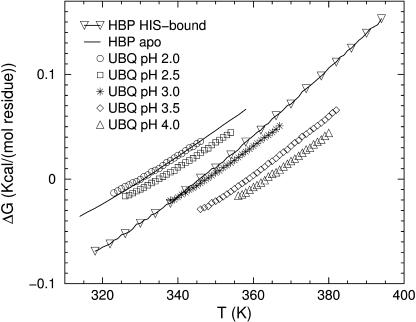
Gibbs free energies and corresponding enthalpies for the folded and unfolded protein are shown in Fig. 5 and Fig. 6 for UBQ (pH 3.0) and HBP, respectively. A dramatic enthalpy-entropy compensation occurs across the transition. Moreover, there is an implication of hysteresis, being a consequence of a first order phase transition. The curves for the folded and unfolded states end at the termination point of coexistence, beyond which it is not possible to be (folded above, unfolded below) the critical end-point temperature. Stability curves are plotted in Fig. 7 showing the change in free energy due to a transition from an unfolded to folded protein. These curves are plotted over a temperature range within the two-phase coexistence. Interestingly, the metastable region for native structure in HBP extends to higher temperatures in holo-form compared to apo-form, whereas the metastable unfolded region is unaffected by the ligand—presumably because the unfolded state does not have the ligand bound.
FIGURE 5.
DCM calculated thermodynamic properties for UBQ (pH 3.0). (Top) The Gibbs' free energy over the range of temperature within the coexistence boundary. (Bottom) Enthalpy for the native (NS) and unfolded (US) states. Solid lines are included to guide the eye.
FIGURE 6.
DCM calculated free energies and enthalpies for HBP in apo and holo forms. (Top) Gibbs' free energy over a temperature range spanning the coexistence boundary. For clarity, the free energy for the native and unfolded states are shifted down by 100 Kcal/mol in the apo form. (Bottom) Enthalpy as a function of temperature. Solid lines are included to guide the eye.
FIGURE 7.
DCM calculated ΔG ≡ GF − GU per residue for HBP for apo and HIS-bound forms and for UBQ at five different pH conditions. The temperature range is limited to where both the native and unfolded states are stable within the coexistence boundary.
Protein flexibility and network rigidity
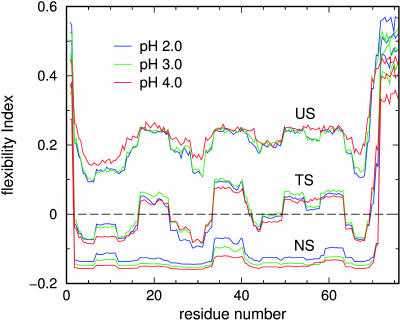
For three distinct states defined by θNS, θTS, and θUS four typical rigid cluster decompositions are shown in Fig. S3 in supplemental materials. These structures are typical realizations of the most probable constraint topologies. The most probable realizations are divided between the native and unfolded states (as shown in Fig. S4 in supplementary materials). At fixed θ, network rigidity properties (clusters of atoms that are found to be mutually rigid or flexible) often appear with regularity, with some variances. To capture characteristic features, a continuous measure, called the flexibility index, is used to quantify the balance and local distribution of independent degrees of freedom and redundant constraints. The flexibility index is a measure used by FIRST (Jacobs et al., 2001) that assigns a weight to rotatable covalent bonds. A density of independent degrees of freedom, ρdof, is defined as the number of independent dof within a flexible region, divided by the number of covalent bonds that can rotate within this region. When a region is overconstrained, a redundant constraint density, ρrdc, is defined as the number of redundant constraints divided by the number of covalent bonds within this region. The last possibility is an isostatic rigid region (ρdof = ρrdc = 0) having the minimal number of constraints to make the region rigid. The flexibility index is the ensemble average of (ρdof − ρrdc).
For UBQ, the conditional flexibility index for the backbone at θNS, θTS, and θUS is shown in Fig. 8 at pH of (2.0, 3.0, 4.0). Backbone flexibility is essentially independent of pH at the respective conditional θ-values, which themselves depend on pH. However, based on G(θ, Tm(pH)) UBQ becomes globally more rigid as pH increases from 2.0 to 4.0, where Tm also increases as pH increases. This result is counter intuitive to the notion that a structure at higher temperatures will be more flexible. However, this intuition can be misleading when comparing two different pH environments. These results suggest side-chain flexibility in UBQ increases as pH is lowered, and this is a plausible explanation for the shifts in Tm as a function of pH.
FIGURE 8.
A comparison of the conditional flexibility index along the backbone for UBQ at pH 2.0, 3.0, and 4.0 calculated at Tm for {θNS, θTS, θUS}. The corresponding θ values at pH 2.0, 3.0, and 4.0 are respectively given as {1.38, 1.66, 2.15}, {1.27, 1.57, 2.04}, and {1.02, 1.29, 1.81}.
Backbone flexibility reflecting thermodynamic equilibrium, calculated in terms of the flexibility index is shown in Fig. 9 on a three-dimensional ribbon-rendering of UBQ for nine distinct cases consisting of pH 2.0, 3.0, and 4.0 at their respective melting temperatures. The coloring gives a qualitative view of the flexibility characteristics. At the respective Tm for each pH, the overall flexibility profile is similar, also observed in Fig. 8. In Fig. 9, the backbone flexibility for HBP in apo and ligand-bound forms are compared. At the same temperature, the apo-form is more flexible than the bound-form. In addition, other flexibility measures can be defined, such as the probability for a covalent bond to rotate (i.e., in a disordered state), which is shown in supplementary materials, Figs. S5 and S6.
FIGURE 9.
DCM predictions for backbone flexibility using the color code to the right for HBP in apo and holo forms, and for UBQ at different pH, temperature conditions.
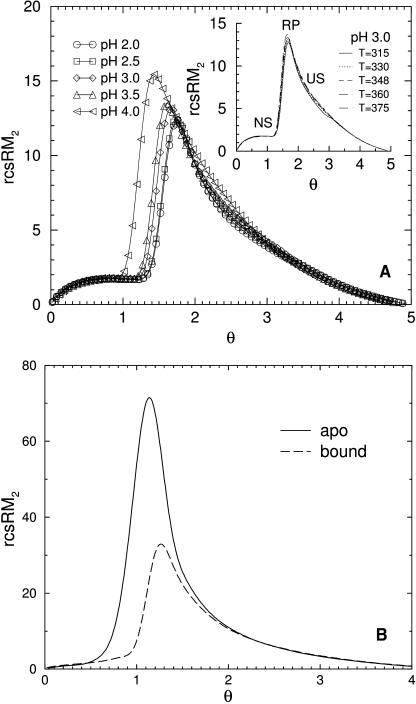
At the transition state for UBQ, Fig. 8 shows the backbone has both flexible and rigid parts. Some local regions fluctuate considerably between flexible and rigid, but on average, the protein is marginally rigid. The degree of rigid cluster size fluctuation is quantified by cluster size statistics as a function of global flexibility order parameter. In Fig. 10 a, the reduced second moment for rigid cluster size is plotted against the global flexibility order parameter. This quantity is referred to as a cluster size susceptibility. The calculation proceeds as a normal second moment over rigid cluster size, except the maximum size is excluded (i.e., reduced). This quantified measure is used in percolation theory to identify a percolation threshold (Stauffer and Aharony, 1994) located at the peak. At the rigidity percolation threshold, denoted as θRP, a system has maximum fluctuation between being globally flexible (with many small rigid clusters) or globally rigid (with some flexible regions and dangling end rotamers). For θ (less, greater) than θRP, the protein is globally (rigid, flexible) with much less fluctuation in rigid cluster size. Cluster size susceptibility is found to be essentially independent of temperature, implying the rigidity transition is driven by constraint topology.
FIGURE 10.
Reduced second moment for rigid cluster size. (a) UBQ at five different pH conditions at their respective Tm. The inset focuses on pH 3.0 for a variety of different temperatures, and the regions in the flexibility order parameter labeled as NS, RP, and US correspond to the native, transition, and unfolded states. (b) HBP in apo- and bound-forms using the respective best-fit parameters.
In the case of UBQ, Fig. 10 a shows that as pH increases the rigidity percolation threshold shifts to lower θ values. For example, θRP = 1.75, 1.67, and 1.43 for pH 2.0, 3.0, and 4.0, respectively. The corresponding values for θNS are {1.38, 1.27, and 1.02}. Therefore, the native state is on the rigid side of the rigidity transition. Recall that the global flexibility order parameter characterizes the net number of independent constraints within a protein, but it does not offer insight into the distribution of rigid clusters. However, looking at the reduced second moment of rigid cluster size helps interpret statistical properties. For example, at θ = 1.67, UBQ (pH 3.0) is at the percolation threshold having greatest fluctuation in cluster size. At pH 4.0 the structure is globally floppy possessing more extended flexible regions that connect many small rigid clusters. At pH 2.0, the opposite is true, where the protein contains a large rigid region possessing only a few small extended flexible regions. Thus, the nature of a rigid cluster decomposition depends on the deviation away from θRP, rather than the value of the global order parameter. As another example, Fig. 10 b shows two rigid cluster susceptibility curves for HBP with a θRP of 1.14 and 1.27 in apo- and bound-forms, respectively. For large θ both curves are nearly identical, presumably because the ligand does not bind at high θ-values. At low θ-values, the bound-ligand substantially reduces rigid cluster fluctuation, as reflected by the lower peak height for the bound-form.
It is found that the rigidity percolation threshold and the transition state are distinctly different. For example, at pH 3.0 for UBQ, θRP = 1.67 whereas θTS = 1.57, and for HBP apo-form θRP = 1.14 whereas θTS = 1.31. It can be seen from these numbers that it is possible to have θRP greater or less than θTS. Presumably, the rigidity transition will have direct affect on kinetics and folding pathways (Rader et al., 2002) controlling the degree to which nativelike substructures fluctuate in the unfolded ensemble. The rigidity transition is a mechanical, not thermodynamic, phenomenon. Deviations between θTS and θRP are in part determined by side-chain entropic effects that are not directly participating in the nucleation of large rigid substructures. At first, we were surprised by this result based on prior work using FIRST by Thorpe and co-workers (Hespenheide et al., 2002; Rader et al., 2002). Therefore, an attempt was made to align the two transitions by augmenting a term in the error function (i.e., (θRP − θTS)2, which proved inadequate. Further supporting evidence for this intrinsic deviation within the minimal three-parameter DCM over a diverse protein dataset was recently reported (Livesay et al., 2004). Although intimately related, mechanical and thermodynamic stability are different quantities. The improbable likelihood that any single parameterization would result in θRP = θTS for all proteins and solvent conditions leads us to make a model independent claim that the locations of the rigidity transition and the transition state are distinctly different.
DISCUSSION
Free energy decomposition schemes
Summation of a free energy decomposition generally fails to accurately predict protein thermodynamic properties because component entropies are nonadditive (Mark and van Gunsteren, 1994; Dill, 1997) over coupled subsystems. The problem appears in protein thermodynamics due to many types of competing weak noncovalent interactions (Dill, 1990), which also include solvent effects. A common strategy is to perform a free energy decomposition using a set of coordinates that partitions a protein into uncoupled subsystems, such as a normal mode analysis. Unfortunately, even restricted to the native state, normal mode analysis fails because a proper description of protein thermodynamics must account for the large ensemble of conformations that are partially unfolded (Pan et al., 2000). One approach that has been demonstrated to be very successful is to expand the free energy decomposition in terms of local geometrical properties of protein structure using accessible solvent surface area (Gómez et al., 1995). An efficient ensemble based approach along these lines has been successfully employed in COREX (Hilser and Freire, 1996; Hilser et al., 1998; Pan et al., 2000).
An alternative approach is to directly account for correlations in entropic components (Brady and Sharp, 1995) that arise because subsystems are coupled. With this perspective, the DCM overcomes the conundrum of nonadditivity of entropy by ascribing both thermodynamic and mechanical properties to component parts of a protein. Correlations are explicitly accounted for by network rigidity, although nonadditivity of entropy is not necessarily an outcome. For the unfolded state additivity in free energy decomposition appears accurate enough to predict heat capacity from sequence (Gómez, et al., 1995; Hedwig and Hinz, 2003). From the perspective of the DCM, these results naturally follow because a low percentage of constraints are found to be redundant in frameworks representing the unfolded ensemble. Nonadditivity in entropy becomes a serious problem only when a substantial fraction of redundant constraints appear. The distribution of where redundant constraints are placed within a given framework (Jacobs et al., 2003) is directly tied to molecular cooperativity. Moreover, an accurate description of protein stability and molecular cooperativity requires an ensemble-based approach (Pan et al., 2000).
In the minimal DCM, torsion constraints do not provide direct cooperative effects because no local correlations are enforced based on backbone Ramachandran plots (Ramachandran et al., 1963) or side-chain rotamer statistics (Koehl and Delarue, 1994). The torsion constraint parameterization also ignores local environment and residue type. The key constraints that reflect local variation in structure is the H-bonds (and salt bridges) because they form cross links in the network and are attune to specificity. The HBN provides an encoded mechanical signature that correlates well with biological function (Jacobs et al., 2001) and folding pathways (Hespenheide et al., 2002; Rader et al., 2002). Hydrophobic interactions and other geometrically nonspecific interactions are lumped together and modeled using effective torsion, v, and H-bond to solvent, u, energy terms.
Improvements on the free energy decomposition scheme to explicitly account for hydrophobic interactions, hydration effects, differences in residues and local environments related to solvent exposed regions, etc., are currently being incorporated. These improvements will affect the stability curves shown in Fig. 7 as additional interactions (physical mechanisms) are explicitly modeled. For example, in prior work (Jacobs and Wood, 2004; Lee et al., 2004) hydration effects are modeled to describe polypeptides undergoing a helix-coil transition in mixed solvent conditions that exhibit both heat and cold denaturation. Although model extensions are currently being developed for proteins, this report firmly establishes the feasibility of simultaneously calculating mechanical and thermodynamic stabilities. The minimal DCM demonstrates a fundamental connection between structure, flexibility, and thermodynamic stability by regarding network rigidity as an underlying interaction.
Mean-field predictions for protein stability and flexibility
The DCM quantifies protein flexibility on long time scales using the same rigidity calculation as FIRST (Jacobs et al., 2001; Hespenheide et al., 2002; Rader et al., 2002; Rader and Bahar, 2004), which is an athermal mechanical model. FIRST is limited to describing mechanical stability of a native fold, presumably valid under conditions where the protein functions. Since constraints modeling noncovalent interactions fluctuate through breaking and forming, it is imperative to sample over different constraint topologies. At the coarse grain level, the DCM resembles an Ising-like model with long-range coupling between the entropic contributions from independent constraints. Conformational sampling over distinct constraint topologies is applied to calculate the partition function. This task is performed within a mean-field approximation combined with perturbing away from the known constraint topology of the native state. It is in this latter aspect that the DCM is similar to COREX (Hilser and Freire, 1996).
The mean-field approximation offers an accurate treatment because of the long-range nature of network rigidity, and the method employed is a hybrid between a mean-field Landau theory and MC sampling. Over the two-dimensional constraint space (see Fig. 1), MC sampling allows the calculation to retain relevant statistical fluctuations. The computational method employed here is ∼1010 times faster than standard molecular dynamics simulations. By constructing a partition function over an ensemble of accessible constraint topologies, the DCM calculates average network rigidity properties consistent with thermodynamic stability—allowing protein stability and flexibility relationships to be directly probed.
In accordance with Landau theory, parameters are expected to be functions of solvent and thermodynamic conditions. For example, for the UBQ heat capacity data in Fig. 2 the u and v parameters were pH dependent. The Landau parameters {v, u, δnat, δdis, γmax} in the minimal DCM have been divided into a transferable set {δdis, γmax} and three free phenomenological parameters that depend on protein architecture and solvent conditions. Of the three pure entropy parameters, δnat significantly reflects protein architecture, whereas γmax reflects the intrinsic property of intramolecular H-bonds. At the level of sophistication in treating all torsion constraints the same, a single global value for δdis is used to characterize a random coil for all proteins. Demanding transferability in {γmax, δdis} helps define a common reference for the degree of conformational flexibility to facilitate quantitative flexibility comparisons between different proteins and solvent conditions.
Operationally, it is important to retain the three nontransferable phenomenological parameters, {δnat, u, v} in the minimal DCM to reflect protein-solvent interactions. Optimizing these parameters using heat capacity data (or other thermodynamic information) allows the minimal DCM to describe stability across a diverse set of proteins under different solvent conditions, account for sequence mutations, and adjust for resolution differences in input structures. The minimal DCM is applied like a three-parameter two-state thermodynamic model is used to fit to heat capacity data. The difference being, is that much more information is predicted involving quantitative relationships between flexibility and stability. The flexibility profiles calculated by DCM have been compared against FIRST and the Gaussian Network Model (GNM) on a diverse set of proteins (Livesay et al., 2004), and it was found that the DCM results were statistically marginally better in correlating to S2-order parameters and B-factors. In addition, all the best-fit parameters obtained to date using the DCM are within physically reasonable ranges. Moreover, if the heat capacity data is arbitrarily rescaled by a factor of 1/2 or 2, the derivative three-parameter DCM often cannot fit to the data, which is an indication that the parameterization is physically based.
To test the sensitivity of the DCM, the best-fit parameters listed in Table 2 were applied to different structures with the following results: using five sets of parameters for UBQ, corresponding to pH from 2 to 4, the average transition temperature ± SD among the five cases were predicted to be (329 ± 15) K and 342 ± 14 K for HBP chain B in the apo and holo forms, respectively. Similarly, for the four different HBP best-fit cases, a prediction of 340K ± 6 K was predicted for UBQ independent of pH. Moreover, as exemplified in Fig. 3 the typical width and height of the heat capacities using transferred parameters were typically within a factor of two. These results are encouraging, showing the parameters are physically based, and despite oversimplifications, the minimum DCM captures the essential features of protein stability and flexibility.
CONCLUSIONS
A free energy decomposition is employed to arrive at a minimal DCM containing five parameters. Two of the parameters that model intramolecular hydrogen bonds are transferable, independent of protein and solvent conditions. Protein size, architecture, and solvent effects are all accounted for through three nontransferable phenomenological parameters within a Landau-like description. Nonadditivity of entropy is directly accounted for by regarding network rigidity as an underlying mechanical interaction that provides an enthalpy-entropy mechanism. Within a novel ensemble-based hybrid mean-field/MC calculation, heat capacity curves are accurately reproduced for ubiquitin at five different pH conditions and histidine binding protein in the apo and holo forms. Without cross-linking hydrogen bonds the minimal DCM has no mechanism to provide any type of cooperative effect. Therefore, the results presented here provide a strong indication that the hydrogen bond network plays an important role in governing protein thermodynamics, flexibility, and molecular cooperativity.
The DCM allows stability and flexibility to both be simultaneously quantified, and stability-flexibility relationships are directly linked through the global flexibility order parameter. It was argued, but remains to be confirmed that the global flexibility order parameter provides a suitable reaction coordinate for governing the progress of protein folding transitions. Under this assumption, the transition state is found to be distinct from the mechanical rigidity percolation threshold. In future work, the prospect of describing protein folding-unfolding kinetics quantitatively is being investigated in conjunction with an improved free energy decomposition scheme to more accurately describe protein stability.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Dennis Livesay and Gregory Wood for many useful discussions.
The authors are grateful for financial support from California State University, Northridge; Research Corporation grant CC5141; and to the National Institutes of Health (S06 GM48680-0952). Generic rigidity algorithm is claimed in US Patent No. 6,014,449, which has been assigned to the Board of Trustees, Michigan State University. Used with permission.
References
- Baker, D. 2000. A surprising simplicity to protein folding. Nature. 405:39–42. [DOI] [PubMed] [Google Scholar]
- Brady, G. P., and K. A. Sharp. 1995. Decomposition of interaction free energies in proteins and other complex systems. J. Mol. Biol. 254:77–85. [DOI] [PubMed] [Google Scholar]
- Cooper, A. 2000. Heat capacity of hydrogen-bonded networks: an alternative view of protein folding thermodynamics. Biophys. Chem. 85:25–39. [DOI] [PubMed] [Google Scholar]
- Dahiyat, B. I., D. B. Gordon, and S. L. Mayo. 1997. Automated design of the surface positions of protein helices. Protein Sci. 6:1333–1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dill, K. A. 1990. Dominant forces in protein folding. Biochemistry. 29:7133–7155. [DOI] [PubMed] [Google Scholar]
- Dill, K. A. 1997. Additivity principles in biochemistry. J. Biol. Chem. 272:701–704. [DOI] [PubMed] [Google Scholar]
- Gómez, J., V. J. Hilser, D. Xie, and E. Freire. 1995. The heat capacity of proteins. Proteins. 22:404–412. [DOI] [PubMed] [Google Scholar]
- Gromiha, M. M. 2003. Importance of native-state topology for determining the folding rate of two-state proteins. J. Chem. Inf. Comput. Sci. 43:1481–1485. [DOI] [PubMed] [Google Scholar]
- Gromiha, M. M., J. An, H. Kono, M. Oobatake, H. Uedaira, and A. Sarai. 1999. ProTherm: thermodynamic database for proteins and mutants. Nucleic Acids Res. 27:286–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedwig, G. R., and H. J. Hinz. 2003. Group additivity schemes for the calculation of the partial molar heat capacities and volumes of unfolded proteins in aqueous solution. Biophys. Chem. 100:239–260. [DOI] [PubMed] [Google Scholar]
- Hespenheide, B. M., A. J. Rader, M. F. Thorpe, and L. A. Kuhn. 2002. Identifying protein folding cores from the evolution of flexible regions during unfolding. J. Mol. Graph. Model. 21:195–207. [DOI] [PubMed] [Google Scholar]
- Hilser, V. J., D. Dowdy, T. G. Oas, and E. Freire. 1998. The structural distribution of cooperative interactions in proteins: Analysis of the native state ensemble. Proc. Natl. Acad. Sci. USA. 95:9903–9908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilser, V. J., and E. Freire. 1996. Structure-based calculation of the equilibrium folding pathway of proteins. Correlation with hydrogen exchange protection factors. J. Mol. Biol. 262:756–772. [DOI] [PubMed] [Google Scholar]
- Huynh, D. H. 2002. Comparison of conformational flexibility in proteins exhibiting hinge-bending motions. Master's thesis. California State University, Northridge, CA.
- Jacobs, D. J., and M. F. Thorpe. 1995. Generic rigidity percolation: the pebble game. Phys. Rev. Lett. 75:4051–4054. [DOI] [PubMed] [Google Scholar]
- Jacobs, D. J., S. Dallakyan, G. G. Wood, and A. Heckathorne. 2003. Network rigidity at finite temperature: Relationships between thermodynamic stability, the nonadditivity of entropy, and cooperativity in molecular systems. Phys. Rev. E. 68:061109–061122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs, D. J., A. Rader, L. A. Kuhn, and M. F. Thorpe. 2001. Graph theory predictions of protein flexibility. Proteins. 44:150–155. [DOI] [PubMed] [Google Scholar]
- Jacobs, D. J., and G. G. Wood. 2004. Understanding the alpha-helix to coil transition in polypeptides using network rigidity: predicting heat and cold denaturation in mixed solvent conditions. Biopolymers. 75:1–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehl, P., and M. Delarue. 1994. Application of a self-consistent mean field theory to predict protein side-chains conformation and estimate their conformational entropy. J. Mol. Biol. 239:249–275. [DOI] [PubMed] [Google Scholar]
- Kreimer, D. I., H. Malak, J. R. Lakowicz, S. Trakhanov, E. Villar, and V. L. Shnyrov. 2000. Thermodynamics and dynamics of histidine-binding protein, the water-soluble receptor of histidine permease. Implications for the transport of high and low affinity ligands. Eur. J. Biochem. 267:4242–4252. [DOI] [PubMed] [Google Scholar]
- Kumar, S., and R. Nussinov. 2001. How do thermophilic proteins deal with heat? Cell. Mol. Life Sci. 58:1216–1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, M. S., G. G. Wood, and D. J. Jacobs. 2004. Investigations on the alpha-helix to coil transition in HP heterogeneous polypeptides using network rigidity. J. Phys.: Condens. Matter. 16:S5035–S5046. [Google Scholar]
- Leonhard, K., J. M. Prausnitz, and C. J. Radke. 2003. 3D-lattice Monte Carlo simulations of model proteins. Size effects on folding thermodynamics and kinetics. Biophys. Chem. 106:81–89. [DOI] [PubMed] [Google Scholar]
- Lifson, S., and A. Roig. 1961. On the helix-coil transition in polypeptides. J. Chem. Phys. 34:1963–1974. [Google Scholar]
- Livesay, D. R., S. Dallakyan, G. G. Wood, and D. J. Jacobs. 2004. A flexible approach for understanding protein stability. FEBS Lett. 576:468–476. [DOI] [PubMed] [Google Scholar]
- Livesay, D. R., P. Jambeck, A. Rojnuckarin, and S. Subramaniam. 2003. Conservation of electrostatic properties within enzyme families and superfamilies. Biochemistry. 42:3464–3473. [DOI] [PubMed] [Google Scholar]
- Madura, J. D., J. M. Briggs, R. C. Wade, M. E. Davis, B. A. Luty, A. Ilin, J. Antosiewicz, M. K. Gilson, B. Bagheri, L. R. Scott, and J. A. McCammon. 1991. Electrostatic and diffusion of molecules in solution: simulations with the University of Houston Brownian Dynamics program. Comp. Phys. Comm. 28:235–242. [Google Scholar]
- Makhatadze, G. I., and P. L. Privalov. 1993. Contribution of hydration to protein folding thermodynamics. I. The enthalpy of hydration. J. Mol. Biol. 232:639–659. [DOI] [PubMed] [Google Scholar]
- Mark, A. E., and W. F. van Gunsteren. 1994. Decomposition of the free energy of a system in terms of specific interactions. Implications for theoretical and experimental studies. J. Mol. Biol. 240:167–176. [DOI] [PubMed] [Google Scholar]
- Okamoto, Y. 1998. Protein folding problem as studied by new simulation algorithms. Rec. Res. Dev. Pure & Appl. Chem. 2:1–23. [Google Scholar]
- Pan, H., J. C. Lee, and V. J. Hilser. 2000. Binding sites in Escherichia coli dihydrofolate reductase communicate by modulating the conformational ensemble. Proc. Natl. Acad. Sci. USA. 97:12020–12025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitera, J. D., and W. Swope. 2003. Understanding folding and design: replica-exchange simulations of “Trp-cage” miniproteins. Proc. Natl. Acad. Sci. USA. 100:7587–7592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rader, A. J., and I. Bahar. 2004. Folding core predictions from network models of proteins. Polymer. 45:659–668. [Google Scholar]
- Rader, A. J., B. M. Hespenheide, L. A. Kuhn, and M. F. Thorpe. 2002. Protein unfolding: rigidity lost. Proc. Natl. Acad. Sci. USA. 99:3540–3545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran, G. N., C. Ramakrishnan, and V. Sasisekharan. 1963. Stereochemistry of polypeptide chain configurations. J. Mol. Biol. 7:95–99. [DOI] [PubMed] [Google Scholar]
- Robertson, A. D., and K. P. Murphy. 1997. Protein structure and the energetics of protein stability. Chem. Rev. 97:1251–1267. [DOI] [PubMed] [Google Scholar]
- Stauffer, D., and A. Aharony. 1994. Introduction to Percolation Theory, 2nd ed. Taylor & Francis, London.
- Torrez, M., M. Schultehenrich, and D. R. Livesay. 2003. Conferring thermostability to mesophilic proteins through optimized electrostatic surfaces. Biophys. J. 85:2845–2853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vijay-Kumar, S., C. E. Bugg, and W. J. Cook. 1987. Structure of ubiquitin refined at 1.8 A resolution. J. Mol. Biol. 194:531–544. [DOI] [PubMed] [Google Scholar]
- Wintrode, P. L., G. I. Makhatadze, and P. L. Privalov. 1994. Thermodynamics of ubiquitin unfolding. Proteins. 18:246–253. [DOI] [PubMed] [Google Scholar]
- Yao, N., S. Trakhanov, and F. A. Quiocho. 1994. Refined 1.89-A structure of the histidine-binding protein complexed with histidine and its relationship with many other active transport/chemosensory proteins. Biochemistry. 33:4769–4779. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.