Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Dec 30;88(3):1684–1691. doi: 10.1529/biophysj.104.046912

Molecular Dynamics Simulations of Duplex Stretching Reveal the Importance of Entropy in Determining the Biomechanical Properties of DNA

Sarah A Harris *, Zara A Sands †, Charles A Laughton †
PMCID: PMC1305225  PMID: 15626714

Abstract

Advances in nanomanipulation techniques have made it possible to measure the response of an individual biomolecule to a force applied in the laboratory. Experiments that stretch a single molecule of duplex DNA have been difficult to interpret theoretically, particularly as the major changes in molecular structure caused by the force cannot be measured. In principle, computer simulation can calculate these conformational changes in atomic level detail, but to date such studies have failed to reproduce the experimental data due to the computational expense of the calculations. Here we show that a combination of molecular modeling and statistical physics can be used successfully to understand the stretching behavior of DNA. Our simulations provide new information about the dynamics of DNA denaturation under force in atomic level detail and also show the importance of entropy in determining biomechanical properties in general.

INTRODUCTION

Single molecule manipulation techniques have provided a wealth of new information about the mechanical properties of both nucleic acids and proteins. Atomic force microscopy (AFM) and optical/magnetic tweezers have been widely used to either stretch a biomolecule or unbind a macromolecular complex (Lavery et al., 2002; Strick et al., 2003). These techniques characterize biomechanical properties by measuring the force required to produce a given molecular extension. Similarly, many of the enzymes responsible for processing DNA in the cell are molecular motors capable of transforming chemical energy into a mechanical force that may stretch, twist, or unzip the double helix. Biological motors and single molecule manipulation experiments both perform work on an energy scale which is comparable to the thermal energy, kT (where k is Boltzmann's constant and T is the temperature). A poor understanding of the mechanics of single molecules under these conditions has limited the insight that force-extension measurements have provided into biological thermodynamics. The complexity of biological macromolecules has meant that computer simulation has played an important role in understanding the response of both proteins and nucleic acids to an applied force, particularly at the atomic level (Lavery et al., 2002). However, a process that takes place experimentally over 1μs-1ms must be compressed in the simulation into a time frame of order 10 ns due to the computational expense of large-scale molecular dynamics (MD) simulations such as these. A fully quantitative agreement between simulation and experiments has therefore proved elusive, primarily due to this large disparity in timescales accessible by simulations and in the laboratory (Balsera et al., 1997; Gullingsrud et al., 1999). Simulations which are able to access longer timescales using coarse-grained representations of proteins have so far obtained better agreement with experimental data, but do not provide the same level of structural detail as atomistic MD (Klimov and Thirumalai, 2000).

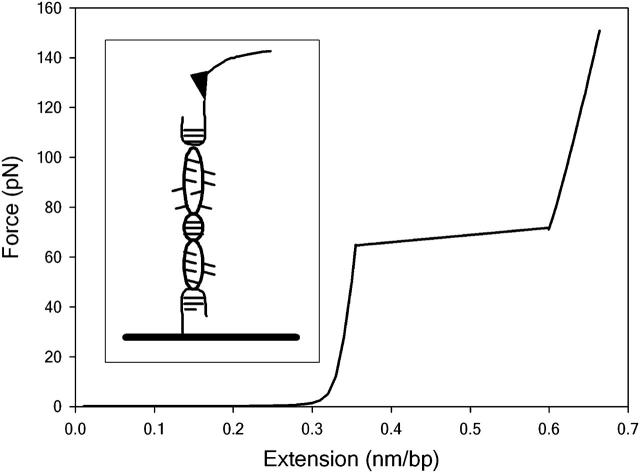
Force-distance measurements on very long (polymeric) DNA sequences observe a characteristic plateau at 65 pN when there is an abrupt extension before the duplex unbinds at forces of ∼150 pN (Clausen-Schaumann et al., 2000; Rief et al., 1999; Fig. 1). However, this plateau is not seen experimentally if the DNA contains <30 basepairs, as short DNA sequences dissociate at considerably lower forces (∼30 pN for a dodecamer; Pope et al., 2001; Strunz et al., 1999). Several steered MD simulations have attempted to mimic the AFM experiment by applying a steadily increasing force to stretch a 12-basepair helix but at vastly elevated pulling rates relative to those accessible in the laboratory (Konrad and Bolonick, 1996; MacKerell and Lee, 1999). These modeling studies obtain (incorrect) force-extension curves containing the plateau only observed experimentally for long DNA polymers. In the simulations, this plateau results from a major conformational change from the canonical B-form DNA usually present in solution to a novel extended configuration known as S-ladder DNA due to the highly untwisted, ladder-like structure of the stretched DNA duplex. Qualitatively similar behavior has also been observed by simulations which calculate the force indirectly from conformational energy changes as the DNA is placed under tension (Kosikov et al., 1999; Lavery and Lebrun, 1999; Lebrun and Lavery, 1996). Understandably, the term “B-S transition” is now commonly used to describe the plateau seen in the experimental force-extension curves of long DNA sequences, based on the assumption that it results from the same conformational change as suggested by simulation.

FIGURE 1.

FIGURE 1

Open in a new tab

A typical force-distance curve for polymeric DNA. Stretching curves were calculated using Eqs. 5 and 12 in Rouzina and Bloomfield (2001a). The flat region of the force-distance curve at 65 pN is commonly known as the B-S plateau. The DNA unbinds at forces of ∼150 pN (depending upon experimental details such as the pulling rate). The inset shows a schematic representation of a DNA molecule stretched between a surface and an AFM cantilever.

However, this assumption has remained the subject of some debate. As the DNA is stretched, it should become thermodynamically unstable and unbind as soon as the reversible work performed by the external force becomes equal to the free energy holding the two strands together. Comparing the binding free energy of duplex DNA (known from conventional thermal melting studies) with the work done by the applied force (obtained by integrating under the force-distance curves) indicates that the helix should melt at forces of ∼65 pN, precisely where the force-plateau is located (Rouzina and Bloomfield, 2001a,b; Williams et al., 2001, 2002). The experimental observation that higher forces are generally required to unbind the duplex than predicted by equilibrium thermodynamics is to be expected, since the experiment does not take place sufficiently slowly to be reversible. This alternative interpretation implies that the plateau signifies a force-induced melting (or overstretching) transition, rather than the B-S conformational change suggested by modeling studies. Such difficulties in interpreting what is arguably the best characterized feature in force-extension measurements to date clearly illustrates the need for a better theoretical understanding of single molecule manipulation experiments in general.

The force-extension behavior of the helix depends on the change in free energy as the molecule is extended, therefore both energetic and entropic terms must be taken into account. Entropic quantities are notoriously difficult to obtain using computer simulation. Therefore, although the energetic changes that accompany DNA stretching have already been calculated (Konrad and Bolonick, 1996;Kosikov et al., 1999; Lavery and Lebrun, 1999; Lebrun and Lavery, 1996; MacKerell and Lee, 1999), considerably less attention has been paid to any dynamic changes that might also occur. We have previously described new methods for extracting the configurational entropy of DNA from MD simulation trajectories using a predictive physical model (Harris et al., 2001). In this study, we have applied these techniques to calculate the configurational entropy change as the DNA molecule is extended. In addition to a conventional steered MD calculation, we have also performed a series of novel MD simulations of a DNA dodecamer at 10 different elongations. The stretched DNA molecules are pinned by harmonic restraints that prevent the molecule from relaxing back to its B-form configuration. This approach, based on thermodynamic arguments, enables us to go some way toward bridging the timescale gap between experiment and simulation and provides quantitative results that are in far better agreement with the laboratory data. This study also sheds some light on the debate about the nature of the B-S transition, and more generally shows the importance of including thermal fluctuations (and hence entropic effects) in the description of mechanical behavior at the molecular level.

METHODS

Simulation setup

All MD simulations were performed with the AMBER 5.1 and AMBER 6 suite of programs (Case et al., 1999). The AMBER-94 force field was used to describe the DNA duplex d(CGCAAAAAAGCG)2 with the TIP3P water model representing the surrounding solvent. Initial coordinates were obtained from the x-ray crystal structure for this sequence (Nelson et al., 1987). The steered MD simulation must stretch the DNA along the helix axis to more than twice its original length. Therefore, an elongated rectangular periodic box containing 12,652 water molecules was required to ensure that the extended structures expected at the end of the simulation are surrounded by at least 8 Å of solvent in each orthogonal direction. The system was then electrically neutralized by the addition of 22 sodium counterions.

Steered molecular dynamics

MD simulations used the fast particle mesh Ewald method to calculate the long-range electrostatic interactions. Constraint of all covalent bonds with SHAKE allowed an integration time step of 2 fs to be used in conjunction with the Verlet integration algorithm (subsequent tests (not shown) revealed that simulations in which SHAKE was only used on bonds to hydrogen did not show significantly modified dynamical behavior). MD was performed at a constant temperature (298 K) and pressure (1 atm). The system was thermalized and equilibrated for 1 ns using a standard multistage protocol (Shields et al., 1997). During the 1.6 ns steered MD run, the DNA was forced to extend from a length of ∼4 0 Å–110 Å by the application of strict restraints to the 5′-terminus of each strand of the molecule. This restraint consisted of a parabolic well with an associated force constant of 100 kcal/mol/Å2. The DNA molecule was stretched by increasing the distance between the two restrained atoms by 1 Å followed by an intervening 10 ps relaxation period. The new positions of these atoms were maintained by the high energetic penalties associated with a deviation from this set value.

‘Pinned’ simulations

Configurations of the DNA sampled from various points along the steered dynamics trajectory were then used as the starting points for nine additional MD simulations of the DNA at various extensions. These were solvated and electrically neutralized, as described above, but without the requirement for the extended box dimension along the helix axis. The appropriate harmonic restraints were used to maintain the molecule in an elongated configuration. These restrained structures were then subject to the standard 1 ns solvent and counterion equilibriation protocols before the 4 ns data production phase. In addition, a conventional 4 ns MD run was also performed on this sequence beginning from the crystal structure to be used as the thermodynamic reference state for comparison with distorted DNA structures.

Energetic analysis

The internal energy change on stretching the molecule and the energies of the restrained simulation were calculated using the MD implementation of the generalized Born/surface area (GB/SA) implicit solvation method developed by Case and co-workers (Tsui and Case, 2000) based on the trajectories obtained using explicit solvent. For comparison with the results obtained by previous simulation studies, a theoretical force-distance curve was calculated from the steered MD simulation. An eighth order polynomial fit was used to describe the change in GB/SA energy as a function of extension (shown in Fig. 2), the force-distance curve could then be obtained by differentiating with respect to the extension. Finally, configurational entropies for each of the ten 4 ns simulations were computed by diagonalization of the Cartesian coordinate covariance matrix following the method described by Schlitter (1993). The procedure has been extensively tested in protein systems by Schafer et al. (2000, 2001), and for DNA by Harris et al. (2001). As previously described, the calculated entropies (S) are dependent on the length (t) of the trajectory that is analyzed, but clearly tend to a limit (S∞) as the width of the sampling window is increased. The entropies calculated for a range of window widths are fitted using the empirical relationship (Harris et al., 2001)

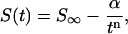graphic file with name M1.gif (1)

where α and n are fitting parameters. This procedure allows for an estimate of S∞ that is independent of the length of the MD simulation. Hydration density maps were also produced by integrating over the equilibrated portions of each trajectory using the methods described previously (Shields et al., 1997; Soliva et al., 2000). The results are presented in the supplemental information.

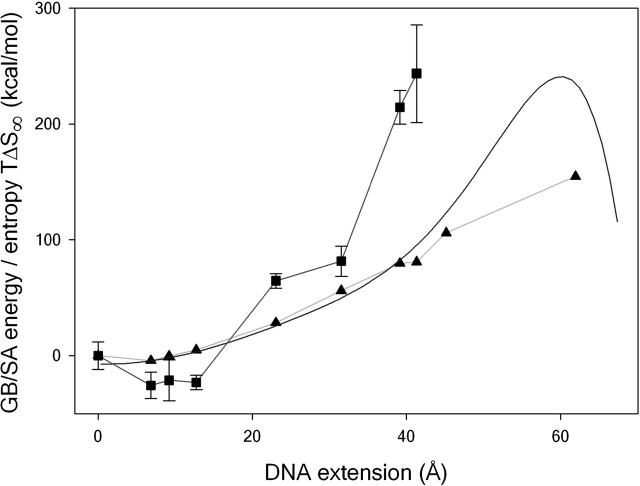
FIGURE 2.

FIGURE 2

Open in a new tab

Thermodynamic changes as the DNA is stretched. The change in GB/SA energy as a function of extension, calculated from the steered MD simulation (smooth curve) and from the restrained simulations (triangles). The change in entropy TΔS∞, calculated from the restrained simulations, is shown for comparison (squares). Error bars are calculated using the standard deviation of ΔS∞ values obtained from increasing simulation window widths, as previously described (Harris et al., 2001).

RESULTS AND DISCUSSION

Thermodynamic analysis

The experimental observations for short DNA sequences can be interpreted using a model which describes unbinding as thermal activation over a single free energy barrier. In this regime, the unbinding force is correlated with the spontaneous dissociation rate of the complex, rather than the equilibrium binding free energy (Schwesinger et al., 2000). The applied force lowers the activation free energy separating bound and unbound states so that the top of the barrier becomes thermally accessible during the experiment (Evans, 2001; Tinoco and Bustamante, 2002). The two strands then disassociate due to a relatively rare, high-energy fluctuation. This process occurs sufficiently slowly for the system to remain in quasi-equilibrium throughout the unbinding. If the force on the DNA increases at a constant rate R, the most probable force required to unbind the duplex will be given by (Strunz et al., 1999, 2000)

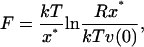graphic file with name M2.gif (2)

where ν(0) is the thermal dissociation rate of the molecule (i.e., when the applied force is zero) which can be extracted from the unbinding experiments by extrapolation (Strunz et al., 1999). The thermal lifetimes obtained by unbinding a DNA duplex with AFM compare well with those obtained using bulk temperature jump measurements, suggesting that these two disassociation processes may follow similar pathways across a common transition state. The position of the transition state x* denotes the DNA extension when the helix disassociates into two single strands (when the molecule is subjected to a ramp of force, the experiment continues until the maximum in the free energy barrier is reached). A theoretical value for the force required to unbind the DNA duplex at experimental pulling rates can therefore be calculated using Eq. 2 if the free energy barrier separating bound and unbound states (and hence x*) can be obtained through simulation. Equation 2 shows that the position of the transition state is the fundamental, time independent quantity which can be directly compared in the simulation and the experiment. The Gibbs free energy change that accompanies DNA stretching (assuming all volume changes are negligible) can be written as (Harris et al., 2001):

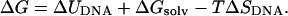graphic file with name M3.gif (3)

The first term is the internal energy change of the DNA as it is stretched. The second term is the change in free energy of solvation of the DNA that accompanies elongation, which includes both energetic and entropic terms related to the reorganization of the solvent (water and counterions). The third term is the change in the configurational entropy of the solute. By analyzing the trajectories using the GB/SA implicit hydration model (Srinivasan et al., 1988; Tsui and Case, 2000), it is possible to compute (ΔUDNA + ΔGsolv; the energetic contribution including a solvation correction) from both the simulations in which the DNA is continuously stretched (given by the smooth curve in Fig. 2) and also the discrete simulations in which elongated configurations are pinned harmonically to hold them at a given length (shown by the triangles and light blue curve in Fig. 2). Surprisingly, the improved equilibration procedure used in the discrete simulations only results in significantly lower GB/SA energies for the most extreme extensions (>40 Å), despite the rapid pulling rate used in the steered MD simulation.

Predictions from steered MD data alone

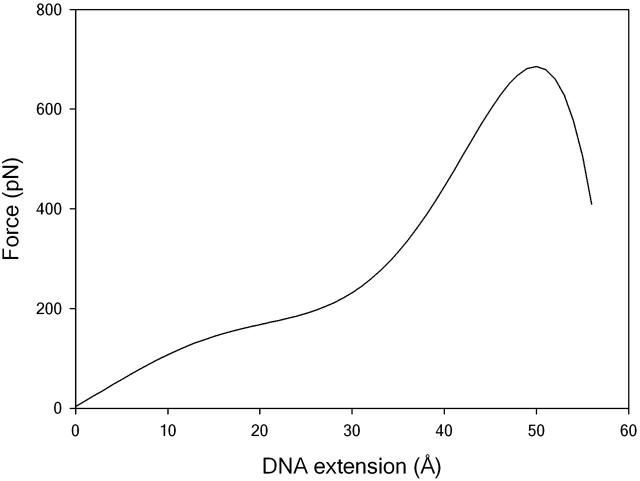
For comparison with earlier modeling studies, we have used the steered MD simulation to calculate a theoretical force-extension curve in which only the energetic contribution 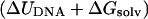Inline graphic is included, as shown in Fig. 3. The DNA becomes mechanically unstable at the transition state (where the GB/SA energy reaches its maximum value). In agreement with previous simulation studies (Konrad and Bolonick, 1996; Kosikov et al., 1999; Lavery and Lebrun, 1999; Lebrun and Lavery, 1996; MacKerell and Lee, 1999), we find that the duplex does not unbind until extensions of ∼50 Å, far higher than those seen experimentally for oligomeric sequences such as this (Pope et al., 2001; Strunz et al., 1999). As previously observed, the theoretical force-extension curves contain a distinctive plateau at an extension of 25 Å only observed in experiments that stretch polymeric DNA. Inspecting the structures before and after this plateau shows that a structural transition has taken place during which the base stacking interactions have switched from being intrastrand (as in B-DNA) to interstrand (as in S-DNA). An example of the S-ladder structures obtained is shown in Fig. 4 (bottom left). Although our observations are similar to those of previous modeling studies, they are in disagreement with the experimental results for short DNA sequences, which find that a dodecamer should unbind at extensions of ∼15 Å and at forces of <30p N, i.e., before any structural transition is seen (Pope et al., 2001; Strunz et al., 1999). At experimental loading rates of between 16 and 4000 pNs−1, the value of x* = 50 Å obtained by simulation actually underestimates the force required to unbind a dodecamer by a factor of ∼3.5 from Eq. 2.

FIGURE 3.

FIGURE 3

Open in a new tab

Force-extension curve calculated by steered MD simulation. A distinct plateau is seen at extensions of 25 Å before the helix unbinds at an extension of ∼50 Å.

FIGURE 4.

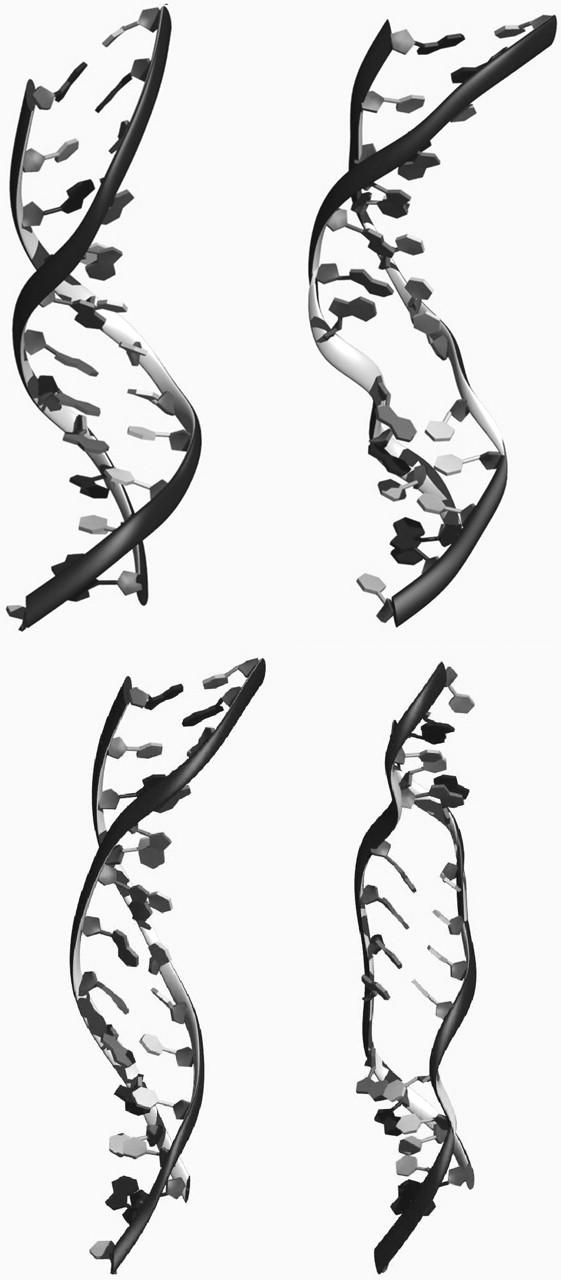
FIGURE 4

Open in a new tab

Formation of “holes” or “denaturation bubbles” in stretched DNA. The initial partially S-form DNA structure (top left) restrained at an extension of 23 Å develops a “hole” or “denaturation bubble” after 3800 ps (top right). A representative S-ladder DNA structure obtained at the beginning of a 4 ns simulation in which the DNA, which is restrained at an extension of 32 Å, (bottom left) develops two “holes” in the central region of the helix after 200 and 550 ps (bottom right).

Addition of configurational entropy terms

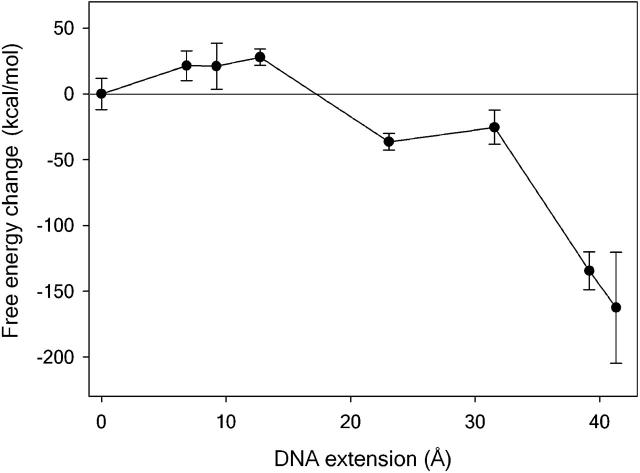
The configurational entropy as a function of extension for each of the increasingly elongated helices is shown by the squares and red line in Fig. 2. As might be expected, the DNA initially stiffens as it is placed under tension; correspondingly, the configurational entropy decreases. However, at extensions of ∼23 Å, the DNA suddenly becomes considerably more flexible. The free energy change as a function of extension ΔG = (ΔUDNA + ΔGsolv) − TΔSDNA is shown in Fig. 5. The maximum in the free energy barrier is now located at DNA extensions of between 13 Å and 23 Å rather than at the 50 Å obtained when the configurational entropy is neglected. The location of the transition state is now consistent with the experimental value of 15 ± 5 Å (Strunz et al., 1999). Consequently, calculating the unbinding force as a function of loading rate using Eq. 2 will give an excellent agreement with the forces measured experimentally (7,8). Furthermore, as the DNA unbinds entropically at extensions before the overstretching transition, these calculations predict that the plateau will not be seen in the force-extension curves for a dodecamer, as is indeed the case.

FIGURE 5.

FIGURE 5

Open in a new tab

The free energy barrier to DNA stretching calculated using the restrained simulations. The transition state is located at DNA extensions of between 13 and 23 Å.

Further experimental evidence illustrating the importance of the entropic contribution is provided by the temperature-dependent unbinding measurements performed for a 16-mer by Schumakovitch et al. (2002). These measurements indicate that the transition state is shifted toward smaller extensions with increasing temperature. The shape of the free energy barrier ΔG(x) = ΔU(x) − TΔS(x) results from the competition between energetic and entropic contributions and will therefore be temperature dependent whenever there is a nonzero entropy change. Assuming that the internal energy increases as the DNA is placed under tension, a decrease in the position of the transition state with increasing temperature indicates that there is a positive entropy change destabilizing the helix close to the transition state. The failure of previous simulation studies to reproduce the experimental data is simply due to the fact that this entropic contribution to the free energy barrier has so far been neglected. When the DNA is unbound using a ramp of force in a relatively short MD simulation, the entropy change is constrained to be close to zero as the molecule can only explore a small region of conformational space over these very limited timescales. Consequently, only energetic changes are able to influence the force-distance curve. This illustrates the difficulties associated with calculating free energies by computer simulation in general when inadequate sampling can significantly alter the behavior of the system. If the change in flexibility of the biomolecule can also be calculated, then such large-scale steered MD calculations can be brought into closer agreement with the experimental results. These new protocols suggest a general method for calculating free energy barriers through MD simulation when an estimate for the entropic contribution can be obtained.

The entropic instability of S-ladder DNA

The results presented in Fig. 5 show that the DNA will unbind at extensions of ∼18 Å due to the increased flexibility of highly elongated structures. Considerable insight into these numerical results can be obtained from a visual inspection of the MD trajectories (animations are provided as supplemental information). The free energy barrier separating bound and unbound states is removed at the point where ΔG = (ΔUDNA+ΔGsolv) − TΔSDNA becomes negative, therefore the DNA should disintegrate spontaneously as soon as this point is reached. For structures at extensions as high as 45 Å and 62 Å, the DNA helix disintegrates significantly even over the relatively short timescale (4 ns) of the simulation. These unstable molecular structures are clearly transient. No entropies were calculated for helices restrained at extensions >45 Å. These systems have been taken so far from local equilibrium that their structures change continuously during the simulation; therefore assigning an entropy would have little meaning. Such structures are simply an artifact of the short simulation times available, and will certainly not be resistant to an applied force over the relatively long timescales of an AFM experiment.

Observation of denaturation bubbles

The MD simulation obtained at an extension of 23 Å (which lies just after the transition state) is of particular interest. At the start of the simulation, the stretched DNA is in an intact partial S-ladder form with a complete set of hydrogen bonds between complementary basepairs (Fig. 4, top left). As the simulation proceeds, the structure clearly develops a “hole” or “denaturation bubble” in which one or more of the interstrand hydrogen bonds break spontaneously (Fig. 4, top right). Such holes appear in the central region of the helix rather than at the ends of the DNA and are separated by intact helical regions. Similarly, denaturation bubbles appear in the more elongated S-ladder helix shown in Fig. 4 (bottom right) after 200 and 550 ps. These denaturation bubbles form at extensions of >15 Å when the flexibility of the duplex suddenly increases (Figs. 2 and 4). The novel S-ladder structure observed in simulations that stretch oligomeric DNA is clearly dynamically unstable. At the transition state, the structure of the duplex is so distorted that hydrogen bonding interactions between complementary bases can be rapidly overcome by thermal fluctuations at room temperature. The conformation closest to the transition state has an average basepair inclination of 38° relative to the helix axis (CURVES; Lavery and Sklenar, 1989). When the bases become so tilted that a sufficient component of the applied tension acts along the hydrogen bond direction, then the basepairing is expected to be irreversibly disrupted and denaturation bubbles should form. We do not observe a gradual increase in average hydrogen bond distances as the DNA is extended. Rather, when the transition state is approached, the largest hydrogen bond distances (>4 Å) are observed more frequently, and occasionally result in basepair separation. A detailed investigation of the kinetics of DNA melting under force over longer timescales is currently in progress.

The term “B-S transition” first arose when the stretching data obtained for polymeric DNA was interpreted as a conformational change using the results from simulation studies on short DNA sequences. Although the validity of this comparison is not clear, our results would suggest that the “B-S” or “overstretching” transition is a force-induced melting transition rather than a conformational change, in agreement with the thermodynamic analysis of Rouzina et al. and Williams et al. These authors propose a model of DNA melting in which intact helical regions separate internal domains of unpaired DNA bases. Unbound domains will propagate and coalesce over longer timescales resulting in two unbound DNA strands (Williams et al., 2002). A theoretical analysis of the force-plateau observed experimentally suggests that S-DNA has a bending stiffness intermediate between double and single stranded DNA, which is consistent with this model (Storm and Nelson, 2003). Although the DNA is thermodynamically unstable at large extensions, it can remain kinetically stable for some time, as the dynamics of melting are notoriously slow. Consequently, unbinding forces >the 65 pN expected from equilibrium thermodynamics are commonly measured experimentally for polymeric sequences (unless the pulling velocities are sufficiently small (Clausen-Schaumann et al., 2000)). The partially disrupted S-ladder structures that appear in our MD simulations over nanosecond timescales seem to be remarkably similar to the early stages of DNA melting proposed previously (Rouzina and Bloomfield, 2001a). Presumably, if it were possible to run simulations of S-ladder DNA over very long timescales, the unbound regions within the molecule would grow until the helix eventually unbinds entropically into two single strands, as suggested by the thermodynamic calculations presented in Fig. 5. This relationship between our thermodynamic and structural data illustrates that statistical physics can provide a quantitative description of a dynamic biological process, and implies it might be developed into a useful theoretical tool for understanding biomolecular mechanics in general.

Biological Implications

The double helix is the quintessential example of the power of a molecular structure to reveal biological function. However, as duplex DNA must be routinely denatured, resealed, unpackaged, and repackaged over a range of cellular timescales by a variety of molecular motor proteins, it is possible that in the future the inherent deformability of DNA and the dynamics of duplex denaturation under force might be considered as relevant biologically as the static structure of the intact helix. The combination of computer modeling and statistical physics we have used to interpret single molecule stretching experiments illustrates the connection between force, thermodynamics, and kinetics in biology. These concepts are also of relevance to the design and function of molecular motors. Evolution must engineer the thermodynamic balance between energy, entropy, and force in such a way that the motor can perform the task required fast enough to be of use in cellular control. We have shown that the energy barrier stabilizing duplex DNA can be overcome by relatively low forces as long as the process takes place sufficiently slowly for unbinding to be assisted by entropic effects. Similarly, the molecular engine will be most efficient if it applies a force over a timescale which is slow compared to thermal fluctuations so that no energy is dissipated through molecular friction. The methods presented here describe biomolecular dissociation in an equilibrium regime when a force applied relatively slowly accelerates thermal activation over a free energy barrier. If the force is applied rapidly under nonequilibrium conditions, then the behavior of the molecule will be modified by dissipative effects that are not readily calculable from equilibrium properties, although the equilibrium free energy can be recovered if sufficient nonequilibrium data are available (Jarzynski, 1997; Ritort et al., 2002; Liphardt et al., 2002). The thermodynamics of nonequilibrium systems still remains one of the least developed areas of theoretical physics. As nanomanipulation techniques provide more detailed information on the kinetic and thermodynamic properties of single molecules, the hope is that new measurements emerging from this branch of biology will inspire progress in some of the unresolved areas of statistical physics.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[Supplemental File]
biophysj_104.046912_index.html (1.2KB, html)

Acknowledgments

We thank Drs. A. Armour, T. Strunz, R. Townsend, and P. Williams, and the theoretical biophysics group at the University of Illinois at Urbana-Champaign, for many useful discussions. We also thank Dr. G. Wells for his help with the figures and Prof. G. Aeppli, Dr. I. Ford, Prof. M. Gillan, Ms. S. Natarajan, and Dr. N. Thompson for reading the manuscript. We are also very grateful to Dr. E. Sherer for providing the unrestrained MD trajectory.

This work was supported by the Biotechnology and Biological Sciences Research Council.

Zara A. Sands' present address is Dept. of Biochemistry, University of Oxford, Oxford OX1 3QU, UK.

References

  1. Balsera, M., S. Stepaniants, S. Izraliev, Y. Oono, and K. Schulten. 1997. Reconstructing potential energy functions from simulated force-induced unbinding processes. Biophys. J. 73:1281–1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Case, D. A., D. A. Pearlman, J. W. Caldwell, T. E. I. I. I. Cheatham, W. S. Ross, C. L. Simmerling, T. L. Darden, K. M. Marz, R. V. Stanton, A. L. Cheng, J. J. Vincent, M. Crowley, V. Tsui, and others. 1999. AMBER 6. University of California, San Francisco
  3. Clausen-Schaumann, H., M. Rief, C. Tolksdorf, and H. E. Gaub. 2000. Mechanical stability of single DNA molecules. Biophys. J. 78:1997–2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Evans, E. 2001. Probing the relation between force-lifetime and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 30:105–128. [DOI] [PubMed] [Google Scholar]
  5. Gullingsrud, J. R., R. Braun, and K. Schulten. 1999. Reconstructing potentials of mean force through time series analysis of steered molecular dynamics simulations. J. Comput. Phys. 151:190–211. [Google Scholar]
  6. Harris, S. A., E. Gavathiotis, M. S. Searle, M. Orozco, and C. A. Laughton. 2001. Cooperativity in drug-DNA recognition: a molecular dynamics study. J. Am. Chem. Soc. 123:12658–12663. [DOI] [PubMed] [Google Scholar]
  7. Jarzynski, C. 1997. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 78:2690–2693. [Google Scholar]
  8. Klimov, D. K., and D. Thirumalai. 2000. Native topology determines force-induced unfolding pathways in globular proteins. Proc. Natl. Acad. Sci. USA. 97:7254–7259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Konrad, M. W., and J. I. Bolonick. 1996. Molecular dynamics simulation of DNA stretching is consistent with the tension observed for extension and strand separation and predicts a novel ladder structure. J. Am. Chem. Soc. 118:10989–10994. [Google Scholar]
  10. Kosikov, K. M., A. A. Gorin, V. B. Zhurkin, and W. K. Olson. 1999. DNA stretching and compression: large-scale simulations of double helical structures. J. Mol. Biol. 289:1301–1326. [DOI] [PubMed] [Google Scholar]
  11. Lavery, R., and A. Lebrun. 1999. Modelling DNA stretching for physics and biology. Genetica. 106:75–84. [DOI] [PubMed] [Google Scholar]
  12. Lavery, R., A. Lebrun, J.-F. Allemand, D. Bensimon, and V. Croquette. 2002. Structure and mechanics of single biomolecules: experiment and simulation. J. Phys. Condens. Matter. 14:R383–R414. [Google Scholar]
  13. Lavery, R., and H. Sklenar. 1989. Defining the structure of irregular nucleic acids—conventions and principles. J. Biomol. Struc. Dyn. 6:655–667. [DOI] [PubMed] [Google Scholar]
  14. Lebrun, A., and R. Lavery. 1996. Modelling extreme stretching of DNA. Nucleic Acids Res. 24:2260–2267. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Liphardt, J., S. Dumont, S. B. Smith, I. Tinoco Jr., and C. Bustamante. 2002. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski's equality. Science. 296:1832–1835. [DOI] [PubMed] [Google Scholar]
  16. MacKerell, A. D., and G. U. Lee. 1999. Structure, force, and energy of a double-stranded DNA oligonucleotide under tensile loads. Eur. Biophys. J. 28:415–426. [DOI] [PubMed] [Google Scholar]
  17. Nelson, H. C. M., J. T. Finch, B. F. Luisi, and A. Klug. 1987. The structure of an oligo(dA).oligo(dT) tract and its biological implications. Nature. 330:221–226. [DOI] [PubMed] [Google Scholar]
  18. Pope, L. H., M. C. Davies, C. A. Laughton, C. J. Roberts, S. J. B. Tendler, and P. M. Williams. 2001. Force-induced melting of a short DNA double helix. Eur. Biophys. J. 30:53–62. [DOI] [PubMed] [Google Scholar]
  19. Rief, M., H. Clausen-Schaumann, and H. E. Gaub. 1999. Sequence-dependent mechanics of single DNA molecules. Nat. Struct. Biol. 6:346–349. [DOI] [PubMed] [Google Scholar]
  20. Ritort, F., C. Bustamante, and I. Tinoco Jr. 2002. A two-state kinetic model for the unfolding of single molecules by mechanical force. Proc. Natl. Acad. Sci. USA. 99:13544–13548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Rouzina, I., and V. A. Bloomfield. 2001a. Force-induced melting of the DNA double helix. 1. Thermodynamics analysis. Biophys. J. 80:882–893. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Rouzina, I., and V. A. Bloomfield. 2001b. Force-induced melting of the DNA double helix. 2. Effect of solution conditions. Biophys. J. 80:894–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Schafer, H., X. Daura, A. E. Mark, and W. F. van Gunsteren. 2001. Entropy calculations on the molten globule state of a protein: side-chain entropies of alpha-lactabumin. Proteins. 43:45–56. [DOI] [PubMed] [Google Scholar]
  24. Schafer, H., A. E. Mark, and W. F. van Gunsteren. 2000. Absolute entropies from molecular dynamics simulation trajectories. J. Chem. Phys. 113:7809–7817. [Google Scholar]
  25. Schlitter, J. 1993. Estimations of absolute and relative entropies of macromolecules using the covariance matrix. J. Chem. Phys. Lett. 215:617–621. [Google Scholar]
  26. Schumakovitch, I., W. Grange, T. Strunz, P. Bertoncini, H. Gütherodt, and M. Hegner. 2002. Temperature dependence of unbinding forces between complementary DNA strands. Biophys. J. 82:517–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Schwesinger, F., R. Ros, T. Strunz, D. Anselmetti, H.-J. Güntherodt, A. Honegger, L. Jermutus, L. Tiefenauer, and A. Plückthun. 2000. Unbinding forces of single antibody-antigen complexes correlate with their thermal dissociation rates. Proc. Natl. Acad. Sci. USA. 97:9972–9977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Shields, G., C. A. Laughton, and M. Orozco. 1997. Molecular dynamics simulations of the d(T·A·T) triple helix. J. Am. Chem. Soc. 119:7463–7469. [Google Scholar]
  29. Soliva, R., E. Sherer, F. J. Luque, C. A. Laughton, and M. Orozco. 2000. Molecular dynamics simulations of PNA·DNA and PNA·RNA duplexes in aqueous solution. J. Am. Chem. Soc. 122:5997–6008. [Google Scholar]
  30. Srinivasan, J., T. E. Cheatham III, P. Kollman, and D. A. Case. 1998. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate-DNA helices. J. Am. Chem. Soc. 120:9401–9409. [Google Scholar]
  31. Storm, C., and P. C. Nelson. 2003. Theory of high-force stretching and overstretching. Phys. Rev. E. 67:051906. [DOI] [PubMed] [Google Scholar]
  32. Strick, T. R., M. N. Dessinges, G. Charvin, N. H. Dekker, J.-F. Allemand, D. Bensimon, and V. Croquett. 2003. Stretching of macromolecules and proteins. Rep. Prog. Phys. 66:1–45. [Google Scholar]
  33. Strunz, T., K. Oroszlan, H. J. Güntherodt, and M. Henger. 2000. Model energy landscapes and the force-induced dissociation of ligand-receptor bonds. Biophys. J. 79:1206–1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Strunz, T., K. Oroszlan, R. Schäfer, and H. Güntherodt. 1999. Dynamic force spectroscopy of single DNA molecules. Proc. Natl. Acad. Sci. USA. 96:11277–11282. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Tinoco, I. Jr., and C. Bustamante. 2002. The effect of force on thermodynamics and kinetics of single molecule reactions. Biophys. Chem. 101–102:513–533. [DOI] [PubMed] [Google Scholar]
  36. Tsui, V., and D. A. Case. 2000. Molecular dynamics simulations of nucleic acids with a generalised Born solvation model. J. Am. Chem. Soc. 122:2489–2498. [Google Scholar]
  37. Williams, M. C., I. Rouzina, and V. A. Bloomfield. 2002. Thermodynamics of DNA interactions from single molecule stretching experiments. Acc. Chem. Res. 35:159–166. [DOI] [PubMed] [Google Scholar]
  38. Williams, M. C., J. R. Wenner, I. Rouzina, and V. Bloomfield. 2001. Entropy and heat capacity of DNA melting from temperature dependence of single molecule stretching. Biophys. J. 80:1932–1939. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental File]
biophysj_104.046912_index.html (1.2KB, html)
Download video file (1.4MB, mpg)
biophysj_104.046912_046912_supplemental_info.doc (23.5KB, doc)
biophysj_104.046912_046912_supplementaryfig1.jpg (611KB, jpg)
Download video file (5.9MB, mpg)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES