Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Dec 21;88(4):2766–2778. doi: 10.1529/biophysj.104.049015

Origin of the Heterogeneous Distribution of the Yield of Guanyl Radical in UV Laser Photolyzed DNA

Dimitar Angelov 1, Benedicte Beylot 1, Annick Spassky 1
PMCID: PMC1305372  PMID: 15613625

Abstract

Oxidative guanine lesions were analyzed, at the nucleotide level, within DNA exposed to nanosecond ultraviolet (266 nm) laser pulses of variable intensity (0.002–0.1 J/cm2). Experiments were carried out, at room temperature, in TE buffer (20 mM Tris-HCl, pH 7.5; 1 mM EDTA) containing 35 mM NaCl, on 5′-end radioactively labeled double-stranded and single-stranded oligomer DNA at a size of 33–37 nucleobases. Lesions were analyzed on polyacrylamide gel electrophoresis by taking advantage of the specific removal of 8-oxodG from DNA by the formamidopyrimidine DNA glycosylase (Fpg protein) and of the differential sensitivity of 8-oxodG and oxazolone to piperidine. The quantum yields of lesions at individual sites, determined from the normalized intensities of bands, were plotted against the irradiation energy levels. Simplified model fitting of the experimental data enabled to evaluate the spectroscopic parameters characterizing excitation and photoionization processes. Results show that the distribution of guanine residues, excited to the lowest triplet state or photoionized, is heterogeneous and depends on the primary and secondary DNA structure. These findings are generalized in terms of excitation energy and charge-migration mediated biphotonic ionization. On the basis of the changes in the yield of the guanyl radical resulting from local helical perturbations in the DNA π-stack, it can be assessed that the distance range of migration is <6–8 bp.

INTRODUCTION

Exposure of DNA to high-intensity ultraviolet (UV) laser pulses has been shown to result in the formation of guanine oxidative lesions with a yield that is strongly modulated by the primary and secondary structure of DNA (Kovalsky et al., 1990; Spassky and Angelov, 1997; Melvin et al., 1998). Moreover, DNA structural deformations, induced by the binding of specific proteins, have been probed through a change in base photoreactivity within the binding site, suggesting a strong correlation of biphotonic ionization processes and secondary as well as higher-order DNA structure (Beylot, 1998; Angelov et al., 1999). Under these irradiation conditions, another major class of oxidative damage occurs, namely the formation of covalent protein-DNA adducts (Pashev et al., 1991; Russmann et al., 1997; Mutskov et al., 1998; Angelov et al., 2000, 2001). Mapping of UV laser-induced lesions allows direct localization of protein-DNA interactions (Abdurashidova et al. 2003; Angelov et al. 2004; Nagaich et al., 2004) and contacts at the nucleotide level (Angelov et al., 2003). Thus, UV laser footprinting and protein-DNA cross-linking have the potential of becoming a unique and powerful tool in high-resolution dynamic studies of DNA-protein interactions. One important limitation of these methods is the lack of sufficient mechanistic information, which is necessary for mathematical modelization of results and their presentation in structural terms. The first step in such studies consists of the identification of the photophysical processes responsible for DNA conformational sensitivity of the photochemical yield.

The goal of this work is to understand the mutual influence of the electronic structure of nucleic bases on biphotonic ionization processes induced by nanosecond UV laser pulses. Under these irradiation conditions, nucleic bases are initially excited via S1 to their lowest triplet state T1 and then they are ionized upon absorption of a second photon giving rise to the chemically reactive transient radical cation (Nikogosyan et al., 1982; Nikogosyan and Letokhov, 1983; Nikogosyan, 1990; Görner, 1994). Taking into account internal and intersystem conversion energy loss of ∼1 eV (Cadet and Vigny, 1990), the overall photonic energy absorbed is ∼8.3 eV. Because it largely exceeds the energy required for ejection of a hydrated electron from nucleotides in aqueous solution (∼6.4 eV) (Candeias et al., 1992; O'Neill and Fielden, 1994), they are readily ionized with a maximum quantum efficiency that is limited essentially by the intersystem-crossing yield. Contrasting with low-intensity monophotonic processes, the efficiency of biphotonic ionization processes depends on the radiation intensity. Theoretical and experimental analyses of such dependences have led to the evaluation of specific electronic transition parameters for free nucleic bases and random DNA, including the intersystem crossing yield ϕ1 and the photoionization parameter ϕ2σ2 (see Appendix) (Nikogosyan et al., 1982; Nikogosyan and Letokhov, 1983; Nikogosyan, 1990). Knowledge of these two parameters for individual bases within DNA permits one to determine the distribution of transient populations for excited molecules and radical cations during the photoprocess.

In a previous study we observed an important increase in the average values of the ionization probability ϕ2 for guanines within DNA duplexes, in comparison with either the remaining three nucleotides within DNA or with free guanine (Angelov et al., 1997; Douki et al., 2001, 2004). This is consistent with the occurrence of hole migration and preferential trapping by guanine in DNA. It should be noted that similar observations on the behavior of the quantum yield of DNA strand breakage and hydrated electron generation upon picosecond laser photolysis have been attributed to a cooperative biphotonic excitation, mediated by a long-range (∼200 bp) energy migration; Nikogosyan et al., 1985). The occurrence of charge-migration phenomena in DNA has been the subject of intense debate among radiation chemists. Most of the data obtained by different techniques, namely low-temperature electron paramagnetic resonance (Gregoli et al., 1979; O'Neill and Fielden, 1994; Becker and Sevilla, 1993; Malone et al., 1994), optical spectroscopy in solutions (Candeias et al., 1992; Candeias and Steenken, 1993; Melvin et al. 1996), and biochemical analysis (Croke et al., 1988; Melvin et al., 1995) are consistent with the occurrence of electron migration although the distance and mechanism of migration remain a matter of much controversy. More recently, long-range hole migration through the DNA π-stack and trapping by guanines has been suggested to occur on the basis of type 1 interactions of covalently bound intercalators or modified DNA bases. This has been demonstrated by using different synthetic DNA assemblies together with time-resolved fluorescence quenching, transient absorption spectroscopy (Kelley et al., 1997; Kelley and Barton, 1999; Fukui and Tanaka, 1998), the induction of oxidative damage (Ly et al., 1999; Henderson et al. 1999; Hall et al., 1996, 1998; Meggers et al. 1998; Giese et al. 1999), or oxidative thymine dimer repair (Dandliker et al., 1997) at a distance of the photoexcited electron acceptor. Pairing and stacking interactions, which are fundamental in maintaining the double helical structure, were suggested to favor the migration of charge along the helix.

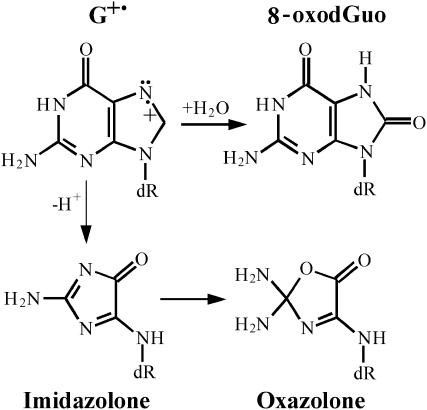
In this study, we have subjected DNA sequences (Fig. 1) to the action of UV nanosecond laser pulses, varying the energy density of the pulses in a wide range and monitoring the quantum efficiency of formation of the two major one-electron oxidative lesions, 8-oxodGuo and oxazolone (Angelov et al., 1997; Douki et al., 2001, 2004) at individual guanines. Because these oxidative guanine lesions result from the decomposition of the guanyl radical through competitive deprotonation and hydration pathways, respectively (Fig. 2) (Kasai et al., 1992; Ravanat et al., 1993; Spassky and Angelov, 1997, 2002; Douki and Cadet, 1999), experimental data enabled us to plot the intensity-response dependency of the radical cation yields for individual guanines. To describe the dependence of the efficiency of biphotonic ionization processes on radiation intensity in terms of quantum yield for triplet formation ϕ1 and photoionization ϕ2, we used a simplified model, previously developed with free bases as well as noninteracting bases in DNA (Nikogosyan et al., 1982; Nikogosyan and Letokhov, 1983; Nikogosyan, 1990). Irradiation has been performed on the duplex or on each single strand separately of several types of DNA sequences, selected to analyze the influence of the sequence context on the yield of guanyl radical. The first type of DNA sequence (Fig. 1, sequences I and II) is a 37-basepair (bp) DNA sequence, including the target site of the endonuclease I-SceI (Beylot and Spassky, 2001). The second type of sequence (33–35 bp) contains two, three, or five guanine runs incorporated in the same environment (Fig. 1, sequences III and IV). The third type of sequences (Fig. 1, sequences V and VI) was chosen to analyze the effect of the destabilization of the helical pairing caused by an additional unpaired base on one strand (“bulge”). This led to the striking result that both probabilities ϕ1 and ϕ2, to excite guanines into T1 and to photoionize them from this state, are strongly dependent on the primary and secondary DNA structures, inferring that the distribution of the relative radical cation yield within DNA is heterogeneous and laser-intensity dependent. These results are discussed in terms of donor-acceptor effects between nucleobases, involving a sequence and structure-dependent redistribution of initially generated excited molecules and radical cations within DNA due to both energy and hole migration within nucleobases and ultimate fixation of the latter species at guanines.

FIGURE 1.

FIGURE 1

Open in a new tab

Sequences of DNA fragments used in our experiments.

FIGURE 2.

FIGURE 2

Open in a new tab

Chemical structures of the major guanine radical cation transformation products arising through competitive deprotonation and water addition.

EXPERIMENTAL SECTION

Chemicals

All chemical products were the highest available purity grade purchased from Sigma (St Quentin en Yvelines, France). Restriction enzymes were purchased from Pharmacia (St Quentin en Yvelines, France). Purified formamidopyrimidine N-glycosylase (Fpg) and E. coli endonuclease III were kindly provided by S. Boiteux, CEA Fontenay-aux-Roses, France. T4 endonuclease V was a kind gift of D. Yarosh at Applied Genetics (Freeport, NY).

Oligonucleotide preparation

Synthetic oligonucleotides for sequences in Fig. 1 were purchased from Genset (Paris, France) and purified on a 20% polyacrylamide gel as previously described (Spassky and Angelov, 1997). Oligonucleotides were 5′-labeled with [γ-32P]ATP (Amersham, Buckinghamshire, UK) in the presence of T4 polynucleotide kinase (New England Biolabs, Beverly, MA). DNA duplexes were prepared by annealing equal amounts of the labeled and unlabeled complementary strands by brief heating at 85°C in TE buffer (10 mM Tris, 1 mM EDTA) containing 10 mM NaCl and cooling slowly to room temperature. Duplex formation was monitored by 15% native polyacrylamide gel electrophoresis. Electrophoresis was carried out in 0.5× TBE buffer at room temperature at 100 V (7–10 V/cm). Oligonucleotides were further purified from background lesions at guanines by Fpg glycosylase treatment and 15% denaturing gel electrophoresis. After elution from the gel and purification on a Sephadex spin column, oligonucleotides were annealed as described above.

The 98-bp EcoRI-HindIII DNA fragment (sequence shown in Fig. 7), which contains a homing endonuclease encoded sequence (the I-SceI recognition sequence) was excised from a pUC 19 plasmid vector derivative supplied by B. Dujon (Colleaux et al., 1988). After 5′-end labeling either at EcoRI or HindIII sides by T4 polynucleotide kinase and [γ-32P]ATP, DNA probes were purified on a 10% preparative native polyacrylamide gel.

FIGURE 7.

FIGURE 7

Open in a new tab

Distribution of cyclobutane pyrimidine dimer yield after subjecting the 98-bp DNA EcoRI-HindIII excision fragment to the action of a single, E = 0.1 J/cm2 (open bars) or multiple, E=0.002 J/cm2 (shaded bars) UV laser pulses at the same total irradiation dose.

UV laser irradiation

DNA samples were exposed to a single or multiple UV laser pulses (λ = 266 nm, τp = 4–5 ns) provided by the fourth harmonics generation of a Q-switched, model 5011 D.NS 10 Nd:YAG laser (BMI, Evry, France). Typically, the irradiation was carried out in 10 μl aliquots (104 cpm, 0.2–0.5 nM) in TE buffer (10 mM Tris, pH 7.5, 1 mM EDTA) containing 35 mM NaCl, at room temperature in small 0.65-ml siliconized Eppendorf tubes. The diameter of the laser beam was adjusted to that of the surface of the irradiated sample (d = 0.25 cm) by means of a circular diaphragm. The energy of individual pulses was measured by using a calibrated pyroelectrical energy meter (Ophir Optronics, Evry, France) and 8% reflection fused silica beam splitter. The irradiation dose E was determined by dividing the laser energy to the area by the beam cross section S = 0.05 cm2.

Determination of the quantum efficiency of lesions at individual sites

After irradiation, DNA samples were incubated for 30 min at 37°C with 5 μg/ml final concentration of an appropriate repair enzyme (Burrows and Muller, 1998), i.e., either formamidopyrimidine DNA glycosylase (Fpg protein) (cleavage at 8oxodG lesions) or endonuclease III (cleavage at thymine glycols) or T4 endonuclease V (cleavage at thymine dimers) in the standard irradiation buffer supplemented with 100 μg/ml BSA and 5 mM β-mercaptoethanol. When single-stranded oligonucleotides or heteroduplexes were used, they were annealed before Fpg treatment with a 50× excess of the correct complementary strand. In the experiments shown in Fig. 5, irradiated DNA was treated with piperidine (1 M final concentration) for 30 min at 90°C. Piperidine was removed by five successive lyophilizations. Dried samples were resuspended in 3 μl of deionized formamide containing 5 mM EDTA, 0.1% xylene cyanol and 0.1% bromphenol blue and run on a 15% polyacrylamide/8 M urea sequencing gel in 1× TBE buffer at a constant 60 W power (temperature ∼55°C). After electrophoresis, gels were dried and autoradiographed on a phosphorimager screen. The maximum total irradiation dose and the DNA size were chosen with respect to single-hit requirement conditions for gel quantification. For 30–40-bp DNA fragments this corresponds to a maximum of 15% depletion of the intact oligonucleotide, which is typically achieved under a single 0.1 J/cm2 laser pulse photolysis.

FIGURE 5.

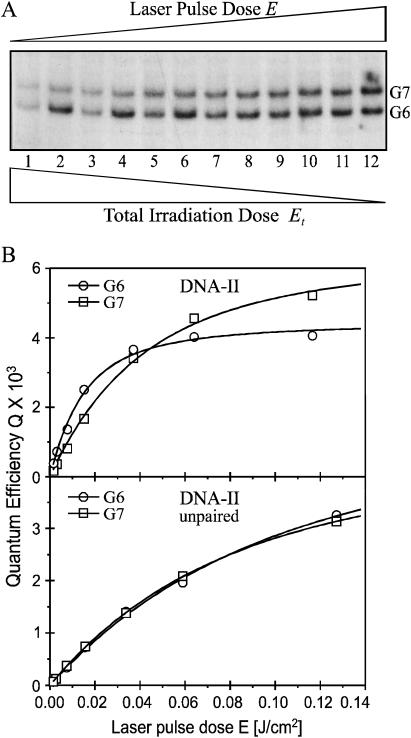
FIGURE 5

Open in a new tab

Distribution of the UV laser induced hot piperidine sensitive lesions: double-stranded versus single-stranded DNA. Oligonucleotides-II, either double-stranded (lines 2, 4, 6, 8, 10, 12 (A) and top frame (B)) or single-stranded (lines 1, 3, 5, 7, 9, 11 (A) and bottom frame (B)) were submitted to UV laser radiation at different pulse intensities and analyzed by sequencing gel electrophoresis after hot piperidine treatment. (A) Gel; (B) quantified quantum yields Qpip as a function of the laser pulse dose and fitted by Eq. 2a. Irradiation conditions were similar to those in Fig. 4.

The apparent quantum yield, or “quantum efficiency” of cleavage at individual DNA bases, was determined by using the formula Q = R/R0σ1Et (see Appendix), where: R/R0 is the normalized photoproduct yield of the corresponding base (integral of the radioactivity in the band, R/integral of total radioactivity loaded, R0); and σ1Et is the number of photons absorbed per nucleotide under linear (low-intensity) absorption approximation and optical thin layer conditions, in which σ1 = 2.3 × 10−17 cm2 (ɛ = 6000 M−1 cm−1) and 1.4 times higher for single-stranded oligonucleotides is the absorption cross section at 266 nm and Et is the total irradiation dose expressed in [photons/cm2] (1 J being the energy produced through the absorption of 1,34 × 1018 266 nm photons, Et[photons/cm2] = 1,34 × 1018 Et [J/cm2]. The values of R and R0 were determined from the digitized phosphorimager pictures of the gels by integration of the corresponding rectangles and respective background freeing using ImageQuant 4.1 software (Molecular Dynamics, Sunnyvale, CA). The fluctuations between the values of Q measured in several independent experiments were usually within 5% for the stronger radioactive bands and up to 10% for the weakest ones.

RESULTS

The dependence of the formation of oxidative lesions on laser intensity is distinct for individual guanines

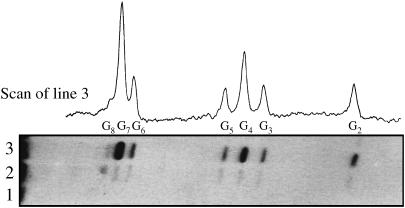
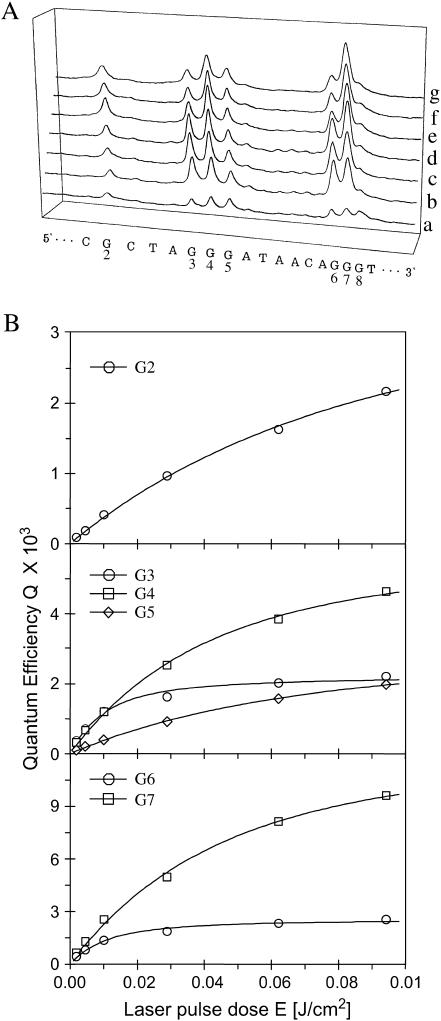
The differential sensitivity toward piperidine and formamidopyrimidine DNA N-glycosylase (Fpg protein) digestion of the two major one-electron oxidative DNA guanine modifications, oxazolone and 8-oxodGuo, has already been exploited to determine the quantum yield of their formation at individual sites of DNA fragments submitted to biphotonic laser photolysis at a fixed irradiation fluence (0.1 J/cm2) (Spassky and Angelov, 1997). Here, duplex DNA fragments as well as each of the complementary oligonucleotides separately (Fig. 1) were exposed to an increasing number of 266-nm laser nanosecond pulses of decreasing laser intensity, from a single pulse of E = 0.1 J/cm2 to 1000 pulses of E = 0.002 J/cm2 before loading on electrophoretic sequencing gels, directly or after treatment with either Fpg protein or hot piperidine. As expected from previous studies (Spassky and Angelov, 1997; Cullis et al., 1996), no significant cleavage was observed in irradiated DNA directly loaded on the gel (Fig. 3, lane 1). In contrast, DNA cleavage bands of variable intensity result at guanine residues of irradiated DNA from the action of either Fpg protein (Fig. 3, compare lanes 2 and 3) or piperidine (not shown). It should be noted that the range of intensity E and the corresponding total irradiation doses Et were chosen to induce in each case a similar extent of DNA cleavage limited to less than a single damage per oligonucleotide required for gel analysis. Interestingly, we observed that the relative distribution of bands varies with the intensity of the radiation (Fig. 4 A). Accordingly, the quantum efficiencies of cleavage QFpg or Qpip were determined at each guanine as a function of the intensity, based on measuring the radioactivity in each band normalized to the total radioactivity in the lane and the radiation energy absorbed per nucleotide (see Experimental Section and Appendix). Fig. 4 B shows the least-square fit by Eq. 2a of the plot of the quantum efficiencies QFpg for each guanine of the duplex-I as a function of the radiation energy density after varying parameters ϕ1 and ϕ2σ2. Consistent with the involvement of a biphotonic resonance ionization process, QFpg first increased linearly with the laser intensity pulses and then reached saturation. The most striking result is that the values of the maximum quantum efficiency Qmax as well as the saturation fluence Es differ markedly from one guanine to another. For the isolated guanine G2 and the guanine G5 located at the 3′ side of the cluster -G3G4G5-, Q slowly increases without reaching saturation even at the end of the entire intensity range. In contrast, the quantum efficiency reaches a maximum for the residues G4 and G7 as well as for the residues G2 and G5, but at the end of the intensity range for the former two and at very low intensity for the latter two. Note also that the value of this maximum of quantum efficiency is two or five times higher for the residues G4 and G7 than for G2 and G5.

FIGURE 3.

FIGURE 3

Open in a new tab

Sequence gel analysis of high-intensity UV laser irradiated DNA-I submitted to Fpg digestion. Double-stranded oligonucleotide-I was submitted to Fpg digestion, directly (lane 2) or after exposition to a single UV laser pulse (E = 0.1 J/cm2) as described in the text (lane 3). UV laser irradiated DNA was directly loaded on the sequencing gel in lane 1, for control.

FIGURE 4.

FIGURE 4

Open in a new tab

Laser pulse intensity dependence of the yield of Fpg enzymatic cleavage at individual guanines within DNA-I. (A) Densitometry scans: nonirradiated control (a); E = 0.002, Et = 2 J/cm2 (1000 pulses) (b); E = 0.005, Et = 1.25 J/cm2 (250 pulses) (c); E = 0.01, Et = 0.5 J/cm2 (50 pulses) (d); E = 0.03, Et = 0.21 J/cm2 (7 pulses) (e); E = 0.06, Et = 0.12 J/cm2 (2 pulses) (f); E = Et = 0.1 J/cm2 (1 pulse) (g). (B) The DNA cleavage bands displayed in panel A were quantified, expressed as quantum efficiencies (QFpg) and plotted versus the laser pulse dose. The open symbols represent experimental values as indicated. The curves were generated by a least-square best-fitting procedure using Eq. 2a.

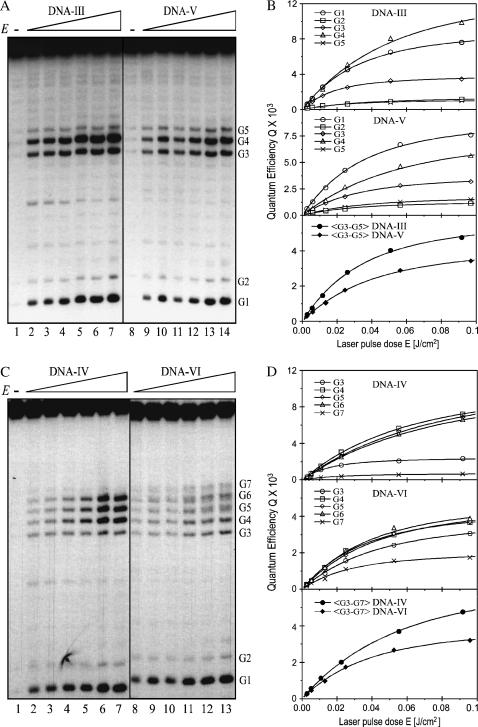
Similarly, Fig. 5 shows that for the duplex-II the maximum of the quantum efficiency is reached at a fluence three times lower for the residue G6 located 5′ to the -GG- run than for G7. These effects were not seen with single-stranded oligonucleotides for which no difference in either the saturation fluence Es or the quantum efficiency Qmax was observed at individual guanines. Interestingly, in single-stranded oligonucleotide-II, saturation is reached at a value of irradiation intensities approximately two times higher than average compared to guanines in the double-stranded DNA. Heterogeneous and intensity-dependent relative distribution of Qmax and Es was also observed in duplexes-III and -IV, containing -GGG- and -GGGGG- clusters, respectively (Fig. 6). However, the very strong 5′-G preference observed at high laser intensity in duplex-III, TG1G2T, contrasts sharply with the similar cleavage of guanines in duplex-II, AG6G7A.

FIGURE 6.

FIGURE 6

Open in a new tab

Effect of base pairing and stacking destabilization on generation of the guanine radical cation. Duplex oligonucleotides are: DNA-III (lines 1–7 in panel A and top frame in panel B) and DNA-IV (lines 1–7 in panel C and top frame in panel D); heteroduplexes are: DNA-V (lines 8–14 in panel A and middle frame in panel B) and DNA-VI (lines 8–13 in panel C and middle frame in panel D) were subjected to the same experiments as in Fig. 4. Also shown are the averaged quantum yield values for clustered guanines as indicated (B and D, bottom frames, solid symbols). (A and C) Gels. (B and D) Gel quantified values of QFpg (symbols) and fitted curves using Eq. 2a.

Distribution of the radical cation within DNA and triplet excited states of individual guanines

The independence of QFpg/Qpip within the whole intensity range was checked for all guanines within DNA-I and -II and for the highest (0.1 J/cm2) and the lowest (0.002 J/cm2) intensities for guanines in duplexes-III to -VI. As expected, no difference was found. Therefore, taking account on the one hand that the chemical transformation pathways of the radical cation do not depend on the laser intensity and on the other hand that the yield of the radical guanyl can be roughly considered as the sum of the yields of the two major decomposition products (Spassky and Angelov, 1997), Q+ = QFpg + Qpip, we derived the corresponding fluence-response dependencies for Q+ (not shown) using the values of QFpg/Qpip at 0.1 J/cm2 as previously determined (Spassky and Angelov, 1997). Thus, we were able to characterize the influence of the sequence environment on biphotonic ionization by determining the corresponding photophysical parameters for individual guanines. The values of the parameters ϕ1 and ϕ2σ2 as well as Q+max and Es, given in Table 1 were determined by best-fit analysis of the experimental data Q+ = QFpg(1 + Qpip/QFpg) using the biphotonic quantum efficiency Eq. 2a. Taking into account the basic relationship of Eq. 3a, the differences in the curve shape for different guanines can be easily related to variations of the indirectly observable parameters ϕ1 and ϕ2σ2. It becomes evident that guanines displaying higher Qmax or lower Es, are those possessing higher values of the intersystem crossing yield ϕ1 or the ionization probability ϕ2, respectively. It should be noted that the spectroscopic meaning of these parameters remains valid in the case of DNA too, but only within the context of the independent-base biphotonic ionization model (see Appendix). In any case, irrespective of the concrete spectroscopic meaning of ϕ1 and ϕ2, these analyses constitute unambiguous evidence that the distribution of the triplet-excited guanines as well as that of the radical cation states are highly heterogeneous in their dependence on flanking bases.

TABLE 1.

Values of the biphotonic ionization parameters obtained by least-square fitting of the experimental values for Q+ with Eq. 2a as explained in the text

Guanines ϕ1 × 10−3 *ϕ1σ1 × 10−20 ϕ2σ2 × 10−17 Q+max × 10−3 Es J/cm2
I-G2 9.7 22.3 1.4 8.2 0.100
I-G3 3.7 8.5 12.1 3.5 0.014
I-G4 9.1 20.9 3.2 8.1 0.046
I-G5 4.7 10.8 2.1 3.7 0.073
I-G6 4.2 9.7 12.5 4.1 0.014
I-G7 18.6 42.8 2.8 15.7 0.050
I-G8 2.3 5.3 3.8 2.2 0.045
I-〈G2-7〉 6.7 15.4 3.6 6.2 0.043
II-G6 12.0 27.6 9.3 11.0 0.017
II-G7 18.9 43.5 3.0 15.6 0.045
II-G6 ss 7.5 17.0 1.5 6.3 0.099
II-G7 ss 8.1 18.5 1.3 6.7 0.107
III-G1 12.2 28.0 4.3 10.1 0.035
III-G2 2.8 6.4 4.4 2.2 0.038
III-G3 5.4 12.4 7.2 5.1 0.023
III-G4 17.1 39.3 2.8 14.5 0.048
III-G5 2.2 5.0 5.5 2.3 0.031
III-〈G3-5〉 8.1 18.6 3.9 7.3 0.040
V-G3 6.4 14.7 4.4 5.9 0.037
V-G4 11.4 26.2 2.6 9.9 0.057
V-G5 3.9 9.5 3.7 3.6 0.043
V-〈G3-5〉 7.1 16.3 3.3 6.4 0.047
IV-G3 3.5 8.0 8.6 3.4 0.020
IV-G4 14.6 33.6 2.1 12.2 0.066
IV-G5 16.1 37.0 1.7 13.1 0.078
IV-G6 15.4 35.4 1.6 12.6 0.080
IV-G7 1.8 4.1 6.3 1.6 0.028
IV-〈G3-7〉 9.4 21.6 2.4 8.2 0.060
VI-G3 7.1 16.3 3.1 6.4 0.050
VI-G4 8.5 19.6 3.9 7.7 0.040
VI-G5 9.7 22.3 3.2 8.6 0.046
VI-G6 10.0 23.0 3.5 8.9 0.042
VI-G7 4.6 10.6 4.6 4.3 0.034
VI-〈G3-7〉 7.9 18.2 3.6 7.2 0.043
†Free Gua 1.3 5.5 0.5 1.2 0.300
Open in a new tab
*

σ1 = 2.3 × 10−17 cm2.

†

Data from Nikogosyan et al. (1982).

〈…〉, average values; ss, single-stranded. The values for G1 and G2 for duplexes-IV to -VI are equals to those for duplex-III. Standard deviations were usually within 5%, but for the weakest guanine cleavage bands they increased to 10–15%.

The following interesting features should shed some light on the mechanism of photoionization in duplex DNA. Clustered guanines are not the only photoionization targets. Single guanines are also ionized, although generally with a lower quantum yield. The distribution of Q+max within clusters containing two or three guanines but in a different sequence environment is not the same and depends on neighboring bases. The almost symmetrical pattern of I-AG3G4G5A and II-AG6G7A sharply contrasts with the asymmetrical distribution in I-AG6G7G8T and III-, IV-TG1G2T. Additionally, by contrasts to single-stranded DNA, there is great diversity in the distribution of photo cleavage for isolated as well as clustered guanines within a wide range of DNA sequences (not shown). As a rule, the highest ionization probability ϕ2 (corresponding to the lowest Es) is observed for guanines located 5′ side within -GG-, -GGG-, -GGGGG- runs. However, this feature is not exclusive, as can be seen for guanine III-G1 and IV-G1. In addition, no simple correlation between the values of Qmax and Es for neighboring guanines can be found. For example, guanines I-G3 and I-G6 display a higher ionization probability ϕ2 (lower saturation dose Es) than I-G4 and I-G7 but a lower intersystem-crossing yield (lower Qmax).

Influence of basepair stacking on the variation in quantum efficiency as a function of laser intensity

The experiments carried out by using duplexes-V and -VI, respectively, including five cytosines opposite three guanines (DNA-V) and five guanines opposite three cytosine residues (DNA-VI), allowed further investigation of the influence of local distortions of the π-stack on the values of Qmax and Es. The results (Fig. 6 and Table 1) show a lowering of Qmax for central guanines, but simultaneous enhancement for 3′- and 5′-side guanines as well as a change in the ϕ2σ2 values for most guanines within clusters of guanines containing bulges. The most obvious variation in ϕ2 was observed at the 5′ guanine, which appeared to partially lose its greater ionization probability. However, no distance effects were observed: the ionization yield of III- to VI-G1G2, located 8 bp from the perturbed guanine cluster, was not affected. These observations are consistent with previously reported results (Spassky and Angelov, 1997): helix destabilization introduced by a single base mismatch at I-G4 or I-G8 induces changes in the radical cation yield as well as its chemical reactivity, but only for the nearest-neighbor guanines. Again, there were no distal effects toward the unmodified -GGG- run, located 6 bp away. Surprisingly, the change in the biphotonic ionization parameters for destabilized sites was not as dramatic as expected. The structure of oligonucleotides containing bulges with two unpaired bases was not solved, but it is likely that these sequences form a heterogeneous population of energetically possible configurations. As a result, the measured photochemical yields might represent values averaged over a set of different configurations, thus smoothing the effect that would occur in a single perturbed conformation.

The decrease in the quantum yield of cyclobutane pyrimidine dimers upon increasing laser intensity is sequence dependent

Treatment by endonuclease III, which recognizes thymine glycols, was not found to yield additional cleavage with regard to directly loaded laser irradiated DNA fragments (not shown). The low level of induction of thymine glycols was further confirmed by direct chemical analysis (Douki et al., 2001, 2004). This observation raised the question of whether triplet-excited pyrimidine can be a substrate for ionization. To this end, we subjected a 98-bp EcoRI-HindIII excision fragment (Beylot and Spassky, 2001; Guillo et al., 1996) containing sequence-I to either a single high-intensity (E = 0.1 J/cm2) pulse or to multiple low-intensity pulses (E = 0.002 J/cm2) with the same total irradiation dose (Fig. 7). The low-lying pyrimidine triplet excited states were probed through induction of cyclobutane pyrimidine dimers as determined by digestion with T4 endonuclease V and sequencing gel electrophoresis of the bottom 5′-labeled pyrimidine-rich strand. Consistent with previous observations (Guillo et al., 1996), the distribution of pyrimidine dimers (Pyr<>Pyr) at low laser intensity (Fig. 7) was irregular and strongly dependent on the neighboring base sequence. Interestingly, the high-intensity pattern displayed substantial differences in the quantum yield for all T<>T dimers, but this difference was not proportionally equal from one site to another. The most dramatic effect was observed for isolated TT, especially within GTTA runs. The decrease in the quantum efficiency at high intensity most likely originates from depletion of the T1 population as a result of leakage through the photoionization channel. Surprisingly, at high intensity, no bleaching of the quantum yield was observed for C<>C dimers within the two -CCC- sequences. This might be attributed to a higher rate of C<>C formation with respect to the inverse of the laser pulse duration, irregardless of the type (triplet, singlet, or excimer) of the low-lying excited state precursor.

This experiment provides clear evidence that transient thymine radical cations are generated in addition to the guanine radical cations. Both radicals arise with a comparable efficiency (the quantum yield of T<>T bleaching is similar to that of G+) from the photoionization of T1 excited molecules. The lack of formation of thymine glycols is evidence for a very short survival time of the thymine radical cation, which decays before chemical reaction.

DISCUSSION

Our main objective was to map the distribution of the T1 excited bases and radical cations generated by high-intensity UV laser photolysis of DNA fragments of defined sequences. It is noteworthy that neither low-intensity monophotonic photochemistry at 254 nm nor time-resolved optical spectroscopy is a straightforward tool to accomplish this task. Therefore, we applied biphotonic photolysis as a variant of single-beam, single-color “pump-probing” technique. The first photon yields metastable T1 excited molecules, which are simultaneously probed by photoionization upon absorption of a second photon at the same wavelength. Because the transient radical cations of individual bases within DNA cannot be monitored by optical spectroscopy, we analyzed the distribution of the resulting oxidative lesions by gel electrophoresis. The enzymatic (Fpg glycosylase) and piperidine-induced cleavage of UV laser-irradiated DNA fragments revealed that cleavage occurred exclusively at guanines. In comparison, control experiments performed with endonuclease III showed an absence of formation of detectable amounts of thymine glycols, in accordance with previous studies (Melvin et al.1998). Keeping this important point in mind, extensive tandem high performance liquid chromatography-mass spectrum/mass spectrum analysis of the major DNA oxidative lesions was carried out (Douki et al., 2001, 2004). Under the same experimental conditions, >85% of oxidative DNA lesions involved guanine residues. Moreover, the saturation fluence was considerably lower for the generation of 8-oxodGuo compared to that of oxidative lesions of cytosine, thymine, and adenine. In contrast, the four nucleobases free in solution displayed similar σ2ϕ2 values, whereas the intersystem-crossing yield of guanine was almost the lowest (Nikogosyan et al., 1982; Nikogosyan and Letokhov, 1983; Nikogosyan, 1990). Together, these data clearly show that guanines are the ultimate target for biphotonic oxidation of DNA. These features have already been tentatively explained by the occurrence of hole migration and preferential trapping by guanines (Angelov et al., 1997; Douki et al., 2001, 2004).

In this work we observed marked variation of Qmax and Es for individual guanines, depending on the primary and secondary DNA structures (Table 1). This corresponds to proportional and inversely proportional variation of ϕ1 and ϕ2, respectively (see Appendix). Note that we consider the variation in the parameter ϕ2σ2 as being exclusively due to the variation in ϕ2, because the σ2 value for the second transition to the highly excited quasi-Rydberg continuum manifold should be relatively independent on the sequence of flanking bases. Thus, the experimental data (Figs. 4–6 and Table 1) unambiguously demonstrate that both the population of T1 and the formation of the radical cation are strongly dependent on neighboring bases and local structural deformations. For example, the T1 excitation probabilities ϕ1 for guanines I-G7 and I-G8 differ by nearly one order of magnitude. The same difference in the value of ϕ2σ2 was observed between I-G2 and I-G3. It is interesting to note that this heterogeneity was not observed in single-stranded oligonucleotides, as all guanines displayed equal ϕ1 and ϕ2σ2 values (Fig. 5 and data not show).

Because the value of Qmax (respectively ϕ1) is a measure of the T1 population, we consider its variation to be a strong indication of energy-transfer processes, which lead to redistribution of the initial excited-state population. The occurrence of energy transfer in DNA has been widely discussed in the literature and all possible mechanisms were proposed to explain divergences of migration distances found, ranging from few angstroms to several tens of nanometers (Isenberg et al., 1967; Guéron et al., 1967; Guéron and Shulman, 1968; Eisinger and Lamola, 1971; Vigny and Ballini, 1977; Nikogosyan et al., 1985; Georghiou et al., 1990). Our data are consistent with the involvement of energy transfer over short distances, not exceeding few nucleotides. Similarly, the strong sensitivity of the value for ϕ2σ2 might be explained by the occurrence of hole transfer and subsequent trapping by guanines. Recent data suggest that this process is highly sensitive to the primary and secondary structure of DNA.

An alternative to the donor-acceptor hypothesis would be a very important change of values of intrinsic parameters ϕ1 and ϕ2 induced by DNA sequence environment. However, this is in contradiction with available experimental results, namely environmental invariability of S1 lifetime (Kang et al., 2002) and phosphorescence quantum yields (Nikogosyan, 1990; Cadet and Vigny, 1990). The electron ejection threshold is below 6.4 eV (Candeias et al., 1992; Candeias and Steenken, 1993; Melvin et al., 1995, 1996) and the quantum yield displays similar values for the four nucleotides, either frees or incorporation into homooligomers, independently on differences in their ionization energies in vacuum (Hush and Cheung, 1975; Orlov et al., 1976; Voityuk et al., 2000). Therefore, it looks very improbable that relatively small variations (Saito et al., 1995; Nakatani et al., 1997; Yoshioka et al., 1999) of the ionization energy induced by the environment can induce such important variations of electron ejection probability ϕ2 we observe at ∼8.3 eV excitation energy.

In the model presented in the Appendix, nucleic acid residues either isolated or within DNA are considered to be independent with respect to the biphotonic ionization process; i.e., energy- and charge-transfer phenomena are not included. To qualitatively illustrate how donor-acceptor effects could be accounted for in this model, we consider the following simplified scheme (Fig. 8). An arbitrary base Bi (energy donor) is excited by one-photon absorption to S1i, then nonradiatively to T1i with a quantum yield (intersystem crossing yield) ϕ1i. Upon energy transfer (or migration) through bases Bi-Bj, at a distance of λij (expressed in number of bases), the base Bj (energy trap) becomes T1j excited by a trapping efficiency ζij, via either the S1j state (S-S energy transfer) or directly (T-T energy transfer). Assuming that the energy migration is faster than the laser pulse duration, the excitation parameter for T1j is K1j(T − T) = ϕ1iλijζijσ1i or K1j(S − S) = ϕ1jλijζijσ1i for T-T or S-S type energy migration, respectively. During the laser pulse, the T1j excited molecules are further photoionized with a probability ϕ2j, via excitation to the Tnj state, and electron ejection in the bulk. Following hole migration over the distance ρjk (in number of bases), presumably through a combination of single-step superexchange and successive electron hopping over bases j–k (Jortner et al., 1998; Bixon et al., 1999; Giese et al., 1999; Giese, 2002), the base Bk ultimately traps the radical cation with the probability ξjk. In general, the expression for the ionization parameter K2k depends on whether the first step of the charge transport τjCT is faster or slower than the laser pulse duration τp. The literature values for τjCT are in the range from subnanoseconds (Wan et al., 1999, 2000) to microseconds. However, under our experimental condition of very low ground-state population depletion, the ratio τjCT/τp does not play an important role. For simplicity we assume that τjCT > τp, thus, the ionization parameter for base Bk is K2k = ρjkξjkϕ2jσ2j. These assumptions were checked by control experiments consisting of comparing values of QFpg for the DNA fragments submitted to exposure on another Nd:YAG laser (Quantel, Les Ulis, France) delivering pulses of 20-ns duration. We found no change of QFpg with the laser pulse duration (5 or 20 ns); i.e., in this time range QFpg depends on the laser pulse dose only. The corresponding expression for the quantum efficiency of ionization of the base Bk is (see Appendix):

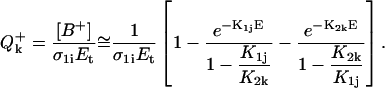graphic file with name M1.gif (1)
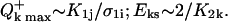graphic file with name M2.gif (2)

FIGURE 8.

FIGURE 8

Open in a new tab

Simplified scheme of the energy-migration mediated biphotonic ionization and hole transport of nucleobases within DNA.

These equations clarify the connection between the measurable Qmax and Es and the donor-acceptor parameters. It should be noted that, based on the values of excited-state energies for the four bases free in solution (Nikogosyan and Letokhov, 1983; Vigny and Ballini, 1977), the preferential energy trap should be thymine or guanine, depending on whether the energy migration involves T-T or S-S channels. Similar considerations suggest that the preferential hole trap should be guanine, which possesses the lowest oxidation potential (Hush and Cheung, 1975; Orlov et al., 1976). Interestingly, 5′-located guanines within clusters of two or more guanines were shown to display the lowest oxidative potential, thereby constituting the most preferential hole traps (Saito et al., 1995; Nakatani et al., 1997; Yoshioka et al., 1999; Breslin and Schuster, 1996). This is consistent with the highest observed values of ϕ2σ2 for these guanines (Table 1). The latter constitute an additional argument in favor of this model.

It should be emphasized that from one side this oversimplified illustrative model cannot describe the real experimental situation and from the other side, it is prematured to undertake a detailed mathematical description of the experimental data using rate equation formalisms. In fact, the corresponding mathematical model for energy- and charge-migration mediated biphotonic ionization in the case of DNA containing N bases, the analysis includes a system of 3N coupled linear differential equations containing a larger number of variable parameters. However, the use of such model calculations will remain dependent on arbitrary variable parameters, giving multiple solutions, unless systematic ab initio calculations and experimental data, aimed at evaluating migration rates and trajectories, are not provided.

Our system differs substantially from others using covalently attached photoexcited electron acceptors. Firstly, there is no charge separation or corresponding Coulomb attraction barrier, because the electron is ejected and hydrated in the bulk directly by photoionization. Secondly, each base is a potential hole injector, thereby its location is random. Thirdly, the distribution of oxidative lesions is probably mediated not only by electron transport, but also by energy migration processes. Although the first point simplifies the analysis, the latter two points make it more challenging. Despite the relatively simple situations so far considered: photoexcited electron acceptor located at a defined DNA site, a considerable discrepancy exists in the literature on such basic questions as the mechanisms, rates, and distances of electron migration. Fortunately, the theoretical basis of electron migration is being investigated to reconcile the divergent experimental data (Jortner, et al., 1998; Bixon et al., 1999; Conwell and Rakhmanova, 2000; Schlag et al., 2000; Bruisma et al., 2000; Giese, 2002). Whatever the exact mechanisms of the nonradiative redistribution of excitation energies and charges, our data (the range of variation of K1 and K2, remote effects to a local structural perturbation) are not consistent with efficient migration of energy and electron holes over long distances (>6–8 bp), at least for the DNA sequences used, which is in agreement with most of the literature data.

Finally, our finding that the distribution of triplet-state molecules is heterogeneous and dependent on DNA sequence and structure might have important implications in DNA-protein footprinting experiments using conventional 254-nm radiation (Becker and Wang, 1984; Becker et al., 1988). Due to its technical simplicity, the latter technique is attractively applied to study DNA-protein interactions. The tacit assumption so far implied is that the excitation yields for each type of nucleobases are constants independently on the sequence environment. Consequently, the conformational sensitivity of DNA toward the generation of monophotonic bimolecular photoproducts such as (6–4) TC adducts and T<>T dimers has been attributed solely to the chemical reactivity of excited nucleobases. Our findings now suggest that the occurrence of photofootprinting originates as well from physical processes, such as energy migration, as from variations in the chemical reactivity. The involvement of donor-acceptor effects also provides a rationale for the interpretation of UV laser-induced DNA-protein footprinting and cross-link formation.

CONCLUSION

Experimental data have been provided demonstrating that lower-lying triplets excited as well as photoionized guanine residues are heterogeneously distributed within duplex DNA with dependence on neighboring base sequences. The introduction of local perturbations in base stacking and basepairing at clustered guanines resulted in variations in the biphotonic ionization yield within the perturbed region, but detectable distal effects were not observed. Rate equation model fitting of the experimental data allowed the results to be generalized in terms of energy-transfer mediated biphotonic ionization and hole transfer toward guanines. Further experiments aimed at establishing correlations between DNA sequence alignment and guanine ionization are under way.

Acknowledgments

We thank Dr. R. Wagner and Dr. J. Cadet for critical input.

D.A. acknowledges the North Atlantic Treaty Organization, grant No. CLG 976174; the National Science Fund, BG grant No. K902; the Université Paris VI and ENS-Lyon for the Invited Professor Fellowship; and the Centre National de la Recherche Scientifique for the Poste Rouge Grant.

APPENDIX

The biphotonic ionization of monomeric DNA compounds under nanosecond UV laser photolysis occurs according to the following simplified scheme (Nikogosyan et al., 1982; Nikogosyan and Letokhov, 1983): 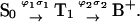Inline graphic In establishing this model, we assume that all relaxation processes from S1 and Tn proceed in a time considerably shorter than the laser pulse duration (Kang et al., 2002), whereas the lifetime of the intermediate T1 state, which is in the microsecond time range, is longer (Vigny and Ballini, 1977; Cadet and Vigny, 1990). For an optical thin layer (optical density < 0.1) condition and assuming a rectangular pulse shape, the normalized radical cation yield at the end of the laser pulse [B+] is given by the following analytical solution of the corresponding rate equations for the populations (Nikogosyan et al., 1982, Nikogosyan and Letokhov, 1983):

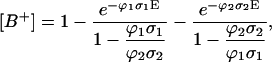graphic file with name M4.gif (1a)

where σ1 and σ2 are the absorption cross sections of the corresponding transitions at 266 nm; for DNA, σ1 = 2.3 × 10−17 cm2 (ɛ = 6000 M−1 cm−1); E is the laser pulse dose in [photons/cm2]; ϕ1 and ϕ2 are the intersystem crossing yield and the quantum yield of photoionization from the state T1, respectively.

In general, precise determination of the true quantum yield of multi- (bi-) photonic processes is very difficult because the actual number of photons absorbed is unknown. Therefore, we deal with the apparent quantum yield or “quantum efficiency”, defined as the quantum yield under linear absorption approximation: Q = N/Pabs, where N is the number of photoproducts (for example radical cations B+) and Pabs is the apparent number of absorbed photons, determined by the ground-state absorption at low photonic intensity (the fraction of photons absorbed measured by a conventional spectrophotometer). In the case of an optical thin layer, from the definition and Eq. 1a it follows:

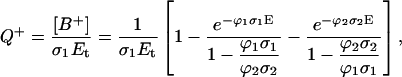graphic file with name M5.gif (2a)

where Et is the total irradiation dose expressed in [photons/cm2].

The curve, representing the dependence of Q on E, displays an initial linear increase followed by saturation and a gradual decrease after passing through a maximum. The dependence is completely defined by a set of two parameters. These may be either the saturation parameters of the two transition steps ϕ1σ1 and ϕ2σ2 present in Eq. 2a, or the maximum value of the quantum efficiency Qmax and the saturation dose Es defined from the equation: Q(Es) = (1 − e−1) × Qmax = 0.63 × Qmax. The latter two parameters are directly measurable from experimental curves, but in the general case they do not have an immediate spectroscopic meaning. In contrast, the former parameters are model derived, but they have a defined spectroscopic meaning. It should be pointed out that each pair of parameters from one set can be presented as a function of the two parameters from the other set, but in the general case the expressions are not simple. In the particular case when the values of ϕ1σ1 and ϕ2σ2 are very different from one another, as in the case of nucleobases, simple relationships between the two sets of parameters exist. Taking into account the experimentally evaluated values of ϕ1, σ1, and ϕ2σ2 for free nucleobases (Nikogosyan et al., 1982), ϕ1 ∼ 10−3–10−2, σ1 ∼ 2.3–5 × 10−17 cm2 (ϕ1σ1 ∼ 2 × 10−20–5.10−19), ϕ2σ2 > 5 × 10−18 cm2 it follows that ϕ1σ1 ≪ ϕ2σ2. The meaning of this inequality is that saturation of Q within the laser pulse dose increase is due to saturation of the second transition, while the ground state still remains very far from depletion. Under these conditions the following approximate relations can be derived:

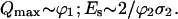graphic file with name M6.gif (3a)

It should be noted that the greater the inequality ϕ1σ1 ≪ ϕ2σ2 the better the approximation is in Eq. 3a.

In general, this model can be applied to polymers (DNA, RNA), with the limitation that no energy- and/or charge-transfer processes are operative. In the latter case a simplified illustrative generalization is presented in the Discussion.

Dimitar Angelov's permanent address is Institute of Solid State Physics, Bulgarian Academy of Sciences, 72 Tsarigradsko Shaussee Blvd., 1784 Sofia, Bulgaria.

References

  1. Abdurashidova, G., M. B. Danailov, A. Ochem, G. Triolo, V. Djeliova, S. Radulescu, A. Vindigly, S. Riva, and A. Filaschi. 2003. Localization of protein bound to replication origin of human DNA along the cell cycle. EMBO J. 22:4294–4303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Angelov, D., M. Charra, C. W. Müller, J. Cadet, and S. Dimitrov. 2003. Solution study of the NF-κB p50-DNA complex by UV laser protein-DNA cross-linking. Photochem. Photobiol. 77:592–596. [DOI] [PubMed] [Google Scholar]
  3. Angelov, D., M. Charra, M. Seve, J. Côté, S. Khochbin, and S. Dimitrov. 2000. Differential remodeling of the HIV-1 nucleosome upon transcription activators and SWI/SNF complex binding. J. Mol. Biol. 302:315–326. [DOI] [PubMed] [Google Scholar]
  4. Angelov, D., F. Lenouvel, F. Hans, C. V. Müller, P. Bouvet, E. Moudrianakis, J. Cadet, and S. Dimitrov. 2004. The histone octamer is “invisible” when NF-κB binds to the nucleosome. J. Biol. Chem. 279:42374–42382. [DOI] [PubMed] [Google Scholar]
  5. Angelov, D., E. Novakov, S. Khochbin, and S. Dimitrov. 1999. Ultraviolet laser footprinting of histone H1(0)-four-way junction DNA complexes. Biochemistry. 38:11333–11339. [DOI] [PubMed] [Google Scholar]
  6. Angelov, D., A. Spassky, M. Berger, and J. Cadet. 1997. High-intensity UV laser photolysis of DNA and purine 2′-deoxyribonucleosides: formation of 8-oxopurine damage and oligonucleotide strand cleavage as revealed by HPLC and gel electrophoresis studies. J. Am. Chem. Soc. 119:11373–11380. [Google Scholar]
  7. Angelov, D., J. M. Vitolo, V. Mutskov, S. Dimitrov, and J. Hayes. 2001. Preferential interaction of the core histone tail domains with linker DNA. Proc. Natl. Acad. Sci. USA. 98:6599–6604. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Becker, M. M., D. Lesser, M. Kurpiewsky, A. Baranger, and L. Jen-Jacobsen. 1988. Ultraviolet footprinting accurately maps sequence-specific contacts and DNA kinking in Eco RI endonuclease-DNA complex. Proc. Natl. Acad. Sci. USA. 85:6247–6251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Becker, D., and M. D. Sevilla. 1993. The chemical consequences of radiation damage to DNA. Adv. Radiat. Biol. 17:121–180. [Google Scholar]
  10. Becker, M. M., and J. C. Wang. 1984. Use of light for footprinting DNA in vivo. Nature. 309:682–687. [DOI] [PubMed] [Google Scholar]
  11. Beylot, B. 1998. PhD thesis. University Paris VI, Paris, France.
  12. Beylot, B., and A. Spassky. 2001. Chemical probing shows that the intron-encoded endonuclease I-SceI distorts DNA through binding in monomeric form to its homing site. J. Biol. Chem. 276:25243–25253. [DOI] [PubMed] [Google Scholar]
  13. Bixon, M., B. Giese, S. Wessely, T. Langenbacher, M. E. Michel-Beyerle, and J. Jortner. 1999. Long-range charge hopping in DNA. Proc. Natl. Acad. Sci. USA. 96:11713–11716. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Breslin, D. T., and G. B. Schuster. 1996. Anthraquinone photonucleases: mechanisms for GG-selective and nonselective cleavage of double-stranded DNA. J. Am. Chem. Soc. 118:2311–2319. [Google Scholar]
  15. Bruisnma, R., G. Grüner, M. R. D'Orsogna, and J. Rudnick. 2000. Fluctuation-facilitated charge migration along DNA. Phys. Rev. Lett. 85:4393–4396. [DOI] [PubMed] [Google Scholar]
  16. Burrows, C. J., and J. Muller. 1998. Oxidative nucleobase modifications leading to strand scission. Chem. Rev. 98:1109–1151. [DOI] [PubMed] [Google Scholar]
  17. Cadet, J., and P. Vigny. 1990. The photochemistry of nucleic acids. In Bioorganic Photochemistry. H. Morrison, editor. John Wiley & Sons, Hoboken, NJ. 1–272.
  18. Candeias, L. P., P. O'Neill, G. D. D. Jones, and S. Steenken. 1992. Ionization of polynucleotides and DNA in aqueous solution by 193 nm pulsed laser light: identification of base-derived radicals. Int. J. Radiat. Biol. 61:15–20. [DOI] [PubMed] [Google Scholar]
  19. Candeias, L. P., and S. Steenken. 1993. Electron transfer in di(deoxy) nucleoside phosphates in aqueous solution: rapid migration of oxidative damage (via adenine) to guanine. J. Am. Chem. Soc. 115:2437–2440. [Google Scholar]
  20. Colleaux, L., L. D'Auriol, F. Galibert, and B. Dujon. 1988. Recognition and cleavage site of the intron-encooled omega transposase. Proc. Natl. Acad. Sci. USA. 85:6022–6026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Conwell, E. M., and S. V. Rakhmanova. 2000. Polarons in DNA. Proc. Natl. Acad. Sci. USA. 97:4556–4560. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Croke, D. T., W. Blau, C. OhUigin, J. M. Kelly, and D. J. McConnell. 1988. Photolysis of phosphodiester bond in plasmid DNA by high-intensity UV laser irradiation. Photochem. Photobiol. 47:527–536. [DOI] [PubMed] [Google Scholar]
  23. Cullis, P. M., M. E. Malone, and L. A. Merson-Davies. 1996. Guanine radical cations are precursors of 7,8-dihydro-8oxo-2′-deoxyguanosine but are not precursors of immediate strand breaks in DNA. J. Am. Chem. Soc. 118:2775–2781. [Google Scholar]
  24. Dandliker, P. J., R. E. Holmlin, and J. K. Barton. 1997. Oxidative thymine dimer repair in the DNA helix. Science. 275:1465–1468. [DOI] [PubMed] [Google Scholar]
  25. Douki, T., D. Angelov, and J. Cadet. 2001. UV laser photolysis of DNA: effect of duplex stability on charge-transfer efficiency. J. Am. Chem. Soc. 123:11360–11366. [DOI] [PubMed] [Google Scholar]
  26. Douki, T., and J. Cadet. 1999. Modification of DNA bases by photosensitized one-electron oxidation. Int. J. Radiat. Biol. 75:571–581. [DOI] [PubMed] [Google Scholar]
  27. Douki, T., J.-L. Ravanat, D. Angelov, J. R. Wagner, and J. Cadet. 2004. Effects of duplex stability on charge transfer efficiency within DNA. Top. Curr. Chem. 236:1–25. [Google Scholar]
  28. Eisinger, J., and A. A. Lamola. 1971. The excited state of nucleic acids. In Excited States of Proteins and Nucleic Acids. R. F. Steiner and I. Weinryb, editors. Plenum Press, New York. 107–198.
  29. Fukui, K., and K. Tanaka. 1998. Distance dependence of photoinduced electron transfer in DNA. Angew. Chem. Int. Ed. Engl. 37:158–161. [Google Scholar]
  30. Georghiou, S., S. Zhu, R. Weidner, C.-R. Huang, and G. Ge. 1990. Singlet-singlet energy transfer along the helix of a double-stranded nucleic acid at room temperature. J. Biomol. Struct. Dyn. 8:657–674. [DOI] [PubMed] [Google Scholar]
  31. Giese, B. 2002. Electron transfer in DNA. Curr. Opin. Chem. Biol. 6:612–618. [DOI] [PubMed] [Google Scholar]
  32. Giese, B., S. Wessely, M. Spormann, U. Lindemann, E. Meggers, and M. E. Michel-Beyerle. 1999. On the mechanism of long-range electron transfer through DNA. Angew. Chem. Int. Ed. Engl. 38:996–998. [DOI] [PubMed] [Google Scholar]
  33. Görner, H. 1994. Photochemistry of DNA and related biomolecules: quantum yield and consequences of photoionization. Photochem. Photobiol. 26:117–139. [DOI] [PubMed] [Google Scholar]
  34. Gregoli, S., M. Olast, and A. Bertinchamps. 1979. Charge migration phenomena in γ-irradiated costacking complexes of DNA nucleotides. II. An ESR study of various complexes in frozen solution. Radiat. Res. 77:417–431. [PubMed] [Google Scholar]
  35. Guéron, M., J. Eisinger, and R. G. Shulman. 1967. Excited states of nucleotides and singlet energy transfer in polynucleotides. J. Chem. Phys. 47:4077–4091. [DOI] [PubMed] [Google Scholar]
  36. Guéron, M., and R. G. Shulman. 1968. Energy transfer in polynucleotides. Annu. Rev. Biochem. 37:571–596. [DOI] [PubMed] [Google Scholar]
  37. Guillo, L. A., B. Beylot, P. Vigny, and A. Spassky. 1996. Formation of cyclobutane thymine dimers from UVA photosensitization of pyridopsoralen monoadducted DNA. Photochem. Photobiol. 64:349–355. [DOI] [PubMed] [Google Scholar]
  38. Hall, D. B., R. E. Holmlin, and J. K. Barton. 1996. Oxidative DNA damage through long-range electron transfer. Nature. 382:731–735. [DOI] [PubMed] [Google Scholar]
  39. Hall, D. B., S. O. Kelly, and J. K. Barton. 1998. Long-range and short-range oxidative damage to DNA: photoinduced damage to guanines in ethidium-DNA assemblies. Biochemistry. 37:15933–15940. [DOI] [PubMed] [Google Scholar]
  40. Henderson, P. T., D. Jones, G. Hampikian, Y. Kan, and G. Schuster. 1999. Long-distance charge transport in duplex DNA: the phonon-assisted polaron-like hopping mechanism. Proc. Natl. Acad. Sci. USA. 96:8353–8358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Hush, N. S., and A. S. Cheung. 1975. Ionization potentials and donor properties of nucleic acid bases and related compounds. Chem. Phys. Lett. 34:11–13. [Google Scholar]
  42. Isenberg, I., R. Rosenbluth, and S. L. Baird, Jr. 1967. Comparative phosphorescence quenching of DNAs of different composition. Biophys. J. 7:365–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Jortner, J., M. Bixon, T. Langenbacher, and M. E. Michel-Beyerle. 1998. Charge transfer and transport in DNA. Proc. Natl. Acad. Sci. USA. 95:12759–12765. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Kang, H., K. T. Lee, B. Jung, Y. J. Ko, and S. K. Kim. 2002. Intrinsic lifetimes of the excited states of DNA and RNA bases. J. Am. Chem. Soc. 124:12958–12959. [DOI] [PubMed] [Google Scholar]
  45. Kasai, H., Z. Yamaizumi, M. Berger, and J. Cadet. 1992. Photosensitized formation of 7,8-dihydro-8-oxo-2′-deoxyguanosine (8-hydroxy-2′-deoxyguanosine) in DNA by riboflavin: a non singlet oxygen mediated reaction. J. Am. Chem. Soc. 114:9692–9694. [Google Scholar]
  46. Kelley, S., and J. K. Barton. 1999. Electron transfer between bases in double helical DNA. Science. 283:375–381. [DOI] [PubMed] [Google Scholar]
  47. Kelley, S. O., R. E. Holmlin, E. D. A. Stemp, and J. K. Barton. 1997. Photoinduced electron transfer in ethidium-modified DNA duplexes: dependence on distance and base stacking. J. Am. Chem. Soc. 119:9861–9870. [Google Scholar]
  48. Kovalsky, O. I., I. G. Panyutin, and E. I. Budowsky. 1990. Sequence-specificity of the alkali-sensitive lesions induced in DNA by high-intensity ultraviolet laser radiation. Photochem. Photobiol. 52:509–517. [DOI] [PubMed] [Google Scholar]
  49. Ly, D., L. Sanii, and G. B. Schuster. 1999. Mechanism of charge transport in DNA: internally-linked anthraquinone conjugates support phonon-assisted polaron hopping. J. Am. Chem. Soc. 121:9400–9410. [Google Scholar]
  50. Malone, M. E., M. C. R. Symons, and A. W. Parker. 1994. DNA in glasses at 77 K: high energy ionizing radiation versus UV electron ejection. Int. J. Radiat. Biol. 66:511–515. [DOI] [PubMed] [Google Scholar]
  51. Meggers, E., M. E. Michel-Beyerle, and B. Giese. 1998. Sequence dependent long range hole transport in DNA. J. Am. Chem. Soc. 120:12950–12955. [Google Scholar]
  52. Melvin, T., S. Botchway, A. W. Parker, and P. O'Neill. 1996. Migration of photo-induced oxidative damage in models for DNA. J. Am. Chem. Soc. 118:10031–10036. [Google Scholar]
  53. Melvin, T., S. M. T. Cunniffe, P. O'Neill, A. W. Parker, and T. Roldan-Arjona. 1998. Guanine is the target for direct ionization damage in DNA, as detected using excision enzymes. Nucleic Acids Res. 26:4935–4942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Melvin, T., M. A. Plumb, S. W. Botchway, P. O'Neill, and A. W. Parker. 1995. 193 nm light induced single strand breakage of DNA predominantly at guanine. Photochem. Photobiol. 61:584–591. [DOI] [PubMed] [Google Scholar]
  55. Mutskov, V., D. Gerber, D. Angelov, J. Ausio, J. Workman, and S. Dimitrov. 1998. Persistent interactions of core histone tails with nucleosomal DNA following acetylation and transcription factor binding. Mol. Cell. Biol. 18:6293–6304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Nagaich, A. K., D. A. Walker, R. Wolford, and G. L. Hager. 2004. Rapid periodic binding and displacement of the glucocorticoid receptor during chromatin remodeling. Mol. Cell. 14:163–174. [DOI] [PubMed] [Google Scholar]
  57. Nakatani, K., J. Shirai, S. Sando, and I. Saito. 1997. Guanine specific DNA cleavage by photoirradiation of dibenzoyldiazomethane-oligonucleotide conjugates. J. Am. Chem. Soc. 119:7626–7635. [Google Scholar]
  58. Nikogosyan, D. N. 1990. Two-quantum photochemistry of nucleic acids: comparison with conventional low-intensity UV photochemistry and radiation chemistry. Int. J. Radiat. Biol. 37:233–299. [DOI] [PubMed] [Google Scholar]
  59. Nikogosyan, D. N., D. A. Angelov, and A. A. Oraevsky. 1982. Determination of parameters of excited states of DNA and RNA bases by laser UV photolysis. Photochem. Photobiol. 35:627–635. [DOI] [PubMed] [Google Scholar]
  60. Nikogosyan, D. N., and V. S. Letokhov. 1983. Nonlinear laser photophysics, photochemistry and photobiology of nucleic acids. Riv. Nuovo Cimento. Soc. Ital. 6:1–74. [Google Scholar]
  61. Nikogosyan, D. N., A. A. Oraevsky, and V. S. Letokhov. 1985. Two-step picosecond UV excitation of polynucleotides and energy transfer. Chem. Phys. 97:31–34. [Google Scholar]
  62. O'Neill, P., and M. Fielden. 1994. Primary free radical processes in DNA. Adv. Radiat. Biol. 17:53–121. [Google Scholar]
  63. Orlov, V. M., A. N. Smirnov, and Y. M. Varshavski. 1976. Ionization potentials and electron-donor ability of nucleic acid bases and their analogs. Tetrahedron Lett. 48:4377–4378. [Google Scholar]
  64. Pashev, I. G., S. I. Dimitrov, and D. Angelov. 1991. Cross-linking proteins to nucleic acids by ultraviolet laser irradiation. Trends Biochem. Sci. 16:323–326. [DOI] [PubMed] [Google Scholar]
  65. Ravanat, J.-L., M. Berger, S. Boiteux, J. Laval, and J. Cadet. 1993. Excision of 7,8-dihydro 8-oxoguanine from DNA by the Fpg protein. J. Chem. Phys. 90:871–879. [Google Scholar]
  66. Russmann, C., M. Truss, A. Fix, C. Naumer, T. Herrmann, J. Schmitt, J. Stollhoff, R. Beigang, and M. Beato. 1997. Crosslinking of progesterone receptor to DNA using tunable nanosecond, picosecond and femtosecond UV laser pulses. Nucleic Acids Res. 25:2478–2484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Saito, I., M. Takayama, H. Sugiyama, and K. Nakatani. 1995. Photoinduced DNA cleavage via electron-transfer: demonstration that guanine residues located 5′ to guanine are the most electron-donating sites. J. Am. Chem. Soc. 117:6406–6407. [Google Scholar]
  68. Schlag, E. W., D.-Y. Yang, S.-Y. Sheu, H. L. Selzle, S. H. Lin, and P. M. Rentzepis. 2000. Dynamical principles in biological processes: a model of charge migration in proteins and DNA. Proc. Natl. Acad. Sci. USA. 97:9849–9854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Spassky, A., and D. Angelov. 1997. Influence of the local helical conformation on the guanine modifications generated from one-electron DNA oxidation. Biochemistry. 36:6571–6576. [DOI] [PubMed] [Google Scholar]
  70. Spassky, A., and D. Angelov. 2002. Temperature-dependence of UV laser one electron oxidative guanine modifications as a probe of local stacking fluctuations and conformational transitions. J. Mol. Biol. 323:9–15. [DOI] [PubMed] [Google Scholar]
  71. Vigny, P., and J.-P. Ballini. 1977. Excited states of nucleic acids at 300 K and electronic energy transfer. In Excited States in Organic Chemistry and Biochemistry. B. Pullman and N. Goldblum, editors. D. Riedel, Boston, MA. 1–13.
  72. Voityuk, A., J. Jortner, M. Bixon, and M. Rösch. 2000. Energetics of hole transfer in DNA. Chem. Phys. Lett. 324:430–434. [Google Scholar]
  73. Wan, C. Z., T. Fiebig, S. O. Kelley, C. R. Treadway, J. K. Barton, and A. H. Zewail. 1999. Femtosecond dynamics of DNA-mediated electron transfer. Proc. Natl. Acad. Sci. USA. 96:6014–6019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Wan, C. Z., T. Fiebig, O. Schiemann, J. K. Barton, and A. H. Zewail. 2000. Femtosecond direct observation of charge transfer between bases in DNA. Proc. Natl. Acad. Sci. USA. 97:14052–14055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Yoshioka, Y., Y. Kitagawa, Y. Takano, K. Yamaguchi, T. Nakamura, and I. Saito. 1999. Experimental and theoretical studies on the selectivity of GGG triplets toward one-electron oxidation in B-form DNA. J. Am. Chem. Soc. 121:8712–8719. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES