Abstract
Mammal life history traits relating to growth and reproduction are extremely diverse. Sibling rivalry may contribute to selection pressures influencing this diversity, because individuals that are relatively large at birth typically have an advantage in competition for milk. However, selection for increased growth rate is likely to be constrained by kin selection and physiological costs. Here, we present and test a model examining the ESS (evolutionarily stable strategy) balance between these constraints and advantages associated with increased prenatal growth in mammal sibling rivalry. Predictions of the model are supported by results of comparative analyses for the Carnivora and Insectivora, which demonstrate an increase in prenatal growth rate with increasing intensity of postnatal scramble competition, and a decrease in postnatal growth rate relative to size at birth. Because increased prenatal growth rates are predicted to select for reduced gestation length under certain conditions, our study also indicates that sibling rivalry may contribute to selection pressures influencing variation in altriciality and precociality among mammals.
Competition between siblings is common among species where young share a “nursery” during early development, because the demand for resources by offspring in such systems commonly exceeds the supply of maternal investment (1, 2). In mammals, several lines of evidence suggest that the intensity of sibling competition within litters is related to the number of offspring competing for access to milk from each nipple. In extreme cases, where offspring numbers actually exceed the number of nipples, the consequences of increased competition for milk can be fatal (3–5). More typically, the average offspring number per nipple is only around 0.5 (6), and so it could be argued that competition for access to nipples is negligible. However, factors such as restriction of access to only one side of the mother during suckling, and the regular depletion of certain mammae for some of the time, mean that two or more siblings often compete for access to each undepleted gland (6, 7). Moreover, because competing siblings typically remain firmly attached to a nipple until it is depleted, there is little opportunity for the same nipple to be used by different offspring in succession (7). Nonlethal effects of sib-competition are thus evident even where offspring numbers are less than the number of available nipples (1, 8).
Productivity gradients across mammary glands are also likely to intensify competition, because siblings will often compete for the most productive nipples. Evidence for variation in milk availability at different nipples is found in a variety of mammals, although patterns differ between taxa (1). In felids, for example, the rear mammary glands are generally more productive (9), whereas in ungulates (especially pigs) anterior nursing sites are favored (10). Individual growth rates vary significantly according to success in competition for these most productive suckling sites, and relatively large individuals are typically more successful in gaining access to them. In domestic pigs, for example, heavier young are most often found sucking the anterior nipples and grow more quickly as a result (10).
Here, we explore the consequences of within-litter sib-competition for pre- and postnatal growth rates in mammals. In particular, we predict that increased prenatal growth rates should generate a competitive advantage in scrambles for access to nipples or teats and hence milk supply, because individuals that are relatively large at birth typically have an advantage in competition with smaller siblings that is maintained during development (1, 11). However, any advantages of increased prenatal growth are likely to be constrained by kin selection (12, 13) and by costs related to higher than optimal prenatal growth (14). An ESS (evolutionarily stable strategy; ref. 15) model, described below, examines the balance between these constraints and the competitive advantages of higher prenatal growth rates. We also explore the potential consequences of increased prenatal growth rates from a maternal perspective, and investigate whether sibling rivalry is likely to have consequences for postnatal growth rates in mammals.
Theoretical Predictions
The model presented is an adaptation of a general scramble model (16), modified for the case of mammalian sibling rivalry for access to milk. Each nipple is seen as a unitary resource around which sibs compete: the more sibs per nipple, the greater the sib competition. We assume that two conditions apply during suckling. In the “uncompetitive” condition each offspring has unrestricted access to at least one undepleted mammary gland. In the “competitive,” access to nipples is restricted, so that there is an advantage to being bigger at birth to gain a greater share of the milk. Here, milk gains depend on size at birth and hence on growth rate during prenatal development.
We make the important assumption that over the range of variation seen, the milk availability per offspring in a litter is independent of the intensity of competition for nipples. Thus, although nipple number is likely to increase across species with litter size and total milk supply, we are assuming that when there are more offspring per nipple, they compete for proportionately more total resource. This assumption has a critical bearing on the ESS solution (see Appendix). It is based on evidence from our comparative analyses for carnivores. After controlling for adult body mass, evolutionary changes in offspring number per nipple are independent of changes in maternal investment measured as offspring mass at first intake of solids (r2 = 0.11; F1,19 = 2.22; P > 0.15). We argue elsewhere (P.S. and G.A.P., unpublished work) that the number of nipples is constrained by maximum litter size, and hence by the variation about the mean litter size. Thus, control of sibling rivalry by changing the number of nipples will be constrained.
An offspring's fitness benefits are expected to be monotonic increasing with its milk uptake, to some asymptotic maximum (Fig. 1a). Given that unilateral increases in fetal growth can increase competitive gains, the relative amounts of milk gained in competitive and uncompetitive conditions are important in determining how much the ESS average prenatal growth rate will be increased by postnatal sib-competition. Our model (see Appendix for analysis) makes the following assumptions:
- 1.
Prenatal growth rate in utero is influenced by genes expressed in the embryo (offspring “control”). If the mother controls prenatal growth rates, offspring growth rate will be independent of competition for nipples.
- 2.
Gains during competitive suckling are proportional to relative size of neonates.
- 3.
Ever-increasing prenatal growth rate—and hence size at parturition—is constrained by two costs. (i) “Individual costs”—i.e., the personal costs of the increased growth rate. Biologically, there must be some “efficiency” cost related to increasing the growth rate above the rate optimal for the uncompetitive condition (h, Fig. 1b). (ii) “Summed costs.” If a given offspring increases its growth rate above h, some costs may be felt equally by all of the litter. Most plausibly, these summed costs would arise as reduced survival of the mother through carrying the summed fetal mass during gestation (Fig. 1c).
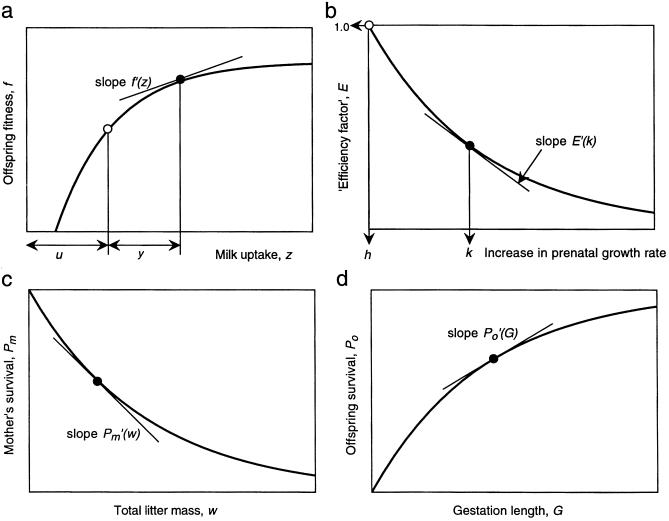
Figure 1.
Relationships assumed in the models. (a) Relation between offspring personal fitness gains, f, and the total milk uptake, z = u + y. The milk gained under uncompetitive suckling (u) takes the offspring to a personal fitness shown by the unfilled circle, and competitive gains add to this to take f to the filled circle, at which the gradient, shown by the slope, is f′(z). In the models, we used f(z) = 1 − e−az, where a is a positive constant; thus f′(z*)/f(z*) = a/(eaz* − 1). (b) Individual costs of increasing growth rate to level k, where h is the optimum in the absence of competition. Personal fitness is reduced as k increases, by multiplying f by factor E, where 1 ≥ E(k) ≥ 0; the slope of the line at k is E′(k*). In the models, we used E(k) = e−ck, thus E′(k*)/E(k*) = −c. (c) Summed costs of increased growth rate. The mother's survival probability Pm (and hence each offspring's survival probability) declines monotonically with the neonatal litter mass w; the slope of the line is the gradient P′m(w*). In the models, we used Pm(w) = e−bw, thus P′m(w)/Pm(w) = −b. (d) The survival probability of each neonate is Po(G), which increases with gestation time, G; the slope of the line is the gradient P′o(G*). We assume that Po(G) = (1 − e−qG).
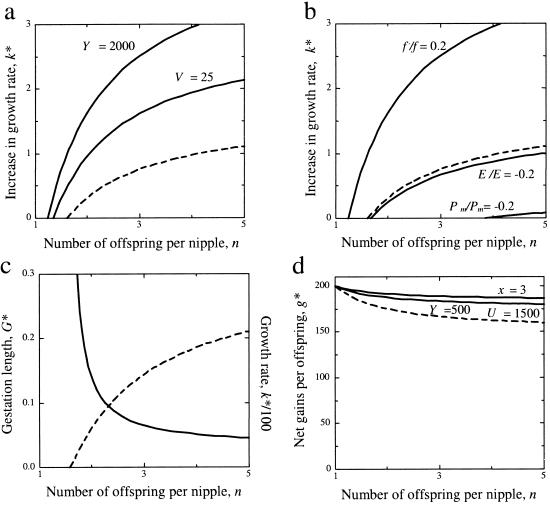
The ESS average growth rate, k*, is shown in Fig. 2 (see Appendix for analysis). To investigate the properties of the ESS growth rate increase, it is necessary to make explicit assumptions (see Fig. 2) about the terms and functions used in the model developed in the Appendix. With these assumptions, Fig. 2 shows how growth rate will change with the number of offspring per nipple. ESS prenatal growth rate increases with the proportion of milk allocated under competition conditions (Fig. 2a), with increases in the relative marginal value of the milk for offspring fitness (Fig. 2b), and decreases with the number of future offspring affected (Fig. 2a) and as the relative marginal individual or shared costs of higher prenatal growth increase (Fig. 2b).
Figure 2.
Predictions of the models in relation to the number of offspring per nipple, n. The explicit functions used (see Fig. 1 legend) allowed several of the parameters in Eq. 3 to be regarded as constants. Unless otherwise stated, we used the following: h = 1.0, f′/f = 0.1, P′m/Pm = −0.1, E′/E = −0.1, n = 10, rc = 0.5, rf = 0.25, V = 50, Y = 1,000. (a) Effects of amount of milk available under scramble conditions (Y), and future sibs (V), on increase in ESS growth rate, k*, when gestation length is fixed at G = 1.0. The broken curve is for Y = 1,000, V = 50. k* with n is greater when more milk is supplied under competitive conditions, (continuous curve for Y = 2,000), and when fewer future offspring are affected by the summed scramble costs (continuous curve for V = 25). (b) Effects of benefits and costs (individual and summed) on increase in growth rate, k*, when gestation length is fixed at G = 1.0. The broken curve shows how k* increases with n when f′/f = 0.1, P′m/Pm = −0.1, E′/E = −0.1. The effect of changing each of parameter unilaterally can be seen by comparing the continuous curves with this broken curve. Doubling the relative individual costs marginally reduces k* (curve for E′/E = −0.2), but doubling the relative summed costs reduces k* sharply (curve for P′m/Pm = −0.2), and doubling the relative benefits strongly increases k* (see curve for f′/f = 0.2). (c) An example of conflict resolution, calculated using the standard parameter values. The ESS gestation length, G* (continuous curve), is iterated from Eq. 5, and with Po(G*)/P′o(G*) = (eqG* − 1)/q; q = 1.0. The ESS growth rate increase, k* (broken curve), is calculated from Eq. 4, which gives k* = [q/{(eqG* − 1)bN}], using the iterated G* values. For low n, the ESS has growth rate h = 1.0 (i.e., k* = 0) so that G remains constant. (d) Net ESS gains, g*, per offspring from the postnatal growth model, calculated from Eq. 8. The broken curve has Y = 1,000, U = 1,000, and x = 1.0. The effect of increasing x to 3.0 (upper continuous curve), or of decreasing the proportion of milk obtained under scramble conditions (changing to Y = 500, U = 1,500; lower continuous curve) is to decrease scramble and to weaken the decline in gains with n.
Mothers may evolve various counterstrategies against reduction in their survival prospects arising from increased offspring growth rates. In the Appendix we examine one possibility (there are several) in which the mother reduces the gestation period. But this is likely to decrease survival of the neonates by making them more vulnerable at the time of birth (Fig. 1d). We show that if the relative marginal costs of increased birth mass to the mother are higher, a reduced gestation length is expected for the same relative offspring mass. Making explicit assumptions, we can show how gestation length is reduced with increased risks to the mother, and with increased prenatal growth rate. Finally, we can predict how parent–offspring conflict may be resolved. This game is a sequential one: the offspring strategy for increased growth rate first invades; “retaliation” follows by invasion of a compensatory reduction in gestation length. At the ESS between mother and offspring, gestation length reduces, and prenatal growth rate increases, with scramble competition for nipples (Fig. 2c). Increased growth rate is now greater than if gestation length remains fixed. This arises from an evolutionary feedback: as gestation length reduces, it relaxes the summed costs constraint on the offspring, allowing growth rate to escalate, favoring further reduction in gestation, and so on, until it pays neither to change further.
Postnatal growth rates will depend on the net energy gained during the suckling period. We again used a modified version of the scramble model of G.A.P. (16) to deduce how postnatal growth rate will be affected by sib competition (see Appendix). We assume that the mother controls the amount of milk available, but the offspring can control the scramble effort it expends in gaining access to nipples under competitive conditions. Postnatal growth rate is expected to be directly proportional to net energetic gains, which is predicted to decline with sib-competition for nipple access (see Fig. 2d).
To summarize our predictions for pre- and postnatal growth rates:
- 1.
If offspring are assumed to exert some control of prenatal growth rates, selection favors increased prenatal growth rates under higher postnatal sib-competition, because of the competitive advantages of being bigger in scrambles for access to nipples. If the mother controls prenatal growth, this effect will not be seen.
- 2.
The mother is assumed to determine the total milk supply. Postnatal growth rates will be lower when sib competition for nipples access is higher, because this favors higher scramble expenditure, reducing the net energetic gain during the suckling period.
These predictions were tested in comparative analyses of the Carnivora and Insectivora.
Methods
Comparative Dataset.
Life history data for the Carnivora and Insectivora were collated from several published reviews (refs. 17–21; see Tables 1 and 2, which are published as supporting information on the PNAS web site, www.pnas.org). Variables included for both orders are number of mammae, litter size, female or adult body mass, neonate mass, and gestation length.
Female body mass is the average body mass of females that are not pregnant or lactating, and neonate mass is the average body mass of young at birth. Errors can arise if weights are taken from captive animals or if seasonal fluctuations in adult body mass are large. Species values were therefore averaged from more than one source where possible, or taken from references in which median values were used to represent those carnivore species that undergo significant seasonal mass fluctuations independent of reproductive state (19). Body mass data were excluded for species in which extreme body mass variation was reported between populations [e.g., brown bear, Ursus arctos (20)]. In some cases, adult body mass was substituted for female body mass where no sex differences were specified. Litter sizes used in the analyses are also average species values. Only species with typical litter size greater than one were included in the dataset, because the focus of the investigation is competition between siblings within litters. For species with delayed implantation, estimates for gestation length were restricted to the period of “true gestation.”
The number of offspring per nipple in a typical litter was calculated by dividing average litter size by mammary number. Prenatal growth rate was quantified as the average daily increase in body mass (g) from conception to birth, calculated for both carnivores and insectivores by dividing average neonate mass (g) by gestation length for each species. Data for postnatal growth rates were also obtained for carnivores from previously published sources (19) and refer to the average daily increase in body mass (g) from birth to weaning. Data were not included if animals were hand-reared, or if rearing conditions were unknown. Data for offspring mass at first intake of solids were also included for carnivores where available (19). Comparable data on postnatal growth rates were not available for insectivores. Sigmoidal growth equations were not used because of the focus on early growth rates, mathematical descriptions of which typically approximate to a simple linear equation (22).
Comparative Analyses.
Species cannot be regarded as statistically independent for the purpose of comparative analyses because closely related taxa are likely to share characteristics of common ancestors (23). The CAIC 2.0 (Comparative Analysis by Independent Contrasts) software package (24) was used to explore evolutionary associations between key variables in the dataset while controlling for phylogenetic effects (25). All data were log transformed before analysis. With all comparative methods, it is desirable that the phylogenies used should be accurate and known without error, although the reliability of phylogenetic information can rarely be guaranteed (23). In the present study, the phylogeny of Bininda-Emonds et al. (26) was used for the Carnivora, and that of Symonds (21, 27) for the Insectivora. The phylogeny of Bininda-Emonds et al. (26) is a complete phylogeny or “supertree” derived from 177 literature sources, most of which give the same general pattern of carnivore phylogeny, regardless of the data or methodology used to generate them. Symonds's (21) phylogeny for the Insectivora is also based on a review of published information, but is likely to be less robust than that of Bininda-Emonds et al. (26). Branch lengths were set at equal in each phylogeny (28), and relationships between hypothesized independent and dependent variables were tested using linear regression analysis, forced through the origin (23).
Results
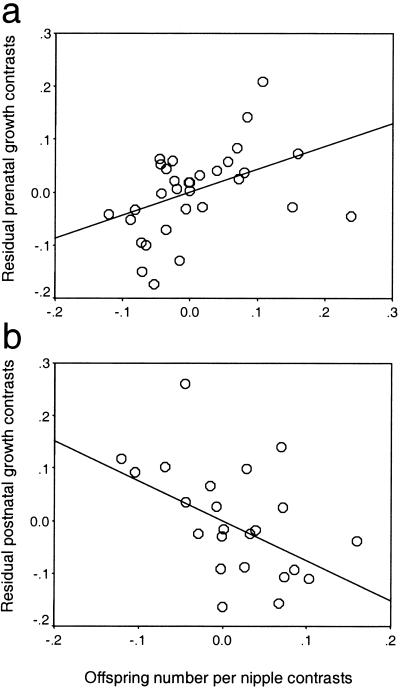
Maternal body mass does not predict the mean number of offspring per nipple within either group (carnivores: r2 = 0.06, F1,44 = 2.63, P > 0.10; insectivores: r2 = 0.001, F1,16 = 0.01, P > 0.90), but does predict prenatal growth rate (carnivores: r2 = 0.19, F1,31 = 6.85; P < 0.02; insectivores: r2 = 0.48, F1,9 = 8.45; P < 0.02). After controlling for this effect, residual prenatal growth rate is significantly positively related to changes in the number of offspring per nipple (carnivores: y = 0.43 ± 0.16x; r2 = 0.19, F1,31 = 7.20; P < 0.02; Fig. 3a; insectivores: y = 0.31 ± 0.11x, r2 = 0.48, F1,9 = 8.18; P < 0.02). Hence, in both groups, species with a relatively high intensity of postnatal sibling competition have relatively high prenatal growth rates for their adult body size.
Figure 3.
Regression analysis for carnivores of independent contrasts between mean offspring number per nipple and (a) residual prenatal growth rate, y = 0.43 ± 0.16x; r2 = 0.19, F1,31 = 7.20; P < 0.02 (after control for relationship between contrasts in prenatal growth rate and maternal body mass, r2 = 0.19, F1,31 = 6.85; P < 0.02) and (b) residual postnatal growth rate, y = −0.76 ± 0.28x; r2 = 0.25, F1,22 = 7.16; P < 0.02 (after control for relationship between contrasts in postnatal growth rate and neonate mass, r2 = 0.42, F1,22 = 15.11; P < 0.001).
After controlling for a strong relationship with contrasts in neonate mass (r2 = 0.42, F1,22 = 15.11; P < 0.001), residual postnatal growth rate in carnivores is significantly negatively related to changes in offspring number per nipple (r2 = 0.25, F1,22 = 7.16; P < 0.02; Fig. 3b). From a comparison of Fig. 3 a and b, it is apparent that although carnivores with relatively high levels of postnatal sibling competition have high prenatal growth rates in relation to maternal body size, their subsequent postnatal growth rates are low in relation to their size at birth. Pre- and postnatal growth rates of carnivores are positively correlated, although not significantly so after control for significant positive relationships of both growth rates with maternal body mass (residual pre- vs. postnatal growth rate: r2 = 0.15, F1,21 = 3.65; P = 0.07).
Finally, we investigated the role of litter size in the relationships described. We found that offspring number per nipple increases with litter size (carnivores: y = 0.29 ± 0.11x, r2 = 0.13, F1,47 = 7.37; P < 0.01), but that litter size per se does not predict variation in pre- or postnatal growth rates, controlled for female and neonatal mass, respectively (carnivore prenatal growth: r2 = 0.01, F1,31 = 0.39; P > 0.50; postnatal growth: r2 = 0.03, F1,22 = 0.46; P > 0.40). Moreover, carnivore species with relatively more offspring per nipple for their litter size also have relatively high prenatal growth rates for their adult body size (r2 = 0.15, F1,31 = 5.46; P < 0.03), and relatively low postnatal growth rates for their size at birth (r2 = 0.26, F1,22 = 7.23; P < 0.02).
Discussion
Prenatal growth rate is known to be an important explanatory variable in mammal life history diversity, although selection pressures contributing to variation in growth rates are not well understood (29, 30). Results of our theoretical and comparative analyses indicate that postnatal sibling competition is likely to be an important factor influencing prenatal growth rate in mammals. After control for adult body mass, prenatal growth rates increase with the intensity of postnatal sibling rivalry, measured as an increase in offspring numbers per nipple, for both carnivores and insectivores. These results are consistent with previous evidence that mammalian offspring exert some control over prenatal growth (31). There is also convincing evidence that prenatal growth rates are influenced by conflict between male and female parents, mediated by different imprinting of growth factor genes in the parental germ lines (32, 33). This parental conflict is expected to be more intense where offspring have different fathers, so prenatal growth rates should typically be faster among lineages where the probability of multiple paternity within or between litters is high. More detailed comparative analyses are needed to investigate this predicted relationship, and to determine whether the probability of multiple paternity within or between litters might also be positively correlated with offspring number per nipple, thus providing an alternative explanation for the results presented in Fig. 3. There are several species in the current dataset for which the probability of multiple paternity is low both within and between litters, including monogamous canids and mongooses (20, 34). However, because these species do not have consistently low average offspring numbers per nipple compared with an overall average of 0.57 for all carnivores (e.g., Canis lupus, 0.65; Canis latrans, 0.75; Cuon alpinus, 0.36; Suricata suricata, 0.67; Cynictis penicillata, 0.33), a confounding influence of parental conflict in the relationship presented appears unlikely.
Increased prenatal growth rates under sib-competition may have important consequences for understanding patterns of life history variation. In particular, where increased prenatal growth rates are costly for females, our analyses show that parent–offspring conflict may lead to escalating coevolutionary reductions in gestation length and increases in prenatal growth rate. Because reductions in gestation length will have consequences for the relative development of young at birth, our findings suggest a new hypothesis that parent–offspring conflict over growth rate could potentially explain the existence of an altricial precocial dichotomy in mammal development. That is, most mammalian orders can be classified as having either largely precocial or altricial neonates, although the reasons for this apparent dichotomy are poorly understood (29, 35). If parent–offspring conflict over prenatal growth rate influences altriciality, we should expect altricial mammals to have relatively high prenatal growth rates for their body size. Interestingly, the results of previous comparative analyses demonstrate just this—altricial mammals have higher fetal growth rates relative to maternal body size than precocial mammals, and shorter gestation lengths (36). Our hypothesis is also consistent with variation in litter size associated with the precocial altricial dichotomy, because precocial species typically give birth to single offspring, and are thus rarely subject to selection pressure for increased prenatal growth rates under sibling rivalry. Investigation of sibling rivalry and costs of increased prenatal growth in precocial species that typically produce more than one offspring (e.g., certain rodents and lagomorphs) would therefore be particularly informative to explore whether parent–offspring conflict over prenatal growth rate is an important factor in the evolution of altriciality.
Whether parent–offspring conflict over prenatal growth rate contributes to selection for altriciality also depends critically on the mechanism by which the timing of parturition is controlled. In particular, our model assumes that females have dominant control over the duration of gestation. Although this assumption appears reasonable on the basis of currently available evidence for carnivores, rodents, lagomorphs, and marsupials, each of which typically produce altricial young, strict maternal control may not apply in the more precocial ungulates (37).
Results of our comparative analyses also provide evidence that postnatal growth rate is typically low in relation to size at birth among species with high levels of postnatal sibling rivalry. This relationship may be a direct consequence of increased prenatal growth rates in species with more intense postnatal sibling rivalry, for example, if there is a tradeoff between pre- and postnatal growth rates, or if species with high prenatal growth rates simply have less growth to achieve during the period of postnatal development. Reduced postnatal growth rate in species with relatively intense sibling rivalry may also be explained in terms of increasing energetic costs of scramble expenditure as described above (see also ref. 16). An effect of scramble competition would be consistent with intraspecific studies demonstrating evidence of reduced protein turnover and growth retardation in mammal litters manipulated to increase competition (38). Growth costs associated with begging have also recently been demonstrated experimentally in birds (39, 40).
In conclusion, results of the theoretical and comparative analyses presented here offer insight for explaining patterns in mammalian growth rates and altriciality, and suggest sibling rivalry to be an important selection pressure in the evolution of mammal life history diversity.
Supplementary Material
Acknowledgments
We thank R. Beynon, J. L. Hurst, and S. P. Jensen for providing references and helpful discussion, and two anonymous referees for constructive reviews.
Abbreviation
- ESS
evolutionarily stable strategy
Appendix
ESS Models of Growth.
There are N young per litter. U units of milk are given in “uncompetitive” suckling (average/young = u = U/N units), and Y units in “competitive” suckling (average/young = ȳ = Y/N). The average total milk gain per young is thus (U + Y)/N = Z/N.
Milk per young is independent of nipple competition. With T nipples, milk available in competitive suckling = R = Y/T per nipple. With n = N/T young competing per nipple, the amount available to each of these competing sib groups is R(n) = (Y/N)n. A young's benefits through suckling are f(z), where z = total milk gained during lactation (= u + ȳ on average). f(z) is monotonic increasing with z, with decreasing gradient (Fig. 1a).
Young's Prenatal Growth Strategy.
Average gain per young in postnatal competition = ȳ = Y/N, but bigger neonates gain more and smaller ones less. We seek an ESS prenatal growth rate increase, k*, caused by sib-competition. Simplistically, let growth be linear during gestation period G; neonate size at gestation time, G, is (h + k*)G, where h is the growth rate optimal for individual costs (see below) without sib-competition. Increasing prenatal growth rate increases relative birth weight, and hence share of milk in competitive suckling. A young playing k, when its littermates play k* is assumed to gain
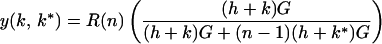 |
1 |
milk units in competitive conditions: it competes with n sibs, rather than with all N littermates. Because y increases with k, benefits f increase with k.
Individual costs are included by multiplying f by a factor, E(k), which decreases below 1.0 as k increases above 0 (Fig. 1b). Summed costs arise by decreased maternal survival with larger fetuses: survival probability to gestation is Pm(w), where w = summed neonate mass (Fig. 1c). Young's survival probability after birth is Po(G), which increases with G (Fig. 1d).
To find k*, we use inclusive fitness rather than “genetic accounting” (both typically give the same ESS; ref. 1). The relatedness between the focal young playing k ≠ k* and its current sibs = rc and that between the focal young and its V expected future sibs is rf. Its inclusive fitness is
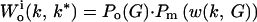 |
2 |
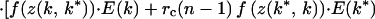 |
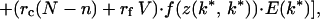 |
where f(z(k, k*)) = benefit to focal when its sibs play k*, f(z(k*, k)) = benefit to each sib playing k* when focal plays k, and f(z(k*, k*)) = benefit per sib when all play k*. The three terms in square brackets give the focal young's gains through self, current competing sibs, and current noncompeting sibs plus future sibs. Neonate mass = w(k, G) = G[(h + k) + (h + k*)(N − 1)].
The ESS, k*, is found by the standard technique (15). Setting R(n) = (Y/N)n, this becomes
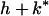 |
3 |
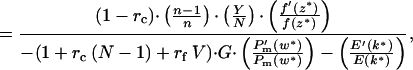 |
where z* = (U + Y)/N. Because both P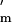 (w) and E′(k) are negative (Fig. 1 c and b) the denominator in Eq. 3 is positive.
(w) and E′(k) are negative (Fig. 1 c and b) the denominator in Eq. 3 is positive.
Note that the numerator in Eq. 3 increases with (n − 1)/n, a general principle for scramble effort when per capita resources remain constant (16). Thus for n > 1, k* increases most at low n, and asymptotes at large n. For n close to 1, Eq. 3 cannot be satisfied for positive h, so k* = 0. ESS growth rate (Fig. 2 a and b) increases if: sibs affected are half rather than full sibs, competitive conditions predominate (Y is high), and relative milk benefits [f′(z*)/f(z*)] are high. The denominator increases (and k* decreases) as the focal's affected sibs [1 + rc(N − 1) + rfV] increase, as relative summed [−P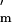 (w*)/Pm(w*)] and individual [−E′(k*)/E(k*)] costs increase, and as gestation length (G) increases.
(w*)/Pm(w*)] and individual [−E′(k*)/E(k*)] costs increase, and as gestation length (G) increases.
The Mother's Gestation Strategy and the ESS Resolution.
There are various plausible evolutionary retaliations. Here we assume that females alter gestation length, G. Female fitness is Wm(G) = Po(G) ⋅ Pm(w(G))[(N + V) ⋅ f(z) ⋅ E(k)]. Maximizing with respect to G
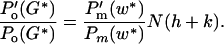 |
4 |
Note that Eq. 3 gives the ESS prenatal growth rate at a given gestation played by the mother, and that Eq. 4 gives (implicitly) the mother's ESS gestation length in relation to the growth rate played by the young. Substituting gives an ESS equation that must be satisfied for two strategies (G*, k*):
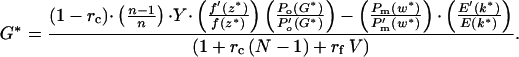 |
5 |
The example in Fig. 2c uses the exponential form Po(G) = 1 − e−qG, Po(G*)/P′o(G*) = (eqG* − 1)/q. Solutions for G* can be iterated. When k* > 0 (i.e., when sib-competition favors an increase in growth rate), G* decreases with n: the mother retaliates against costs of increased fetal growth rate by reducing gestation length. G* falls most steeply at low n (Fig. 2c).
Increase in offspring growth rate, k*, at conflict resolution is found by feeding G* values obtained from the solution to Eq. 5 into Eqs. 4 or 3 (Fig. 2c). Despite the large changes in G* with n, k*(n) retains a similar form to those for fixed G (see Fig. 2 a and b), but is markedly higher because of the feedback described in the text.
Young's Postnatal Growth Strategy.
Assume that postnatal growth rates depend on net gains during suckling, and the mother controls milk supply (U + Y). A young increasing scramble effort, S, increases its access to nipples in competitive conditions. E(S) = energy cost of scrambling to level S. At the ESS, S*, the amount of energy gained by a mutant young scrambling to level S ≠ S* is taken as
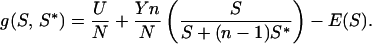 |
6 |
Let f(g) = personal fitness benefits of gaining energy, g. The mutant's inclusive fitness is
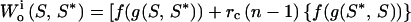 |
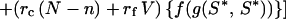 |
cf. Eq. 3. If f′(g) is positive, S* is independent of f(g):
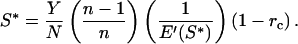 |
Substituting E(S) = jSx, in which j and x are positive constants with x > 1 (energetic costs increase disproportionately with x)
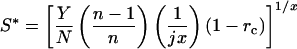 |
7 |
(cf. equation 5 of ref. 16). Net energetic gains at the ESS are found from Eq. 6 with E(S) = jSx, substituting Eq. 7:
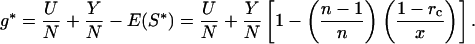 |
8 |
Eq. 8 implies that g* (and hence postnatal growth rate) declines with sib competition for nipple access, n. Note that x ≥ 1.0 (x = 1.0 generates maximum scramble expenditure; ref. 16). The relationship is weak only, especially if Y is low (broken curve, Fig. 2d), or scramble expenditure weak (x = 3, Fig. 2d).
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Mock D W, Parker G A. The Evolution of Sibling Rivalry. Oxford: Univ. Press; 1997. [Google Scholar]
- 2.Mock D W, Forbes L S. Trends Ecol Evol. 1995;10:130–134. doi: 10.1016/s0169-5347(00)89014-x. [DOI] [PubMed] [Google Scholar]
- 3.Cameron G N. J Mammal. 1973;54:489–493. [PubMed] [Google Scholar]
- 4.Schadler M H, Butterstein G M. J Mammal. 1979;60:841–844. [Google Scholar]
- 5.Cockburn A. Behav Ecol Sociobiol. 1994;35:53–62. [Google Scholar]
- 6.Gilbert A N. Proc Natl Acad Sci USA. 1986;83:4828–4830. doi: 10.1073/pnas.83.13.4828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cramer C P, Blass E M. Am J Physiol. 1983;245:154–159. doi: 10.1152/ajpregu.1983.245.2.R154. [DOI] [PubMed] [Google Scholar]
- 8.Fuchs S. Behav Ecol Sociobiol. 1982;10:39–51. [Google Scholar]
- 9.McVittie R. Appl Anim Ethol. 1978;4:159–168. [Google Scholar]
- 10.Fraser D. J Reprod Fertil. 1990;40,Suppl.:355–370. [PubMed] [Google Scholar]
- 11.Clutton-Brock T H. The Evolution of Parental Care. Princeton, NJ: Princeton Univ. Press; 1991. [Google Scholar]
- 12.Hamilton W D. J Theor Biol. 1964;7:1–52. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- 13.Royle N J, Hartley I R, Owens I P F, Parker G A. Proc R Soc London Ser B. 1999;266:923–932. [Google Scholar]
- 14.Stearns S C. The Evolution of Life Histories. Oxford: Oxford Univ. Press; 1992. [Google Scholar]
- 15.Maynard-Smith J. Evolution and the Theory of Games. Cambridge, U.K.: Cambridge Univ. Press; 1982. [Google Scholar]
- 16.Parker G A. Philos Trans R Soc London B. 2000;355:1637–1645. doi: 10.1098/rstb.2000.0726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ewer R F. The Carnivores. New York: Cornell Univ. Press; 1972. [Google Scholar]
- 18.Innes D G L. In: Advances in the Biology of Shrews. Merrit J F, Kirkland G L Jr, Rose R K, editors. Carnegie Museum of Natural History Special Publication No. 18; 1994. pp. 111–136. [Google Scholar]
- 19.Gittleman J L, Oftedal O T. Symp Zool Soc London. 1987;57:41–77. [Google Scholar]
- 20.Nowak R M. Walker's Mammals of the World. 5th Ed. London: The Johns Hopkins Univ. Press; 1991. [Google Scholar]
- 21.Symonds M R E. Funct Ecol. 1999;13:508–513. [Google Scholar]
- 22.Zullinger E M, Ricklefs R E, Redford K H, Mace G M. J Mammal. 1984;65:607–636. [Google Scholar]
- 23.Harvey P H, Pagel M D. The Comparative Method in Evolutionary Biology. In: May R M, Harvey P H, editors. Oxford Series in Ecology and Evolution. Oxford: Oxford Univ. Press; 1991. [Google Scholar]
- 24.Purvis A, Rambout A. Comput Appl Biosci. 1995;11:247–251. doi: 10.1093/bioinformatics/11.3.247. [DOI] [PubMed] [Google Scholar]
- 25.Felsenstein J. Am Nat. 1985;125:1–15. [Google Scholar]
- 26.Bininda-Emonds O R P, Gittleman J L, Purvis A. Biol Rev. 1999;74:143–175. doi: 10.1017/s0006323199005307. [DOI] [PubMed] [Google Scholar]
- 27.Symonds M R E. J Zool. 1999;249:315–337. [Google Scholar]
- 28.Purvis A, Gittleman J L, Luh H K. J Theor Biol. 1994;167:293–300. [Google Scholar]
- 29.Read A F, Harvey P H. J Zool. 1989;219:329–353. [Google Scholar]
- 30.Harvey P H, Promislow D E L, Read A F. In: Comparative Socioecology. Foley R, Standen V, editors. Oxford: Blackwell; 1989. pp. 305–318. [Google Scholar]
- 31.Haig D. Q Rev Biol. 1993;68:495–532. doi: 10.1086/418300. [DOI] [PubMed] [Google Scholar]
- 32.Haig D, Graham C. Cell. 1991;64:1045–1046. doi: 10.1016/0092-8674(91)90256-x. [DOI] [PubMed] [Google Scholar]
- 33.Moore T, Haig D. Trends Genet. 1991;7:45–49. doi: 10.1016/0168-9525(91)90230-N. [DOI] [PubMed] [Google Scholar]
- 34.Macdonald D W. The New Encyclopedia of Mammals. Oxford: Oxford Univ. Press; 2001. [Google Scholar]
- 35.Derrickson E M. Funct Ecol. 1992;6:57–65. [Google Scholar]
- 36.Martin R D, MacLarnon A M. Nature (London) 1985;313:220–223. [Google Scholar]
- 37.Fuchs A R, Fields M J. In: Encyclopedia of Reproduction. Knobil E, Neill J D, editors. Vol. 3. London: Academic; 1999. pp. 703–716. [Google Scholar]
- 38.Johnson J D, Wogenrich W J, Hsi K C, Skipper B J, Greenberg R E. Growth Dev Aging. 1991;55:263–273. [PubMed] [Google Scholar]
- 39.Rodríguez-Gironéz M A, Zúniga J M, Redondo T. Behav Ecol. 2001;12:269–274. [Google Scholar]
- 40.Kilner R. Proc Natl Acad Sci USA. 2001;98:11394–11398. doi: 10.1073/pnas.191221798. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.