Abstract
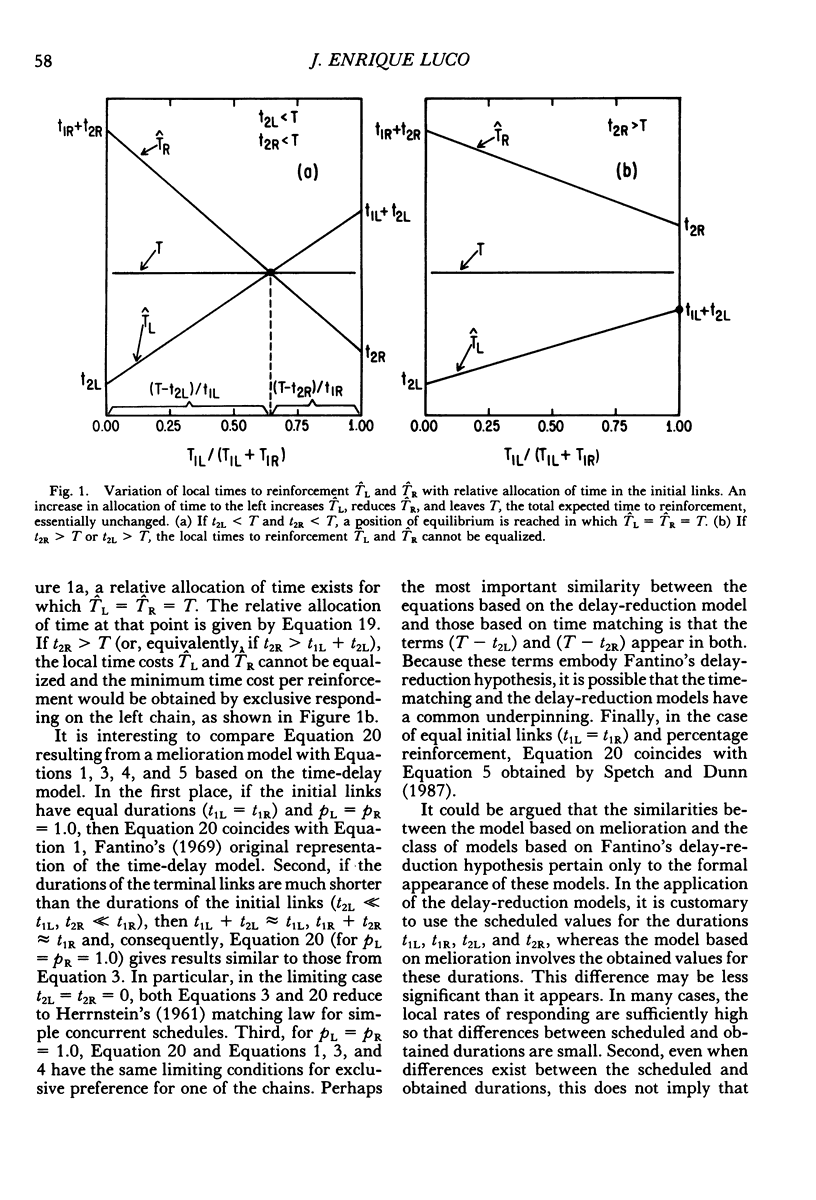
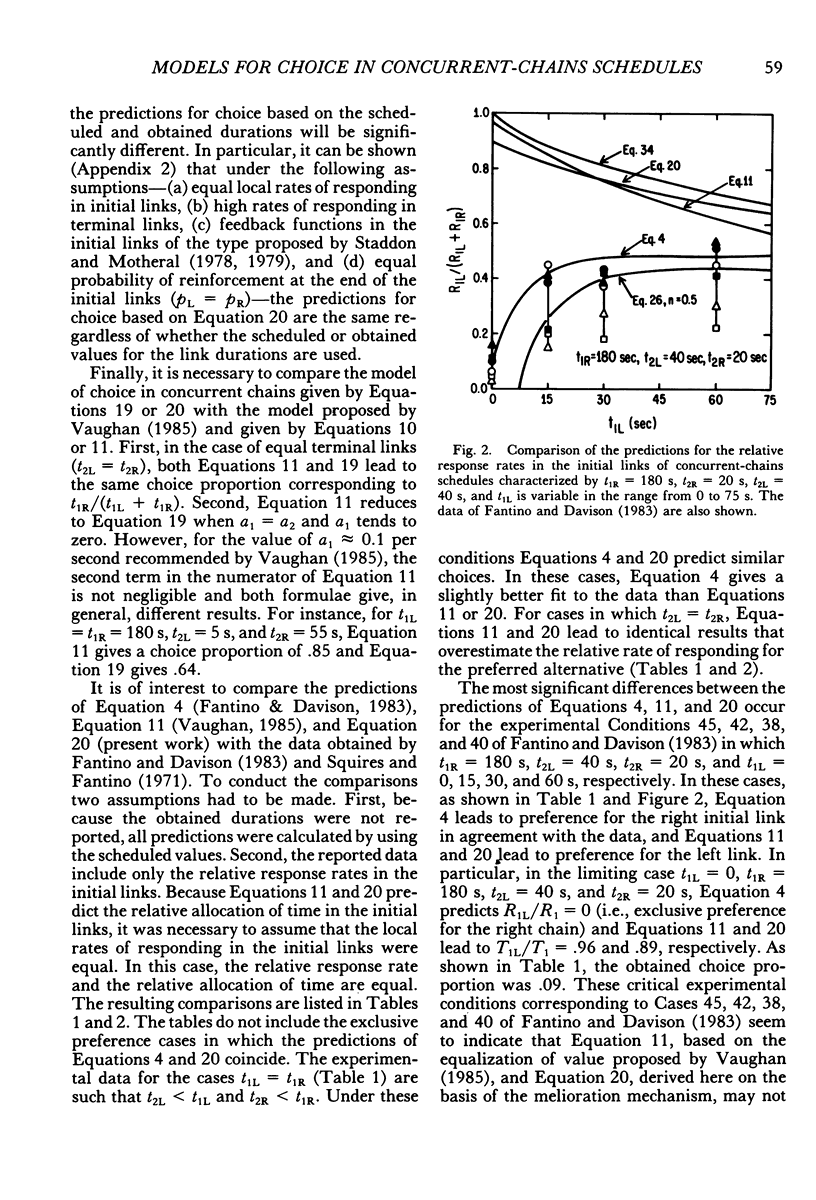
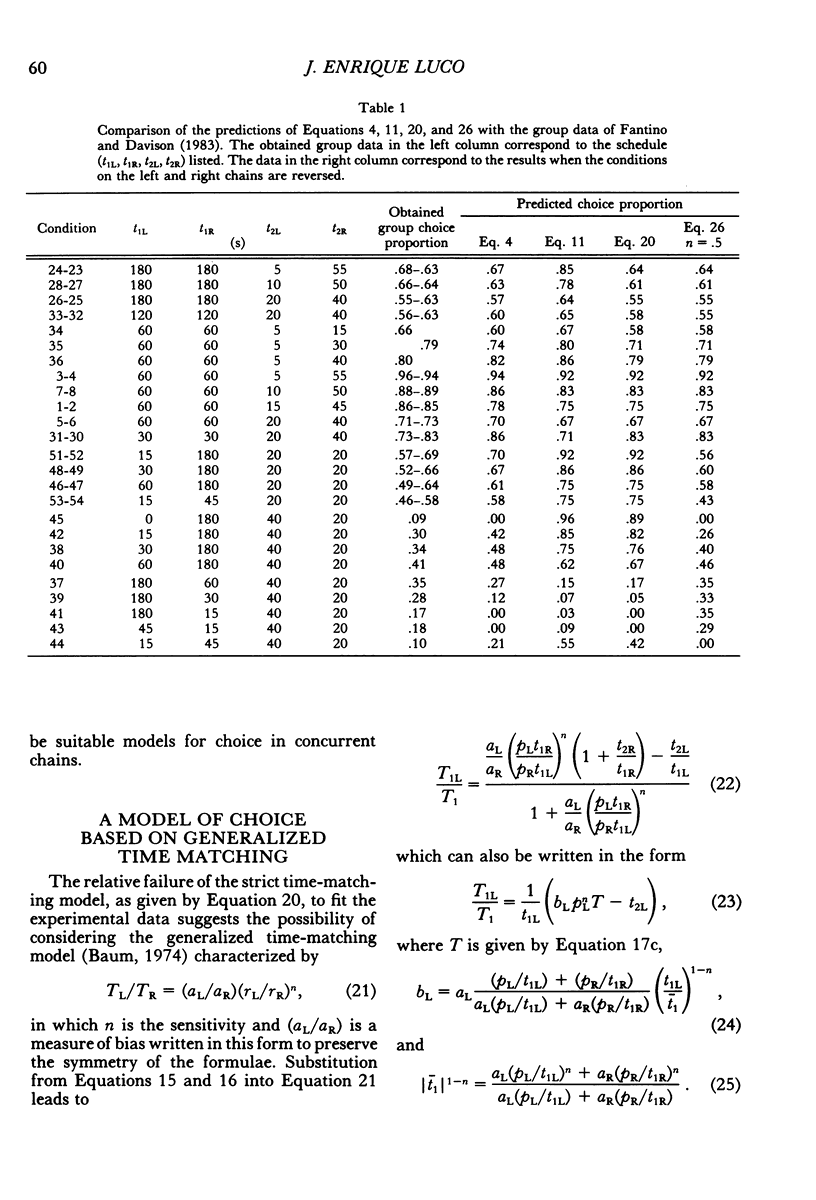
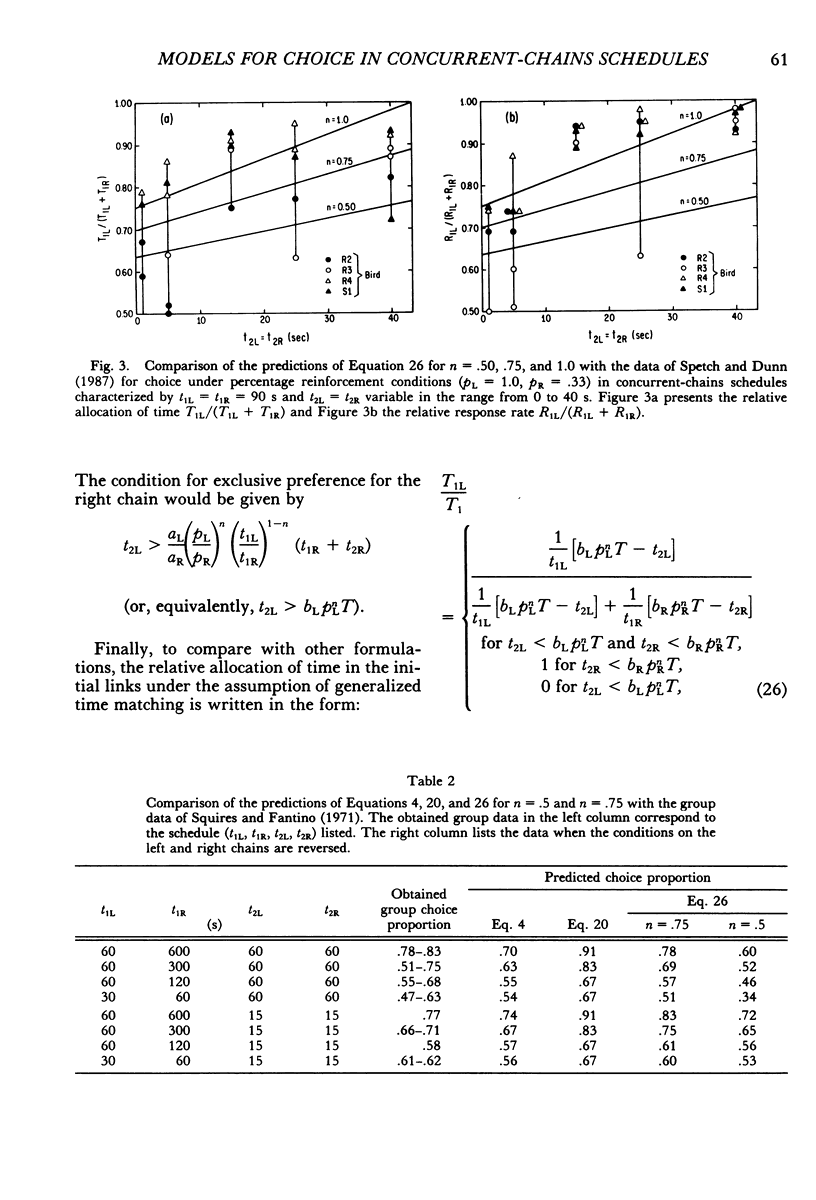
Models of choice in concurrent-chains schedules are derived from melioration, generalized matching, and optimization. The resulting models are compared with those based on Fantino's (1969, 1981) delay-reduction hypothesis. It is found that all models involve the delay reduction factors (T - t2L) and (T - t2R), where T is the expected time to primary reinforcement and t2L, t2R are the durations of the terminal links. In particular, in the case of equal initial links, the model derived from melioration coincides with Fantino's original model for full (reliable) reinforcement and with the model proposed by Spetch and Dunn (1987) for percentage (unreliable) reinforcement. In the general case of unequal initial links, the model derived from melioration differs from the revised model advanced by Squires and Fantino (1971) only in the factors affecting the delay-reduction terms (T - t2L) and (T - t2R). The models of choice obtained by minimizing the expected time to reinforcement depend on the type of feedback functions used. In particular, if power feedback functions are used, the optimization model coincides with that obtained from melioration.
Full text
PDF









Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Baum W. M. On two types of deviation from the matching law: bias and undermatching. J Exp Anal Behav. 1974 Jul;22(1):231–242. doi: 10.1901/jeab.1974.22-231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison M. Bias and sensitivity to reinforcement in a concurrent-chain schedule. J Exp Anal Behav. 1983 Jul;40(1):15–34. doi: 10.1901/jeab.1983.40-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fantino E. Choice and rate of reinforcement. J Exp Anal Behav. 1969 Sep;12(5):723–730. doi: 10.1901/jeab.1969.12-723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fantino E., Davison M. Choice: Some quantitative relations. J Exp Anal Behav. 1983 Jul;40(1):1–13. doi: 10.1901/jeab.1983.40-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HERRNSTEIN R. J. Relative and absolute strength of response as a function of frequency of reinforcement. J Exp Anal Behav. 1961 Jul;4:267–272. doi: 10.1901/jeab.1961.4-267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HERRNSTEIN R. J. SECONDARY REINFORCEMENT AND RATE OF PRIMARY REINFORCEMENT. J Exp Anal Behav. 1964 Jan;7:27–36. doi: 10.1901/jeab.1964.7-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rachlin H. A molar theory of reinforcement schedules. J Exp Anal Behav. 1978 Nov;30(3):345–360. doi: 10.1901/jeab.1978.30-345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spetch M. L., Dunn R. Choice between reliable and unreliable outcomes: mixed percentage-reinforcement in concurrent chains. J Exp Anal Behav. 1987 Jan;47(1):57–72. doi: 10.1901/jeab.1987.47-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Squires N., Fantino E. A model for choice in simple concurrent and concurrent-chains schedules. J Exp Anal Behav. 1971 Jan;15(1):27–38. doi: 10.1901/jeab.1971.15-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan W. Choice: A local analysis. J Exp Anal Behav. 1985 May;43(3):383–405. doi: 10.1901/jeab.1985.43-383. [DOI] [PMC free article] [PubMed] [Google Scholar]


