Abstract
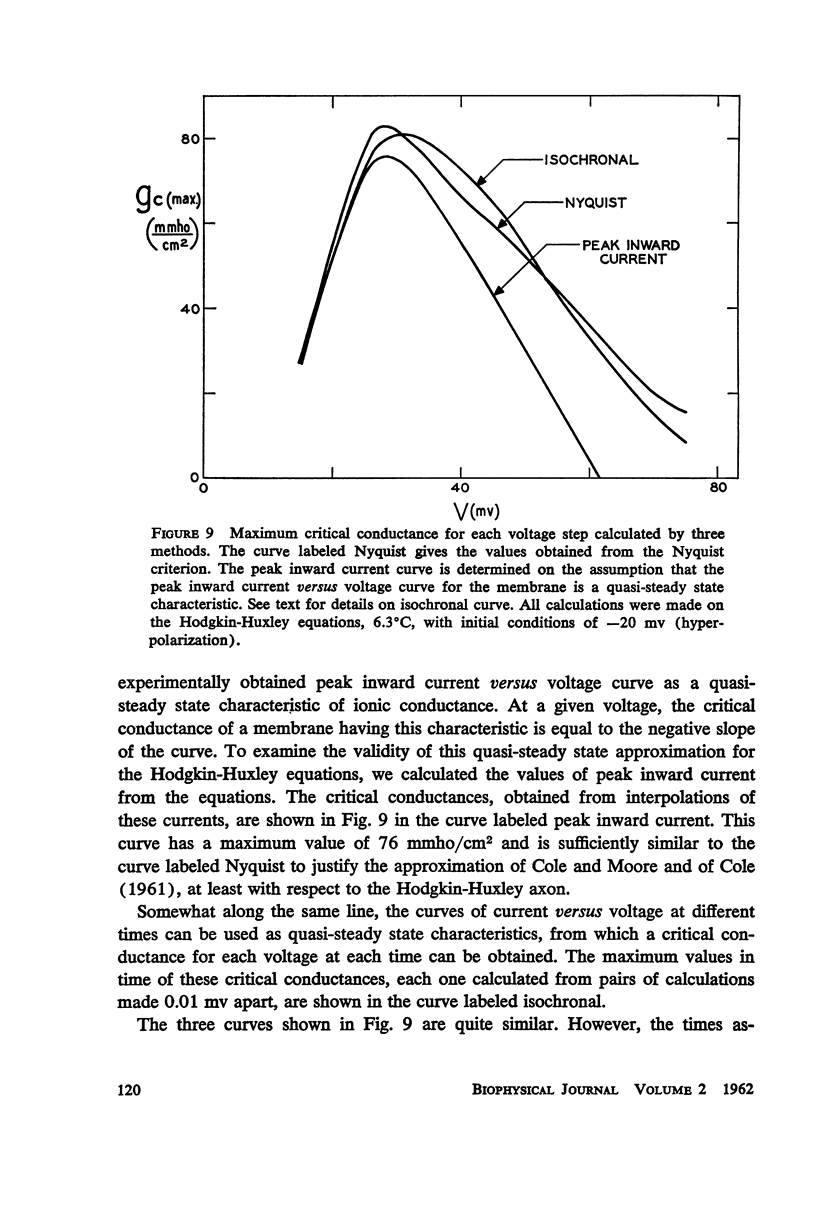
A mathematical method for determining the stability properties of a uniform nerve membrane is developed. Two basically similar tests of stability are considered: examination of the real characteristic roots of the linearized equations and application of a modified Nyquist criterion to the linearized alternating current admittance. The method is applied to the Hodgkin-Huxley equations for the squid axon membrane at 6.3°C to decide theoretically whether stable membrane behavior might be expected in a space clamp experiment. The equations are solved for step depolarizations similar to those used in voltage clamp experiments. Each solution can be represented by a trajectory in the phase space of the variables V, m, h, and n. The stability of motion of a phase point on a given trajectory, and hence the adequacy of the control of the membrane potential, is shown to be a function of the effective conductance in series with the membrane. (For a patch of membrane away from the point controlled by feedback, the effective conductance is the combined conductance of the axial current electrode, axoplasm, and an external layer of sea water, all in series.) In particular, there is a (uniquely determined) critical conductance, defined as the minimum effective series conductance consistent with stability, associated with each point on the trajectory. During a step depolarization the critical conductance goes through a maximum. The values of such maxima as a function of voltage are closely similar to the negative slopes of the peak inward current versus voltage curve. This empirical correlation may be helpfup in the prediction of stability in experimental situations.
Full text
PDF

















Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- COLE K. S. An analysis of the membrane potential along a clamped squid axon. Biophys J. 1961 May;1:401–418. doi: 10.1016/s0006-3495(61)86898-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- COLE K. S., MOORE J. W. Ionic current measurements in the squid giant axon membrane. J Gen Physiol. 1960 Sep;44:123–167. doi: 10.1085/jgp.44.1.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzhugh R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys J. 1961 Jul;1(6):445–466. doi: 10.1016/s0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HODGKIN A. L., HUXLEY A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HODGKIN A. L., HUXLEY A. F., KATZ B. Measurement of current-voltage relations in the membrane of the giant axon of Loligo. J Physiol. 1952 Apr;116(4):424–448. doi: 10.1113/jphysiol.1952.sp004716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HUXLEY A. F. Ion movements during nerve activity. Ann N Y Acad Sci. 1959 Aug 28;81:221–246. doi: 10.1111/j.1749-6632.1959.tb49311.x. [DOI] [PubMed] [Google Scholar]
- TASAKI I., BAK A. F. Discrete threshold and repetitive responses in the squid axon under voltage-clamp. Am J Physiol. 1958 May;193(2):301–308. doi: 10.1152/ajplegacy.1958.193.2.301. [DOI] [PubMed] [Google Scholar]
- TASAKI I., SPYROPOULOS C. S. Nonuniform response in the squid axon membrana under voltage-clamp. Am J Physiol. 1958 May;193(2):309–317. doi: 10.1152/ajplegacy.1958.193.2.309. [DOI] [PubMed] [Google Scholar]
- TAYLOR R. E., MOORE J. W., COLE K. S. Analysis of certain errors in squid axon voltage clamp measurements. Biophys J. 1960 Nov;1:161–202. doi: 10.1016/s0006-3495(60)86882-8. [DOI] [PMC free article] [PubMed] [Google Scholar]


