Force and Flexibility of Flailing Myxobacteria

Abstract

Myxococcus xanthus is a common Gram-negative bacterium that moves by a process called gliding motility. In myxobacteria, two distinct mechanisms for gliding have been discovered. S-type motility requires the extension, attachment, and retraction of type IV pili. The other mechanism, designated as A-type motility, may be driven by the secretion and swelling of slime; however, experiments to confirm or refute this model are still lacking and the force exerted by this mechanism has not been measured. A previously published experiment found that when an M. xanthus cell became stuck at one end, the cell underwent flailing motions. Based on this experiment, I propose an elastic model that can estimate the force produced by the A-motility engine and the bending modulus of a single myxobacterial cell. The model estimates a bending modulus of 3 × 10⁻¹⁴ erg cm and a force between 50–150 pN. This force is comparable to that predicted by slime extrusion, and the bending modulus is 30-fold smaller than that measured in Bacillus subtilis. This model suggests experiments that can further quantify this process.

INTRODUCTION

Bacteria are exceptionally diverse; they have found an enormous number of different ways to achieve similar functions. Even common processes such as motility and maintenance of shape are accomplished by many different mechanisms. A biophysical understanding of these processes requires measurement of some basic features. For motility, one needs to know how much force is required to move the bacterium through its environment and what produces that force. To understand how a bacterium maintains its shape, the material properties of the cell must be measured. In some bacteria these measurements are easier than in others. Since Escherichia coli is an ellipsoidal cell that moves through a fluid environment, it is straightforward to estimate the force that is required to drive this process (for example, see Berg (1). Microscopic advances such as optical traps have also made it possible to measure forces and elastic properties at the cellular level. Using an optical trap to bend filamentous Bacillus subtilis cells enabled the Young's modulus of the cell wall to be estimated (2). The force/velocity relation for Mycoplasma mobile was also measured recently using both optical traps and fluid drag (3).

Myxococcus xanthus is a common Gram-negative bacterium that has been extensively studied due to its complex life cycle (4). When a colony is starved, cell movement and cell-cell signaling lead to rippling motions across the colony and eventually to the formation of fruiting bodies in which some cells sporulate (5). Cells are rod-shaped with an average length of 5–7 μm and a diameter of 0.5 μm (6,7). The inside of the cell is enclosed by an inner membrane bilayer that is surrounded by a cell wall that is composed of a protein meshwork made predominantly of peptidoglycan. The cell wall provides much of the structural rigidity to the cell. Outside the cell wall is a second membrane bilayer.

M. xanthus translocates by gliding. This motility is generically defined as translocation in the direction of the long axis of the cell when in contact with a substrate (8). Due to this vague definition, it is not surprising that there is more than one mechanism by which gliding is achieved. Indeed, M. xanthus possess two distinct mechanisms for gliding motion: adventurous (A) motility and social (S) motility (9). S-motility is driven by type IV pili which extend, attach to nearby cells or the substrate, and then retract, pulling the cell forward (10–14).

A-motility remains more elusive; however, recent experimental evidence strongly suggests that slime extrusion from a surface organelle drives this type of gliding motility. Experiments on cyanobacteria showed that slime is extruded from these cells at velocities comparable to the rate at which the cells glide (15). In addition, electron microscopy revealed a pore-shaped organelle embedded in the cell wall near sites of slime extrusion (15). Investigations on M. xanthus revealed similar pores and showed that slime emanated from the back of the cell in narrow bands near the sites of these pores (16). Wolgemuth et al. developed a mathematical model that showed that hydration of a polyelectrolyte gel could produce sufficient force to propel A-motility in myxobacteria and cyanobacteria (16). If this model is correct, A-motility is driven by a pusher motor: force is generated at the rear of the cell that pushes the cell forward, much like a rear wheel drive car. This model predicts the force/velocity relation and the total force that can be produced by this mechanism. Experiments to measure these properties have not been performed yet.

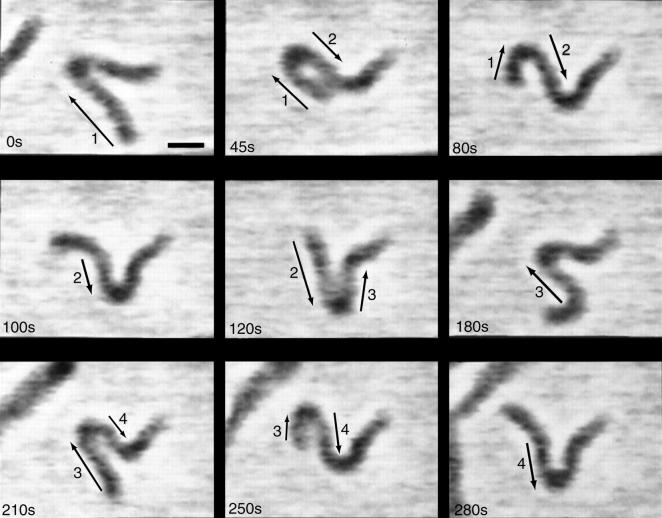
Another unique feature of myxobacteria is its flexibility. Cells can bend much more readily than many other bacteria, which is most likely due to the structure of their peptidoglycan (17). Kaiser and Welch suggested that the flexibility of myxobacteria may provide a method by which “traffic jams” are overcome during rippling and fruiting body formation (6). This flexibility is exemplified in Spormann and Kaiser (18) when a gliding M. xanthus cell became stuck at one end while the other end was still free. Time lapse images of this cell suggest that the free end is still pushing on the cell, trying to move it forward. The stuck end prevents this motion and the cell bends and flails about in a periodic fashion (Fig. 1). Though this case, where one end becomes stuck and the other remains free, is rare, it provides a useful method to study the gliding motility of myxobacteria.

FIGURE 1.

Movement of an M. xanthus cell where the right end is fortuitously stuck to the agar substrate. Note that frames at t = 210 s, 250 s, and 280 s essentially repeat the behavior at t = 45 s, 80 s, and 100 s. Moving segments of the cell are indicated by arrows. Scale bar is 2 μm. Figure reprinted with permission from Spormann and Kaiser (18).

In this article, I propose a model that can explain the periodic motions of a flexible cell that is stuck at one end and propelled by a pusher motor from the other. This model provides an estimate of both the force produced by the motor and the elastic parameters of the M. xanthus cell body. As experiments to measure these parameters have not been possible yet, this model provides a novel method to estimate them in M. xanthus and other gliding bacteria.

THE MODEL

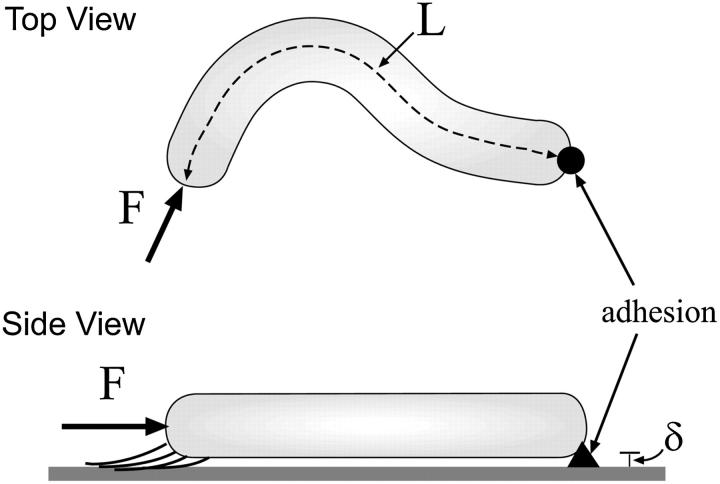
Myxobacteria cells are much longer than they are wide. Therefore, I begin by treating the cell as an elastic filament of length, L, and radius, a. The distance along the filament is parameterized by the arc length, s, and the shape of the filament is described by the vector r(s). At s = 0, the end is clamped in place with r = 0 and ∂r/∂s = 0. The other end (s = L) is acted on by a force, F, produced by the A-motility engine, but is otherwise free. The force is assumed to be applied tangentially at the free end of the cell (Fig. 2). Since the cell is cylindrical and confined to the two-dimensional plane of the surface, the only material parameter that is important is the bending modulus, A. I assume that the cell body is linearly elastic. Therefore, the elastic energy for deforming the cell away from its straight state is quadratic in the curvature, 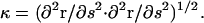The assumption of linear elasticity should hold for curvatures that are less than 1/a. The elastic restorative force per length, f, arises from variational derivatives of the energy (19),

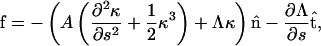(1)

where 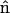is the normal vector and 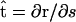is the tangent vector. The function Λ is effectively the tension in the filament, which accounts for the presence of the force, F, as well as maintains the total arc length of the filament.

FIGURE 2.

Schematic of the model. A cylindrically-shaped cell of length, L, is stuck down at one end (black arrow) and is pushed on by a force, F, directed along the tangent at the other end. Due to the slime secreted by the cell, the cell sits at a distance, δ, above the substrate. If the applied force is large enough, the cell bends. The direction of the applied force then torques the free end of the cell about the fixed end, leading to flailing motion.

The cell is in contact with the surface, but presumably this contact is lubricated by the slime that the bacterium secretes. For cellular systems, the force that comes from friction between surfaces or drag from fluids dominates over inertia. Therefore, the force that acts on the cell is proportional to the velocity rather than the acceleration. We define two drag coefficients, ζ_⊥ and 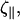which are the proportionality constants for movement perpendicular to or along the tangent direction, respectively. For motion of a filamentary object in bulk fluid, resistive force theory for slender bodies predicts that 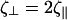(20). This result is not valid for cases where distal points of the filament come in close contact with each other, as the cell does in Fig. 1 at 45 s and 120 s. The presence of the wall, however, damps out nonlocal fluid effects, as the inverse 4th power of distance (21). For cases where the spacing between distal points on the cell is larger than the spacing between the cell body and the substrate, δ, we expect that these effects will be negligible. Furthermore, M. xanthus cells typically follow slime trails (22). If the drag is predominantly due to the slime, rather than the surrounding fluid, nonlocal effects will only be present if the slime bands from distal points on the cell are connected. As the slime is a polymeric fluid, the drag perpendicular to the long axis of the cell may be significantly larger than the parallel drag. Therefore, I will use that 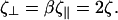Balancing the restorative force with the drag force produces a dynamic equation for the shape of the filament,

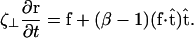(2)

This model does not account for internal drag due to cell wall viscoelasticity. As little is known about the magnitude of viscoelastic effects in bacterial cells, I assume that the external drag due to the slime and/or fluid dominates.

Demanding that the filament is inextensible leads to an ordinary differential equation for Λ (19),

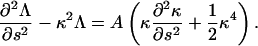(3)

The tangentially directed force at s = L imposes the boundary condtions ∂²r/∂s²(L) = ∂³r/∂s³(L) = 0 and Λ(L) = F. At the clamped end, ∂Λ/∂s(0) = 0.

RESULTS

For small applied forces at the free end, compression is insufficient to bend the cell body, and the bacterial cell remains straight. At higher forcing, the force should buckle the filament. Once bent, though, the direction of the tangentially applied force shifts relative to the position of the clamped end. A component of the force will point in the direction perpendicular to the line defined by the straight filament, which will act to torque the free end about the fixed end. For small deformations of the filament, this torque should cause the free end of the filament to slide roughly perpendicular to the line connecting the free end and the clamped end (Fig. 2) and should lead to periodic oscillations of the free end.

Before solving the full nonlinear model equations (1–3), we note that there are five physical constants that can influence the dynamics of this problem (A, L, F, ζ_⊥, and β). Nondimensionalizing the equations using the filament length, the characteristic timescale (ζ_⊥L⁴/A), and the characteristic force (A/L²), leaves only two dimensionless parameters (FL²/A and β), which completely define the dynamic shape evolution of the oscillating filament.

To solve the model equations, an intrinsic representation (See Appendix) was used to simulate the dynamics of the filament, as this method was found to be more stable numerically than direct solution of Eq. 2. A Crank-Nicolson routine was used to integrate Eq. 4, and Eq. 3 was integrated using an implicit method. All simulations were started using an initial configuration of the filament that was perturbed slightly from the straight state with 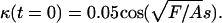For values of F < 37.5 A/L², the straight filament shape was stable, confirming the linear stability analysis (See Appendix). When F > 37.5 A/L², the filament bent and waved back and forth about the line defined by the straight filament. The period of this oscillation was finite at the onset of the instability, which was also consistent with the linear stability analysis. As F was increased beyond this critical force, the amplitude of the oscillation increased. Fig. 3 shows a time series of the simulation with F = 250A/L² and β = 2.0. This instability is the zero Reynolds number version of the fluttering instability of an elastic beam under tangentially applied follower forcing, which has been studied theoretically and experimentally in the inertial limit where the drag is ignored (23). The critical force for the flailing instability calculated here is ∼3 times larger than the critical force for the inertial instability (23).

FIGURE 3.

Simulation of the model equations shown at nine different times, showing periodic flailing motion. F = 250 A/L² and β = 2.0. Comparison of the top three panels to the bottom three panels shows that the induced motion of the filament is periodic. A movie of this simulation is available in the online supplementary material.

Plotting the end displacement as a function of time shows that the deformation of the filament is periodic (results not shown). At values of FL²/A > 100, secondary instabilities begin to incorporate higher frequency oscillations in the shape of the filament. As shown in Fig. 3, the filament oscillates between a U-shaped form and an S-shaped form during each half period; the higher frequency oscillation is at roughly twice the frequency of the primary frequency. At even higher forces, these secondary instabilities can lead to quite interesting dynamical behavior. Fig. 4 shows the results of a simulation with FL²/A = 500 and β = 2.0. During the course of this simulation, the morphology of the filament transitions between a flailing form similar to that seen at lower forcing (similar to that shown in Fig. 3) and a rapid fluctuation with three wavelengths along the length of the filament.

FIGURE 4.

At larger forces, F = 500 A/L², higher order modes influence the dynamics. Simulation of the model equations shown at nine different time segments comprising half a period. In panel 4, the filament transiently bends into a shape with three wavelengths present. β = 2.0. A movie of this simulation is available in the online supplementary material.

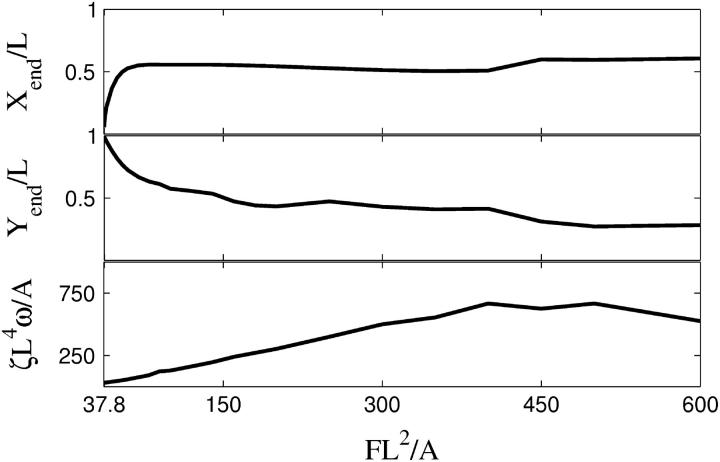
To quantify the magnitude of the oscillation, I used the maximum displacement of the free end in both the x and y directions, which are denoted by X_end and Y_end, respectively. In Fig. 5, the end displacements and the frequency are plotted as a function of the applied force. As is expected, the amplitude of the x displacement is zero at the critical force and the filament is straight (Y_end/L = 1). As the force rises, the amplitude of the deformation increases. At a value of FL²/A ≈ 60, the x displacement plateaus, but the y displacement continues to increase. At higher forces, the filament remains more bent during the course of the motion, and therefore, the end displacements do not continue to increase. The bottom panel of Fig. 5 shows that for FL²/A > 100, the frequency of the oscillation is not strongly dependent on the applied force.

FIGURE 5.

The extreme positions of the free end of the cell (X_end (top), Y_end (middle)), and frequency of flailing (bottom), ζL⁴ω/A, as a function of force with β = 3.

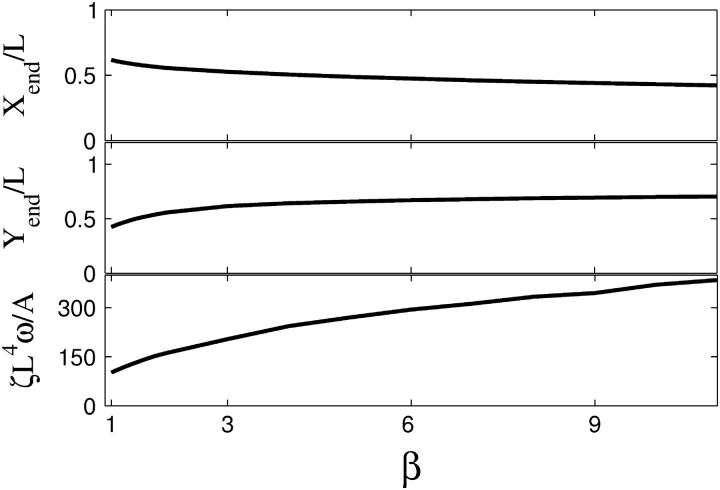
The discrepancy between the tangential and perpendicular drags also affects the dynamics of the instability. For 1 < β < 3, the amplitude of the oscillation is weakly dependent on β, with larger values of β leading to larger displacements of the end of the filament as shown in Fig. 6. For β > 3, the amplitude does not change significantly. Simulations show that smaller values of β lead to higher curvatures along the filament (movies of simulations with β = 1.5 and β = 5.0 are available in the online supplementary material). For β > 6, the filament is more rigid due to the high cost for moving perpendicular to the filament axis. The curvature along the filament at these larger values of β is more uniform than at smaller values of β. The frequency of the oscillation is also not strongly dependent on the value of β (Fig. 6), varying by less than a factor of 3 for 1 < β < 11.

FIGURE 6.

Extreme positions of the free end of the cell (X_end (top), Y_end (middle)), and frequency of flailing (bottom), ζL⁴ω/A, as a function of β with FL²/A = 120.

DISCUSSION

Here I have presented a model that can describe the periodic motions of a gliding myxobacteria with one end stuck to the substrate. The force produced by the A-motility pusher motor at the unstuck end acts as a tangentially directed follower force. If this force exceeds the critical force, then the bacterium bends and periodically flails about. The amplitude of the cell body deformation is dependent on two physical parameters, the force of the A-motility engine and the anisotropy between the tangential and perpendicular drag coefficients.

Simulations of the model equations produce qualitatively similar shapes to time lapse images of M. xanthus cells (18). Based on the amplitude of the oscillations from the experiment, this model suggests that the dimensionless force exerted by the A-motility engine is in the range 100 < FL²/A < 300. In addition, the simulations suggest that 1.5 < β < 4. For a filament immersed in bulk fluid, slender-body hydrodynamics calculations give β = 2 (20), and so the ratio between the tangential and perpendicular drag coefficients is not strongly affected by the presence of the substrate or the lubrication of the secreted slime.

For these ranges on the force and values of β, the frequency of the oscillation is fairly uniform. Therefore, we can estimate that ζL⁴ω/A ∼ 300. If we assume that the tangential drag coefficient between the cell body and substrate can be estimated using the relation derived for a slender body immersed in a fluid of viscosity η moving near a wall, then ζ = 2πη/ cosh⁻¹(1 + δ/a) where δ is the distance between the cell body and the wall and a is the radius of the cell body (21). Following Wolgemuth et al. (16), I assume that η ≈ 10 g/cm s and δ = 10 nm. Therefore, ζ ≈ 300 g/cm s. From the experiment (18), ω = 4 × 10⁻²s⁻¹ (Fig. 1). This analysis leads to a rough estimate for the bending modulus, A ∼ 3 × 10⁻¹⁴ erg cm, which is 30 times smaller than that measured in B. subtilis fibers (2). The smaller radius of myxobacteria compared to B. subtilis can account for a 10-fold difference in bending modulus between these two bacteria. The difference between these values could also be due to reduced cross linking of the peptidoglycan, as has been suggested previously (17). Using this value for the bending modulus, we can estimate the force produced by the A-motility engine using the force estimates from the simulations. We find that F = 50–150 pN, consistent with the force predicted to be generated by hydration of slime (16).

One difficulty with measuring the propulsive force generated in gliding bacteria is that though microspheres will adhere to the cell body, they do not bind rigidly, and therefore can translate along the cell length (24). Applying calibrated forces opposite the direction of motion via optical tweezers or fluid flow is not possible if the beads slide along the cell surface. The model presented here suggests a new method to measure propulsive force in gliding bacteria. Using micropipettes or polylysine coated beads, it should be possible to constrain one end of a gliding cell. By measuring the deformation and frequency of periodic motions of the cell body, the model allows a method to calculate the force produced by the A-motility engine in myxobacteria and may also be applicable for measuring forces in other gliding bacteria such as flexibacteria and cyanobacteria. The one lacking piece of information is the drag coefficient. Applying a calibrated force in the direction of motion using fluid flow or optical tweezers should be possible. Pulling a cell along the surface in the direction of the long axis at different velocities can provide a method for measuring the tangential drag. In addition, adhering two beads to the cell body and pulling perpendicular to the long axis can provide a method for measuring the perpendicular drag coefficient.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX

Intrinsic representation

For problems involving the deformation of elastic filaments, it is often easier to handle the mathematics using an intrinsic representation that does not make reference to the actual spatial coordinate position of the filament and only accounts for the filament conformation. These methods have proven useful in a number of applications (for example, see Goldstein and Langer (19) and Wolgemuth et al. (25)). Using the definition of the curvature, κ, Eqs. 1 and 2 can be rewritten in terms of κ and Λ (19),

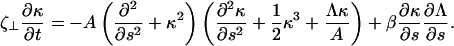(4)

The clamped boundary condition is satisfied by setting the translational and angular velocities of the filament to zero. Therefore, at s = 0,

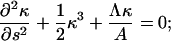(5)

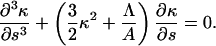(6)

At the forced end, the boundary conditions on κ are

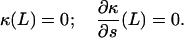(7)

Linear stability

Linearization of Eqs. 3 and 4 about the straight filament (κ = 0) gives that Λ = F and

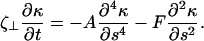(8)

Assuming that the solution is of the form κ = κ(s) exp((γ + iω)t), leads to a system of equations for γ and ω that can be solved if F is known. When γ < 0, the κ = 0 solution is stable and the filament remains straight. When γ > 0, the filament bends. Numerical solution of Eq. 8 found a critical force (the point at which the filament is no longer straight) to be F_cr ≈ 37.5 A/L². In addition, the value for ω was nonzero: this instability is a supercritical Hopf bifurcation (26).