A Quantitative Model of Purinergic Junctional Transmission of Calcium Waves in Astrocyte Networks

Abstract

A principal means of transmitting intracellular calcium (Ca²⁺) waves at junctions between astrocytes involves the release of the chemical transmitter adenosine triphosphate (ATP). A model of this process is presented in which activation of purinergic P2Y receptors by ATP triggers the release of ATP, in an autocrine manner, as well as concomitantly increasing intracellular Ca²⁺. The dependence of the temporal characteristics of the Ca²⁺ wave are shown to critically depend on the dissociation constant (K_R) for ATP binding to the P2Y receptor type. Incorporating this model astrocyte into networks of these cells successfully accounts for many of the properties of propagating Ca²⁺ waves, such as the dependence of velocity on the type of P2Y receptor and the time-lag of the Ca²⁺ wave behind the ATP wave. In addition, the conditions under which Ca²⁺ waves may jump from one set of astrocytes across an astrocyte-free lane to another set of astrocytes are quantitatively accounted for by the model. The properties of purinergic transmission at astrocyte junctions may determine many of the characteristics of Ca²⁺ propagation in networks of these cells.

INTRODUCTION

Purinergic receptors on astrocytes implicated in Ca²⁺ elevation

Application of adenosine triphosphate (ATP) to astrocytes for periods of several hundred seconds gives rise to a transient increase in Ca²⁺ concentration—hereafter denoted by [Ca²⁺]—which then relaxes to a maintained plateau (1–3, but see Koizumi et al. (4)). The sustained response is due to an influx of calcium ions through P2X₇ receptors (1,5). The transient response is most likely mediated by P2Y₁ and P2Y₂ receptors (henceforth P2Y₁ R and P2Y₂ R), involving an increase in inositol 1,4,5-trisphosphate (IP₃) to release calcium from endoplasmic reticulum (ER) stores (4) through G-protein coupling to phospholipase C (PLC) (3,6). The P2Y₂ R agonist uridine 5′-triphosphate (UTP) produces Ca²⁺ in astrocytes through an increase in IP₃ turnover (7) with subsequent release of calcium from thapsigargin-sensitive calcium stores (8) as well as release of ATP (9); however, the mechanism by which ATP is released is as yet unknown. Direct evidence for the existence of functional P2Y₁ R and P2Y₂ R on astrocytes has been obtained by injecting astrocyte mRNA into oocytes and showing subsequently that these give Ca²⁺ upon application of the P2Y₁ R agonist 2-methylthio ATP and the P2Y₂ R agonist UTP (10); see also Zhu and Kimelberg (11). The dominant metabotropic P2YR appears to be P2Y₁ R, according to a combined Western blot pharmacological approach (12).

Involvement of P2Y receptors in junctional transmission of Ca²⁺ between astrocytes

Hassinger et al. (13) have shown that scraping away cells to form a cell-free lane in two-dimensional astrocyte cultures does not interrupt the Ca²⁺ initiated on one side of the lane from propagating to the other side for lane widths <∼120 μm, although the delay time for the Ca²⁺ propagating across the lane is longer the wider the lane. These observations show that transmission of Ca²⁺ may involve the release of a chemical substance from the astrocytes. It is very likely that the principal substance that mediates this Ca²⁺ transmission is ATP. Simultaneous imaging of ATP and Ca²⁺ waves in two-dimensional cortical astrocyte cultures have been obtained after these were initiated by mechanical stimulation of an astrocyte (14). Both waves possess a duration of ∼10s at half-height and both were blocked by the purinergic receptor antagonist suramin. P2YRs, specifically P2Y₁ Rs and P2Y₂ Rs, dominate in the action of the astrocyte transmitter ATP in propagating Ca²⁺ waves (see, for example, Gallagher and Salter (15) and Salter and Hicks (16)). In spinal cord astrocytes, specific P2Y₁ R antagonists, such as adenosine-3′-phospho-5′-phosphosulfate, block transmission (17); see also Fam et al. (18). A fivefold greater concentration of the P2Y₂ R agonist UTP is required to give a [Ca²⁺] comparable to that obtained using the specific P2Y₁ R agonist 2-MeS adenosine diphosphate (henceforth, ADP) (18), although ATP itself is equipotent at P2Y₁ Rs and P2Y₂ Rs (19). Gallagher and Salter (15) have shown that transmission of Ca²⁺ occurs in two-dimensional cultures of human astrocytoma cells heterologously expressing either P2Y₁ Rs or P2Y₂ Rs, with transmission through the latter faster than through the former. They take this to be due to the fact that P2Y₁ Rs take longer than P2Y₂ Rs to generate Ca²⁺ when stimulated with ATP. Since ADP acting on P2Y₁ Rs generates Ca²⁺ much faster than ATP, therefore apyrase, by metabolizing ATP to ADP, accelerates Ca²⁺ release in astrocytes that only express P2Y₁ Rs but blocks release in astrocytes that only express P2Y₂ Rs (15). Although glutamate receptors exist on astrocytes, the release of glutamate onto these is not primarily involved in the transmission of Ca²⁺ waves, but rather that of Na⁺ waves (20).

Mechanism of release of ATP from astrocytes during junctional transmission of Ca²⁺

It is well established that ATP-stimulated release of glutamate from astrocytes involves a calcium-triggered exocytosis of glutamate-containing vesicles (21–24). However, the mechanism of release of ATP from astrocytes has yet to be clearly established. Mechanical stimulation gives rise to an increase in [Ca²⁺], which, if buffered with BAPTA, has been claimed either to block (25,26) or not to block (14) ATP release. However, depletion of intracellular calcium stores with thapsigargin fails to block ATP release (14). Most importantly, ATP waves propagate ahead of calcium waves from the point of stimulation in a two-dimensional astrocyte culture (14) and in the retina (27). Thus, the cumulative evidence is against a Ca²⁺-dependent exocytosis of ATP. Alternative pathways for ATP release from astrocytes that are not dependent on calcium-triggered exocytosis are possible. ATP release is partially blocked by antagonists to ATP-binding-cassette proteins such as glibenclamide (28,9) and there is evidence that elevation of protein kinase C (PKC) enhances a glibenclamide-sensitive chloride efflux from astrocytes through ATP-binding cassette proteins, raising the possibility that PKC stimulation elevates ATP release (28).

Modeling the process of astrocyte junctional transmission of Ca²⁺

Previous models of Ca²⁺ wave propagation in networks of glial cells have assumed that the passive diffusion of IP₃ through gap junctions is the underlying mechanism (29,30). An elevated concentration of IP₃ in a single cell acts on receptors on the ER causing the release of Ca²⁺ into the cytosol, which then activates PLC to produce more IP₃. This IP₃ diffuses to neighboring cells, where the regenerative process is repeated. In contrast, the present model is based solely on purinergic transmission, where the underlying mechanism is the diffusion of ATP in the extracellular space. This ATP binds to P2Y receptors on the astrocyte surface, thus initiating a G-protein cascade that leads to the production of IP₃ and the consequent release of Ca²⁺ from internal stores. This increase in [IP₃] is also assumed to lead to release of ATP into the extracellular space, where it acts back on the initiating cell and also diffuses to neighboring cells, thus propagating an ATP wave and a Ca²⁺ wave. We consider both one-dimensional and two-dimensional networks of these astrocytes and show that the model accounts for most observations on astrocytic transmission and provides a coherent theoretical framework for further experimental research on this subject.

METHODS

Overview

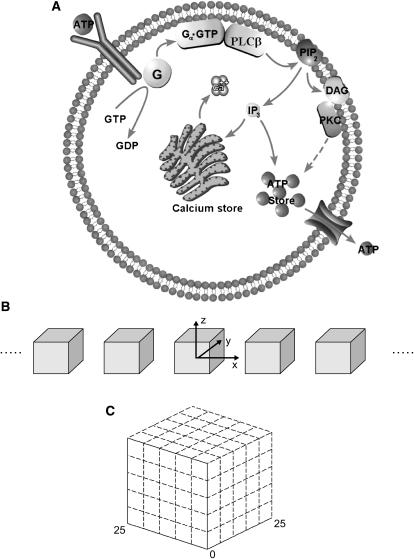
The single-cell model follows that of Lemon et al. (31) with some changes. Simplifications have been made: some processes included in that model are not relevant to astrocytes; others are second-order effects and can be omitted with little change to the final results. The main additions that must be made concern the release of ATP into the extracellular space and the diffusion of IP₃ inside the cell and ATP outside the cell. Fig. 1 A is a schematic diagram showing the main processes that will be used in our model of a single cell; Table 1 gives the parameter values used in the calculations.

FIGURE 1.

(A) Simplified schematic diagram of the steps leading from metabotropic receptor activation to Ca²⁺ release from the calcium store (endoplasmic reticulum) into the cytosol and ATP release from internal stores into the extracellular space. Transmitter (ATP) binds to the receptor which then interacts with the G-protein (G), leading to the replacement of GDP with GTP and the subsequent dissociation of the G-protein into subunits. The subunit G_α·GTP binds to a site on phospholipase C-β (PLC) and this activated unit initiates an interaction with membrane-bound phosphatidylinositol 4,5-bisphosphate (PIP₂), leading to the hydrolysis of PIP₂ and the production of IP₃. This diffuses into the cytosol where it opens IP₃-sensitive channels in the ER, allowing the release of Ca²⁺ into the cytosol. The IP₃ is also assumed to interact with ATP stores inside the astrocyte, leading to the release of ATP into the extracellular space. An alternative pathway, involving diacylglycerol (DAG) and protein kinase C (PKC) is also indicated, though it is not used in the present model. (B) A lane of model astrocytes, represented by cubes of side 25 μm, separated by spaces of width 25 μm. The cubes have their centers in the xy plane (z = 0) and are aligned parallel to the x-axis. (C) A cube of side 25 μm, representing a single astrocyte, subdivided into 5 × 5 × 5 cubes of side 5 μm, as indicated by the broken lines. The grid points used in the numerical integration scheme are placed at the center of each subcube, thus giving 27 interior points and 98 surface points. At all points, the processes implemented are IP₃ diffusion and Ca²⁺ release from the ER; at the surface points, the additional processes implemented are receptor activation, the G-protein cascade leading to IP₃ production, and the release of ATP. The exterior space is likewise divided into subcubes of side 5 μm with grid points at the centers and these are used to implement diffusion of ATP in the extracellular space.

TABLE 1.

Model parameter values

Symbol	Definition	Value	Notes
P2Y Receptor regulation
KR	Dissociation constant for ligand binding to P2YRs	Various	See text
G-protein cascade
kdeg	IP3 degradation rate	1.25 s−1	(31)
ka	G-protein activation rate	0.017 s−1	(31)
kd	G-protein deactivation rate	0.15 s−1	(31)
r*h	IP3 production rate	2 × 10−14μmol μm−2 s−1	Fit to experiment
DIP	IP3 diffusion coefficient	280 μm2 s−1	(30)
ATP production
VATP	ATP production rate	2 × 10−11μmol μm−2 s−1	Fit to experiment
Krel	Kinetic parameter	10 μM	Fit to experiment
[IP3]min	Threshold concentration	0.012 μM	Fit to experiment
kloss	Depletion rate parameter	30 s−1	Fit to experiment
DATP	ATP diffusion coefficient	300 μm2 s−1	(67)
Jmax	Maximum channel current	2880 μM s−1	(36)
KI	IP3 channel kinetic parameter	0.03 μM	(36)
Kact	IP3 channel kinetic parameter	0.17 μM	(36)
kon	IP3 channel kinetic parameter	8.0 μM s−1	(36)
Kinh	IP3 channel kinetic parameter	0.1 μM	(36)
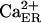[]	Ca2+ concentration in ER	400 μM	(36)
Vmax	Maximum pumping rate into ER	5.85 μM s−1	(36)
Kp	Pump dissociation constant	0.24 μM	(36)
β	Endogenous buffer parameter	0.0244	(36)
Initial values
[IP3]0	Initial IP3 concentration	0.01 μM	(31)
[Ca2+]0	Initial Ca2+ concentration	0.05 μM	(36)

Receptors

A basic model is used in which receptors do not desensitize—they are neither phosphorylated nor internalized and recycled. Thus the reaction is

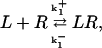(1)

where L is ligand and R receptor. The quantity we want is the ratio of bound to total receptors, ρ = [LR]/[R_T], where [R_T] = [R] + [LR] is the total number of receptors. Under the assumption of fast binding kinetics, Eq. 1 can be assumed to be in equilibrium, leading to

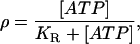(2)

where [L] = [ATP] is the extracellular ATP concentration and 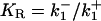is the dissociation constant. Although K_R is defined in relation to the binding of ATP to P2Y receptors, and as such should have a value of the order of 10 μM (32), it can be interpreted more broadly in the context of the model. The crucial quantity is ρ, since this governs the production of active G-protein (see Eq. 3 below), and thus ρ can be interpreted more generally as being a measure of additional aspects of the model such as the density of P2Y receptors and the strength of the coupling of the bound receptors to G-protein activation. To save introducing additional parameters, these aspects have been incorporated in the single quantity K_R, which then becomes an effective, rather than an actual, dissociation constant.

G-protein cascade

The equation describing G-protein activation is Lemon et al. (31), their Eq. 16:

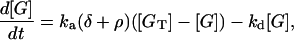(3)

where [G] is the amount of activated G-protein, [G_T] is the total G-protein, ρ is the fraction of bound receptors as given by Eq. 2, δ is the ratio of the activities of the unbound and bound receptors (and thus allows for background activity even in the absence of ligand binding, i.e., unbound receptors can activate a small amount of G-protein), and k_a and k_d are the G-protein activation and deactivation rate parameters, respectively. Eq. 3 is represented by the kinetic scheme

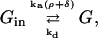(4)

where G_in is inactive G-protein, so [G_in] = [G_T] − [G]. Again assuming fast kinetics, we obtain

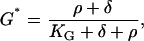(5)

where G* = [G]/[G_T] and K_G = k_d/k_a.

IP₃ production and diffusion

IP₃ production and degradation is governed by Lemon et al. (31), their Eq. 19:

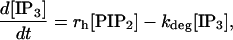(6)

where r_h = α([Ca²⁺]/(K_c + [Ca²⁺]))[G] and the last term accounts for the degradation of IP₃ inside the cell. The Ca²⁺-dependence of r_h allows for the catalytic effect of Ca²⁺ on IP₃ production (it binds to a catalytic site on PLC), but for simplicity this secondary effect is not included in the astrocyte model, so K_c = 0 giving r_h = α[G]. Also, there is assumed to be no depletion of PIP₂, so [PIP₂]= [(PIP₂)_T] and Eq. 6 simplifies to

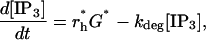(7)

where G* is given by Eq. 5, and r*_h is a constant, independent of [Ca²⁺].

In the above equations [IP₃] is taken to be spatially homogeneous, but now diffusion must be included. IP₃ is produced at the cell wall, it then diffuses into the cytosol and is degraded everywhere, including at the cell wall. Thus [IP₃] is now spatially inhomogeneous, [IP₃] = [IP₃](r, t), and satisfies

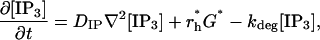(8)

where D_IP is the diffusion coefficient for IP₃ and the term r*_hG* is applied only at the cell wall.

ATP production and diffusion

As stated in the Introduction (see also Discussion), the mechanism by which ATP is released by astrocytes has not been established, although there is evidence that IP₃ is probably involved. We have chosen to use IP₃ as the agent triggering release, but this is not crucial to the model. The release can be linked to the concentration of active G-protein, with essentially the same results. In an even simpler model, ATP release can be taken to depend directly on ATP concentration, with no intermediate steps.

ATP is assumed to be released into the extracellular space at the cell boundary at rate

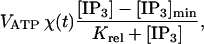(9)

provided [IP₃] is greater than [IP₃]_min; otherwise it is not released. The threshold value [IP₃]_min is necessary to prevent very small levels of [ATP] from being amplified and thus leading to a propagating wave. V_ATP and K_rel are constants and χ(t) is a parameter that accounts for depletion of ATP stores inside the cell; it has initial value 1 and decreases according to

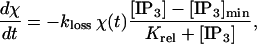(10)

where k_loss is a constant. This depletion is included to terminate ATP release from each cell and thus lead to the correct waveforms for [ATP] and [Ca²⁺]. Some evidence for a depletable ATP store is provided by the observation that there is no ATP release by the third impulse during repetitive stimulation of astrocytes (14). Evidence against such depletion could come from experiments in which astrocytes are exposed to glutamate, leading to the production of IP₃ and hence depletion of ATP stores, but an intercellular wave is still supported (33). However, it may be that only the initial response to glutamate releases significant quantities of IP₃: see especially Fig. 2 A in Kim et al. (34), which shows an initial Ca²⁺ spike followed by much lower oscillations. These oscillations might be supported by a concentration of IP₃ that is below threshold in our model, or they might be the result of Ca²⁺-induced Ca²⁺ release from IP₃-insensitive stores (see Discussion in Charles et al. (33) and the theoretical analysis of Keizer and Levine (35)). Thus, the ATP stores may only be partially depleted by glutamate and also could have time for some refilling. An alternative way of terminating the action of ATP would be to assume that the P2Y receptors desensitize at a sufficient fast rate. Desensitization has been included in the P2Y receptor model in Lemon et al. (31), but the parameter values listed there give a timecourse that is too slow.

FIGURE 2.

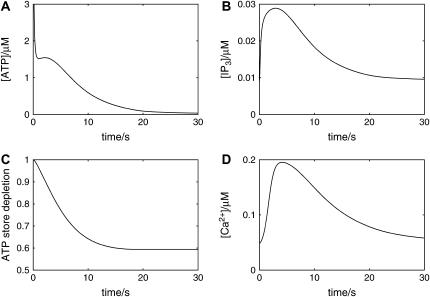
Changes in [ATP], [IP₃], [ATP]_store, and [Ca²⁺] in a single isolated model astrocyte, as functions of time, after its exposure to an initiating instantaneous pulse of ATP of concentration 10 μM applied at time t = 0. (The pulse is applied at each grid point immediately surrounding the astrocyte.) K_R = 25 μM. (A) [ATP], immediately outside the astrocyte. (The initial amplitude is 10 μM, but the range on the ordinate has been reduced for clarity.) (B) [IP₃], at the center of the astrocyte. (C) The depletion of the ATP store inside the astrocyte, expressed as a proportion of the initial [ATP]. (D) [Ca²⁺], at a point just inside the astrocyte.

ATP diffuses in the extracellular space and is thus spatially inhomogeneous, [ATP] = [ATP](r, t), and satisfies

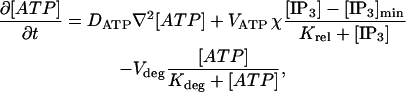(11)

where D_ATP is the diffusion coefficient for ATP and the depletion term is applied only at the cell wall and only when [IP₃] > [IP₃]_min. The last term allows for the breakdown of ATP by an ectonucleotidase. It was found that the inclusion of this term makes no essential difference to the output of the model (see Results) and so it has been omitted in the main calculations reported here.

Ca²⁺ release from internal stores

The steps leading from IP₃ production to Ca²⁺ release from the ER via IP₃ Rs have been modeled in Lemon et al. (31), but here we follow a similar scheme due to Fink et al. (36). Both schemes are based on the original models of De Young and Keizer (37), and Li and Rinzel (38).

The Ca²⁺ dynamics are governed by

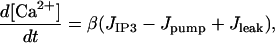(12)

where [Ca²⁺] is the cytosolic Ca²⁺ concentration, J_IP3, J_pump, and J_leak are the rates of Ca²⁺ concentration change due to release through IP₃ R channels, pump uptake into the ER, and leak from the ER, respectively, and β is a factor describing Ca²⁺ buffering. The diffusion of Ca²⁺ has been neglected, since it is much slower that that of IP₃. The IP₃-induced current is

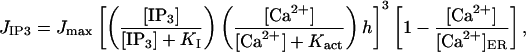(13)

where J_max is the maximum rate, K_I is the dissociation constant for IP₃ binding to an IP₃ R, K_act is the dissociation constant for Ca²⁺ binding to an activation site on an IP₃ R, [Ca²⁺]_ER is the Ca²⁺ concentration in the ER (taken to be constant), and h satisfies

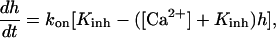(14)

where k_on is the rate of Ca²⁺ binding to the inhibitory site on the IP₃ R and K_inh is the corresponding dissociation constant.

The ATPase Ca²⁺ pump is described by

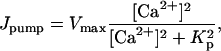(15)

where V_max is the maximum pumping rate and K_p is the dissociation constant. The leak is described by

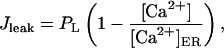(16)

where the constant P_L is determined by steady-state flux balance (see Initialization, below). The buffering is described by the steady-state approximation

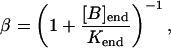(17)

where [B]_end and K_end are the concentration and dissociation constants of the endogenous buffer, respectively.

Geometry

Each astrocyte is represented by a cube of side 25 μm (Fig. 1 C). These cubes are arranged in two-dimensional arrays, on the x,y plane. The minimum spacing between cubes is 25 μm, but this can be altered to investigate the maximum distance over which astrocytes can communicate. A single lane of four cubes with minimum spacing is illustrated in Fig. 1 B. In many calculations, lanes of 19 astrocytes were used in various configurations to investigate communication between lanes. With this simplified geometry we are not attempting to model the spatial complexity of a real astrocyte; rather this is an effective astrocyte in which the processes emanating from a real astrocyte are lumped into a compact space, taken to be cubical for reasons of computational simplicity. Real astrocytes also tend to be space-filling, with their arborizations touching but not overlapping (39); the intercellular gaps in our model reflect the fact that the specific geometry of the astrocytes has not been incorporated.

Initialization

In the absence of ATP there is still background IP₃ and Ca²⁺ resulting from the activation of a small amount of G-protein by unbound receptors (see Eq. 5; in this case, ρ = 0 but δ ≠ 0). If diffusion of IP₃ is neglected, then initial homogeneous concentrations of IP₃ and Ca²⁺, [IP₃]₀, and [Ca²⁺]₀ respectively, can be set. However, this cannot be used as the background state when diffusion is included, since the production of IP₃ at the cell wall and its subsequent diffusion into the interior of the cell violate this homogeneous state and lead to instabilities. Rather, these initial homogeneous concentrations are used to set the activity ratio δ (using Eqs. 5 and 7) as

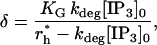(18)

and the Ca²⁺ leak rate, P_L, by setting J_IP3 − J_pump − J_leak = 0. Then the IP₃ equation, Eq. 8, is run, as described in the following section, until a steady-state solution is obtained that is close to the homogeneous one, but of course not identical since it is inhomogeneous. The Ca²⁺ equation, Eq. 12, is now solved to find the corresponding equilibrium Ca²⁺ concentration, which will also be inhomogeneous (even though Ca²⁺ does not diffuse), because of the inhomogeneous distribution of IP₃.

Method of solution

Each cell is represented by a rectangular Cartesian grid with spacing 5 μm (Fig. 1 C), and thus contains 27 interior grid points and 98 surface grid points. The space between the cells is similarly represented by a rectangular grid with the same spacing of 5 μm. The grid extends to ±49 points in the z direction, which is essentially infinite. The lanes of 19 astrocytes use ±99 grid points and thus the grid ends in a space between cells. The boundary conditions are ATP sinks at all boundaries. The ER is present at all 125 grid points of each cell and Ca²⁺ production and IP₃ degradation also occurs at each of these points. On the other hand, IP₃ production occurs only at the 98 surface points, as does ATP binding to P2YRs and the production of ATP.

The background distributions of IP₃ and Ca²⁺ are calculated as described in Initialization, above. In doing these calculations, fluxes need to be converted to concentration changes. A flux of f μmol μm⁻² s⁻¹ through an area a μm² into a volume v μm³ leads to a concentration change of 10¹⁵ (f a/v) μM s⁻¹, so the appropriate conversion factor to be applied to r*_h and V_ATP is 0.2 × 10¹⁵ μm⁻¹. The ATP wave is initiated by setting a step concentration (typically 10 μM) of ATP in the layer surrounding the central cell.

The equations for the diffusion of IP₃, Eq. 8, and of ATP, Eq. 11, are solved using a “leap-frog” method (see the Appendix in Henery (40); in the present case, only the straightforward extension of the one-dimensional case is required since there are only single equations, and not coupled equations). The other differential equations for ATP store depletion, Eq. 10, Ca²⁺, Eq. 12, and h, Eq. 14, are solved using a standard Runge-Kutta method.

RESULTS

P2Y₁ and P2Y₂ receptor generation of Ca²⁺ in a single astrocyte

According to the model in Fig. 1 A, exposure of a single astrocyte to ATP leads to both an increase in [Ca²⁺] as well as the release of ATP, which increases [ATP] and then acts on P2YRs of the cell in an autocrine manner. Fig. 2 shows that exposure of an astrocyte to an initiating pulse of ATP (Fig. 2 A) leads to a fast increase in [IP₃] (Fig. 2 B). Given that the release of ATP is directly coupled to IP₃ (see Eq. 9), the ATP autocrine mechanism gives rise to a relatively sustained increase in [ATP], which is terminated and drops back to basal levels as a consequence of depletion of the store of releasable ATP in the astrocyte (Fig. 2 C). Calcium is released from the ER by IP₃, so that there is a concomitant increase in [Ca²⁺] accompanying, but lagging that of [IP₃] (Fig. 2 D).

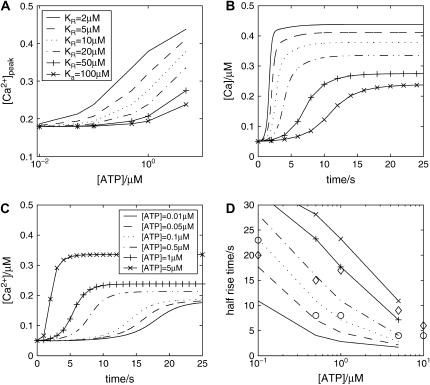
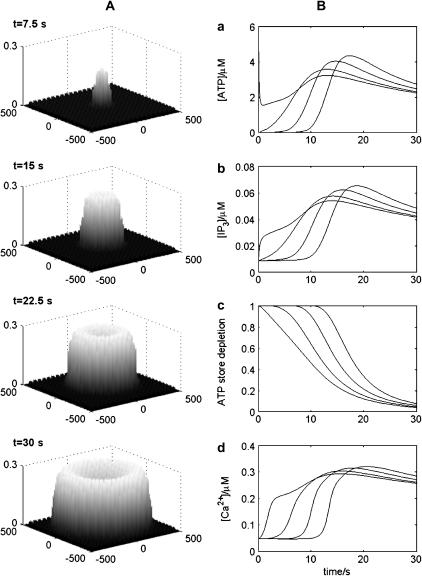
The results of a sustained application of ATP to a single astrocyte are given in Fig. 3. The quantitative relation between peak [Ca²⁺] and [ATP] is shown in Fig. 3 A, with the curves giving higher peak Ca²⁺ as K_R decreases. Fig. 3 B shows that the rate of rise of [Ca²⁺], after application of a fixed concentration (5 μM) of ATP, increases with a decrease in K_R. This rate of rise also increases with an increase in [ATP] (Fig. 3 C). Fig. 3 D plots the half-rise times for [Ca²⁺] as a function of [ATP]. Shown also are the experimental values of Gallagher and Salter (15) for astrocytes in which ATP or ADP acts exclusively on P2Y₁ Rs (diamonds) or ATP acts exclusively on P2Y₂ Rs (circles). It will be noted that the theoretical curves give a best fit to the experimental data for the P2Y₂ Rs if K_R ∼5–15 μM, but that the data for the P2Y₁ Rs is fitted if K_R ∼25–50 μM. Thus ATP acting on P2Y₂ Rs gives a faster rising [Ca²⁺] than when it acts on P2Y₁ Rs, even though both receptors have the same sensitivity to ATP.

FIGURE 3.

Properties of the P2Y₁ and P2Y₂ receptors on a single model astrocyte after sustained application of ATP. (A) Dose-response curve, with [ATP] on the abscissa (logarithmic scale) and peak Ca²⁺ on the ordinate, for receptors with K_R = 2, 5, 10, 20, 50, and 100 μM, as indicated. (B) Time course of Ca²⁺ in an astrocyte, after a step application of ATP (5 μM) to P2Y receptors, for the same range of K_R values as in A. (C) Time course of Ca²⁺ after the step application of various concentrations of ATP (0.01, 0.05, 0.1, 0.5, 1.0, and 5.0 μM), as indicated. K_R = 20 μM. (D) Time for Ca²⁺ to reach 50% of its peak value in response to different concentrations of ATP acting on receptors with the same range of K_R values as in A. Also shown is the experimental data from Fig. 6 d in Gallagher and Salter (15), for P2Y₁ receptors (diamonds) and P2Y₂ receptors (circles).

P2Y₁ and P2Y₂ receptor generation of Ca²⁺ and release of ATP from astrocytes

Consider a network consisting of a lane of astrocytes, each astrocyte making junctions with one another (Fig. 1 B), using the transmitter ATP acting on P2YRs at the junctions. Initiation of the transmission of ATP and of Ca²⁺ waves along the network begins at a cell when the [ATP] immediately surrounding the cell is impulsively raised to 10 μM. A [Ca²⁺] transient is thus initiated in the cell, and the cell also releases ATP, which then acts back in an autocrine manner to release further ATP after this initial application. This released ATP, together with some of that applied, diffuses to the next cell to generate Ca²⁺ and also to trigger the regenerative release of ATP once more through the action of P2YRs. In this manner, the Ca²⁺ and ATP waves are transmitted along the astrocyte network.

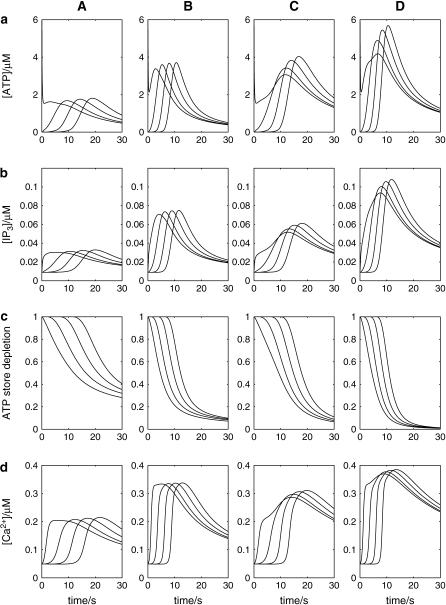
Fig. 4 shows the quantitative relationships between [ATP] (a), [IP₃] (b), the size of the ATP store in the astrocyte (c), and [Ca²⁺] (d). Some data relating to Fig. 4 is summarized in Table 2. Fig. 4, A and B, is for lanes of astrocytes one cell wide and 19 cells long with K_R = 25 μM in Fig. 4 A and K_R = 15 μM in Fig. 4 B. The changes in [IP₃] in each cell are similar to those in [ATP], and they both lead the [Ca²⁺] changes. This happens because the increase in [Ca²⁺] arises only after IP₃ has acted on the calcium store through the mechanism described by Eq. 12, whereas IP₃ causes the immediate release of ATP from stores inside the cell, according to Eq. 9. The release of ATP, involving in part an autocrine mechanism, is terminated by depletion of the ATP store (Fig. 4, Ac and Bc). Comparison between the results for K_R = 25 μM (as for P2Y₁ R, Fig. 4 A) and K_R = 15 μM (as for P2Y₂ R, Fig. 4 B), shows that in the latter case the duration of [Ca²⁺] at 70% height is less, as is that of [ATP] (Table 2). This leads to a faster speed for both the ATP and Ca²⁺ waves (19 μm s⁻¹ compared with 11 μm s⁻¹ for the higher K_R). Gallagher and Salter (15) observed propagation exclusively through P2Y₁ R at 6 μm s⁻¹ (see their Fig. 4 e) and through P2Y₂ R at 18 μm s⁻¹ (see their Fig. 4 e). The velocities for Ca²⁺ for different values of K_R are summarized in Fig. 5 (open bars). For 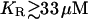the wave decreases rapidly in amplitude and does not propagate beyond the first few astrocytes from the point of stimulation. This is in marked contrast to the behavior for K_R < 33 μM, in which case the wave propagates indefinitely with almost constant amplitude. For 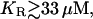and an initial impulsive application of 10 μM ATP, the value of ρ (Eq. 2) is too small for the G-protein cascade to produce sufficient IP₃ to sustain the regenerative release of ATP. The decrease in duration of ATP and Ca²⁺ waves at the lower K_R is due to the faster depletion of the ATP stores by the action of IP₃ (compare Fig. 4 Ac with Fig. 4 Bc). Note also the larger amplitude of [ATP] and therefore of [Ca²⁺] for the receptors with the smaller K_R (compare Fig. 4, A and B).

FIGURE 4.

Propagation of various signals in a lane of model astrocytes. The lane is 19 cells long and either one cell wide (columns A and B) or three cells wide (columns C and D), with spacing of 50 μm between the centers of adjacent cells in all cases. Results are shown for four astrocytes (1−4), situated sequentially along a lane (using the middle row in columns C and D), with initiation occurring in the central astrocyte (number 1). (a) [ATP] immediately outside each astrocyte. (b) IP₃ production in each astrocyte. (c) Depletion of the ATP store in each astrocyte. (d) Ca²⁺ transients in each astrocyte. K_R = 25 μM in columns A and C and 15 μM in columns B and D. The waves are initiated at t = 0 by an instantaneous pulse of ATP of magnitude 10 μM around astrocyte 1.

TABLE 2.

Data from Fig. 4; the durations are calculated at 70% of the height above background

		KR (μM)	Wave speed (μm s−1)	Lag ATP-Ca2+ (s)	Duration (s)
	Lane				ATP	Ca2+
Fig. 4 A	One cell wide	25	11	2.8	10	14
Fig. 4 B	One cell wide	15	19	2.3	4.8	11.2
Fig. 4 C	Three cells wide	25	16	3.0	9.4	18
Fig. 4 D	Three cells wide	15	23	3.0	5.9	17.6

FIGURE 5.

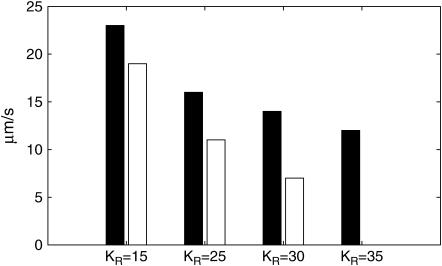
Dependence on K_R of the speed of the Ca²⁺ wave in a lane of astrocytes. The bars show the speed of the wave, from astrocyte to astrocyte, at distances >100 μm from the point of initiation, for K_R = 15, 25, 30, and 35 μM. The open bars are for a lane that is one cell wide and the solid bars are for a lane that is three cells wide. For the one-cell-wide case and K_R = 35 μM, the wave does not propagate beyond three cells, so its speed has not been calculated.

A number of calculations were also done with the inclusion of ATP breakdown, as given by the last term in Eq. 11. There was some diminution in amplitude and some decrease in velocity of the Ca²⁺ wave, but the overall results were very similar to those without this term. For example, for the parameter choice V_deg = 1 μM s⁻¹, K_deg = 5 μM, both the amplitude and velocity declined by <10%.

Consideration next was made of lanes of astrocytes which were three cells wide rather than just one cell. In this case, junctional transmission occurred first at the site of initiation to the immediately surrounding four astrocytes before propagating along this wider lane. Fig. 4, C and D, gives the results for cells possessing receptors with K_R = 25 μM and 15 μM, respectively. In Fig. 4, comparison of C with A shows the effects of increasing the width of the network. For a given K_R value, there is a substantial increase in peak [ATP] (from ∼2 μM to ∼4 μM) with concomitant increase in peak [Ca²⁺] from ∼0.2 μM to over 0.3 μM. Although the ATP store is depleted at a faster rate in the larger network (in Fig. 4, compare Cc with Ac), the time courses of both [ATP] and [Ca²⁺] are not much different in the two cases (in Fig. 4, compare Aa and Ad with Ca and Cd). This occurs because the pooling of ATP in the extracellular space, by the additional astrocytes in the larger network, offsets the loss due to store depletion. The result is to increase the amplitudes of ATP and Ca²⁺ waves with some increase in their speed (Table 2; see also Fig. 5, solid bars).

The transmission of the Ca²⁺ wave along the length of an astrocyte network consisting of a lane of cells using receptors with K_R = 25 μM is shown diagrammatically in Fig. 6. At 7.5 s the Ca²⁺ transient is near its peak value at the site of initiation in the middle of the lane (compare Fig. 6 (t = 7.5 s) with Fig. 4 Aa). Thereafter the wave is transmitted with little change in peak amplitude or speed along the network from the site of initiation (Fig. 6).

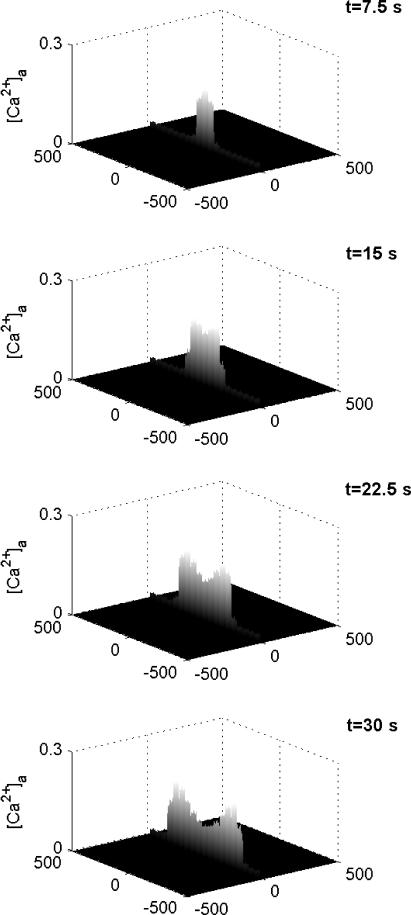
FIGURE 6.

Diagrammatic representation of the spatial and temporal changes in Ca²⁺ in a network consisting of a lane of astrocytes one cell wide, the distance apart of the centers of the astrocytes being 50 μm. The calcium wave is initiated by an instantaneous pulse of ATP of concentration 10 μM at the central astrocyte at time t = 0. The vertical bars give Ca²⁺ in μM at times t = 7.5, 15, 22.5, and 30 s, as indicated. K_R = 25 μM.

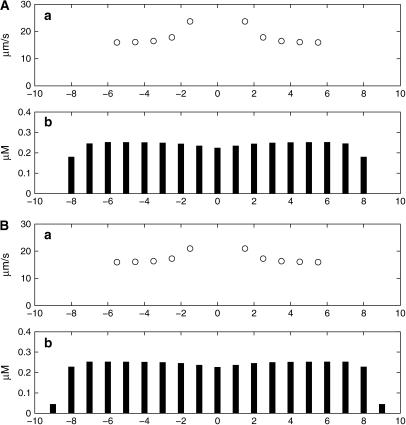
The question arises as to whether changing the size of the initiating [ATP] affects the size and propagation of Ca²⁺ in the remaining astrocytes along a lane of cells. Doubling the initiating [ATP] from 10 μM (Fig. 7 A) to 20 μM (Fig. 7 B) makes little difference to either the peak amplitude of [Ca²⁺] at the site of initiation and in the immediately adjacent cells or the speed of propagation in this vicinity or beyond the initiating region.

FIGURE 7.

Changes in the amplitude of the Ca²⁺ wave and its speed of conduction from astrocyte to astrocyte with changes in the amplitudes of the initiating ATP transient, which is 10 μM in A and 20 μM in B. In each case, the network is a lane of astrocytes three cells wide and initiation takes place at the central astrocyte. K_R = 25 μM. (a) The speed of the Ca²⁺ wave between adjacent astrocytes. (b) The peak amplitude of the Ca²⁺ transient in all the astrocytes.

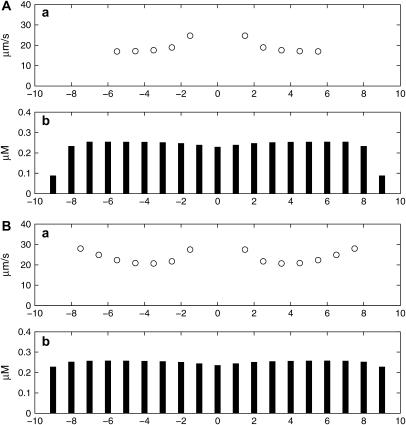
It has been reported that the addition of exogenous ATP can modify the propagation of Ca²⁺ in astrocytes in vivo, by increasing the distance over which the Ca²⁺ wave propagates (Sul et al. (62); see their Fig. 8). Although there is no reason why Ca²⁺ does not propagate over any distance in our model (provided K_R is not too large), it was of interest to observe if raising the ambient level of [ATP] affects the characteristics of propagation. Fig. 8 shows that the effects of increasing the ambient [ATP] from 0.03 μM to 0.07 μM are to marginally increase the speed of propagation (in Fig. 8, compare Aa with Ba) without changing the peak amplitude of the Ca²⁺ wave (in Fig. 8, compare Ab with Bb). Increasing the ambient [ATP] further, for example to 0.1 μM, leads to spontaneous production of ATP and Ca²⁺ in all cells.

FIGURE 8.

Changes in the amplitude of the Ca²⁺ wave and its speed of conduction from astrocyte to astrocyte with changes in the ambient background [ATP], which is 0.03 μM in A and 0.07 μM in B. In each case, the network is a lane of astrocytes three cells wide and initiation is a pulse of ATP of amplitude 10 μM at the central astrocyte. K_R = 25 μM. (a) The speed of the Ca²⁺ wave between adjacent astrocytes. (b) The peak amplitude of the Ca²⁺ transient in all the astrocytes.

P2Y₁ and P2Y₂ receptor generation of Ca²⁺ and release of ATP for a two-dimensional astrocyte network

Nearly all experimental work on astrocytes in vitro employs two-dimensional arrays of these cells (see Introduction). A study has therefore been made of transmission of ATP and Ca²⁺ waves in a two-dimensional plane of astrocytes compared with the one-dimensional lanes of astrocytes. Propagation of the Ca²⁺ wave in the two-dimensional network is illustrated diagrammatically in Fig. 9 A. This shows the wave-front moving out in the plane from its site of initiation in the center. There is an increase in the rates of rise and peak amplitude of [ATP] and [Ca²⁺] between the one-dimensional case (a lane one cell wide, Fig. 4 A) and the two-dimensional case in which each cell has four nearest neighbors with centers 50 μm apart (Fig. 9 B). The rate of decline of the ATP store is greater in the two-dimensional case (compare Fig. 4 Ac with Fig. 9 Bc), but the rate of decline of [ATP], [IP₃], and hence [Ca²⁺], is slower in the two-dimensional case because of the higher pooling of ATP (compare Fig. 4 A with Fig. 9 B). The duration of [Ca²⁺] at half-peak is >30 s (after the wave-front has moved away from the site of initiation; see Fig. 9 Bd), which is similar to that observed by Wang et al. (14) (see their Fig. 4 C). The [ATP] wave has a shorter duration than the Ca²⁺ wave (Fig. 9, Ba and Bd), as is also observed ((14), their Fig. 4 B).

FIGURE 9.

Diagrammatic representation of the spatial and temporal changes in a network consisting of a regular array of cells in a plane, the distance apart of the centers of the astrocytes being 50 μm. The calcium wave is initiated by an instantaneous pulse of ATP of concentration 10 μM around the central astrocyte at time t = 0. (A) The Ca²⁺ response in the whole array, with the vertical bars giving Ca²⁺ in μM at times t = 7.5, 15, 22.5, and 30 s, as indicated. (B) Results for four model astrocytes (1−4), at sequentially greater distances along a line in the array, with initiation occurring in astrocyte 1. K_R = 25 μM. (a) [ATP] immediately outside each astrocyte. (b) IP₃ production in each astrocyte. (c) Depletion of the ATP store in each astrocyte. (d) Ca²⁺ transients in each astrocyte.

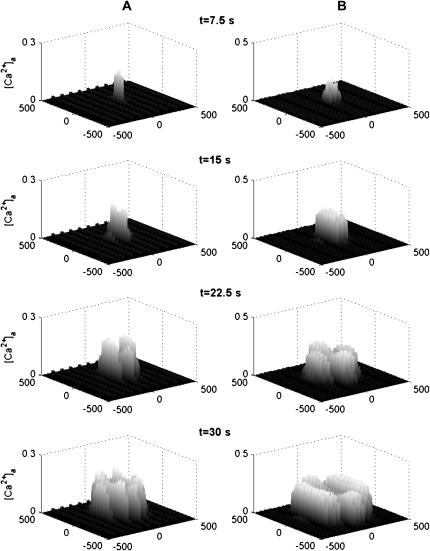
Experiments have been performed on Ca²⁺ propagation in which two-dimensional cultures of astrocytes are manipulated in such a way as to produce an astrocyte-free lane surrounded by astrocytes (see, for example, Fig. 1 B in Hassinger et al. (13)). Propagation of the Ca²⁺ wave is at ∼10 μm s⁻¹ in the absence of the lane (see Fig. 2 A in Hassinger et al. (13)). Successively wider lanes delay the propagation across the lane by successively longer times, consistent with the time taken for diffusion of ATP across the lane to initiate a Ca²⁺ wave in astrocytes on the opposite side of the lane from the side of the mechanically initiated Ca²⁺ wave. An 80-μm lane gave a delay of 18 s (see Fig. 2 B in Hassinger et al. (13)). Our model of Ca²⁺ transmission reproduces many of these features of Ca²⁺ propagation across cell-free lanes. Fig. 10 shows the effects of initiating Ca²⁺ transmission in lanes of cells that are either one cell wide (Fig. 10 A) or three cells wide (Fig. 10 B), when there are parallel lanes of cells on each side of the central lane containing the initiating cell, but the lanes are separated by a 75-μm-wide gap. At t = 22.5 s (for K_R = 25 μM), there is clear indication that the Ca²⁺ has jumped to the adjacent lanes in both cases.

FIGURE 10.

Diagrammatic representation of the spatial and temporal changes in Ca²⁺ in a network consisting of (A) parallel lanes of astrocytes one cell wide separated by empty lanes one cell wide and (B) parallel lanes of astrocytes three cells wide separated by empty lanes one cell wide. The remaining details are as for Fig. 6.

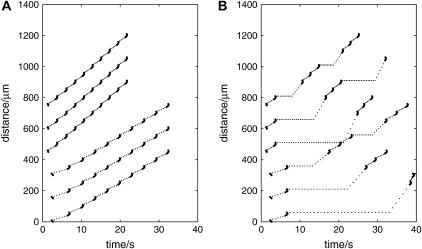
The present model gave a delay of 12 s for a 75-μm lane and 22 s for a 125-μm-wide lane (see Fig. 11 B), with a propagation speed of 16 μm s⁻¹ in the absence of lanes (Fig. 11 A), if K_R = 25 μM. In the case where K_R = 15 μM, the model gave a delay of 8 s for a 75-μm-wide lane (Fig. 11 B) with a propagation speed of 25 μm s⁻¹ in the absence of lanes (Fig. 11 A). For K_R = 25 μM, a jump of 175 μM can occur after ∼40 s (Fig. 11 B).

FIGURE 11.

Transmission of the Ca²⁺ wave along lanes and across cell-free lanes. The network consists of parallel lanes three cells wide separated by cell-free lanes of various widths. The Ca²⁺ wave is initiated at t = 0 by a pulse of ATP of amplitude 10 μM applied to the central astrocyte. (A) The time at which [Ca²⁺] reaches half-maximum in each astrocyte situated along the center of the middle lane. The points (·) show the time at which Ca²⁺ is half-maximum at each grid point inside an astrocyte, the grid points being taken along the central line. The dotted line interpolates between these points and has no physical significance. The upper set of three traces is for K_R = 15 μM and the lower set is for K_R = 25 μM. In each set, starting from the top, the width of the cell-free lanes has been increased by one cell width; thus it is respectively 75, 125, and 175 μm. The speed in the absence of cell-free lanes is 23 μm s⁻¹ for K_R = 15 μM and 16 μm s⁻¹ for K_R = 25 μM. For clarity, each subsequent trace has been displaced by 150 μm, so the ordinate gives relative distance. (Compare with Fig. 2 A in Hassinger et al. (13).) (B) As for A, except the times at which [Ca²⁺] reaches half-maximum are now plotted for a lines of grid points passing through the centers of astrocytes lying transverse to the lanes and thus the Ca²⁺ wave has to cross cell-free lanes. Again, the dotted lines link corresponding data but have no physical significance. The delays for propagation of Ca²⁺ across the cell-free lanes of widths 75, 125, and 175 μM are, for K_R = 15 μM (from the top down), 7, 13, and 21 s, respectively; and for K_R = 25 μM, they are 10, 19, and 30 s, respectively.

DISCUSSION

ATP versus gap-junction transmission

There are considerable contradictions in the literature concerning the question of whether transmission between astrocytes is chemical, involving the release of ATP, or involves gap junctions (for some reviews of the earlier literature, see Charles (41) and Giaume and Venance (42)). For example, blocking gap junctions between astrocytes in the striatum with 18-α-glycyrrhetinic acid is reported to block Ca²⁺ propagation (43–46); blocking these junctions with heptanol blocks 85% of propagation between spinal cord astrocytes (47) and 75% of propagation between cortical astrocytes (48,49). On the other hand, it has been shown that Ca²⁺ propagation is considerably antagonized by purinergic receptor blockade between cortical astrocytes (50) and completely antagonized by such blockade of spinal cord astrocytes (17,15). Some of these apparent contradictions may be attributed to the gap-junction blockers acting to antagonize ATP release (51) and/or to the linkage between purinergic receptor (P2YR) expression and that of connexins (47). Whether endogenous endonucleotidases of astrocytes play a role in limiting access of ATP to P2Y₁ Rs and P2Y₂ Rs is controversial, as some say that it does (52) and others that it does not (15). We have not included any gap-junction transmission mechanism in our model of astrocyte junctions, although this might be necessary in the future when better agreement is reached on the relative contributions of gap junctions and ATP to the Ca²⁺ transmission process.

ATP release mechanisms

As pointed out in the Introduction, the mechanism by which ATP is released by astrocytes has not yet been elucidated as there are contradictory observations on this point. ATP release, due to mechanical or chemical stimulation, has been reported as either unaffected by the blocking of Ca²⁺ with thapsigargin or BAPTA/AM chelators (14,53), or affected by such blocking (26,25). A calcium-independent release of ATP may occur via anion transporters (28,9). Connexin hemichannels that are permselective for ATP release (54) have also been implicated in ATP release from astrocytes (55), as well as from endothelial cells (56), so that a product of G-protein signaling could be envisaged as opening such channels. However, it has been claimed that connexin blockers, such as oleamide, fail to block transmission between astrocytes (57), whereas the connexin hemichannel activator quinine evokes ATP release (58). These uncertainties point to a lack of specificity of these agents and suggest that a knockout of specific connexin genes is needed to establish the role of these in astrocyte transmission (59). We have therefore opted at this stage for a Ca²⁺-independent release of ATP from astrocytes in our model. This is supported by the observation that the ATP wave appears to precede the Ca²⁺ wave in a number of experimental situations (27,14).

Modeling transmission of the Ca²⁺ wave

Transmission at junctions between astrocytes has previously been modeled only in terms of gap junctions mediating transmission (30). It is assumed in these models that there is direct diffusion of inositol trisphosphate (IP₃) between apposing astrocytes at the junctions, with IP₃ generated by a Ca²⁺-sensitive PLC process in addition to the PLC generation of IP₃ after G-protein receptor activation. Given the considerable recent evidence that the major component of junctional transmission involves the release of ATP, at least for astrocytes originating from certain parts of the central nervous system, we have developed a model of this process of transmission.

Modeling conduction of the Ca²⁺ wave

Single astrocytes, when exposed to a ligand such as noradrenaline, release calcium from different endoplasmic reticula in such a way that the process can be modeled as a series of Ca²⁺-coupled oscillators, each of these being equivalent to one ER (60). An individual ER or oscillator is activated by IP₃ generated throughout at the astrocyte plasmalemma by the action of the ligand on G-protein coupled receptors found over the surface of the plasmalemmal membrane. In the present model, IP₃ is also generated throughout the plasmalemma membrane of the astrocyte, but in this case the generation is due to the action of ATP and not noradrenaline. However, this IP₃ then diffuses through the astrocyte to act on ER found at each of the 125 grid points in the numerical representation of the astrocyte and to release Ca²⁺ at each of them. We have not apportioned specialized ER at the grid points, possessing relative high densities of IP₃ receptors, which participate in a calcium-coupled oscillator system as is the case in the model of Roth et al. (60). The incorporation of such specialized ER does not assist in illuminating the ATP transmission mechanisms that are the point of interest or the present work.

Spatial and temporal characteristics of Ca²⁺ wave propagation and transmission in astrocyte networks

In the presence of neurons, astrocytes propagate a Ca²⁺ wave from a point of mechanical stimulation for a distance of 150−250 μm (61,62) and from a point of potassium stimulation for ∼1000 μm (63), there being indications of a diminution in amplitude and speed over the first 150 μm (for a review see Giaume and Venance (42)). In the absence of neurons, Ca²⁺ waves propagate for at least 200 μm from a point of stimulation (see, for example, Takano et al. (64)). However, it is not known if the Ca²⁺ wave propagates in an all-or-none fashion over long distances (>200 μm) when only glial cells are present, although it has been argued that propagation is limited to an approximate distance of 60 astrocytes (42). There is no restriction on the distance of propagation of the Ca²⁺ wave in the present model, which is regenerative due to the mechanism of ATP-induced ATP release. However, increasing the dissociation constant (K_R) of receptors slows the velocity of propagation of the Ca²⁺ wave from its site of initiation, and if K_R is increased to 35 μM in a single lane of astrocytes, propagation ceases at 100 μm from the site of initiation (see Fig. 5). As pointed out in Receptors, above, K_R is an effective dissociation constant and may take values greater than the actual dissociation constant for ATP acting on P2Y receptors. Ectonucleotidases may act to metabolize released ATP (65). As described in Results, above, introduction of such enzymes into our model merely uniformly decreases the amplitude and velocity of the Ca²⁺ wave from its point of origin, without affecting the propagation distance. It remains to be seen whether Ca²⁺ is observed to propagate for distances of >1000 μm in continuous astrocyte networks confined to discrete lanes in the absence of neurons, such as those modeled in Fig. 6 A.

The speed of propagation of the Ca²⁺ wave is critically dependent on the dissociation constant, K_R, of the receptors (see Table 2 and Fig. 5). Gallagher and Salter (15) obtained velocities of 8 μm s⁻¹ and 16 μm s⁻¹ for propagation of the Ca²⁺ wave through the release of ATP at astrocyte junctions using P2Y₁ and P2Y₂ receptors, respectively. This range of velocities is approximately that observed in cultured astrocytes from a variety of sources (see Table 1 in Giaume and Venance (42)). According to the present model, there is a slight decrease in the speed of propagation of the Ca²⁺ wave over the first three or so astrocytes from the site of initiation (∼150 μm), but there is no diminution in the peak amplitude of Ca²⁺ (see Figs. 7 and 8). It has been suggested that the relatively high velocities and amplitudes of Ca²⁺ waves in the vicinity of mechanical stimulation arise as a consequence of a combination of gap junction communication and chemical transmission at the astrocyte junctions at the site of mechanical stimulation (41,64). We have not yet included gap junctions in our model to test this idea; however, it seems implausible that adding a slow process (gap junction communication) to a faster process (extracellular transmission) will result in an overall increase in speed. A further point concerns the common experimental procedure in which Ca²⁺ release is initiated by mechanical stimulation of an astrocyte. If this only increases [IP₃] in the stimulated cell, as has been suggested (66,14), then our method of initiation using a sudden increase in [ATP] surrounding the cell would be equivalent (see Eq. 9). It is interesting in this regard that doubling the step increase in extracellular ATP makes very little difference to the speed or peak amplitudes of the Ca²⁺ wave (see Fig. 7).

Critical tests of the purinergic junction model of astrocyte transmission

As mentioned in the Introduction, Hassinger et al. (13) examined in some detail the extent to which Ca²⁺ waves could jump cell free gaps of different widths. They found that there was a delay in propagation of the Ca²⁺ wave across lanes which increased with gap width until this reached ∼150 μm, when such propagation failed. For a 80-μm-wide cell-free lane the delay was 18 s, whereas our model of this process gave for a 125-μm-wide cell-free lane a delay of 14 s for astrocytes with K_R = 15 μM. More recent research has used micropatterned arrays of astrocytes in which lanes of cells ∼110-μm-wide alternate with cell-free lanes ∼40-μm-wide, with mechanical initiation of Ca²⁺ occurring in just one lane (64). These authors obtained a delay of ∼10 s for the Ca²⁺ wave to traverse the cell-free lane. This may be compared with a delay of 8 s, which our model gives for a cell-free lane of width 75 μm for astrocytes with a K_R = 30 μM. The velocities in the experimental studies were 8–20 μm s⁻¹, which are those found in the modeling study for P2Y receptors with K_R values of ∼35−25 μM, respectively. These quantitative comparisons between experimental and modeling results suggest that the model can account for these observations on micropatterned arrays of astrocytes.