The Dual-Color Photon Counting Histogram with Non-Ideal Photodetectors

Abstract

Dual-color photon counting histogram (PCH) analysis utilizes the photon counts in two detection channels to distinguish species by differences in brightness and color. Here we modify the existing dual-color PCH theory, which assumes ideal detectors, to include the non-ideal nature of the detector. Specifically, we address the effects of deadtime and afterpulsing. Both effects modify the shape of the dual-color PCH and thus potentially lead to incorrect values for the brightness and number of molecules if an ideal model is assumed. We use the modified theory to predict the effects of detector non-idealities on dual-color PCH as a function of concentration and brightness. In addition, we introduce a method based on moment analysis to determine the error in brightness due to non-ideal detector effects. We verify our theory experimentally by measuring a dye solution as a function of concentration and brightness. We determine the deadtime and afterpulse probability of our detectors and show that both effects play an important role in the analysis of dual-color PCH experiments. We demonstrate that resolving a mixture of CFP and YFP requires taking non-ideal detector effects into account. These corrections are also crucial for cellular measurements, as shown for GFP and RFP in mammalian cells.

INTRODUCTION

The resolution of species is of central importance in many biological experiments. One technique capable of quantitatively characterizing a mixture of species is fluorescence fluctuation spectroscopy (FFS). FFS utilizes the fluctuations in light intensity produced by fluorescently-tagged biological molecules diffusing through a very small observation volume (∼0.1 fL). Statistical methods such as fluorescence correlation spectroscopy and photon counting histogram (PCH) analysis are used to extract kinetic and structural information about the biological system from the fluctuations in fluorescence intensity. Fluorescence correlation spectroscopy uses correlation functions, which capture the temporal aspects of the fluctuations, to resolve species while PCH uses the amplitude distribution of the fluctuations to resolve species. The FFS technique has been used extensively to study the association and disassociation of proteins (1–3), kinetics (4–6), diffusion in cells (7), and flow (8,9).

In standard FFS, all the light is collected by one detector. Dual-channel FFS uses a dichroic mirror to separate the emission of two spectrally distinct fluorophores into two different detectors. Dual-channel schemes offer increased specificity when studying heterogeneous biological systems. For example, consider the proteins A and B, which are assumed to dimerize with themselves and each other. If both proteins were labeled with the same fluorophore, then we are able to distinguish monomers (A or B) from dimers (AA, AB, or BB), but not between the three possible forms of dimer or between the two monomers. However, if we were to label protein A with a green fluorophore and protein B with a red one, then in principle, we could clearly distinguish between all five scenarios.

To detect hetero-interactions, dual-channel FFS looks for coincident fluctuations in the two detectors. One may either compare how the fluctuations in fluorescent intensity in one detector (e.g., “red” channel) correlate in time with the fluctuations in the second detector (e.g., “green” channel) or one may compare the fluctuation amplitude in the red channel to that in the green channel. The first approach is termed cross-correlation analysis (10) and the second is termed dual-color photon counting histogram analysis (11) or two-dimensional fluorescence intensity distribution analysis (12). Cross-correlation analysis has been used to study diffusion (13), enzyme kinetics (14), protein-protein interactions (15), and to resolve species (16). However, cross-correlation analysis is often hampered by spectral cross-talk in which some of the green photons leak into the red channel and some of the red photons leak into the green channel due to the overlap of the fluorophores' emission spectra. Cross-talk amounts to false coincidences between the two detection channels and thus must be corrected for or eliminated with additional spectral filters (17). Dual-color PCH analysis, on the other hand, can readily resolve species in the presence of cross-talk (11). Both techniques are ultimately complimentary and the same data set can be used for both analyses.

In our previous work on PCH analysis for a single detector, we found that non-ideal detector effects cause significant changes in the PCH (18). Based upon this experience, we decided to investigate the influence of these effects on the dual-color PCH. The detector effects we are specifically concerned with are deadtime and afterpulsing. Deadtime is a fixed period of time after the registration of a photon in which the detector is unable to detect subsequent photons. The deadtime of nonparalyzable detectors, such as actively-quenched avalanche photodiodes (APD), is unaffected by photons reaching the detector during the deadtime. Afterpulsing is the generation of a spurious pulse after the detection of a real pulse. The dual-color PCH theory developed so far has only considered the case of ideal photodetectors (11,12). We found that just as in the single-channel case, non-ideal detector effects can produce significant changes in the dual-color PCH. These effects, if not accounted for, may lead to erroneous interpretation of experimental data and therefore severely limit the practical use of this analysis method. To overcome these limitations, we develop a new dual-color PCH theory that incorporates both deadtime and afterpulsing effects. We validate our new theory using a simple dye as a model system. In addition, we resolve a mixture of CFP and YFP, which exhibit considerable spectral overlap. We also present methods for determining the deadtimes and afterpulse probabilities of photodetectors. The qualitative effects of deadtime and afterpulsing on the dual-color PCH are the same as in the single-channel case. Both effects turn out to be important in dual-color experiments and thus need to be incorporated into the analysis. The modified dual-color PCH theory allows us to study biological systems at conditions otherwise inaccessible to standard dual-color PCH. As we will show for GFP and RFP, the new theory is particularly important in cellular measurements where the number of molecules is high and the brightness is low. To increase the sensitivity of the dual-color PCH technique, we performed global analysis of FFS experiments with the modified PCH theory.

THEORY

Dual-color PCH resolves species by differences in molecular brightness in the two detectors (ɛ_A, ɛ_B) (11). The subscripts A and B are used throughout this article to identify the detection channel. Molecular brightness is defined as the integrated fluorescence intensity produced by a single molecule in the observation volume and is usually measured as photon counts per molecule per sampling period (cpm). Dividing the brightness in cpm by the sampling period yields the brightness in units of counts per molecule per second. We will report brightness in cpm throughout this article. It should be noted that the brightness depends on the properties of the fluorophore itself and on the physical setup. Dual-color PCH analysis also returns the average number of molecules of each species present in the observation volume.

We employ the same terminology and notation for dual-color (or dual-channel) PCH as we employed for single-channel PCH (18). Throughout this article, we use the terms photon count distribution and photon counting histogram (PCH). The first term is a generic theoretical description that applies to any photon counting experiment and is denoted by p(k) for single-channel and p(k_A,k_B) for dual channel. The second term refers to photon count distributions particular to FFS experiments. The experimental PCH will be denoted π(k) for single-channel PCH or π(k_A,k_B) for dual-channel PCH, and the theoretical PCH will be denoted eithe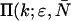r ) or 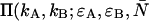). The unprimed quantities refer to those measured by an ideal detector (e.g., ɛ). Primed quantities refer to those measured by detectors with deadtime (e.g., ɛ′). Quantities denoted with an asterisk refer to those obtained from detectors with afterpulsing (e.g., ɛ^*).

Model for deadtime

Consider a time-varying light intensity I(t) incident on a photodetector. In the semiclassical description, the integrated light intensity W(t) falling onto the detector surface during the sampling time T is

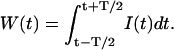(1)

Mandel's formula relates the probability distribution function (pdf) of the integrated intensity p(W) with the pdf of the observed photon counts p(k) (19),

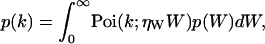(2)

where Poi(k,〈k〉) is the Poisson distribution with expectation value 〈k〉 and k is the number of photon counts observed in a time interval T. The parameter η_W describes the detection efficiency of the photodetector.

We will assume that the sampling time T is chosen short enough, so that the fluctuations in W track the intensity fluctuations of interest. Thus the integrated intensity is given by W(t) = I(t)T, and the pdf of the integrated intensity is proportional to the pdf of the intensity, p(W)dW = p(I)dI. Mandel's formula in the limit of short sampling times written as a function of intensity is

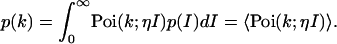(3)

The angular brackets denote the average of the Poissonian shot-noise contribution over the intensity distribution p(I). The parameter η is proportional to the detection efficiency η_W and takes the sampling time into account, η = η_WT.

If an optical filter is inserted into the emission path and the light is split into two beams with each beam being detected by its own photodetector, then the two-dimensional photon count distribution is given by

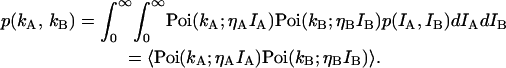(4)

The function p(k_A,k_B) characterizes the joint probability of detecting k_A photons in channel A and k_B photons in channel B during the sampling time T.

To obtain the dual-color PCH function, one must evaluate Eq. 4 with the proper two-channel intensity probability function p(I_A,I_B) for FFS experiments. The distribution p(I_A,I_B) depends on the point-spread function (PSF) and the physical source of fluctuations, namely particles diffusing through a small observation volume. As shown in Appendix A, the dual-color PCH for a single species as measured by an ideal detector is described by three parameters: 1), the molecular brightness ɛ_A in channel A; 2), the molecular brightness ɛ_B in channel B; and 3), the average number of molecules 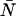in the excitation volume. It is denoted 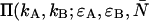). For multiple species, the dual-color PCH is obtained by successive convolutions of the dual-color PCH function of each species (11).

We have so far assumed ideal detectors when deriving the dual-channel photon count distribution. However, detectors are never ideal and the non-idealities of the detector need to be accounted for in the theoretical description of the photon count distribution. The effect of deadtime on the photon count distribution for a single nonparalyzable detector has been addressed in the literature (20,21) and is characterized by the parameter δ = τ_†/T = τ_†f, where τ_† is the deadtime of the detector, T the sampling time interval, and f = 1/T the sampling frequency. A fluctuating light source measured by a detector with deadtime leads to a photon count distribution p′(k),

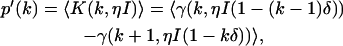(5)

where γ(k,x) is the incomplete γ-function. In other words, the effect of deadtime on photon count distributions is described by replacing the Poissonian kernel of Eq. 3 with the kernel K(k,ηI) of Eq. 5. It is convenient to express K(k,ηI) as a series of Poisson functions (18),

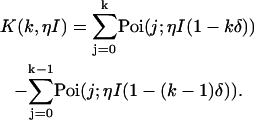(6)

Equation 6 allows us to describe deadtime-affected PCH functions as a mathematical series of ideal PCH functions (18).

We now extend this approach to describe dual-channel photon count distributions in the presence of deadtime by replacing each of the Poissonian kernels of Eq. 4 with the corresponding deadtime-corrected kernel of Eq. 6,

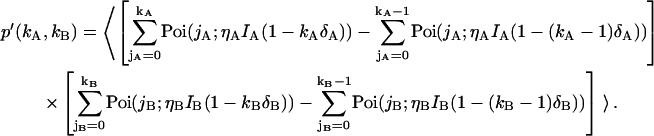(7)

Evaluating Eq. 7 with the proper bivariate intensity distribution function p(I_A,I_B) of dual-channel FFS experiments (Appendix A) ultimately leads to an expression for the deadtime-affected dual-color PCH,

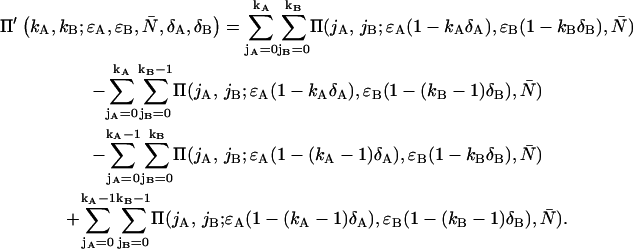(8)

We see that the dual-color PCH function with deadtime Π′ is a summation over ideal dual-color PCH functions Π with modified brightnesses. The deadtime-affected PCH function of multiple species 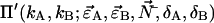is obtained by replacing the ideal single species PCH functions 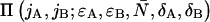in Eq. 8 by the corresponding multiple species PCH function 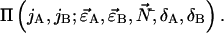We use vector notation to organize the parameters of all species; for example, the brightness vector 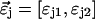characterizes the brightness of species 1 and 2 in channel j (11).

Model for afterpulsing

An algorithm to correct for afterpulses in the photon count distribution for a single detector was developed by Campbell (22). For the single-channel PCH, we inverted this algorithm to obtain afterpulse-affected PCHs in terms of ideal PCHs (18). Here we extend this model to two detection channels. The model assumes that a real event generates a single afterpulse with probability q_A for detector A and probability q_B for detector B, and that afterpulses cannot generate more afterpulses. Applying this model to two independent detectors determines the afterpulse-affected dual-channel photon count distribution p^*(k_A,k_B),

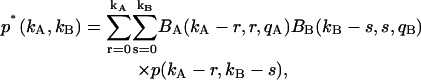(9)

where p(k_A,k_B) is the dual-color photon count distribution in the absence of afterpulsing and B_i(k_i − n,n,q_i) is the probability of n afterpulses following k_i − n real events in detector i with an afterpulse probability q_i. B_i(k_i − n,n,q_i) is given by the binomial distribution,

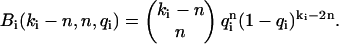(10)

Note that B_i(k_i − n,n,q_i) = 0 for (k_i − n) < n; this ensures that only single afterpulses are allowed. It is easy to verify that the distribution p^*(k_A,k_B) is normalized, 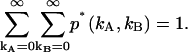Eq. 9 is valid for any photon count distribution. For FFS experiments, we replace p(k_A,k_B) in Eq. 9 by the ideal PCH function Π(k_A,k_B) to determine the afterpulse-affected PCH function Π^*(k_A,k_B).

Implementation of models

The deadtime and afterpulsing models of Eqs. 8 and 9 require a double summation over all photon counts for each value of the corrected distribution p′(k_A,k_B) or p^*(k_A,k_B). Such algorithms are time-consuming because they scale with L⁴, where L represents the linear dimension of the array of photon counts. Thus, we need a more efficient algorithm to model large two-dimensional arrays of photon count distributions.

The afterpulsing probability q_i of each detection channel is ≪1. In other words, the binomial function B_i(k_i − n,n,q_i) rapidly decays to zero with increasing number of afterpulses n. This allows us to truncate the summation in Eq. 9 after a finite number of afterpulses. We write the truncated afterpulsing model as

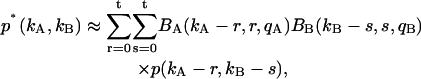(11)

where t represents the maximum number of afterpulses considered in each detection channel. We typically encounter experimental two-dimensional histograms with a maximum photon count of <200 counts per sampling period. After taking the afterpulsing probability of our detectors into account, we found that t = 5 is sufficient for modeling experimental data.

To simplify the deadtime model, we expand the kernel of Eq. 5 in a Taylor series, because the deadtime parameter δ_i of each detection channel is ≪1. We formally write the kernel as

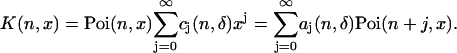(12)

The coefficients a_j are given by (see Appendix B)

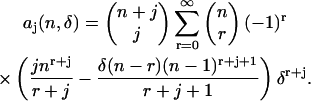(13)

The deadtime-affected photon count distribution p′(k_A,k_B) is determined by

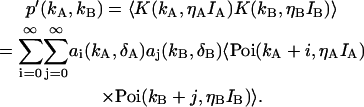(14)

The averaged Poisson distribution above is related to the ideal two-dimensional photon count distribution p(k_A,k_B) via Eq. 4, and thus Eq. 14 becomes

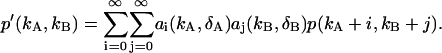(15)

Since the deadtime parameter is ≪1, we can truncate the series of Eq. 15 after a few terms. First, we transform the coefficients a_j by changing the summation parameter from r to m = r + j,

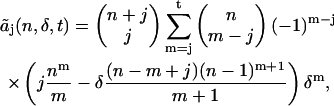(16)

and truncate the series at m = t. The truncated coefficient 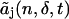includes the deadtime effect up to t^th order of the deadtime parameter δ. Note that 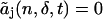for t < j. To model the deadtime-affected photon count distribution to the t^th order in the deadtime parameters δ_A and δ_B, we write Eq. 15 as

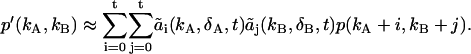(17)

Equation 17 is valid for any photon count distribution and scales as L² rather than L⁴. We found that t = 5 is sufficient to model experimental dual-channel PCHs with a total intensity of up to 2 × 10⁶ cps. Modeling histograms with intensities higher than this limit requires a higher order of t, while a lower order of t is sufficient for histograms with lower intensities.

We implemented Eqs. 11 and 17 in a computer algorithm to model experimental PCH functions. The algorithm first creates the ideal PCH function Π(k_A,k_B) as discussed in Chen et al. (11), and applies Eq. 17 to arrive at the deadtime-affected distribution Π′(k_A,k_B). The distribution Π′(k_A,k_B) is transformed by Eq. 11 to arrive at the deadtime- and afterpulse-affected PCH function Π′^*(k_A,k_B). We have found that applying the afterpulse operation first followed by the deadtime operation results in only a very slight difference in the PCH function and this difference is less than the experimental error. In other words, the order of operation produces negligible differences in Π′^*(k_A,k_B).

Moment analysis

Upon inspection, Eqs. 8 and 9 do not give any insight into the magnitude of deadtime and afterpulsing on dual-color PCH. In particular, they do not provide analytical expressions for predicting the severity of non-ideal detector effects on the brightness. However, a simple analytical prediction for the relative error in the dual-color PCH parameters due to afterpulsing or deadtime is very useful to the experimentalist, because it allows him/her to judge whether non-ideal detector effects can be neglected or need to be accounted for in the data analysis for a given set of experimental conditions.

In the single-channel PCH case, we used the ordinary moments and cumulants of the PCH to derive analytical expressions that describe the relative error in ɛ and 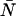due to afterpulsing or deadtime (18). We take a similar approach for dual-color PCH and derive equations from the bivariate cumulants to determine the relative error in the brightnesses ɛ_A and ɛ_B and number of molecules For the dual-color PCH case, we are interested in the two first-order cumulants κ₁₀ and κ₀₁ as well as the three second-order cumulants κ₁₁, κ₂₀, and κ₀₂. We ignore the higher-order cumulants, since these five cumulants are the most statistically significant. The five ideal cumulants are given by (11)

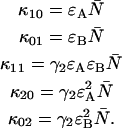(18)

It is convenient to define two new parameters; the first parameter is the total brightness ɛ = ɛ_A + ɛ_B and the second parameter is the fractional brightness f = ɛ_A/ɛ. Using these new parameters, the brightness in each channel is given by ɛ_A = fɛ and ɛ_B = (1 − f)ɛ. Expressing the first-order ideal cumulants in terms of these parameters, we find

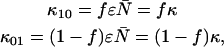(19)

where 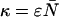is the total photon counts in both channels.

In the presence of non-ideal detector effects, we measure non-ideal cumulants 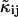instead of ideal ones. Analysis of the non-ideal cumulants assuming the ideal model shown in Eq. 18 leads to biased parameters 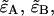and 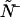instead of the true physical parameters ɛ_A, ɛ_B, and 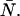We now describe a procedure to estimate the non-ideal parameters and 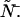Here we specifically focus on the calculation of 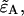because once it is found the calculation of 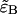and 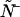are straightforward. The first-order non-ideal cumulants are 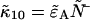and 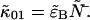Since the first-order cumulants are largely unaffected by non-ideal detector effects and have the smallest error, we make the approximation that 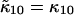and 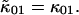We can therefore express the second-order non-ideal cumulants in terms of 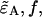and κ,

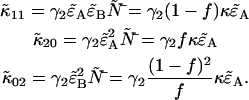(20)

To obtain an expression for 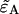we must use least-squares minimization because the system of equations is overdetermined. We have three cumulants and only one unknown parameter. The corresponding χ²-function of the three second-order cumulants is

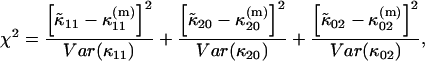(21)

where 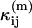is a model of the ij cumulant that includes deadtime or afterpulses, and Var(κ_ij) is the variance of the ij cumulant. The expressions for the 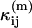and variances are given in Appendix C and are expressed in terms of the ideal parameters () and the non-ideal parameters (δ_A,δ_B,q_A,q_B). We minimize Eq. 21 with respect to 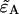as

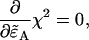(22)

and solve Eq. 22 for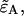

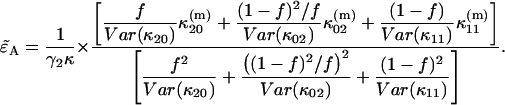(23)

Equation 23 allows us to calculate the deadtime- or afterpulse-affected brightness 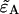from the ideal parameters since the parameters κ and f are given by 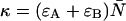and f = ɛ_A/(ɛ_A + ɛ_B).

Evaluating Eq. 23 with the deadtime cumulants 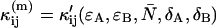given in Appendix C yields an analytical expression for the deadtime-affected brightness (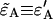). Equation 23 also allows us to calculate the afterpulse-affected brightness (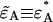) by using the equations in Appendix C that model the afterpulse cumulants 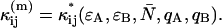The resulting expressions for 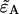in the presence of deadtime and afterpulses are lengthy and cumbersome and are not shown here. However, these expressions are easily implemented and evaluated using a computer algorithm and thus can be used by the experimentalist to determine whether corrections for deadtime and/or afterpulsing are necessary.

To obtain the relative error in brightness when both effects are present, we simply calculate the relative errors due to deadtime and afterpulsing separately and then add them together. This is tantamount to assuming that the two effects are independent of one another. Technically the two effects are not statistically independent (e.g., each afterpulse generates a deadtime in the detector), but to first order they can be treated as such. Afterpulses occur with a probability q and the leading order of correction of afterpulsing to PCH is of order O(q). Similarly, deadtime effects give rise to corrections with leading order O(δ). The corrections due to the interdependency of afterpulses and deadtime is thus of order O(qδ). Since q and δ are small numbers, the correction is of higher order and is neglected because we are only interested in first-order effects. Including the entanglement of the effects in the model would require that the individual corrections for deadtime and afterpulsing include second-order terms as well as a more sophisticated model for afterpulsing. None of these higher-order corrections appear to be necessary to describe our dual-color PCHs as is shown below.

MATERIALS AND METHODS

Instrumentation

The instrumentation for dual-channel fluorescence fluctuation experiments is similar to that described in Chen et al. (11) and consisted of a Zeiss Axiovert 200 microscope (Thornwood, NY) and a mode-locked Ti:Sapphire laser (Tsunami, Spectra-Physics, Mountain View, CA) pumped by intracavity doubled Nd:YVO₄ laser (Millennia Vs, Spectra-Physics). All experiments were performed using a 63X C-Apochromat oil immersion objective (NA = 1.4). Alexa 488 was excited at 780 nm with an average power of 9.6 mW, CFP and YFP were excited at 905 nm with an average power of 2.4 mW, and GFP and RFP were excited at 995 nm with an average power of 0.75 mW. All powers were measured after the objective. The fluorescence emission was separated into two different detection channels by an optical filter. A beam splitter was used for the Alexa 488 sample, a 515-nm dichroic mirror for the CFP/YFP mixture and a 565 nm dichroic for the GFP and RFP cellular measurements. All dichroic mirrors were from Chroma Technology (Rockingham, VT). Photon counts were detected with an avalanche photodiode (APD) (SPCM-AQ-14, Perkin-Elmer, Dumberry, Québec). The output of each APD, namely TTL pulses, was directly connected to one of two dual-channel data acquisition cards (Flex02-12D, Correlator.com, Bridgewater, NJ or ISS, Champaign, IL). The sampling frequency was 100 kHz for the Alexa 488 measurements and 20 kHz for the CFP/YFP experiments and for cellular measurements. The sampling frequencies chosen for the Alexa 488 and CFP/YFP measurements introduce an undersampling effect of ∼10%, which is neglected. No undersampling occurs in the cellular experiments. The recorded photon counts were stored and later analyzed with programs written for IDL (Research Systems, Boulder, CO).

Sample preparation

Alexa 488 was purchased from Molecular Probes (Eugene, OR) and dissolved in water. The dye concentration of the stock solution (∼10 μM) was determined by optical absorption measurements using the extinction coefficient provided by Molecular Probes. Alexa 488 was diluted in water to a concentration of ∼100 nM. Background counts were ∼100 cps in both channels.

Plasmids pRSET A ECFP and EYFP were a kind gift from Dr. Patterson (Cell Biology and Metabolism Branch, National Institutes of Health, Bethesda, MD). His-tagged CFP and YFP were prepared according to Patterson et al. (23) using the Bug Buster protein purification kit (Novagen, San Diego, CA). Stock protein solutions were diluted and measured in phosphate-buffered saline (PBS) (Sigma-Aldrich, St. Louis, MO). Background counts were ∼100 cps in both channels.

pEGFP-C1 plasmid was obtained from Clontech (Mountainview, CA). This was amplified with a 5′ primer that encodes a Nhe I restriction site and a 3′ primer that encodes a BspE I site for mammalian expression. The mRFP pRSET B plasmid was a kind gift from Dr. Tsien (University of California, San Diego). It was spliced into the above GFP plasmid.

COS cells were obtained from ATCC (Manassas, VA) and maintained in 10% fetal bovine serum (Hyclone Laboratories, Logan, UT) and DMEM media. Cells were subcultured into an eight-well cover-glass chamber slides (Naglenunc International, Rochester, NY) and then transiently transfected using Polyfect (Qiagen, Valencia, CA) according to manufacturer's instructions. Before conducting measurements, the growth media was removed and replaced with PBS.

Data analysis

PCH functions are calculated with respect to a three-dimensional Gaussian PSF, whereas a Gaussian-Lorentzian PSF was used in Hillesheim and Müller (18). The choice of PSF and its effect on the PCH parameters is discussed in Chen et al. (11). The histogram of the experimental data is calculated from the recorded photon counts and then normalized to obtain the experimental probability distribution of photon counts π(k_A,k_B). To fit the experimental PCH to the theoretical PCH, we must weigh each element of the PCH with its standard deviation 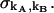The probability of simultaneously observing k_A and k_B counts n times out of M trials is given by the binomial distribution function, and its standard deviation is given by 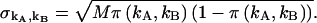The theoretical PCH, denoted 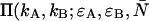), is calculated and the reduced χ² is determined by

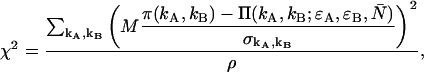(24)

where the sum is taken over all k_A and k_B where π(k_A,k_B) is >0. The degrees of freedom ρ is determined by r₀ − d where r₀ equals the number of terms in the sum and d is the number of free fitting parameters. Because a typical data set contains ∼M = 10⁶ data points, the resulting binomial distribution is well approximated by a normal distribution. Thus the quality of the model can be estimated by the reduced χ² and by the normalized residuals 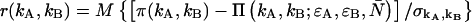of the fit.

Background effects were included in all fits. The brightnesses and number of molecules of the background species were obtained by fitting solvent-only histograms for the solution measurements. For cellular measurements, the background is composed of both scattered light and autofluorescence. Untransfected cells were measured and their histograms were fit to determine the number of molecules and brightness in each channel. Afterpulse effects were included in all background fits.

RESULTS AND DISCUSSION

Determination of τ_† and q

To quantitatively characterize the effect of deadtime and afterpulsing on the dual-color PCH we first need to determine the deadtimes (τ_†A,τ_†B) and afterpulse probabilities (q_A, q_B) of our detectors. In Hillesheim and Müller (18), we measured the deadtime and afterpulse probability of one of our detectors using Mandel's Q parameter. We have since found that this technique of determining the deadtime and afterpulse probability is highly sensitive to external sources of fluctuations, and therefore great care must be exercised to assure the validity of the fitted detector parameters. Thus, we developed new methods for independently determining the deadtime and afterpulse probability for each of our detectors.

Determining the deadtime of the detector is straightforward. We expose the APD to background light with an intensity of ∼10 kcps. The output signal from the APD is connected to a fast digital oscilloscope (Tektronix TDS 3034, Wilsonville, OR) and the deadtime is determined by the shortest time interval between consecutive pulses. The experimentally determined deadtimes of our detectors are shown in Table 1. The deadtime of the data acquisition cards is less than that of the photodetectors and is therefore not a determining factor.

TABLE 1.

Deadtime and afterpulse probabilities of our detectors

	Instrument 1	Instrument 2
Afterpulse probability	qA = 0.002	qA = 0.007
	qB = 0.003	qB = 0.0046
Deadtime	τ†A = 50 ns	τ†A = 50 ns
	τ†B = 48 ns	τ†B = 51 ns

Although the deadtime is comparable for all detectors, the afterpulse probability varies significantly from detector to detector.

We developed two methods for measuring the average afterpulse probabilities of our detectors. The same data set can be used for both methods. The APD is exposed to low levels of light (∼2000 cps) and data is collected in photon mode (see Eid et al. (24)) with a clock of 24 MHz for ∼30 min. The photon count rate is low enough that deadtime effects are negligible. If the light incident on the detector is uncorrelated, any correlations that arise between photon counts are due to afterpulses. The number of afterpulses is directly proportional to the average photon counts 〈k〉 and the probability p_a(τ) to observe an afterpulse at time τ after a real event has occurred. Thus, the autocorrelation function due to afterpulsing is written as

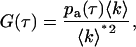(25)

where the mean photon count 〈k〉^* in the presence of afterpulsing is related to the ideal mean photon count by 〈k〉^* = 〈k〉(1 + q). The cumulative probability q that a real photon event will trigger an afterpulse is given by

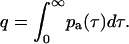(26)

We introduce the function

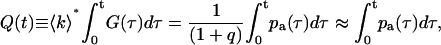(27)

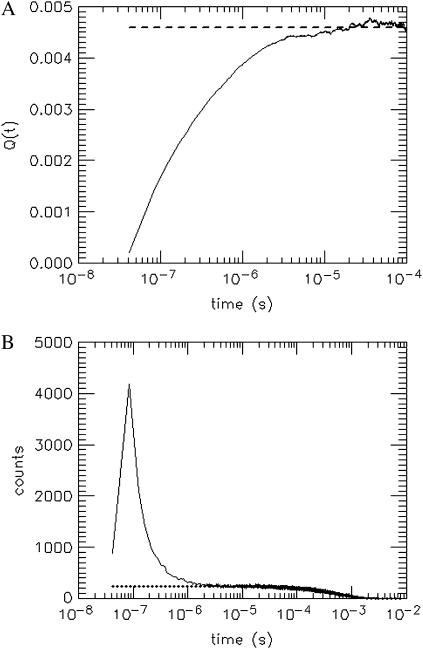
where the approximation introduced in Eq. 27 uses the fact that q is ≪1. Note that for times larger than the timescale t₀ of afterpulse generation the afterpulse probability goes to zero, or p_a(τ) → 0 for τ > t₀. In this limit, Q(t) approaches the afterpulse probability q. A plot of Q(t) vs. t is shown in Fig. 1 A for detector B on instrument 2 (see Table 1). At t ≈ 1 μs, Q(t) becomes constant because nearly all of the afterpulses occur within a few microseconds of their original pulse. The value at which Q(t) stabilizes is 0.0046 and is equal to the afterpulse probability q of the detector.

FIGURE 1.

Determination of the afterpulse probability of one of the detectors used in this study by (A) the integrated autocorrelation function Q(t) (see Eq. 27) and (B) the histogram of the time intervals between photon events. The detector was exposed to light whose intensity is constant on the timescale of the afterpulsing (τ ∼ 1 − 10 μs). Afterpulses generally arrive within a few microseconds after the real pulse that generated them. Therefore any correlations that arise at early times are due to afterpulsing. The value at which Q(t) stabilizes (dashed line) corresponds to the afterpulse probability, which for this detector is 0.0046. The dotted line in B represents the fitted exponential decay due to a constant light source. The large peak above the exponential decay curve at time intervals <1 μs is due to afterpulses.

The second method utilizes the histogram of time intervals between photon arrivals h(t), shown for the same detector in Fig. 1 B. Since the background light is of nearly constant intensity, we expect for an ideal detector a histogram of exponentially distributed arrival times. For a non-ideal detector we observe an excess of counts for time intervals of <1 μs. These excess counts are afterpulses and the hole at the beginning of the histogram is due to deadtime. If we subtract the exponential distribution due to constant light from the histogram in Fig. 1 B, we are left with a histogram h_a(t) of only the afterpulses,

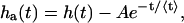(28)

where A is the amplitude of the exponential distribution and 〈t〉 the average time between photon arrivals. The total number of events in the afterpulse-only histogram h_a(t) is the total number of afterpulses N_a. The total number of detected events N_e is the sum of the histogram h(t). We determine the afterpulse probability by q = N_a/(N_e − N_a). Using this method, we obtained an afterpulse probability of 0.0046, in excellent agreement with the result from the first method. The afterpulse probabilities of our detectors are shown in Table 1.

Modeling non-ideal detector effects on the dual-color PCH

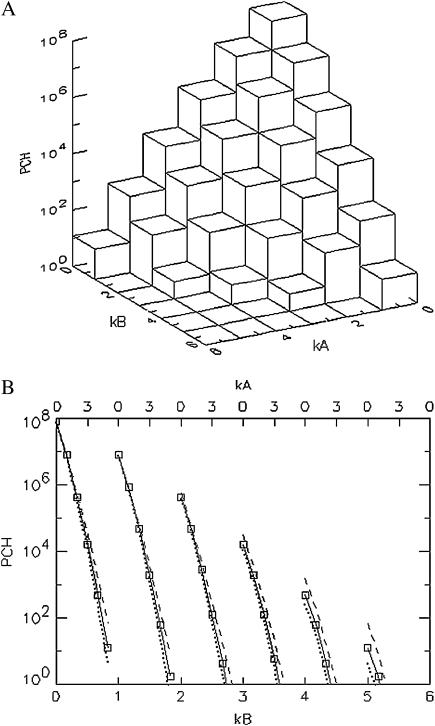
We first model dual-color PCH functions to better understand the influence of deadtime and afterpulsing on the shape of the two-dimensional histograms. An ideal PCH function with ɛ_A = ɛ_B = 0.021 cpm, 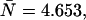and a total of M = 1 × 10⁸ photon events is displayed in Fig. 2 A. The three-dimensional graph shows the number of events with k_A photons detected in channel A and k_B photons in channel B. Overlaying three-dimensional plots of deadtime- and afterpulsing-affected PCH distributions onto the graph of Fig. 2 A makes it difficult to read. Therefore, we project the three-dimensional histogram onto two dimensions, so that changes in its shape due to non-ideal effects are more apparent. In Fig. 2 B, the histogram of Fig. 2 A is plotted row by row, starting with k_B = 0 (squares with solid line). The top axis specifies the photon counts of channel A, whereas the bottom axis indicates the photon counts in channel B.

FIGURE 2.

(A) Three-dimensional representation of an ideal dual-color PCH. The PCH value is displayed as a function of the photon counts (k_A, k_B) in channels A and B. (B) Two-dimensional representation of the ideal three-dimensional PCH shown in A by graphing it row after row starting with k_B = 0 (solid line, squares). The two-dimensional plot facilitates the comparison of the shape changes between ideal and non-ideal PCH functions. Deadtime preferentially decreases the counts of the PCH (dotted line) in the higher channels leading to a narrowing of the function, while afterpulsing increases the counts in the higher channels of the PCH (dashed line), thus broadening the PCH. The data are modeled for ɛ_A = ɛ_B = 0.021 cpm and 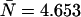and for M = 1 × 10⁸ data points. We used large values of deadtime (δ_A = δ_B = 0.05) and afterpulse probability (q_A = q_B = 0.02) for illustration purposes.

The dotted line of Fig. 2 B represents the same histogram but with deadtime effects (δ_A = δ_B = 0.05), whereas the dashed line represents the afterpulse-affected PCH (q_A = q_B = 0.02). The non-ideal PCH functions are generated using Eqs. 8 and 9. Exaggerated values for the deadtime and afterpulse parameters were chosen to more clearly illustrate non-ideal detector effects. We expect that deadtime and afterpulse effects show up primarily in the higher channels of the PCH. Here the term “channel” refers to the number of photons detected in a sampling period. At high count rates, many photons are lost in the deadtime and thus higher channels are more affected than lower channels. This leads to an overall narrowing of the PCH function as observed in Fig. 2 B. The deadtime-affected PCH (dotted line) is less than the ideal PCH and the deviation grows with increasing photon counts k_A and k_B. Afterpulses, on the other hand, broaden the PCH, as shown in Fig. 2 B. The afterpulsing-affected PCH function (dashed line) exceeds the ideal PCH and the deviation grows with increasing number of photon counts in each channel. With each real pulse, there is a chance that an afterpulse is generated and thus higher channels are more likely to contain afterpulses than lower channels. Afterpulsing and deadtime have opposite effects on the dual-color PCH.

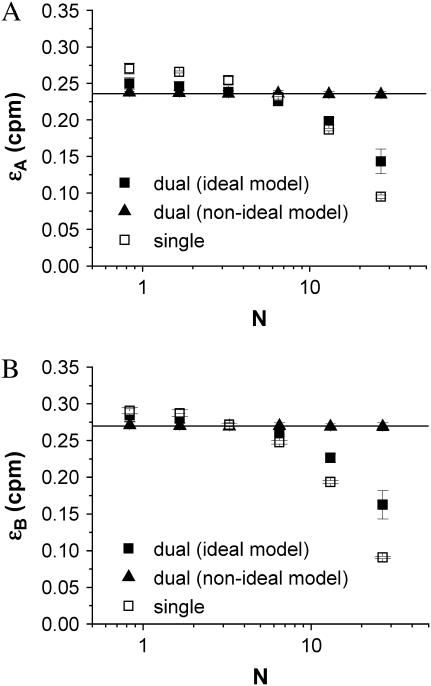
We are specifically interested in how the broadening or narrowing of the dual-color PCH due to afterpulsing and deadtime biases the brightness in each channel and the number of molecules when the histogram is fit using an ideal model. These experimental parameters are crucial for characterizing biological systems and biased parameters would lead to a misinterpretation of the experimental results. In addition, we would like to compare non-ideal detector effects in the dual-channel PCH with those in the single-channel PCH. We earlier found for the single-channel case that deadtime-affected PCH functions fit to the ideal PCH model resulted in a reduced brightness and an elevated number of molecules (18). We expect a similar behavior for dual-color PCH analysis. To better characterize deadtime effects on the dual-color PCH, we generated several deadtime-affected histograms using Eq. 8. Identical brightness values (ɛ_A = ɛ_B = ɛ) and identical deadtime parameters (δ_A = δ_B = δ) were chosen to simplify the comparison with single-channel PCH. 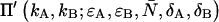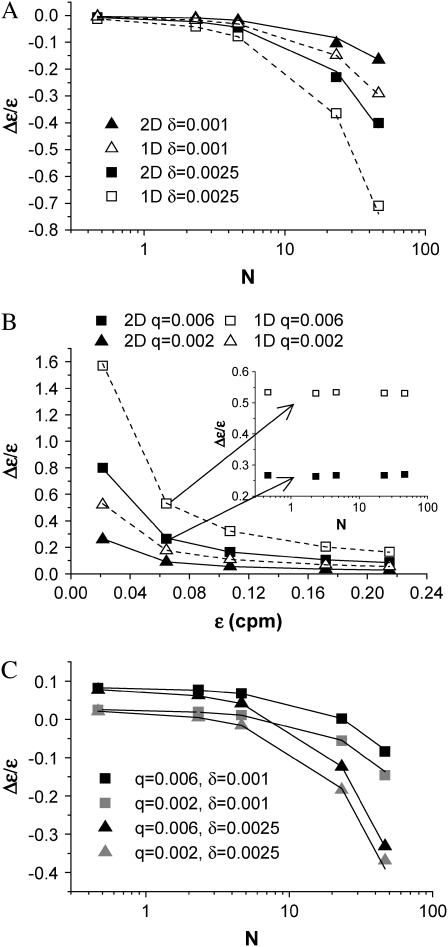The deadtime PCH functions were fit to ideal PCH functions 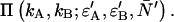The biased brightness values ɛ′_A and ɛ′_B are identical (ɛ′_A = ɛ′_B = ɛ′) since symmetric conditions were chosen for each detection channel. This allows us to simply compare the brightness ɛ with the biased brightness ɛ′. In Fig. 3 A we graph the relative error in the brightness due to deadtime (Δɛ/ɛ)_deadtime = (ɛ′ − ɛ)/ɛ for the dual-color PCH as a function of the number of molecules 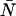for two different deadtime parameters (solid symbols). We also analyzed the effect of deadtime on single-channel histograms using the same brightness and number of molecules as the dual-channel histograms. The relative error in the single-channel histograms is shown in Fig. 3 A as open symbols. The relative error in the brightness of both single- and dual-channel PCH increased as a function of concentration and with increasing deadtime parameter 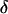(Fig. 3 A).

FIGURE 3.

Relative error in brightness introduced by non-ideal detector effects. The PCH functions are modeled for identical parameters in both channels, i.e., ɛ_A = ɛ_B = ɛ. This simplifies the comparison with single-channel data. (A) The relative error of ɛ due to deadtime is shown for dual-channel (solid symbols) and single-channel (open symbols) histograms as a function of 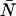for two different deadtime parameters. (B) The relative error of ɛ due to afterpulsing is shown for dual-channel (solid symbols) and single-channel (open symbols) histograms as a function of ɛ for two different afterpulse probabilities. The relative error in ɛ as a function of 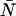for select values of ɛ is shown as an inset. (C) The relative error of ɛ due to the combined effects of afterpulsing and deadtime is shown for dual-channel histograms as a function of 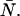We used ɛ = 0.21 cpm in A and C, while we set 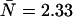in B. The solid and dashed lines are the predictions of the relative error of ɛ based on moment analysis.

We also used moment analysis to calculate the relative error in brightness due to deadtime for each dual-channel histogram according to Eq. 23. The error based on bivariate moment analysis is shown in Fig. 3 A as solid lines and agrees with the observed error of dual-channel PCH. We found that moment analysis reproduces the error introduced by deadtime in the dual-color PCH as long as 〈k〉 × δ < 0.05. This limit is a consequence of the Taylor expansion of the moment equation to first-order. The relative error in brightness for the single-channel PCH by moment analysis is shown as dashed lines and was calculated as previously described (18).

We observed two significant differences between the deadtime-affected dual-color PCH and its single-channel counterpart: the relative error is smaller for dual-channel than for single-channel (Fig. 3 A) and the reduced χ² of the fit to an ideal model is much larger for the dual-channel than for the single-channel case (Table 2). This latter result suggests that, while single-channel PCHs with deadtime can be fit within experimental error by the ideal model, the same is not true for the dual-channel case. In fact, the ideal dual-color PCH model fails to fit most of the dual-color PCH functions that include deadtime.

TABLE 2.

Reduced χ²-values obtained from fits of single- and dual-channel deadtime-affected PCHs to their respective ideal models

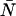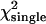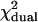0.1	0.0	0.0
0.5	0.0	0.4
1.0	0.0	1.0
5.0	0.0	6.2
10.0	0.0	13.0

The values correspond to the δ = 0.0025 curves in Fig. 3 A. The histograms are generated from a model (Eq. 8) rather than experimentally obtained, so a reduced χ² ≤ 1 implies that the ideal PCH model describes the deadtime modified PCH. A reduced χ² > 1 implies that the ideal PCH model does not describe the deadtime PCH, which is the case for the more severely affected dual-channel PCHs (i.e., those with the highest concentrations). The number of data points used was 6 × 10⁶.

The difference in behavior between single- and dual-channel PCH is best understood in terms of cumulants. The relative error of the cumulant κ_ij introduced by deadtime is calculated from (Δκ_ij/κ_ij)_deadtime = (κ′_ij − κ_ij)/κ_ij, where κ′_ij is the deadtime-affected cumulant. The values and relative errors for the first five cumulants are shown in Table 3 for values of ɛ_A = ɛ_B = 0.21 cpm and 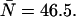The relative error of the first-order cumulants (κ₁₀, κ₀₁) is small and identical to the relative error of the single-channel cumulant κ₁. For the second-order cumulants of κ₂₀ and κ₀₂ the relative error is much larger than for the first-order cumulants, but again identical to the relative error of the single-channel cumulant κ₂. There is, however, one other important second-order cumulant for the dual-color PCH, κ₁₁, and this cumulant is much less affected by deadtime compared to κ₂₀ or κ₀₂. The reason for this lies in the fact that the detection processes of both detectors are independent of one another. In other words, the deadtime experienced by the first detector due to a photon event is not preventing the second detector from detecting a photon.

TABLE 3.

Values for the cumulants calculated from dual-color PCHs with ɛ_A = ɛ_B = 0.21, 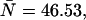and δ-values given below

	δ = 0	δ = 0.001	δ = 0.0025
κ10 = κ01	10	9.90 (−1%)	9.75 (−3%)
κ20 = κ02	0.76	0.53 (−30%)	0.22 (−71%)
κ11	0.76	0.73 (−4%)	0.69 (−9%)

The number in parentheses is the relative error between the ideal PCH (δ = 0) and deadtime-compromised PCHs (δ = 0.001 and δ = 0.0025). The second-order cumulant κ₁₁ is much less affected by deadtime than the other second-order moments, κ₂₀ and κ₀₂.

To understand the extent to which afterpulsing affects the dual-color PCH, we generated several afterpulse-affected dual-color PCHs using Eq. 9 as well as their single-channel equivalents and then fit them to their respective ideal PCH models. As we did for the deadtime modeling, we chose identical parameters for both channels (ɛ_A = ɛ_B = ɛ, q_A = q_B = q). The relative error in brightness due to afterpulsing (Δɛ/ɛ)_afterpulse is given by (ɛ^* − ɛ)/ɛ, where ɛ^* is the biased brightness returned by the ideal fit of the afterpulse-modified histogram and ɛ is the ideal brightness. We find that the relative error due to afterpulsing becomes larger as the brightness decreases, and larger afterpulse probabilities lead to larger errors (Fig. 3 B); this is qualitatively the same behavior as observed for single-channel PCH (18). As is the case for deadtime, dual-color PCH is more robust against afterpulsing effects than single-channel PCH as judged by the approximately twice-larger error for the single-channel PCH compared to the dual-channel PCH (Fig. 3 B). However, the error in brightness of dual-channel PCH, especially at low brightnesses, is still large enough that it cannot be ignored during data analysis. As judged by the reduced χ²-values, the ideal model fails to adequately describe dual-channel histograms in the presence of afterpulsing (Table 4). The relative error in the brightness introduced by afterpulsing is independent of the number of molecules and thus introduces a constant error in any dilution or titration experiment (see inset of Fig. 3 B). We again used moment analysis to calculate the relative error in brightness due to afterpulsing for the histograms shown in Fig. 3 B (lines). The result agrees very well with the error in brightness observed by modeling PCH functions. The reason that the relative error (Δɛ/ɛ)_afterpulse is smaller for the dual-color PCH than for the single-channel PCH is essentially the same reason it is smaller for the deadtime case; namely the relative error of κ₁₁ due to afterpulsing is less than the relative error in κ₂₀ and κ₀₂ because photon detection in detector A is independent from that in detector B.

TABLE 4.

Reduced χ²-values obtained from fits of single- and dual-channel afterpulse-affected PCHs to their respective ideal models

ɛ (cpm)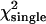
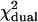0.1	1.3	23.2
0.3	1.0	14.8
0.5	1.1	10.9
0.8	1.1	7.7
1.0	1.2	6.8

The values correspond to the data shown in Fig. 3 B for q = 0.006. The histograms are generated from a model (Eq. 9) rather than experimentally obtained, so a reduced χ² ≤ 1 implies that the ideal PCH model describes the afterpulse-modified PCH. A reduced χ² > 1 implies the ideal PCH model does not describe the afterpulse-affected PCH, as is the case for all the dual-color histograms above. The number of data points used was 6 × 10⁶.

In our previous work on single-channel PCH analysis we concluded that afterpulsing is primarily a problem when the brightness is low (ɛ < 0.09 cpm for q = 0.002) (18). However, the afterpulse probability of some of our detectors is over three-times larger and thus afterpulsing causes significant errors (>10%) in the single-channel PCH even for moderate brightnesses (ɛ = 0.21 cpm). Dual-channel experiments split the brightness of a fluorophore into two detection channels with a dichroic filter. Because emission wavelength is used to separate different fluorophores, the brightness of a dye will usually be high in one channel and weak in the other channel. The low value of the brightness in the weak channel makes it very susceptible to afterpulsing effects. Thus, afterpulsing plays a significant role in the analysis of most dual-color PCH experiments even for detectors with low afterpulse probabilities.

The non-ideal detector effects of deadtime and afterpulsing work in opposite directions on the dual-color PCH: deadtime narrows the distribution resulting in reduced ɛ-values and increased 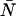-values, while afterpulsing broadens the distribution leading to increased ɛ-values and reduced 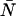-values. The combination of the two effects on the dual-color PCH in a simulated dilution experiment is shown in Fig. 3 C. Again we use identical parameters for both channels (ɛ_A = ɛ_B = ɛ, q_A = q_B = q, and δ_A = δ_B = δ). The relative error in the brightness due to afterpulsing is independent of concentration and introduces a constant error for each dilution step while the error introduced by deadtime decreases with each subsequent dilution. Thus for a given brightness, afterpulse effects dominate at lower concentrations and deadtime effects dominate at higher concentrations. The concentration at which the two sources of error cancel depends on the brightness, the afterpulse probability, and deadtime parameter of each detector. Comparison of Fig. 3 C with Fig. 3, A and B, shows that the relative error in brightness for combined deadtime and afterpulsing effects is just the sum of the relative error of the two effects individually (i.e., (Δɛ/ɛ)_total = (Δɛ/ɛ)_deadtime + (Δɛ/ɛ)_afterpulse). We also predict the error using bivariate moment analysis, where the relative errors due to deadtime and afterpulsing are added together. The results are shown in Fig. 3 C as solid lines. Moment analysis describes the error in brightness obtained from modeling the dual-channel PCH.

Experimental verification: Alexa 488

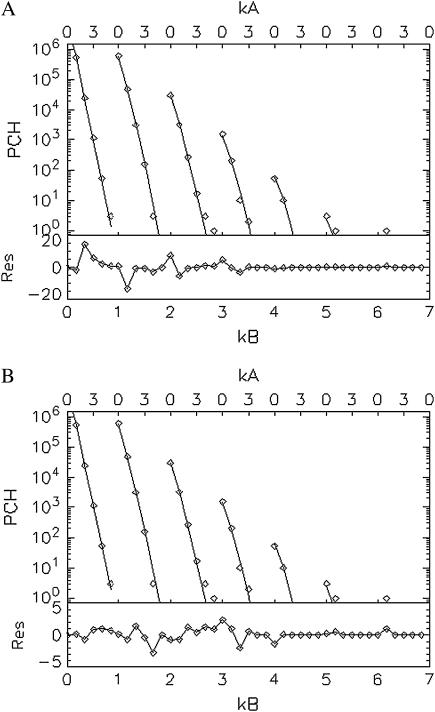
The modeling provided both qualitative and quantitative predictions about the behavior of the dual-color PCH and its parameters in the presence of non-ideal detector effects. To verify these predictions and also test the new theory's ability to describe real data, we performed a simple dilution experiment. A solution of Alexa 488 in water was diluted sequentially by factors of 2. At the lowest concentration, the sample was also measured with a neutral density filter (30% transmission) inserted into the emission path to further reduce the brightness. A 50/50 beam splitter was used to separate the emission into the two detectors.

In our initial attempts to fit experimental histograms to the non-ideal model, we found that a range of deadtimes and afterpulse probabilities could fit the histograms equally well when both effects are included. Since deadtime effects are largely absent at low concentrations and afterpulsing effects are always present regardless of the concentration and the more severe the lower the brightness, we decided to focus first on the low concentration sample with the additional emission filter. Since afterpulsing causes large deviations from the ideal dual-color PCH model (Table 4) we expect that the q parameter for each detector can be accurately determined from histograms obtained from samples with low brightness and low concentrations. The dual-color PCH of the lowest concentration sample (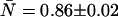) of our dilution experiment was fit to both the ideal model and a model that includes only afterpulses. These fits are shown in Fig. 4. The ideal model fails to describe the data (χ² = 24.0), whereas the afterpulse model describes the data within experimental error (χ² = 1.5). The afterpulse probabilities returned from the fit (q_A = 0.0070 ± 0.0006, and q_B = 0.0070 ± 0.0006) are in excellent agreement with our independent measurements of the afterpulse probabilities for those detectors (see Table 1, Instrument 2). The molecular brightnesses returned from the fit that includes afterpulsing are ɛ_A = 0.073 ± 0.002 cpm and ɛ_B = 0.082 ± 0.002 cpm. Fits using the ideal model yielded ɛ_A = 0.088 ± 0.006 cpm and ɛ_B = 0.099 ± 0.006 cpm for the dual-color PCH, and ɛ = 0.114 ± 0.002 cpm for the single-channel PCH from detector A and ɛ = 0.112 ± 0.002 cpm for the single-channel PCH from detector B. These results are in agreement with our modeling, which predicts that the errors for the single-channel histograms would be larger than for the dual-channel histograms.

FIGURE 4.

Fits (lines) of the experimental dual-color PCH (diamonds) to the ideal model (A) and to a model including afterpulsing (B) and their normalized residuals. The sample is a dilute aqueous solution of Alexa 488 (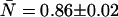) so deadtime effects are negligible. The ideal model fails to describe the experimental dual-color PCH as evidenced by the large reduced χ² (χ² = 24.0) and residuals. Including afterpulses into the model improves the fit significantly, yielding a reduced χ² of 1.5. The afterpulse probabilities returned by the fit are q_A = 0.0070 ± 0.0006 and q_B = 0.0049 ± 0.0006, in excellent agreement with our independent measurements (Table 1, Instrument 2). A neutral density filter was used in the emission path to reduce the brightness of the sample.

To adequately describe the entire dilution experiment both afterpulsing and deadtime effects must be accounted for in the dual-color PCH model. We first fit the dual-color and single-channel histograms for each dilution step to their ideal models (Fig. 5). As expected from the modeling, we observed that the brightness returned by the ideal fit was too large at low concentrations due to afterpulsing, whereas the brightness was too low at high concentrations because of deadtime. The errors for the single channel histograms were also larger than the errors for the dual-channel histograms. Next we performed a global fit of all the dual-color histograms where the brightness of each channel is linked so that it remains the same for all dilution steps. A global fit to an ideal model fails to describe the data (χ² = 29.9). Including deadtime effects in the dual-color PCH model improved the global fit (χ² = 7.3) but this model was still insufficient. The global fit only described all histograms within error (χ² = 1.1) when both deadtime and afterpulsing effects are included in the model. The afterpulsing probabilities were fixed during the global fit to the values obtained earlier by our independent measurements (q_A = 0.0070, q_B = 0.0046), while the deadtime parameters were allowed to vary. The global fit determined values of δ_A = 0.0047 ± 0.0002 and δ_B = 0.0047 ± 0.0002 for the deadtime parameters. These values agree well with the expected value of 0.005 corresponding to a deadtime of 50 ns and sampling frequency of 100 kHz. The brightness for each channel from the global fit for each channel is shown in Fig. 5 as a solid line. We also refit each two-dimensional histogram individually using the non-ideal model (deadtime and afterpulses). The resulting brightness values are shown in Fig. 5 as solid triangles and agree within error with the brightness determined by global analysis.

FIGURE 5.

Alexa 488 was diluted in water by a factor of 2 several times and the dual-color and single-channel PCHs of each sample were fit to their respective ideal models. Shown is the molecular brightness in detector A (A) and in detector B (B) returned from the individual fit of each sample to the ideal model and the non-ideal model (dual-color PCH only). The solid lines represent the brightness in each detection channel determined by global analysis of all dual-color PCH histograms to the non-ideal model. The number of molecules was also determined by the global fit. The ideal model fails to provide a constant brightness. It yields a brightness that is too large at low concentrations due to afterpulse effects, whereas, at high concentrations, the value is too low because of deadtime effects. Since detector A has the larger afterpulse probability of the two detectors, its difference between the single- and dual-channel brightnesses is larger than that for detector B at the lower concentrations. For each dilution step, the dual-channel histogram was fit to the non-ideal model with deadtime and afterpulses. The non-ideal model returned constant ɛ-values as expected.

Experimental verification: CFP and YFP in solution

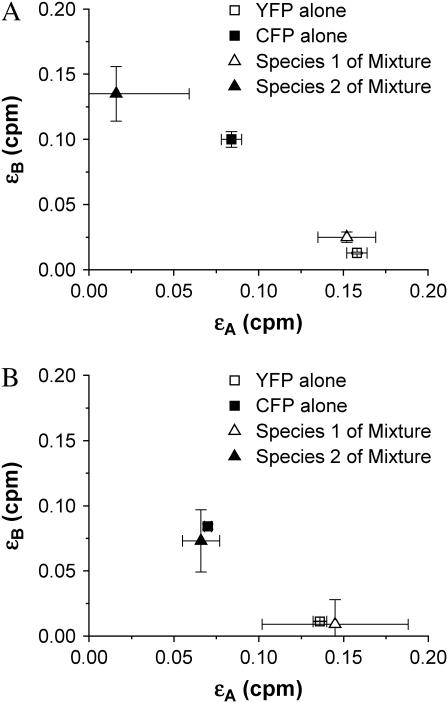
In Chen et al. (11), we resolved a mixture of CFP and YFP using a 525-nm dichroic, although, as we pointed out, a 515-nm dichroic would provide the best signal/noise ratio for separating the mixture. Because the brightness of YFP in the “blue” channel (λ < 515 nm) is very weak, the strong effect of afterpulsing in this channel prevented us from resolving the mixture with the 515-nm dichroic. In addition, we were unable to resolve mixtures at higher concentrations due to deadtime effects. Now with a new PCH theory that includes non-ideal detector effects, we repeated the experiments with CFP and YFP but used a 515-nm dichroic. We prepared an equimolar sample of CFP and YFP in PBS and diluted by factors of 2 in five steps. All of the dual-color histograms were first fit globally to the ideal dual-color PCH model and then to our deadtime- and afterpulse-modified model. The deadtime and afterpulse parameters were fixed to values of δ_A = δ_B = 0.001, q_A = 0.007, and q_B = 0.0046. The brightness in each channel was linked across the data sets since this parameter should not change as a function of concentration. Surprisingly, the reduced χ² of both global fits were ∼1. Based on our earlier modeling, we expected that the ideal model would have difficulty fitting the experimental histograms. However, our result demonstrates that including another species in the model provides enough flexibility to account for the misfit due to afterpulsing and/or deadtime. The brightness values of the global fit to the ideal model are shown in Fig. 6 A. We see that the compensation of non-ideal detector effects by a two-species model leads to biased brightness values that differ from the true brightness values for CFP and YFP. We determined the brightness of CFP and YFP individually by measuring them independently. In fact, we had to include afterpulsing effects to describe the dual-color histograms of CFP alone and YFP alone at low concentrations. Fig. 6 A demonstrates that the ideal model fails to provide the correct brightness values. The global fit includes histograms that are both deadtime-dominated and afterpulse-dominated, and the ideal model compromises between these competing effects by adjusting the brightness and number of molecules of each species. This compensation leads to nonphysical parameters. The brightness values of the global fit to the non-ideal model are shown in Fig. 6 B and match the brightness values expected for CFP and YFP. In other words, the non-ideal model successfully resolves the protein mixture.

FIGURE 6.

A mixture of CFP and YFP in solution. The sample was diluted by factors of 2 in five steps (N_total ≈ 50 for the first histogram and N_total ≈ 5 for the fifth histogram with N_YFP ≈ N_CFP for all histograms). (A) The brightnesses and their standard deviation as determined by global analysis of the dual-color histograms for the mixture fitted to an ideal PCH model with two species (triangles). (B) The same histograms were then globally fit to a PCH model for two species that included afterpulsing and deadtime. The brightness in each channel for species 1 and 2 obtained from the non-ideal fit are shown as triangles. The brightness values of a solution of CFP alone (solid square) and of YFP alone (open square) were also determined by dual-color PCH analysis and serve as a control. The non-ideal model recovers the brightness of CFP and YFP of the mixture, while the ideal model fails to return the proper brightness.

Experimental verification: GFP and RFP in cells

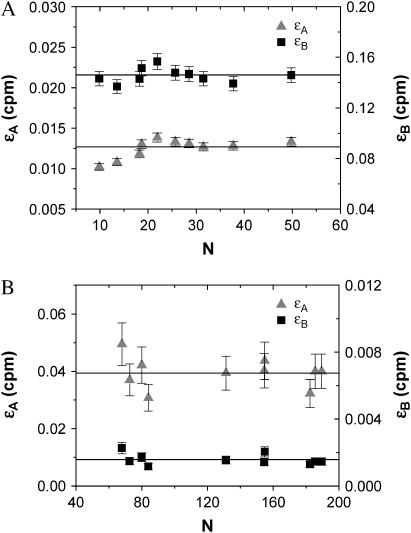
Deadtime and afterpulse corrections are vitally important for PCH analysis of cellular measurements. The intrinsic brightness of the commonly used fluorescent proteins (FPs), such as GFP, is lower than that of most organic fluorophores used for FFS experiments. In addition, the excitation power in cell experiments is lower than in aqueous solution, thus further reducing the brightness, and the concentrations of FPs are typically very high (N ∼ 10 − 100). To demonstrate the utility of the dual-color PCH for analysis of fluorescence fluctuation experiments in living cells, we transiently transfected COS cells with GFP or RFP. In fitting the histogram of each cell, we corrected for deadtime and afterpulse effects (δ_A = δ_B = 0.001, q_A = 0.007, and q_B = 0.0046) as well as for background. The results of the experiment are shown in Fig. 7. We see that the brightness values for each channel are constant for both GFP and RFP, as expected. Without these corrections, the brightness values in each channel would show a concentration-dependent behavior similar to that shown for Alexa 488 in Fig. 5, but the deviations would be more severe because the total brightness is lower and the concentration higher.

FIGURE 7.

The brightness in channels A (triangles) and B (squares) of GFP (A) and RFP (B) in vivo as obtained from dual-color PCH analysis with deadtime and afterpulsing effects. Each data point represents the measurement of a different cell. Background was also taken into account during the fit. Since GFP and RFP are monomeric in the cell, their brightness remains constant as the concentration increases.

Summary of non-ideal corrections for the dual-color PCH

In this article, we have developed a new theory for the dual-color PCH that includes deadtime and afterpulsing (Eqs. 8 and 9). Although this new theory is exact, it is impractical from an experimental point of view. Using Eqs. 8 and 9 to fit large histograms individually or for global analysis often took several minutes or even hours. Thus we developed and implemented the approximations of Eqs. 11 and 17, which have led to enormous gains in fitting time (∼10 s). However, neither the exact theories nor their approximations provide insight into the magnitude of the errors in ɛ_A, ɛ_B, and 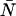introduced by deadtime or afterpulses. For the single-channel PCH, we were able to provide a contour diagram to illustrate these errors (18) but such a diagram is not possible for the dual-color PCH because there are three parameters instead of two. In addition, the afterpulse probability varies considerably between detectors. Thus we developed a simple approach based on moment analysis to predict the severity of the errors in ɛ_A, ɛ_B, and 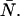Experimentalists can use Eq. 23 to determine the effect of deadtime and afterpulses on ɛ_A, for example, by inputting the ideal parameters and detector properties.

CONCLUSION

We previously demonstrated that dual-color PCH is a powerful tool for resolving mixtures. However, to take full advantage of this analysis method, the effects of deadtime and afterpulsing must be taken into account. These effects complicate the resolution of species at high concentrations, where deadtime effects dominate, or at low brightness, where afterpulse effects dominate. We developed a new theory of dual-color PCH that includes the effects of deadtime and afterpulsing and verified it experimentally. The new theory also allows us to perform global analysis of dual-color PCH experiments, which increases the sensitivity for resolving species. Using this modified dual-color PCH theory we were able to resolve a mixture of CFP and YFP, a protein pair with significant cross-talk. We also demonstrated that the technique is suitable for analysis of cellular experiments by characterizing the brightness of GFP and RFP in mammalian cells.

APPENDIX A

The derivation of the dual-color PCH function presented here is slightly different from that presented in Chen et al. (11). It closely follows the derivation of the single-channel PCH function (25) and has the advantage that it is straightforward to generalize this approach to the case of deadtime-affected dual-color PCH.

We begin by considering a single diffusing particle at position 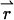within the observation volume V_PSF defined by the PSF. Throughout this derivation we will use the normalized point-spread function psf 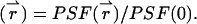The proper dual-channel intensity distribution p⁽¹⁾(I_A,I_B) for a single particle enclosed in a sample volume V is

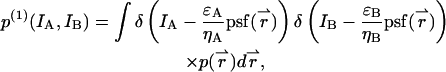(29)

where 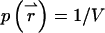is the probability to find the particle at 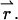Inserting this into Eq. 4, we arrive at the dual-color PCH function Π⁽¹⁾ of a single particle diffusing within the sample volume V,

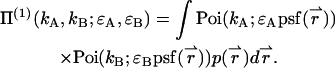(30)

The intensity distribution p⁽²⁾(I_A,I_B) for two identical, but independent, particles is given by

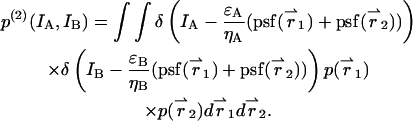(31)

Evaluating Eq. 4 using p⁽²⁾(I_A,I_B) returns the PCH function Π⁽²⁾ for two particles,

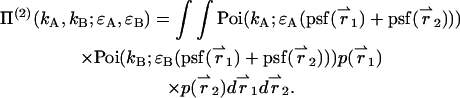(32)

Since the particles are independent we also obtain Π⁽²⁾ by convolution of the single-particle PCH functions Π⁽¹⁾,

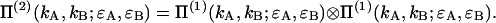(33)

The N-particle dual-color PCH function Π^(N) is obtained by convoluting the single-particle function Π⁽¹⁾ N-times.

We now transform from the closed volume V to the small observation volume V_PSF. The probability to have N particles in the observation volume is 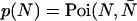), where the average number of particles 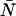is calculated from the bulk concentration c of the sample and Avogadro's constant N_A using 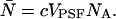The dual-color PCH function for an open volume is given by averaging over all PCH functions with fixed particle number weighted by the probability p(N),

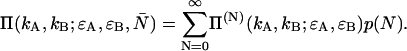(34)

The average number of photon counts of detectors A and B is given by 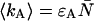and 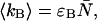respectively.

To obtain the dual-color PCH function (Eq. 8) in the presence of deadtime we rewrite Eq. 7,

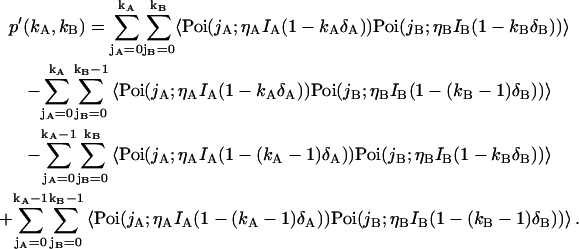(35)

Evaluating Eq. 35 with the dual-channel intensity distribution p⁽¹⁾(I_A,I_B) of a single diffusing particle (Eq. 29) yields the corresponding deadtime-affected PCH function Π⁽¹⁾′,

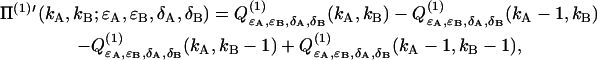(36)

where we introduced

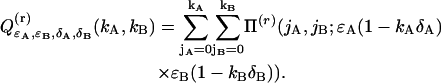(37)

Inserting the intensity distribution p⁽²⁾ (I_A,I_B) into Eq. 35 determines the deadtime-affected PCH function Π⁽²⁾′ of two particles,

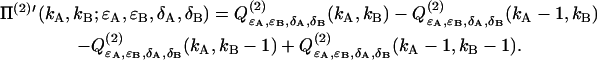(38)

It is straightforward to generalize this approach to the case of N particles to determine Π^(N)′.

Analog to Eq. 34, the deadtime-affected PCH function Π′ is given by averaging over all PCH functions Π^(N)′ weighted by their probability p(N),

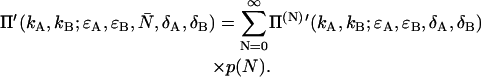(39)

Exchanging the order of summation of Eqs. 39 and 37 allows us to write the deadtime-affected PCH function Π′ in its final form of Eq. 8.

APPENDIX B

To obtain the coefficients c_j in Eq. 12 we first rewrite the kernel in Eq. 5 as (21)

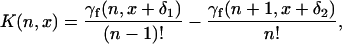(40)

where x = ηI, δ₁ = −x(n − 1)δ, and δ₂ = −xnδ. In Eq. 40, γ_f(n,z) is the incomplete factorial function. We then use the relationship (26)

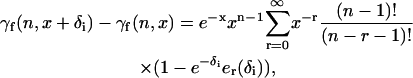(41)

where

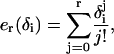(42)

to expand Eq. 40. We then obtain

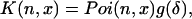(43)

where

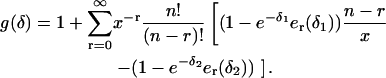(44)

We performed a Taylor expansion of the term in brackets in Eq. 44 and found that this term can be expressed as

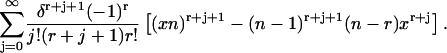(45)

Inserting this back into Eq. 44 results in an expression for g(δ) of

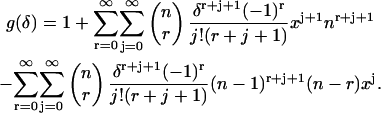(46)

Let us look at the first double summation term in Eq. 46. Let then this term becomes

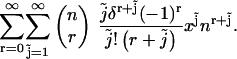(47)

We want to start the 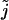summation at zero, so we must evaluate the term (Eq. 47) for 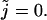We see that the term is zero for r > 0 and one for r = 0. Thus Eq. 47 can be rewritten as

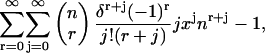(48)

where we have let 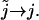And thus

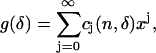(49)

where

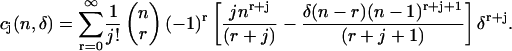(50)

APPENDIX C

The cumulants of the intensity distribution can also be related to the ordinary moments of the photon count distribution and are given by

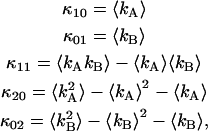(51)

where the ordinary moments of the dual-channel photon count distribution for the ideal case are calculated from

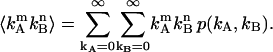(52)

The deadtime- and afterpulse-affected cumulants (denoted with a prime and asterisk, respectively) have the same form as the ideal, but are calculated from the deadtime-affected ordinary moments (e.g., κ′₁₀ = 〈k_A〉′) and afterpulse-affected ordinary moments (e.g., 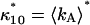), respectively.

The deadtime- and afterpulse-affected moments are obtained by replacing p(k_A,k_B) in Eq. 52 with p′(k_A,k_B) and p^*(k_A,k_B), respectively. We will first consider the deadtime-affected moments. For the single-channel case, O'Donnell (21) found that

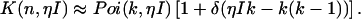(53)

Therefore for the dual-channel case, the photon count distribution is

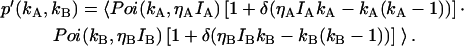(54)

Simplifying the above and keeping only first-order terms (i.e., O(δ_A) or O(δ_B)) yields

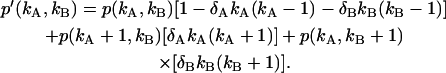(55)

We have also made use of Eq. 4 in deriving the above expression. Inserting Eq. 55 into Eq. 52, we arrive at the following expressions for the deadtime-affected moments in terms of ideal moments,

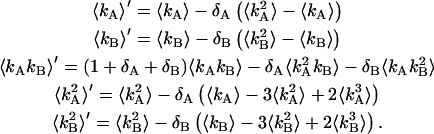(56)

For the afterpulse case, we insert Eq. 9 into Eq. 52 to calculate the afterpulse-affected moments. Keeping only terms of O(q_A) or O(q_B), we find for the five ordinary moments,

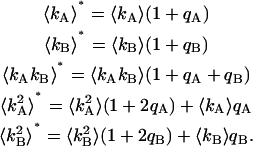(57)

To obtain the deadtime- and afterpulse-affected cumulants (i.e., 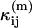), we insert Eqs. 56 and 57, respectively, in Eq. 51. Before this is done, however, the ideal moments in Eqs. 56 and 57 must be related to the ideal PCH parameters ɛ_A, ɛ_B, and This is accomplished by equating Eqs. 18 and 51 (see also Hillesheim and Müller (18)). The final expressions for the are straightforward to derive but are too long to be presented here.

And, finally, the variances of the cumulants are (27),

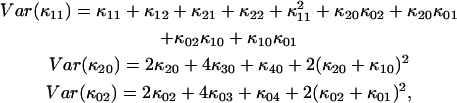(58)

where κ_ij is calculated from

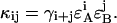(59)

We use the ideal variances rather than the non-ideal variances above. This approximation is sufficient for our purposes and results in simpler expressions.