Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2005 Oct 14;90(1):92–100. doi: 10.1529/biophysj.105.066969

Extending a Spectrin Repeat Unit. I: Linear Force-Extension Response

Sterling Paramore 1, Gary S Ayton 1, Dina T Mirijanian 1, Gregory A Voth 1
PMCID: PMC1367040  PMID: 16227506

Abstract

Nonequilibrium molecular dynamics simulations were used to calculate the elastic properties of a spectrin repeat unit. A contiguous α-helical linker was constructed by employing periodic boundary conditions, allowing a novel scheme for evaluating the thermodynamic force as a function of extension. By measuring the force-extension response under small extensions, spectrin was observed to behave primarily as an elastic material with a spring constant of 1700 ± 100 pN/nm. The implications of this spring constant, in terms of the properties of the spectrin tetramer, are also discussed.

INTRODUCTION

The erythrocyte (red blood cell) offers a novel system for studying how a cell responds to an applied force. Lacking any internal organelles, the plasma membrane and its associated cytoskeleton are the only structures the erythrocyte has available to resist external forces and maintain its unique shape (1). The cytoskeleton of the erythrocyte is primarily composed of a network of large (∼200 nm) rodlike multidomain proteins called spectrin. The organization of the spectrin cytoskeleton spans several distinct time- and length-scales, ranging from the atomistic description of the individual domains of spectrin to the nearly continuum-level description of the entire cell. This article is concerned with the calculation of material properties of spectrin at the atomistic scale that can be used to understand properties of the larger-scale structures composing the erythrocyte.

Spectrin is a tetrameric protein that is formed by the head-to-head association of two heterodimers (2,3). Each heterodimer is composed of antiparallel α- and β-subunits that form a right-handed double-helix (4). These subunits are further divided into ∼20 (for the α-spectrin monomer) and ∼17 (for the β-spectrin monomer) covalently-linked spectrin repeat units. Although the repeat units do not exhibit strict sequence homology, each unit is ∼106 residues in length and is folded into three α-helices (A, B, and C) arranged in an antiparallel coiled coil. Based on crystallographic measurements, helices A and C are thought to compose a contiguous α-helix that forms the linker region between the repeat units (5–10).

Although it seems clear that the erythrocyte derives its shape and resilience from the spectrin cytoskeleton (1), the relationship between the structure and function of spectrin on the atomistic scale (9–14), the scale of the tetramer (2,4,15–17), and the scale of the network (18–22) are still subjects of important research. Our approach to studying these relationships is to build a simulation methodology that spans the multiple time- and length-scales inherent in the construction of the erythrocyte. This article presents simulations characterizing the elastic properties of a spectrin repeat unit, which can be thought of as the basic building block of the erythrocyte cytoskeleton. The information obtained at this scale will aid in understanding the material properties of the spectrin network at larger scales, in particular that of the spectrin tetramer.

The origin of the elasticity of the spectrin tetramer has been the subject of considerable debate. Electron micrographs of spectrin in vitro (2,15) and viscometry studies of the spectrin dimer (23) suggested that spectrin was quite flexible, and could be treated as an entropic polymer. This flexibility has been thought to be a consequence of hingelike functionality of a nonhelical linker connecting repeat units (24). However, as discussed above, recent x-ray crystal structures of multiple-repeat spectrins indicate that the linker likely forms a contiguous α-helix, suggesting that the linker may not be as flexible as originally perceived. Furthermore, electron micrographs of partially expanded membrane skeletons suggested that the tetramer forms a rigid double-helix (4). With this type of structure, the elasticity of the tetramer has been proposed to be dependent more on energetic contributions derived from changes in the helical pitch and diameter of the double-helix (4,25).

More recently, the material properties of spectrin monomers have been studied using atomic force microscopy (AFM) (26–30) to measure a force-extension curve. These experiments show a force-extension curve with a characteristic sawtooth pattern. The peaks in the sawtooth pattern have been attributed to the force required to rupture the individual repeating domains. However, in the absence of external forces, the end-to-end distance of a spectrin tetramer in the cytoskeleton is only approximately one-third or less of its total contour length (16,17,19,20). Rupturing a domain using AFM involves stretching the end-to-end length of spectrin up to, and beyond, its full (folded) contour length. The physiological significance of spectrin's force response under such extreme extensions is not clear, nor is it known if the rupture behavior plays any role in governing the shape or elasticity of the erythrocyte.

Furthermore, the spectrin AFM experiments have not resolved changes in extension to <∼1 nm. Rief et al. (26) were able to fit a spectrin AFM force-extension curve to a two-level model of unfolding and estimated that a spectrin repeat unit needs to be extended only by ∼1.5 nm before rupture occurs and the unit unfolds. This suggests that the AFM experiments are missing information on the prerupture force response of a spectrin repeat unit that may be critical for understanding its function in a biological system.

Molecular dynamics (MD) simulation can complement the experimental studies by providing more detailed atomistic structural information and can also probe force-extension relationships with resolution ≪1 nm. Previous MD simulations of a single isolated (i.e., no linker) spectrin repeat unit (12,13) primarily focused on calculating the force-extension curve under extensions large enough to make comparisons with AFM experiments. This study takes a different approach by examining the force response of a spectrin repeat unit under small extensions. Here, a spectrin repeat unit was extended, and the force response measured, using a method called cyclic expansion nonequilibrium molecular dynamics (NEMD) (31–36). This method facilitates the use of boundary conditions to attach the spectrin repeat unit to its periodic image. These boundary conditions allow for simulation of an intact α-helical linker region, without any noncontiguous helical ends (a distinction that will be addressed in more detail in the companion article (37)). As mentioned above, the force response at small extensions may be more relevant for understanding spectrin under physiological conditions. The small-extension force response will be shown to provide some important details about the nature of the elasticity of the tetramer. Nevertheless, the AFM experiments do provide critical insight into the relationship between the structure of a protein and its response to applied forces. The companion article (37) expands on this work by subjecting the spectrin repeat unit to larger extensions and examining the role of the linker in the rupture process observed by AFM experiments.

METHODS

Molecular dynamics simulations were performed using the DL_POLY simulation package, Ver. 2.12, developed in Daresbury Laboratory (Daresbury, Warrington, England (38)). A modification of the Nosé-Hoover constant NPT algorithm in DL_POLY allowed for the calculation of the NEMD trajectories, as described below. The force-field used was the modified Cornell et al. (39,40) AMBER (parm96) force field. Electrostatic interactions were treated with the smooth particle-mesh Ewald method using a tolerance of 5 × 10−5. The real-space part of the Ewald sum and van der Waals interactions were cut off at 7.6 Å. A flexible TIP3P water model (41) with the intramolecular parameters of Schmitt and Voth (42) was used to solvate the system. All simulations were performed with a 1 fs time step. The temperature was kept constant at 300 K using a Nosé-Hoover thermostat with a relaxation time of 0.1 ps, and the pressure was kept constant with a barostat relaxation time of 1 ps.

The starting structure for all simulations was based on the solution NMR structure of the 16th repeat of chicken-brain α-spectrin (11) (Protein Data Bank ID 1AJ3). Residues 1–9 and 108–110 were not resolved in the NMR experiment and were added to the structure using the Swiss-PDBViewer (43). Multiple-repeat crystal structures of various spectrins (5–10) indicate that repeat units are typically linked by a contiguous α-helical linker. To account for these observations, the missing residues were constructed to adopt α-helical conformations, and the ends of the spectrin repeat unit (residues 1 and 110) were covalently attached by a peptide bond through the periodic boundary conditions along the z axis of the simulation cell. The boundary conditions thus serve as a means by which a periodically replicated system of linked spectrin repeat units can be simulated. The resulting structure was solvated with 2194 water molecules and equilibrated under zero pressure in a constant NPT ensemble for 10 ns. For the last 8 ns, the average length of the box in the z direction was 5.57 nm with a standard deviation of 0.052 nm; in the x and y directions, the average length was 3.76 nm with a standard deviation of 0.020 nm. The total charge of the molecule was −1, so a sodium cation was added to the system to maintain neutrality. The average α-carbon root-mean-squared deviation from the NMR structure was 2.6 Å, indicating that the structure was fairly stable. Configuration snapshots from this equilibration were used as starting points for the NEMD trajectories as described below. The water oxygen radial distribution function and diffusion constant were in agreement with simulations of pure water, indicating that finite size effects originating from the solvent were minimal.

Cyclic expansion NEMD

Cyclic expansion NEMD was used to calculate the force-extension behavior of a spectrin repeat unit. The method has been successfully applied to the study of the viscous properties of simple fluids (31,32) and the elastic properties of lipid bilayers (33,34,35,36). Cyclic expansion NEMD can be used to determine the primary material behavior (e.g., viscous or elastic) of the system under study by measuring the phase relationship between the extension rate and force response. The form of the method used here is largely due to Ayton et al. (35), with some minor modifications to account for the differences in the system studied.

In a cyclic expansion NEMD experiment, the system is subject to an oscillating strain rate given by

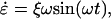graphic file with name M1.gif (1)

where ξ is the amplitude of oscillation and ω is the frequency (λ = 2π/ω is the period). This strain rate is applied along the z direction of the box by scaling the dimensions of the simulation cell at each step by

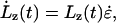graphic file with name M2.gif (2)
graphic file with name M3.gif (3)

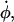where Inline graphic is the extension rate or pulling speed. Although Lz is scaled in a predetermined fashion via Eq. 1, the x and y directions are scaled so as to maintain zero x and y stress and therefore constant volume, on average. This is accomplished through the use of a Hoover barostat term (44,45), Inline graphic which has the equation of motion

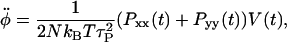graphic file with name M6.gif (4)

where Pαα is the αα component of the instantaneous pressure tensor, N is number of atoms, τP is the barostat relaxation time, T is the temperature, and kB is Boltzmann's constant.

With the exception of the strain rate term of Eq. 1, the equations of motion for the particles of the system experiencing cyclic expansion are identical to those used in the Nosé-Hoover constant NPT algorithm (46). The atom positions ri and momenta pi are governed by

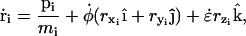graphic file with name M7.gif (5)
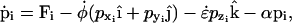graphic file with name M8.gif (6)

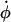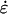where the force, Fi, on each particle i is minus the gradient of the potential of the system. The first term on the right-hand side of Eqs. 5 and 6 is derived from Hamilton's equations of motion. The additional terms involving Inline graphic and Inline graphic induce a flow field, making the momenta pi peculiar (47) (i.e., related to equipartition via Eq. 8). The thermostating variable α keeps the temperature of the system constant by removing or adding heat and evolves according to

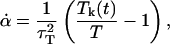graphic file with name M11.gif (7)

where Tk is the instantaneous kinetic temperature,

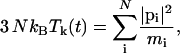graphic file with name M12.gif (8)

and τT is the thermostat relaxation time.

Initial positions and velocities for the NEMD simulations were obtained from configurations sampled along the equilibration trajectory. The equilibration was performed by integrating the equations of motion under an NPT ensemble where the barostat for the z direction was independent of the x and y directions (i.e., using Eqs. 5 and 6 with Inline graphic given by an expression similar to Eq. 4). This resulted in starting configurations with a distribution of initial lengths L that come from an NPT ensemble.

Cyclic expansion NEMD simulations were performed using strain rate periods of 500, 1000, 1500, 2000, 2500, 3000, 3500, and 4000 ps. Twelve starting configurations were used for the 500- and 1000-ps period simulations, seven for the 1500- and 2000-ps period simulations, and four for the rest. For all simulations, the strain rate amplitude ξ was set to 0.02 (giving a maximum strain of 0.04). A full NEMD cycle involves extending the system to maximum strain and then contracting it back down to its initial length. The extension part of the cycle was calculated for all of the above strain rate periods, but the contraction half of the cycle was only calculated for 500-, 1000-, 2000-, and 4000-ps strain-rate periods, using four starting configurations each.

THEORY: FORCE AND FREE ENERGY

Previous implementations of cyclic expansion NEMD focused on measuring the stress-strain relationship of membranes (33–36). However, due to spectrin's heterogeneity along the direction of the applied strain, the cross-sectional area required to calculate a stress is ill-defined. The material properties of spectrin are thus best characterized in terms of its force-extension behavior (i.e., the mean force that the molecule exerts in response to a displacement along its reaction coordinate, or end-to-end length). Formulating the material response of spectrin in terms of force and extension also allows for a more convenient comparison with experiment, since these are the quantities measured by AFM.

Two computational methods which are commonly used to measure force-extension relationships in proteins are steered molecular dynamics (48–50) and biased unfolding (12,51). In steered MD, one end of the molecule is fixed, and the other is subject to a harmonic potential that moves at some given velocity. Biased unfolding also uses a potential to constrain the length of the molecule, but the potential only moves when fluctuations increase the length. Both of these methods use the analogy of an AFM experiment to define a force by adding an extra potential to the system and measuring the displacement of the reaction coordinate along that potential. They have proven to be remarkably useful in describing the molecular origin of the peaks in the AFM force-extension curves for the muscle elasticity protein titin (50–54). However, in the case where the spectrin repeat unit is attached to its periodic image, these methods cannot be applied since there are no ends to attach to the restraining potential.

The force that can be measured using cyclic expansion NEMD arises solely from molecular interactions (there is no added external potential) and is defined as minus the derivative of the free energy with respect to length under isothermal conditions,

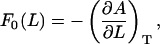graphic file with name M14.gif (9)

where L is the length of the box in the z direction, and the zero subscript signifies that the system is at equilibrium (or in the ω→0 limit). It can be shown (see Supplementary Material) that by using the NEMD equations of motion, the free energy derivative of Eq. 9 can be expressed as

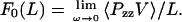graphic file with name M15.gif (10)

Perhaps not surprisingly, the force is just the pressure along the direction of strain multiplied by the cross-sectional area of the box. It is important to point out that this simple expression for the force is a consequence of the equations of motion and that this methodology can only be applied in the case where periodic boundary conditions are employed. If the spectrin repeat unit was not attached through periodic boundary conditions, then the force measured by Eq. 10 would be due to solvent reorganizing around the protein in response to a shape change in the box, and not to an extension of the spectrin repeat unit.

Equation 10 motivates the definition of a finite frequency, or nonequilibrium, force, Fω(L) = 〈PzzV〉/L. This force Fω(L) contains contributions from the irreversible work done on the system, at a finite frequency ω, and is in fact equal to minus the derivative of the work with respect to the length. The equilibrium free energy derivative, Eq. 9, is only obtained in the zero frequency limit. The effective spring constant is similarly defined as k0 = limω→0 kω, and is measured by calculating the slope of the force-extension curve for each trajectory at a particular frequency, averaging over multiple starting configurations, and extrapolating to zero frequency.

RESULTS

Equilibrium properties

One of the key features distinguishing this study from previous MD simulations of a single spectrin repeat unit (12,13) is the presence of a contiguous α-helical linker. The periodic boundary conditions employed conveniently allow modeling of the linker region connecting two repeat units with the computational cost of simulating one repeat unit. This situation thus models an infinitely long chain of attached repeat units. Of course, with a real multiple-repeat spectrin molecule, the repeat units can be bent or twisted relative to one another (see (6,9) for illustrations of this effect), which cannot occur under these boundary conditions. The periodically replicated system simulated here thus corresponds to a prestressed, or hyperstretched, state where all of the long wavelength bending modes have been dampened out. This allows us to examine a situation where the stretching modes are decoupled from the bending modes, a condition unattainable by regular experiment. As a consequence of the boundary conditions, the linker is forced to bend slightly to connect to its periodic image, but the effects of this bend are expected to be small compared to the effects of including the linker.

Many dynamical properties of a system can be obtained from an equilibrium simulation. A property of primary concern to this study is the measurement of an effective spring-constant for the spectrin repeat unit. The equilibrium trajectory (used to generate starting configurations for the NEMD simulations) was integrated under a constant NPT ensemble where the length of the box in the z direction was allowed to fluctuate independently of the other directions. The equipartition theorem states that the average thermal energy associated with each degree of freedom is kBT/2, where kB is Boltzmann's constant and T is the thermodynamic temperature. If the equilibrium energy of the repeat unit follows Hooke's law, then the effective spring constant can be calculated, according to the equipartition theorem, by measuring the fluctuations in the length of the box via 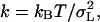Inline graphic where σL is the standard deviation of length of the box in the z direction. Over the course of the last 8 ns of the equilibration trajectory, the average length was measured to be 5.57 nm with a standard deviation of 0.052 nm, giving a spring constant of 1530 pN/nm. This value is close to that obtained using the NEMD methods described later; however, since this method requires the entire equilibrium simulation to calculate σL, an estimate of the error in k is not readily available. The only way to assess the accuracy of σL is to calculate it as a function of time steps and see whether it converges to some value. Even after 8 ns of equilibration, σL did not appear fully converged (data not shown), suggesting that a significantly longer equilibrium trajectory would be necessary to measure a statistically precise value for k.

NEMD control: water

Cyclic expansion NEMD simulations are usually discussed in terms of the system's stress response to an applied strain. However, a spectrin repeat unit is by no means homogeneous along the direction of the applied strain. This makes the definition of a cross-sectional area, which is required to calculate a stress, unclear. It is thus more appropriate to describe spectrin's force response to an applied extension. (Since force and stress are closely related, the terms “force” and “stress” will often be used interchangeably throughout the rest of this article.)

It is important to separate the intrinsic material response of the spectrin repeat unit from that of the solvent. To ensure that the chosen boundary conditions did not generate spurious solvent effects, cyclic expansion NEMD simulations of pure water were performed under conditions nearly identical to those used for the spectrin repeat unit simulations. As discussed in Methods, the simulation box length L is extended only in the z direction, whereas the x and y directions fluctuate under zero pressure. These conditions maintain, on average, constant volume and give rise to a change in the shape of the simulation cell. Under very slow extension rates, water will not respond with a measurable stress response to the applied strain since it is an isotropic liquid and freely adopts any container shape. On the other hand, under exceedingly high extension rates, the water molecules will not be able to adjust to the boundary condition changes quickly enough, resulting in a viscoelastic or even quasi-elastic stress response.

A simulation of 3072 water molecules was equilibrated in a simulation cell with similar dimensions to those used for the spectrin repeat unit simulations (average Lz = 6.24 ± 0.75 nm and Lx = Ly = 3.80 ± 0.23 nm). Preliminary investigations revealed that the force response of water was only detectable at very fast oscillations (with periods of λ = 1–2 ps). To allow the box shape to adjust in response to these high strain-rates, the barostat time constant τP had to be adjusted to 0.1 ps. Strain rate periods of 1–100 ps were imposed on 10 configurations taken from a 1-ns equilibration trajectory.

To get an estimate of the magnitude of the elastic and viscous forces that bulk water responds with under cyclic expansion NEMD, the water force-extension curves were fit to the function

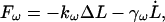graphic file with name M17.gif (11)

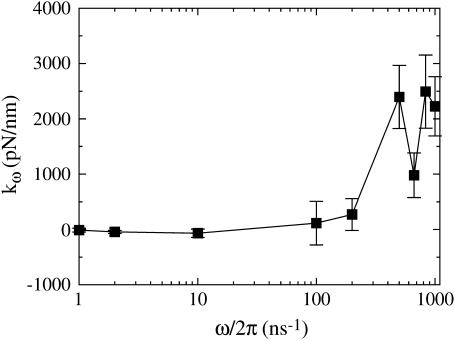
where kω is a finite-frequency effective water spring constant, and γω is a finite-frequency friction coefficient. Note that the friction term, 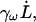Inline graphic corresponds to forces that are out of phase with the imposed extension. Fig. 1 illustrates how the elastic component kω of the water force response varies as a function of frequency (the strange dip observed at ω/2π = 667 ns−1 is likely a consequence of poor sampling due to the very large noise encountered at high frequencies). As expected, very high extension rates gave a measurable elastic response. However, even at frequencies 50-times faster than those used in the spectrin repeat unit NEMD simulations, no significant elastic component was detected. This ensures that when the protein is present, any measured elastic component can be attributed solely to the presence of spectrin. The fits to Eq. 11 also reveal that γω has minimal frequency dependence over this range of frequencies. The average γω was found to be 1200 ± 300 pN ps/nm. For the extension rates used in the spectrin repeat unit NEMD simulations, the force response due to water friction is expected to only account for an insignificant 1–2 pN.

FIGURE 1.

FIGURE 1

Open in a new tab

Fitted spring constant versus strain-rate frequency for 3072 water molecules in a box of the same shape as in the spectrin repeat unit simulations. Error bars represent the standard deviation of the mean.

Elastic properties of the spectrin repeat unit

For small extensions and pulling speeds, the material properties of a spectrin repeat unit were mapped onto a linear elastic constitutive relation given by

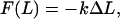graphic file with name M19.gif (12)

where F is the force that the system responds with to the applied strain, ΔL is the displacement in the simulation box length L along the z coordinate from its equilibrium position, and k is an effective spring constant. Of course, this is not the only possible constitutive relation that could be applied to a protein like spectrin. More complex viscoelastic models exist (55,56) which relate both the extension and the extension rate to the force; but the measurement of force (or pressure) in an MD simulation tends to be very noisy and characterization of secondary effects is not always feasible. Equation 12 represents a first approximation to the material behavior of the spectrin repeat unit and is not expected to be valid over a large range of extensions (such as those probed by AFM experiments (26,27,29,30)) or pulling speeds. The complete force response is likely to have complex extension and extension rate dependencies arising from the conformational changes that would result under large strains that no simple linear elastic or viscoelastic model could address. Despite these considerations, our results show that Eq. 12 offers a reasonable description of the spectrin repeat unit up to extensions of ∼3 Å.

Cyclic expansion NEMD subjects the system to a sinusoidal extension rate via Eq. 1. As opposed to a constant rate of extension, this provides us a convenient method for determining the primary material behavior of the spectrin repeat unit (i.e., whether it is viscous, elastic, or viscoelastic). When the system is extended, it responds with a force and if the force response is in phase with the extension, then the material is said to have an elastic response. If the system responds with a force that is in phase with the extension rate, then the material has a viscous response. The material may also have both viscous and elastic properties, in which case a phase-shift in the response from the ideal viscous or elastic behavior would be observed.

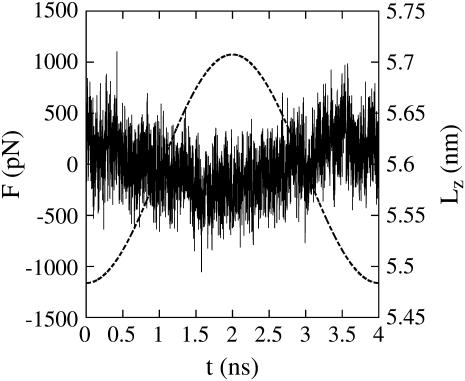
To confirm that Eq. 12 is an appropriate constitutive equation, the phase relationship between the force response and the imposed cyclic extension was measured. Fig. 2 shows that the force is largely in phase with the extension, indicating that under small perturbations, the spectrin unit responds elastically. This observation verifies the use of an elastic constitutive relation, as proposed in Eq. 12. Had a significant phase shift been observed, then the constitutive equation would have needed to be modified to include a viscous component.

FIGURE 2.

FIGURE 2

Open in a new tab

Force (left axis, solid line) and extension (right axis, dashed line) versus time t for a single cyclic expansion NEMD trajectory at λ = 4 ns, as in Eq. 1. Each point of the force curve is the average force of the preceding 1000 time steps.

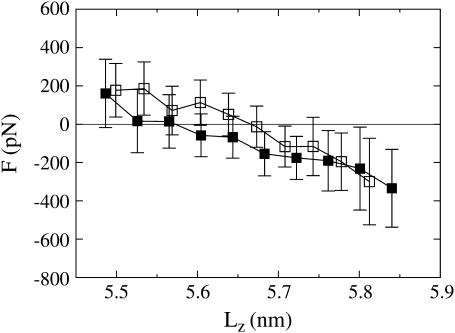
Of course, measuring the phase relationship between the extension and force response does not provide the functional form of the elastic relation. To this end, an explicit force-extension curve was measured and plotted in Fig. 3. This figure shows force-extension curves at λ = 4000 ps for both the extension and contraction trajectories. Each point on the curve is the average force within the nearby range of extensions. Error bars were calculated by treating each NEMD trajectory as an independent measurement and calculating the standard error of the mean force (i.e., the variance of the mean force is the sum of the variance of the average force from each trajectory divided by the square of the number of measurements (57)). These error bars therefore give a measurement of the sampling error. The averaged force-extension curves must be interpreted cautiously since the starting configurations for the NEMD trajectories have some distribution of starting lengths. No two trajectories started from precisely the same length and thus each point along the curve does not correspond to a unique extension rate. However, the end-points of the curve are roughly at a zero extension rate, whereas the middle regions of the curve are roughly at the maximum extension rate. The force-extension curves reveal that, when the spectrin repeat unit is extended up to six-times its equilibrium length fluctuations, it gives a nearly linear force response. When it is then contracted back toward its initial length, the force response is also linear and shows essentially no hysteresis to within the error of the measurements. Therefore, for small amplitude oscillations, the repeat unit can be treated approximately as an ideal spring, validating the constitutive equation proposed in Eq. 12.

FIGURE 3.

FIGURE 3

Open in a new tab

Force versus extension at λ = 4000 ps for extension (solid squares) and contraction (open squares) trajectories.

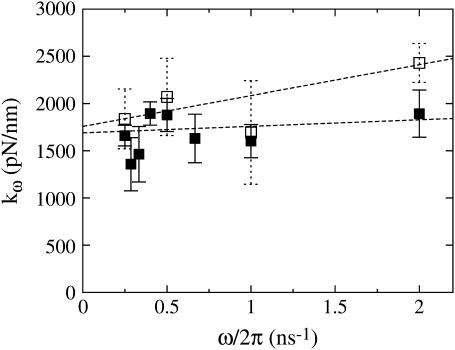
To obtain a quantitative measurement of the spring constant, cyclic expansion NEMD trajectories were generated according to the procedure described in Methods. For all trajectories, a linear fit was performed on the force-extension curve for both the extension and contraction parts of the NEMD cycle. This resulted in a set of finite-frequency spring constants which are plotted in Fig. 4. This figure shows that the frequency dependence of the spring constant for the extension half of the NEMD cycle is minimal. A linear regression of this data gave an extrapolated spring constant of kω→0 = 1700 ± 100 pN/nm, only slightly larger than the value obtained in the equilibrium simulations. It could be argued that tertiary structure rearrangements of the three helices composing the spectrin repeat unit would, on long timescales, lower the measured spring constant. If very long equilibrium MD simulations were available, this effect could manifest itself as large fluctuations in the length of spectrin, lowering the measured effective spring constant. However, any equilibrium tertiary structure rearrangements that persisted over long timescales would likely result in more disordered crystal structures (6,9,10). Given the insensitivity of the measured spring constant over an eightfold difference in pulling speeds, its similarity to the value obtained via equilibrium length fluctuations, and the fact that the available crystal structures are all well resolved, suggests that the spring constant obtained in this study would be applicable at longer timescales.

FIGURE 4.

FIGURE 4

Open in a new tab

Spectrin repeat unit elastic spring constant versus strain-rate frequency on extension (solid squares) and contraction (open squares). Error bars represent the standard deviation of the mean. The extrapolated value of the extension spring constant was found to be 1700 ± 100 pN/nm, and the contraction spring constant was 1800 ± 300 pN/nm.

The spring constant for the contraction half of the NEMD cycle, also shown in Fig. 4, does exhibit a stronger frequency dependence than the extension spring constant. Although the starting configurations for the extension trajectories were sampled from an equilibrium distribution, the contraction half of the cycle originated from the final configurations of the extension trajectories which belong to a nonequilibrium state. Therefore, the structural perturbations resulting from the previous NEMD run alters the frequency dependence of the measured spring constant. However, since extensions and contractions sample the same points on the reaction coordinate, the infinitely slow strain rate response should be the same. As expected, the extrapolated value for the contraction spring constant (kω→0 = 1800 ± 300 pN/nm) agrees well with the value for extension.

DISCUSSION

As mentioned previously, earlier steered and biased MD simulations of a single spectrin repeat unit did not include a contiguous α-helical linker (12,13). Although these earlier studies did not report a value for an effective spring constant, the force-extension curves of (13) reveal that the spring constant, over the first nanometer of extension, is ∼100 pN/nm—approximately an order-of-magnitude smaller than that reported here. This demonstrates that the contiguous α-helical structure of the linker dramatically affects the material properties of the spectrin repeat unit, making it more resistant to external forces. The origin of this effect likely has to do with the network of hydrogen bonds that maintain α-helices. A contiguous α-helical linker is able to form more backbone hydrogen bonds than a ruptured, or nonhelical, linker. With more hydrogen bonds, the contiguous α-helix would be able to withstand stronger forces. These and related issues, such as the recent double-repeat MD simulations of Ortiz et al. (14), are addressed in far more detail in the companion article (37).

When comparing these simulations with experimental results, the effects of the boundary conditions must be carefully considered. The periodic system generated by attaching a spectrin repeat unit to its periodic image corresponds to a highly-stretched multiple-repeat spectrin molecule, where all of the bending interactions between repeat units are absent. The benefits to such a construction is that it allowed for measurement of a spring constant for a spectrin repeat unit that is isolated from any interrepeat bending motions. Experiments to date have only been able to measure force-extension relationships of spectrins consisting of several attached repeat units. In an experiment, the repeat units are able to bend as well as stretch when spectrin is extended. This complicates determining what aspects of the spectrin repeat unit play a role in governing the elasticity of a multiple-repeat spectrin (i.e., bending, stretching, twisting, etc.). In these simulations, the small system size actually provides an advantage over using a larger system consisting of many repeat units, since a larger system would suffer some of the same problems as encountered experimentally. These specially constructed NEMD simulations thus provide unique and valuable information about the elasticity of spectrin that complement the results available from current experiments.

Although no direct experimental measurements of the spring constant of a spectrin repeat unit are available, some comparison with experimental measurements of a different but related system can still provide some insight. AFM experiments (58) estimate that the Young's modulus of the α-helical polypeptide poly-L-glutamic acid is ∼3 × 103 pN/nm2, in good agreement with earlier theoretical estimates of polyglycine and poly-L-alanine (59). The elastic response of a spectrin repeat unit will come primarily from the weakest region, which is expected to be the α-helical linker since it is not part of the heptad repeat pattern (6,9). Assuming that the above AFM measurements of poly-L-glutamic acid represent a typical Young's modulus for an α-helix, the five-residue, 0.75-nm-long linker would be expected to give a spring constant of ∼500 pN/nm (assuming a cross-sectional radius of ∼0.2 nm). The discrepancy between this value and that measured for the spectrin repeat unit using NEMD is within an order of magnitude, but perhaps suggests that interactions with adjacent helices impart extra stabilization on the linker. Another possible reason for the discrepancy could be due to the presence of bending modes in the poly-L-glutamic acid AFM experiments. Part of the force response measured by AFM is likely due to straightening the bending modes, and not stretching the helix, which would lower the measured spring constant. But since bending modes would not be as prevalent over only five residues, the effective spring constant at this length scale could be larger.

Optical tweezer micromanipulation experiments of freshly extracted spectrin skeletons have estimated (21,60) that the spring-constant of the mesoscopic spectrin tetramer is on the order of 0.01 pN/nm. Suppose that the spectrin tetramer could be treated as just a set of two elastic strands in parallel, where each strand is composed of 40 ideal springs in series, and each spring corresponds to a spectrin repeat unit. Using the repeat unit spring constant of k = 1700 pN/nm would result in a spring constant for the tetramer that is almost four orders-of-magnitude larger than that estimated by the experiments described above. This large discrepancy clearly demonstrates that the elasticity of the tetramer cannot be derived from simple linear extension of a series of individual repeat units, but that extra degrees of freedom, such as bending, twisting, or other mesoscale motions, must play an important role.

CONCLUSIONS

Cyclic expansion NEMD has been shown here to be an effective simulation methodology for calculating the material properties of a spectrin repeat unit. The forces were measured via a simple expression that can be related to a derivative of the free energy. A unique feature of these simulations was the use of periodic boundary conditions to simulate a single spectrin repeat unit with a contiguous α-helical linker. This allowed for observation of the stretching contributions to the elasticity, decoupled from the bending contributions, while maintaining the physiological importance of including the linker. Using this method, it was determined that a spectrin repeat unit under these conditions responds elastically to an applied extension. A quantitative estimate of an effective spring constant for the spectrin repeat unit was obtained and found to be 1700 ± 100 pN/nm. By comparison with previous simulations, this result shows that the contiguous α-helical linker significantly strengthens the spectrin repeat unit. Furthermore, the magnitude of this value suggests that bending or twisting interactions must play an important role in governing the elasticity of the spectrin tetramer at higher length scales.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[Supplemental]
biophysj_105.066969_index.html (677B, html)

Acknowledgments

This research was supported by a grant from the National Science Foundation Information Technology Research program (No. CHE-0218739). The computational resources for this work were partially supported by the National Computational Science Alliance under grant No. MCA94P017N and utilized the IA32 and IA64 Linux Superclusters. Allocations of computer time from the Center for High Performance Computing at the University of Utah and the Maui High Performance Computing Center are also gratefully acknowledged.

References

  • 1.Elgsaeter, A., B. T. Stokke, A. Mikkelsen, and D. Branton. 1986. The molecular basis of erythrocyte shape. Science. 234:1217–1223. [DOI] [PubMed] [Google Scholar]
  • 2.Shotton, D. M., B. E. Burke, and D. Branton. 1979. The molecular structure of human erythrocyte spectrin: biophysical and electron microscopic studies. J. Mol. Biol. 131:303–329. [DOI] [PubMed] [Google Scholar]
  • 3.Speicher, D. W., T. M. DeSilva, K. D. Speicher, J. A. Ursitti, P. Hembach, and L. Weglarz. 1993. Location of the human red cell spectrin tetramer binding site and detection of a related “closed” hairpin loop dimer using proteolytic footprinting. J. Biol. Chem. 268:4227–4235. [PubMed] [Google Scholar]
  • 4.McGough, A. M., and R. Josephs. 1990. On the structure of erythrocyte spectrin in partially expanded membrane skeletons. Proc. Natl. Acad. Sci. USA. 87:5208–5212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Yan, Y., E. Winograd, A. Viel, T. Cronin, S. C. Harrison, and D. Branton. 1993. Crystal structure of the repetitive segments of spectrin. Science. 262:2027–2030. [DOI] [PubMed] [Google Scholar]
  • 6.Grum, V. L., D. Li, R. I. MacDonald, and A. Mondragón. 1999. Structures of two repeats of spectrin suggest models of flexibility. Cell. 98:523–535. [DOI] [PubMed] [Google Scholar]
  • 7.Djinović-Carugo, K., P. Young, M. Gautel, and M. Saraste. 1999. Structure of the α-actinin rod: molecular basis for cross-linking of actin filaments. Cell. 98:537–546. [DOI] [PubMed] [Google Scholar]
  • 8.Ylänne, J., K. Scheffzek, P. Young, and M. Saraste. 2001. Crystal structure of the α-actinin rod reveals an extensive torsional twist. Structure. 9:597–604. [DOI] [PubMed] [Google Scholar]
  • 9.Kusunoki, H., R. I. MacDonald, and A. Mondragón. 2004. Structural insights into the stability and flexibility of unusual erythroid spectrin repeats. Structure. 12:645–656. [DOI] [PubMed] [Google Scholar]
  • 10.Kusunoki, H., G. Minasov, R. I. MacDonald, and A. Mondragón. 2004. Independent movement, dimerization and stability of tandem repeats of chicken brain α-spectrin. J. Mol. Biol. 344:495–511. [DOI] [PubMed] [Google Scholar]
  • 11.Pascual, J., M. Pfuhl, D. Walther, M. Saraste, and M. Nilges. 1997. Solution structure of the spectrin repeat: a left-handed antiparallel triple-helical coiled-coil. J. Mol. Biol. 273:740–751. [DOI] [PubMed] [Google Scholar]
  • 12.Paci, E., and M. Karplus. 2000. Unfolding proteins by external forces and temperature: the importance of topology and energetics. Proc. Natl. Acad. Sci. USA. 97:6521–6526. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Altmann, S. M., R. G. Grünberg, P.-F. Lenne, J. Ylänne, A. Raae, K. Herbert, M. Saraste, M. Nilges, and J. H. Hörber. 2002. Pathways and intermediates in forced unfolding of spectrin repeats. Structure. 10:1085–1096. [DOI] [PubMed] [Google Scholar]
  • 14.Ortiz, V., S. O. Nielsen, M. L. Klein, and D. E. Discher. 2005. Unfolding a linker between helical repeats. J. Mol. Biol. 349:638–647. [DOI] [PubMed] [Google Scholar]
  • 15.Morrow, J. S., and V. T. Marchesi. 1981. Self-assembly of spectrin oligomers in vitro: a basis for a dynamic cytoskeleton. J. Cell Biol. 88:463–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Takeuchi, M., H. Miyamoto, Y. Sako, H. Komizu, and A. Kusumi. 1998. Structure of the erythrocyte membrane skeleton as observed by atomic force microscopy. Biophys. J. 74:2171–2183. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Swihart, A. H., J. M. Mikrut, J. B. Ketterson, and R. C. MacDonald. 2001. Atomic force microscopy of the erythrocyte membrane skeleton. J. Microsc. 204:212–225. [DOI] [PubMed] [Google Scholar]
  • 18.Waugh, R., and E. A. Evans. 1979. Thermoelasticity of red blood cell membrane. Biophys. J. 26:115–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Byers, T. J., and D. Branton. 1985. Visualization of the protein associations in the erythrocyte membrane skeleton. Proc. Natl. Acad. Sci. USA. 82:6153–6157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Liu, S.-C., L. H. Derick, and J. Palek. 1987. Visualization of the hexagonal lattice in the erythrocyte membrane skeleton. J. Cell Biol. 104:527–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Lenormand, G., S. Hénon, A. Richert, J. Siméon, and F. Gallet. 2001. Direct measurement of the area expansion and shear moduli of the human red blood cell membrane skeleton. Biophys. J. 81:43–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Lee, J. C.-M., and D. E. Discher. 2001. Deformation-enhanced fluctuations in the red cell skeleton with theoretical relations to elasticity, connectivity, and spectrin unfolding. Biophys. J. 81:3178–3192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Stokke, B. T., A. Mikkelson, and A. Elgsaeter. 1985. Human erythrocyte spectrin dimer intrinsic viscosity: temperature dependence and implications of the molecular basis of the erythrocyte membrane free energy. Biochim. Biophys. Acta. 816:102–110. [DOI] [PubMed] [Google Scholar]
  • 24.Speicher, D. W., and V. T. Marchesi. 1984. Erythrocyte spectrin is comprised of many homologous triple helical segments. Nature. 311:177–178. [DOI] [PubMed] [Google Scholar]
  • 25.Hansen, J. C., R. Skalak, S. Chien, and A. Hoger. 1997. Spectrin properties and the elasticity of the red blood cell membrane skeleton. Biorheology. 34:327–348. [DOI] [PubMed] [Google Scholar]
  • 26.Rief, M., J. Pascual, M. Saraste, and H. E. Gaub. 1999. Single molecule force spectroscopy of spectrin repeats: low unfolding forces in helix bundles. J. Mol. Biol. 286:553–561. [DOI] [PubMed] [Google Scholar]
  • 27.Lenne, P.-F., A. J. Raae, S. M. Altmann, M. Saraste, and J. K. H. Hörber. 2000. States and transitions during forced unfolding of a single spectrin repeat. FEBS Lett. 476:124–128. [DOI] [PubMed] [Google Scholar]
  • 28.Lavery, R., A. Lebrun, J.-F. Allemand, D. Bensimon, and V. Croquette. 2002. Structure and mechanics of single biomolecules: experiment and simulation. J. Phys. Condens. Matter. 14:R383–R414. [Google Scholar]
  • 29.Law, R., P. Carl, S. Harper, P. Dalhaimer, D. W. Speicher, and D. E. Discher. 2003. Cooperativity in forced unfolding of tandem spectrin repeats. Biophys. J. 84:533–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Law, R., G. Liao, S. Harper, G. Yang, D. W. Speicher, and D. E. Discher. 2003. Pathway shifts and thermal softening in temperature-coupled forced unfolding of spectrin domains. Biophys. J. 85:3286–3293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Hoover, W. G., D. J. Evans, R. B. Hickman, A. J. C. Ladd, W. T. Ashurst, and B. Moran. 1980. Lennard-Jones triple-point bulk and shear viscosities, Green-Kubo theory, Hamiltonian mechanics, and nonequilibrium molecular dynamics. Phys. Rev. A. 22:1690–1697. [Google Scholar]
  • 32.Hoover, W. G., A. J. C. Ladd, R. B. Hickman, and B. L. Holian. 1980. Bulk viscosity via nonequilibrium and equilibrium molecular dynamics. Phys. Rev. A. 21:1756–1760. [Google Scholar]
  • 33.Ayton, G., S. G. Bardenhagen, P. McMurtry, D. Sulsky, and G. A. Voth. 2001. Interfacing continuum and molecular dynamics: an application to lipid bilayers. J. Chem. Phys. 114:6913–6924. [Google Scholar]
  • 34.Ayton, G., S. G. Bardenhagen, P. McMurtry, D. Sulsky, and G. A. Voth. 2001. Interfacing molecular dynamics with continuum dynamics in computer simulation: toward an application to biological membranes. IBM J. Res. Dev. 45:417–426. [Google Scholar]
  • 35.Ayton, G., A. M. Smondyrev, S. G. Bardenhagen, P. McMurtry, and G. A. Voth. 2002. Calculating the bulk modulus for a lipid bilayer with nonequilibrium molecular dynamics simulation. Biophys. J. 82:1226–1238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Ayton, G., A. M. Smondyrev, S. G. Bardenhagen, P. McMurtry, and G. A. Voth. 2002. Interfacing molecular dynamics and macro-scale simulations for lipid bilayer vesicles. Biophys. J. 83:1026–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Paramore, S., G. S. Ayton, and G. A. Voth. 2005. Extending a spectrin repeat unit. II: Rupture behavior. Biophys. J. 90:101–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Smith, W., and T. Forester. 1999. The DL_POLY molecular simulation package. http://www.cse.clrc.ac.uk/msi/software/DL_POLY/.
  • 39.Cornell, W. D., P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, Jr., D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
  • 40.Kollman, P. A., R. Dixon, W. Cornell, T. Fox, C. Chipot, and A. Pohorille. 1997. The development/application of a minimalist organic/biochemical molecular mechanic force field using a combination of ab initio calculations and experimental data. In Computer Simulation of Biomolecular Systems, Vol. 3. A. Wilkinson, P. Weiner, and W. F. van Gunsteren, editors. Elsevier, Dordrecht, The Netherlands. 83–96.
  • 41.Jorgensen, W. L., J. Chandrasekhar, and J. D. Madura. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
  • 42.Schmitt, U. W., and G. A. Voth. 1999. The computer simulation of proton transport in water. J. Chem. Phys. 111:9361–9381. [Google Scholar]
  • 43.Guex, N., and M. C. Peitsch. 1997. SWISS-MODEL and the Swiss-PDBViewer: an environment for comparative protein modeling. Electrophoresis. 18:2714–2723. [DOI] [PubMed] [Google Scholar]
  • 44.Hoover, W. G. 1985. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A. 31:1695–1697. [DOI] [PubMed] [Google Scholar]
  • 45.Hoover, W. G. 1986. Constant-pressure equations of motion. Phys. Rev. A. 34:2499–2500. [DOI] [PubMed] [Google Scholar]
  • 46.Melchionna, S., G. Ciccotti, and B. L. Holian. 1993. Hoover NPT dynamics for systems varying in shape and size. Mol. Phys. 78:533–544. [Google Scholar]
  • 47.Evans, D. J., and G. P. Morriss. 1990. Statistical Mechanics of Nonequilibrium Liquids. Academic Press, London, UK.
  • 48.Grubmüller, H., B. Heymann, and P. Tavan. 1996. Ligand binding: molecular mechanics calculation of the streptavidin-biotin rupture force. Science. 271:997–999. [DOI] [PubMed] [Google Scholar]
  • 49.Izrailev, S., S. Stepaniants, M. Balsera, Y. Oono, and K. Schulten. 1997. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 72:1568–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Lu, H., and K. Schulten. 2000. The key event in force-induced unfolding of titin's immunoglobulin domains. Biophys. J. 79:51–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Paci, E., and M. Karplus. 1999. Forced unfolding of fibronectin type 3 modules: an analysis by biased molecular dynamics simulations. J. Mol. Biol. 288:441–459. [DOI] [PubMed] [Google Scholar]
  • 52.Lu, H., B. Isralewitz, A. Krammer, V. Vogel, and K. Schulten. 1998. Unfolding titin immunoglobulin domains by steered molecular dynamics simulation. Biophys. J. 75:662–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Lu, H., and K. Schulten. 1999. Steered molecular dynamics simulations of force-induced protein domain unfolding. Proteins. 35:453–463. [PubMed] [Google Scholar]
  • 54.Krammer, A., H. Lu, B. Isralewitz, and V. Vogel. 1999. Forced unfolding of the fibronectin type III module reveals a tensile molecular recognition switch. Proc. Natl. Acad. Sci. USA. 96:1351–1356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Fung, Y. C. 1993. Biomechanics: Mechanical Properties of Living Tissues. Springer-Verlag, New York.
  • 56.Tschoegl, N. W. 1989. The Phenomenological Theory of Linear Viscoelastic Behavior. Springer-Verlag, New York.
  • 57.Lemons, D. S. 2002. An Introduction to Stochastic Processes in Physics. The Johns Hopkins University Press, Baltimore and London.
  • 58.Idiris, A., M. T. Alam, and A. Ikai. 2000. Spring mechanics of α-helical polypeptide. Protein Eng. 13:763–770. [DOI] [PubMed] [Google Scholar]
  • 59.Suezaki, Y., and N. Gō. 1976. Fluctuations and mechanical strength of α-helices of polyglycine and poly(L-alanine). Biopolymers. 15:2137–2153. [DOI] [PubMed] [Google Scholar]
  • 60.Lenormand, G., S. Hénon, A. Richert, J. Siméon, and F. Gallet. 2003. Elasticity of the human red blood cell skeleton. Biorheology. 40:247–251. [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental]
biophysj_105.066969_index.html (677B, html)
biophysj_105.066969_1.pdf (185.5KB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES