Abstract
In considering the problem of steady-state negative conductance in the squid axon from the standpoint of electrodiffusion, the following assumptions produce results which are in reasonable agreement with experimental observations: (1) The major ion distributions are not significantly perturbed by current flows (2) The electric field in the membrane is essentially uniform. (3) The membrane has certain properties appropriate to solids, particularly with respect to chemical potentials. (4) Na+ and K+ move according to a single-file interstitialcy migration mechanism and independently of each other. (5) The interaction energy of Na+ with membrane sites is about 1.4 times that for K+. Assumptions 1 and 2 are sufficient for the appearance of a negative conductance. Experimental test of the theory is possible and is specifically suggested.
Full text
PDF






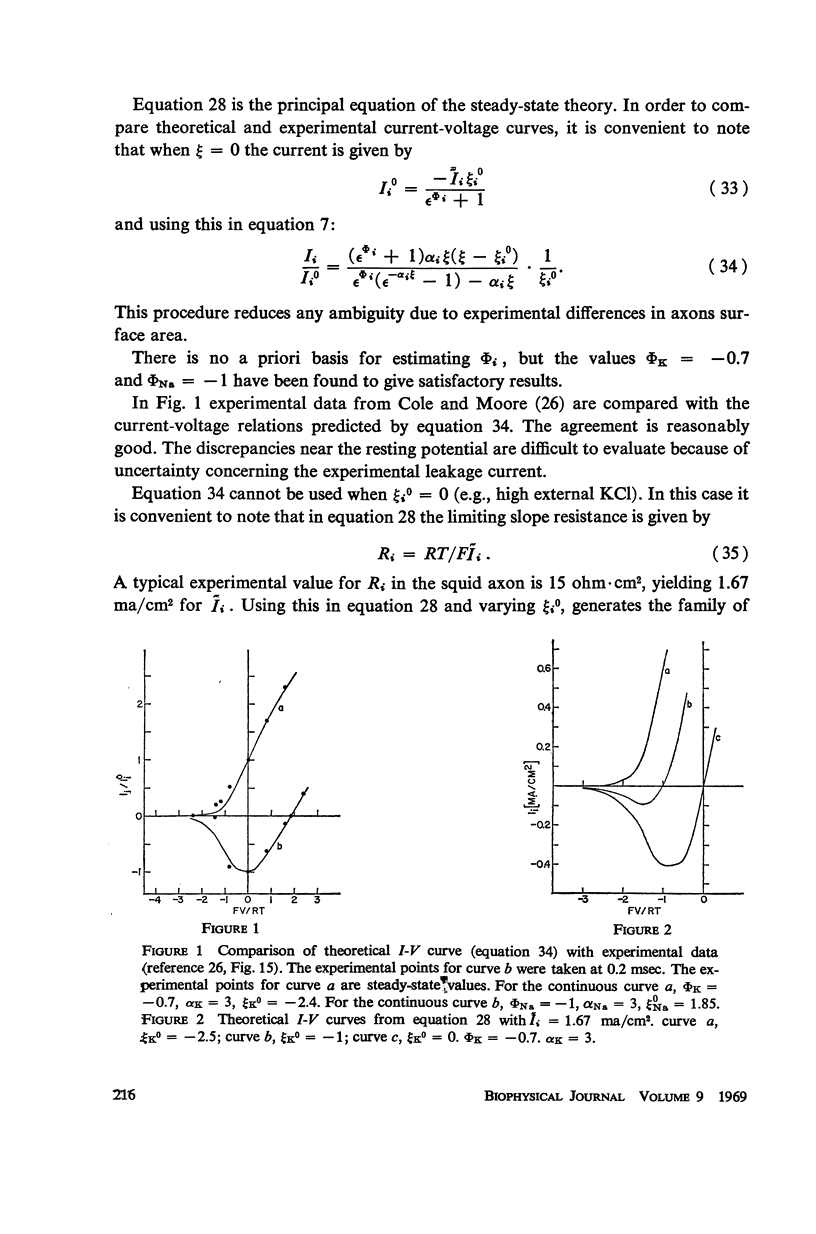
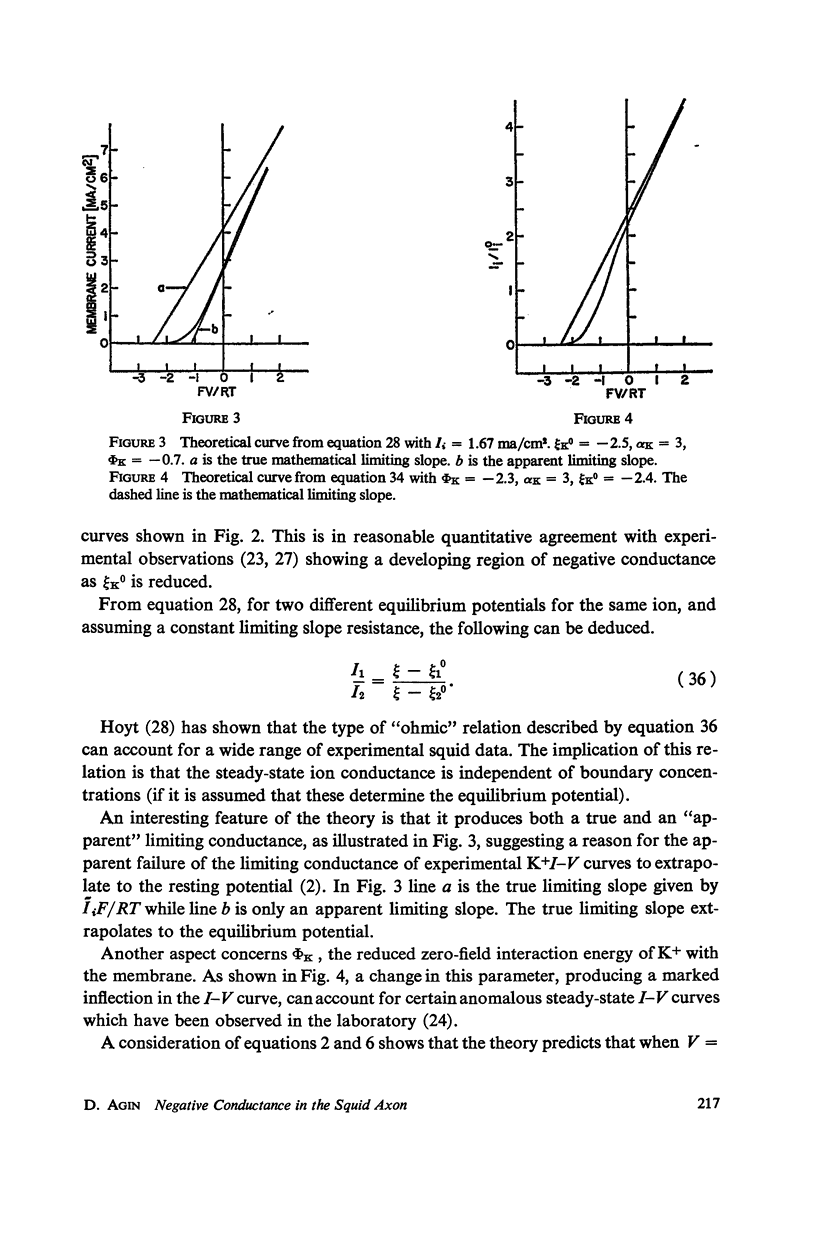




Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Agin D. Electroneutrality and electrodiffusion in the squid axon. Proc Natl Acad Sci U S A. 1967 May;57(5):1232–1238. doi: 10.1073/pnas.57.5.1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agin D., Schauf C. Concerning negative conductance in the squid axon. Proc Natl Acad Sci U S A. 1968 Apr;59(4):1201–1208. doi: 10.1073/pnas.59.4.1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- COLE K. S. ELECTRODIFFUSION MODELS FOR THE MEMBRANE OF SQUID GIANT AXON. Physiol Rev. 1965 Apr;45:340–379. doi: 10.1152/physrev.1965.45.2.340. [DOI] [PubMed] [Google Scholar]
- COLE K. S., MOORE J. W. Ionic current measurements in the squid giant axon membrane. J Gen Physiol. 1960 Sep;44:123–167. doi: 10.1085/jgp.44.1.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- FITZHUGH R. Thresholds and plateaus in the Hodgkin-Huxley nerve equations. J Gen Physiol. 1960 May;43:867–896. doi: 10.1085/jgp.43.5.867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottlieb M. H., Sollner K. Failure of the Nernst-Einstein equation to correlate electrical resistances and rates of ionic self-exchange across certain fixed charge membranes. Biophys J. 1968 May;8(5):515–535. doi: 10.1016/S0006-3495(68)86505-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HODGKIN A. L., HUXLEY A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MAURO A. Anomalous impedance, a phenomenological property of time-variant resistance. An analytic review. Biophys J. 1961 Mar;1:353–372. doi: 10.1016/s0006-3495(61)86894-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MOORE J. W. Excitation of the squid axon membrane in isosmotic potassium chloride. Nature. 1959 Jan 24;183(4656):265–266. doi: 10.1038/183265b0. [DOI] [PubMed] [Google Scholar]
- TEORELL T. Electrokinetic membrane processes in relation to properties excitable tissues. II. Some theoretical considerations. J Gen Physiol. 1959 Mar 20;42(4):847–863. doi: 10.1085/jgp.42.4.847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei L. Y. Possibility of electron tunneling through a nerve membrane. Bull Math Biophys. 1967 Sep;29(3):411–418. doi: 10.1007/BF02476580. [DOI] [PubMed] [Google Scholar]


