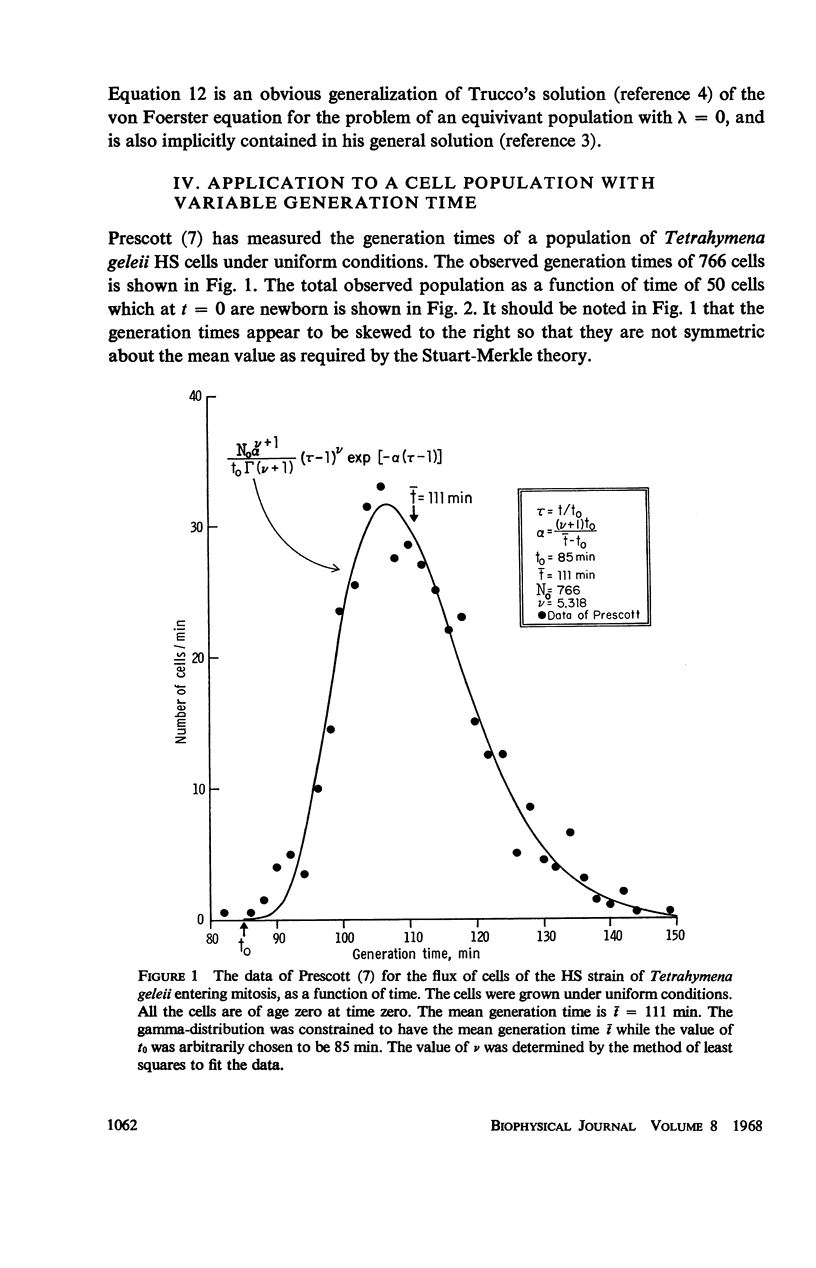
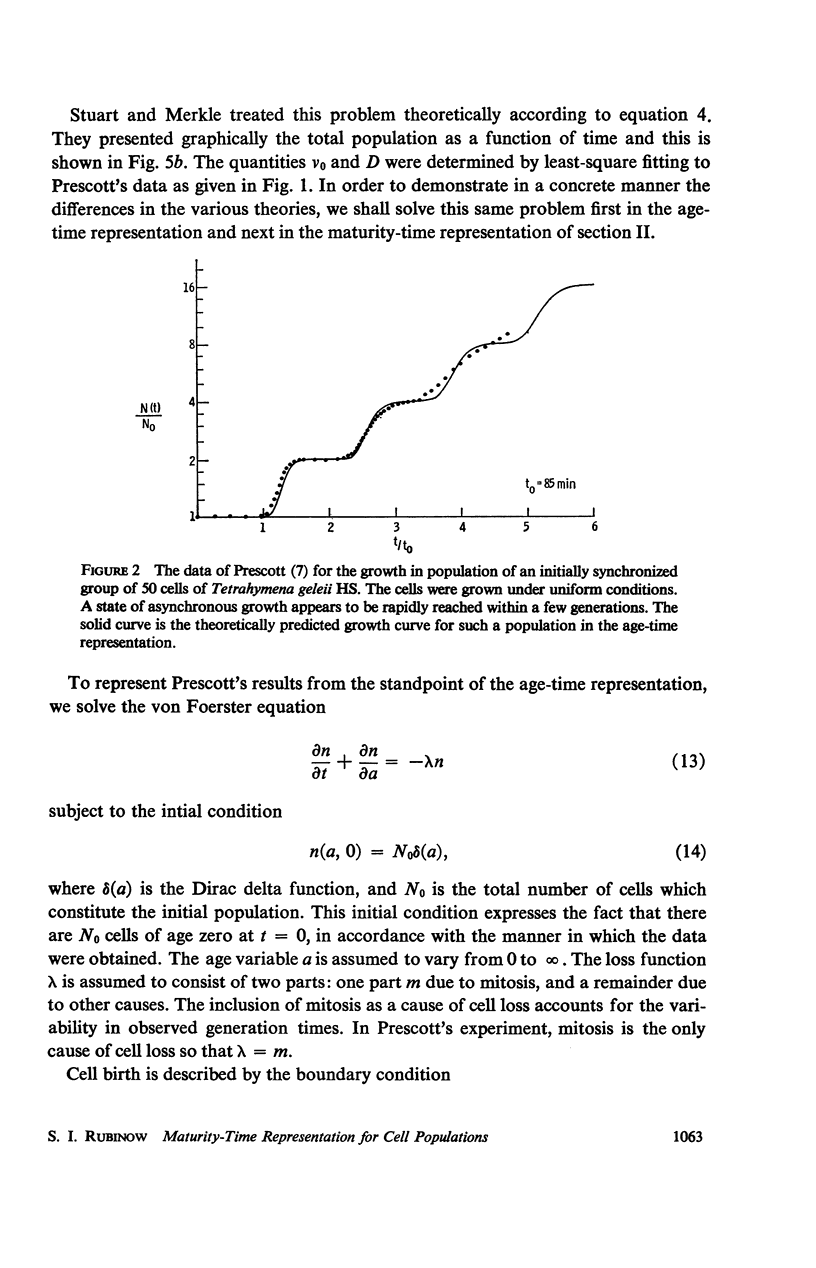
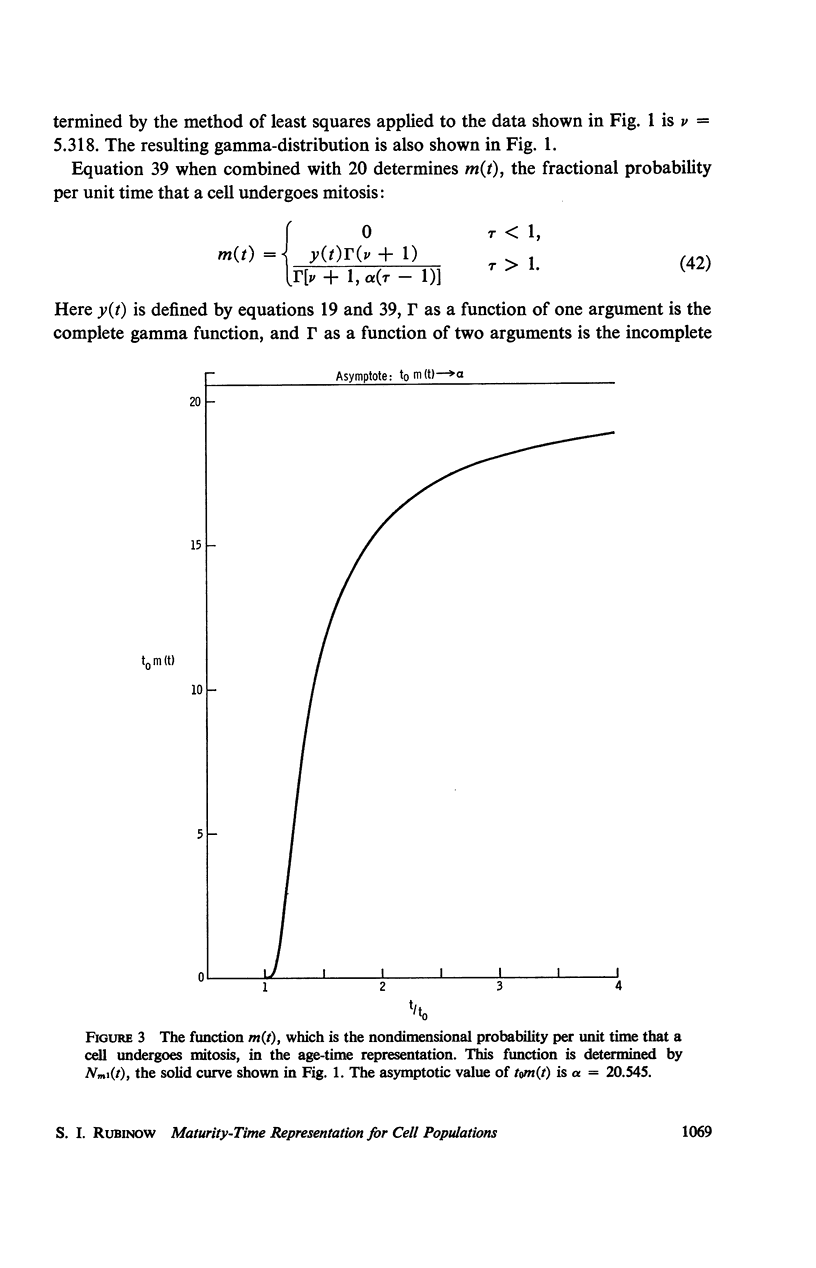
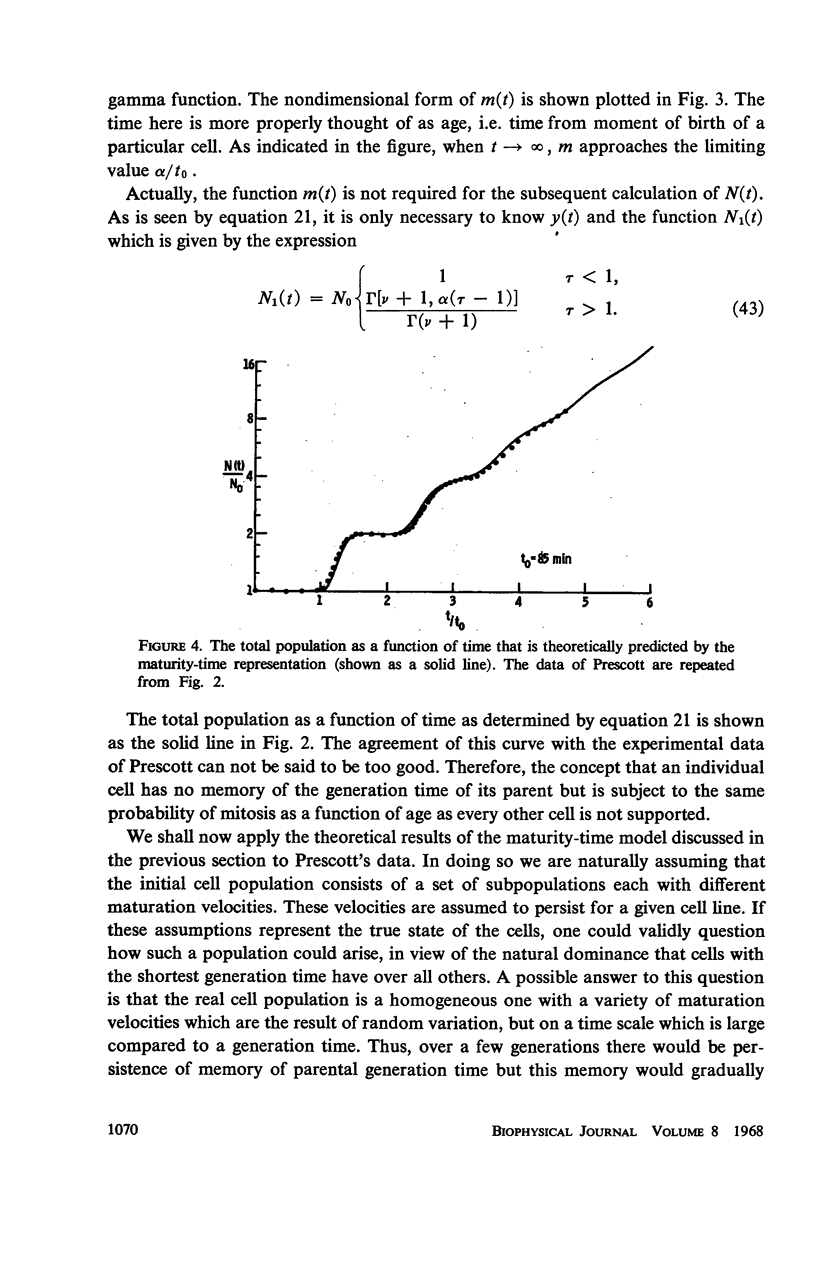
Abstract
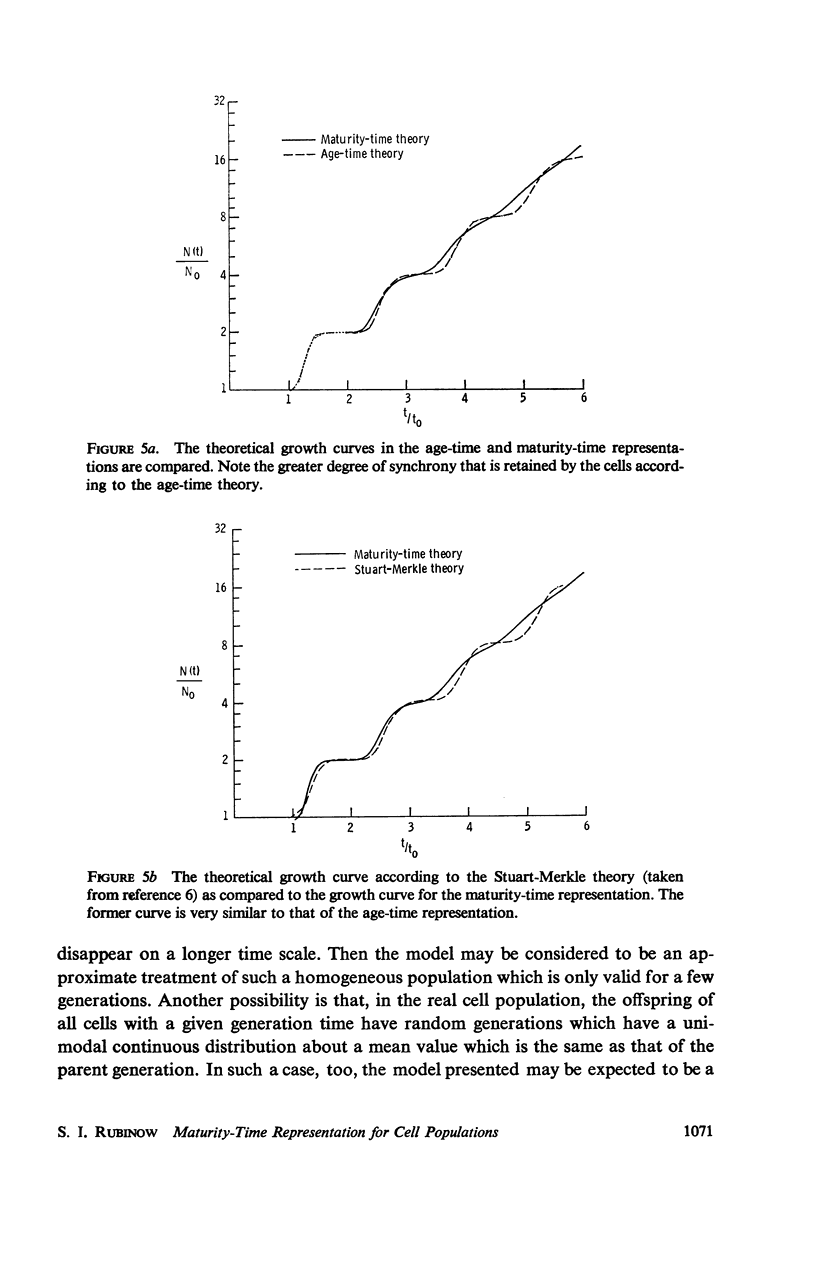
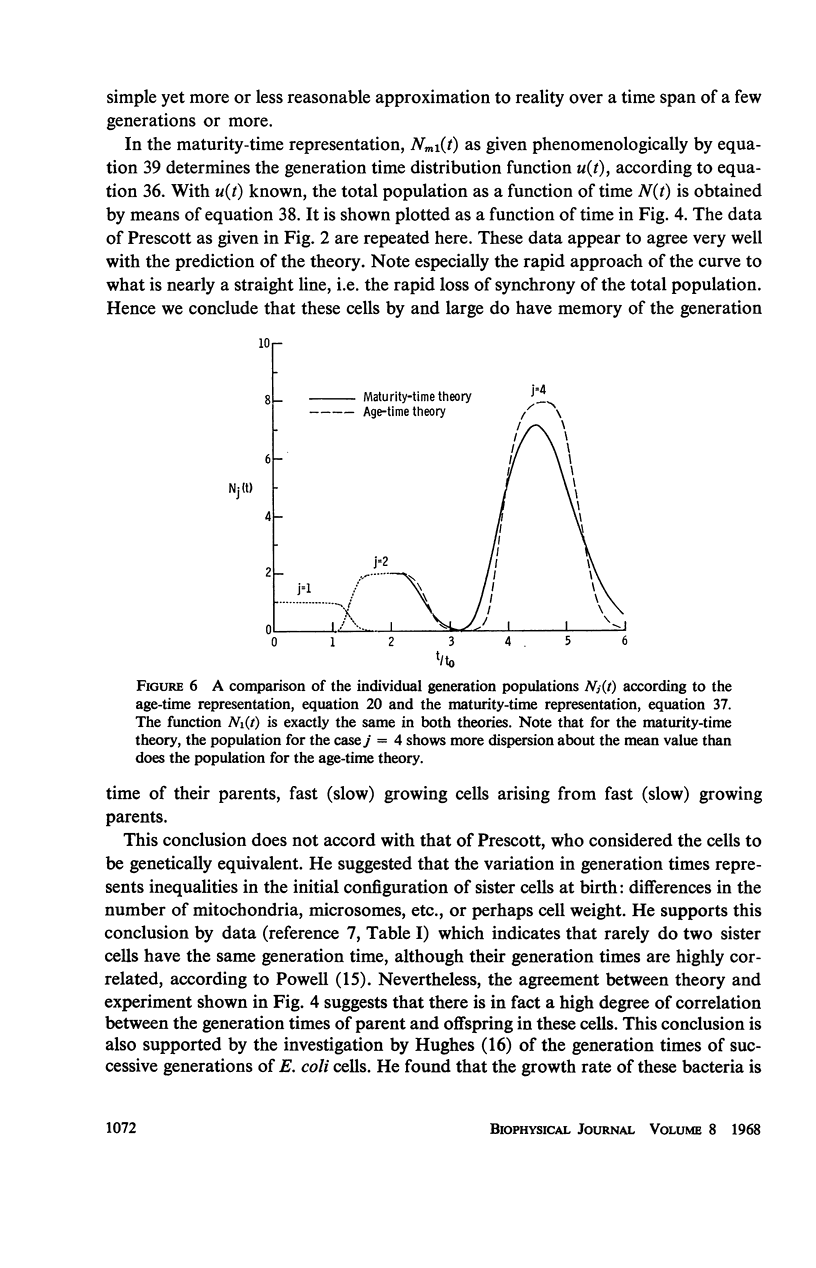
A maturity-time representation for the study of cell populations is introduced, which differs from the age-time representation suggested by von Foerster. A significant feature of the theory is the concept of maturation velocity. A solution to the fundamental equations of the theory is presented in terms of the individual generations which make up the population at any time. The problem of variability of generation time is considered from the differing viewpoints of the two representations, as well as that of an alternate theory due to Stuart and Merkle. The experimental observations of Prescott concerning the generation time distribution and population growth of Tetrahymena geleii HS cells appear to support best the theoretical formulation of the maturity-time representation. In particular, they suggest that memory of the maturation velocity or generation time of a given cell tends to persist from parent to daughter for several generations at least.
Full text
PDF












Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Barrett J. C. A mathematical model of the mitotic cycle and its application to the interpretation of percentage labeled mitoses data. J Natl Cancer Inst. 1966 Oct;37(4):443–450. [PubMed] [Google Scholar]
- Bell G. I., Anderson E. C. Cell growth and division. I. A mathematical model with applications to cell volume distributions in mammalian suspension cultures. Biophys J. 1967 Jul;7(4):329–351. doi: 10.1016/S0006-3495(67)86592-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HUGHES W. H. The inheritance of differences in growth rate in Escherichia coli. J Gen Microbiol. 1955 Apr;12(2):265–268. doi: 10.1099/00221287-12-2-265. [DOI] [PubMed] [Google Scholar]
- Lipkin M., Deschner E. Comparative analysis of cell renewal in the gastrointestinal tract of newborn hamster. Exp Cell Res. 1968 Jan;49(1):1–12. doi: 10.1016/0014-4827(68)90513-2. [DOI] [PubMed] [Google Scholar]
- Nooney G. C. Age distributions in dividing populations. Biophys J. 2008 Dec 31;7(1):69–76. doi: 10.1016/S0006-3495(67)86575-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- POWELL E. O. An outline of the pattern of bacterial generation times. J Gen Microbiol. 1958 Apr;18(2):382–417. doi: 10.1099/00221287-18-2-382. [DOI] [PubMed] [Google Scholar]
- PRESCOTT D. M. Variations in the individual generation times of Tetrahymena geleii HS. Exp Cell Res. 1959 Feb;16(2):279–284. doi: 10.1016/0014-4827(59)90255-1. [DOI] [PubMed] [Google Scholar]
- SCHERBAUM O., RASCH G. Cell size distribution and single cell growth in Tetrahymena pyriformis GL. Acta Pathol Microbiol Scand. 1957;41(3):161–182. doi: 10.1111/j.1699-0463.1957.tb01014.x. [DOI] [PubMed] [Google Scholar]
- Trucco E. Mathematical models for cellular systems the Von Foerster equation. I. Bull Math Biophys. 1965 Sep;27(3):285–304. doi: 10.1007/BF02478406. [DOI] [PubMed] [Google Scholar]
- Trucco E. Mathematical models for cellular systems. The Von Foerster equation. II. Bull Math Biophys. 1965 Dec;27(4):449–471. doi: 10.1007/BF02476849. [DOI] [PubMed] [Google Scholar]


