Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1968 Nov;8(11):1353–1398. doi: 10.1016/S0006-3495(68)86561-0

The Stochastic Theory of Cell Proliferation

Burt V Bronk, G J Dienes, Arthur Paskin
PMCID: PMC1367700  PMID: 5696217

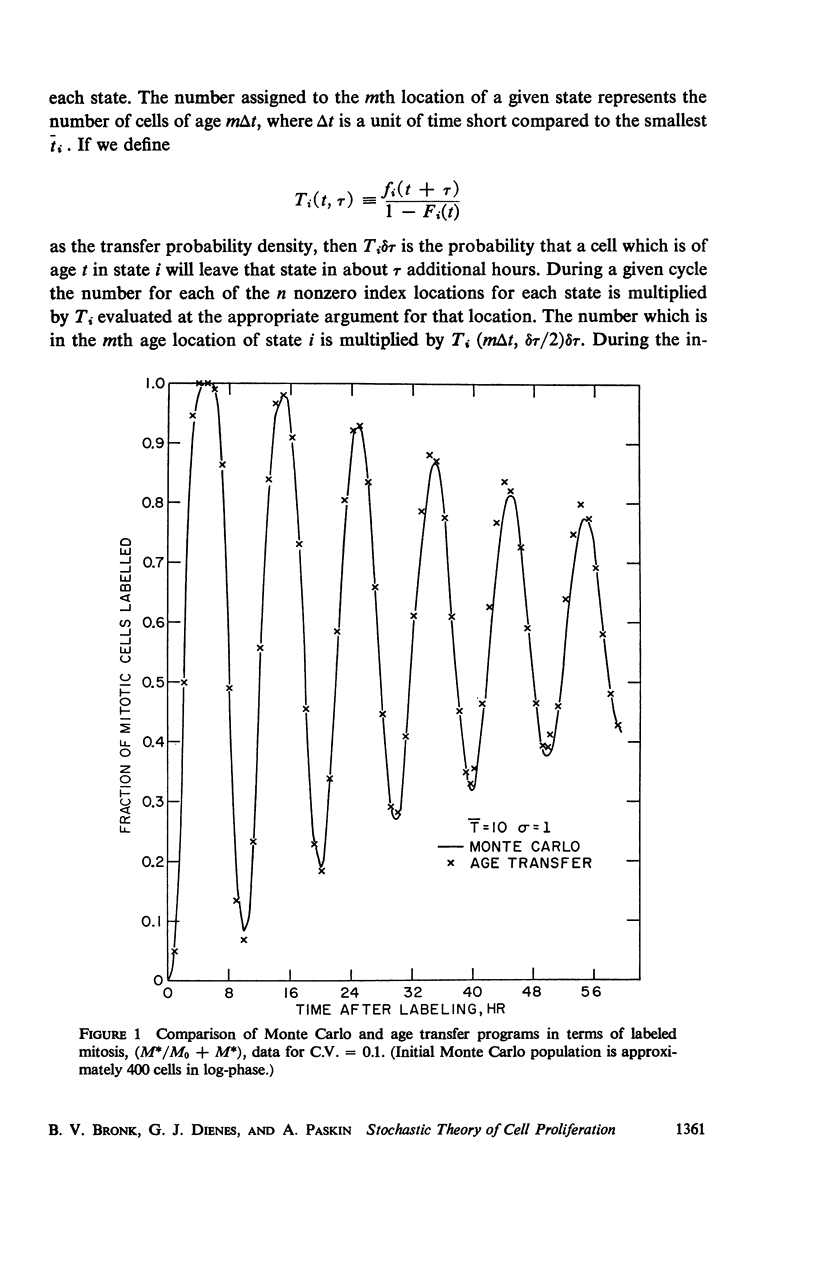
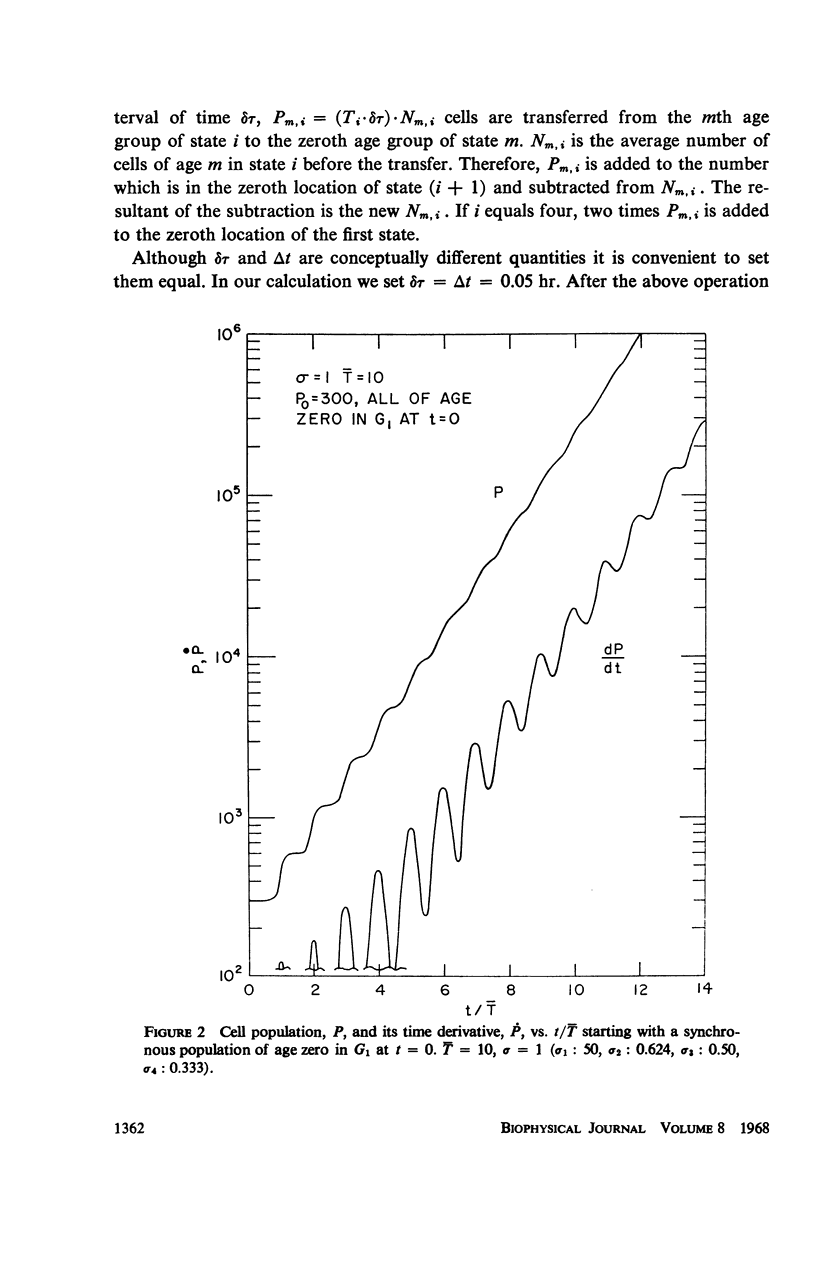
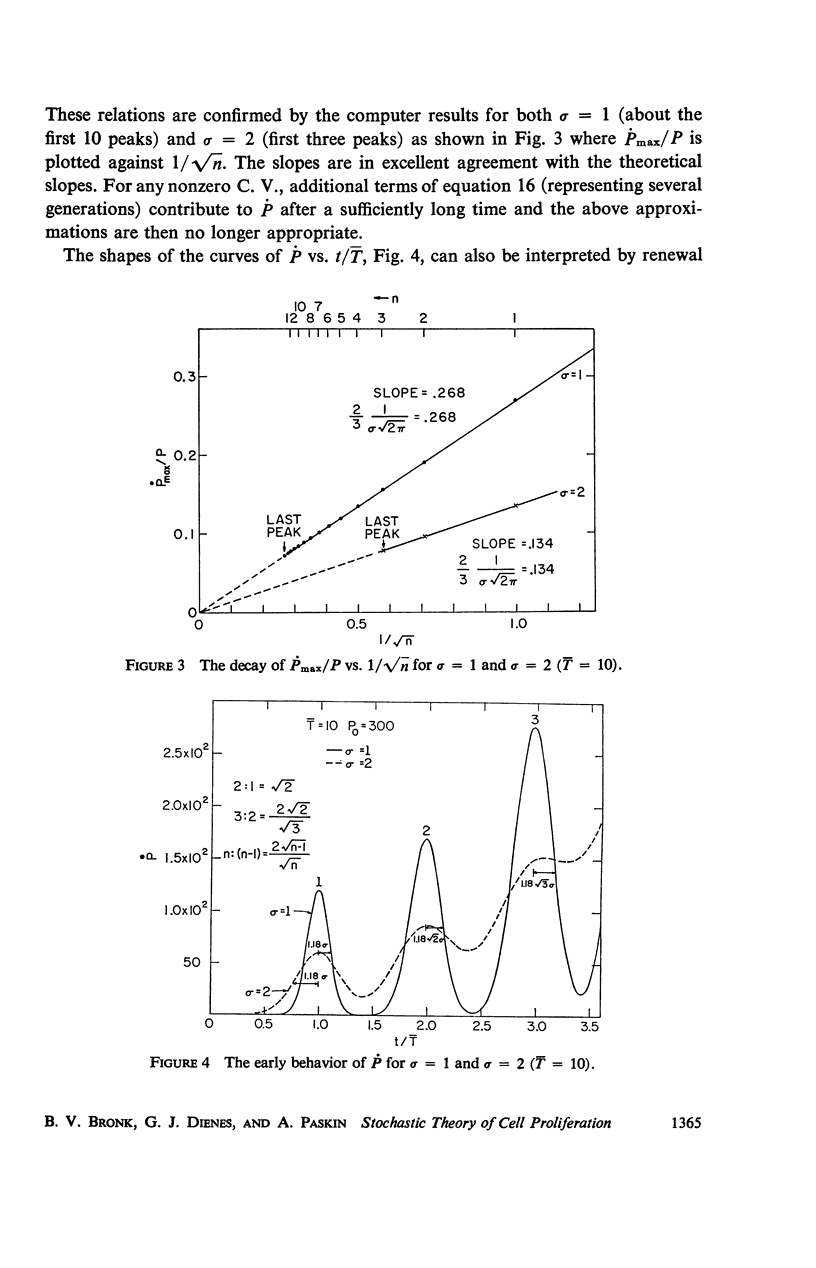
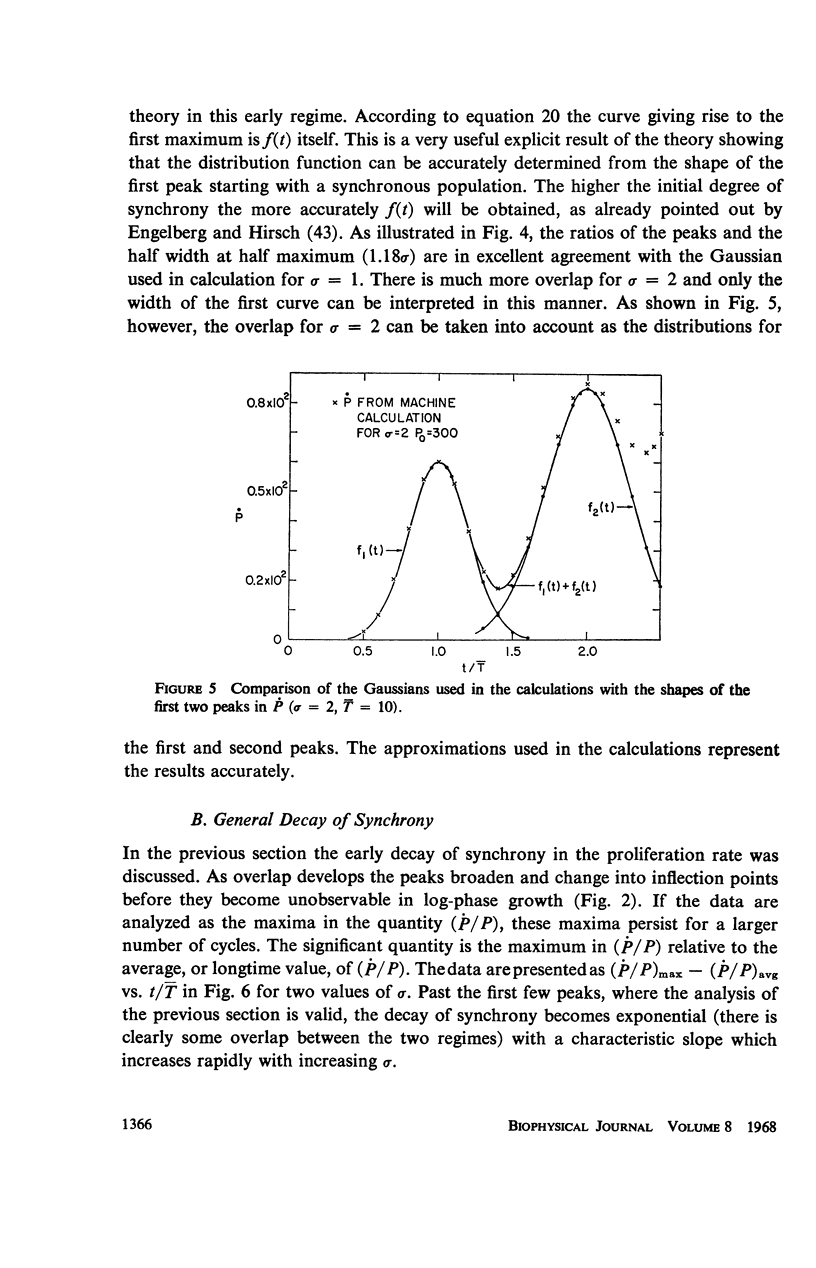
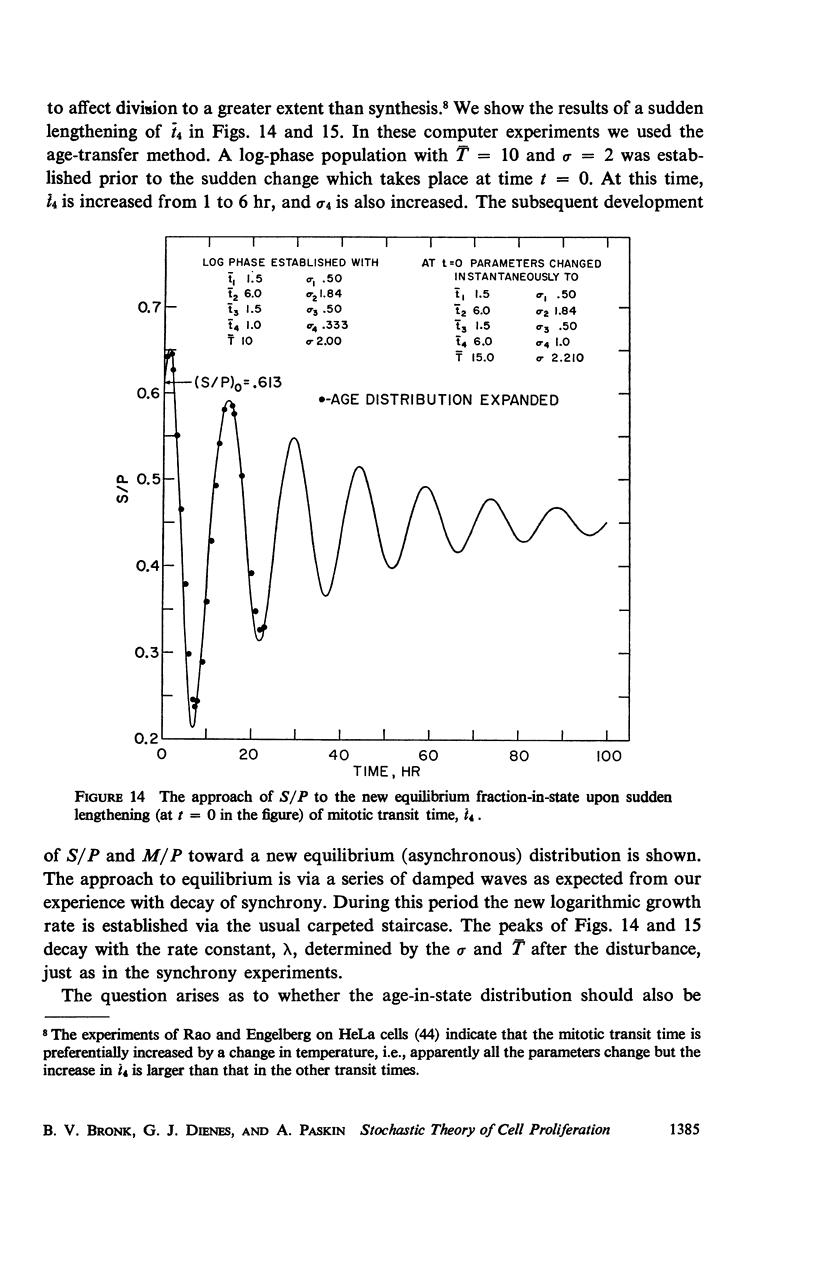
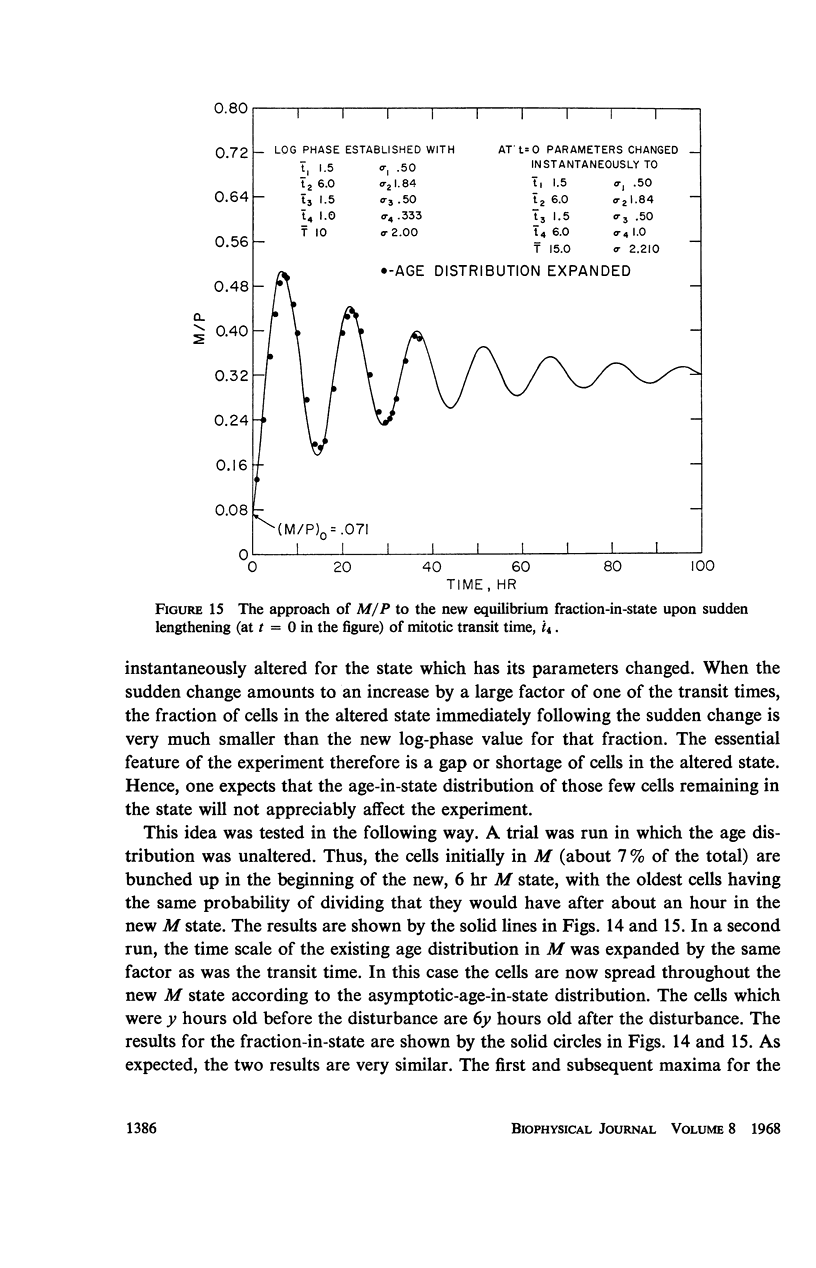
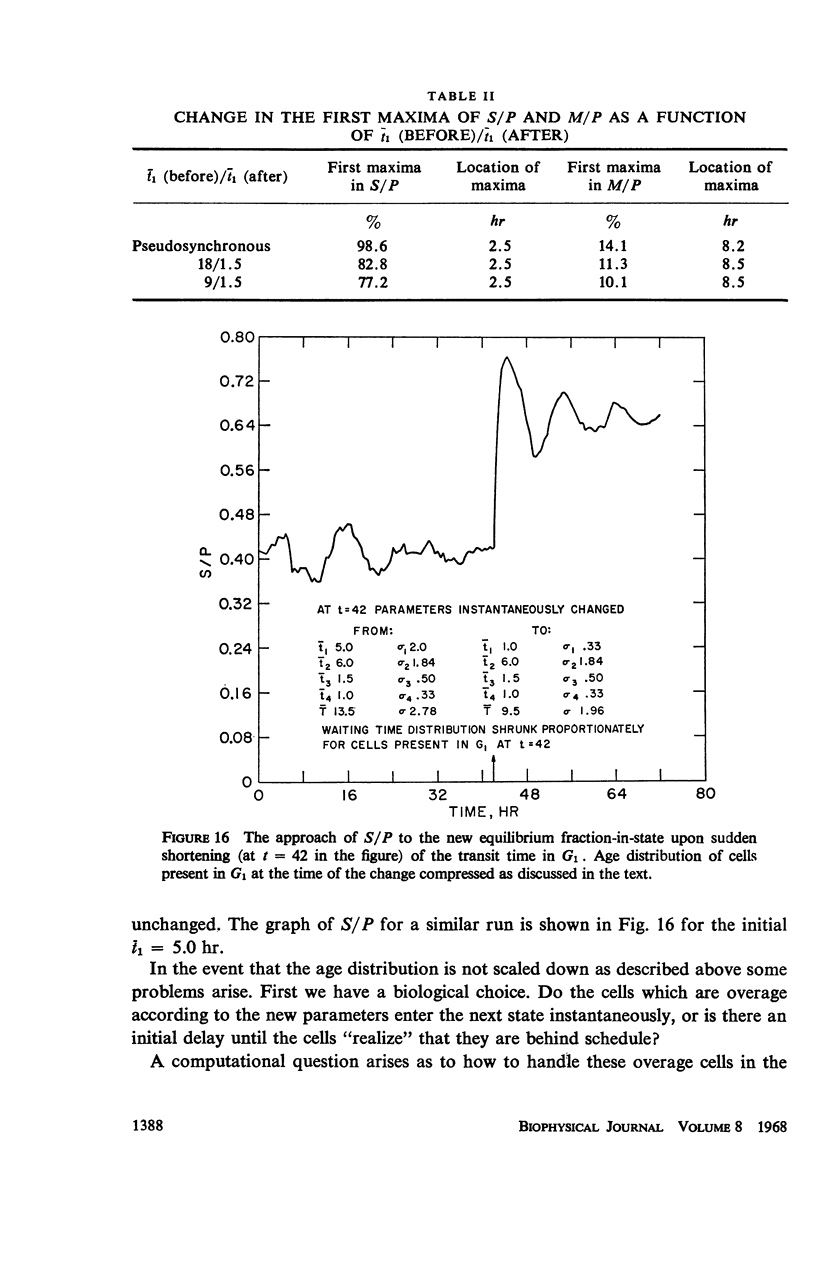
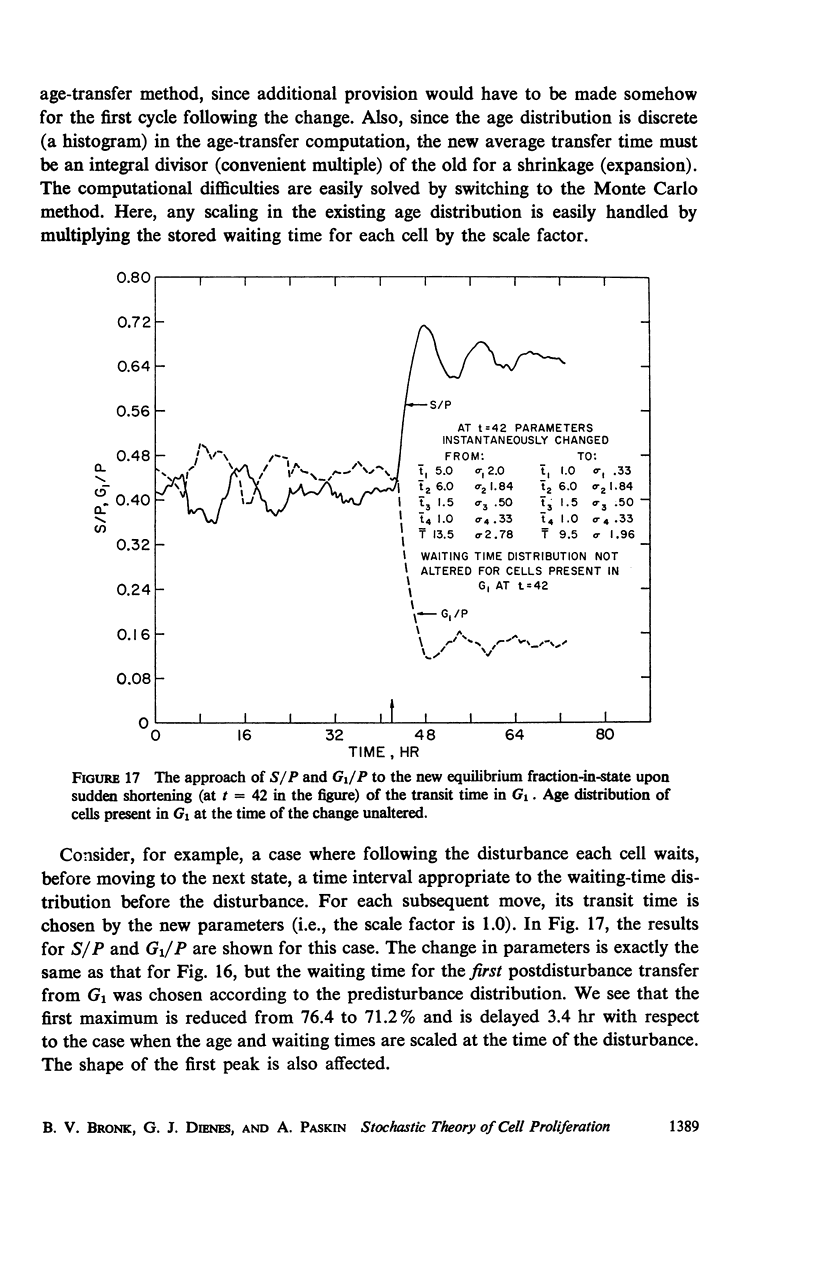
Abstract

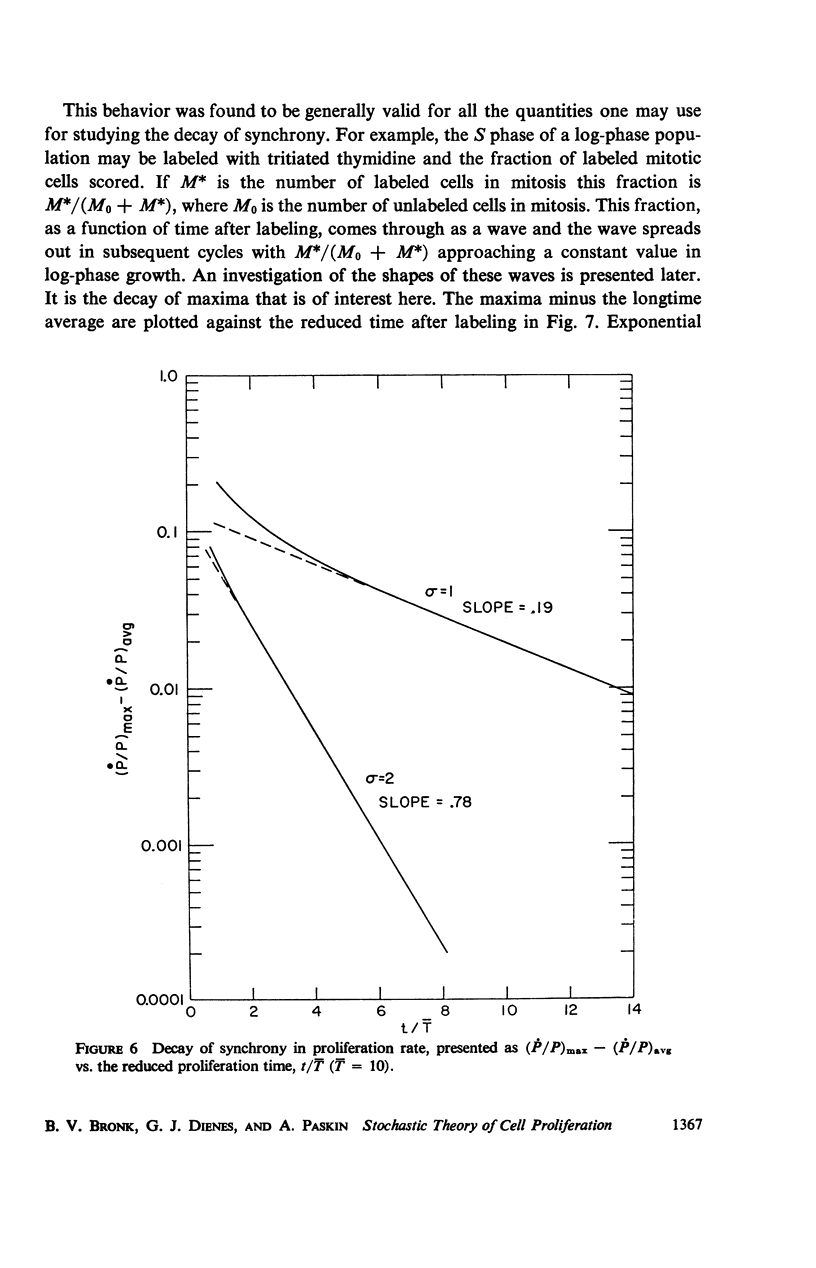
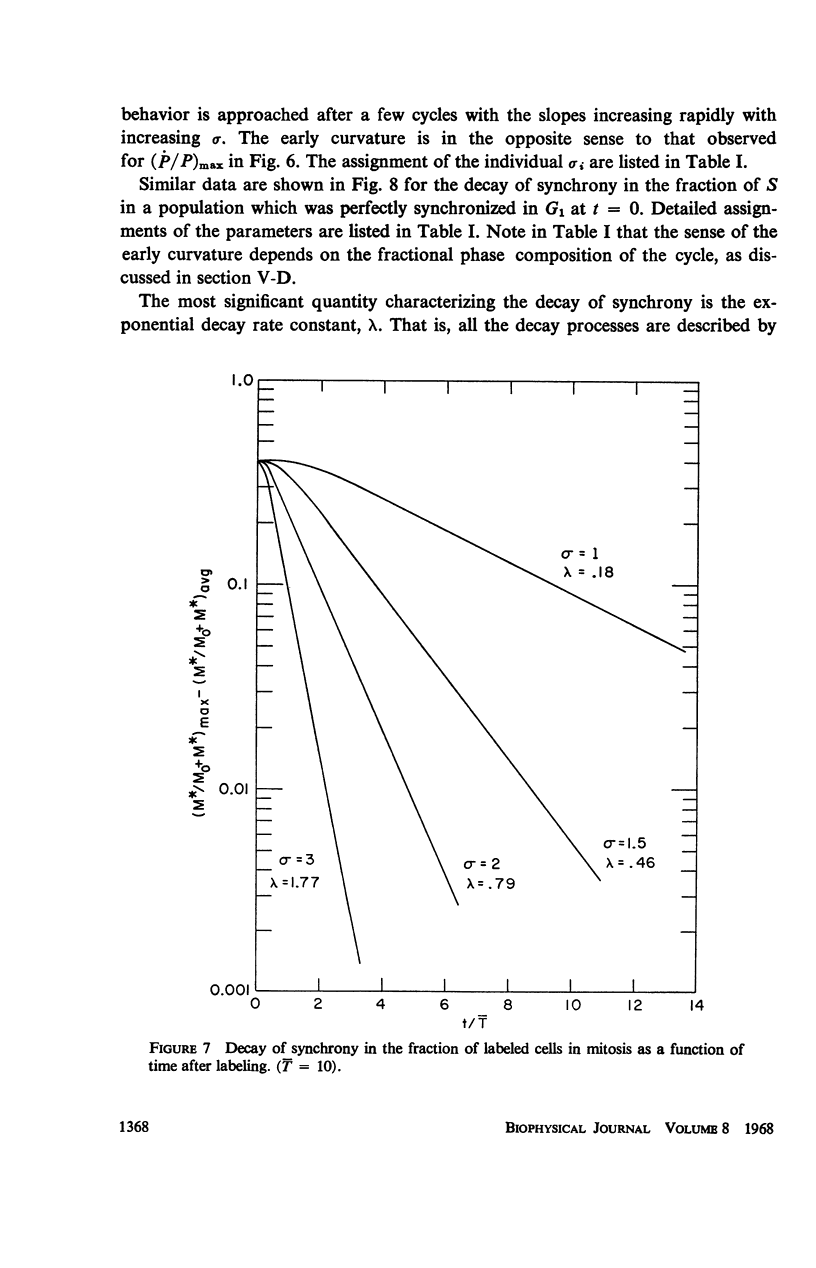
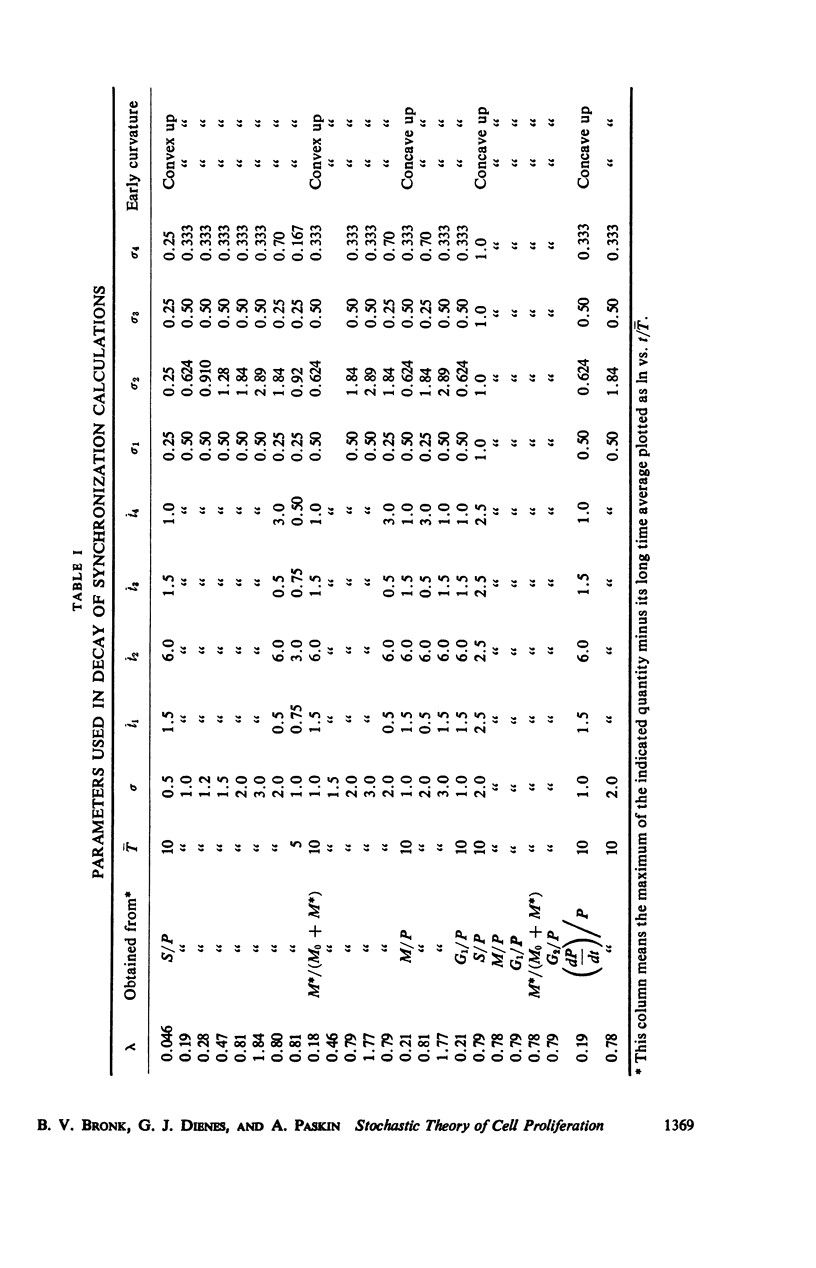
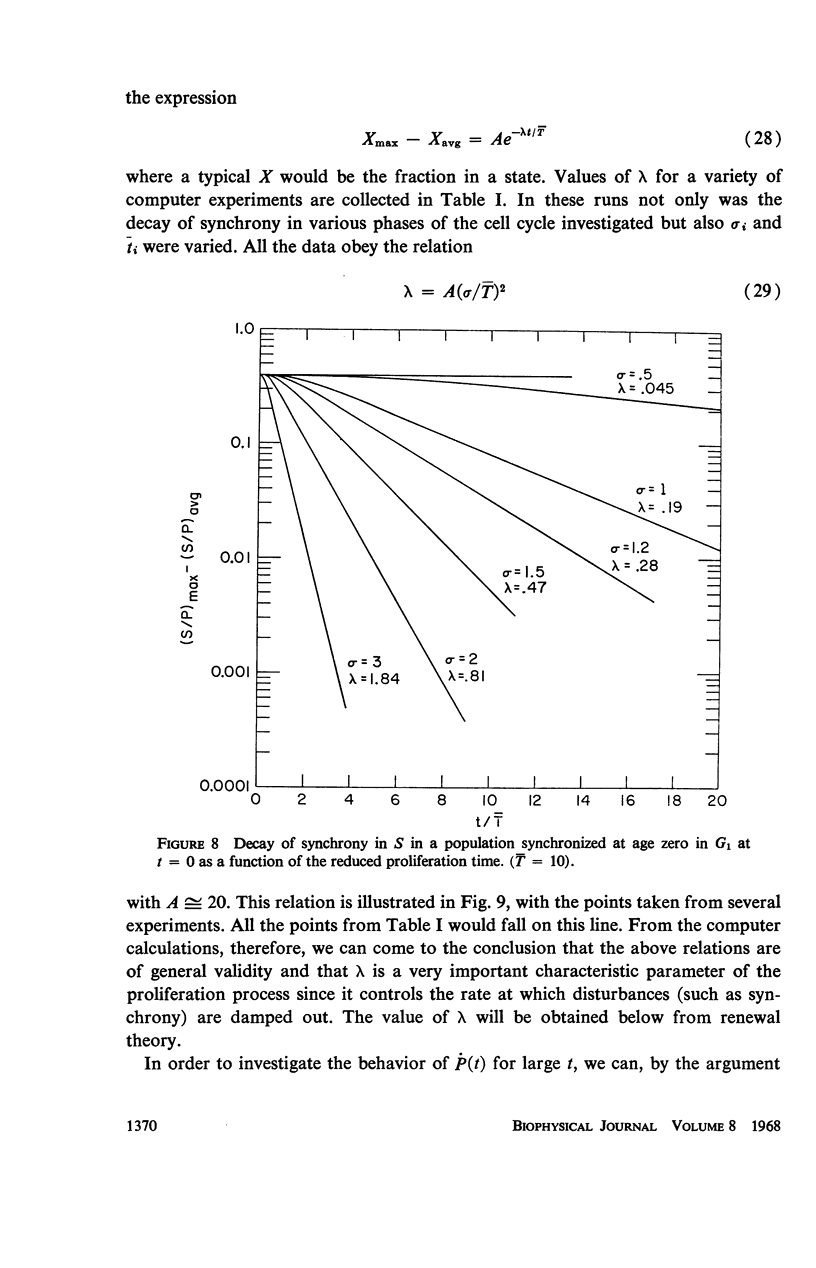
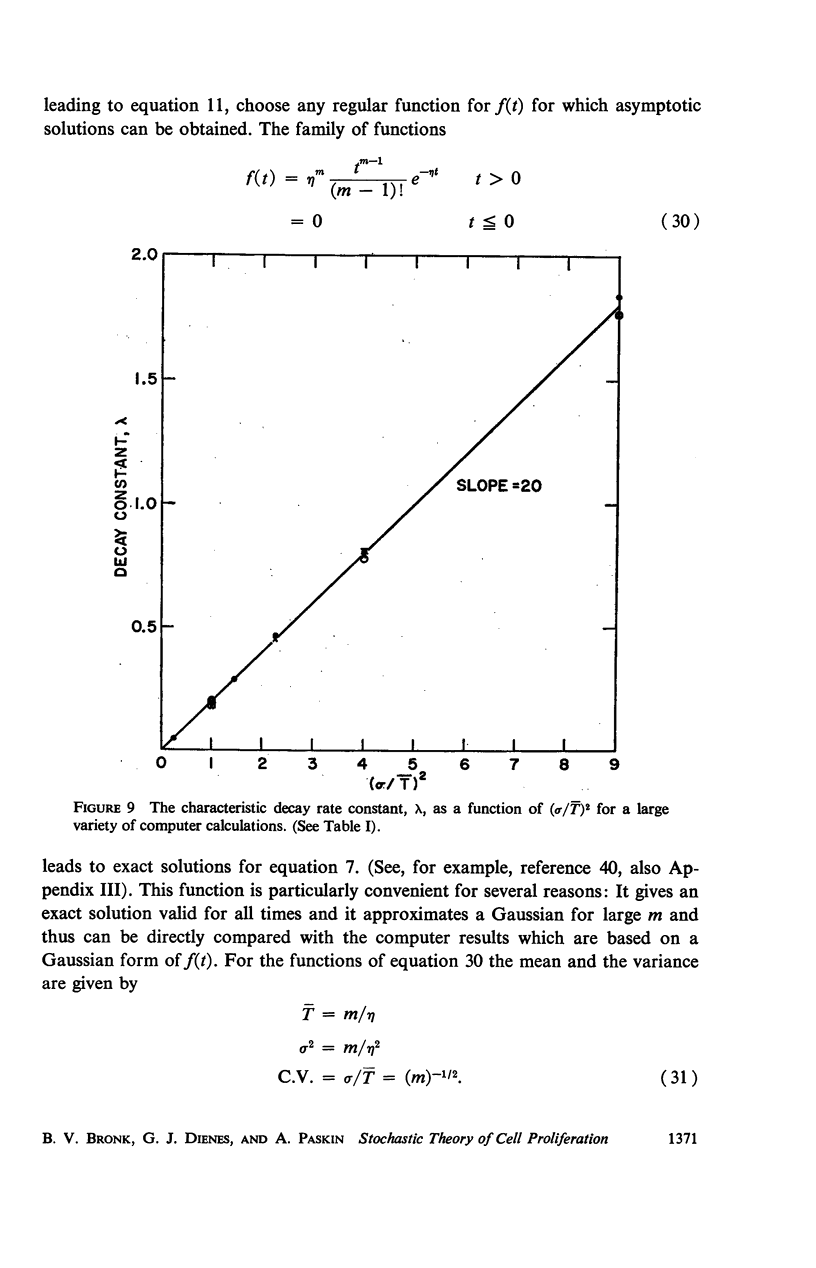
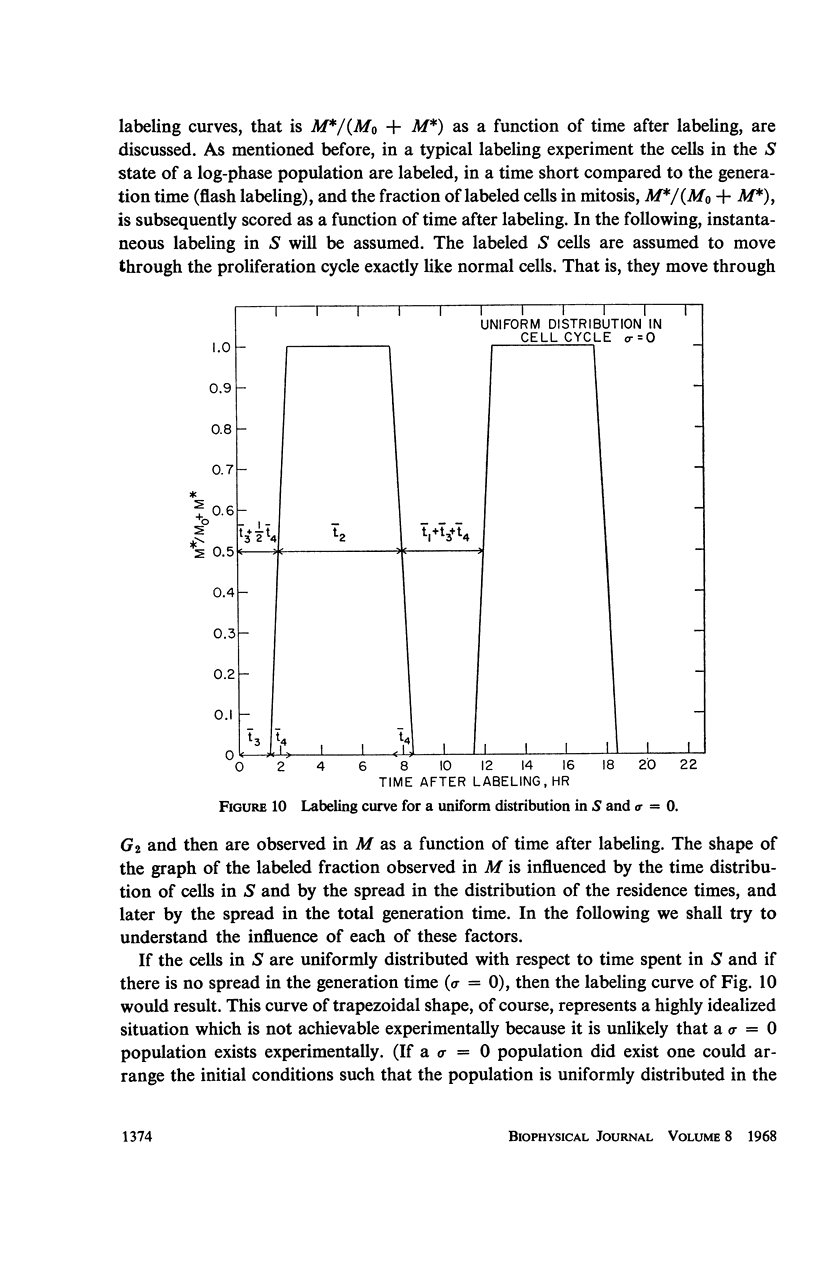
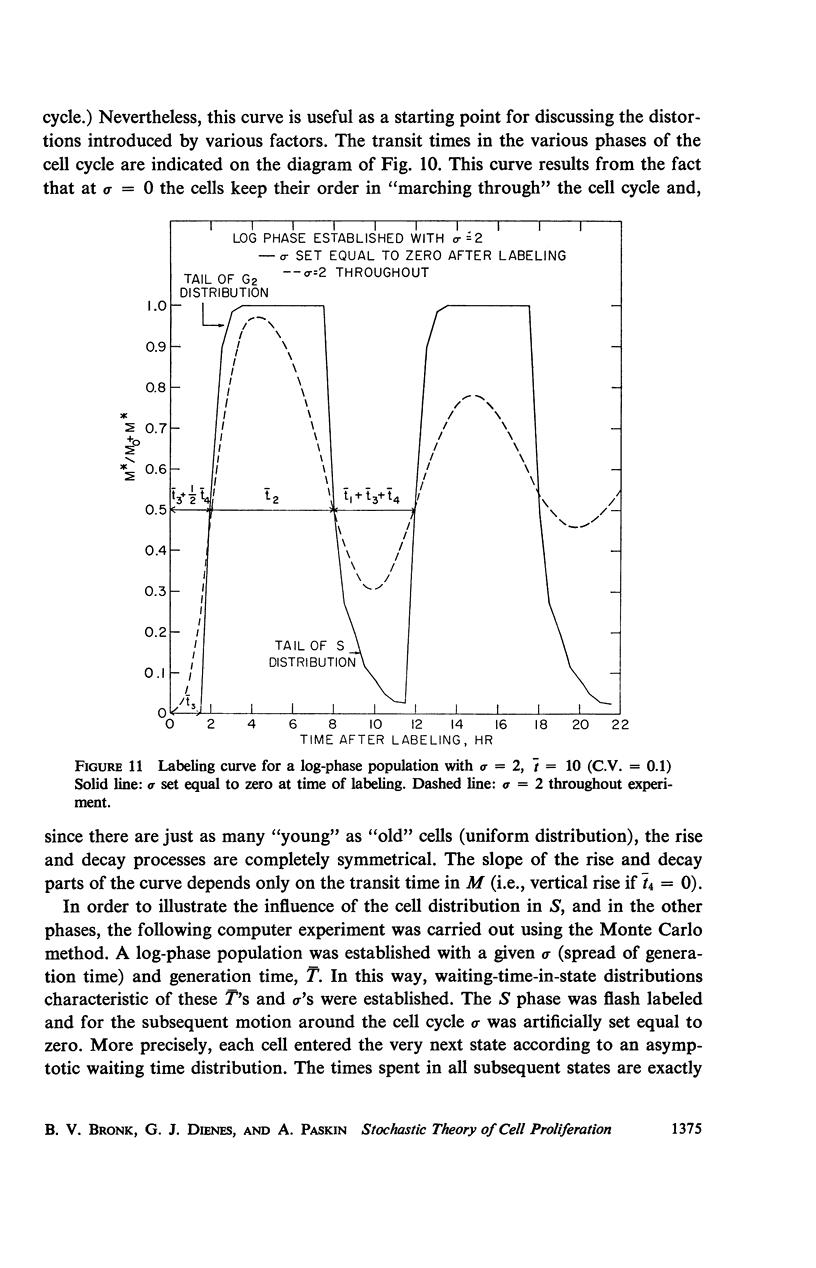
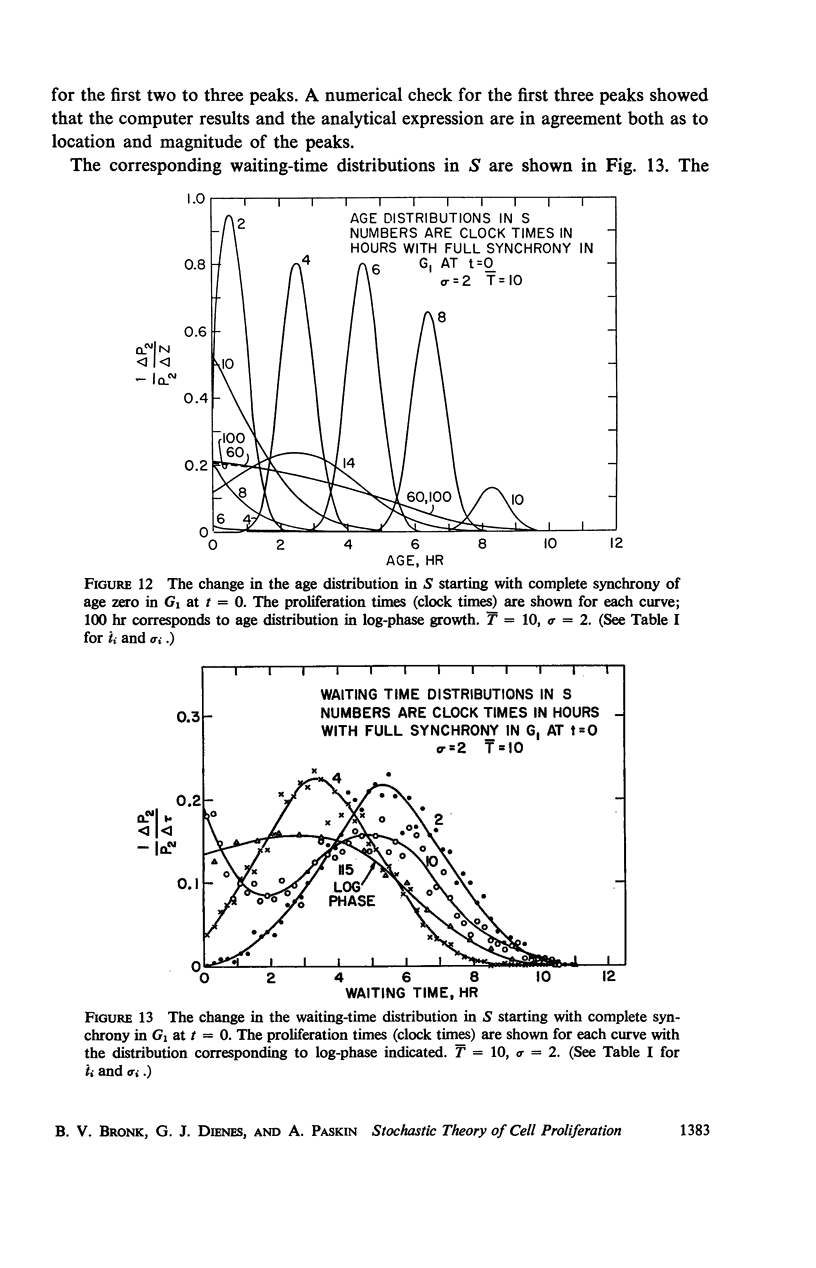
A stochastic theory of cell kinetics has been developed based on a realistic model of cell proliferation. A characteristic transit time, t̄i, has been assigned to each of the four states (G1, S, G2, M) of the cell cycle. The actual transit time, ti, for any cell is represented by a distribution around t̄i with a variance σi2. Analytic and computer formulations have been used to describe the time development of such characteristics as age distribution, labeling experiments, and response to perturbations of the system by, for example, irradiation and temperature. The decay of synchrony is analyzed in detail and is shown to proceed as a damped wave. From the first few peaks of the synchrony decay one can obtain the distribution function for the cell cycle time. The later peaks decay exponentially with a characteristic decay constant, λ, which depends only on the average cell-cycle time, T̄, and the associated variance. It is shown that the system, upon any sudden disturbance, approaches new “equilibrium” proliferation characteristics via damped periodic transients, the damping being characterized by λ. Thus, the response time of the system, T̄/λ, is as basic a parameter of the system as the cell-cycle time.

Full text

PDF
1357

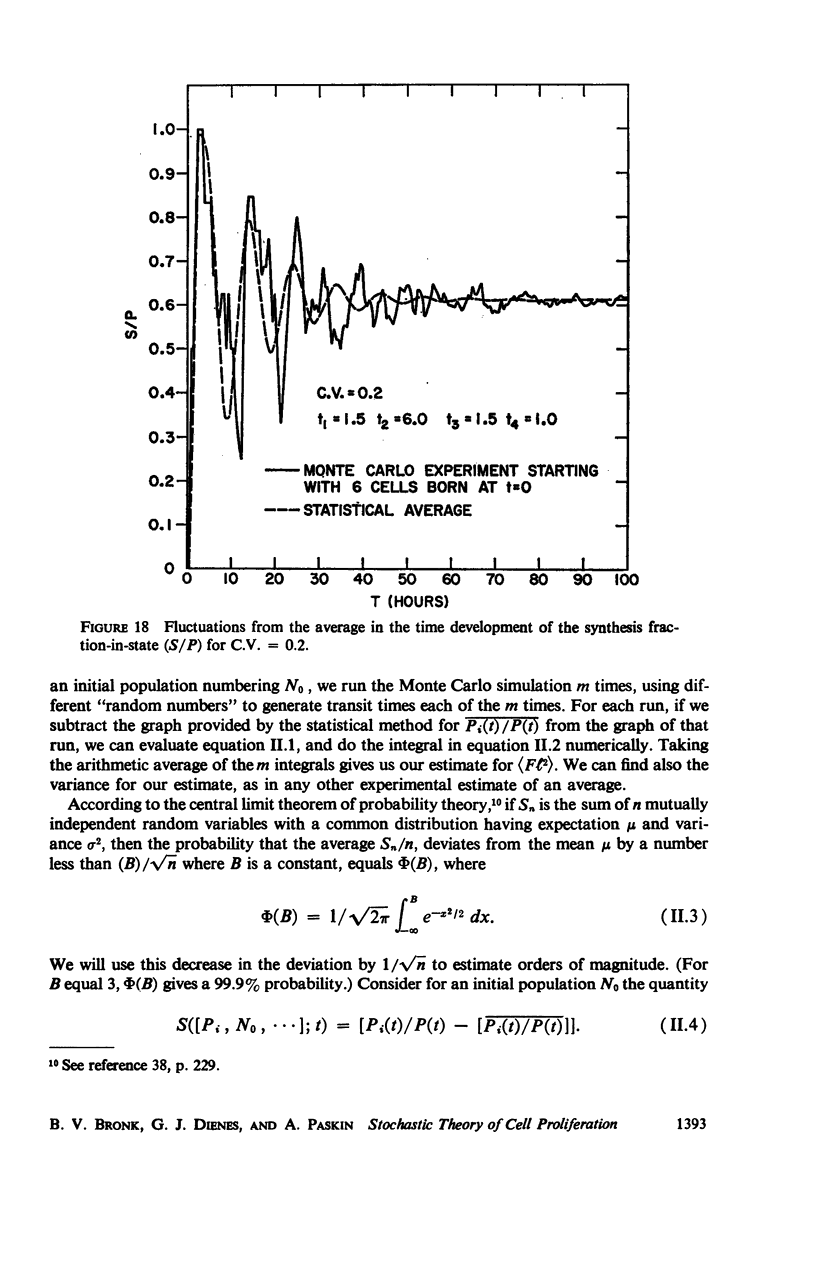
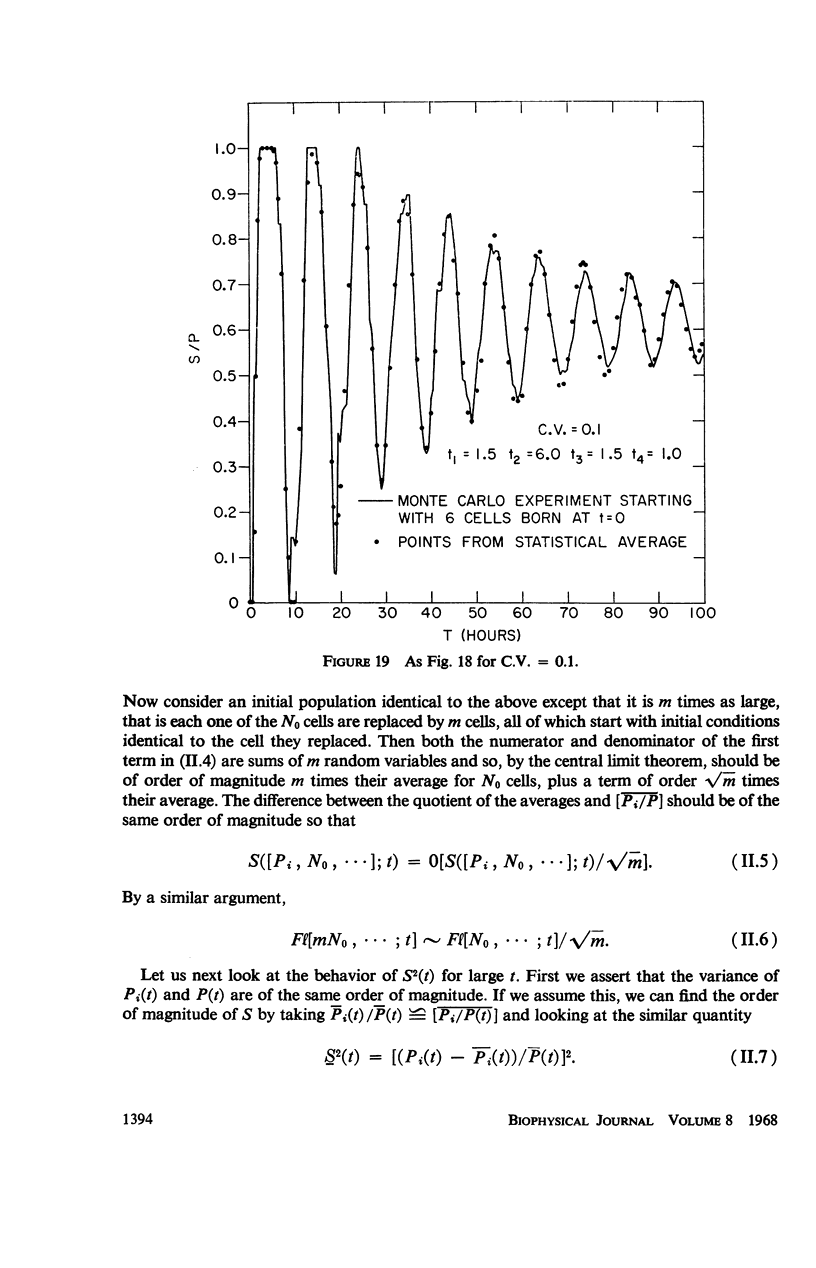
Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Barrett J. C. A mathematical model of the mitotic cycle and its application to the interpretation of percentage labeled mitoses data. J Natl Cancer Inst. 1966 Oct;37(4):443–450. [PubMed] [Google Scholar]
  2. Bellman R., Harris T. E. On the Theory of Age-Dependent Stochastic Branching Processes. Proc Natl Acad Sci U S A. 1948 Dec;34(12):601–604. doi: 10.1073/pnas.34.12.601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. DAWSON K. B., MADOC-JONES H., FIELD E. O. VARIATIONS IN THE GENERATION TIMES OF A STRAIN OF RAT SARCOMA CELLS IN CULTURE. Exp Cell Res. 1965 Apr;38:75–84. doi: 10.1016/0014-4827(65)90429-5. [DOI] [PubMed] [Google Scholar]
  4. ENGELBERG J. THE DECAY OF SYNCHRONIZATION OF CELL DIVISION. Exp Cell Res. 1964 Dec;36:647–662. doi: 10.1016/0014-4827(64)90320-9. [DOI] [PubMed] [Google Scholar]
  5. GARDINER V., HOFFMAN J. G., METROPOLIS N. Digital computer studies of cell multiplication by Monte Carlo methods. J Natl Cancer Inst. 1956 Aug;17(2):175–188. [PubMed] [Google Scholar]
  6. Hahn G. M. State vector description of the proliferation of mammalian cells in tissue culture. I. Exponential growth. Biophys J. 1966 May;6(3):275–290. doi: 10.1016/S0006-3495(66)86656-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hirsch H. R., Engelberg J. An analog of cell-culture growth. J Theor Biol. 1965 Sep;9(2):303–312. doi: 10.1016/0022-5193(65)90115-3. [DOI] [PubMed] [Google Scholar]
  8. Hirsch H. R., Engelberg J. Decay of cell synchronization: solutions of the cell-growth equation. Bull Math Biophys. 1966 Sep;28(3):391–409. doi: 10.1007/BF02476821. [DOI] [PubMed] [Google Scholar]
  9. Hirsch H. R., Engelberg J. Determination of the cell doubling-time distribution from culture growth-rate data. J Theor Biol. 1965 Sep;9(2):297–302. doi: 10.1016/0022-5193(65)90114-1. [DOI] [PubMed] [Google Scholar]
  10. Hughes W. L., Bond V. P., Brecher G., Cronkite E. P., Painter R. B., Quastler H., Sherman F. G. CELLULAR PROLIFERATION IN THE MOUSE AS REVEALED BY AUTORADIOGRAPHY WITH TRITIATED THYMIDINE. Proc Natl Acad Sci U S A. 1958 May;44(5):476–483. doi: 10.1073/pnas.44.5.476. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. KUBITSCHEK H. E. Normal distribution of cell generation rate. Exp Cell Res. 1962 Mar;26:439–450. doi: 10.1016/0014-4827(62)90150-7. [DOI] [PubMed] [Google Scholar]
  12. Lotka A. J. RELATION BETWEEN BIRTH RATES AND DEATH RATES. Science. 1907 Jul 5;26(653):21–22. doi: 10.1126/science.26.653.21-a. [DOI] [PubMed] [Google Scholar]
  13. PUCK T. T., STEFFEN J. LIFE CYCLE ANALYSIS OF MAMMALIAN CELLS. I. A METHOD FOR LOCALIZING METABOLIC EVENTS WITHIN THE LIFE CYCLE, AND ITS APPLICATION TO THE ACTION OF COLCEMIDE AND SUBLETHAL DOSES OF X-IRRADIATION. Biophys J. 1963 Sep;3:379–397. doi: 10.1016/s0006-3495(63)86828-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. QUASTLER H. Cell population kinetics. Ann N Y Acad Sci. 1960 Oct 7;90:580–591. doi: 10.1111/j.1749-6632.1960.tb23274.x. [DOI] [PubMed] [Google Scholar]
  15. QUASTLER H., SHERMAN F. G. Cell population kinetics in the intestinal epithelium of the mouse. Exp Cell Res. 1959 Jun;17(3):420–438. doi: 10.1016/0014-4827(59)90063-1. [DOI] [PubMed] [Google Scholar]
  16. SINCLAIR W. K., MORTON R. A. RECOVERY FOLLOWING X-IRRADIATION OF SYNCHRONIZED CHINESE HAMSTER CELLS. Nature. 1964 Jul 18;203:247–250. doi: 10.1038/203247a0. [DOI] [PubMed] [Google Scholar]
  17. Trucco E. Mathematical models for cellular systems. The Von Foerster equation. II. Bull Math Biophys. 1965 Dec;27(4):449–471. doi: 10.1007/BF02476849. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES