On the simulation of protein folding by short time scale molecular dynamics and distributed computing

Abstract

There are proposals to overcome the current incompatibilities between the time scales of protein folding and molecular dynamics simulation by using a large number of short simulations of only tens of nanoseconds (distributed computing). According to the principles of first-order kinetic processes, a sufficiently large number of short simulations will include, de facto, a small number of long time scale events that have proceeded to completion. But protein folding is not an elementary kinetic step: folding has a series of early conformational steps that lead to lag phases at the beginning of the kinetics. The presence of these lag phases can bias short simulations toward selecting minor pathways that have fewer or faster lag steps and so miss the major folding pathways. Attempts to circumvent the lags by using loosely coupled parallel simulations that search for first-order transitions are also problematic because of the difficulty of detecting transitions in molecular dynamics simulations. Nevertheless, the procedure of using parallel independent simulations is perfectly valid and quite feasible once the time scale of simulation proceeds past the lag phases into a single exponential region.

Theoreticians and experimentalists are now combining forces to describe and predict the pathways of folding and unfolding of proteins (1). Simulation methods place varying demands on computer time. With present technology, theoreticians use simplified models to probe general principles and derive specific details rapidly. At the extreme of resolution, molecular dynamics (MD) simulation of proteins has the potential of predicting the complete pathways of folding and unfolding at atomic resolution. But there is an incompatibility between the time scales accessible to MD simulation, currently of the order of a microsecond for a very small protein, and that observed for folding, which is generally in the upper end of the range of tens to hundreds of thousands of microseconds. However, the pathways of unfolding of several proteins have now been solved with ever-increasing confidence at atomic resolution, thanks to combining simulation with near-atomic level experimental information (reviewed in ref 1). Φ value analysis of transition states and NMR studies of denatured states provide the high-resolution experimental descriptions that are used to benchmark MD simulations, which in turn flesh out the structures and fill in the rest of the folding events. MD simulations of protein unfolding are currently feasible, because the rate of protein unfolding increases with increasing temperature to the nanosecond to tens of nanoseconds time scales that are currently easily accessible to simulation. Also, unfolding starts from the best-defined state on the reaction pathway, the native state. Protein folding, on the other hand, is initiated from the least-defined state in solution, the denatured state, and the rate of protein folding follows a bell-shaped curve with temperature, often peaking at just above body temperature. The first simulations of unfolding were performed at some 200–300°C (2–4) but nevertheless gave results that are consistent with experimental data at 25–50°C (5–8). Recently, experimentalists have sought to bridge the time scale gap by finding small fast folding (in microseconds) and even faster unfolding (in nanoseconds) proteins. Experiment and simulation of the unfolding of the engrailed homeodomain (En-HD) (9) and WW domains (10), for example, have been compared at accessible temperatures. Running the unfolding simulations in reverse gives the folding pathways. But even on current supercomputers, it is still not possible to simulate directly the folding of these very fast proteins.

Now theoreticians have risen to the challenge of microsecond folding by introducing a radically new approach of MD simulation that has the potential of simulating, with current computing technology, the folding of proteins that fold on the tens of microseconds time scale. Instead of attempting a single very long simulation on the tens of microseconds time scale, tens of thousands of very short simulations are performed on screen savers on personal computers throughout the world (“distributed computing”) (11–13). In essence, the philosophy behind the method is that if N₀ simulations are performed of a first-order reaction of rate constant k for a very short time period δt, where δt ≪ 1/k, then the number of simulations going to completion (δN_P) will be N₀kδt (that is, the initial rate of a first-order reaction as δt tends to 0). For example, if k = 10⁵⋅s⁻¹ and δt = 10⁻⁸⋅s⁻¹, then 10 of 10⁴ simulations should lead to complete reaction, even though each individual simulation lasts only 1/1,000th of a half life of the reaction. This procedure is so intriguing that I present an analysis of its scope and potential problems to aid in its development and successful implementation.

True Two-State Folding?

Many small proteins do fold with apparently first-order kinetics. The first question is whether first-order kinetics extends to the very initial stages of folding. The MD procedure is initiated from the polypeptide chain being in an extended conformation (=“U”)† to avoid any bias. In contrast, rapid relaxation kinetics experiments (see, e.g., ref. 9) measure the transition between the denatured state that exists in solution under folding or physiological conditions (D) and the native (N) and any intermediate state (I). D is not an extended polypeptide chain but an equilibrium ensemble of structures with varying degrees of native and nonnative interactions (see, for example, refs. 7 and 8). I is also an ensemble. There is thus an initial energetically downhill progress from the hypothetical extended form U to the denatured state ensemble, D. The folding of the polypeptide chain in these simulations is not a single elementary step of a first-order process, because there is a series of initial conformational events as the chain equilibrates from U to D. These will lead to lag kinetics, with the very early stages not being on the single exponential curve that can be observed experimentally for D to N. First, I deal with the simplest case and then give a more general example.

Very Rapid Transition from U to D and Rapid Equilibration Within D

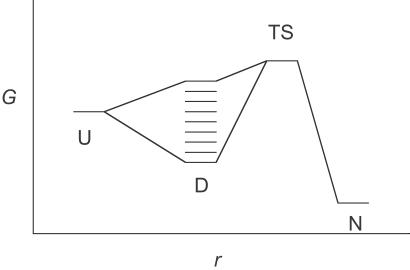
The overall folding kinetics depends on the relative rate constants for collapse, for interconversion of states in the D ensemble, and for the subsequent folding steps, as well as the energetic distribution of states relative to U. One limiting scenario, which is the simplest to analyze, is illustrated in Fig. 1: the collapse is very fast relative to the time scale of experimental observation, and the structures interconvert far more rapidly than they form the native state N. Even though each of the states in D folds with a different first-order rate constant, N is formed according to a single exponential step if there is a common transition state ensemble (see ref. 14 for a rigorous analysis). Suppose the most stable state of the D ensemble, D₀, has a free energy G_D,0, the transition state (average) G_TS, and the extended state G_U. The rate constant for the formation of N from the lowest energy state of I is of the form:

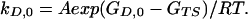Similarly, the rate constant for state D_i that is ΔG_i higher in energy is given by:

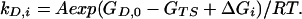In terms of flux (the number of molecules folding via each state in D), the higher rate constant of each state k_D,i is exactly counterbalanced by its lower occupancy, which is proportional to exp(−ΔG_i)/RT, according to a Boltzmann distribution. Thus the same flux, F, passes through each state in D, and is given by:

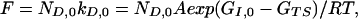where N_D,0 is the number of molecules in the lowest energy state of D. If there are n states in the D ensemble and the total number of molecules is N₀, then the apparent first-order rate constant for folding is given by:

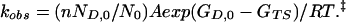Fig 1.

Energy diagram for folding where the denatured state ensemble, D, is formed and equilibrates very rapidly compared with the D to N rate constant.

That each state in the D ensemble contributes the same flux has important consequences for comparing short simulations with experiment, because the equal contribution of each pathway holds throughout the whole folding time course. Suppose that the period of simulation is long with respect to the time of the U to D transition, and that it can sample the initial rates of the D to N transition for a period δt. During δt, a higher energy state D_i folds with a rate constant that, as given by Eq. 2, is higher than for D₀ by a factor of exp(ΔG/RT). Again, the higher rate constant is counterbalanced exactly by the lower occupancy of state D_i, and so the same number of molecules folds via D_i as it does through D₀. Thus, under the special conditions of very rapid formation and equilibration of D compared with the sampling time, short time scale simulations provide a representative sampling of the pathways of folding.

Competing Pathways

Small peptides fold on a time scale of tens of nanoseconds to a microsecond (15), which is highly compatible with the current sampling times of distributed computing. The secondary structural elements in real proteins also fold in this time regime (15), which causes problems because a series of consecutive reactions can generate substantial lag times in the formation of products although each step may be fast. Consider a reaction passing through a series of states as it proceeds to products (Eq. 5).

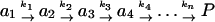If there are n steps, then n relaxation times are observed. The equations cannot be easily solved for more than two steps when each step is reversible, but the solutions are simple when the steps are irreversible.

For a single-step reaction (where P = a₂ in Eq. 5), the analytical solution is

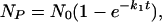where N is either the number of molecules or of simulations. The number of molecules (complete simulations), δN_P, that are produced in a very short time, δt, (≪1/k₁) at the beginning of the reaction, is found from the expansion of the exponential component to be

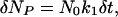which is the basis of the sampling in distributed computing an initial rate kinetics. For a two-step reaction (where P = a₃ in Eq. 5):

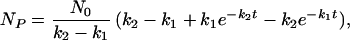which is the simplest example of lag kinetics.

The initial rate for δt ≪ 1/k₁, 1/k₂ is

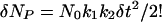In general, the initial rate for an n-step reaction is:

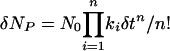Inspection of Eqs. 9 and 10 reveals how the initial rate in the lag phase is greatly attenuated when there is a series of intermediate steps prior to the last step. Note that if there are competing first-order pathways by which U can proceed directly to N, and the sum of their first-order rate constants is k_a, then the rate law for formation of N_P is

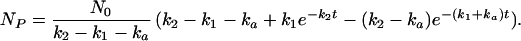The number of molecules folding by the two-step route, N_P(2-step), is

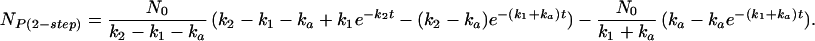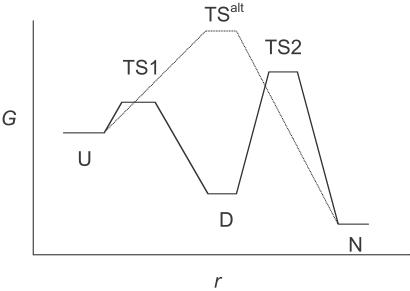
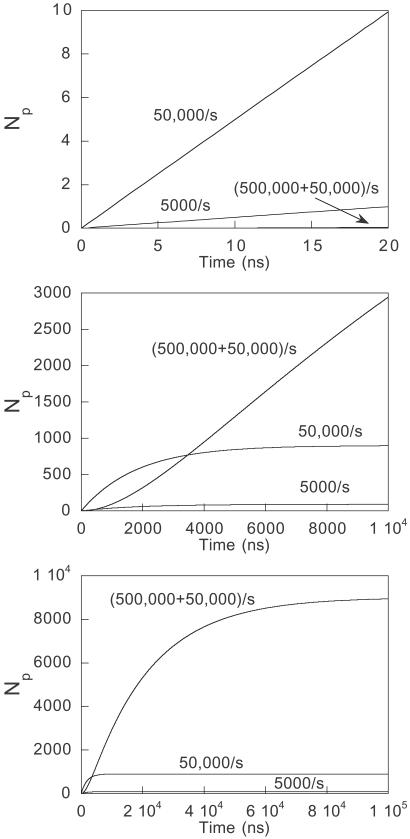
I shall illustrate the importance of lag phases in Eq. 5 by an example based on experimental data. The engrailed homeodomain folds in a two-step process, with a fast collapse at approximately 5 × 10⁵⋅s⁻¹ [an event on the time scale expected for the formation of helices, etc. (15), followed by a docking event at 50,000 s⁻¹ (ref. 9 and unpublished data)]. Other homologues of En-HD with less stable secondary structure fold according to a kinetically single step with rate constants of 5,000–50,000 s⁻¹ via different transition states (unpublished data). It is likely that the folding of En-HD will explore an energy landscape that includes all of these paths. Suppose, as in Fig. 2, En-HD folds by its major pathway from U and there are also two minor pathways that compete and fold without a prior collapse; pathway 1 at 50,000 s⁻¹ and pathway 2 at 5,000 s⁻¹. The kinetics for 10,000 simulations or molecules is plotted in Fig. 3, calculated from Eq. 6 for the minor pathways and Eq. 8 for the major in competition. After 20 ns of reaction (or simulation), 9.9 molecules have folded by minor pathway 1, 1 molecule by pathway 2, and 0.05 molecules by the major route. After 200 ns, minor pathway 1 has produced 95, pathway 2 has produced 9.5, and the major route, 4.8 folded molecules. But, at near completion at 100 μs, minor pathways 1 and 2 have produced only 901 and 90 folded molecules, respectively, whereas the major route overwhelmingly predominates with 8,942. Thus, sampling after 20 ns would have had 99.6% of the successful pathways from minor components that account for only 10% of the total molecules folded. Clearly, a series of independent short simulations over 20 ns, and even a microsecond, will miss the major pathway and pick up only the slower high-energy pathways with fewer intermediates.

Fig 2.

Illustration of a two-step folding reaction, where both rate constants are significant, and a competing one-step reaction via a different transition state.

Fig 3.

Number of molecules found to be folded by experiment at different time intervals when 10,000 molecules partition through three parallel pathways: two minor one-step pathways at 5,000 s⁻¹ and 50,000 s⁻¹, and a two-step at 5 × 10⁵⋅s⁻¹ followed by 50,000 s⁻¹, according to the mechanism in Fig. 2. Mechanisms other than those in Fig. 2 can produce progress curves with early bursts that have a different initial pathway distribution from that expected from those found later. Attila Szabo has pointed out the pedagogical example that where there are two competing pathways, one a single-step with a rate constant of k₂ and a two-step of first rate constant k₁ and second rate constant k₂ (the same as for the single-step), then N is formed according to a perfect single exponential of rate constant k₂. The ratio of molecules folding by the two-step route to the one step is given by: (k₁ − (k₁ + k₂)exp(−k₂t)+k₂exp(−(k₁ + k₂)t))/(k₂(1 −exp(−(k₁ +k₂)t)). This reduces to k₁/k₂ as t tends to infinity and to k₁t/2 as t tends to zero, as expected from Eqs. 7 and 9.

Discontinuous Simulation Methods

Voter has devised a method that avoids the difficulties associated with lag kinetics (16); different simulations are loosely coupled, whereby they are stopped after one simulation has successfully crossed a barrier and are all restarted from the successful configuration (11–13). For example, consider the kinetics of the major pathway that begins with the step of 5 × 10⁵⋅s⁻¹. After 20 ns, nearly 100 of the 10⁴ simulations should have crossed the barrier that has the rate constant of 5 × 10⁵⋅s⁻¹, and 5 would have crossed in the first nanosecond. Accordingly, the simulations would have to be rapidly stopped and restarted from the conformations corresponding to this transition and so avoid the minor pathway. But the crucial factor in the loosely coupled procedure is to identify when the transitions occur, and the means for their identification is an inherent weakness in the method (12, 13). It is extremely difficult to detect transitions in MD simulations, because they do not directly calculate free energy, and so indirect methods must be used. For example, Daggett and coworker have used a structural clustering method to detect transition states (17), and others use the experimentally determined structures (6) in MD simulations. For En-HD, a structural approach would require identifying the 1% of structures that have relaxed into the intermediate ensemble. Pande and coworkers use the criterion of a surge in heat capacity as being characteristic of a transition (12, 13). Experimentally, changes in the heat capacity of a protein are dominated by solvation; 95% of ΔC_P results from changes in hydration and only 5% from changes in noncovalent interactions (18). The largest changes in solvation result from hydrophobic collapse. The actual quantity used by Pande and coworkers (the time-resolved energy variance, 〈E²〉_c) may differ somewhat from the experimentally observed value, but it has yet to be established as an unbiased discriminator and whether it will detect members of the relatively heterogenous ensembles that typify folding intermediates. Thus, the loosely coupled procedure may have a bias toward detecting pathways that are based on the features implicit in the criterion for discrimination, such as those dominated by hydrophobic collapse, or that just fail to detect intermediates. Not only may the loosely coupled procedure miss pathways because they do not generate the right signals, they will also be dogged by the problems of lag phases in the generation of intermediates.

Conclusion

Distributed computing is a very exciting development for simulating protein folding pathways cheaply over otherwise currently inaccessible long time regimes. But there are inherent problems, because the early phases of protein folding of up to at least the microsecond region are rich in events that may not be representative of the major pathways of folding. Simulations made in the early time regions before the system relaxes will be biased toward overall folding routes that have the least number of intermediates but that may be very minor pathways. Strategies to overcome the problems of intermediates, such as that devised by Voter (16), are problematic because it is so difficult to identify intermediates in MD simulation. Simple criteria for detection of intermediates will bias the search to pathways that have the sought-for intermediates, which again may be misleading. Nevertheless, the procedure using parallel independent simulations is perfectly valid and quite feasible once the time scale of simulation proceeds past the lag phases into the single exponential region. This can be done with some smaller peptides at present. To be reliable for larger proteins, simulations will have to be extended into the microsecond region or greater. Perhaps, starting distributed computing from denatured states, transition states or intermediates that have been generated by other simulation procedures may be a way forward now. As always, benchmarking by experiment is necessary because of the approximations in the empirical energy functions that are used in simulation.

Abbreviations

• MD, molecular dynamics

• En-HD, engrailed homeodomain