X-ray diffraction “fingerprinting” of DNA structure in solution for quantitative evaluation of molecular dynamics simulation

Abstract

Solution state x-ray diffraction fingerprinting is demonstrated as a method for experimentally assessing the accuracy of molecular dynamics (MD) simulations. Fourier transforms of coordinate data from MD simulations are used to produce reciprocal space “fingerprints” of atomic pair distance correlations that are characteristic of the ensemble and are the direct numerical analogues of experimental solution x-ray diffraction (SXD). SXD experiments and MD simulations were carried out to test the ability of experiment and simulation to resolve sequence-dependent modifications in helix conformation for B-form DNA. SXD experiments demonstrated that solution-state poly(AT) and poly(A)-poly(T) duplex DNA sequences exist in ensembles close to canonical B-form and B′-form structures, respectively. In contrast, MD simulations analyzed in terms of SXD fingerprints are shown to deviate from experiment, most significantly for poly(A)-poly(T) duplex DNA. Compared with experiment, MD simulation shortcomings were found to include both mismatches in simulated conformer structures and number population within the ensembles. This work demonstrates an experimental approach for quantitatively evaluating MD simulations and other coordinate models to simulate biopolymer structure in solution and suggests opportunities to use solution diffraction data as experimental benchmarks for developing supramolecular force fields optimized for a range of in situ applications.

Characterization of the structure and dynamics of biological macromolecules in liquids and other physiologically relevant noncrystalline media is critical for achieving a full understanding of chemical and biological function at the molecular level (1, 2). Molecular dynamics (MD) simulations based on molecular mechanical force fields and Ewald-type treatments for the long-range electrostatic interactions have been remarkably successful in simulating the general features of DNA sequence-dependent conformations, conformational transitions, and nucleic acid–drug interactions (3–5). However, variances in the details of simulated DNA structure based on choice of force fields and simulation conditions (4, 6) suggest levels of uncertainty in the prediction of DNA structure that are likely to undermine attempts to understand function at the atomic scale.

A general problem for the evaluation of MD simulation is the lack of a sufficient experimental database on solution-state DNA structure. Crystal-packing distortions of DNA and the intrinsic lack of long-range structural data from NMR measurements restricts the reliable database on DNA structure to local structural parameters (7, 8). It is an open question whether force fields focused primarily on local structure parameters are sufficient to accurately model the full range of DNA conformational landscapes in solution.

Recently, a number of reports have shown that wide-angle x-ray scattering provides a direct measure of macromolecular conformation in solution (9–15). Wide-angle x-ray scattering measures rotationally averaged molecular diffraction. Solution x-ray diffraction (SXD) patterns provide one-dimensional (1D) “fingerprints” of 3D structure that are directly relatable to atomic configuration by Fourier transform (14–17). In previous work, we demonstrated that SXD patterns have sufficient resolution to characterize protein and DNA conformations in solution and to discriminate between close but distinguishable crystallographic and NMR models (11, 15). Observed broadening of the SXD features compared with those calculated from static structures further indicated that experimental SXD patterns include information on configurational landscapes in solution that can be parameterized in terms of a mean configuration and breadth of the dispersion (14, 15).

Here, we report on the use of SXD measurements to test the accuracy of MD simulations by directly comparing Fourier transforms of MD coordinate ensembles with experimental SXD patterns measured for solution-state DNA. Experimental SXD patterns are quantitatively compared with those calculated from coordinate models and MD simulations for three AT-rich duplex DNA sequences, d(A)₁₀, d(A)₂₀, and d(AT)₁₀. SXD experiments show that the alternating poly(deoxyadenosine–deoxythymidine)–poly(deoxyadenosine–deoxythymidine) duplex [poly(AT)] and homopolyer poly(deoxyadenosine)–poly(deoxythymidine) duplex [poly(A)–poly(T)] sequences differ in solution-state conformation and adopt conformations close to canonical B-form and B′-form conformations (18–21), respectively. In contrast, MD simulations for a variety of AT-rich sequences were found to be biased toward similar B-form conformations, and clear discrepancies are resolved between experimentally observed and simulated ensembles. This work demonstrates the opportunity to use SXD measurements as quantitative benchmarks for evaluating MD simulations and to guide the development of experimentally verified force fields that more accurately predict supramolecular structure.

Results and Discussion

General Features of X-Ray Solution Diffraction for DNA.

Correlations between DNA fiber diffraction patterns and helical DNA structures were established in the 1950s and are widely used for the classification of DNA structures (21, 22). Fiber diffraction measurements have shown that in the solid-state duplex poly(AT) adopts a B-form conformation, whereas poly(A)–poly(T), also called A-tract DNA, adopts a B′-form conformation, having 10.0 base pairs (bp) per turn instead of 10.6 for B-form. B′-form DNA also has a narrower minor groove and shorter base rise than canonical B-form (18, 19).

SXD patterns reflect rotationally averaged molecular diffraction in the solution state and thus are analogous to fiber diffraction patterns. Scattering from structural repeats in duplex helical DNA produces a series of diffraction peaks in SXD patterns that vary in position and intensity depending on the molecular conformation. Positions of the SXD peaks are correlated to the structural repeat spacing, d = 2π/q, where q = (4π/λ)sinθ, and λ is the x-ray wavelength and 2θ is the scattering angle, and correspond directly to peaks measured by fiber diffraction. Peak lineshapes reflect the overlapping effects of coherence length and dispersion in atomic pair distances within a molecular structure. Hence, SXD patterns provide a summary of molecular structure by providing a measure of the spatially resolved atomic pair correlations. Comparisons between experiment and model can either be made at the level of the reciprocal space SXD patterns or the corresponding real space pair distance distribution functions (PDDF). In the present context, we have chosen to use SXD patterns as fingerprints for comparison of experiment with models for DNA conformation in solution. SXD patterns can be calculated rigorously by Fourier transform of coordinate data (14–17), and comparison of experimental and model SXD patterns avoids the possible introduction of artifacts by inverse transforms of imperfect experimental SXD data into PDDF.

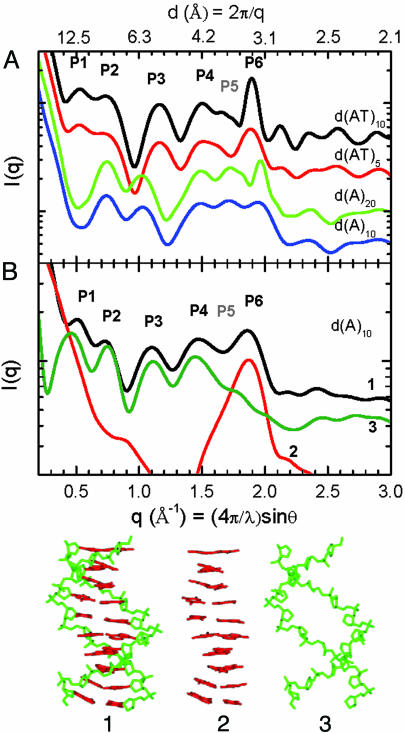
Fig. 1A shows SXD patterns calculated for fiber diffraction models for canonical B- and B′-form conformations of DNA compared pairwise for 20- and 10-bp sequences. The sharpening of diffraction peaks in the longer sequences results from the increased coherence length in these conformer models with exact helical symmetry. The SXD fingerprints can be compared by the positions and intensities of diffraction peaks, labeled P1–P6 in Fig. 1. Notably, peak P5 is attenuated for the B-form duplex poly(AT) with 20 alternating A-T bp [d(AT)₁₀] and d(AT)₅ duplex models but is prominent in the duplex poly(A)–poly(T) with 20 A-T bp [d(A)₂₀] and duplex poly(A)-poly(T) with 10 A-T bp [d(A)₁₀] B′-form conformers, whereas the converse is seen for peak P1. Characteristic shifts in position, lineshape, and intensity also occur for each of the other peaks. Calculated SXD patterns of B-form duplex models built by using d(A)₂₀ and d(AT)₁₀ sequences are almost identical (data not shown), indicating that characteristic B- and B′-form SXD patterns arise from conformational differences and not sequence differences.

Fig. 1.

SXD fingerprint patterns calculated from DNA models. (A) SXD fingerprints calculated from canonical duplex models: B-form d(AT)₁₀ (black), B-form d(AT)₅ (red), B′-form d(A)₂₀ (green), and B′-form d(A)₁₀ (blue). (B) SXD fingerprints calculated from a d(A)₁₀ MD B-form conformer using the complete structure (black), the base pair atoms only (red), and sugar–phosphate backbone atoms only (green). The atomic groups are shown as structures 1–3, respectively.

The structural basis for the SXD features can be demonstrated by scattering calculations based on partial structures. Fig. 1B shows full and partial structure SXD patterns calculated for a d(A)₁₀ B-form duplex conformer (structure 1 in Fig. 1), taken from the MD simulation described below. The SXD pattern features calculated for the MD conformer are softened by deviations from exact helical symmetry. Contributions due to the stacked nucleotide bases can be calculated from the partial structure 2 in Fig. 1, which gives rise to a single diffraction peak P6 shown by the red line in Fig. 1B. The position and linewidth of this diffraction peak scale directly with the mean distance and uniformity of base pair stacking (15). Peaks at lower angle, P1–P4, are dominated by scattering from the sugar–phosphate backbone, as shown by the green line SXD pattern calculated from the partial structure 3 in Fig. 1. Similarly, peaks P1 and P2 can be demonstrated to arise from helical interstrand pair distance correlations and reflect the combined effects of interference due to the major and minor groove spacing and the helix radius (data not shown). The P5 peak contains a mixture of atomic pair contributions that arise predominately from cross-terms between the backbone and stacked base pairs and vary significantly with conformation. From these models the shift of peak P6 to higher angle for the B′-form conformer can be shown to arise from the closer base pair stacking distance in the B′-form DNA, whereas the changes in P1–P5 reflect the differences in the helicoidal parameters of the two conformers.

Experimental Solution-State Diffraction for d(AT)₁₀ and d(A)_20,10 Duplexes.

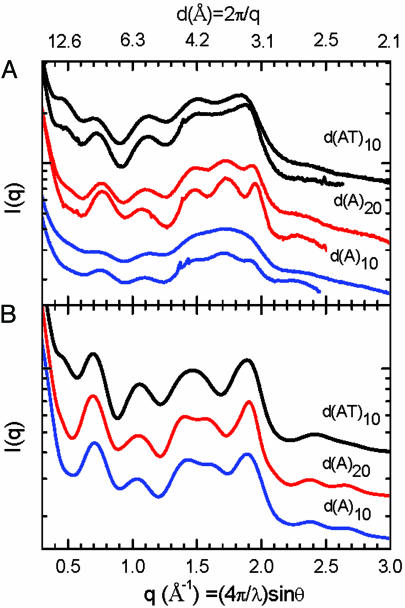
Fig. 2A shows experimental SXD patterns measured for d(AT)₁₀, d(A)₂₀, and d(A)₁₀ duplexes from top to bottom, respectively, each recorded in 100 mM NaCl solution at two temperatures, room temperature and 3°C. The detection of diffraction peaks for solution-state DNA is significant because it provides a direct measure of in situ structure and configurational dispersion. Clear evidence for the influence of configurational broadening on SXD patterns is shown by the significant narrowing of diffraction peaks upon cooling. Evidence that the SXD pattern changes reflect thermal transitions in DNA and not distortions due to solvent and other artifacts is demonstrated by the broadness of the water diffraction peak (see Figs. 5 and 6, which are published as supporting information on the PNAS web site), the relative insensitivity of solvent scattering to temperature changes in this range, and observed correlations between DNA sequence melting temperatures and the onsets of temperature-dependent SXD peak broadening. Peak broadening is particularly severe for the short d(A)₁₀ sequence compared with the d(A)₂₀ homologue. By reference to model calculations discussed below, the extensive broadening for the d(A)₁₀ duplex can be identified as because of increased configurational disorder in the shorter sequence. Also noticeable are slight shifts in diffraction peak positions for each sequence that reflect temperature-dependent changes in conformation, in particular, the shift to higher q for P6 for both d(AT) and d(A) duplexes that reflects an average decrease in the base pair stacking by ≈0.05 Å upon cooling.

Fig. 2.

SXD patterns from experiment and MD simulation of duplex poly(A)–poly(T) and poly(AT) DNA. (A) Experimental SXD patterns for d(AT)₁₀ (top two traces), d(A)₂₀ (middle two traces), and d(A)₁₀ (bottom two traces) shown pairwise recorded at room temperature (upper trace) and 3°C (lower trace). (B) Ensemble-averaged SXD patterns calculated from MD simulations for d(AT)₁₀ (top trace), d(A)₂₀ (middle trace), and d(A)₁₀ (bottom trace) using simulation conditions AT10.2, A20.2, and A10.3 in Table 2, respectively.

The SXD features measured for solution-state d(AT)₁₀ and d(A)_20,10 duplex samples mirror those calculated from the canonical B- and B′-form models. Notably, the experimental SXD pattern for d(AT)₁₀ is missing diffraction peak P5 (top pair of traces in Fig. 2A), whereas d(A)₂₀ and d(A)₁₀ are missing a clearly resolved P1 peak (lower pairs of traces in Fig. 2A). In addition, P6 and P2 show shifts in positions and intensities. Real space PDDF patterns derived from the experimental SXD patterns are presented in Fig. 7, which is published as supporting information on the PNAS web site. The PDDF patterns show analogous temperature- and sequence-dependent shifts and broadening.

The SXD data presented here provides a measurement of homopolymeric poly(A)–poly(T) and poly(AT) duplex conformations in solution. The close correspondences between diffraction peak positions measured in solution and those calculated from fiber diffraction models (Table 1) demonstrates that the experimental solution-state d(AT)₁₀ and d(A)_20,10 duplex structures are centered on conformations close to the canonical B-form and B′-form conformers, respectively. However, noticeable broadening of the experimental patterns and the loss of well resolved diffraction features beyond the P6 peak reflects temperature-dependent configurational dispersion in solution that is absent in the static models.

Table 1.

Experimental and model SXD peak positions

Peak	Exp.	Fiber	MD
B-form DNA, d(AT)10
P1	0.45 (0.03)	0.53	0.47
P2	0.72 (0.01)	0.74	0.69
P3	1.12 (0.01)	1.16	1.05
P4	1.51 (0.02)	1.51	1.46
P5	—	—‡	—
P6	1.87 (0.01)	1.89	1.89
rmsd		0.042	0.043
B′-form DNA, d(A)20
P1	—	—	—
P2	0.77 (0.01)	0.75	0.70
P3	1.07 (0.02)	1.03	1.05
P4	1.49 (0.02)	1.48	1.41
P5	1.73 (0.01)	1.72	1.56
P6	1.95 (0.01)	1.96	1.91
rmsd		0.021	0.091

Peak positions were determined from zero crossing points in first derivative plots. Values are in Å⁻¹.

*Experimental positions were determined from 10 point smoothed derivative plots of 3°C data. Uncertainties were determined from experimental half-width noise.

^†Ensemble averaged SXD patterns in Fig. 2B.

^‡A partially resolved shoulder is only seen in longer (≈20 bp) sequences with strictly canonical B-form structure but is not resolved in shorter sequences or sequences that deviate from ideal symmetry.

MD Simulations of Homopolymeric d(AT)₁₀ and d(A)_20,10 Duplexes.

MD simulations were performed by using amber 8.0 (23) to simulate the solution-state structures for d(AT)₁₀, d(A)₂₀, and d(A)₁₀ duplexes. A range of simulation parameters, including solvent box dimensions, nonbonded interaction cutoffs, and starting conformations, were tested. A summary of the simulation conditions are listed in Table 2. The MD ensembles were characterized by calculating the SXD pattern from each conformer, and then the ensemble-averaged SXD fingerprint pattern was compared with experiment.

Table 2.

MD simulations

Trial	Time, ns	Initial structure	Box,* Å	Cutoff,† Å	B′-form,‡ %	B′-form rmsd§
d(A)10
A10.0	2.0	B	—	—	14.3	0.096
A10.1	10.8	B	8	8	21.8	0.076
A10.2	8.6	B	10	8	23.4	0.071
A10.3	8.2	B	10	12	46.2	0.069
A10.4	1.7	B	10	15	41.8	0.067
A10.5	6.0	B′	8	8	13.2	0.078
A10.6	4.8	B′	10	12	47.0	0.072
d(A)20
A20.1	6.7	B	8	8	19.5	0.092
A20.2	4.8	B	10	12	49.6	0.071
d(AT)10
AT10.1	6.7	B	8	8	5.2	—
AT10.2	2.8	B	10	12	9.1	—

Explicit water (TIP3P model) was used in all simulations except A10.0, where a generalized Born model was used. Structural parameters tabulated for the MD simulations are listed in Tables 3 and 4, which are published as supporting information on the PNAS web site.

*Minimum distances between DNA and solvent box perimeter.

^†Limits for nonbonded interactions.

^‡Percentage of the ensemble having B′-form conformations, defined as having the same number of resolved SXD peaks as the experimental d(A)₂₀ SXD pattern.

^§The variance between the B′-form MD ensemble subset SXD peak positions and d(A)₂₀ experiment (3°C).

Fig. 2B shows ensemble average SXD patterns calculated from simulations of d(AT)₁₀, d(A)₂₀, and d(A)₁₀ duplexes that used a 12-Å nonbonding interaction cutoff (simulations AT10.2, A20.2, and A10.3 respectively; Table 2). The MD simulations only partially reproduced sequence-dependent SXD features observed in experiment. The MD SXD fingerprint pattern for the d(AT)₁₀ duplex shows agreement with experiment in the number of discernable peaks and their approximate positions, including the absence of a P5 peak and presence of a weak P1 diffraction peak, reflecting predominately B-form conformers in the simulated ensemble. However, variances between simulated and experimental SXD peak positions for d(AT)₁₀ (Table 1) reflect differences in the details of the mean conformations, whereas lineshape differences reflect variances in the distribution of structures within the simulated and experimental ensembles.

In contrast to the general agreement between experiment and simulation for the d(AT)₁₀ duplex, MD simulations for the for the d(A)₂₀, and d(A)₁₀ duplexes yield SXD patterns that only incompletely replicate experimental patterns. The d(A)_20,10 SXD simulations show a loss of the P1 diffraction peak and emergence of a partially resolved feature near P5 that are consistent with the altered base pair stacking and change in helical conformation expected for a shift toward B′-form resembling structures. However, the generally poor correspondence between the simulated SXD peak positions with those measured in experiment (Table 1) demonstrates the inadequacy of the simulation to accurately represent the experimental solution-state ensemble for A-tract DNA.

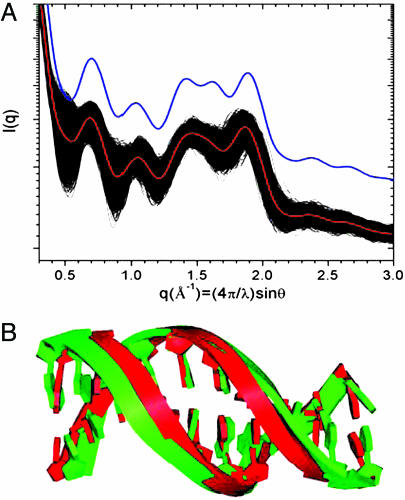
The MD simulations can be considered in further detail by examining the SXD patterns for individual conformers within the ensemble. For example, Fig. 3 shows SXD patterns calculated for each of the >2,000 individual MD conformers from the A10.1 simulation along with the ensemble average SXD pattern. Significant dispersion can be seen in each of the fingerprint peak regions. The d(A)₁₀ MD ensemble was searched for conformers that have a SXD fingerprint resembling the experimental pattern. An averaged SXD pattern for a subset comprising 21.8% of the total ensemble is shown plotted in blue in Fig. 3A. The subset SXD fingerprint shows a resolved P5 peak, the absence of P1, and a shift to higher angle and narrowing of the P6 peak that are characteristic of B′-form resembling conformers. The B′-form resembling conformers were distributed in clusters throughout the MD simulation trajectory as shown in Fig. 8, which is published as supporting information on the PNAS web site. This subset ensemble has a significantly improved agreement with d(A)₂₀ data (3°C) compared with the ensemble average, as indicated by the comparison of root mean square deviations (rmsds) in SXD peak positions compared with experiment (Table 2). However, the MD subset still fails to accurately replicate the experimental ensemble.

Fig. 3.

Examination of conformer SXD fingerprints within the d(A)₁₀ MD ensemble. (A) SXD patterns calculated for each of the 2,200 conformers generated in simulation A10.1 (black), the ensemble-averaged SXD pattern (red), and a subset-averaged SXD pattern for conformers with B′-form fingerprints (blue), offset for clarity. (B) Overlap of structures representative of the ensemble (green) and B′-form subset (red) averages.

An illustration of the structural differences linked to the variances in SXD patterns is shown in Fig. 3B by an overlap of structures representative of the subset and ensemble averages. The subset conformer has a minor groove spacing of 10.3 Å, which is smaller than the 11.7-Å spacing measured in the B-form conformer representative of the ensemble average but still significantly larger than the 8.8-Å spacing in the canonical B′-form conformer that is in accord with both experimental fiber and solution diffraction data.

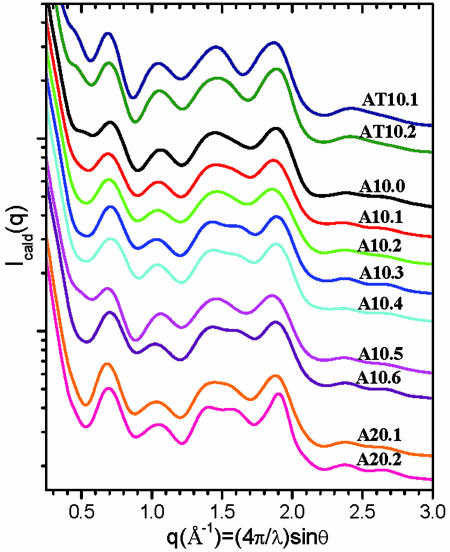
The simulation of the d(AT) and d(A) duplex sequences were tested as a function of starting geometry, simulation box sizes, nonbonding interaction cutoff, and solvent model, as summarized in Table 2. With the procedures described in Materials and Methods, each MD simulation was stable in the time range of 1–10 ns, as judged by the system energies, rmsds, and other frequently monitored parameters during the time course of MD simulations (see Fig. 9, which is published as supporting information on the PNAS web site). The ensemble-averaged SXD fingerprint patterns for all MD simulations of the d(A)₁₀, d(A)₂₀, and d(AT)₁₀ duplexes are displayed in Fig. 4. The usefulness of the SXD presentation is that it provides a graphical comparison of the simulations based on spatially resolved pair correlations and magnitudes of the ensemble dispersions and quantitative benchmarks for comparison with experiment.

Fig. 4.

A series of MD simulations compared by ensemble-averaged SXD fingerprints. The simulation conditions and parameters are listed in Table 2. Structural parameters tabulated for the MD simulations are listed in Tables 3 and 4.

For example, the comparison of simulations A10.0 and A10.1 tested the effect of using implicit Born or explicit coordinate models for solvent on the d(A)₁₀ simulation. The SXD patterns for both simulations are quite similar, except for slight changes in the lineshape in the P1 region. Both simulations failed to produce a well resolved P5 diffraction peak seen in the experiment. An increase of simulation box size from 8 Å in A10.1 to 10 Å in A10.2 did not significantly change the ensemble. However, an increase of a cutoff for nonbonded interactions from 8 to 12 Å in simulation A10.3 caused a shoulder to appear in the P5 region. An examination of the ensemble shows that this shoulder arises from a subset of conformers having a well resolved P5 diffraction peak at q = 1.62 Å⁻¹. Increasing the nonbonding interactions cutoff to 15 Å in A10.4 did not significantly alter the ensemble SXD fingerprint. The simulations were found to be insensitive to starting structure, as shown by simulations A10.5 and A10.6 that used the expected B′-form instead of the B-form structure for the d(A)₁₀ sequence. The B′-form conformers were found to be lost during the equilibration procedures before the MD trajectories.

Simulations of longer d(A)₂₀ and d(AT)₁₀ duplexes showed similar increases in the population of B′-form conformers upon increasing the cutoff for nonbonded interactions to 12 Å. The sharply reduced population of B′-form conformers in the d(AT)₁₀ duplex ensembles demonstrates that the amber force field recognizes the conformational difference between poly(A)–poly(T) and poly(AT) sequences. However, the B′-form conformers emergent in the simulations poly(A)–poly(T) simulations are found to be a relatively poor match to experiment, as indicated in Table 2 by the rmsd in diffraction peak positions.

Experimental Evaluation of MD Simulations.

Although the currently available force fields for DNA have been found to be remarkably successful for simulating a broad range of sequence-dependent structural features (3–5), variances between simulations suggest a significant level of uncertainty in the prediction of structural details (4, 6, 24–26). In the present work, we have extended these findings by using SXD measurements to provide indices for tabulating goodness-of-fit between experiment and coordinate models. These analyses showed that simulation shortcomings, particularly for A-track sequences, arise both from mismatches in the structures of conformers that provide the closest match to data and from their underpopulation within simulated ensembles.

Discrepancies between simulation and experiment could arise from the restricted range of molecular motions sampled by simulation. However, we found no discernable evolution in the mean conformation or amplitude of the dispersion for MD trajectories across the 1- to 10-ns time frame (Figs. 8 and 9), suggesting that simulated DNA structure reached equilibration by 1 ns. Similar findings were previously noted in simulations carried out to 60 ns, although counterion distributions were found not to have equilibrated (27). These observations and the present data suggest a possibility that final DNA structure equilibration might be linked to long-range counterion redistribution. A scale of the mismatch between experiment and simulation is illustrated by the finding of minor groove spacing near 8.8 Å for B′-form conformers that are representative of experimental SXD, whereas the subset of B′-form resembling conformers in MD simulation were found to have minor groove spacing near 10.3 Å. Reconciling structural differences between simulation and experiment is anticipated to be necessary for accurately modeling of sequence-dependent DNA function in ion binding, molecular recognition, photo-damage, and charge transfer.

Prior experimental validation of MD simulation have compared crystallographic and NMR data (8, 24, 26, 28, 29). However, potential distortions of DNA conformation by crystal packing forces and the short-range nature of solution NMR interactions have largely limited the reliable experimental database to local structural parameters. For example, MD simulations for the (CGCGAATTCGCG)₂ duplex were previously concluded to be in good agreement with 2D NOESY NMR data and heliocoidal structural parameters derived from a NMR model that included residual dipolar couplings (30). However, our recent SXD measurements demonstrated that of the four NMR structures available for the (CGCGAATTCGCG)₂ duplex, an alternative model by Kuszewski et al. (31) provided the best fit of calculated and experimental SXD peak positions (15). The mismatch between MD simulation and experiment for the (CGCGAATTCGCG)₂ duplex is shown by comparison of calculated and experimental SXD patterns (see Fig. 10, which is published as supporting information on the PNAS web site). Besides mismatches in the diffraction peak positions, the SXD fingerprints of MD ensemble failed to simulate the presence of a P1 diffraction peak that is resolved in both the experimental SXD pattern and the best-fit NMR model calculation. This comparison illustrates the problem that even when local helicoidal parameters are in good accord, the global DNA conformation deduced from local structural parameters can deviate significantly from experiment. SXD measurements provide a direct method for assessing global solution-state conformation and provide benchmarks for quantitatively indexing goodness-of-fit between simulation and experiment.

The SXD analyses presented here expose the limits of current MD simulations. Although largely insensitive to aperiodic short-range structures, SXD measurements are found to be quite sensitive to the details of global DNA conformation. The complementarity of NMR and SXD data suggest the opportunity of combining global SXD experimental measurements with short-range NMR distance constraints to achieve optimized, more accurate empirical force fields for DNA structure simulation. This level of refinement is likely to be critical for achieving progress in the resolution of molecular mechanisms for DNA function in ion binding, molecular recognition, photo-damage, and long-range charge transfer.

Materials and Methods

DNA Samples.

Oligodeoxyribonucleotides were either prepared by conventional phosphoramidite chemistry using DNA synthesizer and purified by HPLC or obtained commercially (Integrated DNA Technologies, Coralville, IA). Samples for x-ray scattering were prepared by dissolving DNA in 100 mM NaCl and 50 mM Tris·HCl buffer, with a concentration of 1–10 mg/ml. Tris·HCl buffer was prepared from Trizma Preset crystals (pH 7.0) (Aldrich).

SXD and Data Analyses.

X-ray scattering measurements were carried out on the undulator (12-ID) and bending magnet (12-BM) beam lines at the Advanced Photon Source, Argonne National Laboratory (32). The x-ray wavelength was set at λ = 0.62 Å, and the sample to charge-coupled device (CCD) detector (MAR Research, Hamburg) distances were adjusted to achieve scattering measured across the range of momentum transfer 0.04 Å⁻¹ < q < 3.0 Å⁻¹. Radiation damage was prevented by flowing samples at 5 × 10⁻⁵ liters/min in a 2-mm capillary cell that provided a complete exchange of the x-ray irradiated volume in <1 s. Accumulated CCD detector image exposure times ranged between 3 and 20 s, and azimuthally averaged data from 5 to 10 images were averaged. Methods for solvent subtraction and other corrections are described in Supporting Text, which is published as supporting information on the PNAS web site. Temperature-dependent scattering data were collected with the sample flow cell sandwiched between a pair of air-cooled Pelletier thermoelectric coolers (Melcor, Trenton, NJ) that provided temperature control to a precision of better than ±0.1°C. PDDFs were calculated from the scattering data by using the program gnom (33). Coordinate-based simulations of SXD patterns used computational approaches described in refs. 11 and 14–17 and are outlined in Supporting Text.

MD Simulations and Structural Analyses.

MD simulations at 300 K and 1 atmosphere were carried out by using the sander module in amber 8 (23) by using the ff99 force field (34) on jazz, a 350-node computer cluster, in the Laboratory Computing Resource Center at Argonne National Laboratory. The particle mesh Ewald method was used to calculate the long-range, nonbonding electrostatic and van der Waals interactions (35). Cutoffs for real-space nonbonded interactions were tested in the range 8–15 Å. Canonical structures of B-form were built by using program nucgen in amber, and canonical B′-form structures were built by using model 18 (18) in 3dna (36). An appropriate number of counterions (Na⁺) were placed around the DNA molecule to achieve a neutral system, which was subsequently solvated by using the TIP3P water model (37) in a rectangular periodic box with a distance from each wall to the closest solute atoms at least 8 or 10 Å as noted in the different simulation runs. All bonds with hydrogen atoms involved were constrained with shake (38). The whole system then was equilibrated by using a protocol similar to that described in ref. 39, except that sodium ions were equilibrated with the solute DNA. Equilibration was followed by 2- to 11-ns production runs using 2-fs time steps, during which snapshots were collected every 2.5 or 5.0 ps. Structural parameters of MD conformers were calculated by using the program 3dna (36).

Abbreviations

MD

molecular dynamics

rmsd

rms deviation

PDDF

pair distance distribution function

poly(A)–poly(T)

homopolyer poly(deoxyadenosine)–poly(deoxythymidine) duplex

poly(AT)

alternating poly(deoxyadenosine–deoxythymidine)–poly(deoxyadenosine–deoxythymidine) duplex

d(A)₁₀

duplex poly(A)–poly(T) with 10 A-T bp

d(A)₂₀

duplex poly(A)–poly(T) with 20 A-T bp

d(AT)₁₀

duplex poly(AT) with 20 alternating A-T bp

SXD

solution x-ray diffraction.