Nondiffusive mechanisms enhance protein uptake rates in ion exchange particles

Abstract

Scanning confocal fluorescence microscopy and multiphoton fluorescence microscopy were used to image the uptake of the protein lysozyme into individual ion exchange chromatography particles in a packed bed in real time. Self-sharpening concentration fronts penetrating into the particles were observed at low salt concentrations in all of the adsorbents studied, but persisted to 100 mM ionic strength only in some materials. In other adsorbents, diffuse profiles were seen at these higher salt concentrations, with the transition region exhibiting a pronounced fluorescence peak at the front at intermediate salt concentrations. These patterns in the uptake profiles are accompanied by significant increases in protein uptake rates that are also seen macroscopically in batch uptake experiments. The fluorescence peak appears to be a concentration overshoot that may develop, in part, from an electrokinetic contribution to transport that also enhances the uptake rate. Further evidence for an electrokinetic origin is that the effect is correlated with high adsorbent surface charge densities. Predictions of a mathematical model incorporating the electrokinetic effect are in qualitative agreement with the observations. These findings indicate that mechanisms other than diffusion contribute to protein transport in oppositely charged porous materials and may be exploited to achieve rapid uptake in process chromatography.

The dramatic growth of the biotechnology industry in recent years has depended critically on preparative separation techniques for protein products. Ion exchange chromatography, introduced for protein separations in the 1950s, remains one of the most widely used preparative-scale purification and separation methods (1). Ion exchange adsorbents have been designed to offer a range of mechanical and chemical properties for chromatographic separation and purification (2), but a fundamental understanding of transport mechanisms in these materials remains elusive. For most materials, simple diffusive mechanisms are thought to control intraparticle transport, but studies using batch or column techniques (3–7) yield model-dependent transport coefficients, and they cannot definitively determine the physical transport mechanism. With the projected acceleration in the discovery and development of protein therapeutics as a result of the human genome project, the demand for improved chromatographic materials and methods for optimizing protein separation and purification will increase. Therefore, a more fundamental understanding of the transport mechanisms in these materials is required to develop better heuristics for process development as well as methodologies for the design of new adsorbents.

A key complication in the interpretation of batch or column studies is that the transport is coupled to adsorption, making additional assumptions regarding the adsorption behavior necessary to characterize the transport. Microscopic techniques have a greater potential to resolve the resulting ambiguities regarding transport mechanisms. Korthauer et al. (8) used optical interferometery coupled with a flow cell to study the transport of albumin in an individual agarose bead for nonadsorbing conditions. From this method they were able to determine intraparticle concentration profiles and an effective diffusion coefficient. Despite its advantage over previous methods, this technique was not used further to study transport behavior under adsorptive conditions. A second promising route is the use of scanning confocal microscopy to image protein uptake into individual chromatography particles. Results reported thus far have been limited to studies of large proteins with relatively slow transport rates because contacting and imaging were performed sequentially rather than simultaneously, introducing a time lag (9–12). We report here results using confocal microscopy to perform imaging of protein uptake into single ion exchange particles packed in a flow cell. The temporal resolution attained allows uptake profiles to be observed in real time, and the results suggest that the mechanisms of protein uptake may be considerably more complex than is usually assumed. This method greatly expands current capabilities for studying and understanding biomolecule transport in porous materials.

Materials and Methods

Materials.

The experiments reported here studied the uptake of hen egg white lysozyme into a variety of commercial cation-exchange stationary phases, namely SP Sepharose FF (Amersham Biosciences), Toyopearl SP 650 C and SP 550 C (Tosoh Biosep, Tokyo), and SP Spherodex (Biosepra, Marlborough, MA). Lysozyme was obtained from Sigma and used without further purification. Lots 57H7045 and 20K0956, with manufacturer-reported purities of 94% and 98% by SDS/PAGE, were used. Lysozyme concentrations were calculated from the absorbance at 280 nm and an extinction coefficient of 2.54 cm²/mg (13). The pH for all experiments was maintained at 7 with a sodium phosphate buffer, resulting in a net charge of ≈+8 on the lysozyme molecule (14). Phosphate concentrations were 10 mM for all buffers except for the 2 and 6 mM ionic strength experiments, where the phosphate concentrations were 1 and 3 mM, respectively.

Fluorescence labeling reactions for confocal experiments were performed at pH 9.3 for 30 min in 100 mM carbonate buffer to conjugate the lysozyme with Cy5 (Amersham Biosciences). Labeled protein was separated from unreacted dye by using a gravity-fed Sephadex G25 size exclusion column. The labeled protein cut, the first band to elute, was collected by visual inspection. To avoid total internal filtering of the confocal laser light by the fluorescent dye, the labeled protein solution was diluted with unlabeled protein solution to achieve a final molar label ratio (dye/protein) <0.01. For experiments with FITC (Molecular Probes) the conjugation reaction was performed in a 100 mM carbonate buffer at pH 8.5 with DMSO added to the reaction mixture (10% vol/vol) to help solubilize the dye. The FITC labeling reaction was quenched with 10% (vol/vol) of 1.5 M hydroxylamine at pH 8.5.

Confocal Microscopy.

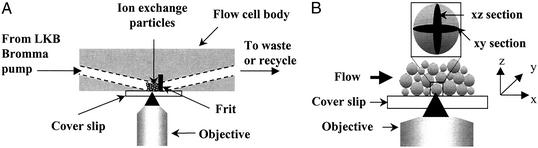
The real-time studies were made possible by a flow cell into which chromatographic particles are packed behind a coverslip (Fig. 1A). A 1/16-inch-diameter channel was drilled through either side of a solid Delrin block (51 × 55 × 19 mm) at the same angle from the horizontal; the channels meet and penetrate through one face of the block. A stainless steel frit installed in the flow cell body holds the particles in place and the coverslip is attached to the face of the block with a silicone sealant (Silicone II, General Electric). The protein solution is recirculated with a LKB Bromma positive displacement pump at a specified rate through the flow cell to enhance external mass transfer and simulate column conditions. The residence time in the chromatographic bed (V_bed ≈ 5 μl) is ≈3 s even at the lowest flow rate used (0.1 ml/min), and the overall depletion in the recirculated feed solution was minimal (<5%), so the set-up was operated as a differential bed at essentially constant concentration.

Figure 1.

Cross-sectional view of confocal flow cell (A) and expanded view (B) showing xz and xy optical sectioning of single particles within the particle bed in the flow cell during protein uptake. The xz section (shown as a shaded oval in the expanded particle) is parallel to the direction of flow.

Imaging was performed with a Zeiss 510 laser scanning microscope in which the laser is focused to a spot size of ≈230 nm. Vertical (xz image) or horizontal (xy image) sections may be acquired (Fig. 1B), with lateral and axial resolutions of ≈320 and 1,200 nm, respectively (15). Typical diameters of preparative chromatographic particles, including those used in this study, are of order 100 μm, so spatial changes in the fluorescence intensity profiles as a function of time can be measured accurately.

Isotherms.

Adsorption isotherms for lysozyme in the different stationary phases were measured by dosing a known volume of particles into a known volume of protein solution contained in 15-ml sterile centrifuge tubes. The tubes were rotated slowly, end over end, for ≈24 h. The supernatant protein concentration was determined by absorbance, and the protein taken up by the stationary phase was calculated by material balance.

Batch Uptake.

Batch uptake experiments were performed in a baffled 100-ml beaker stirred by a paddle supported from above on a glass rod. Protein solution was continually withdrawn through a 10-μm stainless steel filter (model A302, Upchurch Scientific, Oak Harbor, WA) by a peristaltic pump, passed through a spectrophotometric detector (model 226, ISCO) and returned to the beaker through a side port near the base. The protein concentration in the supernatant was monitored via absorbance at 254 nm, with the linearity of the response verified.

Experiments were performed by first establishing a baseline for 74 ml of buffer solution in the beaker, then adding and mixing an appropriate volume of concentrated protein solution and re-establishing a stable absorbance measurement. A measured volume of particles was added and absorbance measurements continued, typically for 90 min. The contents of the beaker were then transferred to a Nalgene bottle and placed on a shaker board for 24 h to confirm consistency of long-time uptake data with batch isotherm measurements.

Results and Discussion

Ionic Strength Effects on Protein Uptake Profiles.

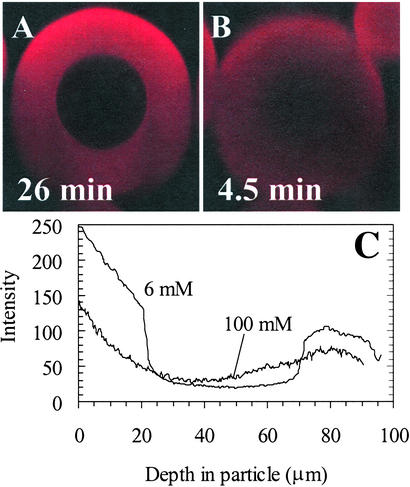
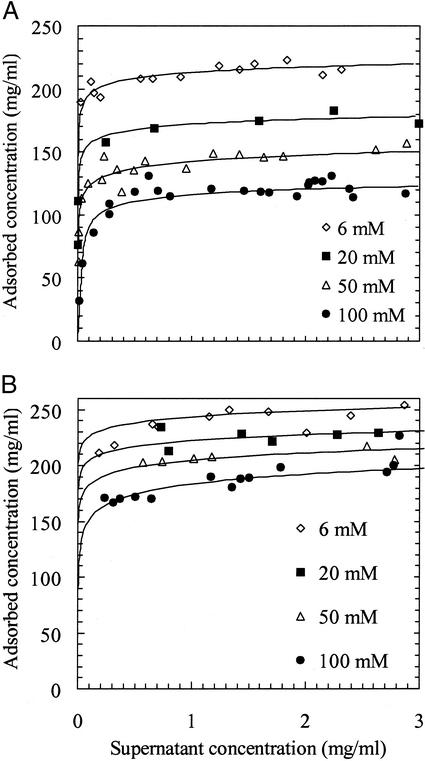
The key effect studied in the experiments was that of ionic strength on lysozyme uptake into cation exchangers. For SP Sepharose Fast Flow at a relatively low ionic strength of 6 mM, a sharp front develops as the protein penetrates into the particle (Fig. 2A). This phenomenon is a classic example of a self-sharpening front that results from pore diffusion with local adsorption equilibrium described by a near-rectangular isotherm (16), known in the limit of a perfectly rectangular isotherm as shrinking core behavior (17). Indeed, isotherms measured for lysozyme in all of the stationary phases in this study were nearly rectangular over the full range of ionic strengths reported; data for SP Sepharose FF and SP 550 C are shown in Fig. 3. Within the framework of the shrinking core model, values of the effective diffusivity can be extracted from the microscopy images directly by using the position of the adsorption front as a function of time (18).

Figure 2.

Digital xz optical sections during lysoyzme-Cy5 uptake into SP Sepharose FF. The attenuation of the signal intensity with depth is caused by absorption and scattering of the incident laser and emitted fluorescent light caused by the base matrix, adsorbed protein molecules, and fluorescence labels. (A) Image using 40 × 1.2 numerical aperture water immersion objective for 6 mM ionic strength and 26 min of uptake of 2.1 mg/ml lysozyme solution at a superficial flow rate of 2,100 cm/h. The time for front penetration to the particle center was ≈40 min. (B) Image using 63 × 1.2 numerical aperture water objective for 100 mM ionic strength and 5 min of uptake of 2.2 mg/ml lysozyme solution at a superficial flow rate of 1,060 cm/h. The time for complete uptake (no significant increase in the image intensity) was ≈15 min. (C) Vertical intensity profiles for images in A and B obtained by drawing a box 10 pixels wide vertically through the center of the particle in Scion (Frederick, MD) image software and averaging the pixels in the horizontal direction to reduce noise in the profiles. (Magnifications: ×330.)

Figure 3.

Adsorption isotherms for lysoyzme on different cation exchangers as a function of ionic strength. (A) SP Sepharose FF. (B) SP 550C.

In contrast to the sharp fronts at low ionic strength, the intraparticle profiles in SP Sepharose FF are unexpectedly diffuse at an ionic strength of 100 mM (Fig. 2B), despite the similarly rectangular isotherms for these conditions. These profiles also indicate that uptake reaches completion much more quickly in this limit than at low ionic strength. A similar transition from sharp fronts to diffuse profiles has been reported in confocal uptake studies of proteins in SP Sepharose FF after increases in the ionic strength and pH (12).

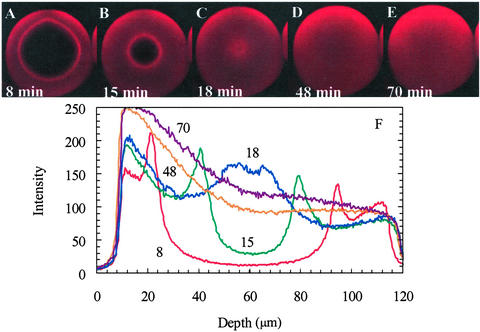
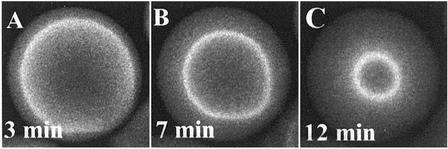
The transition between the two forms of uptake profiles for lysozyme in SP Sepharose FF, at intermediate ionic strengths, is manifested by fluorescence profiles that take on the very intriguing form of a sharp front at which a focused overshoot in intensity appears and propagates into the particle (Fig. 4). The overshoot suggests that there is an increase in the protein concentration at the front, contradicting standard diffusion theories that predict decreasing protein concentration with increasing penetration depth into the particle. In addition, progression of the front is much faster than in the case shown in Fig. 2A, with the time to reach the particle center reduced >2-fold. Furthermore, the full intensity profiles (Fig. 4F) indicate that there is additional uptake after the front reaches the center of the particle, as evidenced by the increase in the intensity profiles on the upper half of the particle between 18 and 54 min. This behavior suggests that local equilibrium, which is usually assumed for intraparticle transport models, is not attained during the initial phase of the uptake.

Figure 4.

(A–E) Time series of xz optical sections during lysozyme-Cy5 uptake in the same SP Sepharose FF particle at 50 mM ionic strength by using a ×63 water objective. The superficial velocity through the bed was 500 cm/h and the lysozyme concentration was 2.3 mg/ml. (F) Vertical intensity profiles from images A–E were obtained by using the same method as in Fig. 2. The focused overshoot at the front is compelling evidence for a nondiffusive contribution to transport. (Magnifications: ×220.)

We have conducted additional characterization experiments to verify that the unexpected fluorescence peak corresponds to an overshoot in lysozyme concentration and is not an artifact of the label or protein impurities. First, the effect appears to be invariant with fluorescent probe type and label ratio over 2 orders in magnitude (Fig. 8, which is published as supporting information on the PNAS web site, www.pnas.org). Second, a confocal uptake experiment using lysozyme-FITC doped with ovalbumin-Cy5 shows that ovalbumin penetrates only the outer region of the particle, ruling out the possibility that the overshoot is caused by ovalbumin, one of the predominant impurities in the lysozyme preparation (Fig. 9, which is published as supporting information on the PNAS web site). Third, confocal uptake experiments with lysozyme lots of different purities (98% and 94%) showed the same overshoot magnitude. If impurities were the cause of the overshoot, the 3-fold change in the impurity content would likely have been observed in the confocal results. Fourth, an isoelectric focusing gel of the unlabeled lysozyme showed only one band, indicating that the lysozyme preparation was very pure in terms of the charge of its constituent proteins, reducing the likelihood that impurities or lysozyme isoforms are the source of the observed overshoot. Finally, to eliminate fluorescent probes completely, we conducted experiments using multiphoton excitation to obtain uptake images from the intrinsic fluorescence of the tryptophan residues in lysozyme (19). Excitation was with a mode-locked titanium:sapphire laser (Coherent Radiation, Palo Alto, CA) with λ = 718 nm and a pulse frequency of ≈80 MHz. The images (Fig. 5) with lysozyme at 50 mM ionic strength reveal an overshoot during uptake, and the time scale for front penetration to the center of the particle is in agreement with the results from the experiments using lysozyme-Cy5.

Figure 5.

Time series of xy optical sections recorded by using multiphoton excitation during uptake of unlabeled lysozyme into SP Sepharose FF with a ×40 oil objective, with the focal depth approximately at the center of the particle. The superficial velocity through the bed was 360 cm/h and the lysozyme concentration was 1.8 mg/ml. The image contrast was enhanced by using Scion image software because of the low signal-to-noise ratio. The particle diameter for this experiment was 87 μm, compared with 105 μm for the lysozyme-Cy5 case, explaining the slightly faster uptake in this case. (Magnifications: ×250.)

The same uptake behavior is reproduced for labeled lysozyme in Toyopearl SP650 C under the same solution conditions as for SP Sepharose FF. In addition, results with α-lactalbumin in Q Sepharose FF, and with ribonuclease A and lactoferrin in SP Sepharose FF, have produced similar overshoots, with a double ring observed in the latter two cases (Fig. 10, which is published as supporting information on the PNAS web site). In contrast, only sharp fronts, as observed for SP Sepharose FF in Fig. 2A, are observed in Toyopearl SP 550 C and SP Spherodex for a range of ionic strengths up to 200 mM at pH 7 (Fig. 11, which is published as supporting information on the PNAS web site).

Batch and Confocal Estimates of Protein Diffusivities.

In view of the large variations in uptake rate apparent from the confocal microscopy data, a comparison with macroscopic batch uptake rates is informative. For batch experiments, the amount of protein taken up as a function of time was determined from the supernatant absorbance measurements by mass balance. Values of effective pore diffusivities can then be estimated by fitting the uptake data to an appropriate transport model. Because the shrinking core model is appropriate for most of the conditions examined, as verified by the confocal images, pore diffusivities (D_p) were estimated by linear regression of the uptake as a function of time t, using the finite volume solution of the model (18). Pore diffusivities from confocal images were calculated from estimates of the fractional uptake, based on the radial position of the adsorption front and the assumption that the adsorption layer was saturated, using linear regression of the infinite volume solution of the model (18):

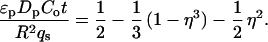1

Here η is the fractional uptake, ɛ_p is the intraparticle porosity, C_o is the feed protein concentration, R is the particle radius, and q_s is the capacity from the measured equilibrium adsorption isotherm.

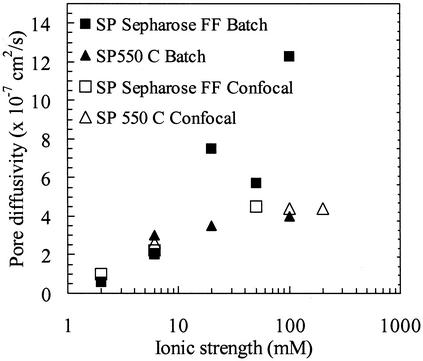
Estimates of the diffusivities from both batch and confocal data are shown in Fig. 6 for SP Sepharose FF and SP 550C over a range of ionic strengths, for experiments with initial protein concentrations of 1.5–2 mg/ml. Excellent agreement is seen between the batch and confocal values for SP 550C, with the diffusivity values varying little over the range of ionic strengths studied. These values, corresponding to ≈40% of the free solution value, are consistent with expectations for lysozyme diffusion in porous media. For SP Sepharose FF, estimates from the batch experiments cover the full range of ionic strengths, whereas those for confocal experiments are shown only where sharp fronts were seen in the images. The agreement between the data from the two methods is reasonable, but most notable is the increase of almost an order of magnitude in the effective pore diffusivity for SP Sepharose FF as the ionic strength is increased. The value at 100 mM ionic strength is higher than the lysozyme free solution diffusivity [1.1 × 10⁻⁶ cm²/s (14)]. This finding confirms the acceleration of uptake with increasing ionic strength, but the value is not a true pore diffusivity in view of the inapplicability of the shrinking core model, as evidenced by the diffuse profiles observed for this condition by confocal microscopy (Fig. 2B).

Figure 6.

Effective diffusion coefficients regressed from the shrinking core model for the batch and confocal uptake of lysozyme in SP Sepharose FF and SP 550 C as a function of the ionic strength for initial lysozyme concentrations of ≈1.5–2 mg/ml. Diffusivity estimates were obtained from measurements of the supernatant concentration as a function of time for batch experiments and from measurements of the adsorption front position for confocal experiments. The free solution diffusivity of lysozyme is 1.1 × 10⁻⁶ cm²/s.

The contrast between the two data sets emphasizes that the change in the confocal intensity profiles in SP Sepharose FF is correlated with a significant acceleration in macroscopic uptake rate that could be exploited to improve column loading efficiency in large-scale separations.

Mechanistic Basis.

The key structural characteristic of the materials showing the change in uptake behavior appears to be the surface charge density, which is significantly higher for SP Sepharose FF and SP 650 C than for the other stationary phases (Table 1). This finding suggests a physical rather than a chemical origin of the effect, which is supported by the fact that SP 550 C and SP 650 C are chemically identical, differing only in pore size distribution and surface charge density, yet only the latter material displays the change in uptake behavior. The fact that the overshoot phenomenon occurs in a narrow range of ionic strength, and correlates with materials with high surface charge densities and with rapid uptake transport, implicates electrostatic effects in its origin. The sharpness of the overshoot also implicates an additional nondiffusive transport mechanism.

Table 1.

Estimated surface charge densities for strong cation-exchange stationary phases

Stationary phase	Surface charge density, C/m2
SP Sepharose	0.36–0.50
Toyopearl SP 650 C	0.44–0.63
Toyopearl SP 550 C	0.066–0.099
SP Spherodex	0.17

These values were determined from manufacturers' ion-exchange capacity information and surface area estimates based on pore size distributions (20). 

We believe that the effect is driven by the radial gradients in the adsorbed protein concentration that develop within the particle during uptake. These concentration gradients give rise to corresponding gradients in the local electrostatic potential caused by screening of the negative surface charge on the adsorbent by the positively charged protein. Adsorption of lysozyme on CM Sephadex (a cellulose-based exchanger similar to SP Sepharose) has been shown to result in a change in sign of the zeta potential from negative to positive (21). These results and our hypothesis suggest that local electric fields in the direction of transport may produce an electrophoretic or other electrokinetic contribution to the protein flux. Similar theories for ion transport in charged membranes have been proposed (22).

We have tested this theory by using a 1D transport model accounting for pore diffusion, electrophoresis of the pore protein, local adsorption kinetics, and a nonlinear adsorption isotherm. The pore protein concentration c and the adsorbed protein concentration q are found as functions of time, t, and radial position, r, from a numerical solution of the governing transport equation

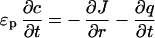2

augmented by the Nernst–Planck equation for the flux,

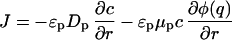3

and a kinetic expression for the local adsorption rate,

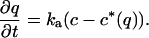4

Here ɛ_p is the particle porosity, D_p and μ_p are the diffusivity and the electrophoretic mobility, respectively, of the protein in the pores, k_a is an adsorption rate constant, c*(q) is the hypothetical pore concentration in equilibrium with the actual adsorbed concentration, and φ(q) is the average electrostatic potential near the stationary-phase surface in the particle. The ratio of the electrophoretic mobility to the diffusivity in the particle pores was assumed to be equal to the corresponding ratio in free solution. The equations were solved by using the method of lines with finite differencing of the spatial derivatives.

The adsorbed layer was assumed to comprise a thin electrolyte layer between a plane containing the stationary-phase surface charge and the adsorbed protein molecules. The average electrostatic potential near the outer surface of the adsorbed layer was estimated by solving the Poisson–Boltzmann equation in the aqueous layers and the Poisson equation in the protein layer, assuming that the charge density at the two aqueous–protein interfaces was equal to the average surface charge density of the protein. A difference of +20 mV in average pore potential for monolayer coverage compared with that for no adsorption was estimated. For low surface coverage, the negative surface potential of the stationary phase should dominate local behavior because the surface is still accessible to protein, whereas for high coverage, the positive potential caused by the adsorbed lysozyme should dominate the local behavior. Therefore, a nonlinear relation (concave up) between the average potential and the protein surface coverage was assumed.

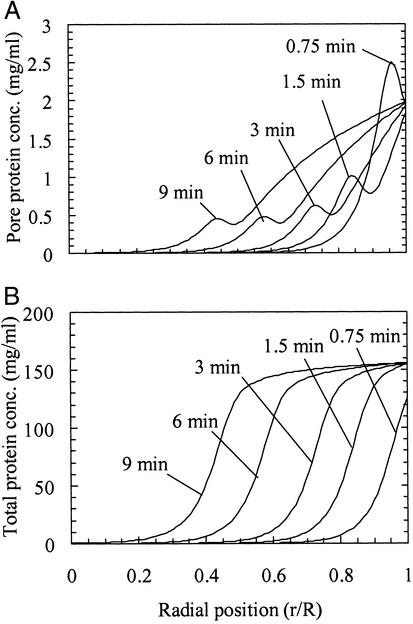
The results of the calculations indicate that an overshoot at the front in the pore concentration profile is possible depending on the value of the Damköhler number (Da = k_aR²/D_p, where R is the particle radius), which characterizes the relative rates of adsorption and diffusion. For very high values of Da, implying local equilibrium, no overshoot in the pore protein concentration is predicted. However, for Da = 200, an overshoot in the pore concentration appears and persists as the protein front penetrates into the particle (Fig. 7A). Therefore, accounting for finite adsorption kinetics leads to an overshoot in pore concentration when electrophoresis is included in the description; the lack of an overshoot for the materials with lower surface charge densities would then be caused by weaker potential gradients along the pore. This finding agrees qualitatively with experiment because the intraparticle intensity profiles from confocal microscopy show that local equilibrium is not attained during the initial front propagation for the 50-mM case (Fig. 4F). In addition, the simulated intraparticle concentration profiles for discrete times during the uptake were integrated to estimate the amount of protein taken up; interpretation of the values in terms of the shrinking core model gave a pore diffusivity of 5.9 × 10⁻⁷ cm²/s, close to the values obtained experimentally from confocal and batch experiments (Fig. 6).

Figure 7.

Calculated concentration profiles for Da = 200 and R = 50 μm. (A) Pore concentration. The calculations show an overshoot in the pore concentration at the front. The finite adsorption rate causes radial gradients in adsorbed protein concentration to be gradual, thus causing the electrophoretic contribution to transport to be significant for the pore protein. (B) Total protein concentration. No overshoot is predicted, because of the near-rectangular adsorption isotherm.

Although the model qualitatively captures the overshoot and accelerated uptake observed experimentally, the theory is not quantitative, because the model does not predict an overshoot in the total protein concentration, which is ≈2 orders of magnitude larger than the pore concentration (Fig. 7B). This finding is not surprising given the highly simplified physical picture captured in the 1D model. We believe that accounting for the protein concentration distribution in the pore cross section will amplify the overshoot caused by the electrophoretic effect, because protein concentrations and electric fields near the surface are expected to be much higher than in the bulk. Other electro-kinetic effects such as electroosmosis may also play a role in this transport behavior.

Seen in isolation, the transition to diffuse profiles at 100-mM ionic strength (Fig. 2B) for the high surface charge density materials suggests a surface diffusion mechanism. However, in light of the overshoot behavior and the apparent importance of sorption kinetics at intermediate salt concentrations, the diffuse profiles may be evidence for weaker adsorption, which would enhance the effective diffusive and electrokinetic mobility of the protein. Because this weaker adsorption can be a consequence, within a mass action framework, of more rapid desorption kinetics, the diffuse profiles may also be consistent with the proposed model.

There are other effects that may contribute to explaining the observed behavior as well. Multicomponent coupled diffusion and adsorption can cause concentration overshoots; as discussed earlier, however, we have gone to great lengths to ensure that such effects are absent for the lysozyme results, although they may contribute to the double rings seen for some other proteins. Purely electrostatic effects resulting from release of counterions from both protein and surface may be a factor, as may effects of coupled diffusion among these species (23). However, one would expect these effects to be most pronounced at very low ionic strengths, where our experiments show behavior completely consistent with the shrinking core model as expected, whereas our more surprising results are seen at moderately high ionic strengths. Coupling effects have also been invoked in another model (24), but several of the diffusivity and adsorption isotherm parameter values used there are unrealistic for our experimental system. Furthermore, the coupling there was implemented via an electroneutrality constraint, but because the transport description did account explicitly for the elecrostatic coupling of diffusion fluxes, the formulation could lead to inconsistencies (G. Carta, personal communication).

Conclusions

The anomalous overshoot in fluorescence intensity at the front penetrating the particle, observed in a variety of systems, suggests that there is a significant nondiffusive contribution to protein transport in ion exchange chromatography, with an electrokinetic model providing results that are qualitatively consistent with the experimental observation. Although the complexity of this system makes a detailed accounting for all of the factors that affect the transport behavior extremely difficult, our model paints a qualitative picture of a possible origin of this very interesting anomalous effect. The correlation with high adsorbent surface charge density also supports this argument. In addition to the mechanistic insights provided by confocal imaging, the correlation of the anomalous behavior with increased uptake rates shows the importance of these findings for bioprocessing productivity. In particular, our results provide clearer guidelines for optimizing protein capture by using existing ion exchange materials. The results may also aid in the design of new materials with improved mass transfer properties as well as new devices for analytical and preparative separations.