Determination of the geometric structure of the metal site in a blue copper protein by paramagnetic NMR

Abstract

The biological function of metalloproteins is closely tied to the geometric and electronic structures of the metal sites. Here, we show that the geometric structure of the metal site of a metalloprotein in solution can be determined from experimentally measured electron-nuclear spin–spin interactions obtained by NMR. Thus, the geometric metal site structure of plastocyanin from Anabaena variabilis was determined by including the paramagnetic relaxation enhancement of protons close to the copper site as restraints in a conventional NMR structure determination, together with the distribution of the unpaired electron onto the ligand atoms. Also, the interproton distances (nuclear Overhauser enhancements) and dihedral angles (scalar nuclear spin–spin couplings) normally used in NMR structure determinations were included as restraints. The structure calculations were carried out with the program x-plor and a module that takes into account the specific characteristics of the paramagnetic restraints. A well defined metal site structure was obtained with the structural characteristics of the blue copper site, including a distorted tetrahedral geometry, a short Cu–Cys S^γ bond, and a long Cu–Met S^δ bond. Overall, the agreement of the obtained metal site structure of Anabaena variabilis plastocyanin with those of other plastocyanins obtained by x-ray crystallography confirms the reliability of the approach.

The biological function of many metalloproteins stems from the geometric and electronic structures of the metal sites imposed by the protein environment. In the blue copper proteins, such as plastocyanins, amicyanins, and azurins, the geometry of the copper site is unusual as compared with small-molecule copper complexes (1–15). In particular, the metal sites of blue copper proteins are characterized by a short copper–sulfur bond. This unusual geometry is believed to be the main reason for the strong covalency of the metal site (10, 16, 17) and, thus, responsible for the rapid and long-range electron transfer reactivity (18–22) that characterizes the blue copper proteins. Detailed knowledge of the geometric and electronic metal site structures of the blue copper proteins is, therefore, imperative for understanding the function of the proteins at the molecular level.

So far, the geometric structure of the metal site in blue copper proteins (12–14) has been determined primarily by x-ray crystallography and extended x-ray absorption fine structure (3, 23, 24), whereas the electronic structure of the blue copper site has been determined theoretically from quantum chemical calculations (5, 25–27) and experimentally by x-ray absorption spectroscopy (16, 17), and more recently by nuclear paramagnetic relaxation (28–31). These structures have formed the basis for a detailed understanding of the biological function of the proteins by elucidating the interplay between the electronic and geometric structure of the metal site (8, 15, 32–34). However, the geometric structures were all determined in the solid state. Yet, the function of metalloproteins refers to the structure and dynamics of the metal sites in solution. Detailed knowledge of the characteristics of the solution structure of the metal site is, therefore, of interest. Previously, it was found that the overall solution structure of an oxidized blue copper protein is very similar to the solution structure of the reduced protein. Thus, the overall structure of oxidized plastocyanin from Synechocytis was determined by NMR and paramagnetic nuclear relaxation (35), by imposing the crystal structure of the first copper coordination sphere on the NMR solution structure.

Here, we present an approach that allows a determination of the geometric structure of the metal sites of paramagnetic metalloproteins in solution. The approach is based on experimental NMR measurements. Thus, the electron–nuclear spin–spin interactions derived from paramagnetic NMR relaxation rates are included as restraints in a conventional NMR structure determination, together with interproton distance restraints (nuclear Overhauser enhancements; NOEs) and dihedral angle restraints (scalar nuclear spin–spin couplings) normally used for structure determination of proteins by NMR (36). Because the paramagnetic restraints are derived from the relaxation rates of nuclei close to the metal site, the point dipole approximation of the electron spin fails and a description of the paramagnetic relaxation that takes the electron delocalization into account must be used (37). Therefore, the approach requires knowledge of the distribution of the unpaired electron spin, which can be obtained experimentally by x-ray absorption spectroscopy (16, 17), electron nuclear double resonance (38), paramagnetic NMR (28–31) spectroscopy, or theoretically by quantum chemical calculations (5, 25–27). The blue copper protein, plastocyanin from Anabaena variabilis (A.v.), was used as an example. So far, the metal site structure of this plastocyanin has not been determined, yet recent detailed spectroscopic studies (31) indicate that the structure is similar to those of other plastocyanins (9, 11, 22).

Theory

The paramagnetic relaxation enhancements of the nuclei in metalloproteins are caused by the time-dependent modulation of the spin–spin interactions between the nuclei and the unpaired electron spin. Two different mechanisms contribute to the interaction, namely the dipolar spin–spin interaction (through space) and the scalar Fermi contact interaction (through bonds). Because of the relatively long electron relaxation time, τ_s, of the blue copper proteins (28, 39), the longitudinal paramagnetic relaxation rate, R_1p, of the protons is, to a good approximation, affected only by the dipolar interaction (37, 40–43)

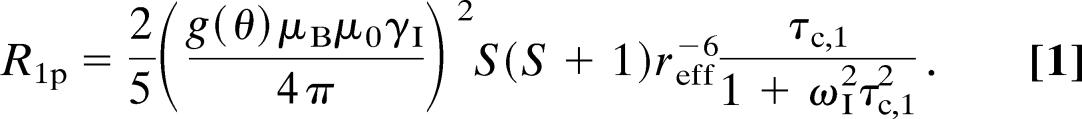Here, μ₀ is the magnetic permeability of free space, μ_B is the Bohr magneton, γ_I is the nuclear gyromagnetic ratio, S is the spin quantum number of the unpaired electron(s), ω_I is the Larmor frequency of the protons, and r_eff is the effective electron–proton distance. Furthermore, τ_c,1 is the correlation time for the modulation of the electron–nuclear dipolar interaction and is given by τ_c,1⁻¹ = τ_R⁻¹ + τ_s⁻¹ , where τ_R is the rotational correlation time of the protein. Finally, g(θ) is the electron g-factor at the position of the proton, where θ is the polar angle of the proton position in the principal coordinate system of the axial g-tensor (42, 43). The axial and equatorial value of the g-tensor used in the analysis was determined previously by EPR (5) (g_‖ = 2.226 and g_⊥ = 2.054). The effective electron–nucleus distance, r_eff, depends on the metal–nucleus distance and the unpaired electron spin distribution. A detailed analysis of r_eff and the structural information of this parameter is given below.

In contrast to the longitudinal paramagnetic relaxation, the transverse relaxation, R_2p, is affected both by the dipole interaction and the Fermi contact interaction (37, 40, 44)

where

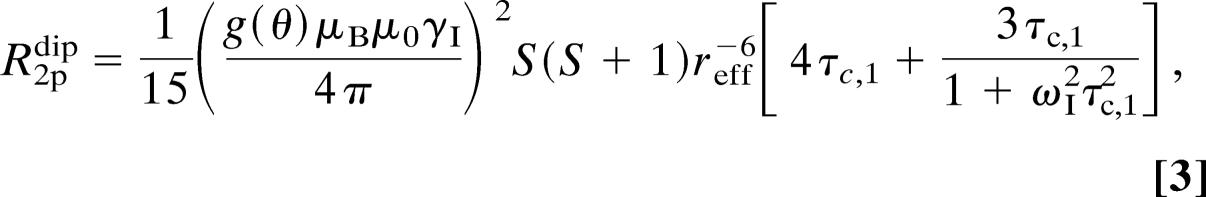and

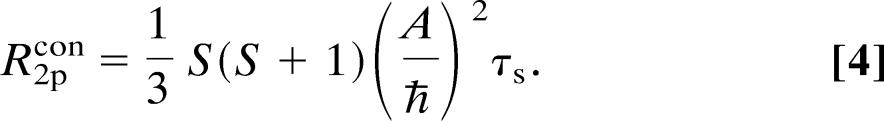Here, A is the electron–nucleus hyperfine scalar coupling constant and ħ is the Planck constant divided by 2π, and the remaining symbols are as defined above.

Also, the chemical shifts of the nuclei are affected by both of the electron–nuclear interactions, giving rise to a pseudo-contact shift (dipolar) and a Fermi contact shift (scalar), respectively. For nuclei located within a few bonds from the metal site, the Fermi contact shift will dominate, and the hyperfine shift is given by (45)

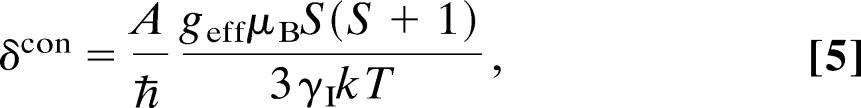where g_eff is the effective value of the g-tensor, k is the Boltzmann constant, and T is the absolute temperature.

Results and Discussion

Effective Nucleus–Electron Spin Distance r_eff.

If the point dipole approximation (40) applies, that is, the unpaired electron spin is located exclusively at the center of the metal ion, the effective distance, r_eff, in Eq. 1 reduces to the geometric distance between the nucleus and the metal ion. However, the point dipole approximation does not apply to the relaxation of nuclei close to the metal ion, because the unpaired electron spin is delocalized onto the ligand atoms, as demonstrated in previous studies of the paramagnetic relaxation of nuclei near metal sites (30, 41, 46). Therefore, to derive metal–nucleus distances from the paramagnetic relaxation rates of nuclei close to the metal site, the electron spin must be described by a density function, ρ(r), that takes into account the spatial distribution of the unpaired electron(s). Thus, for protons close to the metal ion, the effective nucleus–electron distances, r_eff, that is obtained from the dipolar paramagnetic relaxation rates, Eqs. 1 and 3, is given by (37)

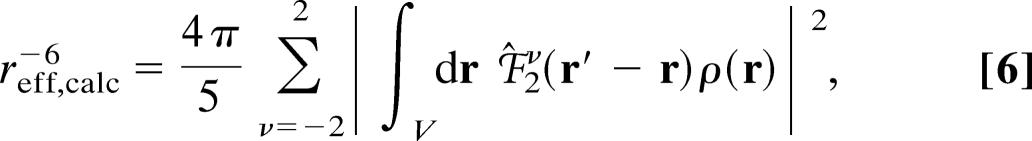where ρ(r) is the density of the unpaired electron spin, $\widehat{ℱ}$₂^ν(r) = ‖r‖⁻³ Y₂^ν (r/‖r‖) is the spatial component of the electron–nucleus dipolar operator, and r′ is the position of the proton. Furthermore, Y₂^ν (r/‖r‖), ν = −2, … , 2, is the five-dimensional irreducible tensor component of the spherical harmonics. Hence, r_eff, which can be derived from the paramagnetic relaxation rate, depends on both the electron spin distribution, ρ(r), and the position, r′, of the proton relative to the metal site.

Distribution of the Unpaired Electron Spin in Plastocyanin.

The copper ion in plastocyanin is coordinated to the S^γ atom of a cysteine and the aromatic N^δ atom of two histidines with strong covalent bonds. Furthermore, the copper is weakly coordinated to the S^δ atom of a methionine, resulting in a distorted tetrahedral coordination sphere (5, 9–11, 16, 17, 38). The electronic structure of the blue copper site of plastocyanin has been studied extensively during the last decades both by experimental approaches (5, 16, 17, 38) and quantum chemical calculations (5, 10, 25–27, 47). It was found that the unpaired electron spin density is located predominately at the atomic orbitals of the four atoms in the trigonal NNS-plane, i.e., the copper atom, the Cys S^γ ligand, and the two aromatic His N^δ ligands (5, 16, 17, 25–27, 30), whereas the electron spin density at the Met S^δ atom and the Cys H^β is small (26–28, 38). Yet, it was found recently (31) that also the latter orbitals must be included in the description of the unpaired electron spin density to obtain a reliable prediction of the paramagnetic relaxation of the protons close to the copper site. Therefore, the total unpaired electron spin density was described by seven hydrogen-like atomic orbitals, that is, a 3d orbital centered at the copper atom, a 3p orbital centered at each of the ligand sulfur atoms Cys S^γ and Met S^δ, a 2p orbital centered at each of the His N^δ ligands, and a 1s orbital centered at each of the β-protons of the ligand cysteine (see Table 2, which is published as supporting information on the PNAS web site). The integral in Eq. 6 was evaluated, assuming that the unpaired electron spin density, ρ(r), is parameterized by the hydrogen-like Slater-type atomic orbitals mentioned above and that overlap spin population can be neglected (37). Thus

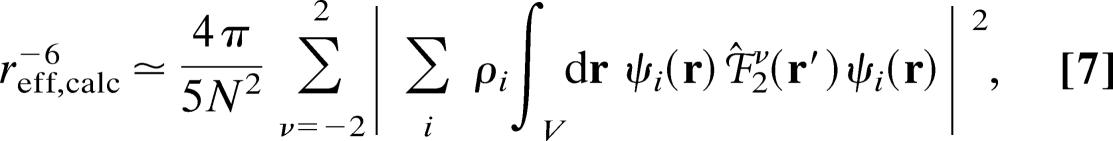where ψ_i(r) are the hydrogen-like orbitals, N is a normalization constant, and ρ_i are the atomic spin densities of the individual atoms included in the parameterization of the spin density. The effective charge, Z_eff, used for the individual hydrogen-like orbitals was determined from the radial function of the pure natural atomic orbitals (48) obtained in a density functional theory calculation (31). The integral in Eq. 7 was solved as described in Supporting Text, which is published as supporting information on the PNAS web site.

Solution Structure of the Copper Site.

According to Eq. 7, the geometric structure can be determined from the paramagnetic relaxation rates, provided the overall electron spin distribution, ρ(r), is known. Here, the latter was described by the seven hydrogen-like atomic orbitals mentioned above and given in Table 2. The paramagnetic relaxation rates were included as restraints in the structure calculations by a module written for the program x-plor 3.851 (49). The module calculates the effective electron–nucleus distances, r_eff, (Eq. 7) from the unpaired electron spin density. Furthermore, the module includes a pseudopotential, E_prlx, which ensures that the paramagnetic restraints are weighted according to their relative uncertainties, as detailed in Eq. 9. Only paramagnetic relaxation restraints of backbone and ligand residue protons were used to avoid additional complexity arising from dynamical processes.

Thus, the geometric structure was obtained by including the paramagnetic relaxation rates as restraints in the structure calculations together with the electron spin distribution, ρ(r), and the conventional interproton distances and dihedral angle restraints (50, 51), except for those close to the metal site. The applied procedure is further detailed in Supporting Text. The total energy, E_total, for the target function, obtained in each of the structure calculations, is given by

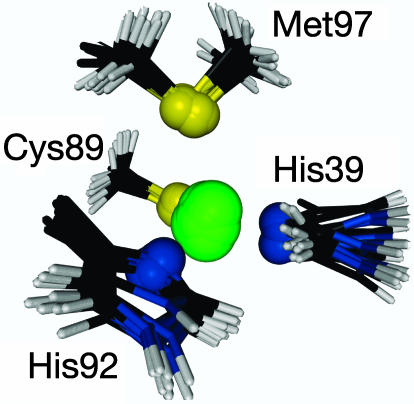
where E_prlx is the energy of the paramagnetic restraints given by Eq. 9, E_chem is the energy that corresponds to the deviation from an ideal chemical geometry, E_dihed is the energy of the dihedral angle restraints, E_vdw is the van der Waals energy, and E_noe is the energy of the interproton distance restraints (49). The final set of geometric structures was determined as the set of 10 structures with the lowest total energy, E_total. That is, the 10 structures selected are those with the best simultaneous agreement of all of the restraints included in the structure calculation. The copper coordination sphere of these structures is shown in Fig. 1.

Fig. 1.

The first coordination sphere of the copper site of A.v. plastocyanin. The superimposed structures are the 10 structures with lowest E_total energy. The rms deviation of the ligand atoms of the 10 structures is 0.17 Å. The figure was made with the program molmol (57).

To evaluate the robustness of the method, the structure calculations were repeated for a series of different combinations of the unpaired spin densities on the copper and the ligand atoms, as shown in Fig. 5, which is published as supporting information on the PNAS web site. For the variation of ρ_Cu within the region from 0.40 to 0.50 or 0.85 < ρ_Cu/ρ_S < 1.35, which is considered as the region for the covalency of the blue copper site (15), the copper–ligand distances vary in a smooth manner, illustrating the robustness of the method. For the variation of ρ_Cu within the larger region from 0.35 to 0.55, the copper–ligand distances still vary in a smooth manner. Moreover, a more precise location of the Met-97 S^δ atom is obtained, if a single diverging structure is neglected from the ensemble of 10 calculated structures, as shown in Fig. 5.

Evaluation of the Obtained Metal Site Structure.

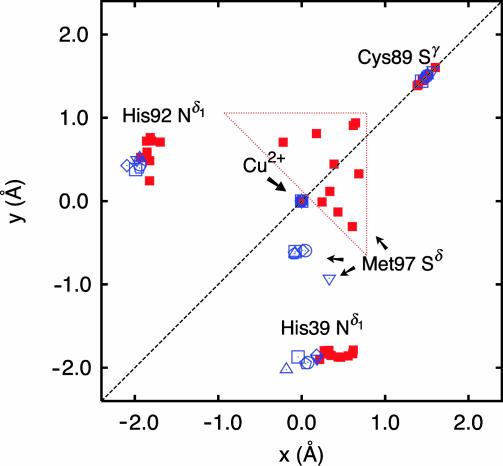
As shown in Table 1, a well-defined solution structure of the metal site of A.v. plastocyanin is obtained from the nuclear paramagnetic restraints. The metal site has a distorted tetrahedral geometry with the copper atom bound to the same ligands as found previously for other plastocyanins by x-ray crystallography (2, 4, 12–14, 52), EPR spectroscopy (5, 10), and extended x-ray absorption fine structure spectroscopy (23). This similarity also includes a long Cu–Met S^δ bond and a relative short Cu–Cys S^γ bond. Table 1 summarizes the average bond lengths and angles of the copper site of the 10 A.v. plastocyanin structures shown in Fig. 1 and compares them with the corresponding bond lengths and angles of other plastocyanins obtained by x-ray crystallography. The position in the NNS plane of the ligand atoms of the 10 A.v. plastocyanin structures and the crystal structures are illustrated in Fig. 2.

Table 1.

Comparison of bond lengths and dihedral angles in the catalytic site of plastocyanins

Structural parameters	A.v.*	P.n.†	S.o.‡	U.p.§	D.c.¶	E.p.∥	S. sp.**
Bond lengths, Å
Cu–NH39	1.94 ± 0.01	1.91	1.96	2.08	1.99	1.90	1.97
Cu–SC89	2.12 ± 0.03	2.07	2.15	2.18	2.23	2.12	2.14
Cu–NH92	1.98 ± 0.01	2.06	2.01	2.06	2.06	2.17	2.01
Cu–SM97	2.80 ± 0.04	2.82	2.88	2.69	2.94	2.92	2.64
Bond angles, °
NH39–Cu–SC89	118 ± 2	132	130	133	128	125	131
NH39–Cu–NH92	116 ± 3	97	103	96	106	104	101
NH39–Cu–SM97	106 ± 5	89	87	90	81	90	86
SC89–Cu–NH92	114 ± 2	121	120	115	119	120	121
SC89–Cu–SM97	88 ± 2	110	106	105	107	108	108
NH92–Cu–SM97	105 ± 2	101	102	113	108	102	99
Geometric distances, Å
Cu–NNS††	0.35 ± 0.07	0.36	0.31	0.47	0.35	0.38	0.29

*The average of the 10 structures with lowest energy shown in Fig. 1. The uncertainties are the standard deviations of the mean for the bond lengths and angles calculated for the structures in Fig. 1.

^†Angles and distances from the crystal structure of poplar plastocyanin from Populus nigra at pH 6.0 (9) (PDB ID code 1PLC).

^‡Angles and distances from the crystal structure of spinach plastocyanin from Spinacia oleracea at pH 4.4 (11) (1AG6).

^§Angles and distances from the crystal structure of oxidized plastocyanin from the green alga Ulva pertusa at pH 6.0 (14) (1IUZ).

^¶Angles and distances measured in the crystal structure of oxidized plastocyanin from Dryopteris crassirhizoma at pH 4.5 (12) (1KDJ).

^∥Angles and distances from the crystal structure of plastocyanin from the green alga Enteromorpha prolifera (7) (7PCY).

**Angles and distances measured in the crystal structure of oxidized plastocyanin from the cyanobacterium Synechococcus sp. at pH 5.0 (13) (1BXU).

^††The distance from the copper ion to the plane formed by His-39 N^δ1, His-92 N^δ1, and Cys-89 S^γ. The positive value indicates that the copper atom is located toward the Met-97 S^δ ligand from the NNS-plane.

Fig. 2.

The location in the NNS-plane (the x, y-plane) of the ligand atoms, His-39 N^δ1, Cys-89 S^γ, and His-92 N^δ1 of the 10 structures in Fig. 1; ■, shown in red, and of six different crystal structures, shown in blue. The six crystal structures are as follows: □, the crystal structure of poplar Populus nigra plastocyanin at pH 6.0 (9) (Protein Data Bank ID code 1PLC); ○, the crystal structure of spinach plastocyanin from Spinacia oleracea at pH 4.4 (11) (1AG6); ▵, the crystal structure of oxidized plastocyanin from the green alga Ulva pertusa at pH 6.0 (14) (1IUZ); ▿, the crystal structure of oxidized plastocyanin from Dryopteris crassirhizoma at pH 4.5 (12) (1KDJ); (◇), crystal structure of plastocyanin from the green alga Enteromorpha prolifera (7) (7PCY); ⌂, crystal structure of oxidized plastocyanin from the cyanobacterium Synechococcus sp. at pH 5.0 (13) (1BXU). The dashed line corresponds to the pseudo C_s symmetry mirror plane.

Overall, the metal site structure obtained here for A.v. plastocyanin in solution is in good agreement with the structures determined previously for other plastocyanins by x-ray crystallography. This agreement includes the relative position of the covalently bound ligands in the trigonal NNS plane, as shown in Fig. 2 and Table 1. Thus, the bond lengths and bond angles of the strongly bound Cys S^γ and His N^δ atoms of the 10 structures obtained here are in agreement with the crystal structures. Furthermore, the paramagnetic NMR restraints predict a Cu–His-92 N^δ bond that is longer than the Cu–His-39 N^δ bond, in agreement with the crystal structures.

A significant difference is observed only for the weakly bound Met S^δ ligand atom. Thus, even though the long and weak bonding of this ligand atom in the 10 NMR solution structures (Fig. 1) is in agreement with the corresponding distance in the crystal structure of other plastocyanins (8), the Met S^δ ligand atom is closer to the pseudo C_s symmetry plane in the NMR structures than it is in the crystal structures (see Fig. 2). The significance of this deviation from the crystal structure is confirmed by the paramagnetic relaxation rates of the Met H^γ atoms in spinach plastocyanin. For this plastocyanin, the experimental paramagnetic relaxation rates of the Met H^γ side-chain protons are at variance with the corresponding rates obtained by density functional theory calculations based on the crystal structure (31). This finding is in contrast to the paramagnetic relaxation of the side-chain protons of the other ligand residues, which are predicted correctly by the density functional theory calculations. Yet, the ensemble of NMR structures in Fig. 1 is in good agreement with the paramagnetic relaxation of all the side-chain protons of the ligand residues. Therefore, the results here indicate a small difference between the solution and crystal structures of the metal site of plastocyanin at the position of the Met S^δ ligand atom. Still, the location of this ligand atom is relatively uncertain as indicated in Fig. 2, which could be due to a relatively large flexibility of the residue in the structure calculation.

Conclusions

It is shown that the geometric structure of the copper site of a blue copper protein can be determined by paramagnetic NMR relaxation restraints that are derived from the spin–spin interactions between the unpaired electron of the copper site and the protons of residues close to the metal site. The analysis takes into account the distribution of the unpaired electron onto the ligand nuclei, which allows a correct description of the paramagnetic relaxation of the protons close to the copper site and, thereby, a reliable determination of the geometric structure from the paramagnetic relaxation rates. Overall, the obtained structure of the metal site of A.v. plastocyanin is in agreement with the crystal structures of the copper site of other plastocyanins. In particular, good agreement is obtained for the relative position of the strongly covalently bound ligands in the trigonal NNS plane, the short Cu–Cys S^γ bond, and the long Cu–Met S^δ bond. Only the Met S^δ ligand atom seems closer to the pseudo C_s symmetry plane in the NMR structure than it is in the crystal structures. Finally, the approach presented here is, in principle, applicable to other paramagnetic metalloproteins, if the electron spin density can be parameterized and the paramagnetic relaxation enhancements can be obtained for a sufficient number of protons close to the metal site.

Materials and Methods

Sample Preparation.

Plastocyanin from the blue-green bacteria A.v., prepared and purified as described in refs. 50 and 53, was kindly supplied by Jens Ulstrup and Hans E. M. Christensen (Technical University of Denmark, Kongers Lyngby, Denmark). The protein was dissolved in 99.99% D₂O at pH 7.0 (meter reading). All samples contained 100 mM NaCl.

NMR Experiments.

The NMR experiments were performed at 298.2 K and a ¹H frequency of 800 MHz. The signal eliminating relaxation filter experiment (54) was used for measuring the relaxation rates of the fast relaxing contact shifted signals, as described in ref. 30. The saturation transfer experiment (28), which detects paramagnetically broadened signals not observed in the NMR spectrum, was performed by using a water-eliminated Fourier transform sequence (55) with selective saturation during the interpulse delay: Δ − 180_x − SAT(on, off) − 90_x − Acq(t_a). Two spectra were recorded in difference mode with different radiation frequencies for the saturation pulse, that is “on” and “off.” The saturation frequency on was varied between 200 and 1,010 ppm in steps of 90 ppm, whereas the off saturation frequency was positioned symmetrically to the on values with respect to the HDO solvent signal. The acquisition time, t_a, was 60 ms, the saturation delay was 43 ms, and the recycle delay, Δ, was 3 ms.

Determination of the Paramagnetic Relaxation Enhancement.

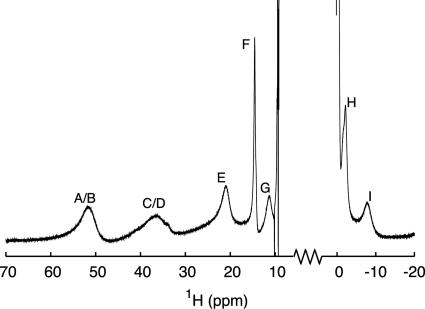
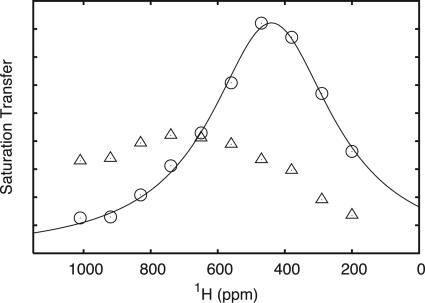
The paramagnetic relaxation enhancements used as restraints in the structure determination were obtained by one of two different procedures. The majority of the relaxation enhancements, which stems from protons observable in the signal eliminating relaxation filter experiment (Fig. 3; see also Fig. 6, which is published as supporting information on the PNAS web site), were determined directly as the relaxation rates of the hyperfine shifted signals of a 1.8 mM fully oxidized A.v. plastocyanin sample. A diamagnetic contribution of 1 s⁻¹ was subtracted from the measured rates. For the Cys-89 H^β2 proton, the hyperfine shifted signal was too broad to be observed directly, and the paramagnetic dipolar relaxation of this proton was determined as R_2p^dip (Eq. 3), derived from the transverse paramagnetic relaxation (Eq. 2), the Fermi contact relaxation (Eq. 4), and the Fermi contact shift (Eq. 5). The R_2p rate and δ_con shift were obtained by a series of saturation transfer experiments (28), using a 50% oxidized sample, and derived from the linewidth and frequency of the Cys-89 H^β2 signal defined by the intensity profile (Fig. 4). Stereospecific assignment of the Cys-89 β-protons was made as described in Supporting Text (see also Table 3, which is published as supporting information on the PNAS web site).

Fig. 3.

A ¹H signal eliminating relaxation filter spectrum showing the hyperfine shifted signals in oxidized A.v. plastocyanin. The spectrum was recorded at 800 MHz by using the following parameters: R₁^o = 50 s⁻¹, R₁^S = 2s⁻¹, t_a (Δ₀) = 90 ms, ζ = 1, and τ = 91 ms. The assignment is (22): His-92 H^δ2 (A), His-39 H^δ2 (B), His-92 H^ε1 (C), His-39 H^ε1 (D), Met-97 H^γ2 (E), Asn-40 H^α (F), Met-97 H^γ1 (G), His-39 H^β1 (H), and Cys-89 H^α (I). The spectrum is in good agreement with those of other plastocyanins (22), indicating a close similarity of the metal site structures.

Fig. 4.

The profiles of the hyperfine shifted signals of Cys-89 H^β1 (▵) and the Cys-89 H^β2 (○) obtained by a series of saturation transfer experiments with different saturation frequencies (28) (see text). The full-drawn line corresponds to a least-squares fit of a Lorentzian function to the saturation transfer of Cys-89 H^β2. The spectral parameters obtained in the least-squares fit are as follows: ω₀ = 440 ± 4 ppm, Δν_1/2 = 221 ± 8 ppm, in good agreement with the corresponding parameters obtained for other plastocyanins (28).

Pseudopotential for the Paramagnetic Relaxation Restraints.

The structure calculations were carried out as detailed in Supporting Text by using the program x-plor (49). A module for analyzing the paramagnetic relaxation was integrated in the program.

The pseudopotential, E_prlx, included in the target function of x-plor by the module was defined as

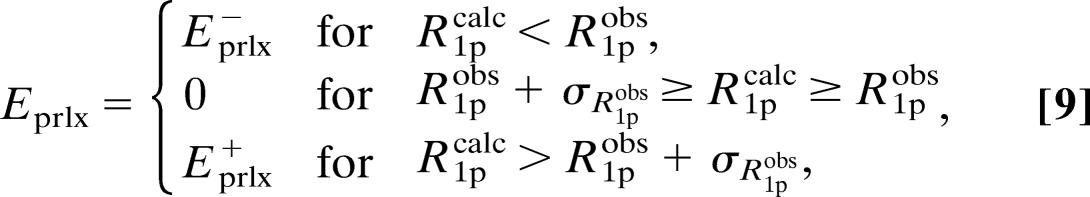and

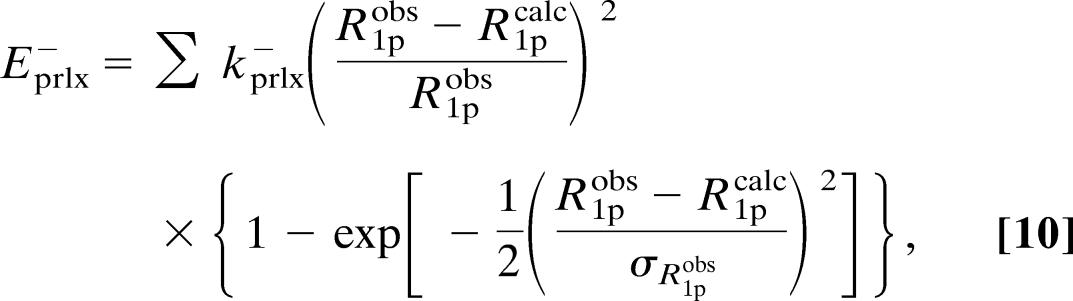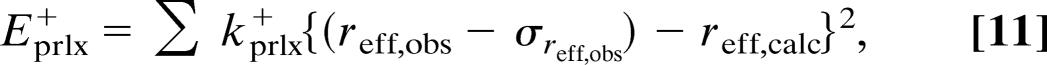where the summation includes all of the paramagnetic relaxation restraints. Furthermore, k_prlx^± is the force constant, R _1p ^obs is the experimentally observed paramagnetic relaxation enhancement, and R_1p^calc is the relaxation enhancement calculated from the structure using Eq. 1, the dipole integral, Eq. 7, and the unpaired electron spin density parameterized as described in the text and shown in Table 2. Finally, σ R_1p^obs is the uncertainty of the observed paramagnetic relaxation rate, R_1p^obs. The definitions in Eq. 9 ensure that the pseudopotential and its first derivative are continuous for all values of R_1p^obs, R_1p^calc, and σ R_1p^obs.

The pseudopotential, E_prlx, given in Eqs. 9–11, is the normalized form of the potential applied in ref. 56. The normalization used here ensures that restraints with identical relative uncertainty are weighted equally in the structure calculation. Furthermore, the Gaussian function (Eq. 10) ensures a correct incorporation of the paramagnetic restraints and their uncertainties in the structural calculation, assuming the uncertainties are Gaussian. To avoid unrealistically high E_prlx energies for R_1p^calc > R_1p^obs + σ R_1p^obs, a quadratic extension of the pseudopotential (Eq. 11) was implemented as suggested in ref. 56. Finally, the pseudopotential in Eq. 9 is asymmetric in the distance domain, which ensures that the nuclei with paramagnetic relaxation restraints are not pulled too close to the paramagnetic center by the r⁻⁶ distance dependence, if fluctuations in the structure occur. This approach prevents a violation of the conventional diamagnetic NOE and dihedral angle restraints.

Structure Calculations.

A total of 11 paramagnetic relaxation restraints were included in the structure calculations, together with the majority of the conventional NOE and dihedral angle restraints determined previously (51) from reduced A.v. plastocyanin. Only paramagnetic restraints from the ligand residues and the hydrogen-bonded asparagine were included in the calculations. These residues are His-39, Asn-40, Cys-89, His-92, and Met-97 (see Table 4, which is published as supporting information on the PNAS web site). Most of the conventional restraints from the protein framework were used, including the interresidue NOEs between the ligand residues and the protein frame. Only the NOEs between side-chain atoms of the ligand residues (His-39, Cys-89, His-92, and Met-97) were excluded, to allow the metal site to be defined exclusively by the paramagnetic restraints. Also, the hydrogen bonds from slowly exchanging amide protons used previously as restraints were left out here.

The crystal structures of other plastocyanins show a pseudosymmetry of the copper site. Thus, for five of the six crystal structures listed in Table 1 the His-39 N^δ–Cu–Cys-89 S^γ angle is within 11° of the His-92 N^δ–Cu–Cys-89 S^γ angle. Therefore, in the high-temperature part of the structure calculation (>800 K; see Supporting Text) of A.v. plastocyanin these two angles were allowed to vary within 15°. More specifically, a flat-bottomed quadratic potential with a force constant of 100 kcal·mol⁻¹·rad² was used for this restrain. This symmetry potential keeps the structure of the metal site within reasonable limits during the high-temperature dynamics. The symmetry restrain was not included in the final low-temperature structure calculation. The final angles obtained are within 10°, as shown in Table 1.

Computational Details.

All data analyses and computations, including the structure calculations, were carried out on an Apple xserve cluster with 34 processors.

Abbreviations

A.v.

Anabaena variabilis

NOE

nuclear Overhauser enhancement