Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1985 Mar;47(3):357–366. doi: 10.1016/S0006-3495(85)83926-6

Bursting, beating, and chaos in an excitable membrane model.

T R Chay, J Rinzel
PMCID: PMC1435203  PMID: 3884058

Abstract

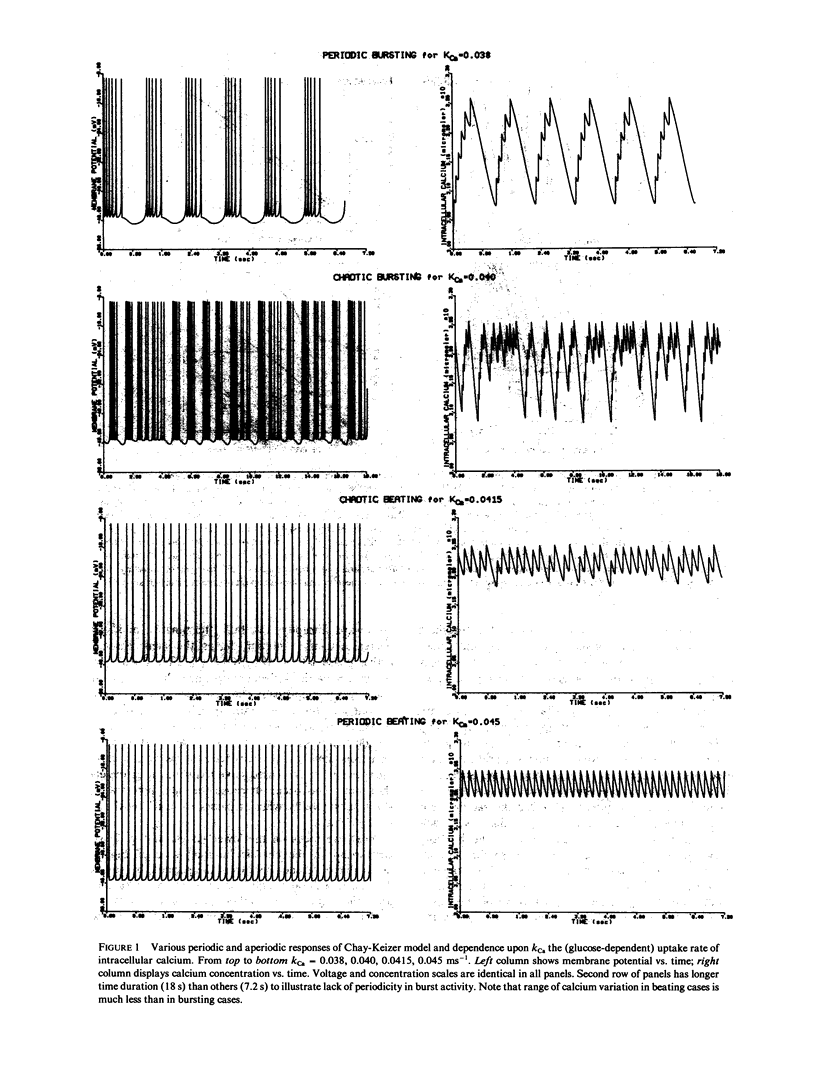
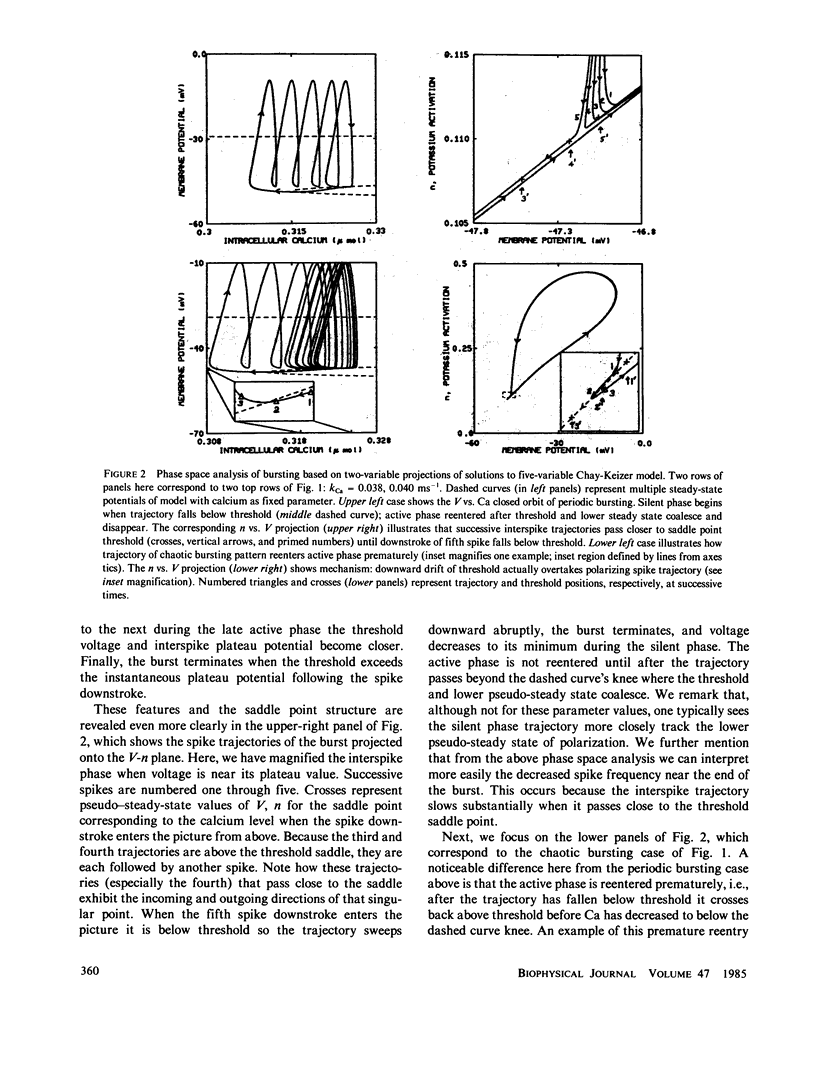
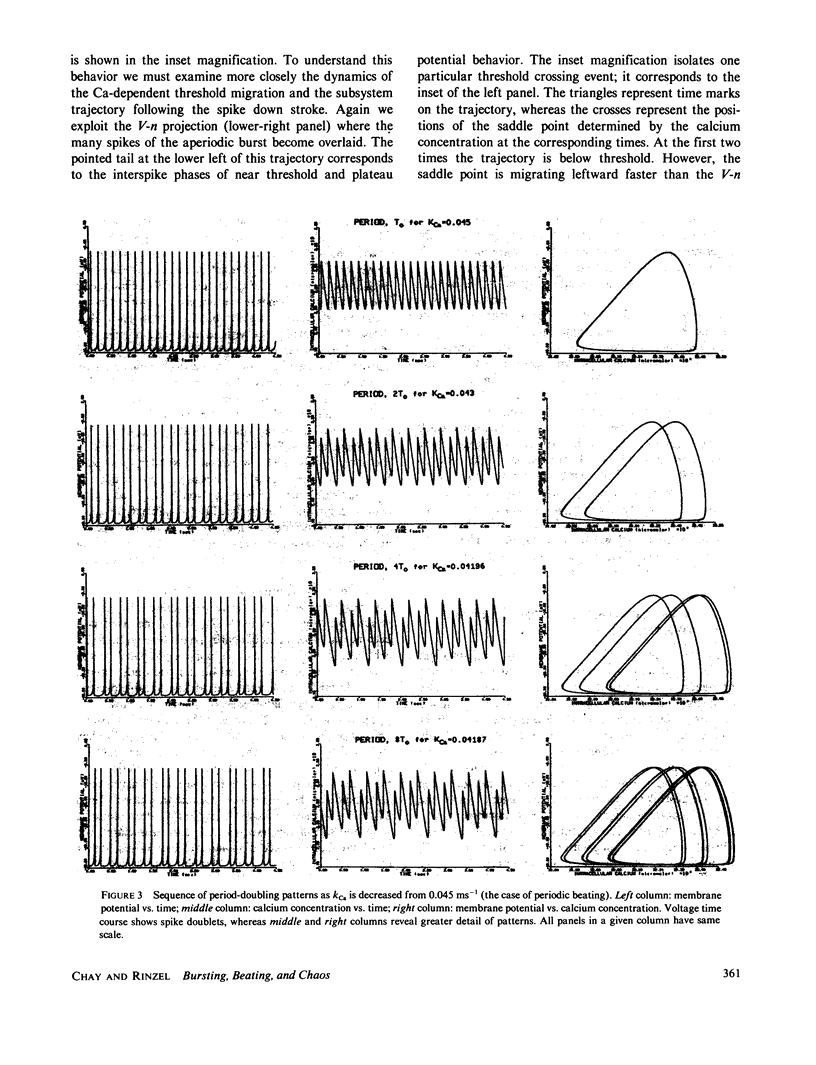
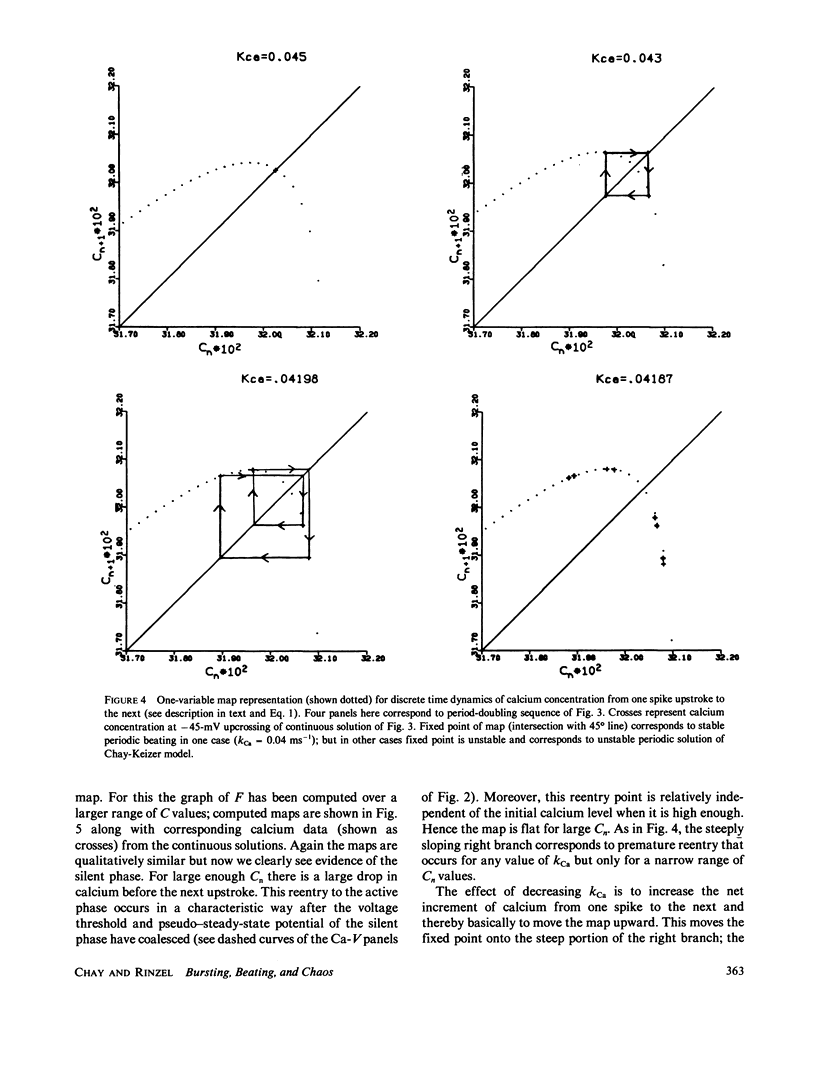
We have studied periodic as well as aperiodic behavior in the self-sustained oscillations exhibited by the Hodgkin-Huxley type model of Chay, T. R., and J. Keizer (Biophys. J., 1983, 42:181-190) for the pancreatic beta-cell. Numerical solutions reveal a variety of patterns as the glucose-dependent parameter kCa is varied. These include regimes of periodic beating (continuous spiking) and bursting modes and, in the transition between these modes, aperiodic responses. Such aperiodic behavior for a nonrandom system has been called deterministic chaos and is characterized by distinguishing features found in previous studies of chaos in nonbiophysical systems and here identified for an (endogenously active) excitable membrane model. To parallel the successful analysis of chaos in other physical/chemical contexts we introduce a simplified, but quantitative, one-variable, discrete-time representation of the dynamics. It describes the evolution of intracellular calcium (which activates a potassium conductance) from one spike upstroke to the next and exhibits the various modes of behavior.

Full text

PDF
361

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Atwater I., Dawson C. M., Scott A., Eddlestone G., Rojas E. The nature of the oscillatory behaviour in electrical activity from pancreatic beta-cell. Horm Metab Res Suppl. 1980;Suppl 10:100–107. [PubMed] [Google Scholar]
  2. Chay T. R. Abnormal discharges and chaos in a neuronal model system. Biol Cybern. 1984;50(4):301–311. doi: 10.1007/BF00337079. [DOI] [PubMed] [Google Scholar]
  3. Chay T. R., Keizer J. Minimal model for membrane oscillations in the pancreatic beta-cell. Biophys J. 1983 May;42(2):181–190. doi: 10.1016/S0006-3495(83)84384-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. FITZHUGH R. Thresholds and plateaus in the Hodgkin-Huxley nerve equations. J Gen Physiol. 1960 May;43:867–896. doi: 10.1085/jgp.43.5.867. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Glass L., Mackey M. C. Pathological conditions resulting from instabilities in physiological control systems. Ann N Y Acad Sci. 1979;316:214–235. doi: 10.1111/j.1749-6632.1979.tb29471.x. [DOI] [PubMed] [Google Scholar]
  6. Guevara M. R., Glass L., Shrier A. Phase locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cardiac cells. Science. 1981 Dec 18;214(4527):1350–1353. doi: 10.1126/science.7313693. [DOI] [PubMed] [Google Scholar]
  7. HODGKIN A. L., HUXLEY A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Meissner H. P. Electrical characteristics of the beta-cells in pancreatic islets. J Physiol (Paris) 1976 Nov;72(6):757–767. [PubMed] [Google Scholar]
  9. Plant R. E., Kim M. Mathematical description of a bursting pacemaker neuron by a modification of the Hodgkin-Huxley equations. Biophys J. 1976 Mar;16(3):227–244. doi: 10.1016/S0006-3495(76)85683-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Ritzenberg A. L., Adam D. R., Cohen R. J. Period multupling-evidence for nonlinear behaviour of the canine heart. Nature. 1984 Jan 12;307(5947):159–161. doi: 10.1038/307159a0. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES