Abstract
The structure and stabilities of the intermediates affect protein folding as well as misfolding and amyloid formation. By applying Kramer's theory of barrier crossing and a Morse-function-like energy landscape, we show that intermediates with medium stability dramatically increase the rate of amyloid formation; on the other hand, very stable and very unstable intermediates sharply decrease amyloid formation. Remarkably, extensive molecular dynamics simulations and conformational energy landscape analysis of Aβ25–35 and its N27Q mutant corroborate the mathematical description. Both experimental and current simulation results indicate that the core of the amyloid structure of Aβ25–35 formed from residues 28–35. A single mutation of N27Q of Aβ25–35 makes the Aβ25–35 N27Q amyloid-free. Energy landscape calculations show that Aβ25–35 has extended intermediates with medium stability that are prone to form amyloids, whereas the extended intermediates for Aβ25–35 N27Q split into stable and very unstable species that are not disposed to form amyloids. The results explain the contribution of both α-helical and β-strand intermediates to amyloid formation. The results also indicate that the structure and stability of the intermediates, as well as of the native folded and the amyloid states can be targeted in drug design. One conceivable approach is to stabilize the intermediates to deter amyloid formation.
INTRODUCTION
Polypeptide chains can exist in many structural forms, such as unfolded, natively folded, and misfolded. The native folded state is the biological functional state. Some proteins exist in the natively disordered state; however, they transform into the folded state by favorable binding interactions. Misfolded proteins may form disordered aggregates or ordered amyloid fibrils, which are irreversible and toxic (1). Various intermediate states relate to the transformation between the native and the amyloid states. The structure and stabilities of the intermediates can be dependent on or independent of the folding/unfolding processes (2,3). Some of the intermediates may assemble to form soluble oligomers, which then lead to amyloid fibrils (4). The prion disease is a well known example where the normal form of the prion proteins (PrPC) converts to misfolded PrPSc intermediates, which then form amyloids (5). Amino acid mutations in the protein sequence can affect both folding and amyloid formation processes (6).
Nature optimizes the protein sequence to escape amyloid formation (1,4,7). It appears to do that in two ways—by stabilizing the folded state and destabilizing the amyloid state. The structure and stabilities of the intermediates, especially those linked to the amyloid pathway, may also perturb nature's selection. The intermediates are usually more flexible and broadly distributed; it is thus probably harder to control intermediates than to control the folded and amyloid states. In addition, it is unclear whether one should stabilize or destabilize intermediates to modulate amyloid formation.
The possible effects of the intermediate stability may account for amyloid-related diseases. Alzheimer's disease is a neurodegenerative disorder characterized by the dysfunction and death of nerve cells responsible for the storage and processing of information (8). The disease is mainly related to the altered proteolytic processing of the amyloid precursor protein, which leads to aggregation of neurotoxic forms of the amyloid β (Aβ)-peptide. One characteristic of Alzheimer's disease is the extracellular aggregation of the Aβ peptide. Both the full-length form (Aβ1–40 and Aβ1–42) and the key fragment (Aβ25–35) form fibrils that are neurotoxic (8–10). Recently, alternative propositions have been put forward to explain the pathogenesis of Alzheimer's disease with the possibility that a fraction of these Aβ peptides stay at the membrane lipid bilayer after they are generated (11). One critical mechanism of the cytotoxicity is that the amyloid proteins/peptides form unregulated ion channels in membranes (12). Ion channels formed by the Alzheimer's peptide have been implicated in Alzheimer's disease pathophysiology (13,14). In the pore-formation/ion-channel mechanisms, it also appears that small oligomers play critical roles.
The sequence of Aβ25–35 (GSNKGAIIGLM) has a positively charged N-terminus and a hydrophobic C-terminus. The solution structures of the Aβ25–35 are a mixture of random coil, β-strand, and α-helix (15,16). Hydrogen/deuterium (H/D)-exchange NMR experiments indicate that the Aβ25–35 amyloid fibrils have a core formed from residues 28–35, with residues 31 and 32 being the most protected (17). Even though the H/D-exchange NMR results indicate that N27 is only marginally protected in the Aβ25–35 amyloid fibril, the Aβ25–35 Asn27Gln mutant does not form amyloids (18). It seems that the difference in amyloid formation for the Aβ25–35 and Asn27Gln mutant does not come from the perturbation of the amyloid fibril core. To understand why the N27Q mutation blocks in vitro amyloid formation we carried out exhaustive simulation studies of both Aβ25–35 and Asn27Gln mutant sequences to investigate 1), the stability of candidate amyloid oligomers and 2), distributions of free energies for candidate intermediate monomer states with partial secondary structure formation. Indeed, our molecular dynamics simulations did not show destabilization effects of the Asn27Gln of the oligomer clusters of Aβ25–35. In contrast, the relative conformational stabilities of the Aβ25–35 monomers are altered in the Asn27Gln mutant, which may slow the amyloid formation process.
In particular, we find a single-mode distribution of the model free energies for the Aβ25–35 peptide in the region of high extension favorable for amyloid formation, whereas the mutant peptide has a two-mode ensemble with energies bracketing those of the Aβ25–35 peptide. The mode of the energy landscape may be used to explain the different behavior of amyloid formation. Using Kramer's theory of barrier crossing and a Morse-function-like energy landscape, we show that the change of the stability of the intermediates dramatically increases or decreases the rate of amyloid formation. By considering the barrier-crossing times for a three-state free energy functional with fixed globally stable disordered and metastable “amyloid” minima but a tunable intermediate state, we argue that this observation can explain the blocking of amyloid formation by the mutant sequence. The key to the argument is that weakly stable intermediates too easily flip back to the disordered minimum, whereas highly stable intermediates kinetically trap, so only intermediates with medium stability can make the transition to the amyloid form.
METHODS
Energy landscape functions and rate of barrier crossing
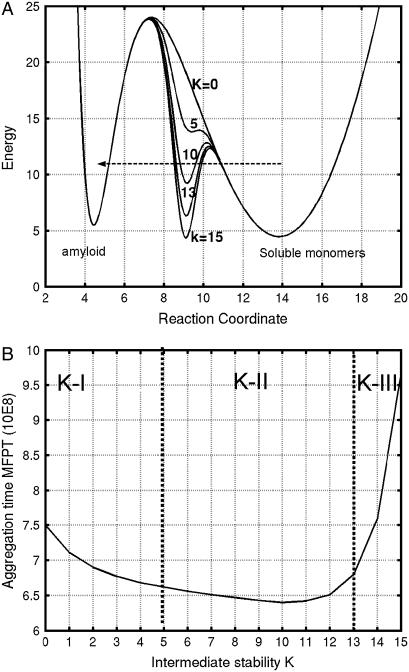
To describe the protein aggregation, a double-well potential (Fig. 1) has been constructed using two Morse functions, one to describe the well of the tightly bound amyloid (Uamyloid) and another corresponding to the broad distribution of native states (Unative). The stability of an intermediate is modeled by a Gaussian function (Uint). The energy of the amyloid state is adjusted to be slightly higher than the native state (Fig. 1), whereas the stability of the intermediates varies with the parameter K. A constant of 95.0 brings the value of U to the near-conventional 0.
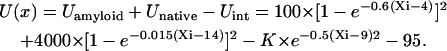 |
(1) |
FIGURE 1.
(A) Plot of energy landscape function with different intermediate stability (see Eq. 1). (B) The aggregation time, computed using Eq. 3. In the K-I region, intermediates are not stable and amyloid formation is slow. In the K-II region, intermediates have medium stability and amyloid formation is fast. In the K-III region, the intermediates are very stable and amyloid formation is sharply slower.
Wagner and Kiefhaber (19) have applied Kramer's theory of diffusive barrier crossing in the high-friction limit to solve the Langevin equation
 |
(2) |
The average time to cross the barrier (the mean first-passage time) (19) is determined by
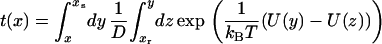 |
(3) |
In Eqs. 2 and 3, D is the diffusion coefficient, xr is the reflecting boundary, which is set at xr = 20, and xs is the absorbing boundary, which is set at xs = 4.5. We calculate the mean first-passage time of the particle starting at x = 14 to reach the position of xs = 4.5. The interstrand distance between the peptide chains in an amyloid β-sheet is around 4.5 Å, and the intersheet distance is ∼10 Å. Thus, the xs = 4.5 reflects a tightly bound amyloid state and x = 14 refers to the unbound state. The reflecting boundary, xr = 20, may be interpreted as peptides in the well separated state.
Stabilities of the peptide β-sheet oligomers
In all our computations, peptides were not capped. The stabilities of peptide β-sheet oligomers are simulated with molecular dynamics (MD) simulations at 330 K. Molecular dynamics simulations were performed in the canonical ensemble (NVT) with periodic boundary conditions by using the program Charmm with Charmm22 force field. The system consisted of eight peptides solvated with 3200 water molecules placed in a rectangular box (dimensions 70 × 40 × 40 Å3). The overall charge of the system is 8. All atoms of the system were considered explicitly. The time step in the MD simulations is 2 fs, and snapshots from the trajectories were saved every 1 ps. Nonbonded pairs were updated within 12 Å every 25 steps and the nonbonded interactions were smoothed to zero from 8 to 10 Å.
Peptide conformational search
The conformational space of the Aβ25–35 monomer is systematically examined by changing the Φ/Ψ angles of Aβ25–35. We used the coarse-grained Φ/Ψ state sets developed by Park and Levitt (20), combined with MD simulated annealing. Thus, all Φ/Ψ angles of the peptide Aβ25–35 and its N27Q mutant have been exhaustively sampled by all combinations of the Park-Levitt states, with Φ/Ψ of (−63,−63), (−132,115), (−42,−41), and (−44,127). The peptide is first minimized by 100 cycles with backbone constraint. Then 10 additional conformations are sampled near the given Φ/Ψ states by MD simulations. The MD sampling has 100 steps with the temperature increasing from 0 to 800 K. Thus, each Park-Levitt Φ/Ψ state has 11 conformations. The total number of conformations sampled is 262,144 for Aβ25–35 and similarly 262,144 for its N27Q mutant.
Peptide conformation free energy
The free-energy landscapes are constructed by evaluating the free energies for individual conformers (21,22). Each conformer is first subjected to energy minimization of 5000 steps with distance-dependent dielectric constant. We compute the vibrational free-energy Gvibration of the minimized structure. The vibrational free energy has both enthalpic and entropic contributions at 300 K:
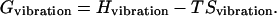 |
(4) |
At the minimized state, we compute the conformational energy. The solvation energies are calculated using the generalized Born method with molecular volume (GBMV) (23). In the GBMV calculation, the dielectric constant of water is set to 80, and no distance cutoff is used. The overall conformational free energy has the following terms:
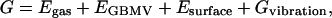 |
(5) |
where Egas is the gas phase potential energy, EGBMV represents the electrostatic contributions to the solvation energy, Esurface is the cavity and exposed surface effect on the solvation energy, and Gvibration is solute vibrational free energy.
RESULTS
Effects of the intermediate stability on the rate of barrier crossing
A generic model free energy functional with three stable states is constructed to crudely model amyloid formation. One minimum is an unfolded monomer, one is a partially folded intermediate, and one is an attempt to represent an amyloid. As indicated in Fig. 1 A, the energy landscape has two stable minima, at U(x = 4.44) = 5.49 and U(x = 13.82) = 4.48. The barrier is located at U(x = 7.35) = 24.01. Therefore, the amyloid state at x = 4.44 is a little higher in energy than the native state at x = 13.82. With K = 15 to describe the intermediate state, the two energy minima are U(x = 4.44) = 5.48 and U(x = 13.82) = 4.48, and the overall barrier is at U(x = 7.35) = 24.01. The intermediate minimum is at U(x = 9.01) = 4.54. Thus, the intermediate states described by our functions do not perturb the thermodynamic stabilities of the native state, transition state, and final amyloid state. The effects of the intermediate stability on the rate of barrier crossing are purely kinetic.
Essentially, we can define three regions based on the intermediate stability (Fig. 1 B). In the K-I region from K = 0 to K = 5, the intermediates are not “stable,” as the potential function has only shoulder regions corresponding to the intermediates. However, the shoulder region still increases the rate of barrier crossing. In the K-II region, the highest rate of barrier crossing occurs with the medium-stability intermediate states with a well-defined local minimum around K = 10. Afterwards, in the K-III region, which corresponds to highly stable intermediate states, the rate of barrier crossing sharply decreases. Thus, intermediates with medium stability will increase the rate of crossing, i.e., amyloid formation.
The current generic functions may have no direct physical correspondence to the kinetics of amyloid formation. For example, the amyloid minimum in the free-energy function does not explicitly contain the collective effects associated with amyloid aggregation. Nevertheless, although not a quantitative model, the results described here are suggestive and can be used to explain how the kinetics of amyloid formation can be changed by the intermediate free-energy ensembles, as discussed in the next two sections.
Stability of the oligomeric Aβ24–36 octamer, Aβ25–35 octamer, and Aβ25–35NQ mutant octamer
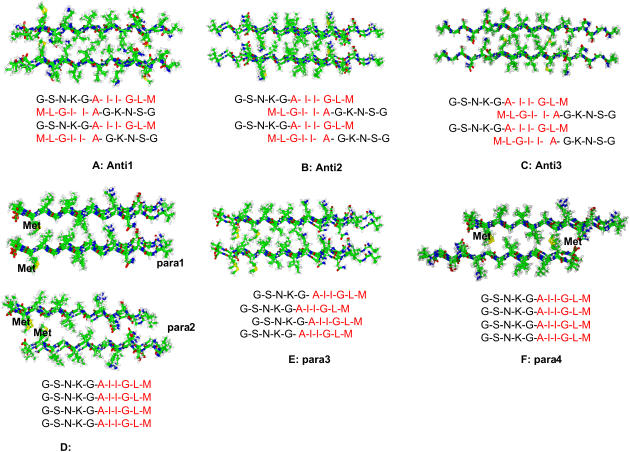
First, we investigate the ability of Aβ peptide fragments to form β-sheet structures in aqueous solution. Experimentally, amyloid fibrils have been observed for the Aβ25–35 sequence (8–10,18,24). In the initial studies, conducted together with other fragments (Aβ16–22, Aβ16–35, and Aβ10–35) of the Aβ peptide (25), we used the Aβ24–36 fragment in our simulations. We considered three antiparallel and four parallel β-sheet complexes for this Aβ24–36 fragment, all in a double-layered octamer organization (Figs. 2 and 3). We counted the number of backbone hydrogen bonds and side-chain contacts between the β-strands in the oligomers to characterize the stabilities of the models. The cutoff distance of a hydrogen bond is 2.5 Å, and the cutoff distance of the Cβ side-chain contact is 7.0 Å.
FIGURE 2.
The various antiparallel and parallel arrangements of β-strands in the β-sheet oligomer which are simulated in this work. The oligomers shown are snapshots from the simulation of Aβ24–26. All models consist of two sheets, each with four strands. In some sheets (anti2, anti3, para3), the strands are shifted with respect to each other within the sheet. In some models (e.g., para2 and para4), the sheets are shifted with respect to each other. The sequence given is for Aβ25–35. Hyrdrophobic regions are in red. (A–C) Antiparallel oligomers. (D) Two parallel oligomers (para1 and para2). (E–F) Two parallel ologimers.
FIGURE 3.
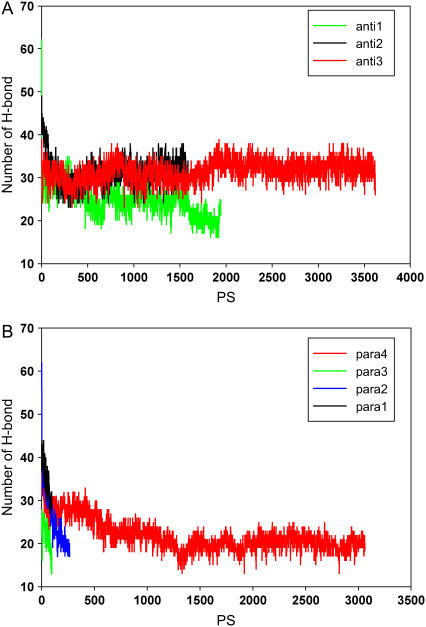
The stability of various tested models of Aβ24–36 oligomers in the MD simulations. We count the number of hydrogen bonds in the snapshots along the trajectory for (A) antiparallel oligomers and (B) parallel oligomers.
In the antiparallel β-sheet, the hydrophobic interactions (Fig. 2, residues in red letters) are optimized within the sheet. All antiparallel β-sheet oligomers are relatively stable. The stabilities increase with the overlap of the hydrophobic residues. Since the strands are increasingly shifted (translated) with respect to each other from anti1 to anti2 to anti3, the number of possible hydrogen bonds should decrease from anti1 to anti2 to anti3. Yet the anti3 model is the most stable in terms of hydrogen bonds retained during the 330 K simulations (Fig. 3 A). The core hydrophobic region of the anti3 model holds the octamer together. With respect to the four parallel β-sheet complexes, three do not survive the high-temperature simulations and readily dissociate (Fig. 3 B). The only stable parallel complex is para4, with the two layers being antiparallel and forming intersheet hydrophobic clusters between –I-G-M- and -M-G-I– (Figs. 2 and 3). Hydrophobic interactions, rather than hydrogen bonding, are more important in stabilizing β-sheet clusters.
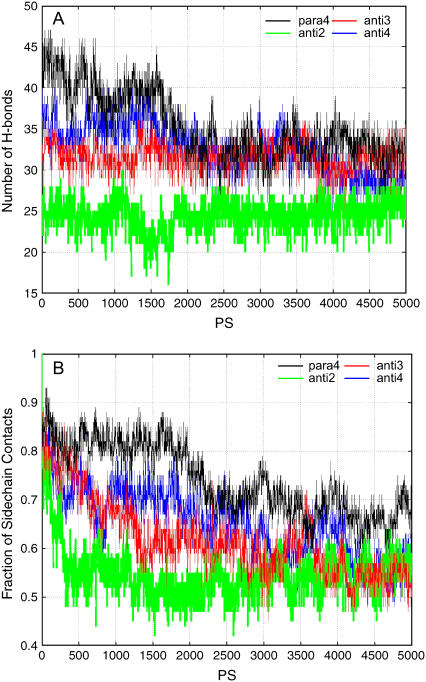
Based on the results of the Aβ24–36 simulations, we next simulated the Aβ25–35 octamers. The conformations used are anti2, anti3, and para4 (Fig. 2). In addition, we tested a variation of anti3 with a different intrasheet association (anti4). The stabilities of the octamer are reported in Fig. 4. Fig. 4 A plots the trajectory of the hydrogen bonding number, and Fig. 4 B is the trajectory of side-chain contacts. Generally, the stabilities for the Aβ24–36 and Aβ25–35 oligomers are similar, and both para4 and anti3 octamers have good stabilities. But the parallel conformation para4 is the most stable for Aβ25–35, and it retains most of the hydrogen bonds and side-chain contacts (Fig. 4). These results are consistent with experiment. H/D-exchange NMR experiments indicate that the core of Aβ25–35 amyloid fibrils is formed from residues 28–35, with residues 31 and 32 being the most protected (17). Structures derived from the NMR experiments (17) are consistent with both anti3 (and anti4) and para4 oligomers.
FIGURE 4.
The stability of tested models of Aβ25–35 oligomers in the MD simulations. On the top, we count the number of hydrogen bonds in the snapshots along the trajectory; at the bottom are the side-chain contacts.
The Aβ25–35 fibrils have amide band infrared absorptions around 1632 cm−1 and 1672 cm−1, indicating a possible antiparallel β-sheet arrangement (18). However, the x-ray diffraction data do not give a clear pattern of periodicities, indicating a disoriented β-crystalline (26,27). This could be the result of the flexible ends of either anti3 or the para4 models disrupting the β-crystalline. Even though, as shown in Fig. 3, our simulations indicated that the para4 is the best candidate for the Aβ25–35 amyloid, we do not focus on the absolute stabilities of the parallel or antiparallel oligomers. Rather, we focus on the question of why a mutation that is not in the protected core region can nevertheless lead to a change in the pattern of amyloid formation.
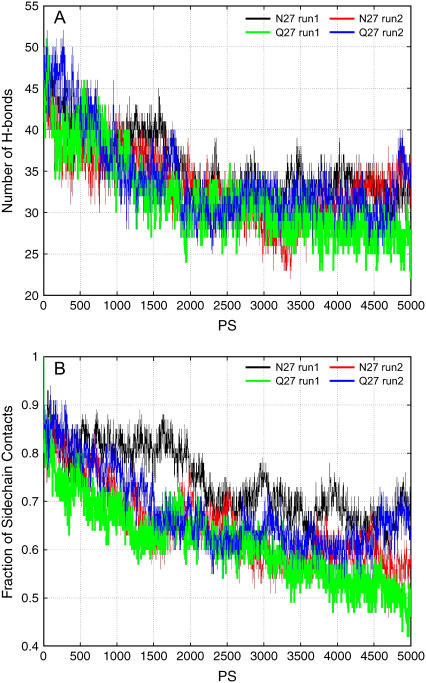
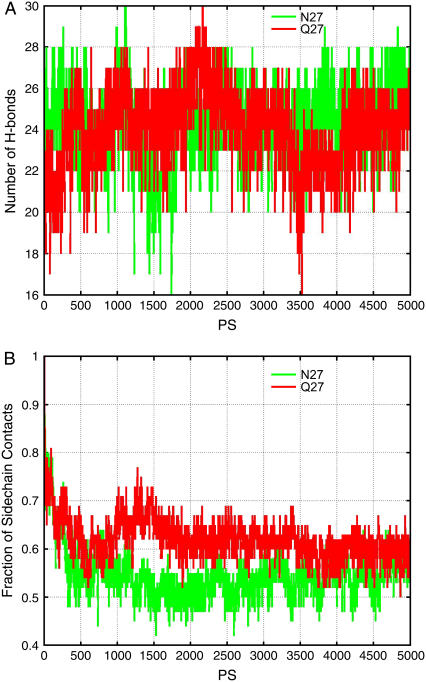
Experimentally, a single mutation of N27 in Aβ25–35 to Q27 completely blocks the aggregation of Aβ25–35. Therefore, to see if the mutation disrupts the β-sheet oligomer, we also simulated the oligomeric stabilities of the Aβ25–35NQ octamers in the conformations of anti3 and para4 (Fig. 2) that are consistent with NMR-deduced aggregation forms. Two independent simulations (run1 and run2) are performed with different initial minimization and heating processes for para4 oligomers. The comparison of the stability for parallel oligomers of the Aβ25–35 and its N27Q mutant is reported in Fig. 5. The black and red lines are trajectories for the the Aβ25–35, and the green and blue lines are for the N27Q mutant. The comparison of the wild-type with the mutant oligomer in the anti3 form is represented in Fig. 6, where the green lines are trajectories for the wild-type and the red lines for the mutant. Our results indicated that the Aβ25–35 N27Q octamers have stabilities similar to the wild-type Aβ25–35 octamers, whether they are in the anti3 or the para4 oligomer form (Figs. 5 and 6). In the antiparallel orientation, the Aβ25–35 N27Q even has better side-chain contacts during the 1- to 4-ns simulation run, but the Aβ25–35 and its N27Q mutant have similar stabilities at the end of the simulation (Fig. 6).
FIGURE 5.
The stability of the Aβ25–35 N27Q mutant oligomer in MD simulations as compared to the wild-type in para4 oligomer. The black and red lines are trajectories for the Aβ25–35, and the green and blue lines are for the N27Q mutant.
FIGURE 6.
The stability of the Aβ25–35 N27Q mutant oligomer in the MD simulations as compared to the wild-type in anti3 oligomer. Green lines are trajectories for the wild-type and red lines for the mutant.
The results are understandable based on the structure of the octamer, since the N27 is not in the hydrophobic core of the cluster. Thus, the N27Q mutation does not alter the oligomer organization. Other factors must exist to cause the different aggregation behavior of the N27Q mutant. One possibility is that the N27Q mutation could lead to a very different oligomer structure apart from the parallel/antiparallel structure examined here. Here we focus on another possibility, indicated already in our study of barrier-crossing kinetics, relating to the monomeric intermediate stabilities. Even though the chemical structures of Asn and Gln are similar, they have significant differences in secondary-structure preference. Asn is known to strongly stabilize β-turn conformations (Pturn = 1.56 for Asn and 0.98 for Gln) (28), whereas Gln shows a preference to form β-strand (Pβ = 1.10 for Gln and 0.89 for Asn) (28). To characterize the conformational behavior, we explored the energy landscapes of the monomeric Aβ25–35 peptide and the Aβ25–35 N27Q mutant.
Energy landscape of the Aβ25–35 monomer and the Aβ25–35 N27Q monomer
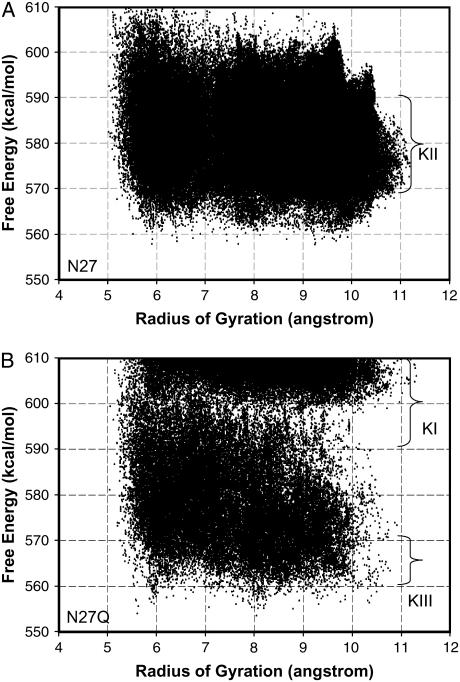
To characterize the conformational energy landscape of the peptides, we calculated the conformational free energies for the 262,144 conformers of the Aβ25–35 monomer and for the same number of conformers of its N27Q mutant. Our exhaustive combinations of the Park-Levitt Φ/Ψ states ensured the thoroughness of our conformational energy landscape. Here, we use the radius of gyration (Rg) to characterize the extent of the extended state of the peptide conformations. The larger the radius of gyration, the more extended is the peptide. Fig. 7 A plots the energy landscape for all conformations sampled for the Aβ25–35 monomer, and Fig. 7 B plots that for its N27Q mutant. In Fig. 7, the radii of gyration for the extended structures are >10 Å.
FIGURE 7.
The energy landscape of monomeric Aβ25–35 and Aβ25–35 N27Q. (Left) Wild-type sequence. (Right) Mutant sequence. For the N27 (wild-type), the energies of intermediates with extended conformations (radii of gyration 10–11 Å) fall within the intermediate range (K-II). For the mutant, no extended-state intermediates fall within the intermediate stability range.
For the Aβ25–35 monomer, the energies for the lowest 30 conformers range from 557.8 to 560.4 kcal/mol with the radii of gyration ranging from 5.5 to 9.9 Å. For the N27Q mutant, there is still a broad distribution of conformations for the lowest 30 conformers (radii of gyration range from 5.59 to 10.35 Å).
Three NMR structures of the Aβ25–35 monomer were solved in different media (16). In 100 mM sodium dodecyl sulfate micelles environment, the Aβ25–35 assumes a well-ordered α-helical structure involving residues 28–34 (PDB code 1qxc, Rg 5.87 Å). The α-helical structure is still well folded (PDB code 1qwp, Rg 6.05 Å) in the 80/20 hexafluoroisopropanol/water mixture. But in the 20/80 hexafluoroisopropanol/water mixture, the α-helical structure unfolded to form a turn (loop) centered at residues 26 and 27 (PDB code 1qyt, Rg 5.64 Å). The Aβ25–35 peptide is stable in these solvent media, without aggregation over several weeks. In aqueous solution, none of the three conformations are within the lowest 30. The computed energies for the three known structures are 586 kcal/mol (1qxc), 579 kcal/mol (1qwp), and 565.4 kcal/mol (1qyt). The energy ranking correlates well with the trend of decreasing α-helical conformation in aqueous solution.
The energy landscapes of the Aβ25–35 and its N27Q mutant explain the difference in the amyloid formation behavior, as predicted by the kinetic analysis in Fig. 1. The most favorable intermediates to form amyloids should be the extended structures with the largest radius of gyration around 10–11 Å. As can be seen from Fig. 7 A, the energies for these extended conformations have medium stabilities (K-II). A single N27Q mutation changes the energy landscape significantly (Fig. 7 B). The energies for these extended conformations for N27Q mutant fell into two regions, one with stable intermediates (K-III) and the other with unstable intermediates (K-I).
Therefore, taking Figs. 1 and 7 together, the energy landscapes of the Aβ25–35 peptide and its N27Q mutant indicate a difference in their amyloid formation kinetics. For the Aβ25–35 peptide, there is a dense population of intermediates with extended conformations of medium stability, which correspond to the K-II region in Fig. 1. The K-II ensemble has the fastest rate of barrier crossing, and the high speed of barrier crossing is consistent with the rapid rate of amyloid formation by Aβ25–35. On the other hand, for the N27Q mutant, the population of the extended intermediates shifted to the K-I and K-III regions, which have much slower rates of amyloid formation.
The remarkable correspondence between the monomeric energy landscape (Figs. 1 and 7) and amyloid formation for the Aβ25–35 peptide and its N27Q mutant argues for assembling extended conformations in the amyloid formation process. The propensities of Asn and Gln for β-strand and β-turn (28) correlate with our energy landscape calculations. Asn is known to strongly stabilize β-turn conformations (28), which makes the extended structure of only medium stability in solution and thus easily able to form amyloids. The propensity to form β-strand is much larger for Gln than for Asn (28). Therefore, for the N27Q mutant, a portion of the extended structure is stabilized (Fig. 7). However, extended intermediates with high stability apparently decrease the rate of amyloid formation.
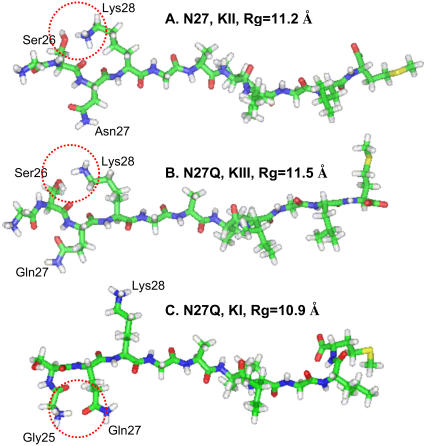
Examination of the peptides' structures in the regions with a large radius of gyration confirmed the β-strand conformations and pointed to a difference in the side-chain hydrogen-binding pattern. Fig. 8 illustrates three representative structures of the peptide conformation with the largest radius of gyration in the three intermediate modes. Fig. 8 A is the structure of Aβ25–35 with the largest Rg value in the K-II region, Fig. 8 B shows the structure of Aβ25–35 N27Q with the largest Rg value in the K-III region, and Fig. 8 C illustrates the structure of Aβ25–35 N27Q with the largest Rg value in the K-I region. In Fig. 8, A and B, we observed hydrogen bonds between the side chains of Ser26 and Lys28. A new hydrogen-bonding pattern appears in the most stable intermediate K-I region for the Aβ25–35 N27Q. With a longer side chain, Gln27 can form multiple hydrogen bonds. Highlighted in the Fig. 8 C is the hydrogen bonding between the N-terminal group and Gln27. In the K-I region we also see the hydrogen bonding between the Gln27 with Ser26 (not shown). These hydrogen bonds do not disturb the β-strand conformation in the central region and provide additional stabilizing force. Of course the side-chain interactions only represent one factor, other interactions (solvent and entropy) may also collectively contribute to the difference of the ensemble of free energies.
FIGURE 8.
Representative structures for the intermediates in the three regions. (A) The structure of Aβ25–35 with the largest Rg value in the K-II region. The side-chain hydrogen bond between Ser26 and Lys28 is highlighted. (B) The structure of Aβ25–35 N27Q with the largest Rg value in the K-III region; the side-chain hydrogen bond between Ser26 and Lys28 is highlighted. (C) The structure of Aβ25–35 N27Q with the largest Rg value in the K-I region. The hydrogen bond between Gly25 and Gln27 is highlighted.
DISCUSSION AND CONCLUSIONS
Using a one-dimensional potential barrier model to study the effects of intermediates on protein folding revealed that intermediates can accelerate the folding reaction (19,29). The Wagner and Kiefhaber solution of Eq. 2 provided an effective way to explore how a change in the potential function affects the rate of barrier crossing (19). Wagner and Kiefhaber used the polynomial V(x) = aX6 – bX4 + cX2 + d to correlate barrier-crossing and protein-folding intermediates. By changing the symmetric barrier height, they showed that intermediates with medium stability can accelerate protein folding, through a favorable entropy contribution. Jun and Weaver (29) used a discontinuous potential with a square barrier to correlate with protein-folding kinetic intermediates. They also found that the intermediates can either speed up or slow down folding, depending on their energy barrier to the final folded state.
We extend the approach from protein folding to protein misfolding in amyloid formation. The extension is natural in two respects. First, the general mathematical description of the barrier-crossing property applies equally to protein folding and to amyloid formation. Our applications with a Morse-like potential function are closer to the chemical-binding problem. The Morse function with the form: D*[1 − e−α(Xi−Re)]2 describes a chemical bond with the strength of D and equilibrium distance of Re. Therefore, our function may be interpreted as describing an amyloid system with interstrand distance of 4.5 Å.
Second, protein folding and misfolding are controlled by the same energy landscape with the same physicochemical principles. Protein folding is a diffusion, collision, and coalescence process. Amyloid formation, due to its polymerization nature, is more diffusion- and collision-controlled. Amyloid formation is very slow compared to protein folding. The lag time for amyloid formation depends on the speed of seed formation. The conformational and diffusion entropy change collectively, constituting a barrier for seed formation. Even though the size of a stable seed depends on the protein sequences, it seems that the dimer formation is the most important step in the amyloid formation (30).
Jang, Hall, and Zhou studied kinetic assembly pathways of a tetrameric β-sheet complex (31) using molecular dynamics simulations. With off-lattice protein models, they found that the “folding” and equilibrium properties of the β-sheet complex strongly depend on the interaction parameter η. The “folding” yield is high at medium η, but low at both small and large values of η. In the small value of η, there are many trapped intermediates that cannot cross the “folding” barrier. Jang and co-workers' results also reflect the kinetic nature of the amyloid β-sheet formation, similar to our current analysis of the effects of intermediate stability.
The nature of the “intermediate” described in both protein folding (19,29) and amyloid formation is not explicitly defined. In principle, any intermediates on the pathway to amyloid formation could have kinetic effects on the rate. For amyloid formation, the intermediates close to the final β-sheet organization should be β-strands. Nevertheless, α-helical intermediates have been shown to be important for amyloid formation, especially for the Aβ peptide (32). Chiti et al. showed that the free energy changes of coil to both α-helices and β-strands affect amyloid formation (33). Fezoui and Teplow found that the α-helix stabilization is especially important for the Aβ peptide amyloid formation (34). The contribution of the α-helix stability to the amyloid formation is often interpreted as the formation of helix-containing oligomers, followed by conformational reorganization to form the extended β-sheet.
Our intermediate stability analysis indicates that the stabilization of an α-helix even before oligomerization can provide the same rate enhancement effect in amyloid formation. The stabilization of the α-helix-containing oligomers is not necessary for amyloid formation. It was found that the assembly of Aβ16–22 into dimers follows multiple routes, but α-helical intermediates are not obligatory (35). Rather, the α-helix appears to provide a stable intermediate on the pathway to amyloid, accelerating β-strand formation. Andrec et al. found that the coil-to-β-hairpin folding is dominated by pathways that visit metastable helical conformations for the C-terminal peptide from the B1 domain of protein G (36). Even for the folding/unfolding of the three-helix bundle protein A, a stable β-hairpin persists in the unfolded ensemble and converts to a helix (37). Thus, the stability of the extended conformation, together with the stability of the α-helix “precursor,” is likely to be important for peptide oligomerization leading to amyloid formation.
How the stability of the extended conformations controls amyloid formation can also be explained in simple terms of solubility. Highly soluble intermediates do not easily aggregate, which corresponds to the K-III region in Fig. 1. The highly insoluble intermediates, which correspond to the K-I region (Fig. 1), have short population time and can easily flip back to the native state. For the K-II region, the barrier to the native state is quite high, but to the amyloid it is still not too high, thus offering a higher chance for aggregation to proceed. The ensemble with the intermediate stability of the K-II region has medium solubility and population time, and is thus prone to form amyloids.
In conclusion, we have studied barrier crossing and intermediate stability. Using conformational landscape analysis and MD simulations, we have investigated the monomeric energy landscape and amyloid formation of the native Aβ25−35 peptide and its N27Q mutant, which does not form amyloids experimentally. Our results indicate that Aβ25−35 intermediates with very low and very high stability will decrease the rate of amyloid formation. In contrast, intermediates with medium stability will accelerate the rate of amyloid formation. Remarkably, although the stability of the N27Q mutant oligomers is similar to that of the wild-type, the distribution of the N27Q monomer intermediates has a significantly lower population of these medium-stability conformer species. The significance of these results is not only in explaining the mutational effects of the Aβ25−35 peptide and N27Q; rather, these results assist in the comprehension of the structure and stability of intermediates, as well as the native folded state and the amyloid state, and can be of use in our fight against misfolded-protein diseases.
Acknowledgments
Computations were conducted using the Biowulf cluster at the National Institutes of Health, Bethesda, Maryland. The content of this publication does not necessarily reflect the views or policies of the Department of Health and Human Services, nor does mention of trade names, commercial products, or organizations imply endorsement by the United States government.
This project was funded in whole or in part with federal funds from the National Cancer Institute, National Institutes of Health, under contract number NO1-CO-12400, and by the United States Army Medical Research Acquisition Activity under grant W81XWH-05-1-0002. The research of R. Nussinov in Israel was supported in part by the Center of Excellence in Geometric Computing and its Applications, funded by the Israel Science Foundation (administered by the Israel Academy of Sciences). This research was supported in part by the Intramural Research Program of the National Institutes of Health, National Cancer Institute, Center for Cancer Research.
References
- 1.Bucciantini, M., E. Giannoni, F. Chiti, F. Baroni, L. Formigli, J. Zurdo, N. Taddei, G. Ramponi, C. M. Dobson, and M. Stefani. 2002. Inherent toxicity of aggregates implies a common mechanism for protein misfolding diseases. Nature. 416:507–511. [DOI] [PubMed] [Google Scholar]
- 2.Houry, W. A., J. M. Sauder, H. Roder, and H. A. Scheraga. 1998. Definition of amide protection factors for early kinetic intermediates in protein folding. Proc. Natl. Acad. Sci. USA. 95:4299–4302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hao, M. H., and H. A. Scheraga. 1998. Molecular mechanisms for cooperative folding of proteins. J. Mol. Biol. 277:973–983. [DOI] [PubMed] [Google Scholar]
- 4.Dobson, C. M. 2003. Protein folding and misfolding. Nature. 426:884–890. [DOI] [PubMed] [Google Scholar]
- 5.Prusiner, S. B. 1998. Prions. Proc. Natl. Acad. Sci. USA. 95:13363–13383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Isaacson, R. L., A. G. Weeds, and A. R. Fersht. 1999. Equilibria and kinetics of folding of gelsolin domain 2 and mutants involved in familial amyloidosis-Finnish type. Proc. Natl. Acad. Sci. USA. 96:11247–11252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dobson, C. M. 2001. The structural basis of protein folding and its links with human disease. Philos. Trans. R. Soc. Lond. B Biol. Sci. 356:133–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mattson, M. P., J. G. Begley, R. J. Mark, and K. Furukawa. 1997. Aβ25–35 induces rapid lysis of red blood cells: contrast with Aβ1–42 and examination of underlying mechanisms. Brain Res. 771:147–153. [DOI] [PubMed] [Google Scholar]
- 9.Pike, C. J., D. Burdick, A. J. Walencewicz, C. G. Glabe, and C. W. Cotman. 1993. Neurodegeneration induced by β-amyloid peptides in vitro: the role of peptide assembly state. J. Neurosci. 13:1676–1687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yankner, B. A., L. K. Duffy, and D. A. Kirschner. 1990. Neurotrophic and neurotoxic effects of amyloid β protein: reversal by tachykinin neuropeptides. Science. 250:279–282. [DOI] [PubMed] [Google Scholar]
- 11.Marchesi, V. T. 2005. An alternative interpretation of the amyloid Aβ hypothesis with regard to the pathogenesis of Alzheimer's disease. Proc. Natl. Acad. Sci. USA. 102:9093–9098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lashuel, H. A., D. Hartley, B. M. Petre, T. Walz, and P. T. Lansbury Jr. 2002. Neurodegenerative disease: amyloid pores from pathogenic mutations. Nature. 418:291. [DOI] [PubMed] [Google Scholar]
- 13.Lin, H., R. Bhatia, and R. Lal. 2001. Amyloid β protein forms ion channels: implications for Alzheimer's disease pathophysiology. FASEB J. 15:2433–2444. [DOI] [PubMed] [Google Scholar]
- 14.Kagan, B. L., Y. Hirakura, R. Azimov, R. Azimova, and M. C. Lin. 2002. The channel hypothesis of Alzheimer's disease: current status. Peptides. 23:1311–1315. [DOI] [PubMed] [Google Scholar]
- 15.Shanmugam, G., and R. Jayakumar. 2004. Structural analysis of amyloid β peptide fragment (25–35) in different microenvironments. Biopolymers. 76:421–434. [DOI] [PubMed] [Google Scholar]
- 16.D'Ursi, A. M., M. R. Armenante, R. Guerrini, S. Salvadori, G. Sorrentino, and D. Picone. 2004. Solution structure of amyloid β-peptide (25–35) in different media. J. Med. Chem. 47:4231–4238. [DOI] [PubMed] [Google Scholar]
- 17.Ippel, J. H., A. Olofsson, J. Schleucher, E. Lundgren, and S. S. Wijmenga. 2002. Probing solvent accessibility of amyloid fibrils by solution NMR spectroscopy. Proc. Natl. Acad. Sci. USA. 99:8648–8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Konno, T. 2001. Amyloid-induced aggregation and precipitation of soluble proteins: an electrostatic contribution of the Alzheimer's β(25–35) amyloid fibril. Biochemistry. 40:2148–2154. [DOI] [PubMed] [Google Scholar]
- 19.Wagner, C., and T. Kiefhaber. 1999. Intermediates can accelerate protein folding. Proc. Natl. Acad. Sci. USA. 96:6716–6721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Park, B. H., and M. Levitt. 1995. The complexity and accuracy of discrete state models of protein structure. J. Mol. Biol. 249:493–507. [DOI] [PubMed] [Google Scholar]
- 21.Ma, B., and R. Nussinov. 2003. Energy landscape and dynamics of the β-hairpin G peptide and its isomers: Topology and sequences. Protein Sci. 12:1882–1893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ma, B., C. J. Tsai, and R. Nussinov. 2000. A systematic study of the vibrational free energies of polypeptides in folded and random states. Biophys. J. 79:2739–2753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lee, M. S., M. Feig, F. R. Salsbury, Jr., and C. L. Brooks 3rd. 2003. New analytic approximation to the standard molecular volume definition and its application to generalized Born calculations. J. Comput. Chem. 24:1348–1356. [DOI] [PubMed] [Google Scholar]
- 24.Hughes, E., R. M. Burke, and A. J. Doig. 2000. Inhibition of toxicity in the β-amyloid peptide fragment β-(25–35) using N-methylated derivatives: a general strategy to prevent amyloid formation. J. Biol. Chem. 275:25109–25115. [DOI] [PubMed] [Google Scholar]
- 25.Ma, B., and R. Nussinov. 2002. Stabilities and conformations of Alzheimer's β-amyloid peptide oligomers (Aβ16–22, Aβ16–35, and Aβ10–35): sequence effects. Proc. Natl. Acad. Sci. USA. 99:14126–14131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Serpell, L. C. 2000. Alzheimer's amyloid fibrils: structure and assembly. Biochim. Biophys. Acta. 1502:16–30. [DOI] [PubMed] [Google Scholar]
- 27.Inouye, H., P. E. Fraser, and D. A. Kirschner. 1993. Structure of β-crystallite assemblies formed by Alzheimer β-amyloid protein analogues: analysis by x-ray diffraction. Biophys. J. 64:502–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chou, P. Y., and G. D. Fasman. 1978. Empirical predictions of protein conformation. Annu. Rev. Biochem. 47:251–276. [DOI] [PubMed] [Google Scholar]
- 29.Jun, B., and D. L. Weaver. 2002. One-dimensional potential barrier model of protein folding with intermediates. J. Chem. Phys. 116:418–426. [Google Scholar]
- 30.Urbanc, B., L. Cruz, S. Yun, S. V. Buldyrev, G. Bitan, D. B. Teplow, and H. E. Stanley. 2004. In silico study of amyloid β-protein folding and oligomerization. Proc. Natl. Acad. Sci. USA. 101:17345–17350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jang, H., C. K. Hall, and Y. Zhou. 2004. Assembly and kinetic folding pathways of a tetrameric β-sheet complex: molecular dynamics simulations on simplified off-lattice protein models. Biophys. J. 86:31–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Klimov, D. K., and D. Thirumalai. 2003. Dissecting the assembly of Aβ16–22 amyloid peptides into antiparallel β sheets. Structure. 11:295–307. [DOI] [PubMed] [Google Scholar]
- 33.Chiti, F., M. Stefani, N. Taddei, G. Ramponi, and C. M. Dobson. 2003. Rationalization of the effects of mutations on peptide and protein aggregation rates. Nature. 424:805–808. [DOI] [PubMed] [Google Scholar]
- 34.Fezoui, Y., and D. B. Teplow. 2002. Kinetic studies of amyloid β-protein fibril assembly. Differential effects of α-helix stabilization. J. Biol. Chem. 277:36948–36954. [DOI] [PubMed] [Google Scholar]
- 35.Santini, S., G. Wei, N. Mousseau, and P. Derreumaux. 2004. Pathway complexity of Alzheimer's β-amyloid Aβ16–22 peptide assembly. Structure. 12:1245–1255. [DOI] [PubMed] [Google Scholar]
- 36.Andrec, M., A. K. Felts, E. Gallicchio, and R. M. Levy. 2005. Protein folding pathways from replica exchange simulations and a kinetic network model. Proc. Natl. Acad. Sci. USA. 102:6801–6806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Garcia, A. E., and J. N. Onuchic. 2003. Folding a protein in a computer: an atomic description of the folding/unfolding of protein A. Proc. Natl. Acad. Sci. USA. 100:13898–13903. [DOI] [PMC free article] [PubMed] [Google Scholar]