Abstract
We performed a 1012-generation mutation-accumulation (MA) experiment in the yeast, Saccharomyces cerevisiae. The MA lines exhibited a significant reduction in mean fitness and a significant increase in variance in fitness. We found that 5.75% of the fitness-altering mutations accumulated were beneficial. This finding contradicts the widely held belief that nearly all fitness-altering mutations are deleterious. The mutation rate was estimated as 6.3 × 10−5 mutations per haploid genome per generation and the average heterozygous fitness effect of a mutation as 0.061. These estimates are compatible with previous estimates in yeast.
THE frequency of spontaneously arising beneficial mutations has recently become a subject of debate. The prevalent opinion is that the vast majority of mutations affecting fitness are deleterious. This opinion found early theoretical support when Fisher (1930) used a geometric model to explain why most mutations should be deleterious. Recent molecular data on the ratio of nonsynonomous to synonomous substitution rates also indicate that the majority of nonsynonomous mutations affecting fitness are deleterious (Eyre-Walker et al. 2002). Several mutation-accumulation (MA) studies have observed a decline in mean fitness due to the accumulation of mutations. This has been interpreted as evidence that the vast majority of mutations are deleterious (Lynch et al. 1999; Keightley and Lynch 2003). However, declines in mean fitness are also consistent with deleterious and beneficial mutations occurring at similar frequencies, but with deleterious mutations having larger average effects (Shaw et al. 2003).
Several recent studies suggest that advantageous mutations may be more common than is generally believed. Shaw et al. (2002) performed a mutation-accumulation experiment in Arabidopsis thaliana and found that half of all mutations affecting fitness are beneficial. Garcia-Dorado (1997) reanalyzed the data from three Drosophila MA experiments and found a better fit with a model incorporating 10% beneficial mutations for one of the studies. In Saccharomyces cerevisiae, one MA study found slightly <2% of mutations were beneficial (Wloch et al. 2001) and another has suggestive evidence for a relatively high fraction of beneficial mutations (see Zeyl and DeVisser 2001, Figure 1).
We performed a mutation-accumulation experiment in the yeast, S. cerevisiae, to estimate the frequency of spontaneously arising beneficial mutations, the genome-wide mutation rate, and the average effect of spontaneous mutations. Our study improves on previous yeast MA experiments in three ways. First, we used a genotype that allowed us to circumvent petite mutations. These mitochondrial mutations cause a substantial reduction in fitness and are lethal on nonfermentable carbon sources (Wilkie 1983). Because they have substantial effects on growth rate and occur at high frequency (often 1% or more), petites overwhelm the fitness effects of nuclear mutations and substantially reduce the number of MA lines that are informative. Zeyl and DeVisser (2001) accumulated petite mutations in 19 of 50 lines, while all 16 of Korona's lines became petite (Korona 1999). The petite mutation is not seen in most eukaryotes (Piskur 1994), presumably because it is lethal in those organisms (Bernardi 1979), and should be avoided for mutation parameters to be comparable to other eukaryotes. Second, we used many more MA lines and accumulated mutations for more generations than in previous experiments. Finally, we used a different technique for estimating line fitness, which allowed us to perform more replicates per line than in previous studies.
We chose to accumulate mutations in diploid rather than haploid yeast for two reasons. First, most MA experiments have been performed on diploid eukaryotes, making a direct comparison easier. Second, more mutations can be accumulated in diploids. It is impossible to completely remove selection from an MA experiment but the fitness effects of mutations may be at least partially masked in diploids because they are heterozygous.
We accumulated spontaneous mutations in 151 MA lines established from a diploid strain. Every 48 hr each MA line was bottlenecked to a single cell for a total of 50 bottlenecks. The fitness of each line was then measured. The mean fitness of the MA lines showed a small, but significant, decline and the variance in fitness increased significantly. Despite the decline in mean fitness, 5.75% of mutations were estimated to be beneficial. The maximum-likelihood estimate for the genome-wide mutation rate to alleles that alter fitness was 6.3 × 10−5 per haploid genome generation with an absolute value of the average heterozygous effect of 0.061.
MATERIALS AND METHODS
Ancestral genotype:
The yeast strain used to establish our MA lines was produced by sporulating a diploid strain (DBY4974/DBY4975), obtained from Dr. Clarence Chan at the University of Texas, to yield a haploid strain of genotype ade2, lys2-801, his3-Δ200, leu2-3.112, ura3-52, Gal+, ho. The haploid strain was then transformed with a HO marker plasmid to induce diploidization, after which the plasmid was removed. The resulting diploid strain, which we term the ancestral strain, was initially homozygous at all loci except the mating-type locus, which was aα. A sample of the ancestral strain was frozen in 15% glycerol at −80°.
This ancestral strain was chosen for two reasons. First, it is mutant at only a few loci and thus is a good representative of mutational processes in a wild-type strain. Second, it is homozygous for ade2, which causes the buildup of a metabolite (phosphoribosylaminoimidazole) in the adenine biosynthetic pathway (Dujon 1981). In the presence of oxidative respiration, this metabolite gives the colonies a reddish color and in its absence, colonies are white. This color marker allowed us to visually screen for the presence of a petite mutation.
MA line establishment and propagation:
One hundred fifty-one MA lines were established from the ancestor. Each MA line was grown on YPD solid medium (1% yeast extract, 2% peptone, 2% dextrose, and 2% agar) at 30° and passaged by single-cell transfer. Eight lines, in individual sectors, were grown per petri plate. For each line, passages were conducted by selecting the nonwhite colony closest to a mark made in each sector of the petri dish. This colony was then streaked onto the appropriate sector of a fresh petri plate. The plate was incubated for 48 hr until the next transfer. Isolated colonies were assumed to originate from a single cell. Every 5 passages, a sample of each line was frozen at −80° in 15% glycerol. When a petite colony was accidentally passaged, which occurred 38 times, all resulting colonies were white (see above). In those cases, we went back to the previous petri dish (which was stored at 4°) and passaged that line again using the colony that was the second closest to the mark. The MA phase of the experiment was continued for one hundred passages. On the basis of previous mutation rate estimates in yeast, we chose to analyze the lines after the first 50 passages.
The ade mutant typically causes colonies to turn pink after 48 hr of growth. Very slow-growing colonies may appear white after 48 hr, even though they are not petite. In addition, ade revertants form white colonies. Under our experimental design, both of these types of colonies would not have been passaged. Thus, our screening procedure may have biased our experiment against accumulating highly deleterious mutations and ade revertants. We investigated these potential sources of bias in a series of experiments outlined in the appendix. The results of these experiments strongly suggest that during the MA experiment we were able to accurately score petite colonies after 48 hr and that ade revertants are rare enough that they are not an important source of bias. We thus believe that our experiment was not substantially biased by our protocol to avoid accumulating petite mutations.
We estimated the average number of generations assuming exponential growth from counts of the number of cells per colony. The number of cells per colony was estimated approximately every seven transfers by choosing a single colony from each of 10 petri dishes. We then suspended the colony in 1 ml of water and estimated cell density using a hemacytometer (Reichert Bright Line, 0.1 mm depth).
To address the possibility of contamination, a marker strain genetically identical to the ancestral strain, with the exception of a homozygous trp1-1 mutation, was interdigitated into four of the sectors of four of the petri dishes. Displaced lines were moved to new petri dishes. The MA lines and the marker strain were passaged together for 69 passages and then checked for contamination. None of the 32 lines on the four plates were cross-contaminated by an adjacent strain. Setting the cutoff probability for seeing zero contaminants in any of the 32 lines at 5% implies that the frequency of across-line contamination is no >8.9% over 69 transfers. This sets the upper limit for contamination frequency at 6.6% over 50 transfers, indicating that at most 10 of our 151 lines were cross-contaminated.
Fitness assays:
The fitness of each MA line was estimated after 50 passages by comparing the maximum growth rate of 10 replicate colonies of the MA line to 10 replicates of the ancestor. Maximum growth rates were estimated from optical density measurements obtained using a Bioscreen C microbiological workstation (Thermo Labsystems).
We first streaked line and ancestor samples from the freezer onto solid YPD and let them grow for 2 days. Ten colonies from each line and 10 ancestral colonies per line were then used to inoculate test tubes containing 2 ml of liquid YPD. These cultures were grown overnight on a test-tube rotator at 30° for a minimum of 14 hr. During this time the overnight cultures reached stationary phase at a density of ∼1 × 107 cells/ml. Forty microliters of each overnight culture was then used to inoculate 2 ml of YPD, giving an initial density of ∼2 × 105 cells/ml. These day cultures were grown at 30° on a test-tube rotator for 6 hr to a final density of ∼1 × 106 cells/ml. One hundred fifty microliters of each day culture was added to 2 ml of YPD, giving a density of ∼1 × 105 cells/ml from which 150 μl was loaded into a Bioscreen C microplate well. Each culture should have been in logarithmic growth phase when loaded into the microplate. Line replicates and matched ancestor replicates were kept interdigitated prior to and during the Bioscreen C runs. The Bioscreen C incubated the microplates at 30°, with continuous, intense shaking and measured the absorbance of 600 nm light for each well every 10 min for 46 hr. Absorbance readings were log-transformed and used to generate growth curves (log absorbance vs. time). Replicates that showed unusual growth curves (either no change in absorbance or an extremely long delay before absorbance increased) were rerun on a different day. Less than 1% of all replicates had unusual growth curves. Maximum growth rates for the ancestor corresponded to changes in absorbance of ∼0.122 log units per hour. From standard curves, this indicates that the average minimum generation time was ∼1.3 hr.
A least-squares regression of log absorbance on time was calculated for a sliding 140-min window. For each replicate, the regression with the largest slope was designated the maximum growth rate of that replicate. The correlation coefficient within this 140-min interval corresponding to the maximal growth rate, averaged over all 3020 growth curves, was 0.999 and the smallest value obtained was 0.937.
The maximum growth rate of each line replicate was standardized by dividing by the mean maximum growth rate of the 50 ancestor replicates on the same Bioscreen plate. The standardized maximum growth rate of a replicate is referred to as the fitness of that replicate. The average fitness of the 10 replicates of each line was designated as the fitness of the line. Each ancestor replicate was standardized in the same manner.
General statistical analysis:
Most statistical tests were performed using JMP statistical software (SAS Institute 2000). We used nonparametric statistics to analyze fitness distributions of the MA lines and ancestor replicates because they were not normally distributed (P < 0.0001, Shapiro-Wilk W-test for both ancestor and MA line distributions) and their variances were unequal (Levene's test, P < 0.0001).
Likelihood analysis:
We used log-likelihood to estimate the proportion of mutations that are beneficial (P), the genome-wide mutation rate to alleles that alter fitness (U), and the absolute value of the mean heterozygous fitness effect of mutations [E(a)]. The maximum-likelihood (ML) estimates were calculated using a program provided by Dr. Peter Keightley. The ML program (Keightley 1994; Keightley and Ohnishi 1998) estimates the parameters from the fitness of the MA lines and the ancestor. The ML program assumes that the number of mutations accumulated in each MA line is Poisson distributed and that the effects of mutations follow a reflected gamma distribution with a fraction P of the mutations having positive (beneficial) effects. The positive and negative parts of the distribution are assumed to have the same scale parameter α and shape parameter β. The mean heterozygous fitness effect of mutations, E(a), is equal to β/α.
Because a thorough ML analysis with the full data set required an excessive amount of computer time, we reduced the size of our data set by an order of magnitude. To do this, MA line fitness was used instead of the 10 replicates of each MA line. In addition, the mean fitness of each group of 10 matched ancestor replicates was used. The reduced data set consisted of 151 MA line fitness measures and 151 ancestor fitness measures.
With the reduced data set, we performed a search of the parameter space by first choosing values of β and P and then running the program to find the ML values of α and U. We tried all combinations of β = 0.01, 0.05, 0.1, 0.5, 1, 2, 3, 4, 6, 8, 10, and 50 and P = 0, 0.01, 0.025, 0.05, 0.1, 0.125, 0.15, 0.2, 0.3, 0.4, and 0.5. We also ran an equal-effects model for all values of P. Upper and lower bounds of the 95% confidence intervals were the parameter values at which the log-likelihood dropped 2 units below the maximum value obtained (Keightley 1994).
RESULTS
Fitness distribution:
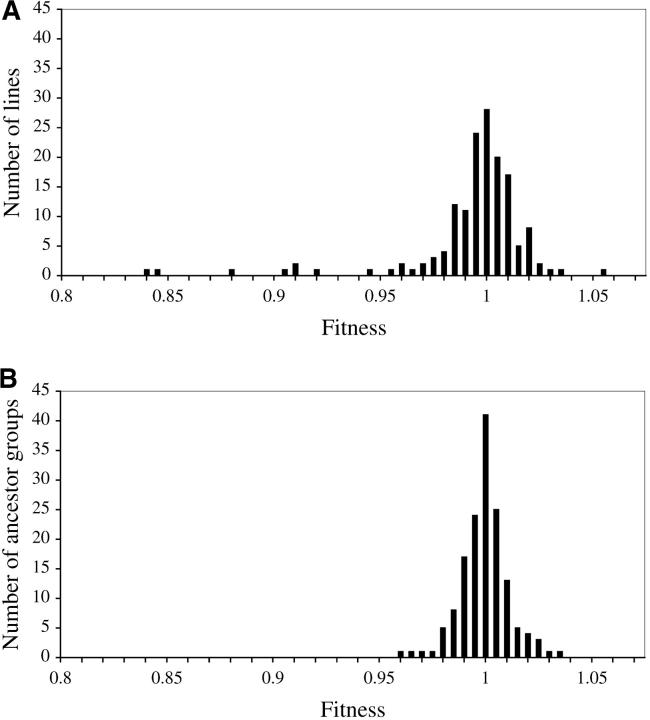
The fitness distributions of the MA lines and ancestors are plotted in Figure 1, A and B, respectively. For each line a Kruskal-Wallis test was performed to determine whether the 10 replicates of that line differed significantly from the 1510 ancestor replicates. After a Bonferroni correction for multiple comparisons, 16 MA lines were identified as having a fitness significantly different from that of the ancestor (Kruskal-Wallis test; α = 0.05). These lines represent 16 of the 18 lines with mean fitness >2.5% different from that of the ancestor. Three of the 16 (19%) have fitness greater than that of the ancestor.
Figure 1.—
Fitness estimates of 151 MA lines (A) and 151 ancestor groups (B). Each point is the mean maximum growth rate of 10 replicates, standardized to the average maximum growth rate of the 50 ancestor replicates on the Bioscreen C microplate.
The mean fitness of the ancestor replicates is 1.0 (by definition) and the variance is 7.95 × 10−4. The mean fitness of the MA line replicates is 0.994 and the variance is 1.4 × 10−3. The MA line fitness variance can be partitioned into within-line variance, = 6.6 × 10−4, and between-line variance, = 7.5 × 10−4. The mean fitness of the MA line replicates is significantly smaller than the mean of the ancestor replicates (Kruskal-Wallis, P = 0.0015) and the variance is significantly larger (Levene's test, P < 0.0001). The genetic variance in fitness of the MA lines due to mutations σ2m increased by 7.45 × 10−7 per generation. This variance was standardized to yield a mutational heritability h2m of 1.1 × 10−3. The fitness distribution of the MA lines is leptokurtic (kurtosis = 4.69) and skewed to the left (skew = −1.26). The fitness distribution of the ancestor lines is leptokurtic (kurtosis = 9.78) and slightly skewed to the right (skew = 0.55).
Estimates of mutational parameters:
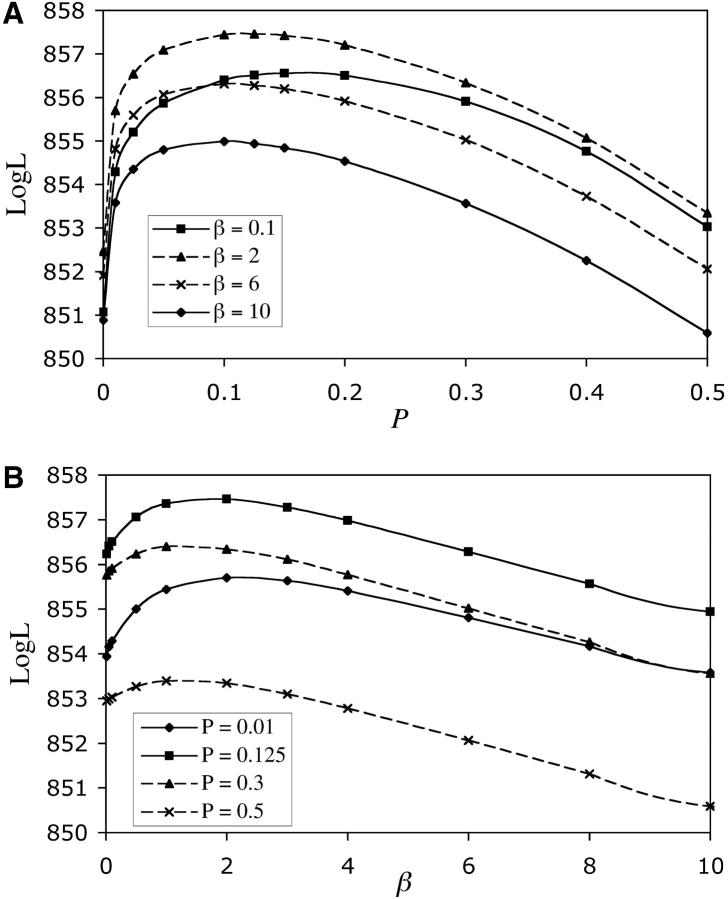
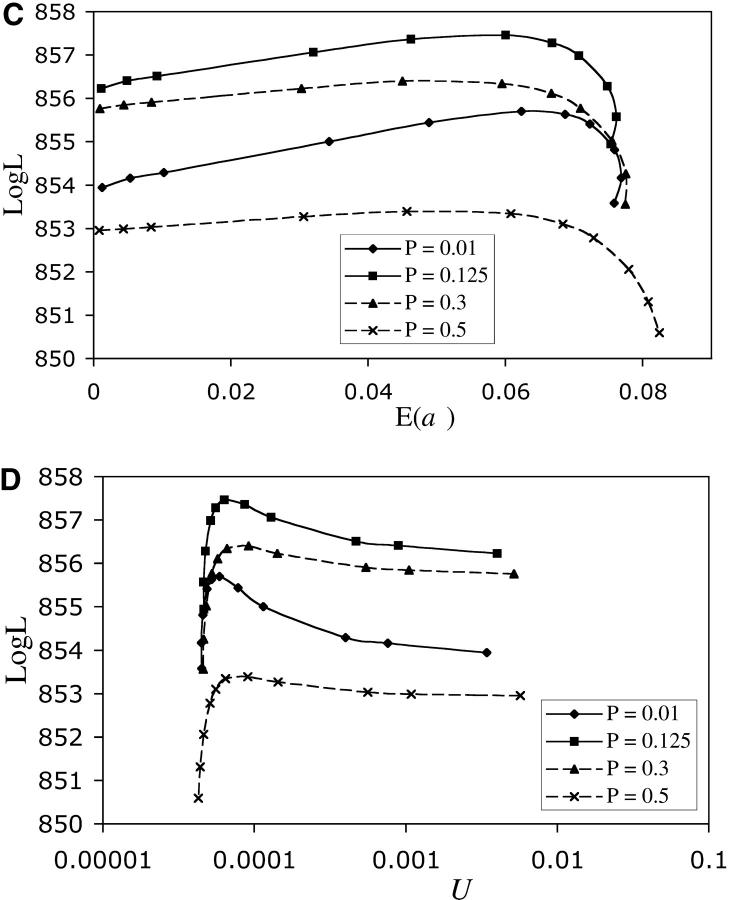
Results from the likelihood analysis are shown in Figure 2. The ML estimate for α is 33 and for β is 2. The equal-effects model gave likelihoods that were >9 log units smaller than the maximum and is a significantly poorer fit to the data (likelihood-ratio test, P < 0.0005). From our analysis, the ML estimates (and 95% confidence intervals) are: P = 0.125 (0.008–0.38), E(a) = 0.061 (0–0.077), and U = 6.3 × 10−5 (4.6 × 10−5–∞) per haploid genome.
Figure 2.—
Profile log-likelihood curves as a function of mutational parameters. (A) the proportion of beneficial alleles, P. (B) The shape parameter of the gamma distribution, β. (C) The average effect of a mutation, E(a). (D) The genome-wide mutation rate, U. ML runs involved setting P and β and then determining the values of E(a) and U that maximized the likelihood. Thus, in A and B, x-axis values are those that were entered into the ML runs (see materials and methods). In C and D, x-axis values are those that were estimated in each of the ML runs. Each point represents the maximum likelihood obtained for a particular combination of β and P, after performing several searches with different starting values of E(a) and U. The reported estimates for each parameter in the text are those values that give the maximum likelihood over all combinations of β and P (= 857.46). Confidence intervals around these estimates are determined by extrapolating the curves to determine the parameter values at which there is a 2 log-unit reduction in likelihood (to 855.46).
We attempted to separately analyze the beneficial and deleterious sides of the distribution of MA line fitness. However, there were not enough lines different from the ancestor on the beneficial side of the distribution to allow separate estimation of the effects for beneficials. As a result we retained the assumption of a reflected gamma distribution.
Generations and effective population size:
For forty-eight of the 50 passages, average colony size was estimated to be 1.4 × 106 cells, which represents ∼20.4 generations between passages, or one cell division every 141 min. For passages 23 and 24, colony size was much smaller, 0.11 × 106 cells, representing ∼16.8 generations between passages. Due to lab error, the medium for these two passages had a different peptone source, which accounts for the less vigorous growth. Combining these estimates, transfers occurred every 20.3 generations and the mutation-accumulation period was 1012 generations. The harmonic mean population size of our MA lines, which serves as an estimate of the effective population size, is 10.7 cells per line. There was no trend toward reduced population size over the course of the experiment.
DISCUSSION
Frequency of beneficial mutations:
Both the ML analysis and the Kruskal-Wallis test indicate that beneficial mutations accumulated in our MA lines. The ML analysis estimates 0.8–38% of our mutations are beneficial and the Kruskal-Wallis test indicates that 19% of the lines with fitness significantly different from that of the ancestor have higher fitness. These results support Shaw et al.'s recent proposal that a substantial fraction of mutations that affect fitness are beneficial (Shaw et al. 2002, 2003). Zeyl and DeVisser (2001) also found suggestive evidence for beneficial mutations in their yeast MA experiment. In their Figure 1A, it appears that among 31 non-petite MA lines, 18 had fitness greater than that of the ancestor, 9 had equal fitness, and only 4 had fitness less than that of the ancestor. However, a model incorporating nonzero P did not improve the fit to their data, although they do not report the confidence interval for P.
Given that the vast majority of mutations are expected to be deleterious, our result requires explanation. There are five possibilities. First, selection may have greatly enriched beneficial and greatly diminished deleterious mutations in our experiment. A fitness-altering mutation that arises during colony growth results in variation upon which selection will act. Faster-growing mutants will be overrepresented and slower-growing mutants will be underrepresented at the time of transfer. The probability of fixing a mutation in a line is proportional to its frequency in a colony at the time of transfer and is thus altered by selection. We estimated this bias using a method developed by Otto and Orive (1995). They model how selection among cell lineages can change the probability that a mutant cell will contribute to the next generation. Their model considers selection on somatic mutations within an individual but is applicable to our situation. We used their Equation 4 and assumed a per-division mutation rate of 6.3 × 10−5 per haploid genome, 20.3 generations per passage, and the gamma distribution of effects estimated by the ML analysis. We then numerically integrated over this distribution using Mathematica (Wolfram 1999) to obtain our correction. Using this procedure, our ML estimate of the frequency of fitness-altering mutations that are beneficial is reduced to 5.75%. Note that selection is expected to be very efficient at eliminating large-effect deleterious mutations, which will be thus be underrepresented in any MA experiment (dominant lethal mutations cannot be accumulated, for example). In nature these mutations will also be efficiently eliminated and it is the mildly deleterious mutations that will be of greatest importance in evolution (see Lynch et al. 1999).
Second, the ancestral strain used in our experiment may have been poorly adapted to the experimental conditions. If this is true, a higher proportion of mutations are expected to be beneficial because the ancestral genotype was far from its fitness optimum (Fisher 1930; Orr 1998). Supporting this hypothesis, the accumulation of the metabolic intermediate in ade-2 mutants is known to slow the growth rate (Ugolini and Bruschi 1996). In addition, an adaptation experiment performed with the ancestral strain found a 14% improvement in fitness in an environment similar to that of the fitness assay (D. W. Hall, unpublished data). Part of this improvement was due to fixation of ade revertants, which are too rare to have been accumulated in the MA experiment (see appendix).
Third, the protocol for measuring fitness may cause mutations that are deleterious in nature to be beneficial in the lab. In the complete medium of our growth assays, several metabolic pathways, such as those involved in amino acid synthesis, are not required. The production of enzymes in some of these pathways might represent a metabolic load on a cell and cause reduced growth in complete medium. Similarly, our fitness measure ignores other aspects of yeast life history, such as haploid growth and sporulation ability, and proteins involved during those stages might also represent a metabolic load on diploid growth rate. Mutations that reduce or preclude production of proteins in these types of pathways might be beneficial to diploid mitotic growth rate, even though they represent deleterious mutations in nature. Testing this hypothesis would require examining lines possessing beneficial mutations in other environments and at other life-history stages.
Fourth, it may be that a relatively small proportion of all mutations are deleterious in yeast due to relaxed purifying selection acting on duplicated genes. The S. cerevisiae genome underwent a duplication event ∼150 million years ago (Langkjaer et al. 2003) and up to 30% of yeast genes remain duplicated (Rubin et al. 2000). Mutations that reduce fitness when they occur in an unduplicated gene may have little effect on fitness if they occur in a duplicated gene, because a fully functional copy of the gene remains in the genome. In contrast, mutations that increase fitness when they occur in an unduplicated gene are also likely to increase fitness when they occur in a duplicated gene, because the mutation would improve the function of one copy of the gene. Furthermore, duplicates may undergo subfunctionalization, in which each copy takes on a subset of the original functions (Lynch and Force 2000). Subfunctionalization reduces pleiotropy in the genome and possibly reduces the deleterious effects of mutations. Support for the effects of duplication comes from recent empirical work in yeast that shows deletions of duplicated genes are less likely to affect fitness than deletions of genes without a duplicate (Gu et al. 2003). Reducing the proportion of mutations that are deleterious will necessarily increase the proportion of fitness-altering mutations that are beneficial. It seems unlikely that this effect could be the only explanation for the observed proportion of beneficial mutations, since that would require an excessive decline in the proportion of mutations that are deleterious. For example, if 0.1% of mutations are beneficial, halving the frequency of deleterious mutations increases the proportion that are beneficial to only 0.2%.
Finally, dominance may have biased our estimates. If deleterious mutations are more likely than beneficials to be recessive, then they would appear underrepresented because we are measuring heterozygous fitness. This possibility is consistent with the empirical observation that most deleterious mutations are recessive (Simmons and Crow 1977; Charlesworth 1979; Orr 1991; Korona 1999; Szafraniec et al. 2003). Information concerning the dominance of beneficial mutations is rare and usually comes from studies of adaptive substitutions, which selection may bias toward dominant mutations (Orr and Betancourt 2001). In addition to different levels of dominance exhibited by deleterious and beneficial mutations, some mutations exhibit overdominance. Overdominance has been observed in both S. cerevisiae (Zeyl et al. 2003) and Caenorhabditis elegans (Peters et al. 2003, but see Fry 2004) and would elevate the apparent frequency of beneficial mutations. Wloch et al. (2001) found slightly <2% of mutations were beneficial in their haploid MA experiment. If our estimate for diploid growth in lab yeast is accurate, their result suggests that a mutation that is beneficial when heterozygous in a diploid may be deleterious or neutral when haploid, consistent with overdominance. This possibility requires further investigation.
Keightley and Lynch (2003) challenged the conclusions of Shaw et al. (2002) regarding the high frequency of beneficial mutations they obtained on three grounds. We address each of these criticisms in the context of our study. First, Keightley and Lynch suggested that the traits examined by Shaw et al. might be under stabilizing selection and so are not “genuine major fitness components” (Keightley and Lynch 2003). In our study, we examined maximum growth rate that empirical work suggests is a major component of competitive fitness in Escherichia coli (Lenski et al. 1998) and is likely a critical fitness component for other microorganisms such as yeast. Second, Keightley and Lynch suggest that the length of Shaw et al.'s experiment may have been insufficient to reveal a significant change in mean phenotype. We are in agreement with Shaw et al. (2003) that finding a significant change in mean phenotype does not shed light on the ratio of deleterious to beneficial mutations, since their average effects may differ. Regardless, the mean fitness of our MA lines declined significantly. Third, Keightley and Lynch criticize Shaw et al.'s failure to consider alternative models for the distribution of mutational effects. In our ML analysis, we examined models of equal and variable mutational effect. The variable-effects model allowing beneficial mutations yielded the highest likelihood scores.
The large proportion of beneficial mutations observed in our experiment may in part reflect a combination of factors: the ancestor's distance from the fitness optimum, yeast's recent genome duplication, our examination of only a single environment and life-history stage, and the recessive nature of deleterious mutations. Even taking these into account, the value obtained suggests that beneficial mutations may be more common than expected in yeast.
Although it has received little theoretical consideration, a high proportion of beneficials have substantial implications for the fitness and persistence of yeast populations. In large populations, the rate of adaptation increases with the proportion of beneficial mutations and plateaus when that proportion becomes exceedingly high (Campos and De Oliveira 2004). In small populations, the probability of population persistence increases with the proportion of beneficial mutations (Whitlock et al. 2003). This occurs because small populations readily accumulate deleterious mutations that can drive them to extinction if not offset by the effects of beneficial mutations (Lande 1994; Lynch et al. 1995).
Genome-wide mutation rate, U:
Our ML estimate of U is 6.3 × 10−5 per haploid genome with a 95% confidence interval ranging from 4.6 × 10−5 to infinity (Figure 2). The unbounded confidence interval surrounding our estimate of U is typical for ML analyses of MA data and prevents us from ruling out the possibility that the actual mutation rate is much larger than estimated (Keightley 1998). Using our ML estimate for U, ∼18 mutations (2 × 6.3 × 10−5 mutations per diploid genome per generation × 151 lines × 1012 generations) are expected to have accumulated during the course of the experiment. Accounting for the excess fixation probability of beneficial mutations (i.e., using the uncorrected ML frequency of beneficial mutations, P = 0.125), 2.3 of the 18 mutations are expected to be beneficial and 15.7 deleterious. These numbers agree quite well with the 3 beneficial and 13 deleterious lines identified by the Kruskal-Wallis test as having significantly different fitness. This suggests that the change in fitness in lines exhibiting significantly different fitness from that of the ancestor may be caused by single mutations.
Our confidence interval for U includes the value reported by Wloch et al. (2001), which is 18-fold higher (Table 1). Wloch et al.'s higher estimate may be because they examined haploid yeast and thus their estimate includes recessive mutations whose effects are masked in heterozygous diploids. Our estimate is similar to that found by Zeyl and Devisser (2001). This is not unexpected since both experiments used a similar design and the same likelihood analysis to estimate U and E(a).
TABLE 1.
Some estimates of haploid mutation rates and effects of mutations from previous MA experiments
| Taxon | Fitness component |
U | E(a) | Reference |
|---|---|---|---|---|
| D. melanogaster | Viability | 0.35 | 0.027 | Mukai (1964) |
| Viability | 0.47 | 0.023 | Mukai et al. (1972) | |
| Viability | 0.14 | 0.03 | Ohnishi (1977) | |
| Viability | 0.02 | 0.1 | Garcia-Dorado et al. (1999) | |
| Viability | 0.052 | 0.11 | Fry et al. (1999) | |
| A. thaliana | LRS | 0.05 | 0.23 | Schultz et al. (1999) |
| Fruit no. | 0.06 | 0.06a | Shaw et al. (2002) | |
| C. elegans | r | 0.0035 | 0.1 | Keightley and Caballero (1997) |
| r | 0.008 | 0.2 | Vassilieva and Lynch (1999) | |
| S. cerevisiae | MGR | 0.000063 | 0.061a | S. B. Joseph and D. W. Hall (this study) |
| r | 0.0011 | 0.086b | Wloch et al. (2001) | |
| r | 0.000048 | 0.217a | Zeyl and DeVisser (2001) | |
| r | — | 0–0.049a,c | Zeyl and DeVisser (2001) | |
| E. coli | r | 0.00017 | 0.012b | Kibota and Lynch (1996) |
The effect of mutations is measured in homozygotes, except where noted. LRS, lifetime reproductive success; MGR, maximum growth rate; r, growth rate. Modified from Bataillon (2000).
Mean effect in heterozygotes.
Mean effect in haploids.
Data from a mutator line.
Mean effect of mutations, E(a):
Our ML estimate of E(a) is 0.061. Our 95% confidence interval (0–0.077) substantially overlaps that found by Zeyl and Devisser (2001) for their mutator strain (0–0.049). Their estimate from a nonmutator strain is substantially larger (0.217) and is based on a single line, perhaps containing a single mutation, and thus little confidence can be given to that estimate. The only other estimate in yeast of mean mutational effect is for haploid fitness (Wloch et al. 2001) and is somewhat larger than our upper confidence bound (Table 1). The difference may be due to mutations tending to be partially masked in heterozygous diploids.
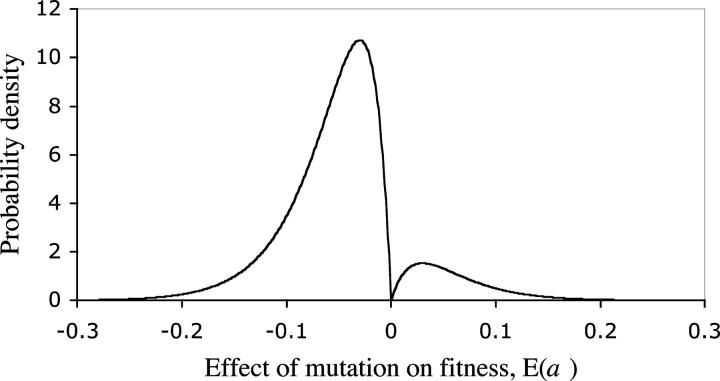
Using the ML estimates of the two parameters of the gamma distribution, β and α, we can determine the shape of the distribution of mutational effects (Figure 3). The wide confidence interval associated with the estimates of β and α implies that other distributions in which the majority of mutations have heterozygous fitness effects of <1% are also possible.
Figure 3.—
The distribution of the effect of accumulated heterozygous mutations. The parameters of the reflected gamma distribution are obtained from the maximum-likelihood estimates: P = 0.125, β = 2, and α = 33.
The ML analysis assumes that the distribution of mutational effects is identical for deleterious and beneficial mutations. However, selection would have enhanced the frequency of large-effect beneficial and reduced the frequency of large-effect deleterious mutations. We were unable to determine the degree to which this bias altered our estimate of the distribution of mutational effects.
Mutational heritability, h2m:
The estimate of mutational variance in our MA lines was standardized to yield a mutational heritability (h2m) of 1.1 × 10−3. This estimate is slightly larger than that of Zeyl and DeVisser (2001), who estimate the mutational heritability of their MA lines to be 4.8 × 10−4. Our estimate is, however, nearly identical to that of Lynch (1988) who estimated the average mutational heritability across many organisms to be 1 × 10−3. This similarity is surprising given the low mutation rate and intermediate mutational effects observed in yeast. The similarity is likely due to the low environmental variance (VE) observed in our experiment.
Four decades of MA experiments have left us with many questions concerning parameters of spontaneous mutations (Lynch et al. 1999). For example, we still do not know the genome-wide mutation rate for Drosophila melanogaster, even within an order of magnitude (Table 1). The only pattern that seems real is that microorganisms have substantially smaller genome-wide mutation rates than multicellular organisms. There are two explanations for this observation.
First, the mutation rate reported for multicellular organisms is per generation and for microbes it is per cell division. D. melanogaster has ∼36 cell divisions in the germ line per generation (Drost and Lee 1995) and thus the mutation rate per cell division is ∼0.005 (Lynch et al. 1999). This value is more similar to the values obtained for yeast and E. coli (Table 1), supporting the conclusion that the total number of mutations per cell division is relatively constant across taxa (Drake 1991; Drake et al. 1998). However, even per cell division, yeast and E. coli appear to have a lower mutation rate than multicellular eukaryotes and additional work addressing this difference is needed.
Second, theoretical work predicts that a greater percentage of mutations will be deleterious, and thus fewer will be beneficial, in more complex organisms (Fisher 1930; Orr 2000). If true, a slower decline in line fitness in MA experiments involving less complex organisms is expected because beneficial mutations would offset the effects of deleterious mutations to some degree. This would result in lower estimates of genome-wide mutation rates, particularly if the possibility of beneficial mutations was not included in the analysis.
A great deal of work remains to be done in yeast. Additional experiments are needed to determine the variation in mutation rates and effects seen across different strains and across different stages of the life cycle. Such experiments will help us to understand the high rate of beneficial mutations reported here and perhaps the variation seen within and across taxa.
Acknowledgments
We thank T. Bataillon, J. Bull, A. Johnson, P. Keightley, and especially S. Otto, M. Kirkpatrick, and two anonymous reviewers for discussions and comments that improved the study and manuscript; P. Keightley for supplying his maximum-likelihood program and suggesting how to search the parameter space; and C. Chan and A. Johnson for providing yeast strains and plasmids. This work was supported in part by National Science Foundation grant DEB-09973221 (to Mark Kirkpatrick) and by a graduate fellowship from the University of Texas Department of Integrative Biology (to S.J.).
APPENDIX
Here we present the results of a series of experiments to address possible sources of bias caused by our use of the ade mutant to screen for petite mutations. Bias would have occurred if we had chosen not to passage colonies that appeared white but were not petite. Non-petite colonies that appeared white after 48 hr of growth could have been either white ade revertants, white mutants that suppressed the red pigment, or red colonies that grew so slowly that their red color had not developed after 48 hr. Thus, bias could be due to inaccurately scoring white or to white colonies sometimes being non-petite.
To test how accurately we scored white colonies, we first streaked the ancestor from the −80° freezer onto solid YPD. After 48 hr we then streaked 56 plates using individual ancestor colonies at a density similar to that obtained during our MA experiment. We then scored all individual colonies as red, white, or unknown (a category that would have been passaged during our experiment). We scored a total of 4537 colonies: 4279 red, 93 white, and 164 unknown. We then stored the 56 plates at 4° for 5 days. Under these conditions red colonies become more vividly red and white colonies become whiter. After 5 days at 4°, we rescored the colonies as 4365 red, 172 white, and zero unknown. In no instance did we inaccurately score a colony as white after 48 hr of growth and red after 5 days at 4° or vice versa.
We also tested how often white colonies were in fact non-petite. We accomplished this by first streaking 100 plates, eight sectors per plate, using a different ancestor colony for each sector. After 48 hr of growth, we spotted a single white colony onto YPD from each sector containing white colonies. This guaranteed that each white colony selected was independent of the others. We then grew the white colonies for 48 hr and replica plated them onto YPG, which contains a nonfermentable carbon source. All 198 independent white colonies were unable to grow on YPG, indicating that they were indeed petite.
Finally, we addressed how often the ade mutant reverts. To do this we grew five replicates of the ancestor for 24 hr in liquid media to a final density of ∼1 × 107 cells/ml. We then plated 1 ml of this solution onto five petri dishes of adenine dropout medium. After 72 hr, we scored the number of ade revertant colonies present on each plate (0, 1, 3, 4, and 4). We then used the Luria-Delbruk method to calculate a reversion rate (Luria and Delbruk 1943). We estimate the reversion rate at the ade locus to be ∼1.6 × 10−7 revertants per cell generation. Since there were 7550 colony passages during the MA experiment, there is a 99.8% chance that there were no revertants in our MA experiment, and we can ignore them as a source of bias.
These experiments indicate that we were able to accurately score colonies and that all colonies scored as white were indeed petites. We thus believe that bias due to our use of the ade mutant was not a problem in our MA experiment.
References
- Bataillon, T., 2000. Estimation of spontaneous genome-wide mutation rate parameters: Whither beneficial mutations? Heredity 84: 497–501. [DOI] [PubMed] [Google Scholar]
- Bernardi, G., 1979. The petite mutation in yeast. Trends Biochem. Sci. 4: 197–201. [Google Scholar]
- Campos, P. R. A., and V. M. De Oliveira, 2004. Mutational effects on the clonal interference phenomenon. Evolution 58: 932–937. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., 1979. Evidence against Fisher's theory of dominance. Nature 278: 848–849. [Google Scholar]
- Drake, J. W., 1991. A constant rate of spontaneous mutation in DNA-based microbes. Proc. Natl. Acad. Sci. USA 88: 7160–7164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake, J. W., B. Charlesworth, D. Charlesworth and J. F. Crow, 1998. Rates of spontaneous mutation. Genetics 148: 1667–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drost, J. B., and W. R. Lee, 1995. Biological basis of germline mutation—comparisons of spontaneous germline mutation—rates among Drosophila, mouse, and human. Environ. Mol. Mutagen. 25: 48–64. [DOI] [PubMed] [Google Scholar]
- Dujon, B., 1981 Mitochondrial genetics and functions, pp. 505–635 in The Molecular Biology of the Yeast Saccharomyces, edited by J. N. Strathern, E. W. Jones and J. R. Broach. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY.
- Eyre-Walker, A., P. D. Keightley, N. G. C. Smith and D. Gaffney, 2002. Quantifying the slightly deleterious mutation model of molecular evolution. Mol. Biol. Evol. 19: 2142–2149. [DOI] [PubMed] [Google Scholar]
- Fisher, R. A., 1930 The Genetical Theory of Natural Selection. Oxford University Press, Oxford.
- Fry, J. D., 2004. How common are overdominant mutations? Genetics 167: 1031–1032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fry, J. D., P. D. Keightley, S. L. Heinsohn and S. V. Nuzhdin, 1999. New estimates of the rates and effects of mildly deleterious mutation in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 96: 574–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Dorado, A., 1997. The rate and effects distribution of viability mutation in Drosophila: minimum distance estimation. Evolution 51: 1130–1139. [DOI] [PubMed] [Google Scholar]
- Garcia-Dorado, A., C. Lopez-Fanjul and A. Caballero, 1999. Properties of spontaneous mutations affecting quantitative traits. Genet. Res. 74: 341–350. [DOI] [PubMed] [Google Scholar]
- Gu, Z. L., L. M. Steinmetz, X. Gu, C. Scharfe, R. W. Davis et al., 2003. Role of duplicate genes in genetic robustness against null mutations. Nature 421: 63–66. [DOI] [PubMed] [Google Scholar]
- Keightley, P. D., 1994. The distribution of mutation effects on viability in Drosophila melanogaster. Genetics 138: 1315–1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley, P. D., 1998. Inference of genome-wide mutation rates and distributions of mutation effects for fitness traits: a simulation study. Genetics 150: 1283–1293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley, P. D., and A. Caballero, 1997. Genomic mutation rates for lifetime reproductive output and lifespan in Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA 94: 3823–3827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley, P. D., and M. Lynch, 2003. Toward a realistic model of mutations affecting fitness. Evolution 57: 683–685. [DOI] [PubMed] [Google Scholar]
- Keightley, P. D., and O. Ohnishi, 1998. EMS induces polygenic mutation rates for nine quantitative characters in Drosophila melanogaster. Genetics 148: 753–766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kibota, T. T., and M. Lynch, 1996. Estimate of the genomic mutation rate deleterious to overall fitness in E. coli. Nature 381: 694–696. [DOI] [PubMed] [Google Scholar]
- Korona, R., 1999. Genetic load of the yeast Saccharomyces cerevisiae under diverse environmental conditions. Evolution 53: 1966–1971. [DOI] [PubMed] [Google Scholar]
- Lande, R., 1994. Risk of population extinction from fixation of new deleterious mutations. Evolution 48: 1460–1469. [DOI] [PubMed] [Google Scholar]
- Langkjaer, R. B., P. F. Cliften, M. Johnston and J. Piskur, 2003. Yeast genome duplication was followed by asynchronous differentiation of duplicated genes. Nature 421: 848–852. [DOI] [PubMed] [Google Scholar]
- Lenski, R. E., J. A. Mongold, P. D. Sniegowski, M. Travisano, F. Vasi et al., 1998. Evolution of competitive fitness in experimental populations of E. coli: What makes one genotype a better competitor than another? Antonie Leeuwenhoek Int. J. Genet. 73: 35–47. [DOI] [PubMed] [Google Scholar]
- Luria, S. E., and M. Delbruk, 1943. Mutations of bacteria from virus sensitivity to virus resistance. Genetics 28: 491–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch, M., 1988. The rate of polygenic mutation. Genet. Res. 51: 137–148. [DOI] [PubMed] [Google Scholar]
- Lynch, M., and A. G. Force, 2000. The probability of duplicate gene preservation by subfunctionalization. Genetics 154: 459–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch, M., J. Conery and R. Burger, 1995. Mutation accumulation and the extinction of small populations. Am. Nat. 146: 489–518. [Google Scholar]
- Lynch, M., J. Blanchard, D. Houle, T. Kibota, S. Schultz et al., 1999. Perspective: spontaneous deleterious mutation. Evolution 53: 645–663. [DOI] [PubMed] [Google Scholar]
- Mukai, T., 1964. The genetic structure of natural populations of Drosophila melanogaster. I. Spontaneous mutation rate of polygenes controlling viability. Genetics 50: 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukai, T., S. I. Chigusa, L. E. Mettler and J. F. Crow, 1972. Mutation rate and dominance of genes affecting viability in Drosophila melanogaster. Genetics 72: 333–355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohnishi, O., 1977. Spontaneous and ethyl methanesulfonate-induced mutations controlling viability in Drosophila melanogaster. II. Homozygous effect of polygenic mutations. Genetics 87: 529–545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr, H. A., 1991. A test of Fisher's theory of dominance. Proc. Natl. Acad. Sci. USA 88: 11413–11415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr, H. A., 1998. The population genetics of adaptation: the distribution of factors fixed during adaptive evolution. Evolution 52: 935–949. [DOI] [PubMed] [Google Scholar]
- Orr, H. A., 2000. Adaptation and the cost of complexity. Evolution 54: 13–20. [DOI] [PubMed] [Google Scholar]
- Orr, H. A., and A. J. Betancourt, 2001. Haldane's sieve and adaptation from the standing genetic variation. Genetics 157: 875–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto, S. P., and M. E. Orive, 1995. Evolutionary consequences of mutation and selection within an individual. Genetics 141: 1173–1187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters, A. D., D. L. Halligan, M. C. Whitlock and P. D. Keightley, 2003. Dominance and overdominance of mildly deleterious induced mutations for fitness traits in Caenorhabditis elegans. Genetics 165: 589–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piskur, J., 1994. Inheritance of the yeast mitochondrial genome. Plasmid 31: 229–241. [DOI] [PubMed] [Google Scholar]
- Rubin, G. M., M. D. Yandell, J. R. Wortman, G. L. G. Miklos, C. R. Nelson et al., 2000. Comparative genomics of the eukaryotes. Science 287: 2204–2215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SAS Institute, 2000 JMP 4.0.4. SAS Institute, Cary, NC.
- Schultz, S. T., M. Lynch and J. H. Willis, 1999. Spontaneous deleterious mutation in Arabidopsis thaliana. Proc. Natl. Acad. Sci. USA 96: 11393–11398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw, F. H., C. J. Geyer and R. G. Shaw, 2002. A comprehensive model of mutations affecting fitness and inferences for Arabidopsis thaliana. Evolution 56: 453–463. [DOI] [PubMed] [Google Scholar]
- Shaw, R. G., F. H. Shaw and C. J. Geyer, 2003. What fraction of mutations reduces fitness? A reply to Keightley and Lynch. Evolution 57: 686–689. [Google Scholar]
- Simmons, M. J., and J. F. Crow, 1977. Mutations affecting fitness in Drosophila populations. Annu. Rev. Genet. 11: 49–78. [DOI] [PubMed] [Google Scholar]
- Szafraniec, K., D. M. Wloch, P. Sliwa, R. Borts and R. Korona, 2003. Small fitness effects and weak genetic interactions between deleterious mutations in heterozygous loci of the yeast Saccharomyces cerevisiae. Genet. Res. 82: 19–31. [DOI] [PubMed] [Google Scholar]
- Ugolini, S., and C. V. Bruschi, 1996. The red/white colony color assay in the yeast Saccharomyces cerevisiae: epistatic growth advantage of white ade8-18, ade-2 cells over red ade-2 cells. Curr. Genet. 30: 485–492. [DOI] [PubMed] [Google Scholar]
- Vassilieva, L. L., and M. Lynch, 1999. The rate of spontaneous mutation for life-history traits in Caenorhabditis elegans. Genetics 151: 119–129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock, M. C., C. K. Griswold and A. D. Peters, 2003. Compensating for the meltdown: the critical effective size of a population with deleterious and compensatory mutations. Ann. Zool. Fenn. 40: 169–183. [Google Scholar]
- Wilkie, D., 1983 Yeast Genetics: Fundamental and Applied Aspects, pp. 255–267. Springer-Verlag, New York.
- Wloch, D. M., K. Szafraniec, R. H. Borts and R. Korona, 2001. Direct estimate of the mutation rate and the distribution of fitness effects in the yeast Saccharomyces cerevisiae. Genetics 159: 441–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfram, S., 1999 The Mathematica Book. Wolfram Media, Champaign, IL.
- Zeyl, C., and J. DeVisser, 2001. Estimates of the rate and distribution of fitness effects of spontaneous mutation in Saccharomyces cerevisiae. Genetics 157: 53–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeyl, C., T. Vanderford and M. Carter, 2003. An evolutionary advantage of haploidy in large yeast populations. Science 299: 555–558. [DOI] [PubMed] [Google Scholar]