Abstract
An international consortium has launched the whole-genome sequencing of potato, the fourth most important food crop in the world. Construction of genetic linkage maps is an inevitable step for taking advantage of the genome projects for the development of novel cultivars in the autotetraploid crop species. However, linkage analysis in autopolyploids, the kernel of linkage map construction, is theoretically challenging and methodologically unavailable in the current literature. We present here a theoretical analysis and a statistical method for tetrasomic linkage analysis with dominant and/or codominant molecular markers. The analysis reveals some essential properties of the tetrasomic model. The method accounts properly for double reduction and incomplete information of marker phenotype in regard to the corresponding phenotype in estimating the coefficients of double reduction and recombination frequency and in testing their significance by using the marker phenotype data. Computer simulation was developed to validate the analysis and the method and a case study with 201 AFLP and SSR markers scored on 228 full-sib individuals of autotetraploid potato is used to illustrate the utility of the method in map construction in autotetraploid species.
POLYPLOIDY has played an important role in the evolution of eukaryotes, particularly flowering plants, and has implications for genetic improvement of many important agricultural crops such as alfalfa, potato, sugarcane, and cotton (Grant 1971; Lewis 1980; Otto and Whitton 2000). In the era of genomics, genetic linkage maps exist or are rapidly becoming available for most important diploid animal and plant species and provide the springboard for genome projects in these species. In sharp contrast, the corresponding study in autopolyploid species is still in its initial stages. As the theoretical kernel of genetic map construction, linkage analysis in this group of species has been a historical challenge since the years of pioneering quantitative geneticists such as Haldane (1930), Mather (1936), and Fisher (1947). This is largely due to the complexities of gene segregation and recombination during meiosis in such organisms, namely: (i) multiplex allele segregation; (ii) double reduction, a phenomenon in which sister chromatids enter in the same gamete and cause systematic segregation distortion and complex segregation pattern; and (iii) mixed bivalent and quadrivalent pairings among homologous chromosomes.
The current data sets available for linkage analyses in autotetraploids are DNA molecular polymorphisms that exhibit either dominant (e.g., AFLPs and RAPDs) or codominant (e.g., RFLPs and SSRs) segregation in a mapping population. In addition to the aforementioned complexities (i–iii), challenges in modeling these PCR-based genetic markers involve (iv) occurrence of null alleles due to experimental failure to identify the presence of some alleles and (v) one phenotype representing several genotypes. Linkage analyses of autopolyploids in the current literature have been based either on the use of single-dose (simplex) dominant markers (e.g., AFLPs and RAPDs) that segregate in a simple 1:1 ratio in mapping populations (Wu et al. 1992; Meyer et al. 1998; Brouwer and Osborn 1999; Barcaccia et al. 2003) or on assuming solely random bivalent pairing among homologous chromosomes (Ripol et al. 1999; Hackett et al. 2001; Luo et al. 2001; Bradshaw et al. 2004; Cao et al. 2005). These have effectively avoided the analytical complexities but at the same time ignored some essential features of the problems.
Having considered these analytical complexities, we developed a statistical framework for genetic linkage analysis in autotetraploid species (Luo et al. 2004). The basis of the analysis is the theoretical model that relates the coefficients of double reduction at two loci with recombination frequency between them. A likelihood-based approach was developed to estimate the model parameters and to test their significance. In this article, the method is elaborated in detail with the aims of investigating the statistical properties of tetrasomic linkage analysis and demonstrating its utility and efficiency in genetic map construction in autotetraploid species. It is illustrated through a case study of constructing genetic linkage maps of microsatellite and AFLP markers collected from a mapping population of cultivated autotetraploid potato (Solanum tuberosum).
METHODS
The current data sets available for linkage analyses in autotetraploids are DNA molecular polymorphisms that exhibit either dominant (e.g., AFLPs and RAPDs) or codominant (e.g., RFLPs and SSRs) segregation in a mapping population. We have summarized the challenges in tetrasomic linkage analysis with these PCR-based genetic markers in the Introduction. Here we illustrate a general method of tetrasomic linkage analysis between two loci, taking all these problems into account. The method analyzes marker phenotypic data (usually gel bands) scored on two autotetraploid parental lines and their offspring at any two marker loci and has the following steps:
We calculate the probability distribution of all possible parental genotypes that is consistent with the observed phenotypes given the parental phenotypes and phenotypes of their offspring, independently at each of the two loci. A simulation study showed that both the parental genotypes can be correctly identified with a probability of nearly 1.0 even with a modest population size of 100 (Luo et al. 2000). At this step, the maximum-likelihood estimate (MLE) of the coefficient of double reduction can be independently worked out at each of the two loci. Whenever there are several probable parental genotypes, the most probable two genotypes will be considered in the next step of linkage analysis.
From the predicted parental genotypes at each of two loci, we can construct two-locus genotypes of the parents by considering all possible linkage phases. For a given pair of parental genotypes, we calculate the probability distribution of offspring genotypes as a function of λ (the probability of a randomly chosen diploid gamete from bivalent pairing), α (the coefficient of double reduction at the putative locus A), and r (recombination frequency between the two loci) by making use of a computer-based algorithm developed in Luo et al. (2001, 2004). The genotypic distribution is then converted into the phenotypic distribution according to the rules that account for dominance/codominance of markers under question and the possibility of the null allele at each of the loci.
With the phenotypic distribution and the numbers of different phenotypes observed from the mapping population, we developed an EM (expectation-maximization) algorithm to estimate the model parameters and to test their significance on the basis of a likelihood-ratio test. The algorithm is detailed in methods.
We can repeat the above steps 1–3 for all possible parental genotypes (different configurations of allelic constitution at each of the two loci and their linkage phase) and make a statistical inference about the most likely model.
Maximum-likelihood estimation of the model parameters:
Here we present a statistical framework to analyze phenotypic data of dominant or codominant markers under the two-locus tetrasomic inheritance model. We have shown that the probability of the ith phenotype in the mapping population can be expressed as
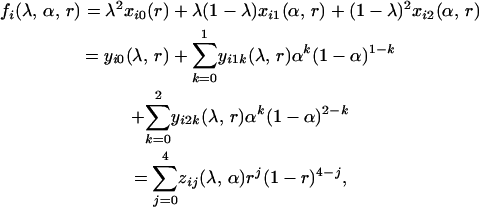 |
(1) |
in which the coefficients 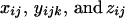 depend on the model parameters λ, α, and/or r. The second subscript of yijk refers to the possible number of double-reduction gametes (j = 1, 2). We developed a computer-based algorithm to calculate these parameters for any given pair of parental genotypes, dominance model of marker alleles, and model parameter values. The algorithm first mimics two cases of gametogenesis, respectively, involving bivalent and quadrivalent pairing of homologous chromosomes of a given parental genotype. Then gamete genotypes generated from the two parents are paired into all possible offspring genotypes under each of these two pairing cases or a mixture of them. For each of the three possible pairing types, the offspring genotypes were sorted according to the number of double-reduction gametes if the gametogenesis involved quadrivalent chromosomal pairing and the number of recombinant gametes. These offspring genotypes are sorted again into phenotype groups by summing up the individuals that turn up in the same phenotype. In parallel with these sorting processes, double-reduction and recombinant statuses for the individuals (also the coefficients of the offspring genotypic frequencies) within the same phenotype groups are also updated and stored, yielding the xij's, yijk's, and zij's.
depend on the model parameters λ, α, and/or r. The second subscript of yijk refers to the possible number of double-reduction gametes (j = 1, 2). We developed a computer-based algorithm to calculate these parameters for any given pair of parental genotypes, dominance model of marker alleles, and model parameter values. The algorithm first mimics two cases of gametogenesis, respectively, involving bivalent and quadrivalent pairing of homologous chromosomes of a given parental genotype. Then gamete genotypes generated from the two parents are paired into all possible offspring genotypes under each of these two pairing cases or a mixture of them. For each of the three possible pairing types, the offspring genotypes were sorted according to the number of double-reduction gametes if the gametogenesis involved quadrivalent chromosomal pairing and the number of recombinant gametes. These offspring genotypes are sorted again into phenotype groups by summing up the individuals that turn up in the same phenotype. In parallel with these sorting processes, double-reduction and recombinant statuses for the individuals (also the coefficients of the offspring genotypic frequencies) within the same phenotype groups are also updated and stored, yielding the xij's, yijk's, and zij's.
If a random sample of n individuals is collected from the mapping population and there are M different marker phenotypes observed in the sample, the likelihood function of the parameters 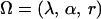 given the parental genotypes G1, G2 and the observed phenotypic data O can be written as
given the parental genotypes G1, G2 and the observed phenotypic data O can be written as
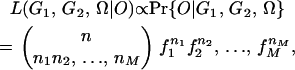 |
(2) |
where ni (i = 1, 2, … , M) is the number of individuals with the ith phenotype class in the sample. Since the phenotype data provide only partial information on offspring genotypes, the log-likelihood function can be analyzed with the EM algorithm (Dempster et al. 1977), a statistical approach appropriate for missing data. The EM algorithm in the present context involves iterating the following two steps from initially given values of parameters:
- The E-step calculates the probability of individuals with the ith phenotype having k (k = 0, 1, 2) gametes from meiosis with bivalent chromosome pairing from
the probability of these individuals carrying a k (k = 0, 1) double-reduction gamete from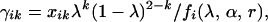
(3a)
and the probability of having k (k = 0, 1, … , 4) recombinant chromosomes from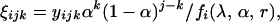
(3b)
where xij's, yijk's, and zij's are those given in Equation 1.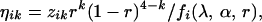
(3c) - The M-step updates the model parameters from
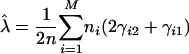
(4a) 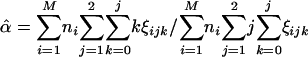
(4b)
Iteration of the two steps generates a series of the parameter estimates, which monotonically converge to local maxima of the log-likelihood function depending on the values used to initiate the algorithm (McLachlan and Krishnan 1997), particularly when parameter λ needs to be modeled. Thus, we suggest the use of different sets of initial values to search for the maximum-likelihood estimates of the parameters.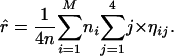
(4c)
Simulation model of multilocus tetrasomic inheritance:
The simulation model mimics gametogenesis of an autotetraploid individual whose meiosis involves quadrivalent pairing of homologous chromosomes. The model considers m loci on a chromosome: L1, L2, … , Lm. For simplicity, we assume that L1 is the most proximal to the centromere and Lm is the most distal. There are at most four distinct alleles at any locus of an autotetraploid individual genotype. When quadrivalent pairing forms among homologous chromosomes, crossing over can occur between any pair of nonsister chromatids. Sexual differentiation in recombination frequency and interference are assumed to be absent. The gametogenesis is simulated as a Markovian process: the gamete genotype at L1 is randomly sampled following the probability distribution given by
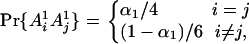 |
(5) |
where 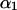 is the coefficient of double reduction at the locus. The distribution implies that there are a total of 10 possible gamete genotypes when double reduction occurs and that the number reduces to 6 when double reduction is absent.
is the coefficient of double reduction at the locus. The distribution implies that there are a total of 10 possible gamete genotypes when double reduction occurs and that the number reduces to 6 when double reduction is absent.
Given the gamete genotype at 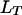 being
being 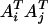 , the probability of the genotype at
, the probability of the genotype at 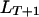 being
being 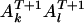 is given by
is given by
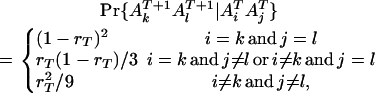 |
(6) |
where 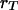 is the recombination frequency between the loci
is the recombination frequency between the loci 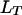 and
and 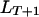 . The equality in subscripts means that alleles locate on the same chromosomes. We can show that the coefficient of double reduction at the locus
. The equality in subscripts means that alleles locate on the same chromosomes. We can show that the coefficient of double reduction at the locus 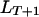 is determined by both
is determined by both 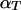 , the coefficient of double reduction at the locus
, the coefficient of double reduction at the locus 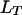 , and r, the recombination frequency between the two loci, through Equation 1 (Luo et al. 2004).
, and r, the recombination frequency between the two loci, through Equation 1 (Luo et al. 2004).
We have described another simulation model that mimics the multiple-locus gametogenesis of an autotetraploid individual whose meiosis involves bivalent pairing only (Luo et al. 2001). These two simulation models are programmed into two computer subroutines to generate gametes from any given multilocus tetraploid genotype under either a quadrivalent or a bivalent pairing setting. The gametes are randomly united to form zygotes.
RESULTS
Properties of the two-locus tetrasomic model:
The theoretical model of tetrasomic linkage analysis considers segregation of alleles at two linked loci in a full-sib family derived from crossing two autotetraploid parental individuals. We consider here the scenario that the two loci are in the same arm of a chromosome. Let α and β be the coefficients of double reduction at two loci, respectively, with α ≤ β indicating that the first locus locates more proximally to the centromere than the second. If r denotes the recombination frequency between the two loci, we show that the relationship between the two double-reduction coefficients is mediated by the recombination frequency in the form of
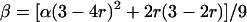 |
(7) |
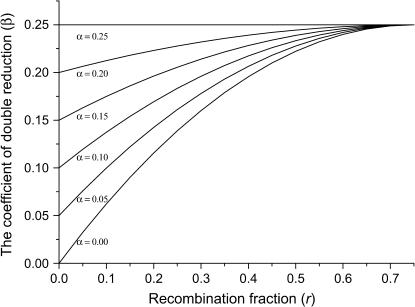
(Luo et al. 2004). It reveals that any recombination occurring between a locus and the centromere may cause double reduction at that locus. Second, the level of double reduction at a locus is linearly related to that of a linked locus by an extent depending on their recombination frequency. Figure 1 illustrates a numerical evaluation of the coefficient of double reduction, β, for various values of α over all possible values of recombination frequency. It shows that the upper limit for the coefficient of double reduction is 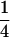 rather than
rather than 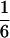 as cited in historical literature (Muller 1914; Mather 1935; Bailey 1961) and in more recent publications (Ronfort 1998; Butruille and Boiteux 2000) and that the maximal value of recombination frequency in autotetraploids is 0.75, at which double reduction reaches its highest frequency, rather than 0.5 as in diploid species. With the assumption of a Poisson distribution of crossovers and absence of interference in recombination, we are able to work out a mapping function that is analogous to Haldane's mapping function in autotetraploid species as
as cited in historical literature (Muller 1914; Mather 1935; Bailey 1961) and in more recent publications (Ronfort 1998; Butruille and Boiteux 2000) and that the maximal value of recombination frequency in autotetraploids is 0.75, at which double reduction reaches its highest frequency, rather than 0.5 as in diploid species. With the assumption of a Poisson distribution of crossovers and absence of interference in recombination, we are able to work out a mapping function that is analogous to Haldane's mapping function in autotetraploid species as
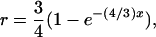 |
(8) |
where x is the genetic distance in map units of centimorgans.
Figure 1.
Expected value of the coefficient of double reduction, β, at a locus that locates more distally to the centromere than its linked locus at which the coefficient of double reduction is α. The value of β is evaluated at different values of α over all possible r, the recombination frequency between the two linked loci.
It is not difficult to explain 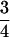 as the upper limit value of recombination frequency in autotetraploids if one notes that only one-fourth of the gametes are nonrecombinants when two marker loci segregate independently when a quadrivalent forms at the first division of meiosis. This was also observed in Sved (1964). The maximum value of
as the upper limit value of recombination frequency in autotetraploids if one notes that only one-fourth of the gametes are nonrecombinants when two marker loci segregate independently when a quadrivalent forms at the first division of meiosis. This was also observed in Sved (1964). The maximum value of 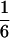 for the coefficient of double reduction was originally predicted as the product of two probabilities:
for the coefficient of double reduction was originally predicted as the product of two probabilities: 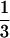 , the probability that two homologous chromosomes with the crossover go to the same pole at the first anaphase, and
, the probability that two homologous chromosomes with the crossover go to the same pole at the first anaphase, and 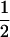 , the probability that sister chromatids in the homologous chromosomes enter in the same gamete. However, this prediction is questionable in at least two aspects. First, crossovers may occur between any pair of the four homologous chromosomes when a quadrivalent forms (Welch 1962). The probability of
, the probability that sister chromatids in the homologous chromosomes enter in the same gamete. However, this prediction is questionable in at least two aspects. First, crossovers may occur between any pair of the four homologous chromosomes when a quadrivalent forms (Welch 1962). The probability of 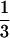 would underestimate the probability that two homologous chromosomes with the crossover go to the same pole at the first anaphase and thus underestimate the upper bound of the double-reduction coefficient. In fact, there has been experimental evidence supporting the coefficient of double reduction in autotetraploid potato being substantially >
would underestimate the probability that two homologous chromosomes with the crossover go to the same pole at the first anaphase and thus underestimate the upper bound of the double-reduction coefficient. In fact, there has been experimental evidence supporting the coefficient of double reduction in autotetraploid potato being substantially >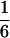 (Mather 1936; Haynes and Douches 1993). Second, the prediction ignores the fact that the level of double reduction at a given locus depends on its recombination frequency with the centromere. On this principle, the maximum value of the coefficient of double reduction should coincide with the limit of recombination frequency. The model presented by Equation 7 accounts for these issues properly.
(Mather 1936; Haynes and Douches 1993). Second, the prediction ignores the fact that the level of double reduction at a given locus depends on its recombination frequency with the centromere. On this principle, the maximum value of the coefficient of double reduction should coincide with the limit of recombination frequency. The model presented by Equation 7 accounts for these issues properly.
Two-locus tetrasomic linkage analysis:
To illustrate the above procedure, we first analyzed simulated data that mimic quadrivalent pairing of homologous chromosomes (i.e., λ = 0.0), recombination, and segregation of alleles at 10 linked marker loci. Table 1 lists the simulated values of the coefficient of double reduction at each locus and recombination frequency between adjacent loci. The simulated parental genotypes at each of the marker loci were determined by independently sampling from six possible alleles whose population frequencies were assumed to be 0.3 (allele A), 0.2 (allele B), 0.2 (allele C), 0.1 (allele D), 0.1 (allele E), and 0.1 (null allele O), respectively. The coefficient of double reduction was estimated either at step 1 as 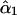 or at step 3 as
or at step 3 as 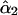 . It can be seen that
. It can be seen that 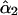 has a consistently smaller sampling variance than
has a consistently smaller sampling variance than 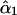 , reflecting the fact that the two-locus analysis takes advantage of using information at two linked marker loci. Moreover, the estimates show a pattern of increase in their values as the frequency of recombination increases from the first to the last locus as expected from the theoretical model. It is clear that the recombination frequency is consistently estimated.
, reflecting the fact that the two-locus analysis takes advantage of using information at two linked marker loci. Moreover, the estimates show a pattern of increase in their values as the frequency of recombination increases from the first to the last locus as expected from the theoretical model. It is clear that the recombination frequency is consistently estimated.
TABLE 1.
Mean and standard deviation of the maximum-likelihood estimates of recombination frequency and the coefficient of double reduction from 100 replicates of simulation of a full-sib population of 200 autotetraploid individuals
| Locus | G1 | G2 | r | α | 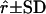 |
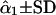 |
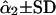 |
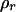 |
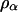 |
|---|---|---|---|---|---|---|---|---|---|
| L1 | CABB | DCEO | 0.00 | 0.0500 | — | 0.0504 ± 0.0210 | 0.0498 ± 0.0197 | — | 0.98 |
| L2 | CABA | BCCA | 0.10 | 0.0998 | 0.1024 ± 0.0211 | 0.0955 ± 0.0410 | 0.0978 ± 0.0340 | 1.00 | 0.95 |
| L3 | BCAE | ACAB | 0.10 | 0.1372 | 0.1036 ± 0.0337 | 0.1369 ± 0.0365 | 0.1386 ± 0.0247 | 1.00 | 1.00 |
| L4 | OBCA | AABD | 0.05 | 0.1517 | 0.0517 ± 0.0168 | 0.1625 ± 0.0428 | 0.1539 ± 0.0291 | 1.00 | 1.00 |
| L5 | AAAO | CDCC | 0.10 | 0.1762 | 0.0934 ± 0.0442 | 0.1767 ± 0.0355 | 0.1786 ± 0.0300 | 1.00 | 1.00 |
| L6 | DOAE | ABAB | 0.05 | 0.1857 | 0.0560 ± 0.0317 | 0.1828 ± 0.0426 | 0.1878 ± 0.0356 | 1.00 | 1.00 |
| L7 | BOAA | DABB | 0.10 | 0.2017 | 0.0969 ± 0.0339 | 0.1994 ± 0.0485 | 0.1981 ± 0.0348 | 1.00 | 1.00 |
| L8 | BBDB | ABAD | 0.05 | 0.2079 | 0.0539 ± 0.0335 | 0.2045 ± 0.0377 | 0.2024 ± 0.0307 | 1.00 | 1.00 |
| L9 | DDBE | BBAD | 0.10 | 0.2184 | 0.1021 ± 0.0395 | 0.2127 ± 0.0319 | 0.2136 ± 0.0307 | 1.00 | 1.00 |
| L10 | AEDE | DACA | 0.05 | 0.2225 | 0.0511 ± 0.0144 | 0.2150 ± 0.0290 | 0.2182 ± 0.0276 | 1.00 | 1.00 |
G1 and G2 are simulated parental genotypes at the 10 marker loci, r and α are the simulated values of recombination frequency between adjacent loci and the coefficient of double reduction. 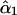 is the estimate of double-reduction coefficient obtained by the single-locus method and
is the estimate of double-reduction coefficient obtained by the single-locus method and 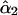 is the estimate of double-reduction coefficient obtained by the two-locus method.
is the estimate of double-reduction coefficient obtained by the two-locus method. 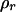 and
and 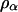 represent the empirical statistical power for testing significance of genetic linkage and double reduction.
represent the empirical statistical power for testing significance of genetic linkage and double reduction.
We tested for the significance of these parameters against their hypothesized null values (α = 0.0, r = 0.75) separately by approximating the log-likelihood ratio as a chi-square test statistic with 1 d.f. (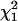 ). The proportion of the significant test statistic in the repeated simulations was calculated as the empirical power for testing the significance of double reduction (ρα) and linkage (ρr). The analysis has a statistical power of nearly 1.0 in detecting significance of these parameters in all of the simulated cases studied. However, it is important to explore the effect of the presence of double reduction on the test of linkage because the linkage test is one of the major components in the following map construction. To explore this question, we carried out independent simulation with r being fixed at its boundary value of 0.75 but the double-reduction coefficient having three different values. Table 2 lists the basic statistics of the log-likelihood ratio for the linkage test. It shows that the log-likelihood ratio has the mean, variance, and 95th percentile that are approximately equal to those of
). The proportion of the significant test statistic in the repeated simulations was calculated as the empirical power for testing the significance of double reduction (ρα) and linkage (ρr). The analysis has a statistical power of nearly 1.0 in detecting significance of these parameters in all of the simulated cases studied. However, it is important to explore the effect of the presence of double reduction on the test of linkage because the linkage test is one of the major components in the following map construction. To explore this question, we carried out independent simulation with r being fixed at its boundary value of 0.75 but the double-reduction coefficient having three different values. Table 2 lists the basic statistics of the log-likelihood ratio for the linkage test. It shows that the log-likelihood ratio has the mean, variance, and 95th percentile that are approximately equal to those of 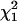 when double reduction was absent (α = 0.0), as expected. However, in the presence of double reduction, the large sample distribution of the likelihood-ratio statistic under the null hypothesis (r = 0.75) is equivalent to the case considered by Self and Liang (1987) that one parameter takes the true value on the boundary of the parameter space and another parameter has the true value not on the boundary. The likelihood-ratio test statistic in this situation has a mixture distribution of
when double reduction was absent (α = 0.0), as expected. However, in the presence of double reduction, the large sample distribution of the likelihood-ratio statistic under the null hypothesis (r = 0.75) is equivalent to the case considered by Self and Liang (1987) that one parameter takes the true value on the boundary of the parameter space and another parameter has the true value not on the boundary. The likelihood-ratio test statistic in this situation has a mixture distribution of 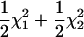 , indicating that the use of a significant threshold based on
, indicating that the use of a significant threshold based on 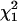 is no longer appropriate for testing linkage. Large variation in the 95th percentile when α > 0.0 in Table 2 agrees well with this prediction. Thus, we suggest the use of
is no longer appropriate for testing linkage. Large variation in the 95th percentile when α > 0.0 in Table 2 agrees well with this prediction. Thus, we suggest the use of 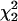 as an approximate distribution for the test statistic of linkage to be conservative. Under the more stringent criterion, ρr in Table 1 remains unchanged.
as an approximate distribution for the test statistic of linkage to be conservative. Under the more stringent criterion, ρr in Table 1 remains unchanged.
TABLE 2.
Estimated mean, variance, and 95th percentile of the log-likelihood ratio in the simulation with recombination frequency r = 0.75
| Marker locia | α |
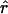 ± SD ± SD |
Mean | Variance | 95th percentile |
|---|---|---|---|---|---|
| L1–L2 | 0.00 | 0.74 ± 0.0650 | 0.9058 | 2.6070 | 4.23 |
| L1–L2 | 0.10 | 0.74 ± 0.0574 | 0.7487 | 0.8711 | 2.53 |
| L1–L3 | 0.00 | 0.74 ± 0.0600 | 1.1400 | 2.7500 | 4.85 |
| L1–L3 | 0.05 | 0.75 ± 0.0565 | 1.0220 | 2.0871 | 3.98 |
| L1–L3 | 0.10 | 0.75 ± 0.0495 | 0.8410 | 1.9072 | 3.14 |
| L1–L4 | 0.00 | 0.74 ± 0.0521 | 1.0264 | 1.6878 | 3.65 |
| L1–L4 | 0.05 | 0.73 ± 0.0217 | 1.3997 | 2.9630 | 5.25 |
| L1–L4 | 0.10 | 0.75 ± 0.0555 | 1.3068 | 3.4320 | 5.66 |
| L1–L6 | 0.00 | 0.75 ± 0.0504 | 1.0200 | 1.8761 | 3.30 |
| L1–L6 | 0.05 | 0.75 ± 0.0472 | 0.9137 | 3.4365 | 3.21 |
| L1–L6 | 0.10 | 0.74 ± 0.0409 | 0.7302 | 1.2361 | 2.95 |
Parental genotypes at the marker loci are identical to those listed in Table 1.
Given that current linkage analyses have been carried out with mostly dominant markers, we explored consequences of ignoring double reduction in analyzing dominant marker data. We simulated 10 linked dominant markers on which there were varying levels of double reduction due to quadrivalent pairing. The simulated parental genotypes at the marker loci are listed together with other simulated parameters in Table 3. The simulation data were analyzed by algorithm I developed in Luo et al. (2001), which assumes randomly bivalent pairing between homologous chromosomes and thus ignores the presence of double reduction, and by algorithm II that models double reduction. Table 3 also tabulates mean and standard deviation of the maximum-likelihood estimates of the simulated parameters over 100 repeated simulations of a full-sib population comprising 200 individuals. It shows that both algorithms provide comparable estimates of recombination frequency. In addition, algorithm II estimates the coefficient of double reduction adequately. It is seen that algorithm II yields smaller deviation of the recombination frequency estimates from the corresponding simulated parameters than algorithm I. The LOD score values for testing for significance of linkage between the dominant markers are usually slightly larger from algorithm II than from algorithm I, suggesting that the algorithm properly accounting for double reduction has a better power to test for linkage than the algorithm ignoring double reduction even when dominant markers are considered. Moreover, we explored performance of algorithm II in analyzing the simulation data generated from bivalent pairing solely and from a mixture of both bivalent and quadrivalent pairings. The algorithm provides nearly identical estimates of simulated recombination frequencies to those from algorithm I when double reduction is actually absent and to those from the algorithm when a mixture of bivalent and quadrivalent pairing is modeled. It accurately estimates the linkage parameters but may underestimate the degree of double reduction to the extent depending on the proportion of bivalent pairing in the simulated meioses (data not shown). This indicates that the algorithm considering quadrivalent pairing only will not influence adequacy of estimation of recombination frequency even though the mapping population is generated from mixing both bivalent and quadrivalent pairings. The biased estimates of the double-reduction parameter will not influence prediction of genetic maps. We found that to ignore the mixed chromosome pairing by making use of algorithm II will effectively improve robustness of the EM algorithm to converge to the maximum-likelihood estimates of the recombination parameter.
TABLE 3.
Mean and standard deviation of the maximum-likelihood estimates of recombination frequencies and the coefficient of double reduction over 100 replicates of simulation of a full-sib population comprising 200 autotetraploid individuals
| Algorithm I
|
Algorithm-II
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Locus | G1 | G2 | r | α | 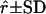 |
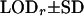 |
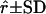 |
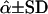 |
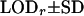 |
| L1 | AOOO | OOOO | 0.00 | 0.000 | — | — | — | 0.000 ± 0.000 | — |
| L2 | OAOO | OOOO | 0.10 | 0.062 | 0.096 ± 0.064 | 19.07 ± 8.48 | 0.095 ± 0.047 | 0.065 ± 0.047 | 20.10 ± 7.76 |
| L3 | OOAA | OOOO | 0.10 | 0.109 | 0.153 ± 0.053 | 27.11 ± 10.25 | 0.108 ± 0.054 | 0.116 ± 0.064 | 28.74 ± 8.98 |
| L4 | OOAO | OOOO | 0.05 | 0.127 | 0.037 ± 0.029 | 49.43 ± 11.62 | 0.058 ± 0.039 | 0.142 ± 0.071 | 48.18 ± 11.17 |
| L5 | OOOA | OOOO | 0.10 | 0.158 | 0.131 ± 0.084 | 12.37 ± 7.84 | 0.109 ± 0.055 | 0.177 ± 0.097 | 13.93 ± 6.94 |
| L6 | OOOA | AOOO | 0.05 | 0.169 | 0.043 ± 0.026 | 73.40 ± 12.64 | 0.051 ± 0.028 | 0.176 ± 0.073 | 74.72 ± 11.16 |
| L7 | AOAO | OOOO | 0.10 | 0.189 | 0.218 ± 0.084 | 3.47 ± 8.58 | 0.107 ± 0.050 | 0.195 ± 0.082 | 9.72 ± 5.38 |
| L8 | AOOO | OOOO | 0.05 | 0.197 | 0.042 ± 0.028 | 50.13 ± 10.79 | 0.058 ± 0.038 | 0.194 ± 0.086 | 52.56 ± 11.63 |
| L9 | OAOO | OOOO | 0.10 | 0.211 | 0.149 ± 0.076 | 8.88 ± 7.41 | 0.104 ± 0.049 | 0.200 ± 0.092 | 13.43 ± 6.69 |
| L10 | AOOO | OOOO | 0.05 | 0.216 | 0.134 ± 0.072 | 10.10 ± 7.65 | 0.086 ± 0.039 | 0.210 ± 0.098 | 15.65 ± 6.61 |
G1 and G2 are simulated parental genotypes at the 10 marker loci, r and α are the simulated values of recombination frequency between adjacent loci and the coefficient of double reduction. Also, LODr is the mean LOD score value for testing for significance of linkage. The simulation mimics multivalent pairings of a homologous chromosome that carries 10 dominant markers and the simulation data were analyzed by algorithm I proposed by Luo et al. (2001), which ignores the presence of double reduction, and by algorithm II that models double reduction.
Map construction based on pairwise-locus linkage analysis:
There has been cytological evidence that meioses of autotetraploids may involve a mixture of bivalent and quadrivalent pairings of homologous chromosomes (Swaminathan and Howard 1953; Wallace and Callows 1995; Stein et al. 2004). Here we present an analysis of a data set from a computer simulation that mimics the mixed bivalent and quadrivalent pairings of homologous chromosomes at an equal proportion (λ = 0.5), recombination and segregation of alleles at 10 linked marker loci. The parental genotypes at the linked loci and the other genetic parameters are the same as those in Table 1. Under this scenario, the genotypic distribution in the mapping populations is a mixture of distributions of diploid gamete genotypes from bivalent and quadrivalent chromosomal pairings during meiosis. In each of 100 repeated simulation data sets, we obtained the MLEs of the model parameters λ, α, and r for all pairs of the 10 markers, giving 45 different pairs. With the MLEs of r and the corresponding LOD scores, we constructed a genetic linkage map of these linked loci using two different approaches: JoinMap (Stam 1993), a least-squares approach that minimizes the difference between expected and estimated mapping distances, and simulated annealing (Hackett et al. 2003). Table 4 summarizes the frequency of the correctly predicted location for each of the simulated marker loci. It shows that the markers were individually mapped to a correct location order in the linkage map in ∼ >90 of 100 repeated simulations. There is a clear decrease in the proportion of the correct location orders predicted from L1 to L10, which is in parallel with the increasing level of double reduction. There is no remarkable difference in the rate of correctly predicted orders of individual markers between the two approaches. However, the JoinMap method yielded 65 linkage maps with all the marker locus orders being correctly recovered, whereas the simulated annealing method achieved only 56 linkage maps of the same kind. Table 4 also tabulates the means of estimated genetic distances of the linkage maps in the cases that all markers were predicted with correct location orders. It can be seen that the increment in the estimated map distances between adjacent markers agrees well with the simulated values for both methods. The linkage maps constructed from the JoinMap method are shorter than those from the simulated annealing method, reflecting the fact that the former favors a shorter map in the optimization procedure.
TABLE 4.
Frequency of the correctly predicted location of each marker locus in a simulated genetic linkage map with 10 marker loci from JoinMap (JM) and simulated annealing (SA), respectively, and the means of estimated mapping distances from the two methods (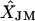 and
and 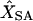 )
)
| Position | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | L10 | XT | 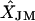 |
 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L1 | 98 | 2 | 0.00 | 0.00 | 0.00 | ||||||||
| 95 | 5 | ||||||||||||
| L2 | 2 | 98 | 10.73 | 9.56 | 12.29 | ||||||||
| 5 | 95 | ||||||||||||
| L3 | 98 | 2 | 21.47 | 17.63 | 25.47 | ||||||||
| 94 | 6 | ||||||||||||
| 4 | 97 | 1 | |||||||||||
| L4 | 6 | 93 | 1 | 26.64 | 25.65 | 30.71 | |||||||
| L5 | 1 | 88 | 11 | 37.37 | 33.43 | 43.66 | |||||||
| 1 | 90 | 9 | |||||||||||
| L6 | 11 | 89 | 42.54 | 38.39 | 49.19 | ||||||||
| 9 | 91 | ||||||||||||
| L7 | 89 | 11 | 53.27 | 46.10 | 61.00 | ||||||||
| 85 | 15 | ||||||||||||
| L8 | 11 | 89 | 58.44 | 53.17 | 66.79 | ||||||||
| 15 | 85 | ||||||||||||
| L9 | 91 | 9 | 69.17 | 62.91 | 78.08 | ||||||||
| 88 | 12 | ||||||||||||
| L10 | 9 | 91 | 74.34 | 66.67 | 84.55 | ||||||||
| 12 | 88 |
Numbers (in L1–L10) in top row are from JM and numbers in bottom row are from SA. XT, the simulated mapping distances.
Construction of linkage maps with DNA molecular markers in autotetraploid potato:
Here we demonstrate the tetrasomic linkage analysis for the construction of genetic linkage maps with dominant and codominant DNA molecular markers in cultivated autotetraploid potato. The marker data set comprised 197 AFLP markers and 4 microsatellite markers scored on 228 offspring from a cross between two parental lines: the advanced potato breeding line 1260lab1 and the cultivar Stirling (Bradshaw et al. 2004). Some of the AFLP markers were present in one parent and absent in the other and some were present in both parents. Details for developing the markers are described in Isidore et al. (2003). First, the clustering approach described in Luo et al. (2001) was used to classify all the 201 markers into linkage groups, yielding 11 (rather than the expected 12) groups when a significance level of 10−10 was used. In other words, a combined map of two parents was produced. We predicted the most probable genotypes of the parental lines at each of the markers on the basis of marker phenotypes of the parents and their offspring (Luo et al. 2000). The most probable parental genotypes were predicted with a probability of nearly 1.0 (≥0.95) at all these marker loci and used as the estimated parental genotypes in the linkage analysis below.
Second, the linkage analysis was carried out within each of the linkage groups on the basis of the analytical algorithm that models only quadrivalent homologous chromosome pairing. This may underestimate the coefficients of double reduction but will not influence the estimation of the recombination frequency and the prediction of the linkage maps as explained in the above simulation study. The analysis considered the two possible orders of putative loci A and B in the model presented above. The LOD score was used to infer the most likely order. Of the 201 markers, 36 showed significant double reduction (3.66 ≤ LOD score ≤ 21.64). The MLEs of the model parameters and the corresponding LOD scores for all possible pairs of marker loci within each of the linkage groups were estimated.
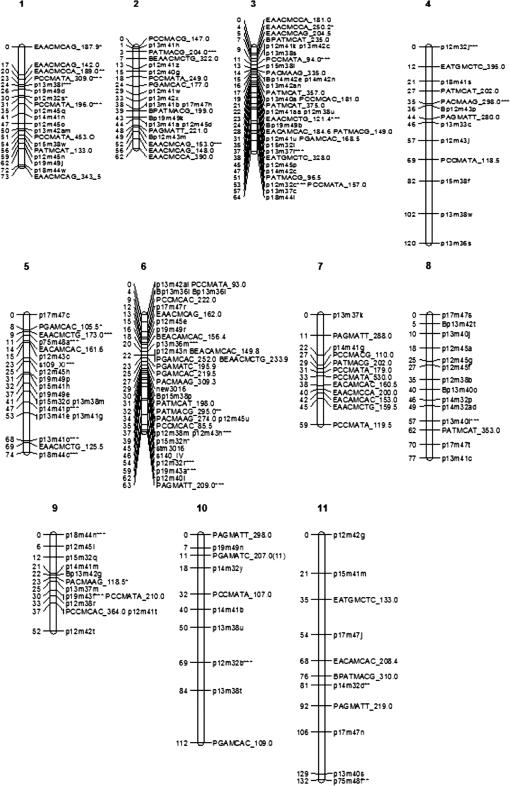
Finally, we loaded the MLEs of the recombination frequencies for all pairs of marker loci and the corresponding LOD scores into JoinMap analysis to work out the map order and map distance of the markers in each of the linkage groups. Figure 2 gives the 11 estimated linkage groups, which have a total map distance of 888 cM. The SSR markers on linkage groups 5 and 6 are known to be located on chromosomes 11 and 4, respectively. The other linkage groups cannot be assigned to known chromosomes, but this was not necessary for the purpose of this article. The markers that show significant double reduction are marked with asterisks in the maps in Figure 2. It can be seen that double reduction occurs unevenly among the linkage groups with assemblies on linkage groups 1, 2, 3, 4, and 6. The markers exhibiting double reduction are usually mapped together and at the ends of their corresponding linkage groups.
Figure 2.
Genetic linkage maps of 201 AFLP or SSR markers in autotetraploid potato (Solanum tuberosum).
DISCUSSION
An international consortium has launched a project to sequence the whole genome of potato, the fourth most important food crop in the world. The project aims at paving the way for the development of novel cultivars comprising a large variety of high performance characteristics, such as disease resistance and processing quality. To achieve the targets, we need a good knowledge of genetic control of the quantitative traits. The genome sequence project will yield an abundance of DNA molecular genetic markers for construction of genetic linkage maps of the molecular markers and for mapping the quantitative trait loci (Xie and Xu 2000; Hackett et al. 2001), in turn, to facilitate marker-assisted breeding programs. This article provides a statistical method and algorithm for constructing genetic linkage maps in autotetraploid species with dominant and codominant genetic markers. The method was demonstrated by a simulation study and by a case study analyzing the phenotype data of 201 AFLP and SSR markers scored on 228 full-sib individuals from crossing two parental lines of tetraploid potato.
Built on the theoretical model of tetrasomic linkage analysis (Fisher 1947; Luo et al. 2004), the method takes appropriate account of essential features of tetrasomic inheritance and various complexities of analyzing marker phenotypic data in autotetraploids. Double reduction, a consequence of quadrivalent pairing and recombination between homologous chromosomes, is one of the distinctive features of tetrasomic inheritance. It causes not only distorted segregation of marker alleles but also a more complicated distribution of offspring genotypes. To avoid the analytical complexity of double reduction in linkage analysis of tetraploids, the current literature on linkage analysis of tetraploids has relied on a random bivalent pairing model (Ripol et al. 1999; Hackett et al. 2001; Luo et al. 2001; Bradshaw et al. 2004; Cao et al. 2005) or on an oversimplified assumption (refer to Luo and Zhang 2005 for details). The methods based on the bivalent pairing model may not be used to analyze the data properly when double reduction does exist. For example, there are a total of 41 possible phenotypes in the offspring of parental lines with genotypes AA/BB/BB/OB and CA/DA/EC/EO when double reduction is present. However, the number reduces to 36 when double reduction is absent. The method presented in this article allows appropriately modeling not only quadrivalent pairing but also a mixture of bivalent and quadrivalent pairings in tetrasomic linkage analysis. In addition, it is well known that double reduction is a position-dependent phenomenon; i.e., the coefficient of double reduction at a locus increases as its distance from the centromere increases. This raises a theoretical question about the limiting values of the genetic parameters in the tetrasomic model. We demonstrate that the upper limits for the coefficient of double reduction and the recombination frequency are 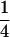 and
and 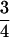 , respectively. Butruille and Boiteux (2000) showed that a level of double reduction as small as 0.04 was able to reduce greatly the equilibrium frequencies of gametophytic lethal alleles. Given that the upper limit is much greater than the rate cited above, we may anticipate that double reduction is effective in eliminating lethal alleles along autotetraploid chromosomes. On the other hand, the recombination frequency in autotetraploids could be as high as
, respectively. Butruille and Boiteux (2000) showed that a level of double reduction as small as 0.04 was able to reduce greatly the equilibrium frequencies of gametophytic lethal alleles. Given that the upper limit is much greater than the rate cited above, we may anticipate that double reduction is effective in eliminating lethal alleles along autotetraploid chromosomes. On the other hand, the recombination frequency in autotetraploids could be as high as 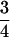 , as opposed to the upper limit of
, as opposed to the upper limit of 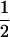 in diploids, supporting the observation that the evolution of polyploid genomes was an extremely dynamic process compared to that of diploids (Song et al. 1995; Luo et al. 2006).
in diploids, supporting the observation that the evolution of polyploid genomes was an extremely dynamic process compared to that of diploids (Song et al. 1995; Luo et al. 2006).
It must be pointed out that segregation distortion may occur at loci under selection in addition to double reduction in the tetrasomic linkage analysis. Selection may favor particular genotype(s) but double reduction leads to excessive homozygosity when compared to random allelic segregation. However, it may be difficult to distinguish the distortion due to selection from that due to double reduction. The linkage analysis proposed in this article models the double-reduction-caused segregation distortion but this does not necessarily mean it models properly the segregation distortion due to selection or other different factors. Thus, it will be useful to develop an appropriate statistical method to test the alternative hypotheses of the segregation distortion factors.
Built on the theoretical model of double reduction and recombination of genetic markers such as AFLPs, RFLPs, and SSRs in tetrasomic chromosomes, this method accounts for partial information of the phenotype of the markers in regard to their genotypes in mapping populations. A simulation study demonstrated the adequacy of the method in estimating the model parameters and in testing their significance. We exploited the efficiency of the pairwise linkage analysis in map construction by using JoinMap and simulated annealing algorithms and found that the former provided a slightly higher rate of correctly predicting the order of all markers in the simulated linkage group (65% vs. 56%). It should be pointed out that these algorithms search for the optimal map order and distance of genetic markers by using information from pairwise linkage analysis. A multilocus approach like that used in diploids (Lander and Green 1987) could be developed on the basis of the two-locus linkage model and the mapping efficiency would be expected to be improved even though tedious algebraic formulation and programming efforts are inevitable.
We analyzed a data set comprising 201 AFLP and SSR markers scored on 228 individuals of a full-sib family and their parental lines. Of the 201 markers, 36 (∼18%) displayed significant double reduction. Double reduction occurred on 10 of the 11 linkage groups and the markers exhibiting double reduction tended to be at the tips of their linkage groups, revealing the chromosome and location dependence of the meiotic events. It should be pointed out that it is difficult to infer relative locations of these marker loci in each of the linkage maps to that of the centromere solely on the basis of distribution of double reduction events predicted in the linkage groups. However, this problem could become tractable by incorporating the markers whose physical map information is known into the linkage analysis.
The analysis developed in this article can be extended for interval mapping of QTL under a tetrasomic model. In fact, the conditional probability distribution of genotypes at a putative QTL given genotypes at its flanking markers can be calculated by making use of the analytical tools developed in the study. Also, given the double-reduction coefficients at the flanking markers and the tested position of QTL given the double-reduction coefficient of its left flanking marker and recombination frequency between the QTL and the marker, the expected coefficient of double reduction at the QTL may be predicted from Equation 7. The conditional probability distribution can thus be worked out as a function of the double-reduction and recombination parameters by modeling gametogenesis at the three loci as a Markovian process described in Equations 5 and 6.
All data analyses and computer simulations presented in this article have been programmed in Fortran-90 computer language and are available upon request from the corresponding author.
Acknowledgments
We thank Christine Hackett for her generosity in providing us with the key subroutine for simulated annealing analysis in this article and Barnaly Pande for kindly providing the molecular marker data. Two anonymous reviewers and the associated editor offered constructive critical comments that have been helpful in improving presentation of this article. This study is supported by research grants from the Biotechnology and Biological Science Research Council and the Natural Environment Research Council of the United Kingdom. Z.W.L. and R.Z. are also supported by China's National Natural Science Foundation (30430380), Basic Research Program (2004CB518605), and Shanghai Science and Technology Committee (04ZR14014).
References
- Bailey, N. T. J., 1961. Introduction to the Mathematical Theory of Genetic Linkage. Clarendon Press, Oxford.
- Barcaccia, G., S. Meneghetti, E. Albertini, L. Triest and M. Lucchin, 2003. Linkage mapping in tetraploid willows: segregation of molecular markers and estimation of linkage phases support an allotetraploid structure for Salix alba × Salix fragilis interspecific hybrids. Heredity 90: 169–180. [DOI] [PubMed] [Google Scholar]
- Bradshaw, J. E., B. Pande, G. J. Bryan, C. A. Hackett, K. McLean et al., 2004. Interval mapping of quantitative trait loci for resistance to late blight, height and maturity in a tetraploid population of potato. Genetics 168: 983–995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brouwer, D. J., and T. C. Osborn, 1999. A molecular marker linkage map of tetraploid alfalfa (Medicago sativa L.). Theor. Appl. Genet. 99: 1194–1200. [Google Scholar]
- Butruille, D. V., and L. S. Boiteux, 2000. Selection-mutation balance in polysomic tetraploids: impact of double reduction and gametophytic selection on the frequency and subchromosomal localization of deleterious mutations. Proc. Natl. Acad. Sci. USA 97: 6608–6613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao, D. C., B. A. Craig and R. W. Doerge, 2005. A model selection-based interval-mapping method for autopolyploids. Genetics 169: 2371–2382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster, A. P., N. M. Laird and D. B. Rubin, 1977. Maximum likelihood from incomplete data via EM algorithm (with discussion). J. R. Stat. Soc. Ser. B 39: 1–38. [Google Scholar]
- Fisher, R. A., 1947. The theory of linkage in polysomic inheritance. Philos. Trans. R. Soc. Lond. Ser. B 23: 55–87. [Google Scholar]
- Grant, V., 1971. Plant Speciation. Columbia University Press, New York/London.
- Hackett, C. A., J. E. Bradshaw and J. W. McNicol, 2001. Interval mapping of quantitative trait loci in autotetraploid species. Genetics 159: 1819–1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hackett, C. A., B. Pande and G. J. Bryan, 2003. Constructing linkage maps in autotetraploid species using simulated annealing. Theor. Appl. Genet. 106: 1107–1115. [DOI] [PubMed] [Google Scholar]
- Haldane, J. B. S., 1930. Theoretical genetics of autotetraploids. J. Genet. 22: 359–372. [Google Scholar]
- Haynes, K. G., and D. S. Douches, 1993. Estimation of the coefficient of double reduction in the cultivated tetraploid potato. Theor. Appl. Genet. 85: 857–862. [DOI] [PubMed] [Google Scholar]
- Isidore, E., H. van Os, S. Andrzejewski, J. Bakker, I. Barrena et al., 2003. Toward a marker-dense meiotic map of the potato genome: lessons from linkage group I. Genetics 165: 2107–2116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander, E. S., and P. Green, 1987. Construction of multilocus genetic linkage maps in humans. Proc. Natl. Acad. Sci. USA 84: 2363–2367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis, W. H., 1980. Polyploidy: Biological Relevance. Plenum Press, New York.
- Luo, Z. W., and Z. Zhang, 2005. Commentary on Wu and Ma. Genetics 171: 2149–2150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo, Z. W., C. A. Hackett, J. E. Bradshaw, J. W. McNicol and D. Milbourne, 2000. Predicting parental genotypes and gene segregation for tetrasomic inheritance. Theor. Appl. Genet. 100: 1067–1073. [Google Scholar]
- Luo, Z. W., C. A. Hackett, J. E. Bradshaw, J. W. McNicol and D. Milbourne, 2001. Construction of a genetic linkage map in tetraploid species using molecular markers. Genetics 157: 1369–1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo, Z. W., R. M. Zhang and M. J. Kearsey, 2004. Theoretical basis for genetic linkage analysis in autotetraploid species. Proc. Natl. Acad. Sci. USA 101: 7040–7045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo, Z. W., Z. Zhang, R. M. Zhang, M. Pandey, O. Gailing et al., 2006. Modeling population genetic data in autotetraploid species. Genetics 172: 639–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mather, K., 1935. Reductional and equational separation of the chromosomes in bivalents and multivalents. J. Genet. 30: 53–78. [Google Scholar]
- Mather, K., 1936. Segregation and linkage in autotetraploids. J. Genet. 30: 287–314. [Google Scholar]
- McLachlan, G. J., and T. Krishnan, 1997. The EM Algorithm and Extensions. Wiley, New York.
- Meyer, R. C., D. Milbourne, C. A. Hackett, J. E. Bradshaw, J. W. McNicol et al., 1998. Linkage analysis in tetraploid potato and associations of markers with quantitative resistance to late blight (Phytophthora infestans). Mol. Gen. Genet. 259: 150–160. [DOI] [PubMed] [Google Scholar]
- Muller, H. J., 1914. A new mode of segregation in Gregory's tetraploid primulas. Am. Nat. 48: 508–512. [Google Scholar]
- Otto, S. P., and J. Whitton, 2000. Polyploid incidence and evolution. Annu. Rev. Genet. 34: 401–437. [DOI] [PubMed] [Google Scholar]
- Ripol, M. I., G. A. Churchill, J. A. G. da Silva and M. Sorrells, 1999. Statistical aspects of genetic mapping in autotetraploids. Gene 235: 31–41. [DOI] [PubMed] [Google Scholar]
- Ronfort, J. L., E. Jenczewski, T. Bataillon and F. Rousset, 1998. Analysis of population structure in autotetraploid species. Genetics 150: 921–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Self, S. G., and K. Y. Liang, 1987. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under non-standard condition. J. Am. Stat. Assoc. 82: 605–610. [Google Scholar]
- Song, K., P. Lu, K. Tang and T. C. Osborn, 1995. Rapid genome change in synthetic polyploids of Brassica and its implications for polyploid evolution. Proc. Natl. Acad. Sci. USA 92: 7719–7723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam, P., 1993. Construction of integrated genetic linkage maps by means of a new computer package: JoinMap. Plant J. 3: 739–744. [Google Scholar]
- Stein, J., C. L. Quarin, E. J. Martinez, S. C. Pessino and J. P. A. Ortiz, 2004. Tetraploid races of Paspalum notatum show polysomic inheritance and preferential chromosome pairing around the apospory-controlling locus. Theor. Appl. Genet. 109: 186–191. [DOI] [PubMed] [Google Scholar]
- Sved, J. A., 1964. The relationship between diploid and tetraploid recombination frequencies. Heredity 19: 585–596. [DOI] [PubMed] [Google Scholar]
- Swaminathan, M. S., and H. W. Howard, 1953. The cytology and genetics of the potato (Solanum tuberosum) and related species. Bibliogr. Genet 16: 1–19. [Google Scholar]
- Wallace, A. J., and R. S. Callows, 1995. Meiotic variation in an intergenomic autopolyploid series. 2. Pairing behavior. Genome 38: 133–139. [DOI] [PubMed] [Google Scholar]
- Welch, J. E., 1962. Linkage in autotetraploid maize. Genetics 47: 367–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, K. K., W. Burnquist, M. E. Sorrells, T. L. Tew, P. H. Moore et al., 1992. The detection and estimation of linkage in polyploids using single-dose restriction fragments. Theor. Appl. Genet. 83: 294–300. [DOI] [PubMed] [Google Scholar]
- Xie, C., and S. Xu, 2000. Mapping quantitative trait loci in tetraploid populations. Genet. Res. 76: 105–115. [DOI] [PubMed] [Google Scholar]