Abstract
Fluctuations in protein numbers (noise) due to inherent stochastic effects in single cells can have large effects on the dynamic behavior of gene regulatory networks. Although deterministic models can predict the average network behavior, they fail to incorporate the stochasticity characteristic of gene expression, thereby limiting their relevance when single cell behaviors deviate from the population average. Recently, stochastic models have been used to predict distributions of steady-state protein levels within a population but not to predict the dynamic, presteady-state distributions. In the present work, we experimentally examine a system whose dynamics are heavily influenced by stochastic effects. We measure population distributions of protein numbers as a function of time in the Escherichia coli lactose uptake network (lac operon). We then introduce a dynamic stochastic model and show that prediction of dynamic distributions requires only a few noise parameters in addition to the rates that characterize a deterministic model. Whereas the deterministic model cannot fully capture the observed behavior, our stochastic model correctly predicts the experimental dynamics without any fit parameters. Our results provide a proof of principle for the possibility of faithfully predicting dynamic population distributions from deterministic models supplemented by a stochastic component that captures the major noise sources.
Keywords: gene networks, systems biology
One of the central goals of systems biology is to predict the dynamic behavior of a cell’s genetic and metabolic networks. These predictions traditionally stem from models in which discrete molecular events, such as transcription and translation, are represented by continuous and deterministic differential equations. Such equations are valid when behavior of individual cells is very similar to the average behavior of the population. However, in many cases, the inherently stochastic nature of biological systems leads to significant cell-to-cell variability (1–3), and previous studies indicate that individual cells often behave very differently from the population average in response to external stimuli. For example, studies of bacterial persistence indicate that the population survival rate can be fundamentally different from the average cell’s survival rate in response to environmental stress (4, 5). The impact of noise-induced population heterogeneity is also relevant when studying cellular memory, where fluctuations in protein numbers can cause the stability of epigenetic memory to degrade by effectively causing cells to forget their original states (6, 7). In these cases, stochastic modeling techniques must be used to describe the large cell-to-cell variability.
Although deterministic models can describe dynamic network behavior and analytical stochastic models can faithfully predict steady-state population distributions (8), little work has been done to connect dynamic cellular behavior with noise models. It is important that stochastic models of biological systems correctly capture system dynamics because few biological systems ever reach steady state. Prior pioneering studies aimed at predicting stochastic dynamics have modeled stochastic effects by including high levels of microscopic detail (9). Although this approach is correct in principle, it is often too complicated to have general applicability because the parameters required are usually unmeasured or difficult to acquire. Since the advent of these microscopic approaches, much has been learned about sources and propagation of noise in gene networks (8, 10–21), leading to comprehensive models of stochastic behavior. However, these previous models have lacked a sufficiently detailed set of dynamic data on which to test predictions of dynamic population distributions (22–24). Thus, it has still not been demonstrated that the current understanding of noise, which accurately describes distributions of protein concentrations in steady state, can be applied to predict dynamic distributions reflecting noise-induced behavior.
In this work, we investigate the predictive power of stochastic dynamics by using an integrated experimental and computational approach in which we construct a stochastic model of cellular dynamics. To test the model’s predictions, we experimentally measure population distributions of protein levels over time in the lactose uptake network of Escherichia coli and then compare these data to the predicted population distributions. To construct our predictive model, we first build a deterministic model that incorporates relevant network components. Next, we use steady state measurements of this network to characterize the magnitude of the relevant noise sources. Finally, by combining these noise sources with the deterministic model, we create a dynamic stochastic model that is able to predict the dynamic behavior of distributions. Using this technique, we show that once macroscopic rates are known, we only need two additional parameters that characterize the noise in each gene to faithfully predict experimental dynamic population distributions without any fit parameters.
The Lactose Uptake Network
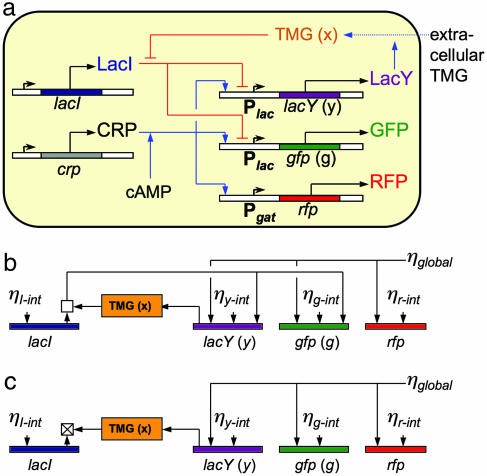
At the systems level, the lactose uptake network in single E. coli cells displays an “all or nothing” response depending on the extracellular concentration of the inducer (25, 26). This ability to display different phenotypes at a single extracellular inducer concentration has been attributed to a positive feedback loop, which is shown in Fig. 1a. LacY (indicated by purple in Fig. 1) is a transmembrane protein involved in active uptake of the inducer thiomethylgalactoside (TMG) (indicated by orange in Fig. 1). The synthesis of LacY is under the control of the lac promoter, which is repressed by the lac repressor, LacI (indicated by blue in Fig. 1), in the absence of TMG. However, intracellular TMG molecules bind to LacI tetramers, causing their dissociation from DNA and an increase in lacY transcription. lacY transcription can be further activated by the cAMP receptor protein (CRP) (indicated by gray in Fig. 1), which upon association with cAMP binds to an activator site in the lac promoter and increases the probability of transcription. In summary, this positive feedback loop is composed of two negative connections and one positive connection: TMG inhibits LacI, LacI represses lacY transcription, and LacY increases the intracellular TMG concentration. In addition to this natural endogenous network, we constructed two fluorescent reporter systems to monitor the state of the network in single cells. The gene encoding for GFP (gfp) (indicated by green in Fig. 1) under control of the lac promoter was integrated into the genome and reports the concentration of LacY. Additionally, we placed a red fluorescent protein (RFP) gene (rfp) (indicated by red in Fig. 1) under the control of the gat promoter on a plasmid, which contains a CRP activation region and a gat repressor binding site. Because wild-type K12 E. coli strains lack a functional gat repressor protein, GatR (27), RFP is a faithful reporter for the activity of CRP (28).
Fig. 1.
Network and noise diagram. (a) Diagram of the lactose utilization network. Blue arrows indicate positive interactions, red bars indicate negative interactions, and black arrows denote protein production. A positive feedback loop from LacY to TMG to LacI back to LacY creates the potential for multistability (high and low steady states). The fluorescent reporter GFP integrated in the genome is expressed in parallel with LacY under control of the lac promoter and reports the induction level of the cell. RFP under control of the gat promoter reports activity of the activator CRP. (b) The noise network for the lactose utilization network. Intrinsic noise is fed into each protein level and is propagated through the network. The square above LacI represents the combination and propagation of noise from total LacI and TMG through the active fraction of LacI tetramers, which depends on the concentration of intracellular TMG. (c) The effective noise network for induced cells with high levels of intracellular TMG, where LacI tetramers are highly inactivated. The crossed square represents the effective inactivation of this feedback by increased levels of intracellular TMG.
Experimental Results
To model the stochastic dynamics of the lactose uptake network, it is first necessary to understand single-cell behavior. At steady state, the positive feedback loop causes cells to be in either an ON (induced) state, during which they maximally produce LacY and GFP, or an OFF (uninduced) state, during which LacY and GFP are produced at a minimal, basal rate. In ON cells, LacY imports enough extracellular TMG to maximally produce LacY, whereas OFF cells do not have enough LacY or extracellular TMG to produce LacY molecules faster than they are lost. These circumstances mean that cells do not generally contain intermediate concentrations of LacY and GFP when in steady state.
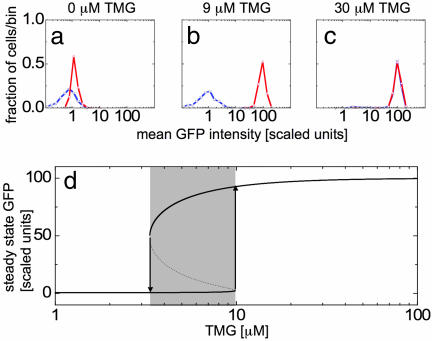
To observe this behavior, we prepare cells in either the ON or OFF state by growing them for 24 h in media with 100 μM TMG or 0 μM TMG, respectively. We then remove the cells from this preparation media and subsequently grow them in fresh media containing an intermediate concentration of extracellular TMG. Cells are grown for 20 h (approximately seven cell generations), at which point the population distributions are no longer changing quickly. For cultures resuspended in very high or low concentrations of TMG, cells occupy either the ON or OFF state, respectively, independent of their induction history (Fig. 2a and c). However, resuspension in intermediate concentrations of TMG maintain an ON or OFF population for extended periods of time in either the higher or lower peak, respectively (Fig. 2b), indicative of hysteresis (Fig. 2d).
Fig. 2.
Demonstration of hysteresis in the long time limit. Histograms of mean GFP fluorescence are shown for cells with a fully induced (red) and fully uninduced (blue) history resuspended and grown for 20 h in 0 (a), 9 (b), and 30 (c) μM TMG. Induced cells grown in 0 μM TMG for 20 h still contain slightly higher quantities of GFP than uninduced cells, and this difference is roughly equivalent to that expected from exponential decay of fluorescence due to dilution of GFP during cell division. (d) Steady-state solutions of the deterministic model. The induced state is shown as the upper dark line whereas the uninduced state is shown as the lower dark line. The intermediate unstable steady state is shown as a dashed line in the shaded bistable region. Cells remain in either the induced or uninduced states until they are moved to a concentration of inducer at which the previous state is unstable (vertical arrows).
Although we find that individual cells are either in the OFF or ON states after 20 h, measurements at shorter time intervals must reveal transient, intermediate distributions that reflect the population morphing from its initial state (Fig. 2a, blue curve) to its final state (Fig. 2c, blue curve). To characterize the dynamics of these population distributions in response to changes in inducer concentration, we sample the population at various times and measure GFP levels in single cells. Fully induced or uninduced cells are washed and subsequently resuspended in media with an intermediate concentration of TMG. Next, the mean GFP fluorescence levels of individual cells are measured. Histograms are generated every 1 or 2 hours for several hours after resuspension in media with intermediate TMG concentration.
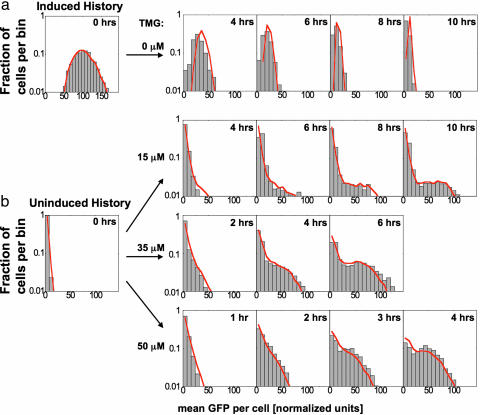
Two types of dynamic responses are observed: ballistic and stochastic. An example of a ballistic transition is shown in Fig. 3a, where ON cells resuspended in 0 μM TMG collectively switch OFF, drifting toward the new stable state. By contrast, Fig. 3b illustrates stochastic transitions, where some initially OFF cells remain OFF while a subpopulation switches to the ON state. Characteristic of a stochastic response, the OFF peak decreases in magnitude exponentially with time.
Fig. 3.
Comparison between our stochastic model and experiments for transitions between OFF and ON steady states. Gray boxes are histograms of single cell GFP fluorescence for populations of 2,000–6,000 cells, and red lines represent a population of 10,000 simulated cells using a Monte-Carlo algorithm. (a) ON cells grown in 50 μM TMG and then placed in 0 μM TMG transition as a uniform population to the uninduced state with a single “ballistic” peak. (b) OFF cells grown at 0 μM TMG are transferred to 15, 35, and 50 μM TMG. These three populations display stochastic switching behavior, where cells randomly leave the uninduced state and move toward the induced state. Simulations predict the ballistic behavior associated with cells turning OFF and the stochastic behavior associated with cells turning ON. In both cases, the experimental distributions are well matched by the model without any additional fit parameters.
Deterministic Model
Several deterministic models have been used to explain the bistable behavior observed in the lactose utilization network (28–31). We augment a model that has been used to describe the strains analyzed in this study (28). Our model is composed of three equations:
and
Here, x, y, and g represent intracellular concentrations of TMG, LacY, and GFP, respectively. TMG denotes the extracellular concentration of TMG. 1/τx represents the rate of loss of intracellular TMG due to export, degradation, or dilution from cell division and growth. 1/τy and 1/τg represent the combined loss from dilution and degradation of LacY and GFP, respectively. The rate constant of active uptake of TMG per LacY molecule is proportional to β, which is a function of extracellular TMG, whereas λ represents passive uptake of TMG independent of LacY. We assume that GFP is transcribed at a rate identical to that of LacY because both are expressed under control of the lac promoter. Therefore, we set α as the maximal production rate of both LacY and GFP. ρ is the repression factor representing the ratio of transcription rates at the lac promoter between induced and uninduced cells. This factor accounts for the effect of fully activating all present LacI tetramers in the absence of intracellular TMG. Derivations of these equations can be found in the supporting information, which is published on the PNAS web site.
By using these equations, it has been shown that the system can have either a single stable steady state (monostable) or two stable steady states separated by an unstable steady state (bistable), depending on the concentration of extracellular TMG (Fig. 2d). Previously, the parameters α, β, and ρ have been determined by fitting the theoretical monostable–bistable boundaries (vertical arrows in Fig. 2d) to those measured experimentally (28). Because the network used in our study is identical, we will use the parameters α, β, and ρ as determined in this previous study (Table 1). We set τy and τg equal to the dilution time scale due to cell growth, τ1/2 = τdivision, because we assume that the active degradation rate of GFP and LacY is much smaller than the dilution rate due to cell growth; here, τdivision is the estimated average time between cell divisions. This approximation leaves τx and λ as the only undetermined parameters in the deterministic model.
Table 1.
Parameters used in the dynamic stochastic model
| Parameter | Value | Error | Source |
|---|---|---|---|
| α | 100 | 16 | Ref. 28 |
| β | 0.123(TMG)0.6 | 15% | Ref. 28 |
| ρ | 170 | 34 | Ref. 28 |
| λ | 0.06 | (0.03, 0.12) | This study |
| τx | 0 min | 35 | This study |
| τ1/2 | 216 min | 43 | This study |
| NLacY | 790 proteins | 210 | This study |
| NGFP | 790 proteins | 210 | This study |
| NLacl | 50 proteins | — | Ref. 34 |
| bLacY | 34.8 proteins | 10.1 | This study |
| bGFP | 34.8 proteins | 10.1 | This study |
| bLacl | 5 proteins | — | Ref. 34 |
—, not applicable.
We estimate the decay time of intracellular TMG, τx, by measuring how quickly the average GFP levels of a fully induced population decrease when placed in media without TMG (Fig. 3a). In this scenario, LacY no longer affects the dynamics of the cells because there is no extracellular TMG to complete the feedback loop. We assume the parameter τx to be much smaller than τ1/2 because cells cease GFP production within 10–20 min after removal of extracellular TMG (see the supporting information for further details), and a fit of the deterministic model to the decreasing GFP levels yields τx = 0 min. This effect could be due to rapid loss of intracellular TMG through efflux, which is known to occur for other inducers (32, 33). Thus, we equilibrate Eq. 1 in relation to Eqs. 2 and 3 by setting: τx(dx/dt) = 0.
In induced cells with many TMG-transporting LacY molecules, passive TMG uptake, λ, should contribute only a small fraction to the intracellular TMG concentration. However, in uninduced cells with few LacY molecules, this passive “leak” rate may be significant. To estimate this rate, the full deterministic model is fit to the population average of fully uninduced cells placed in 50 μM TMG, giving λ = 0.06 (see the supporting information).
Noise and Stochastic Measurements
To make predictions about switching transitions and dynamic population distributions, we must include the effect of stochastic fluctuations in our model. It has been shown (8, 12, 13, 15, 17, 18, 20, 21) that noise in protein levels comes mainly from discreteness of mRNA and protein numbers (intrinsic noise) as well as from global changes in intracellular environment that affect decay and production rates (global noise). To model intrinsic noise, we must estimate two parameters for each gene: the average number of proteins produced from a single mRNA (burst size) and the conversion factor between absolute protein numbers and fluorescence counts.
Fig. 1b contains a diagram indicating the generation and propagation of noise in the network. First, LacY, LacI, and GFP are sensitive to their corresponding intrinsic noise terms ηy-int, ηi-int, and ηg-int, respectively (Fig. 1b). These terms are due to the random creation and destruction events of lacY, lacI, and gfp mRNA and the corresponding proteins. The RFP reporter generates an intrinsic noise term, ηr-int (Fig. 1b), which contains fluctuations due to RFP mRNA and RFP proteins as well as fluctuations in plasmid number. Noise generated by CRP and other factors, such as RNA polymerase and ribosomes, is combined into the term ηglobal, which we treat as a multiplicative factor on the production rates of LacY, GFP, and RFP.
Fluctuations in LacI numbers are propagated directly into LacY and GFP, and the strength of this transmission depends greatly on the intracellular TMG concentration because TMG binding decouples LacI from the production of LacY and GFP (8, 13). Finally, noise in LacY will cause fluctuations in intracellular TMG concentration that affect the binding of LacI to the lac promoter. This effect causes LacY fluctuations to be transmitted into both LacY and GFP noise with a magnitude dependent on TMG concentration.
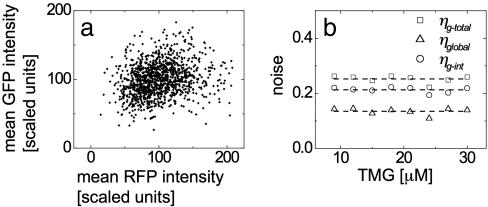
Extrinsic noise can be determined by examining correlations between levels of proteins influenced by the same upstream regulators. To extract the noise parameter, ηglobal, from the distribution of GFP concentrations, it would generally be necessary to solve a set of equations describing the propagation of noise through the entire network (8). However, the network can be simplified greatly by considering only fully induced cells, where TMG-bound and inactivated LacI no longer affects GFP and LacY production. In this case, fluctuations in LacY, GFP, and RFP expression levels are dependent only on extrinsic noise levels, ηglobal, as well as each protein’s intrinsic noise level ηy-int, ηg-int, and ηr-int (Fig. 1c). Because the term ηglobal is shared by GFP and RFP, it is possible to separate the total GFP noise into intrinsic and extrinsic components (see the supporting information for details). GFP and RFP fluorescence levels are measured in individual cells on several populations induced with different concentrations of extracellular TMG. For 30 μM TMG, this distribution is shown in Fig. 4a, indicating a weak correlation between GFP and RFP levels. For GFP, the total noise, ηg-total, and extrinsic noise, ηglobal, are measured directly from the GFP and RFP distributions in the induced population using the relations
and
Here brackets 〈…〉 represent the population average of fluorescent levels of single cells in the ON state only. The intrinsic GFP noise, ηg-int2 = ηg-total2 − ηglobal2, is calculated for extracellular TMG ranging from 9 to 30 μM (Fig. 4b), and mean values of the noise measurements are ηg-total = (0.25 ± 0.04), ηg-int = (0.21 ± 0.03), and ηglobal = (0.14 ± 0.02). These values remain constant over the range of measurement, indicating that the ON cells have similar noise characteristics regardless of the concentration of extracellular TMG.
Fig. 4.
Measurement of intrinsic and extrinsic noise is accomplished by comparing RFP and GFP concentrations in individual cells. (a) RFP and GFP concentrations for individual cells grown in media containing 30 μM TMG for 24 h. A slight correlation between the two concentrations is present, indicating that the two share a weak source of global noise. (b) Measurement of this correlation allows division of total noise in GFP into intrinsic and extrinsic components, each of which are calculated from 9 to 30 μM TMG.
To calibrate between fluorescence and the absolute number of molecules, it is sufficient to determine the number of GFP molecules in an induced cell, N. Rosenfeld et al. (18) showed that intensity fluctuations introduced by cell division vary with the number of fluorescent molecules in the cell. Upon cell division, each molecule will be independently and randomly partitioned into one of the two daughter cells. This process can be described by a binomial distribution, where the difference between the numbers of molecules in each daughter cell will, on average, be proportional to N1/2, meaning that as the number of molecules decreases (increases) the fractional asymmetry introduced by division, N1/2/N = N−1/2, will increase (decrease). Therefore, by using this as a calibration tool, we measure the mean GFP fluorescence in pairs of cells that have recently undergone cell division and estimate that the average number of GFP proteins in an induced cell is NGFP = 790 ± 210 molecules (see the supporting information for details).
We next estimate the second missing noise parameter, burst size, which can be determined from the intrinsic noise, ηg-int, by using the relation 〈δn2〉 = 〈n〉 (b + 1) (11, 12), where n is the number of protein molecules and b is the average number of proteins produced from a single mRNA. This relation stems from the fact that translation effectively amplifies the noise associated with low levels of mRNA. We find that the burst size for GFP is bGFP = 35.3 ± 9.7, consistent with other burst size measurements in E. coli (8). Because the same promoter is regulating GFP and LacY expression, we assume that the production rate of mRNA should be similar for the two proteins. Thus, we set (NLacY/bLacY) = (NGFP/bGFP), where NLacY is the number of LacY molecules in a fully induced cell, and bLacY is the burst size of a LacY mRNA. We could reduce the ratio NLacY/bLacY to a single parameter analytically because the mRNA production rate for LacY is proportional to NLacY/bLacY, and the burst size in units of fluorescence is proportional to (NLacY/bLacY)−1. However, to proceed later with simulations that model explicit molecular events, we need to assign values for both NLacY and bLacY. Therefore, without loss of generality, we choose values for these parameters that maintain the required ratio by setting them equal to those measured for GFP: NLacY = NGFP and bLacY = bGFP.
We expect noise to be transmitted from the LacI component as well, but to analyze these contributions it is necessary to examine steady state distributions around the uninduced fixed point. However, a small signal to noise ratio combined with increasing nonlinearity at these low concentrations makes extraction of relevant information difficult. Instead, we use published estimates of the molecule counts and burst sizes of LacI, which we interpret as bLacI = 5 and NLacI = 50 in our strain (34).
Stochastic Model and Predictions
We now have a full set of parameters for the dynamic deterministic model, as well as all parameters necessary to describe the steady state noise properties of the lactose uptake network. To determine whether these parameters can be used to predict the full dynamic distributions measured in the experimental section, we construct a dynamic stochastic model. In principle, we have already fully defined the model, but for simulation purposes we use a reduced model that contains only essential events. The model consists of three processes: (i) mRNA production followed immediately by a burst of protein production and mRNA degradation, (ii) protein degradation, and (iii) extrinsic or global noise. We therefore ignore specific events, such as binding of LacI or CRP to operator sites and timing between productions of individual protein molecules. These processes and the corresponding rates are summarized in Table 2 and described in greater detail in the supporting information. We use a modified Gillespie’s Monte-Carlo method (35) to simulate large populations of individual cells. Fig. 3a shows the results of the simulation (red solid lines) for induced-to-uninduced transitions where induced cells are placed in 0 μM TMG. Fig. 3b shows simulations (red solid lines) of uninduced cells grown in 15, 35, and 50 μM TMG, respectively.
Table 2.
Stochastic Model
| Protein | Event | Reaction | Rate |
|---|---|---|---|
| GFP | Burst | G → G + B(bGFP) | f(x(Y), I) NGFP/(bGFP τ1/2)ε |
| Decay | G → G − 1 | G/τ1/2 | |
| LacY | Burst | Y → Y + B(bLacY) | f(x(Y), I) NLacY/(bLacY τ1/2) ε |
| Decay | Y → Y − 1 | Y/τ1/2 | |
| LacI | Burst | I → I + B(bLacI) | NLacY/(bLacY τ1/2) |
| Decay | I → I − 1 | I/τ1/2 |
f(x, I) = ({[(ρ − 1)I]/[NLacI(1 + x2)]} + 1)−1 with x(Y) = Y (αβ/NLacY) + λ·TMG models the effect of LacI repression based on instantaneous values of Y and I. ε represents a correlated extrinsic noise, with 〈ε〉 = 1 and 〈ε(t)ε(t + Δt)〉 = 2ηglobal2 exp(−Δt/τ1/2). Capital variables are absolute molecule numbers of the respective lowercase concentrations scaled to the deterministic model as defined in the supporting information: G ≡ g NGFP/α and Y ≡ y NGFP/α. B(b) is an exponentially distributed random integer with mean equal to burst size b.
The stochastic model reproduces ballistic and stochastic switching, whereas the deterministic model does not distinguish between these types of behavior. For the case shown in Fig. 3a, the experiments and simulations both show that every cell moves like the average obtained from the deterministic model. In addition to demonstrating average behavior, the stochastic model also correctly predicts the widths of the distributions. For the data shown in Fig. 3b, the individual cells behave very differently from the average, and the stochastic simulation captures this behavior. In this case, the peak at uninduced GFP levels slowly decays as a subpopulation of cells begins to transition to the induced state. In addition to demonstrating the general behavior, the model matches the rate of transitions out of the uninduced peak and predicts the shape of the population distribution over a wide range of TMG and time.
It is noteworthy that ballistic switching does not always occur when the initial state becomes unstable. For instance, although the OFF state is no longer stable in media with 50 μM TMG, the timing of an OFF-to-ON switching event depends on a cell’s rare production of LacY mRNA and subsequent protein creation. It is this rare, stochastic burst of LacY that ultimately triggers the positive feedback loop and drives the OFF-to-ON transition. Conversely, the ON-to-OFF transition is ballistic because it requires the dilution of intracellular TMG and GFP, both of which are low-noise events involving high molecule numbers.
Discussion
We introduced a method that should have general applicability for the prediction of stochastic cellular dynamics. The first step includes characterization of a deterministic model that matches known steady-state behavior. Rate constants in this model can be estimated from published values, by fitting to steady state measurements, or through direct biochemical assays. Next, the magnitudes of noise sources are extracted from distributions of fluorescent counts and correlations between different expression reporters measured in steady state. The sources of intrinsic noise are then characterized by the discrete molecule numbers, N, and mRNA burst sizes, b. By combining these reaction rates and noise sources, a stochastic model is produced containing three important stochastic factors: mRNA production, protein degradation, and global noise.
The model is in good agreement with experimental data and can predict the type of response (ballistic versus stochastic), the escape rates from a state, and the distribution of reporter fluorescence values without any fit parameters. Furthermore, the predicted distributions proved to be robust against parameter variation in both magnitude and general behavior (see the supporting information). The precision of our model’s predictions could be improved by careful measurement of individual model parameters; however, we have shown that previously obtained parameter estimates are sufficient to provide interesting quantitative information about network behavior not available from deterministic equations alone.
Materials and Methods
We calculate the experimental error in noise measurements [ηg-total = (0.25 ± 0.04), ηg-int = (0.21 ± 0.03), ηglobal = (0.14 ± 0.02)] by setting error bars equal to the standard deviation of the noise values measured during independent experiments from 9 to 30 μM TMG. We determine the error in the value of bGFP by calculating propagated errors from NGFP and ηg-int.
Model predictions were generated by Monte-Carlo simulation by implementation of a modified Gillespie’s stochastic simulation algorithm (35) in matlab (MathWorks, Natick, MA). Cells are initialized at steady state protein numbers and then simulated for 12 “Monte-Carlo hours” to generate an equilibrium distribution at the initial TMG concentration. Results of the deterministic model were calculated by integrating Eqs. 1–3 using Euler’s method with Δt = 1 min.
Because not all parameters used in the analysis are measured explicitly, it is important to test the model’s behavior for robustness against parameter error (see supporting information). Although the theoretical predictions change quantitatively as individual parameters are varied, the important features are preserved through a wide range of parameter values.
Supplementary Material
Acknowledgments
We thank Drs. Mukund Thattai and Attila Becskei for fruitful discussions and Dr. Han Lim and Suzanne Komili for technical assistance and helpful discussions. This work was supported by National Institutes of Health Grant GM068957 and National Science Foundation Faculty Early Career Development Grant PHY-0094181. J.T.M. and D.M. are supported by National Science Foundation graduate research fellowships.
Abbreviations
- TMG
thiomethylgalactoside
- CRP
cAMP receptor protein
- RFP
red fluorescent protein.
Footnotes
Conflict of interest statement: No conflicts declared.
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Rao C. V., Wolf D. M., Arkin A. P. Nature. 2002;420:231–237. doi: 10.1038/nature01258. [DOI] [PubMed] [Google Scholar]
- 2.Kaern M., Elston T. C., Blake W. J., Collins J. J. Nat. Rev. Genet. 2005;6:451–464. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
- 3.Raser J. M., O’Shea E. K. Science. 2005;309:2010–2013. doi: 10.1126/science.1105891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kussell E., Kishony R., Balaban N. Q., Leibler S. Genetics. 2005;169:1807–1814. doi: 10.1534/genetics.104.035352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Balaban N. Q., Merrin J., Chait R., Kowalik L., Leibler S. Science. 2004;305:1622–1625. doi: 10.1126/science.1099390. [DOI] [PubMed] [Google Scholar]
- 6.Acar M., Becskei A., van Oudenaarden A. Nature. 2005;435:228–232. doi: 10.1038/nature03524. [DOI] [PubMed] [Google Scholar]
- 7.Hasty J., Pradines J., Dolnik M., Collins J. J. Proc. Natl. Acad. Sci. USA. 2000;97:2075–2080. doi: 10.1073/pnas.040411297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pedraza J. M., van Oudenaarden A. Science. 2005;307:1965–1969. doi: 10.1126/science.1109090. [DOI] [PubMed] [Google Scholar]
- 9.Arkin A., Ross J., McAdams H. H. Genetics. 1998;149:1633–1648. doi: 10.1093/genetics/149.4.1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kepler T. B., Elston T. C. Biophys. J. 2001;81:3116–3136. doi: 10.1016/S0006-3495(01)75949-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Thattai M., van Oudenaarden A. Proc. Natl. Acad. Sci. USA. 2001;98:8614–8619. doi: 10.1073/pnas.151588598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ozbudak E. M., Thattai M., Kurtser I., Grossman A. D., van Oudenaarden A. Nat. Genet. 2002;31:69–73. doi: 10.1038/ng869. [DOI] [PubMed] [Google Scholar]
- 13.Elowitz M. B., Levine A. J., Siggia E. D., Swain P. S. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 14.Swain P. S., Elowitz M. B., Siggia E. D. Proc. Natl. Acad. Sci. USA. 2002;99:12795–12800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Blake W. J., Kærn M., Cantor C. R., Collins J. J. Nature. 2003;422:633–637. doi: 10.1038/nature01546. [DOI] [PubMed] [Google Scholar]
- 16.Paulsson J. Nature. 2004;427:415–418. doi: 10.1038/nature02257. [DOI] [PubMed] [Google Scholar]
- 17.Raser J. M., O’Shea E. K. Science. 2004;304:1811–1814. doi: 10.1126/science.1098641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rosenfeld N., Young J. W., Alon U., Swain P. S., Elowitz M. B. Science. 2005;307:1962–1965. doi: 10.1126/science.1106914. [DOI] [PubMed] [Google Scholar]
- 19.Hooshangi S., Thiberge S., Weiss R. Proc. Natl. Acad. Sci. USA. 2005;102:3581–3586. doi: 10.1073/pnas.0408507102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Becskei A., Kaufmann B. B., van Oudenaarden A. Nat. Genet. 2005;37:937–944. doi: 10.1038/ng1616. [DOI] [PubMed] [Google Scholar]
- 21.Colman-Lerner A., Gordon A., Serra E., Chin T., Resnekov O., Endy D., Pesce C. G., Brent R. Nature. 2005;437:699–706. doi: 10.1038/nature03998. [DOI] [PubMed] [Google Scholar]
- 22.Isaacs F. J., Hasty J., Cantor C. R., Collins J. J. Proc. Natl. Acad. Sci. USA. 2003;100:7714–7719. doi: 10.1073/pnas.1332628100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Vilar J. M., Guet C. C., Leibler S. J. Cell Biol. 2003;161:471–476. doi: 10.1083/jcb.200301125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Simpson M. L., Cox C. D., Sayler G. S. Proc. Natl. Acad. Sci. USA. 2003;100:4551–4556. doi: 10.1073/pnas.0736140100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Novick A., Weiner M. Proc. Natl. Acad. Sci. USA. 1957;43:553–566. doi: 10.1073/pnas.43.7.553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Maloney P. C., Rotman B. J. Mol. Biol. 1973;73:77–91. doi: 10.1016/0022-2836(73)90160-5. [DOI] [PubMed] [Google Scholar]
- 27.Nobelmann B., Lengeler J. W. J. Bacteriol. 1996;178:6790–6795. doi: 10.1128/jb.178.23.6790-6795.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ozbudak E. M., Thattai M., Lim H. N., Shraiman B. I., van Oudenaarden A. Nature. 2004;427:737–740. doi: 10.1038/nature02298. [DOI] [PubMed] [Google Scholar]
- 29.Chung J. D., Stephanopoulos G. Chem. Eng. Sci. 1996;51:1509–1521. [Google Scholar]
- 30.Wong P., Gladney S., Keasling J. D. Biotechnol. Prog. 1997;13:132–143. doi: 10.1021/bp970003o. [DOI] [PubMed] [Google Scholar]
- 31.Yildirim N., Mackey M. C. Biophys. J. 2003;84:2841–2851. doi: 10.1016/S0006-3495(03)70013-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Liu J. Y., Miller P. F., Willard J., Olson E. R. J. Biol. Chem. 1999;274:22977–22984. doi: 10.1074/jbc.274.33.22977. [DOI] [PubMed] [Google Scholar]
- 33.Le T. T., Harlepp S., Guet C. C., Dittmar K., Emonet T., Pan T., Cluzel P. Proc. Natl. Acad. Sci. USA. 2005;102:9160–9164. doi: 10.1073/pnas.0503311102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Muller-Hill B., Crapo L., Gilbert W. Proc. Natl. Acad. Sci. USA. 1968;59:1259–1264. doi: 10.1073/pnas.59.4.1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gillespie D. T. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.