Abstract
This paper draws attention to selected experiments on enzyme-catalyzed reactions that show convex Arrhenius plots, which are very rare, and points out that Tolman's interpretation of the activation energy places a fundamental model-independent constraint on any detailed explanation of these reactions. The analysis presented here shows that in such systems, the rate coefficient as a function of energy is not just increasing more slowly than expected, it is actually decreasing. This interpretation of the data provides a constraint on proposed microscopic models, i.e., it requires that any successful model of a reaction with a convex Arrhenius plot should be consistent with the microcanonical rate coefficient being a decreasing function of energy. The implications and limitations of this analysis to interpreting enzyme mechanisms are discussed. This model-independent conclusion has broad applicability to all fields of kinetics, and we also draw attention to an analogy with diffusion in metastable fluids and glasses.
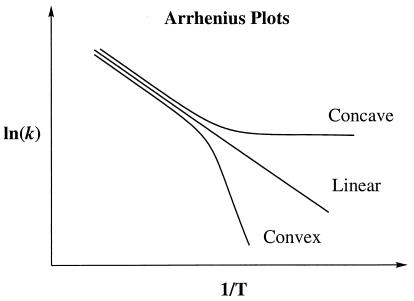
In recent years, an increasing number of studies have measured the temperature dependence of enzyme reactions for both thermostable and mesostable enzymes (enzymes from organisms that grow optimally at high temperature and at normal body temperature, respectively). The temperature dependence is usually exhibited in an Arrhenius plot, which is the natural logarithm of the rate coefficient vs. reciprocal of the absolute temperature (Fig. 1). Some of the methodologies for measuring the temperature dependences of reaction rates have been applied to measure the temperature dependences of the kinetic isotope effects (KIEs) of the catalyzed reactions as well, and such experiments provide experimental data very relevant to characterizing the dynamical bottlenecks of the reactions (1–6). A large number of theoretical models have been advanced for the interpretation of this kind of data (7–19).
Figure 1.
Concave, linear, and convex Arrhenius plots where k is rate coefficient, and T is the absolute temperature.
Experiments on reactions catalyzed by a variety of thermostable and mesostable dehydrogenase and oxidase enzymes have shown that in some cases the Arrhenius plot for the chemical step is convex (20–23). In the present paper, we comment on the significance of this observation, and we provide an interpretation of this finding that places it in the broader perspective of nonbiological chemical as well as biochemical kinetics. This paper points out that the convex Arrhenius behavior places a severe constraint on the microcanonical unimolecular rate coefficient for the chemical step. In particular, we can go beyond the obvious interpretation that a convex Arrhenius plot can be interpreted as a lower than expected rate at high temperatures, and we can say, under certain conditions, that the microcanonical unimolecular rate coefficient for the chemical step must actually decrease with increasing energy.
In general, it is desirable to separate the interpretation of experimental data into two steps. First, we infer general consequences that rest on solid foundations such as thermodynamics and general principles of statistical mechanics. Second, we proceed to more microscopically detailed models that rest on less sure footing. The new aspect of the present analysis is concerned entirely with the first step.
The striking feature of the reactions in refs. 20–23 that we discuss here is the positive convexity C of their Arrhenius plots, where
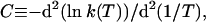 |
1 |
k(T) is the catalytic rate coefficient, and T is temperature. We write
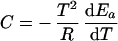 |
2 |
where
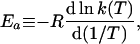 |
3 |
Ea is the temperature-dependent phenomenological energy of activation, and R is the gas constant. Thus a positive convexity means that Ea decreases with increasing temperature. In the broad field of kinetics, not restricting consideration to enzyme kinetics, when nonlinear Arrhenius plots can be observed, they are almost always concave, i.e., C is negative. This general result is explained by Tolman's interpretation of the activation energy, which may be written as (25–27)
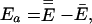 |
4 |
where a double overbar denotes an average over all reacting systems, and a single overbar denotes an average over all systems, whether or not they react. In words, Tolman's Eq. 4 states that the negative of the local slope of an Arrhenius plot can be interpreted as equal to the average energy of molecules that react minus the average energy of all possible reactants. For unimolecular reactions of a thermally equilibrated species:
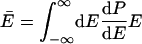 |
5 |
and
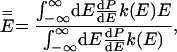 |
6 |
where E is total energy, dP/dE is the normalized probability density that a system has energy E in a canonical ensemble at temperature T, and k(E) is the unimolecular rate coefficient for a microcanonical ensemble at energy E.§ Usually, E̿ increases more rapidly than Ē with increasing T because k(E) is usually an increasing function of energy.¶ This explains why Ea usually increases with T and hence why C is negative. A convex Arrhenius plot means that E̿ decreases or that it increases less rapidly than Ē as temperature increases, and in the next paragraph we argue that this ordinarily implies that k(E) decreases with increasing energy over the region of energy that dominates the integrals in Eq. 6.
One can make a more precise statement about the consequence of E̿ decreasing or increasing less rapidly than Ē as temperature increases. By noting that
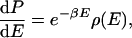 |
7 |
where β is 1/RT, and ρ(E) is the density of states, and by using Eqs. 4–6, one can easily show that
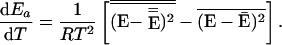 |
8 |
Thus the statement that dEa/dT is negative is the same as the statement that the distribution of reaction energies is narrower than the distribution of reactant energies. If dP/dE were symmetric about Ē, then the sign of dEa/dT would depend on the shape of the function k(E), and not just its sign. But dP/dE is actually a highly skewed function. For typical molecules, its shape is well approximated by setting ρ(E) in Eq. 7 equal to En−1, where n is approximately equal to the number of degrees of freedom (31). If one assumes this form and also assumes that k(E) varies slowly and linearly over the important range of the integrals in Eq. 6, one can show that the right-hand side of Eq. 8 is proportional to dk/dE with a positive constant of proportionality. For more complicated k(E) functions, one no longer has exact proportionality, but the direction of the effect is established by the positive skewedness of dP/dE. Although the identity of the signs of dEa/dT and dk/dE is not a mathematical theorem, it is expected to hold for normal densities of states and smooth k(E) functions.
This result presents a constraint on any microscopic interpretation, and—equally importantly—it suggests new microscopic interpretations. For example, suppose that the reactant configuration space may be partitioned into two types of conformations, one of which (called type R) is reactive with rate coefficient kR(E) and the other of which (called type N) is nonreactive with zero rate coefficient. Then
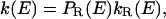 |
9 |
where PR(E) is the conditional probability that a system having energy E is in a conformation of type R. This provides a mechanism for k(E) to decrease with E, i.e., PR(E) decreases with E faster than kR(E) increases. This could occur because higher-energy systems visit a wider region of phase space and hence spend a smaller fraction of their time in any single constrained region. This interpretation may be of special importance for enzymology. In recent years, several studies have been concerned with understanding the role of conformational sampling in enzyme catalysis (17, 18, 22, 32–37). In a recent review, Bruice and Benkovic (17) argued that the active configurations sampled by the enzymatic complex are not of higher energy than the general population of conformers and that populating these conformations may determine the reaction rate. In contrast to the sometimes detailed models in the papers cited, the present interpretation proceeds on very general grounds without invoking any particular microscopic molecular mechanism or model such as tunneling promoted by thermally excited enzyme fluctuations (11, 13, 38, 39), free energy of activation calculations including proper sample over conformations (40), or specific mechanisms of transitions between microstates of varying conformational flexibility (41–44). Nevertheless, it can clearly accommodate more specific interpretations such as a protein that is rigid at low T or a dynamical motion that requires population of specific low-energy vibrational states. However, nothing we have said here gives specific support to such models, whose validity should be examined by further experiments and detailed simulations. The present discussion does not specifically invoke effects associated with the breakdown of transition state theory. Quantum effects like tunneling can be accommodated by simply including them in k(E) or kR(E).
In the context of our analysis, the results mentioned above for thermophilic alcohol dehydrogenase ADH-hT (22, 32) can be interpreted in terms of the relative trends in E̿ and Ē when temperature is changed. A widely advanced hypothesis is that thermophilic enzymes have evolved to function in their physiological niche, that is, at elevated temperature, and are less active at room temperature (even less active, in some cases, than anticipated by their enthalpy of activation at physiological temperature). Our analysis may offer a connection between that notion and calculations concerned with the identification of active and nonactive conformations (16, 17). For example, Wrba et al. (21) reported an empirical observation that, for enzymes with different melting temperatures, the difference in the temperatures of maximum curvature in Arrhenius plots is similar to the difference in melting temperature. This may be related to shifts in PR(E) and kR(E) dependencies on E in the ranges that are important at the transition temperatures for denaturation and activity. As an additional example, we note that it was recently suggested that it is “perhaps not surprising that, for C—H-bond cleavage reactions, a partitioning of thermal energy into low-frequency protein modes is a major factor. These modes can become significantly excited at ambient temperature, in contrast to the C—H stretching mode, which is expected to be largely confined to its zero-point energy level” (22). These kinds of considerations can be related to the temperature dependence of E̿ and Ē and hence to the concavity or convexity of Arrhenius plots.
The general conclusion about the energy dependence of the microcanonical rate coefficient is also applicable to convex Arrhenius plots that are occasionally observed in other studies. If one is to apply these arguments, one must be careful to ensure that the convex Arrhenius plot represents a true elementary reaction with internally equilibrated reactants. For example, in the prototype steady-state problem
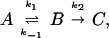 |
10 |
where
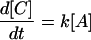 |
11 |
with
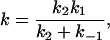 |
12 |
it can be applied to k1, k−1, or k2, but not generally to k. However, if k−1 and k1 are much larger than k2, then k becomes an elementary rate coefficient for A → C, and no conclusions are changed by the pre-equilibrium before the rate-determining step. This further applies to the case in which k2 is much greater than k1 and k−1, where k becomes k1. A special case where the steady-state approach may be applied is that in which A corresponds to unbound reactant and enzyme, state B is the Michaelis complex, and state C is the product (45). Note that in this case k1 (in Eq. 12) should be a second order rate constant leading to the Michaelis equation:
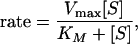 |
13 |
where [S] is the reactant (substrate) concentration, Vmax is the reaction rate at [S] much higher than KM, which is the Michaelis constant, (k2 + k−1)/k1, for Eq. 10. The discussion does not apply to effective rate coefficients resulting from a change in the rate-determining step or to changes in effective enzyme concentration [irreversible denaturation or a reversible inhibition equilibrium of the reactants (46)], nor does it apply to rate coefficients with hysteresis attributable to glass formation. This point should be emphasized for enzymatic reactions: do the rates measured actually represent a meaningful consistent rate constant over the whole temperature range? For example, in an early report of convex Arrhenius plot for the thermophilic alcohol dehydrogenase from Bacillus stearothermophilus (ADH-hT), all measurements were conducted with the same substrate concentration (that was saturating the enzyme at room temperature), and Vmax was presented (47). A later report (22) found that KM increases with temperature so at high temperature [S] was not sufficiently larger than KM, and the measured rate was found to be slower than Vmax, presenting an apparently convex Arrhenius plot. Even for the simplest realistic enzyme kinetics, mechanism 10 should be augmented by a product release step, and the data should be analyzed with due regard for the commitment to catalysis and the ratio of catalysis (48, 49); otherwise, the measured kcat may show a different temperature dependence than the intrinsic k2. Refs. 20–24 have been selected as examples where particular care was taken to ensure and demonstrate that the Arrhenius plot corresponds to a single rate-limiting elementary chemical reaction step as function of temperature. Rubach and Plapp (personal communication of unpublished results), for example, used stopped-flow pre-steady state techniques to measure KIEs on microscopic rate constants to study the reaction catalyzed by horse liver alcohol dehydrogenase. They found convex Arrhenius plots for both hydride and deuteride transfer, but no temperature dependence of the KIEs, and they demonstrated that no change in the rate-determining step was likely to affect their results. We further excluded cases for which the temperature range allows for irreversibly melted or partially melted protein. In contrast to the enzymatic examples showing convex Arrhenius behavior involving a single elementary step, we mention the case of skin permeation of drugs, where convex Arrhenius behavior has been observed, but where the elementary steps have not been or cannot be sorted out (50, 51). For comparison with permeation through skin, we also mention that the somewhat better defined case of non-Arrhenius temperature dependence of diffusion in amorphous solids has been modeled by a multistep site-hopping model (52, 53).
An example from organic chemistry provides a useful illustration of these concepts in conjunction with a temperature-dependent structural reorganization. Limbach has observed convex Arrhenius plots (personal communication of unpublished results) for the base-catalyzed intramolecular proton transfer in 1,3-bis-(4-fluorophenyl)-triazene dissolved in ethyl methyl ether [this can be thought of as a model system for enzymatic processes (55)]. The rate coefficient represents an average over different hydrogen-bonded forms of the reactant, especially the free molecule and the complex with base. The proton transfer takes place in the complex. The convex Arrhenius curvature arises from the fact that the molecule changes at high temperature into the noncomplexed form where the barrier to proton transfer is larger (ref. 55 and H. H. Limbach, personal communication). Thus the Tolman interpretation does not strictly apply because the rate coefficient does not represent a single elementary step. The Arrhenius plot of the reaction from either form separately would presumably be quasilinear or concave. If, however, the different hydrogen-bonded forms are considered to be conformers of a single reactant, the Tolman interpretation may be applied, and it provides an illustration of a molecule that reacts more slowly at higher energy because it explores a wider region of phase space that includes essentially nonreactive conformers. Similarly, Massey et al. (23) suggest a possible explanation of their convex Arrhenius plot involving two competing enzymatic forms, each dominating in a different temperature range. This model is one particular example of a model that could be consistent with the model-independent result presented here. For nonbiological reactions we expect that particularly reactive configurations will often be high-energy species. It is possible that convex Arrhenius plots will be more common in biological systems because an enzyme may have specifically evolved such that the lowest-energy states (i.e., the most accessible ones at ambient T) are the reactive ones, thereby leading to low E̿ even as T is increased.
Convex Arrhenius plots have also been observed for diffusion in supercooled liquids and glasses. Such cases, like the skin permeation problem mentioned above, may be complicated by multiple parallel pathways, but nevertheless have yielded to detailed analysis. One widely quoted explanation is that molecules in low-temperature liquids diffuse by crossing appreciable potential barriers, whereas at high-temperature, diffusive motions are almost free (24, 56). This model recognizes that as temperature is raised, thermal energies will become larger compared to barrier heights; what is required for a convex Arrhenius plot is that the average energy of molecules making transitions (in this case, diffusive hops from one local minimum to another) rises more slowly than the average energy of all molecules. There are many detailed theories of non-Arrhenius behavior in metastable fluids and glasses that do not explicitly address the temperature dependence of the activation energy in terms of Tolman's interpretation (58), but any consistent explanation of a convex Arrhenius plot in terms of local equilibrium elementary rate coefficients must be consistent with Tolman's result at some underlying level, even if this is not explicit or not even recognized.
In summary, the present article has pointed out the fundamental microcanonical information that is provided by an observation of Arrhenius plot convexity, but which has apparently not previously been interpreted. The analysis has widespread applicability and makes a definite model-independent prediction about average energies of systems making transitions. The result is relevant to all fields of kinetics (in enzymes, in atmospheric chemistry, in cluster reactions, etc.) where convex Arrhenius plots may be observed, and we have therefore kept the presentation as general as possible, while citing recent experiments with thermostable and mesostable dehydrogenase and oxidase catalysts as specific examples exhibiting the phenomenon. We have also made a connection to the theory of diffusion. We hope that the point of view espoused in this paper will stimulate new ways of thinking about reaction rates, catalysis, and diffusion.
Acknowledgments
We appreciate helpful discussion with Dan Geselter, Jan Jensen, Judith Klinman, and Hans Limbach. This work was supported in part by the National Science Foundation.
Abbreviation
- KIE
Kinetic isotope effect
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
Recall that a canonical ensemble is one characterized by a temperature, and a microcanonical ensemble is a slice out of a canonical ensemble such that the slice contains all systems with a given total energy. Note that Ea, E̿, Ē, and dP/dE are all associated with the canonical ensemble and therefore are functions of T, and dP/dE equals the Boltzmann-weighted density of states times a normalization constant (28).
References
- 1.Kohen A, Klinman J P. Acc Chem Res. 1998;31:397–404. [Google Scholar]
- 2.Kohen A, Klinman J P. Chem Biol. 1999;6:R191–R198. doi: 10.1016/s1074-5521(99)80058-1. [DOI] [PubMed] [Google Scholar]
- 3.Rickert K W, Klinman J P. Biochemistry. 1999;38:12218–12228. doi: 10.1021/bi990834y. [DOI] [PubMed] [Google Scholar]
- 4.Basran J, Sutcliffe M J, Scrutton N S. Biochemistry. 1999;38:3218–3222. doi: 10.1021/bi982719d. [DOI] [PubMed] [Google Scholar]
- 5.Scrutton N S. Biochem Soc Trans. 1999;27:767–779. doi: 10.1042/bst0270767. [DOI] [PubMed] [Google Scholar]
- 6.Harris R J, Meskys R, Sutcliffe M J, Scrutton N S. Biochemistry. 2000;39:1189–1198. doi: 10.1021/bi991941v. [DOI] [PubMed] [Google Scholar]
- 7.Warshel A. Proc Natl Acad Sci USA. 1984;81:444–448. doi: 10.1073/pnas.81.2.444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Warshel A, Sussman F, Hwang J-K. J Mol Biol. 1988;201:139–159. doi: 10.1016/0022-2836(88)90445-7. [DOI] [PubMed] [Google Scholar]
- 9.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solutions. New York: Plenum; 1991. [Google Scholar]
- 10.Hwang J-K, Warshel A. J Am Chem Soc. 1996;118:11745–11751. [Google Scholar]
- 11.Borgis D, Hynes J T. In: The Enzyme Catalysis Process. Cooper A, Houben J, Chien L, editors. New York: Plenum; 1989. pp. 293–303. [Google Scholar]
- 12.Bruno W J, Bialek W. Biophys J. 1992;63:689–699. doi: 10.1016/S0006-3495(92)81654-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Antoniou D, Schwartz S D. Proc Natl Acad Sci USA. 1997;94:12360–12365. doi: 10.1073/pnas.94.23.12360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kuznetsov A M, Ulstrup J. Can J Chem. 1999;77:1085–1096. [Google Scholar]
- 15.Truhlar D G, Morokuma K. Transition State Modeling for Catalysis. Washington, DC: Am. Chem. Soc.; 1999. [Google Scholar]
- 16.Alhambra C, Corchado J C, Sánchez M L, Gao J, Truhlar D J. J Am Chem Soc. 2000;122:8197–8203. [Google Scholar]
- 17.Bruice T C, Benkovic S J. Biochemistry. 2000;39:6267–6273. doi: 10.1021/bi0003689. [DOI] [PubMed] [Google Scholar]
- 18.Radkiewicz J L, Brooks C L. J Am Chem Soc. 2000;122:225–231. [Google Scholar]
- 19.Wilson E K. Chem Eng News. July 17, 2000;78:42–45. [Google Scholar]
- 20.Lakatos S, Halasz G, Zavodszky P. Biochem Soc Trans. 1978;6:1195–1197. doi: 10.1042/bst0061195. [DOI] [PubMed] [Google Scholar]
- 21.Wrba A, Schweiger A, Schultes V, Jaenicke R, Zavodszky P. Biochemistry. 1990;29:7584–7592. doi: 10.1021/bi00485a007. [DOI] [PubMed] [Google Scholar]
- 22.Kohen A, Cannio R, Bartolucci S, Klinman J P. Nature (London) 1999;399:496–499. doi: 10.1038/20981. [DOI] [PubMed] [Google Scholar]
- 23.Massey V, Curti B, Ganther H J. Biol Chem. 1966;241:2347–2357. [PubMed] [Google Scholar]
- 24.Ullo J, Yip S. Phys Rev A. 1989;39:5877–5886. doi: 10.1103/physreva.39.5877. [DOI] [PubMed] [Google Scholar]
- 25.Tolman R C. J Am Chem Soc. 1920;42:2506–2528. [Google Scholar]
- 26.Tolman R C. Statistical Mechanics with Applications to Physics and Chemistry. New York: Chemical Catalog Co.; 1927. pp. 260–270. [Google Scholar]
- 27.Truhlar D G. J Chem Educ. 1978;55:309–311. [Google Scholar]
- 28.Denbigh K. The Principles of Chemical Equilibrium. Cambridge, U.K.: Cambridge Univ. Press; 1971. p. 342. [Google Scholar]
- 29.Skinner J L, Trommsdorff H P. J Chem Phys. 1988;89:897–907. [Google Scholar]
- 30.Wonchoba S E, Hu W P, Truhlar D G. Phys Rev B. 1995;51:9985–10002. doi: 10.1103/physrevb.51.9985. [DOI] [PubMed] [Google Scholar]
- 31.Rice O K. Statistical Mechanics, Thermodynamics, and Kinetics. San Francisco: Freeman; 1967. p. 565. [Google Scholar]
- 32.Kohen A, Klinman J P. J Am Chem Soc. 2000;122:10738–10739. [Google Scholar]
- 33.Gregory R B. Protein-Solvent Interactions. New York: Dekker; 1995. [Google Scholar]
- 34.Scrutton N S, Basran J, Sutcliffe M J. Eur J Biochem. 1999;264:666–671. doi: 10.1046/j.1432-1327.1999.00645.x. [DOI] [PubMed] [Google Scholar]
- 35.Northrop D B. J Am Chem Soc. 1999;121:3521–3524. [Google Scholar]
- 36.Ostermann A, Waschipkyo R, Parak F G, Nienhaus G U. Nature (London) 2000;404:205–208. doi: 10.1038/35004622. [DOI] [PubMed] [Google Scholar]
- 37.Liebl U, Lipowski G, Négrerie M, Lambry J C, Martin J L, Vos M H. Nature (London) 1999;401:181–184. doi: 10.1038/43699. [DOI] [PubMed] [Google Scholar]
- 38.Antoniou D, Schwartz S D. J Chem Phys. 1998;108:3620–3625. [Google Scholar]
- 39.Borgis D, Hynes J T. Chem Phys. 1993;170:315–346. [Google Scholar]
- 40.Warshel A. Curr Opin Struct Biol. 1992;2:230–236. [Google Scholar]
- 41.Vihinen M. Prot Eng. 1987;1:477–480. doi: 10.1093/protein/1.6.477. [DOI] [PubMed] [Google Scholar]
- 42.Varley P G, Pain R H. J Mol Biol. 1991;220:531–538. doi: 10.1016/0022-2836(91)90028-5. [DOI] [PubMed] [Google Scholar]
- 43.Rasmussen B F, Stock A M, Ringe D, Petsko G A. Nature (London) 1992;357:423–424. doi: 10.1038/357423a0. [DOI] [PubMed] [Google Scholar]
- 44.Zavodszky P, Kardos J, Svingor A, Petsko G A. Proc Natl Acad Sci USA. 1998;95:7406–7411. doi: 10.1073/pnas.95.13.7406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Fersht A. Structure and Mechanism in Protein Sciences: A Guide to Enzyme Catalysis and Protein Folding. New York: Freeman; 1998. [Google Scholar]
- 46.Kistiakowsky G B, Lumry R. J Am Chem Soc. 1949;71:2006–2013. [Google Scholar]
- 47.Guagliardi A, Martino M, Iaccarino I, Derosa M, Rossi M, Bartolucci S. Int J Biochem Cell Biol. 1996;28:239–246. doi: 10.1016/1357-2725(95)00138-7. [DOI] [PubMed] [Google Scholar]
- 48.Northrop D B. In: Enzyme Mechanism from Isotope Effects. Cook P F, editor. Boca Raton, FL: CRC; 1991. pp. 181–202. [Google Scholar]
- 49.Malany S, Sawai M, Sikorski R S, Seravalli J, Quinn D M, Radi Z, Taylor P, Kronman C, Velan B, Shafferman A. J Am Chem Soc. 2000;122:2981–2987. [Google Scholar]
- 50.Ohara N, Takayama K, Machida Y, Nagai K. Int J Pharm. 1994;105:31–38. [Google Scholar]
- 51.Ohara N, Takayama K, Nagai T. Biol Pharm Bull. 1995;18:439–442. doi: 10.1248/bpb.18.439. [DOI] [PubMed] [Google Scholar]
- 52.Chang W, Xu G. J Chem Phys. 1993;99:2001–2003. [Google Scholar]
- 53.Xu G J. Non-Cryst Sol. 1994;170:68–72. [Google Scholar]
- 54.Ediger M D, Angell C A, Nagel S R. J Phys Chem. 1996;100:13200–13212. [Google Scholar]
- 55.Mannle F, Limbach H H. Agnew Chem Int Ed. 1996;35:441–442. [Google Scholar]
- 56.Goldstein M. J Chem Phys. 1969;51:3728–3739. [Google Scholar]