Controlling the Protein Dynamical Transition with Sugar-Based Bioprotectant Matrices: A Neutron Scattering Study

Abstract

Through elastic neutron scattering we measured the mean-square displacements of the hydrogen atoms of lysozyme embedded in a glucose-water glassy matrix as a function of the temperature and at various water contents. The elastic intensity of all the samples has been interpreted in terms of the double-well model in the whole temperature range. The dry sample shows an onset of anharmonicity at ∼100 K, which can be attributed to the activation of methyl group reorientations. Such a protein intrinsic dynamics is decoupled from the external environment on the whole investigated temperature range. In the hydrated samples an additional and larger anharmonic contribution is provided by the protein dynamical transition, which appears at a higher temperature T_d. As hydration increases the coupling between the protein internal dynamics and the surrounding matrix relaxations becomes more effective. The behavior of T_d that, as a function of the water content, diminishes by ∼60 K, supports the picture of the protein dynamics as driven by solvent relaxations. A possible connection between the protein dynamical response versus T and the thermal stability in glucose-water bioprotectant matrices is proposed.

INTRODUCTION

Internal dynamics plays a key role in protein function. In fact, the biological activity of proteins requires flexibility because all interactions, such as that with a specific substrate, usually involve at least small rearrangements of atoms in response to those events. Proteins display such a flexibility over a wide range of timescale and distances. Time windows from femtoseconds (individual bond vibrations) to picoseconds (small group fluctuations) to nano- and microseconds and longer (collective motions of groups of bounded atoms) are covered by the internal motions of these biomolecules, over a corresponding distance scale of fractions of an angstrom to nanometers (1). Since all these motions are thermally driven, the study of their temperature dependence deserves special attention. In particular, both molecular dynamics (MD) simulation studies (2,3) and experiments performed with many techniques such as Mossbauer (4), x-ray (5), and neutron scattering (6) have shown that the dynamics of hydrated proteins shows an unusual temperature dependence, undergoing a dynamical transition at a certain temperature T_d around 180–200 K (7). In terms of the atomic mean-square displacements (MSD), which describe the amplitude of the protein internal fluctuations in the picosecond timescale, such a transition consists in the departure from the low-temperature trend (6,8), with the appearance of remarkable anharmonic degrees of freedom, related to collective motions of groups of atoms. In terms of a well-known theoretical approach, the structural fluctuations responsible for the dynamical transition are just schematized as jumps between nearly isoenergetic protein conformations, the so-called conformational substates (9). These structural fluctuations have been proposed to be necessary for biological functionality (10–14), even though this point is still controversial (15). When temperature is lowered, transitions among conformational substates can be partly or totally suppressed and the biological functionality inhibited. As the dynamical transition is not detectable when the protein is dehydrated (11,14,16) one can infer that the water environment around the surface of the biomolecule acts as a plasticizer by determining the protein thermal fluctuations. This picture is also supported by MD simulation studies that showed that the mobility of the solvent determines the structural fluctuations of proteins at and above 180 K (3,17), whereas intrinsic protein effects are prevalently important at lower temperatures (3). Moreover the solvent determines the amplitudes of atomic fluctuations not only at the protein surface but also in the core (3,18). A hydrogen bond network, whose essential ingredients are cooperativity and a distribution of hydrogen-bonded clusters, would be at the basis of the cross correlation between protein structural fluctuations and the thermal motion of bound water (19). In the past, the features of proteins have been principally investigated when they are solved with water, which is the classic physiological milieu. However an increasing attention is now devoted to the study of the intriguing properties of biomolecules when they are in the presence of organic solvents (20,21) and in particular of bioprotectant (or stabilizer) media (22). In fact, these bioprotectant media, such as polyol- and particularly sugar-water matrices, show an outstanding ability in preserving structure and functionality of biomolecules, which has been often largely exploited in food, pharmaceutical, and biotechnology sciences to optimize lyophilization and long-term storage of biological samples (22–26). Glassy matrices of simple carbohydrate are of capital importance in protecting biological molecules and cells against stresses induced by potentially detrimental freezing, drying, and heating processes (27–29). Despite this importance, the nanoscopic mechanisms through which such matrices act as stabilizers are still unclear. Both the interaction of the matrix molecules with the protein surface groups via direct hydrogen bond (30,31) and the glassy nature of the surrounding environment (32,33) seem to be decisive. Yet, this scenario is incomplete without the comprehension of the way the protein dynamics is affected by the external media. On these grounds, many efforts in the last decade were done to clarify this point (34–40). Bioprotectant glassy matrices were proven not only to induce a noticeable retardation of protein molecular movements (41–43) but also to reduce their extent (34–36), thus preventing physical and chemical protein degradations. The degree of fragility of the glassy matrices where the protein is embedded has been suggested to be a key parameter to quantify their bioprotectant aptitude (44). The protein dynamics seems to be slaved to the environment (13,36,45), even if the question is still debated (46). In particular it has been suggested that it is the molecular environment occupying the shell immediately around the protein surface that controls the fast fluctuations of proteins (13). A new insight on the intimate coupling of the protein with the surrounding environment has been recently provided with the discovery of a quantitative relationship between the local protein relaxational dynamics and the bulk viscosity of the enclosing glassy matrices (47).

Neutron scattering spectroscopy is very sensitive to the single-particle dynamics of hydrogen atoms (48). Therefore such a technique gives invaluable information on the behavior of proteins, where hydrogen atoms are abundantly and almost homogeneously distributed, in the nano- and picosecond time window over the angstrom spatial scale (2). Here we report a neutron scattering study we performed on lysozyme embedded in glucose-water matrices. In these matrices, which are the archetype of bioprotectant mixtures, two transitions in the molecular mobility have been observed through proton magnetic resonance (¹H-NMR) experiments (49). The first one corresponds to the well-known glass transition, whereas the other is related to collapse phenomena in glasses and is 20–30 K higher. Both the transition temperatures, respectively T_g and T_c, can be largely varied by changing the water content, thus emphasizing the dependence of the protein dynamics on the external environment (49). By characterizing the extent of the protein MSD we were able to quantify the dramatic variation of the protein dynamical response to temperature and water content changes, with particular attention to the dynamical transition phenomenon. We have found that the onset of the anharmonic protein motions related to this transition occurs just in correspondence to the dynamical activation of the surrounding glassy matrix. When the water content increases, the dynamical coupling between protein and environment becomes more and more effective.

MATERIALS AND METHODS

Samples preparation

Salt-free lyophilized lysozyme from chicken egg white has been purchased from Sigma-Aldrich (St. Louis, MO). As deuterium has an incoherent neutron scattering cross section much lower that hydrogen (48), we maximized the signal from the protein relative to the solvent by using only fully deuterated glucose (Euriso-Top, Saclay, France) and heavy water (Sigma-Aldrich) in sample preparation.

To avoid the exchange of protons between enzyme and solvent the exchangeable hydrogens of the protein have been D-substituted by leaving in solution 1 g of lysozyme in 20 ml of D₂O at room temperature for 1 day. Using this procedure we can affirm, on the basis of what has been reported by Gregory and Lumry (50), that the spurious contribution to the incoherent quasielastic scattering due to the proton exchanging with the solvent is <1% of the total signal. The solution was freeze-dried into a powder and then desiccated under vacuum in the presence of P₂O₅ to reduce the water content to a value as low as possible.

The protein and an equal weight of deuterated glucose were then dissolved in D₂O and lyophilized again to obtain a mixture of dry lysozyme (∼330 mg) and glucose in proportion in weight 1:1. Finally, the samples were hydrated by putting them in the presence of a KCl-saturated solution of D₂O and varying the equilibration time. The water content w (w = g D₂O/g glucose) was determined by weighing the sample before and after the hydration process. In such a way samples at 0.7w, 0.6w, 0.4w, 0.15w, and 0w have been obtained. After the preparation, they were held in a standard flat aluminum cell (inner thickness of 1 mm) sealed with an indium wire to ensure a constant hydration level, which was also checked by weighing the sample before and after the measurement.

For all the examined w values, the water contained in the samples is in a strongly coordinated form, as it interacts with both glucose and protein molecules. This prevents the ice formation in the subzero temperature range. On the other hand, the presence of crystalline ice would produce Bragg peaks that have not been revealed in the measured elastic intensities.

Incoherent neutron scattering

Neutron scattering spectroscopy is a powerful technique used to directly probe protein motions. In a neutron scattering experiment the relevant quantity is the dynamical structure factor S(Q,E), which represents the probability for an incident neutron to be scattered by the sample with energy and momentum transfer E = ℏω and ℏQ, respectively. S(Q,E) is the Fourier transform of the time-correlation function of the density fluctuation in the system, which provides information on both the structure and the dynamics of the sample through its Q and E dependence. Since our samples are isotropic, the dynamical structure factor depends only on the modulus of the momentum transfer. Moreover, the dominant contribution to the revealed signal is due to nonexchangeable protein hydrogen atoms, whose neutron cross section of hydrogen is by far higher than that of deuterium or of any other atom, and is almost exclusively incoherent in nature (σ_inc = 79.90 barns, σ_coh = 1.76 barns) (48). More in particular, incoherent scattering from these atoms is on average 75% of the total signal, whereas the rest is the coherent contribution from the deuterated matrix and the protein.

In this study the neutron-scattered intensity has been recorded within a narrow energy interval of 2 μeV centered at the elastic peak (E ≈ 0), and in the incoherent approximation can be described by the law (6,36):

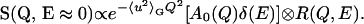(1)

The Gaussian term in Eq. 1 is the so-called Debye-Waller factor, which accounts for the Q-dependence of the elastic intensity due to the vibrational atomic MSD 〈u²〉_G. The protein internal motions are described by the term within square brackets convoluted with the experimental resolution function R(Q,E). This function can be approximated, in the narrow energy interval where our data were acquired, by a Q-independent Gaussian function 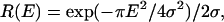where the half-width at half-maximum (HWHM) is 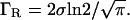A₀(Q) is the elastic incoherent structure factor (EISF), which represents the space-Fourier transform of the scatterers distributions taken at infinite time, averaged over all the possible initial positions. It shows a characteristic modulation in Q, depending on the geometry and type of motion of the scatterers. Therefore the EISF Q-dependence is sensitive to the local dynamics. The dynamics of protein hydrogen atoms can be schematized with the so-called double-well jump model. Such a model has been successfully exploited in describing the picosecond dynamics of protein powders in different environments, such as water (6,16) and glycerol (36). Within this framework, which is an oversimplified description of the complex protein energy landscape, the protein protons are considered dynamically equivalent and their motions are schematized as jumps between two distinct sites with a free energy difference ΔG. The corresponding EISF is

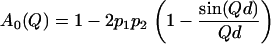(2)

The confined dynamics of hydrogen atoms is described in terms of the distance d between the two potential wells and of the occupation probabilities p₁ and p₂ of the ground and the excited state. The double-well model allows us to directly calculate the total MSD:

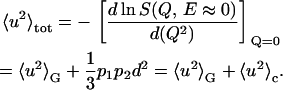(3)

In this equation, 〈u²〉_G is the Gaussian vibrational MSD term, whereas p₁p₂d²/3 = 〈u²〉_c is the conformational contribution to MSD (13) and quantifies the proton mobility due to the jumping between the two energetic sites.

Neutron scattering experiment

The measurements were performed on the high-resolution backscattering spectrometer IN13, at the Institut Laue-Langevin in Grenoble (France). The energy resolution of Γ_R = 4.5 μeV (HWHM) makes accessible motions faster than ∼150 ps. The data were collected in the wide Q-range 0.3–4.5 Å⁻¹, with an average wave-vector transfer resolution of ∼0.2 Å⁻¹. The sample holder was placed at an angle of 135° with respect to the incident beam direction. All the samples were investigated from 20 K to 320 K. The acquired data were corrected to take into account for incident flux, cell scattering, self-shielding, and detector responses. Finally, the elastic intensity of each sample relative to a given temperature was normalized with respect to the data collected at the lowest measured temperature (20 K). Since an average transmission of ∼91% was obtained, we neglected the multiple scattering contribution.

RESULTS AND DISCUSSION

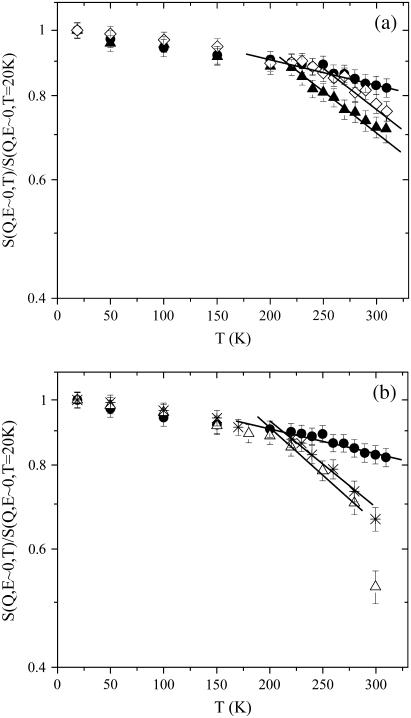
In Fig. 1 we plotted the elastic intensities, integrated over a range of small Q values, as a function of the temperature for all the measured samples (0.3 Å⁻¹ < Q < 1.6 Å⁻¹, with a corresponding average wave-vector transfer Q_av = 1.0 Å⁻¹). In the small Q limit (〈u²(T)〉_totQ² < 1), Eqs. 1–3 lead to S(Q, E ∼ 0) = 1 − Q²(〈u²(T)〉_G + 〈u²(T)〉_c), then the departure from unity gives a tentative measure of the protein mobility. The intensity profiles result in being noticeably affected by the water content. Above a certain temperature the elastic intensity of hydrated samples is definitely lower than that of the dry sample. The temperature at which the departure from the dry curve occurs lowers with increasing w, in particular in the hydration degree range 0w ÷ 0.4w (see panel a), whereas for higher hydration degrees the differences between the experimental data are less marked (see panel b). A closer inspection of this departure will be done below on the basis of the double-well model. Nevertheless, this behavior is qualitatively consistent with MSD of increasing amplitudes from the dry to the most hydrated sample.

FIGURE 1.

Normalized incoherent elastic intensities as a function of T integrated over a small Q-range (0.3 Å⁻¹ < Q < 1.6 Å⁻¹, with a corresponding average wave-vector transfer Q_av of 1.0 Å⁻¹). (a) Lysozyme in glucose at 0w (•), 0.15w (⋄), 0.4w (▴). (b) Lysozyme in glucose at 0w (•), 0.6w (*), and 0.7w (▵). Solid lines are guides for the eye.

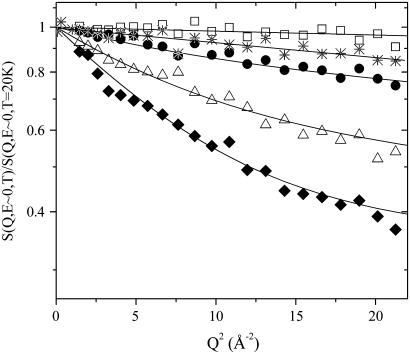
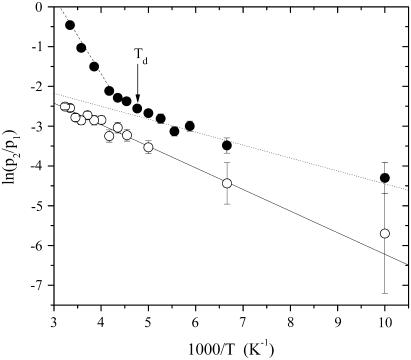
The dependence of the elastic intensities from temperature is shown in Fig. 2, where the S(Q, E ∼ 0, T) versus Q² in the wide investigated Q-range are reported for lysozyme in glucose at 0.4w, at five different temperatures. As emphasized by the logarithmic scale, at 100 K the data exhibit a Gaussian-like trend. When temperature increases, already at 150 K, a departure from such Gaussian behavior becomes more and more evident, resulting in a nonlinear trend of the data. In the past the protein dynamics in the picosecond timescale was considered mainly as harmonic for temperatures lower than the dynamical transition temperature T_d (13). However, recent MDs simulation (51), NMR (52), and neutron scattering (14) studies showed that even below T_d there exists a nonnegligible anharmonic contribution, which comes principally from reorientation motions of methyl groups (14,52). In this alternative description, purely vibrational motions take place only for temperatures up to ∼100 K. Then, when we applied Eq. 1 to fit the measured elastic intensities, we estimated the Gaussian contribution from the slope of 〈u²(T)〉_G versus temperature till 100 K. The fitting procedure directly provides the occupation probabilities ratio p₂/p₁ as a function of T, which quantifies the ability of mobile protein protons to jump from the ground to the excited state. As shown in Fig. 3, the trend of p₂/p₁ for the dry sample can be well described with a single Arrhenius function p₂/p₁ ≈ exp(−ΔG/RT) starting from ∼100 K up to room temperature, where ΔG = ΔH − TΔS is the free energy change due to the jump, ΔH = 4.0 ± 0.5 KJ/mol and ΔS/R = 1.0 ± 0.5 are the corresponding enthalpy and entropy change, respectively. Such an Arrhenius trend suggests that, even in the case of lysozyme embedded in a pure glucose matrix, there is an onset of anharmonicity already at low temperature where the excited state of the double-well begins to be occupied. Methyl-bearing side chains motion makes a significant contribution to the lysozyme neutron spectra because ∼26% of all the nonexchangeable H atoms in lysozyme are on methyl groups. On these grounds, the noticeable departure from the harmonic behavior observed at ∼100 K in lysozyme embedded in glucose can be mainly ascribed to the dynamical activation of methyl groups. Actually, the double-well model gives a schematic view of all the protein relaxation processes (53), even of those originating from protons not belonging to methyl groups, that may be of the order of 20–30% of the total anharmonic contribution, as it happens in dry protein powders (14). In this context, an estimate of the mean spatial extent over which thermal fluctuations take place is the value we found for d = 1.1 ± 0.2 Å, which is nearly constant as a function of the temperature and of the hydration degree. This value can be related to side chains torsional motions, involving or not methyl groups (6,36).

FIGURE 2.

Normalized incoherent elastic intensities versus Q² of lysozyme in glucose 0.4w, at five different temperatures: 50, 100, 150, 240, and 280 K, from top to bottom. Solid lines are fits to Eq. 1.

FIGURE 3.

Occupation probabilities ratio p₂/p₁ for lysozyme in glucose at 0w (○) and lysozyme in glucose at 0.6w (•) with solid, dotted, and dashed lines representing the Arrhenius-like trends fitted as described in the text. The solid arrow indicates the dynamical transition temperature T_d for the sample at 0.6w, as estimated from temperature where the p₂/p₁ ratio deviates from the low-temperature Arrhenius trend (see the text).

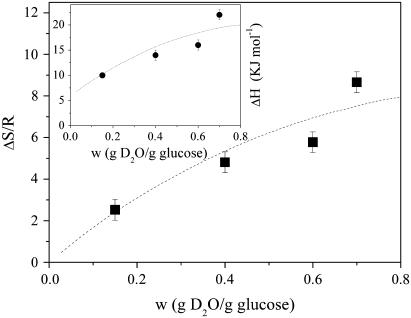
At variance with the dry case, the p₂/p₁ ratio of hydrated samples shows the existence of two different Arrhenius-like trends, as is shown in Fig. 3 for lysozyme in glucose at 0.6 w sample. The first one describes the p₂/p₁ low-temperature region above ∼100 K and is characterized for all the water contents by values of ΔH = 3.0 ± 0.5 KJ/mol and ΔS/R = 1.0 ± 0.5 quite similar to the dry case, thus suggesting that it is related to the methyl group rotation process. At a certain temperature p₂/p₁ begins to deviate from this low-T curve, then a second Arrhenius trend is needed to represent the ratio up to 320 K. This behavior seems to indicate the onset of a second anharmonic process corresponding to the protein dynamical transition. We take as operative definition of T_d the temperature where the p₂/p₁ ratio deviates from the low-temperature Arrhenius trend, as illustrated in Fig. 3. More in particular, T_d is fixed as the first experimental point which departs from the Arrhenius trend by more than the root MSD of the p₂/p₁ values with respect to the same curve. The enthalpy and the entropy change we estimated for the second Arrhenius trend, which are shown in Fig. 4 as a function of the water content, are in general much higher than the low-temperature values. This is consistent with the activation of a dynamical process quite distinct from methyl group reorientation. The enthalpy asymmetry to be overcome during the protein fast fluctuations increases with w, attaining a value of 22.1 ± 0.5 KJ/mol. To explain this trend, we may suppose that, when the water content gets higher, the number of hydrogen bonds per mole of hydrogen atoms in the matrix also increases. This makes the motion of surface protein side chains that have to break an increasing number of hydrogen bonds more difficult, i.e., overcome progressively larger energy barriers. On the other hand, the trend of the excess entropy, which increases with hydration up to ΔS/R = 8.2 ± 0.5 counterbalances this effect. The entropic contribution quantifies the excess of configurations accessible to H atoms via jumps from the ground to the excited state, within the double-well model schematization. From the increase of ΔS/R we can infer that the addition of water makes accessible to the protein side chains a higher number of substates, thus contributing to the plasticization of the whole biomolecule.

FIGURE 4.

Entropy change as a function of the water content for the anharmonic process taking place at the dynamical transition temperature. The dashed line is a guide for the eye. (Inset) Enthalpy change as a function of the water content for the anharmonic process taking place at the dynamical transition temperature. The dashed line is a guide for the eye.

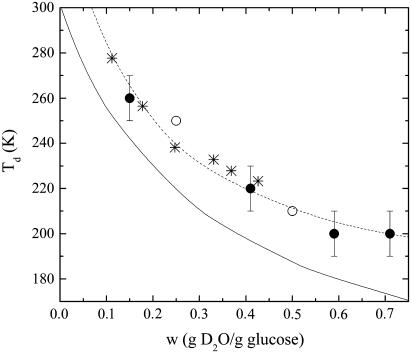
The dynamical transition marks the onset of new anharmonic degrees of freedom beyond the mobility of methyl groups. These new degrees of freedom show a behavior that depends on the composition of the external environment. Fig. 5 shows that the T_d estimated for lysozyme in glucose-water samples may be changed in the investigated water content range by ∼60 K. Of course there is a certain arbitrariness in the definition of T_d, as the dynamical transition appears as a continuous variation of p₂/p₁ as a function of the temperature. However the reliability of this definition comes also from the fact that the behavior of T_d versus w is consistent with the departure of the elastic intensity of the hydrated samples from the dry sample that can be observed in Fig. 1. In the same figure we report for comparison also the dynamical transition temperatures relative to glucose-water mixtures (at 0.25w and 0.5w) (54), derived as well from elastic neutron scattering data, and the temperatures T_c where the molecular mobility of glucose-water systems undergoes a further transition above T_g (49) as a function of w. Such a temperature T_c has been also put in relationship with the so-called critical temperature predicted by the idealized mode coupling theory, where spontaneous breaking of ergodicity occurs (55). More in detail, the T_d trend for lysozyme embedded in glucose-water matrices almost superimposes to T_c values of the homologous glucose-water mixtures. This strikingly close resemblance suggests that the lysozyme dynamical transition is strongly affected by the critical behavior of the surrounding glucose-water glassy matrix and that the main anharmonic onset of protein motions in the picosecond timescale takes place only above T_c, where the solvent is able to sustain protein fast fluctuations. We may then speculate that the solvent has a vital role in promoting the lysozyme internal dynamics, finally allowing the enzyme functional rearrangements (14). This is in agreement with what has been found for lysozyme embedded in glycerol-water matrices (36) and is consistent with the hypothesis of the protein dynamics as slaved to the environment (13).

FIGURE 5.

Dynamical transition temperatures for lysozyme embedded in glucose-water matrices (•) and for glucose-water matrices (○) as a function of the water content, obtained from neutron scattering spectroscopy (this work and Di Bari et al. (54)), as described in the text. To approximately account the uncertainty in the determination of T_d, the temperature step between the experimental points has been taken as error bar. For comparison, the critical temperatures T_c of glucose-water mixtures (*) obtained from ¹H-NMR measurements (49) are also reported. The continuous line represents the glass transition temperatures of glucose-water systems determined through differential scanning calorimetry (32) and dielectric relaxation technique (62). The dashed line is a guide for the eye.

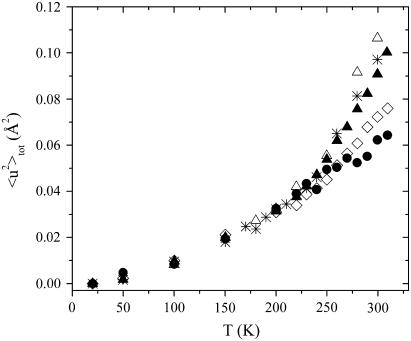
The total MSD 〈u²〉_tot calculated from Eq. 3 are shown in Fig. 6 as a function of T for all the samples. Equation 3 clearly suggests that both the amplitude and the temperature behavior of 〈u²〉_tot are strictly related to the occupation probabilities p₁ and p₂, thus sharing features with the p₂/p₁ behavior. A linear temperature dependence for 〈u²〉_tot was found at low T, where the main contribution is provided by the vibrational term 〈u²〉_G. At ∼100 K, a first onset of anharmonicity takes place in all the samples, regardless of water content, consistent with methyl group rotation. Then a second dynamical transition, observed only in the hydrated lysozyme-glucose systems, occurs at the previously estimated temperature T_d. As it is visible in Fig. 5, T_d attains lower and lower values when water content increases, coherent with the definitively plasticizing role of hydration. More in detail, in the T < T_d range the total MSD show comparable magnitudes for all the samples, whereas for T > T_d they clearly get larger and larger with the water content at any temperature. The addition of water has the macroscopic effect to increase the liquid-like nature of the whole molecular environment, thus supporting a larger mobility of the solvent-exposed protein H atoms. Thus, the trend of 〈u²〉_tot shows that the magnitudes of the protein fluctuations, particularly above the dynamical transition, seem to be driven by the physical liquid-like character of the enclosing molecular environment.

FIGURE 6.

Total MSD versus T for all the investigated samples. Symbols are the same as Fig. 1.

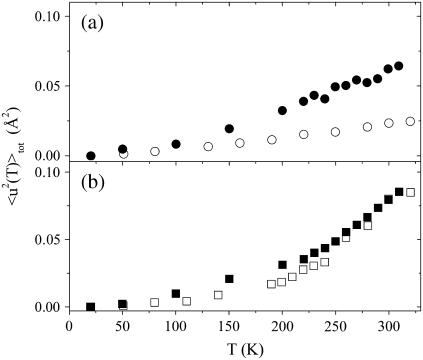
To better investigate the coupling degree between solvent and protein dynamics, we made a comparison of the MSD of lysozyme embedded in the glucose-water matrix with those of the matrix alone taken from Di Bari et al. (54). In that work, the authors investigated glucose-D₂O mixtures at three w values (0, 0.25, and 0.5) at the same instrument, operative conditions, and temperature range as this article. Also the data analysis was carried out by applying the double-well model to the elastic intensities after the normalization to the data at T = 20 K. Fig. 7 a shows that the total MSD of lysozyme embedded in glucose are larger than those of pure glucose. This different dynamical response versus T indicates that the intrinsic dynamics of the nonexchangeable hydrogen atoms, mostly located in the biomolecule core and possibly related to methyl group reorientations, is much more activated than that of the pure glucose matrix. This behavior is quite in agreement with theoretical (3) and experimental (56,57) results, which suggest that internal protein motions do not vanish even with rigid surroundings, becoming independent of the solvent dynamics above a critical solvent viscosity. When the solvent mobility decreases, the protein motions in the core appear to be rather decoupled from the surrounding environment (3), as the relaxations of the neighboring environment become too slow compared to the protein intrinsic dynamical processes, i.e., to protein methyl group reorientation.

FIGURE 7.

Comparison between the 〈u²〉_tot of lysozyme in glucose-made solvent and of the homologous solvent. (a) Total MSD of lysozyme in glucose (•) and glucose (○) (54). (b) Total MSD of lysozyme in glucose at 0.25w (▪ and glucose-D₂O at 0.25w (□) (54). The former are obtained by linearly interpolating the 〈u²〉_tot of the two measured samples at 0.15w and 0.4w at all the investigated temperatures.

Further information on the role of the solvent is given in Fig. 7 b by the comparison between lysozyme in glucose at 0.25w and glucose-D₂O at 0.25w from Di Bari et al. (54). The total MSD of the protein were estimated by interpolating the 〈u²〉_tot of the two samples at 0.15w and 0.4w at all the investigated temperatures. In this case the MSD of the embedded protein are quite similar to those of the mixture. As we cannot exclude systematic errors due to interpolation and minor differences between this data treatment with that of Di Bari et al. (54), we prefer to not discuss the details of the plot. Nevertheless, Fig. 7 b suggests that at 0.25w the dynamics of the protein and that of the matrix around the protein surface is quite coupled. Addition of water could contribute to establish new dynamical connections between the protein side chains and the matrix network at the interface, which in turn propagate to the protein inner molecular groups. With this respect, Figs. 5–7, taken together, suggest that the protein internal dynamics is effectively driven by the surrounding matrix relaxations only in presence of even small water contents when the environment approaches a liquid-like character.

Finally, we focused on the important aim of characterizing the protein average flexibility at physiological temperatures, i.e., in the anharmonic regime. As previously said, in terms of the double-well model, the protein configurational picosecond fluctuations are represented by the second contribution in Eq. 3. At sufficiently high temperatures, the confining conformational space accessible to protein atoms can schematically be described in terms of a harmonic average potential V(r) = br²/2, so that we may write (13,16)

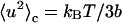(4)

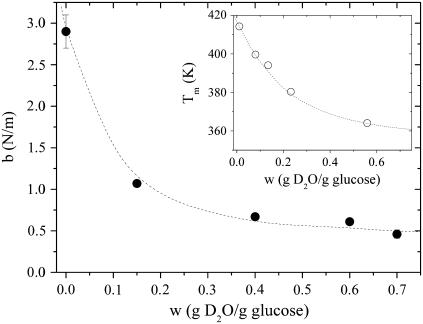
The parameter b provides a measure of the protein rigidity, as it quantifies the linear response of protein fast fluctuations versus T, sampled with this experimental time resolution. If Eq. 4 is used to describe the 〈u²〉_c trend above the protein dynamical transition, b can be directly calculated. A similar approach, where the protein dynamical features are described in terms of an effective force constant, has been already proposed elsewhere (8,58). Fig. 8 shows that the protein rigidity exhibits a sharp decrease with increasing water content and reaches a nearly stable value of ∼0.5 N/m for the more hydrated samples. Such an asymptotic value is somewhat higher than the rigidity estimated for lysozyme in glycerol-water mixtures, i.e., ∼0.39 N/m (59) and for hydrated lysozyme powders at 0.4w, for which a value around 0.35 N/m was obtained (16). It has been recently proposed that flexibility is related to protein thermal stability (8,60). In the inset of Fig. 8 it is reported the melting temperature T_m of lysozyme embedded in sucrose-water mixtures as a function of the water content (61). This trend can be reasonably supposed to be similar to the melting temperatures of lysozyme in glucose-water solutions, which at the best of our knowledge are not available. The T_m values, which quantify the protein thermal stability, strongly decrease as the moisture content increases. Thus a relationship of direct proportionality seems to exist between the b calculated for our samples and the T_m plotted in Fig. 8. This comparison suggests that stiffer systems are characterized by a greater thermal stability, in agreement with the results found for lysozyme in glycerol systems (59).

FIGURE 8.

Protein rigidity b versus w as obtained from Eq. 4. (Inset) Melting temperatures T_m for lysozyme in sucrose-water mixtures as a function of the water content (61). The dashed lines are guides for the eye.

CONCLUSION

Through elastic incoherent neutron scattering technique we studied the dynamics of lysozyme in the picosecond timescale at the atomic level, as affected by the presence of the external matrix composed by a glucose-water mixture. This environment can be considered as a prototype of bioprotectant glass. The protein dynamics is characterized by two different anharmonic processes. The first one, which takes place at ∼100 K, is attributed to the onset of methyl group reorientations. Then, at a higher temperature T_d, the activation of additional degrees of freedom is the signature of the so-called protein dynamical transition. This latter phenomenon seems to be piloted by the environment which, as hydration increases, is more and more dynamically coupled with the protein. The comparison of the protein dynamical response to the temperature variation with the thermal stability, as quantified by the melting temperature, suggests that these properties are connected. We may argue that, as the protein dynamics is piloted by the external matrix relaxations, those relaxations will also determine the thermal stability of the biomolecule.