Testing Simplified Proteins Models of the hPin1 WW Domain

Abstract

The WW domain of the human Pin1 protein for its simple topology and large amount of experimental data is an ideal candidate to assess theoretical approaches to protein folding. The purpose of this work is to compare the reliability of the chemically based Sorenson/Head-Gordon (SHG) model and a standard native centric model in reproducing, through molecular dynamics simulations, some of the well known features of the folding transition of this small domain. Our results show that the Gō model correctly reproduces the cooperative, two-state, folding mechanism of the WW-domain, while the SHG model predicts a transition occurring in two stages: a collapse, followed by a structural rearrangement. The lack of a cooperative folding in the SHG simulations appears to be related to the nonfunnel shape of the energy landscape featuring a partitioning of the native valley in subbasins corresponding to different chain chiralities. However, the SHG approach remains more reliable in estimating the Φ-values with respect to Gō-like description. This may suggest that the WW-domain folding process is stirred by energetic and topological factors as well, and it highlights the better suitability of chemically based models in simulating mutations.

INTRODUCTION

The WW domains are a family of fast-folding, compact, modular domains featuring a triple-stranded, antiparallel β-sheet owing their name to the presence of two highly conserved Triptophanes (W). Recent studies (1) suggested that these domains may fold at a rate close to the speed limit for β-sheet formation, offering the opportunity to investigate the pathways of β-sheet kinetics (2). In particular, the human Pin1 protein WW domain, due to the availability of several structural (3,4), thermodynamical, and kinetic (5) experimental data, represents an excellent target to test computational techniques and theoretical approaches.

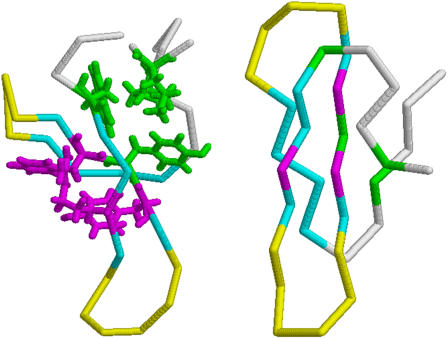
The structure of this domain, resolved through NMR (4) and x-ray diffraction (3) (Fig. 1), is characterized by hydrophobic clusters providing the largest contribution to the thermodynamic stability (5). Cluster 1 (CL1) involves residues Leu⁷, Trp¹¹, Tyr²⁴, and Pro³⁷, the second cluster (CL2) comprises Tyr²³, Phe²⁵, and Arg¹⁴. The stability of the molecule also derives from a network of hydrogen bonds whose central element is the highly conserved Asn²⁶ located on strand β₂ and acting both as donor and acceptor in bonds with Pro⁹, Trp¹¹, Ile²⁸, and Thr²⁹, thus linking strands β₁ and β₃. Two loops are present: Loop I (L1) plays a key role in substrate recognition (3), since it binds to the phosphate of the pS-P motif of the Proline-rich ligands; Loop II (L2), on the other hand, gives an important contribution to thermal stability (5). Thermal denaturation experiments (5) and simplified statistical physics approaches (6) have shown that the Pin1 WW domain folds following a cooperative two-state mechanism at the temperature T_M = 332 K. The mutagenesis analysis performed by the same authors (5) identified the mutations on Ser¹⁶, Ser¹⁸, and Ser¹⁹ in Loop I as maximally destabilizing for the transition state, so that the formation of L1 appears to be the rate-limiting step in the folding/unfolding process. Loop II (L2) is involved in the formation of the transition state only at high temperatures (5). Due to the ability of inducing conformational changes in Proline-rich, phosphorylated substrates, Pin1 is a potential regulator of the cell cycle, and may be involved in pathologies like Liddle's syndrome, muscular dystrophy, and Alzheimer's disease (7,8).

FIGURE 1.

Backbone representation of the NMR structure of Pin1 WW domain (PDB No. 1NMV, Left) and simulated structure Γ₀ (Right). Residues in the three β-strands are colored in blue, those belonging to loops L1 and L2 in yellow. The side chains of residues participating in CL1 (Leu⁷, Trp¹¹, Tyr²⁴, Pro³⁷) are shown in green stick representation, whereas those participating in CL2 (Arg¹⁴, Tyr²³, Phe²⁵) are represented through magenta sticks. Figures were drawn with RASMOL.

The aim of this work is the comparison of two off-lattice protein descriptions: the Gō-model (9), which customarily allows our studying the influence of the native state structure on the folding process, and a model proposed by Sorenson and Head-Gordon (10,11) (the model hereafter referred to as SHG), mainly based on the primary and secondary structural information. The conceptual justification of topology-based or native centric models relies on the observation that the topology of native states can play a crucial role in selecting some features of the folding mechanism (12–15). The main experimental finding supporting the above statement can be summarized (16) as 1), the similarity shared by transition-state conformations and folding mechanisms of proteins having structurally related native states despite their low sequence homology (17–19); and 2), the correlation that certain simple topological properties, such as contact order, may have with protein folding rates (20,21).

The Gō-force field is independent of the amino-acid sequence, and it requires the knowledge of the tertiary structure of native states to identify native interactions. Accordingly, the native centric approach cannot be used for ab initio predictions of native folds, even if recent works (22–26) provide growing evidence that it can be confidently used for the characterization of transition states of real small, fast-folding (submillisecond) (27,28) proteins that are characterized by a low level of energetic frustration. However, topological models might not correctly reproduce the folding process when chemical interactions play a relevant role. The SHG model, which is instead based on the chemical and physical properties of amino acids such as hydrophobicity, is, in principle, better applicable to proteins with a higher level of energetic frustration. Moreover, requiring the knowledge of primary and secondary structures only, the model has a greater predictive power, and in this sense, could be considered closer to an ab initio representation. The above arguments motivate a detailed comparison between the two protein models to assess their applicability and potentialities in the study of biomolecules.

THEORY AND METHODS

When native state topology plays the relevant role in driving the folding process, many molecular details of protein structures can be mapped onto simplified coarse-grained models encoding the overall topology through knowledge of the native contacts. These models, neglecting side chains and peptide groups, reduce a protein chain to its backbone, where amino acids are assimilated to beads centered on their α-carbon atoms. The Gō energy function, mimicking a perfect funnel landscape, assigns to the native state the lowest energy by simply promoting the formation of native interactions. Here we employ the force field proposed by Clementi et al. (22), with distance cutoff R_c = 6.5 Å (29) to identify native contacts in the structure 1NMV.pdb. A native contact means that the distance, R_ij, of C_α atoms relative to residues i and j (|i – j| ≥ 3) is less than R_c in the native state. This pair undergoes an attractive LJ-interaction

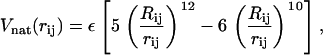(1)

with equilibrium distance R_ij. When two residues are not in a native contact (R_ij > R_c), they interact through a repulsive potential

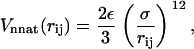with σ = 4.5 Å. These nonnative interactions, besides ensuring the self-avoidance of the chain, generally enhance the cooperativity of the overall folding process (30). A further bias toward the native secondary structure is introduced through a bending and a dihedral potential. The former is modeled as an harmonic function and allows only small oscillations around the native angles (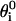) formed by three consecutive residues

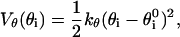with harmonic constant k_θ = 20ε. The most important determinant of the secondary structure is the dihedral potential arising from the torsional energy. Each dihedral angle, identified by four consecutive beads, contributes to the potential with the terms

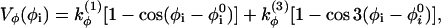where 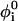is the value of angle i in the native structure, k_φ(1) = ε and k_φ(3) = 0.5ε. Finally, consecutive residues interact with each other through the potential harmonic in their distance r_{i, i+1},

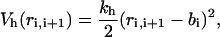(2)

which maintains the chain connectivity, with b_i being the native bond-length and Therefore, the global Gō-potential reads

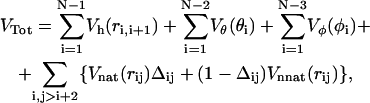where Δ_ij = 1 (0) if the contact is native (nonactive). Gō models of the type just outlined may produce a gradual folding behavior incapable of reproducing the typical kinetic cooperativity of two-state folders. Experimental studies suggest (31,32) that the origin of cooperativity lies in specific interactions appearing only after the assembly of nativelike structures. These particular interactions can be modeled by imparting an extra energetic global stabilization to the native state (33) through a different analytical form of the energy function when the chain visits the native basin. In this work we need to implement the rescaling method to make the folding transition highly cooperative, in agreement with the experiments on the WW domain. The interaction forces on the residues are thus computed according to the rule

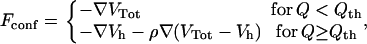(3)

where Q is the fraction of formed native contacts and ρ = 2 is the scaling factor. The force rescaling determines a higher free energy barrier between the folded and unfolded states in correspondence to the folding temperature, which results in a higher cooperativity. Therefore, the residence times in the folded and unfolded state are expected to be significantly longer.

The SHG model is an off-lattice minimal model that generalizes a previous model introduced by Thirumalai and co-workers (34,35). This approach represents α-carbons with beads of three possible types: hydrophobic (B), hydrophilic (L), and neutral (N), according to Table 1. The driving force responsible for the collapse onto a compact structure is the attraction between B-beads, whereas the repulsion between L and N beads determines the rearrangements of the compact structure into the native topology. The long-range interaction between residues, which may be far apart in sequence space, is modeled through the potential

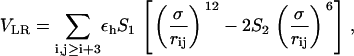(4)

where ε_h (1.65 Kcal mol⁻¹ see below) sets the energy scale and σ = 4.0 Å. The attractive forces between hydrophobic residues is attained by setting S₁ = S₂ = 1 for BB pairs, while the interactions involving the LL and LB pairs are characterized by S₁ = 1/3 and S₂ = −1. This interaction is repulsive and the r⁻⁶ term, which accounts for the hydration shell around the hydrophilic residues, makes the potential longer-ranged than the usual r⁻¹². The forces involving neutral residues are also repulsive and amount to an excluded volume potential by setting S₁ = 0 and S₂ = 0. The secondary structure arises as a result of bending and dihedral interactions, which subrogate side-chain packing and hydrogen-bonding. The analytic expression of the dihedral potential is

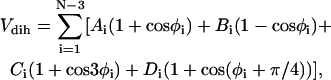(5)

where φ_i indicates the angle between the two adjacent planes identified by the positions of four consecutive beads. The information on secondary structures is systematically stored in the coefficients A, B, C, and D, which determine a bias on the angles reflecting the propensity of residues to form a specific secondary motif. Indeed, each dihedral in the chain is defined to be either Helical (H: A_i = 0, B_i = C_i = D_i = 1.2ε_h), or Extended (E: A_i = 0.9ε_h, C_i = 1.2ε_h, B_i = D_i = 0), or Turn (T: A_i = B_i = D_i = 0, C_i = 0.2ε_h). Therefore, the primary structure must be complemented with the auxiliary sequence of E,H,T symbols assigning the appropriate set of coefficients. The decoupling between primary and dihedral sequence, not present in similar models (40,41), increases the possibilities in the modulations of relative strengths between local and nonlocal interactions, which results in a finer structural tuning (11). The Head-Gordon force field is completed by a bond-angle interaction modeled as a harmonic potential

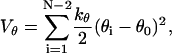(6)

with a constant k_θ = 20ε_h/(rad)², so that large deviations from the equilibrium value θ₀ = 1.8326 rad are unlikely, and bond angles result basically fixed. Also in this model, stiff springs (2) with equilibrium distance r₀ = 3.8 Å, maintain the chain connectivity mimicking the presence of covalent peptide bonds between successive amino acids. This stiff interaction allows us to keep the bond-length approximately fixed, while being less computationally demanding than the RATTLE algorithm used in previous works (34,36) to enforce fixed bond-lengths. The SHG model retains only the minimal number of elements needed to capture the essential features of protein molecules; however, some strong determinants such as hydrogen-bonding and side chains are missing. These limitations should be compensated through a design strategy (37) for optimizing the sequence. Here, we used the sequence LBBNN-BLBLB-NLNNN-LBBBB-LLNNL-BNBBL-LBNNL proposed in Brown et al. (11) for the hPin1 WW domain and designed via a threading approach based on energy-gap maximization (42). The secondary structure propensity, selecting the nativelike dihedral angles, is encoded in the auxiliary sequence TTTTT-EEEEE-TTTTT-TEEEE-TTTTT-EETTT-EET, built directly through the information contained in the PDB file 1NMV.pdb. To control the temperature, we performed constant temperature MD simulations within the isokinetic scheme (38) using dimensionless quantities. The temperature was measured in units of ε_h/R = 1070.96 K, time in units of t = σ(ε_h/M)^1/2= 4.44 ps (σ = 4.0 Å is the equilibrium length of Lennard-Jones interactions, M = 110 is the average amino-acid mass), energy in units ε_h, specific heat in units R = 1.9872 × 10⁻³ Kcal mol⁻¹ K⁻¹, and the radius of gyration in units σ. The energy scale ε_h was set to 1.65 Kcal mol⁻¹ to reach a denaturation temperature compatible with experimental data (5) T = 332 K. For the Gō-model, the same units apply, except for the energy scale set to ε = 0.66 Kcal mol⁻¹. During the simulations, we monitored the difference from the native state or reference state through the overlap Q, representing the fraction of formed native contacts as

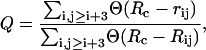where the sum runs over all pairs of native contacts, r_ij and R_ij are the distances of residues i and j in the current and in the reference conformation, respectively, and Θ(u) indicates the unitary step function. A value Q ≅ 1, indicates that the conformation is nativelike, while values close to zero refer to denatured states. We also considered, as further reaction coordinates of the folding/unfolding process, the gyration radius and the root mean-square distance (RMSD) between the current and reference conformations after an optimal superposition performed according to Kabsch's algorithm (39). The thermodynamics of the folding/unfolding transition was obtained via the weighted histogram method (40,41). This technique offers the possibility to gain a better sampling of the conformation space than by ordinary methods. The procedure consists in storing bidimensional histograms of the number of contacts N(E, Q) as a function of the energy E and coordinate Q at each temperature run. Such histograms are then optimally combined to reconstruct the best estimate of the density of states Ω(E, Q), which, in turn, will be used to compute the thermodynamics of the system. The knowledge of Ω(E, Q) can be also employed to derive the probability that, at temperature T, the protein states are characterized by energy E and reaction coordinate Q,

where β = 1/RT and F is the total free energy of the system coming from the normalization of P_T(Q, E). The sum of P_T(E, Q) over all possible energies E provides the probability for the system to have a specific value Q at temperature T, which, in turn, by reversing the Boltzmann's weight, gives the potential of mean force along the reaction coordinate Q,

TABLE 1.

Translation of three-letter code of the 20 natural amino acids into the “three-flavor” code (11)

A.A.	F	A.A.	F	A.A.	F	A.A.	F
Ala	B	Met	B	Gly	N	Asn	L
Cys	B	Val	B	Ser	N	His	L
Leu	B	Trp	B	Thr	L	Gln	L
Ile	B	Tyr	B	Glu	L	Lys	L
Phe	B	Pro	B	Asp	L	Arg	L

We computed the specific heat profile as a function of the temperature: its peaks and shoulders locate those temperatures at which the main structural chain rearrangements occur. A detailed characterization of the folding/unfolding process can be obtained by measuring the probability of native contact formation as the temperature is varied, as

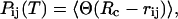where the average 〈···〉 is taken over time, assuming the dynamics to be ergodic. The value P_ij(T) typically features a sigmoidal shape, keeping values close to 1 at low temperatures and decreasing to zero at high temperatures. The knowledge of probabilities P_ij(T) allows for a classification and ranking of native contacts according to their thermodynamic relevance (42–44) thus suggesting possible reaction pathway, key residues (45), and folding nucleus (46).

Φ-values

The comparison of the Gō and SHG models on the WW domain provide the opportunity to study the relevance of topological versus energetic frustration (47) in the folding mechanism. This can be accomplished by Φ-values computation and by the further comparison with experimental data. The Φ-values (15) measure the perturbation effects of a site-directed mutation which, by altering the free energy difference among native, transition, and unfolded states, may affect the thermodynamics and the kinetics of the reaction. A prevalence of topological or energetic frustration may be argued from a better fit with the experiments of the Gō-derived or SHG-derived Φ-values, respectively (22,45). The Φ-values can be computed through a kinetic approach from the folding and unfolding rates of the mutant and wild-type protein (48),

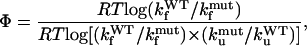(7)

where R is the ideal gas constant, T is the absolute temperature, and k_f and k_u are the folding and unfolding rates, respectively. The denominator of the above expression is just the total stability change ΔΔG⁰. The use of Eq. 7 is computationally demanding, as it requires a simulation for each mutation. This motivates the use of a thermodynamic strategy for the Φ-value evaluation (48),

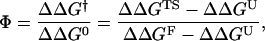(8)

where ΔΔG^† is the change in stability of the free-energy barrier between the native and denatured state. Equation 8 is equivalent to Eq. 7 when Kramer-like theory applies (47).

If the effect of the mutations is sufficiently small, then, following Clementi et al. (22), the Φ-values can be derived by a free-energy perturbation approach,

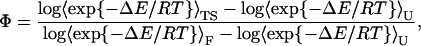(9)

where the Boltzmann factors depend on the energy difference between the mutant and the wild-type (WT) and the averages are computed over WT-conformations of the folded (F), transition state (TS), and unfolded (U) ensembles.

In this article, the Φ-values are computed according to Eq. 9, using a method developed in Clementi et al. (22) that can be summarized in the following steps:

1. Determination of the folding temperature T_f from the specific heat plot.

2. Analysis of the free energy profile at temperature T_f plotted as a function of a suitable reaction coordinate. The free energy profile of a two-state folder typically shows a double-well shape, allowing us to choose three windows of the reaction coordinate identifying the folded, transition state, and unfolded ensembles, respectively.

3. Dynamic simulation at T = T_f and storage of conformations belonging to the F, TS, and U ensembles.

4. Choice of mutations and computation of free-energy perturbation Φ-values.

Structural information about the native-like-ness of the transition state was also gained from the so-called structural Φ-values (49),

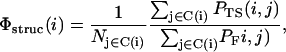(10)

where P_F(i, j) and P_TS(i, j) are the frequencies of the native contact i–j in the folded and transition ensembles, respectively, and the sums run over the set C(i) of native contacts in which residue i is involved.

RESULTS

We report on the thermodynamic properties and contact formation patterns observed in unfolding/refolding equilibrium MD simulations of the WW domain. We first analyze the simulations based on Gō-model and then we discuss the corresponding scenario in the SHG-model approach. Since the implementation of the SHG model requires a well-designed sequence, we employed the 6–40 truncated sequence already optimized in Brown et al. (11). For the sake of a consistent comparison with Gō-simulations, the corresponding fragment was extracted from the NMR structure stored in the PDB file 1NMV (4).

Gō-model

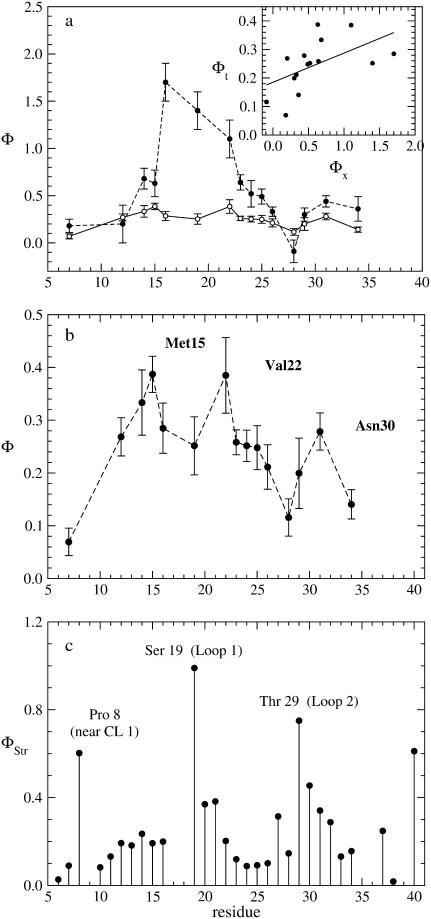
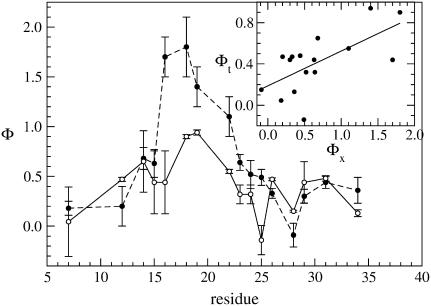
A folding simulation was performed through a gradual cooling of a random coil structure from a temperature T = 1.5 down to 0.5 in 40 steps. The specific heat profile, Fig. 2, is characterized by a single narrow peak at temperature T_f = 1.0, suggesting a possible two-state process. The same conclusion can be drawn from the ratio of van 't Hoff over the calorimetric enthalpy changes amounting to 0.74 without and 0.99 with standard baseline subtraction (50). The folding/unfolding processes are reversible in temperature, as shown by the agreement between specific heat plots. The other observables used to characterize the folding transition such as, RMSD, overlap, and gyration radius exhibit an abrupt change in correspondence to the folding temperature T_f (Fig. 3). Free energy profile (Fig. 4) as a function of the overlap, around the folding temperature, clearly features two distinct wells identifying the folded and unfolded ensembles separated by a barrier corresponding to the transition-state conformations. The shape of the free-energy plot suggests a choice of overlap windows for the sampling of conformations in the three ensembles F, U, and TS (see Fig. 4 legend) for the computation of Φ-values (Methods). In Fig. 5 we compare our single-site simulated Φ-values (Eq. 9) with the experimental data by Gruebele (5). In the Gō-like approach, a mutation can be modeled as the removal of a single native contact (22) or in alternative, as an average over all possible removals of contacts involving the same residue. We followed the second strategy, considering only contacts |i – j| ≥ 3. In this scheme, we cannot evaluate Φ-value of Ser¹⁸ because it lacks such contacts. The theoretical Φ-values in Fig. 5 vary in the range [0.0, 0.5], whereas the experimental ones are distributed in a much wider interval. This feature is an expected result of the very limited energetic frustration of the Gō-force fields (47). The discrepancy is reflected by the modest value of the linear correlation coefficient r = 0.54 (see regression line in the Fig. 5 a, inset). Of course we cannot exclude that a possible improvement of Φ-value accuracy might be achieved either by employing other mutation implementations or by using alternative contact maps accounting for the high flexibility of the native structure of peptides and small proteins (51). Despite this not-high correlation, the theoretical Φ-values provide a qualitative indication about the molecule regions that are still nativelike in the transition state. The plot in fact indicates that the sites most sensitive to mutations are those in the region of loops L1 and L2, in agreement with experimental results (see Fig. 5 b).

FIGURE 2.

Heat capacity as a function of temperature in Gō-model simulations: folding (solid), unfolding (dotted). (Inset) Thermal behavior of energy; dotted lines represents quadratic fits of the baselines.

FIGURE 3.

Structural parameters monitored during the Gō-model folding simulations. Triangles are the reduced gyration radius; solid circles indicates reduced RMSD; open circles refer to the fraction of native contacts Q magnified by a factor 4. Each point in the plots corresponds to an average of 6 × 10⁶ conformations sampled every 10³ time-steps. RMSD and Q are computed using the PDB structure as a reference.

FIGURE 4.

Free energy profiles at different temperatures as a function of the overlap Q (lower panel). Vertical lines indicate the boundaries of the sampling windows for F (0.85 < Q < 1.00) U (0.20 < Q < 0.35) and TS (0.60 < Q < 0.65); see text. (Upper panel) Time evolution of Q at the folding temperature T = 1 oscillating between the minima of the free energy wells.

FIGURE 5.

(a) Comparison between experimental (solid circles) and theoretical (open circles) Φ-values restricted to the mutations performed in Jäger et al. (5) except for Ser¹⁸. The Φ-values were computed from the conformations sampled in a Gō simulation at folding temperature using the perturbation method (8). The inset show the linear regression analysis between the two data sets with a correlation coefficient 0.54. (b) Enlargement of theoretical Φ-value shown in a). (c) Structural Φ-values computed from Eq. 10, using the (F) and (TS) ensemble structures. The three peaks in the plot show that the two loops and the first hydrophobic cluster are nativelike in the transition state.

The picture provided by the structural Φ-values (Fig. 5 c) is consistent with that derived from the perturbation method. In fact, in this case, the highest Φ-values also correspond to residues located in L1 (Ser¹⁹), L2 (Thr²⁹), or in the neighborhood of the first hydrophobic cluster CL1 (Pro⁸). The low Φ-values pertain mainly to residues in strands β₁ and β₂, suggesting that these two regions are unlikely to be in contact in the transition state.

SHG-model

Ten independent folding simulations starting from random-coil conformations were performed through a gradual cooling schedule from temperature T = 1.0 to T = 0.01 in 40 steps. The final structures were further relaxed by a steepest-descent cycle until the maximal total force per monomer reached a value smaller than 10⁻⁸ Kcal mol⁻¹ Å⁻¹. We obtained different folds, and chose the conformation with lowest energy (E = −19.0035ε) and lowest RMSD (4.74 Å) from the PDB structure as the reference structure Γ₀ (Fig. 1). However, the simulations revealed also the existence of another degenerate minimum with the same energy and specular to Γ₀ resulting in much higher RMSD.

Despite the large value of RMSD, Γ₀ correctly displays the topology of a triple-stranded, antiparallel β-sheet; this lacks the typical twist of the PDB structure, though, making loop L2 almost perpendicular to loop L1 (see Fig. 1). As a result, the folded structure is much more compact than the real protein and has a much larger number of native contacts (71 vs. 41). The fact that 22 out of the 41 PDB contacts are also present in the folded structure is an indication of the satisfactory structural performance of the SHG simulation.

Structure Γ₀ was then denatured through 10 independent runs with the same but inverse temperature schedule, involving a thermalization stage of 6 × 10⁶ time steps (Δt = 0.005) at each temperature, followed by a run over the same length, where control parameters were measured to assess the unfolding progress. The course of both folding and unfolding simulations was monitored through the analysis of the energy, the specific heat, RMSD from Γ₀, the overlap, and the radius of gyration, R_g.

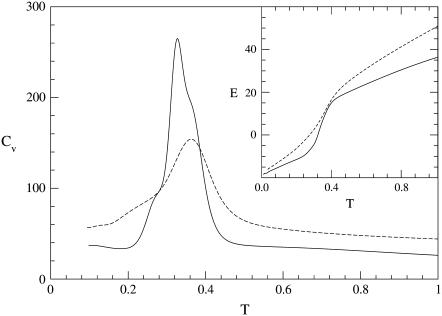
Both the folding and unfolding specific heat plots (Fig. 6) are characterized by the presence of a main peak and a shoulder. The peaks of the folding and unfolding thermograms P_f and P_u are located at T_f = 0.36 and T_u = 0.33, respectively, whereas the shoulders S_f and S_u correspond to T_Sf = 0.24 and T_Su = 0.28. The folding process appears not to be fully reversible, probably due to the fact that the sequence, although designed, is not yet a good folder.

FIGURE 6.

Thermal behavior of heat capacity (main figure) and energy (inset) during unfolding (solid lines) and folding (dashed lines) SHG simulations. The thermodynamic observables have been computed using the weighted histogram method.

The existence of the shoulder in the folding C_v plot is a signature of a noncooperative folding mechanism in which an initial collapse is followed by a structural chain rearrangement, characterized by a significant increase in the number of native contacts unaffecting the overall compactness of the molecule (see Fig. 7). This is confirmed by the thermal fluctuation of the structural overlap

featuring the highest peak, not in correspondence of the main peak P_f but at the temperature T_Sf of the shoulder (inset of Fig. 7).

FIGURE 7.

Noncooperativity of the SHG folding simulation yielding our best final structure Γ₀. After a first collapse, the radius of gyration remains constant, whereas the structural difference from the reference structure 1 – Q keeps on decreasing at temperatures corresponding to the shoulder of the C_V plot signaling a massive structural rearrangement. (Inset) Temperature dependence of fluctuations of the structural overlap. The main peak, located at the same temperature as the heat capacity shoulder, corresponds to the folding temperature.

The marked difference between the folding and unfolding specific heat suggests the opportunity to consider the free energy profiles W_T(Q) to better determine the folding temperature. The profiles (lower panel of Fig. 8) indicate that the transition is characterized by the presence of two wells separated by a barrier and the temperature where these two wells are evenly populated is T = 0.237. This confirms that the peak of C_v is mainly related to the Θ-collapse, whereas the shoulder corresponds to the folding transition. In fact, kinetic simulations at temperature T = 0.237 show that the time evolution of Q(t) exhibit jumps between the two free energy wells (upper panel of Fig. 8). The double-well shape of the free-energy profile again allows us to sample conformations in the folded (F), transition state (TS), and unfolded (U) ensemble used to implement the perturbation technique for Φ-value computation (Methods). The plot in Fig. 9 shows the Φ-values restricted to the set of residues mutated by Gruebele (5). For each site we tested the effect of all the possible single mutations allowed by the model, namely two hydrophobicity shifts and two shifts in the secondary structural bias for each of the two dihedral angles flanking the residue under examination. For each site we chose the least perturbative mutations. Theoretical Φ-values feature two major peaks in correspondence with loop L1 and loop L2, which is a qualitative resemblance with experiments. A more quantitative comparison is provided by the correlation coefficient between theoretical and experimental data amounting to r = 0.65.

FIGURE 8.

Free energy profile as a function of the overlap Q at the folding temperature T = 0.237 (lower panel). The vertical lines mark the boundaries of the Folded (0.78 < Q < 0.90), Transition State (0.53 < Q < 0.61), and Unfolded (0.30 < Q < 0.47) ensembles. The upper panel shows the typical temporal evolution of the overlap in a subinterval of a simulation at folding temperature. The overlap was sampled every 5 × 10³ time-steps.

FIGURE 9.

Experimental (solid circles) and computed (open circles) Φ-values. The Φ-values were computed from the conformations sampled in a SHG simulation at folding temperature using the perturbation method. The two profiles show a qualitative agreement although the correlation coefficient of the regression line (see inset) is r = 0.65.

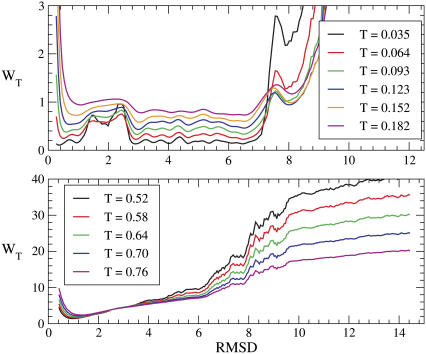
The set of native conformations collected during the kinetic simulation provides a structural characterization of the ensemble F, whose most interesting feature is the clustering of native-basin conformations in two main subsets characterized by nonoverlapping distributions of RMSD from the reference structure Γ₀. This is a further indication of the high level of frustration of the free-energy landscape associated to the sequence, and it is in agreement with the findings by Miller and Wales (52) about the glasslike structure of the energy landscape in a closely related model (35). This partitioning of the native basin is evident in Fig. 10, where we plot the free energy versus the RMSD—a structural indicator more sensitive than the overlap. A finer analysis reveals that the structures in the two subbasins of the native valley correspond to different chiralities but similar energies. The absence of such a partitioning in the same plot for the Gō force field, indicates that this feature is mainly peculiar to the model, rather than to this specific protein.

FIGURE 10.

(Upper panel) Low-temperature free energy profiles of the SHG model as a function of the RMSD from the reference conformation Γ₀. The native valley appears to be partitioned in two main subbasins separated by a barrier. The subbasin corresponding to the RMSD range [0.25–1.00] is populated by conformations with the same chirality as the PDB structure, whereas the subvalley in the range [2.80–6.50] corresponds to the opposite chirality. (Lower panel) Low-temperature free-energy profiles of the Gō model as a function of the RMSD from the native conformation (PDB No. 1NMV). The native valley shows a single basin as opposed to the partitioning in two subvalleys typical of the Gō model.

To clarify how the landscape properties affect the reversibility of the folding process, we studied the folding/unfolding transition from the contact formation probabilities P_ij. In particular, as the plots P_ij(T) are typically sigmoid, a contact can be regarded as broken/formed in correspondence of the temperature, where the absolute value of the slope of the probability curve is maximal. This allows us to identify the contacts whose formation/breakdown occurs at a given temperature.

To analyze the folding/unfolding process, we considered three temperature windows corresponding to different regions of the specific heat plots. The first window (T < 0.15) refers to the pre-transition baseline of the C_v plot, the second window (0.15 ≤ T ≤ 0.30) insists on the region of the shoulder, and the third window (T > 0.30) includes the main peak. The contacts appearing or disappearing in correspondence of the three windows are shown in black, red, and green, respectively, in the contact maps (Fig. 11) summarizing the main events of the pathway. Shaded symbols represent weak interactions with probability of formation below 50% at the lowest simulation temperature T = 0.01.

FIGURE 11.

Contact maps summarizing the folding and unfolding SHG process. The color code identifies three temperature ranges: black, T < 0.15; red, 0.15 ≤ T ≤ 0.30; and green, T > 0.30. Shaded symbols refer to weak contacts with low probability of formation (P_ij < 0.5) at the lowest simulation temperature T = 0.01.

The contact map shows that the first contacts formed during folding are located in the intermediate part of sheet β₁-β₂ and in the region of sheet β₂-β₃ most distant from loop 2. The formation of these contacts is responsible for the collapse of the molecule into a compact but not completely folded conformation. The map also shows that the shoulder of the C_v plot is characterized by the zipping of sheets β₁-β₂ and β₂-β₃ toward loop 1 and loop 2, respectively. During the process there also occurs the locking of β₁-β₃, β₂-tail and head-β₂ contacts (hereafter, the terms head and tail indicate the amino-terminal region Lys⁶-Gly¹⁰ and the carboxy-terminal residues Asn³⁶-Asn⁴⁰, respectively). These contacts are not present in the PDB structure and they arise as a consequence of the higher compactness of Γ₀, so that their formation probabilities are always below 50%. The folding is completed by the appearance of a few contacts between residues very far from each other along the protein chain.

During the unfolding reaction, no native (with respect to Γ₀) contact breaks down in the low-temperature window because the heating schedule enables the protein to escape easily from kinetic traps, making the process much less gradual than folding. This reflects on the smaller number of contacts broken in the shoulder region as compared to the number of contacts formed in the same temperature range during folding. In particular, the cleavage occurs of β₁-β₃, β₂-tail and head-β₂ contacts, whereas the dissolution of the contacts of loop 1 and loop 2 is delayed to the region of the peak of the C_v plot where most β₁-β₂ and β₂-β₃ contacts also disappear.

The comparison of the two contact maps thus reveals that the sequences of the molecular events in the folding and unfolding processes are basically reverse to each other, even if the unfolding is a more abrupt phenomenon occurring in a narrower temperature window.

DISCUSSION

Our results indicate how the different approaches of structure-based and sequence-based description exemplified by the Gō and SHG models are appropriate to simulate complementary features of the folding process. The Gō model, in fact, being based on the influence of the native-state topology on the folding process, is independent from the amino-acid sequence and it completely disregards the chemical properties of the molecule. The SHG model, on the other hand, is a minimal model, where the chemical features of amino acids are partially included, determining the folding driving force.

Our simulations showed that the Gō model with angular bias (22) and rescaling (33) can correctly reproduce the reversible, cooperative, two-state mechanism of folding of hPin1 WW domain (5). The reversibility, indeed, appears from the almost perfect superposition of the C_V plots of folding and unfolding. Several elements, on the other hand, suggest a cooperative, two-state mechanism: the C_V plots show a single sharp peak, the ratio of the van 't Hoff to calorimetric enthalpy is close to 1 (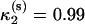) (53), all the indicators used to monitor the similarity with the native state exhibit a sharp sigmoidal thermal behavior, and the barrier between the two free-energy wells at the folding temperature is very high (54,55). The results from the simulation using the SHG model were rather ambiguous. The simulated thermograms featured not only a peak, but also a shoulder at lower temperature. This is the signature of a noncooperative folding involving a collapse into a compact, only partially structured globule, followed by a rearrangement into a native conformation. This scenario is confirmed by the thermal behavior of the structural parameters (overlap, gyration radius, and RMSD from native structure) used to monitor the folding reaction. The results are consistent with the findings by Nymeyer et al. (56) and by Guo and Brooks III (41), in their simulations on the model by Honeycutt and Thirumalai (34). The SHG formulation, although being an improvement of the latter model, still retains some of its drawbacks. Indeed, the conformations of the native ensemble (F), sampled at the folding temperature, can be clustered in two groups with nonoverlapping RMSD distributions and opposite chiralities (57). The existence of two distinct clusters of nativelike conformations can be easily explained by examining the low-temperature free-energy profiles as a function of the RMSD (from reference structure Γ₀): the native basin appears to be partitioned in subbasins separated by barriers. The partitioning of the native basin is likely a feature that the SHG model inherited from the Thirumalai model. Miller and Wales (52), in fact, analyzed the disconnectivity graph of the potential energy surface of Thirumalai's force field, drawing the conclusion that the energy hypersurface is not a single funnel, but it contains low-energy minima separated by high barriers.

Presumably, the reason for the degeneration of the native state of the SHG model relies on the symmetry of the dihedral potential V_φ (Eq. 5). In particular, the sequence designed to represent the hPin1 WW domain, contains only Extended or Turn symbols, so that V_φ is a polynomial in cos(φ) and becomes symmetric for the inversion φ → −φ. The symmetry of the V_φ term, however, is not the only reason for the poor performance of the SHG model. In fact, we find that the energy histograms of the folded- and unfolded-state ensembles are significantly overlapping, thus suggesting the existence of many low-energy, nonnative conformations (41).

We suspect that this is an effect of the only approximated maximization of the energy gap between the native conformation and the decoy set used in the sequence optimization procedure (11). This would call for further refinements of the threading procedure.

Despite the several drawbacks, the SHG model enabled the computation of perturbation Φ-values in qualitative agreement with experimental data. The linear correlation coefficient between theoretical and experimental Φ-values (r = 0.65) is actually better than the one yielded by the Gō simulation (r = 0.54). The explanation of these results must be sought in the partial incorporation of the chemistry in the SHG description. Indeed, real mutations are chemical transformations of the molecule and they are better simulated by a chemically based model such as the SHG rather than by a topological model. In the Gō model, in fact, mutations are generally simulated by the removal of native contacts (22); however, they may affect all the interactions in which a residue is involved. The SHG model, conversely, offers the possibility to treat mutations in a more realistic way because it implements shifts in the hydrophobic character of residues or changes in the secondary structural bias of dihedral angles. Moreover, the better agreement of experimental data with the SHG-computed Φ-values may show that the folding mechanism of hPin1 WW domain is controlled not only by topological but also by energetic factors.

The significant differences, beyond statistical errors, between the Φ-values profiles yielded by the two models, in our opinion, reflect the different strategies upon which the two models are built.

A final issue that deserves some discussion is the quality of the structural prediction using the SHG model. The SHG is a minimal model based on chemical properties of the system and a good outcome of the simulation is not a-priori guaranteed. The simulations show that, apart from chirality problems, the best final structure Γ₀ (Fig. 1) presents the correct topology of a three-stranded antiparallel β-sheet of the hPin1 WW domain, even if the structure appears to be more compact. This, however, does not prevent the correct formation of both hydrophobic clusters. Moreover, Γ₀ shares 22 of the 41 native contacts of the PDB structure.

CONCLUSIONS

We performed folding and unfolding simulations of the WW domain of hPin1 protein, which represents an excellent candidate to test folding algorithms and models due to the availability of a large amount of structural, thermodynamical, and kinetic experimental data. The purpose of the work was to compare the performance of the Gō and SHG models that represent two different strategies to the folding problem. Our simulations indicated that for the specific WW domain considered in this work, the Gō model, with angular bias and rescaling, correctly reproduces the cooperative, two-state, reversible folding mechanism, whereas the SHG model does not. The reasons for the limitations of the SHG model must be sought in the insufficient optimization the sequence and in the nonfunnel shape of the landscape. As a consequence, the present version of the SHG model does not allow reliable predictions of the folding mechanism. The satisfactory performance of the SHG model in the computation of Φ-values, however, clearly shows the importance of incorporating the chemical properties of the sequence in a protein model. Our work, highlighting the limits of the SHG model, is thus intended to be a starting point for a further refinement of the model, in the firm belief that coarse-grained, minimal models represent viable alternatives to computationally demanding all-atom simulations in investigations of large-sized, slow-folding proteins.