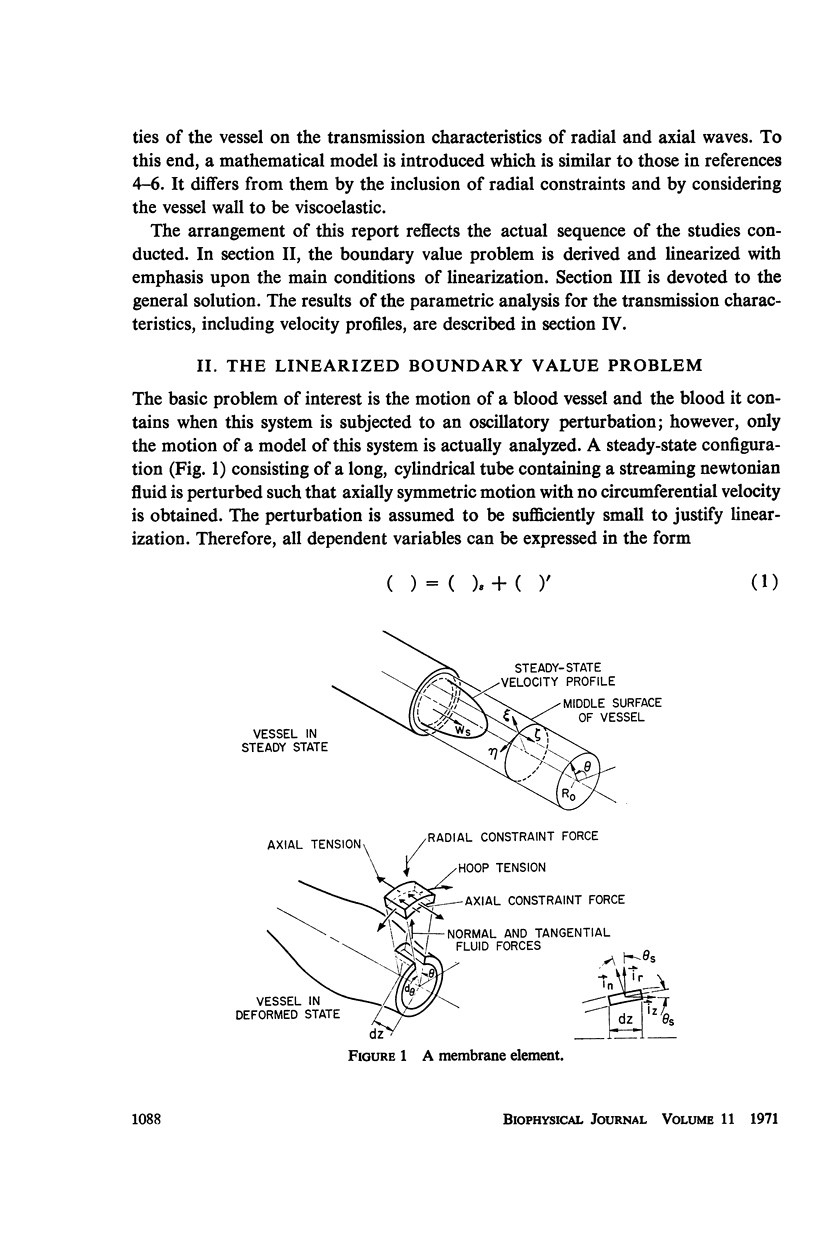
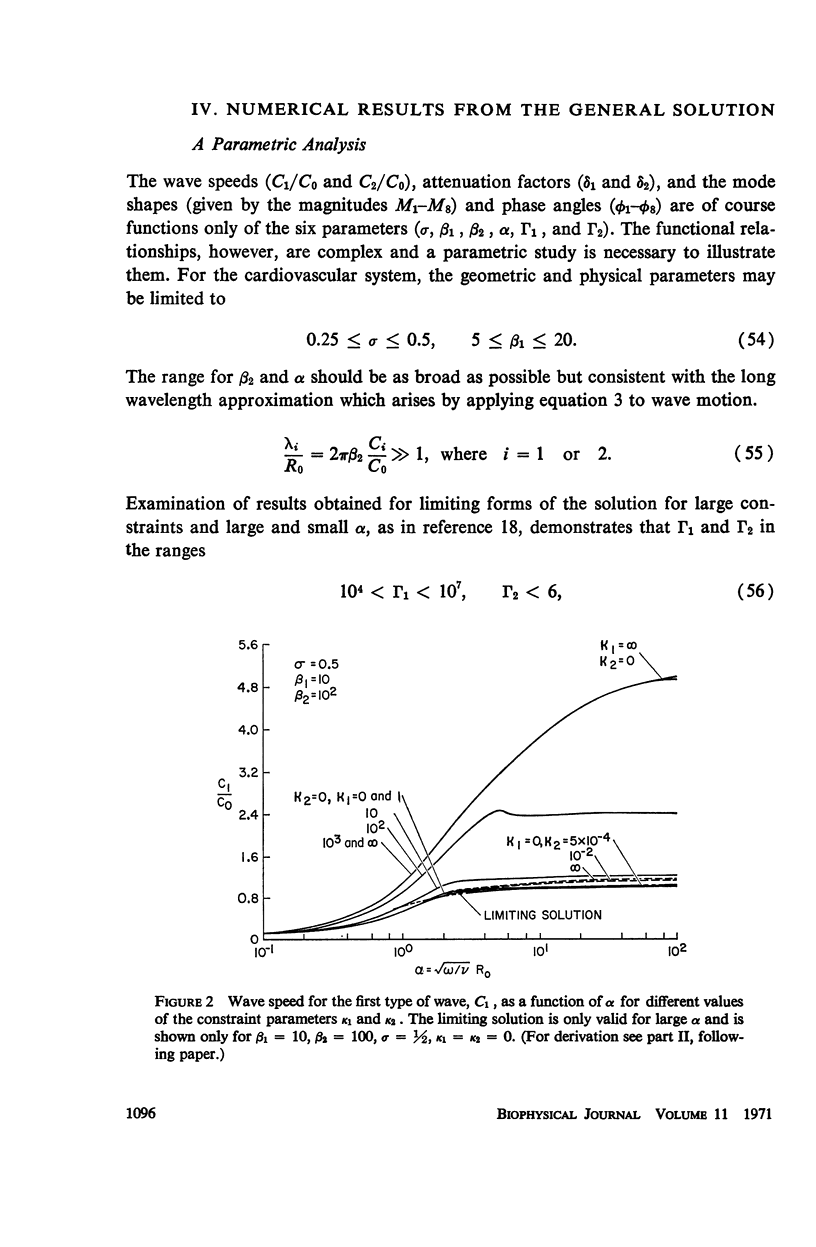
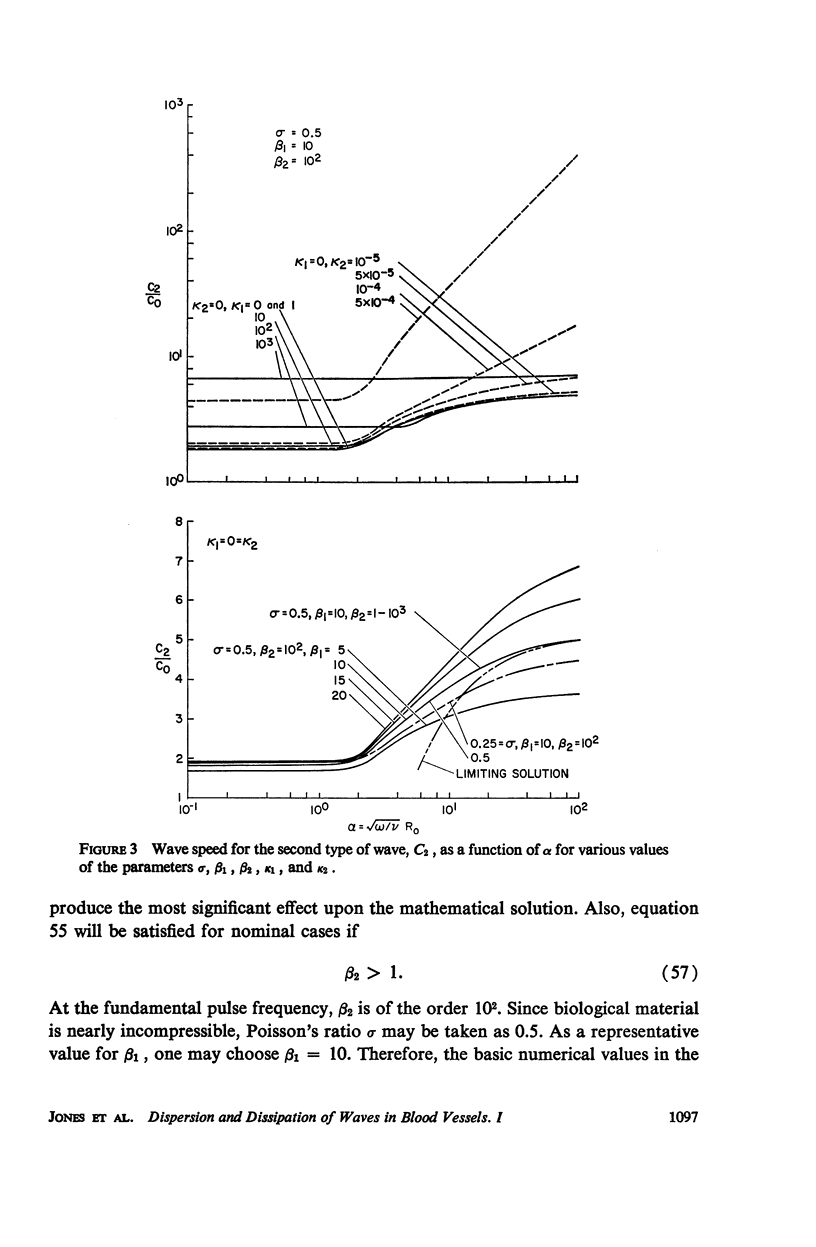
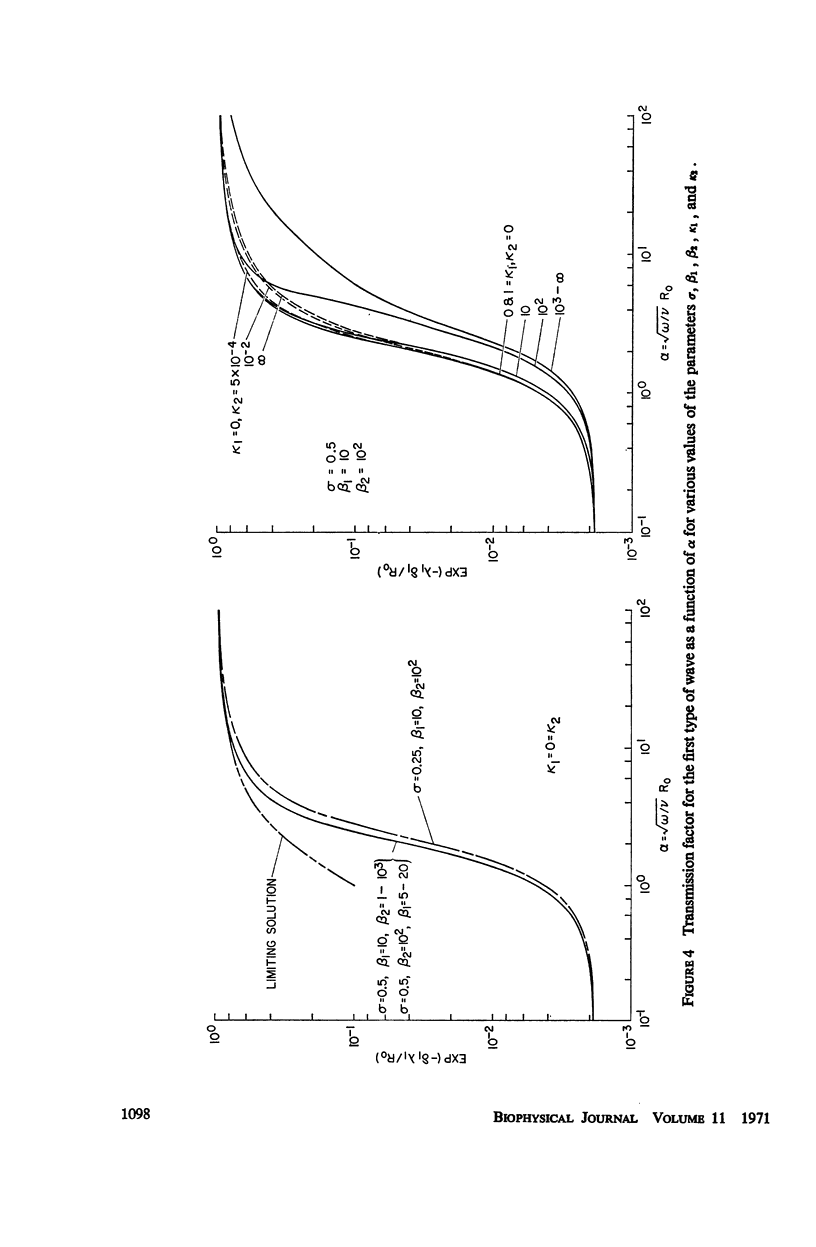
Abstract
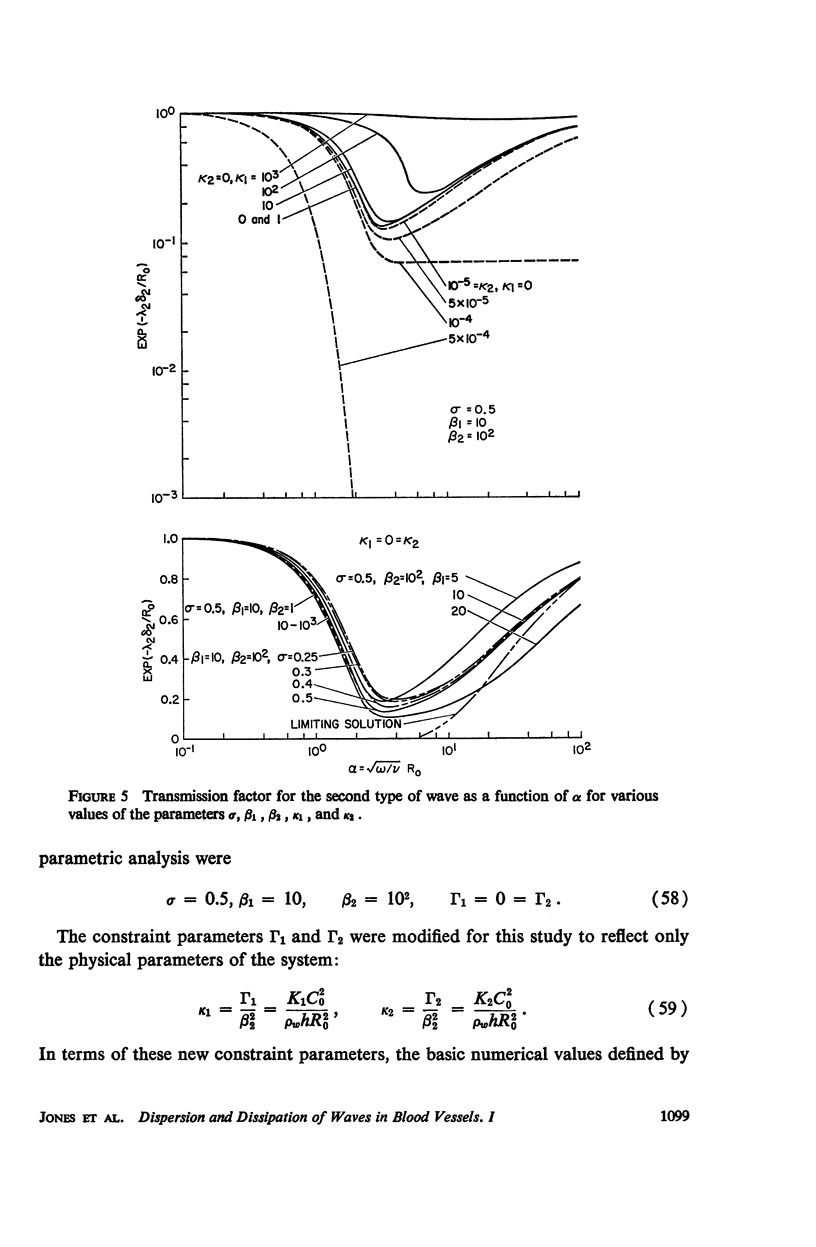
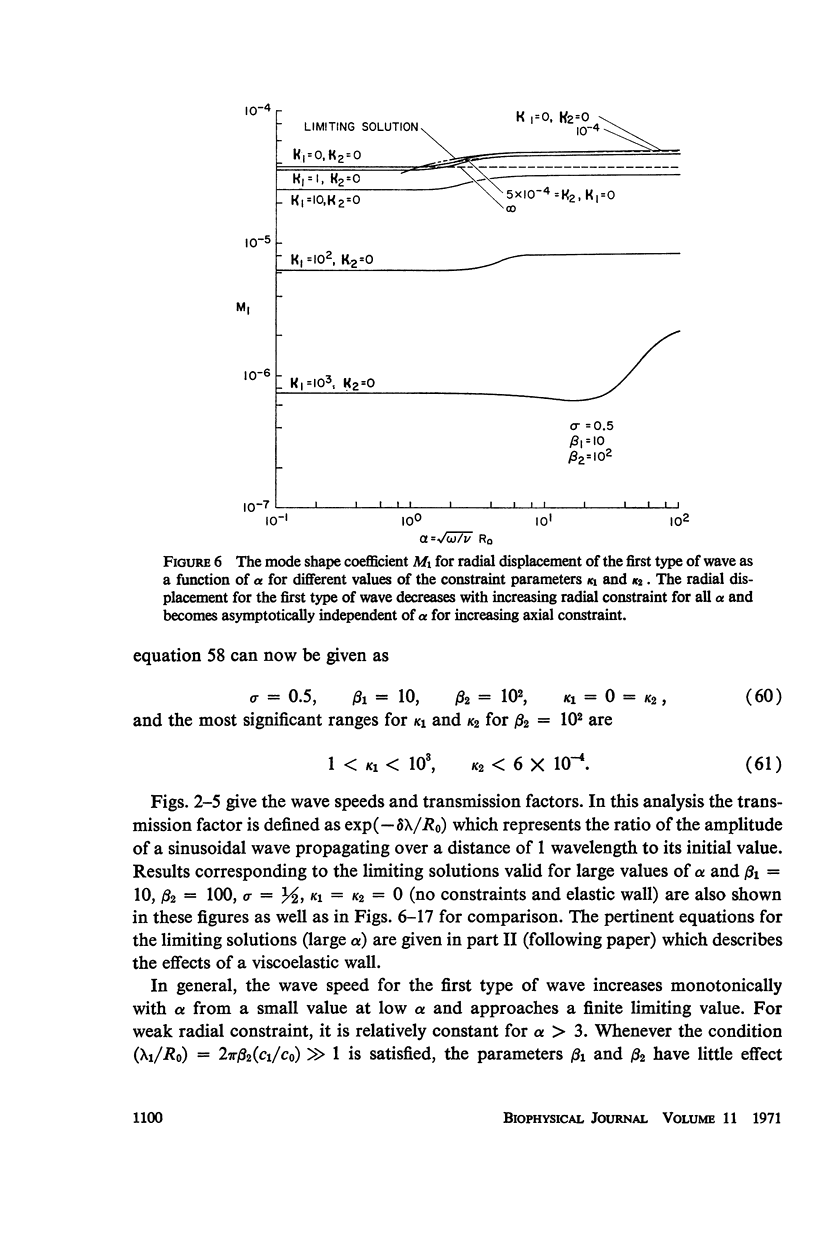
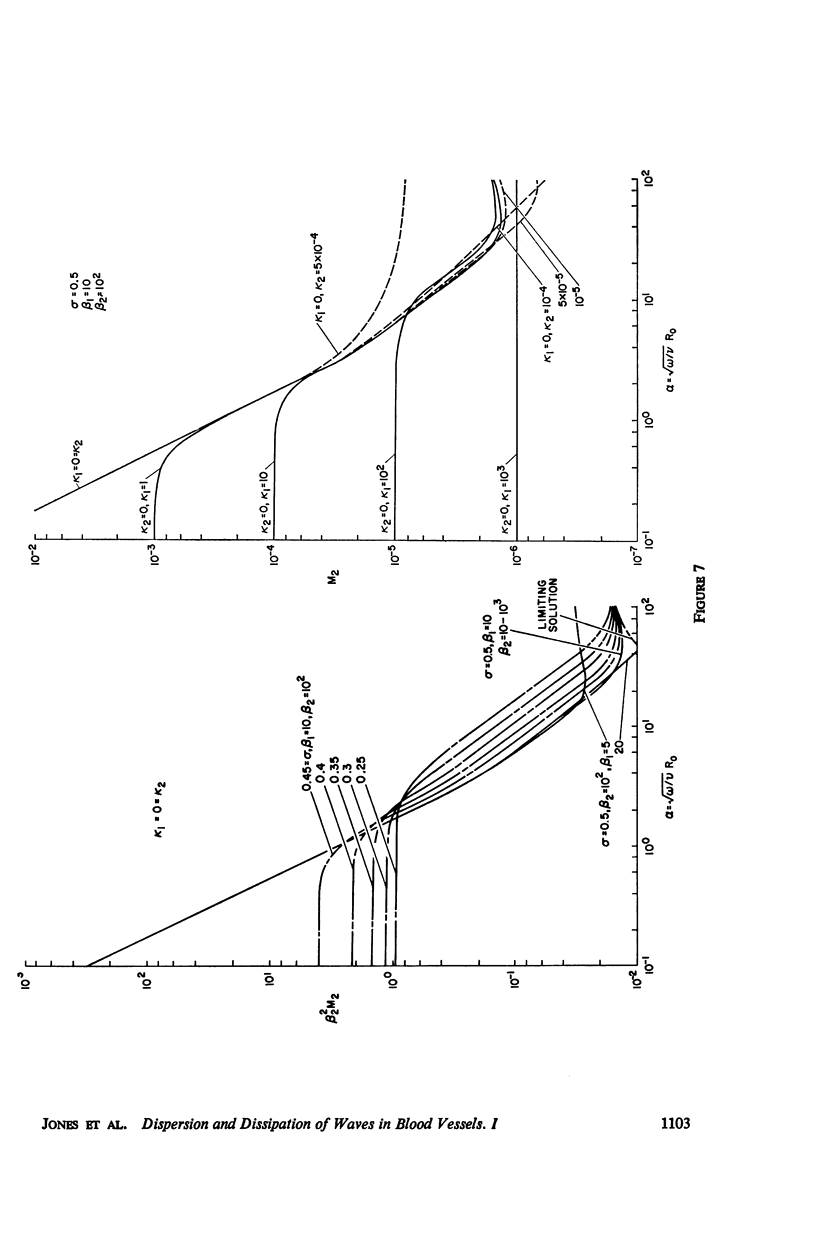
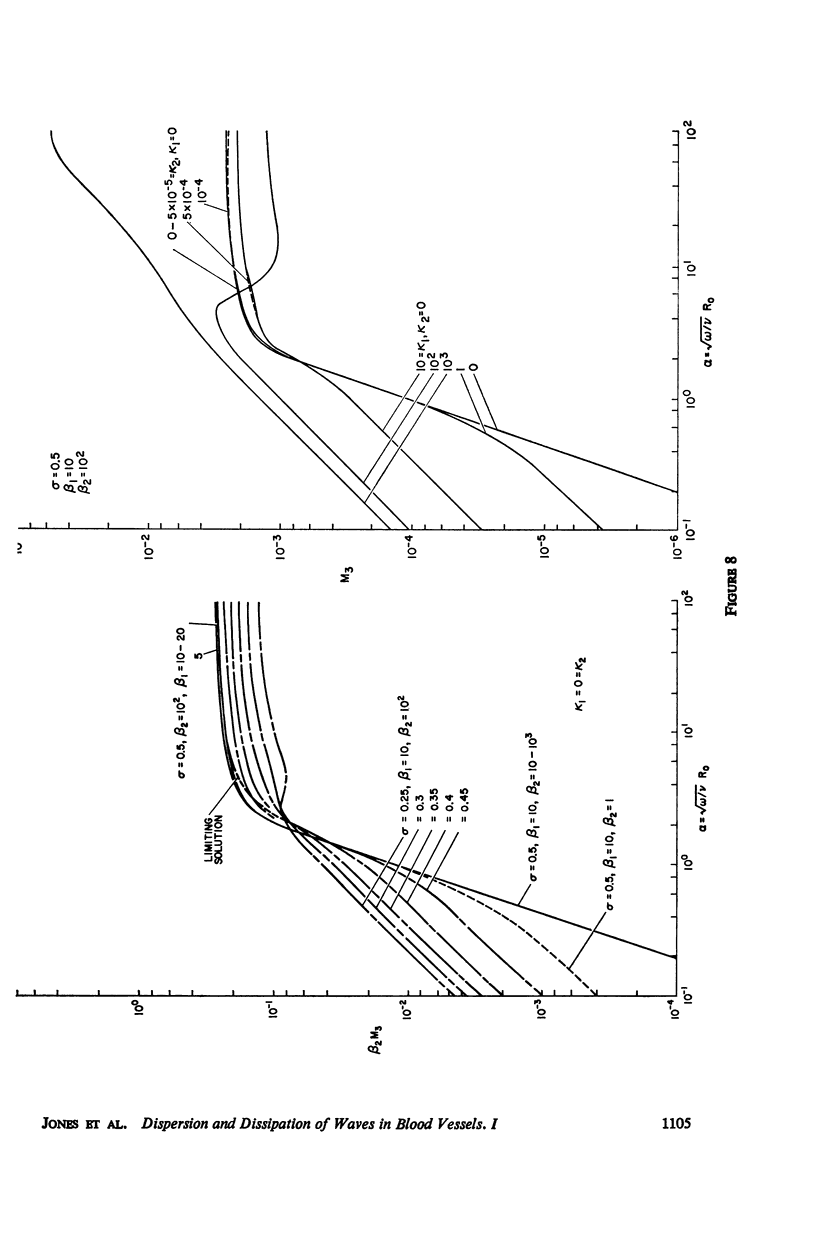
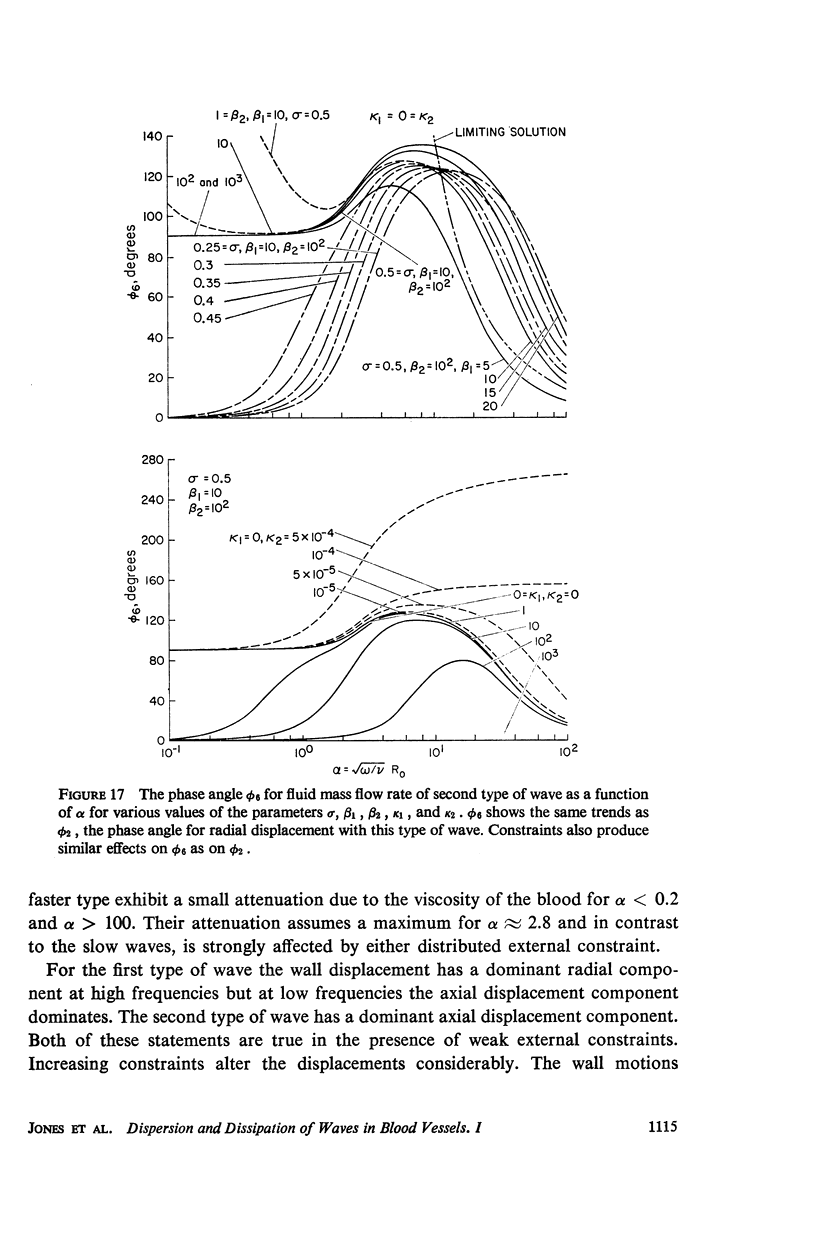
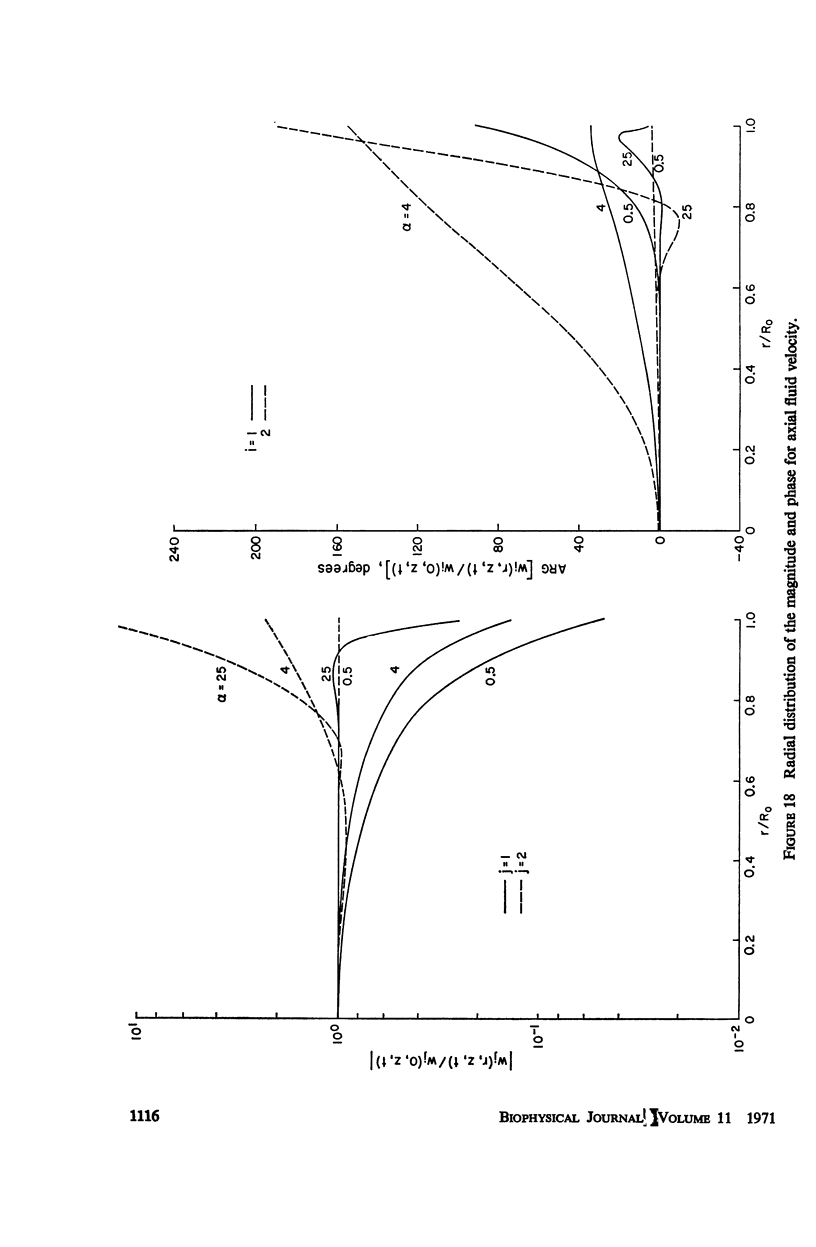
The propagation of sounds and pulse waves within the cardiovascular system is subject to strong dissipative mechanisms. To investigate the effects of blood viscosity on dissipation as well as dispersion of small waves in arteries and veins, a parametric study has been carried out. A linearized analysis of axisymmetric waves in a cylindrical membrane that contains a viscous fluid indicates that there are two families of waves: a family of slow waves and one of fast waves. The faster waves are shown to be more sensitive to variations in the elastic properties of the medium surrounding the blood vessels and at high values of the frequency parameter α defined by α = √ρωR20/μ the blood viscosity attenuates them more strongly over a length than the slow waves. At low values of α, the effects of viscosity on attenuation are reversed; that is, the family of slow waves is much more attenuated than the family of fast waves. For the slow waves the radial displacement component generally exceeds the axial component except at very low frequencies. Conversely the axial displacements are much larger than the radial displacement for the faster waves. The presence of external constraints, however, can modify these results. In the case of the slow waves the phase angle between pressure and radial wall displacement is virtually negligible in the presence of mild external constraints, while the phase angles between pressure and fluid mass flow are at most 45°. The corresponding phase angles for the fast waves exhibit much larger variations with changes in the elastic properties of the surrounding medium.
Full text
PDF

















Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Anliker M., Moritz W. E., Ogden E. Transmission characteristics of axial waves in blood vessels. J Biomech. 1968 Dec;1(4):235–246. doi: 10.1016/0021-9290(68)90019-5. [DOI] [PubMed] [Google Scholar]
- Atabek H. B., Lew H. S. Wave propagation through a viscous incompressible fluid contained in an initially stressed elastic tube. Biophys J. 2008 Dec 31;6(4):481–503. doi: 10.1016/S0006-3495(66)86671-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atabek H. B. Wave propagation through a viscous fluid contained in a tethered, initially stresses, orthotropic elastic tube. Biophys J. 1968 May;8(5):626–649. doi: 10.1016/s0006-3495(68)86512-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergel D. H. The dynamic elastic properties of the arterial wall. J Physiol. 1961 May;156(3):458–469. doi: 10.1113/jphysiol.1961.sp006687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chien S., Usami S., Taylor H. M., Lundberg J. L., Gregersen M. I. Effects of hematocrit and plasma proteins on human blood rheology at low shear rates. J Appl Physiol. 1966 Jan;21(1):81–87. doi: 10.1152/jappl.1966.21.1.81. [DOI] [PubMed] [Google Scholar]
- Chow J. C., Apter J. T. Wave propagation in a viscous incompressible fluid contained in flexible viscoelastic tubes. J Acoust Soc Am. 1968 Aug;44(2):437–443. doi: 10.1121/1.1911100. [DOI] [PubMed] [Google Scholar]
- Cox R. H. Comparison of linearized wave propagation models for arterial blood flow analysis. J Biomech. 1969 Jul;2(3):251–265. doi: 10.1016/0021-9290(69)90082-7. [DOI] [PubMed] [Google Scholar]
- Maxwell J. A., Anliker M. The dissipation and dispersion of small waves in arteries and veins with viscoelastic wall properties. Biophys J. 1968 Aug;8(8):920–950. doi: 10.1016/S0006-3495(68)86529-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel D. J., Fry D. L. Longitudinal tethering of arteries in dogs. Circ Res. 1966 Dec;19(6):1011–1021. doi: 10.1161/01.res.19.6.1011. [DOI] [PubMed] [Google Scholar]
- TAYLOR M. G. An experimental determination of the propagation of fluid oscillations in a tube with a visco-elastic wall; together with an analysis of the characteristics required in an electrical analogue. Phys Med Biol. 1959 Jul;4:63–82. doi: 10.1088/0031-9155/4/1/308. [DOI] [PubMed] [Google Scholar]


