Associative memory Hamiltonians for structure prediction without homology: α/β proteins

Abstract

We describe a method for predicting the structure of α/β class proteins in the absence of information from homologous structures. The method is based on an associative memory model for short to intermediate range in sequence contacts and a contact potential for long range in sequence contacts. The coefficients in the energy function are chosen to maximize the ratio of the folding temperature to the glass transition temperature. We use the resulting optimized model to predict the structure of three α/β protein domains ranging in length from 81 to 115 residues. The resulting predictions align with low rms deviations to large portions of the native state. We have also calculated the free energy as a function of similarity to the native state for one of these three domains, and we show that, as expected from the optimization criteria, the free energy surface resembles a rough funnel to the native state. Finally, we briefly demonstrate the effect of roughness in the energy landscape on the dynamics.

The rapid expansion of the protein sequence databases brought about by, among other things, the various genome sequencing projects has intensified interest in the problem of protein structure prediction. In recent years, there has been much progress toward the goal of predicting protein structure from sequence. Indeed, prediction is now almost routine for sequences with a moderate degree of homology (typically 30–50% sequence identity) to a protein of known structure (1). When homologous structures are not available prediction is more difficult, but even here, there has been much progress (2). Following Anfinsen's (3) thermodynamic hypothesis, algorithms for ab initio prediction typically involve the minimization of some model energy function. Although several energy functions (4–7) have been successful in generating low-resolution structures most suffer from an incomplete correlation between the energy and the quality of the prediction (2, 8, 9).

Advancing in parallel with techniques for structure prediction has been the theoretical understanding of the protein folding reaction itself. The large number of degrees of freedom needed to characterize a folding protein chain naturally leads to the adoption of a statistical characterization of the protein energy landscape (10). Such a characterization reveals that the ability of a protein to reliably find its native state among the exponentially large number of conformations is caused by the topography of the landscape. Inter-residue contacts that appear in the native state are, on average, more stabilizing than random contacts so that both the energy and entropy drop as the protein approaches the native state, and the landscape resembles a rough funnel. Bryngelson and Wolynes (11) have termed this property of the landscape the “principle of minimal frustration.” Model energy functions for structure prediction must also be minimally frustrated, and for the same reason, to overcome the multiple minima problem. This insight, that the essential physics of folding is contained in the requirement of minimal frustration, and not so much in the detailed form of the interaction potentials, is at the heart of a fruitful interaction between analytical models of the folding reaction and the development of practical methods of structure prediction.

We have developed a series of models (7, 12–14) based on associative memory energy functions. By formulating a quantitative version of the principle of minimal frustration, we have optimized the coefficients in our models to achieve a minimally frustrated landscape and have shown that the resulting energy function can successfully predict low-resolution structures in the absence of homology information for α-helical proteins. Moreover, we are able to calculate the free energy as a function of similarity to the native state and thereby quantify the success of the optimization procedure in achieving a funneled landscape. Here we further develop this approach and report the successful ab initio prediction of α/β proteins.

The organization of this article is as follows. First, we describe a number of changes we have made to the energy function and the optimization procedure needed to adapt it to α/β structures. We then describe the results of prediction runs on members of the set of the proteins used to optimize the model and on three α/β proteins not related to any of the training proteins. Finally, we discuss the full free energy surface of one of the test proteins as a function of similarity to the native state, and we briefly discuss the dynamics of the model.

Materials and Methods

Potential Function for α/β Structures.

The structure prediction protocol reported here is a modification of the one described in detail in refs. 7, 9, and 14 and is based on the associative memory energy functions first introduced by Friedrichs and Wolynes (12). For completeness, we will briefly review the main features of the earlier work. The energy of a protein conformation is a function of the similarity of the set of pair distances associated with that conformation to the aligned pair distances in a database of known protein structures. For de novo protein prediction, the database contains only proteins that are globally unrelated to the target sequence.

We use a reduced representation of the chain consisting of C_α, C_β, and O atoms. For short to intermediate sequence separations the conformational energy is given by an associative memory energy function: (V_AM = −∑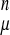 ∑ 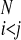γ(P_i,P_j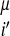,P,P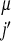,(j − i),SS_i′, SS_j′)Θ(r_ij − r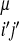). The coefficients, γ, weight the different types of interactions and are functions of the chemical properties (P) of the amino acids i and j, their sequence separation, the identity of residues i′ and j′, in the database protein μ (13) and the secondary structure, SS_i′ and SS_j′, of the database residues. We use a previously described sequence–structure alignment algorithm to associate the ij and i′j′ pairs (15). We use a four-letter code for the amino acid properties, hydrophobic, polar, acid/hydrophilic, and base, along with three sequence proximity classes, short (j − i ≤ 4), intermediate (5 ≤ j − i ≤ 12), and tertiary (j − i ≥ 13). In contrast to previous work we do not allow the interaction between residues to depend on their order in the chain and set γ_{i,j,i′,j′} = γ_{j,i,j′,i′}.

At large sequence separations the conformational energy is given by a simple contact potential with the form:

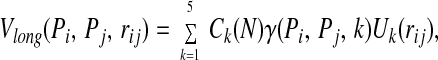1

where the U(r_ij) are designed to approximate square-well potentials about the distance ranges 4.5–6.5 Å, 6.5–8.5 Å, 8.5–10.5 Å, 10.5–12.5 Å, and 12.5–15.0 Å. To increase the discriminatory power of the tertiary potential, we have increased the number of wells since our earlier work (14). C_k(N) is a scaling term that accounts for the variation in the number of contacts in each of the five wells in native protein structures of N residues in length. It has the form a_kN/(1.0 + b_kN). The values of the parameters are given in Table 1.

Table 1.

Parameters of the contact potential scaling term, C_k(N)

k	ak	bk
1	0.0298	0.0298
2	0.0390	0.0211
3	0.0597	0.0133
4	0.0681	0.0100
5	0.0729	0.0035

The formation of β-stranded structures critically depends on the stabilization from interstrand hydrogen bonding, a feature absent from helical proteins. For this reason, we have added several new patterns of interactions to our previous hydrogen bond term:

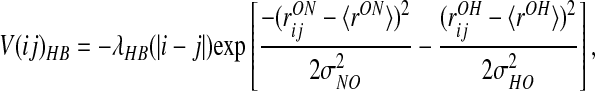2

where r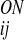 denotes the distance from the carbonyl oxygen on residue i to the nitrogen on residue j, and r 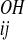denotes the distance from the oxygen on residue i to the H-bonded hydrogen on residue j. First, in an effort to foster the cooperative formation of regular secondary structure elements, we added an additional dependence on the presence or absence of hydrogen bonds between nearby residues:

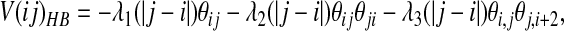where the θ functions are exponentials of the form given in Eq. 2. The λ₂ term gives an additional stabilization to an antiparallel β hydrogen bonding, and the λ₃ does the same for parallel β patterns. The dependence on |j − i| indicates that the coefficients are set separately for each proximity class. The final values of the coefficients were optimized to maximize the free energy difference between the native and unfolded states as described (16) and are listed in Table 2.

Table 2.

Coefficients of the hydrogen bond term

	λ1	λ2	λ3	α1	α2	α3	α4	α5
|(j − i) < 13|	1.79	3.05	0.0	−0.74	0.54	0.60	0.42	0.0
|(j − i) ≥ 13|	1.62	3.47	4.09	−0.74	0.93	1.02	0.42	2.31

All data are given in units of ɛ. The zero values for λ₃ and α₅ indicate that the parallel sheet interaction is turned off in the intermediate range proximity class. 

The registry of β strands is often poorly encoded by the Hamiltonian using only a four-letter code. To correct this we have made use of a suggestion by Regan and others (17, 18) that β secondary structures are stabilized by specific pair interactions as well as amino acid preferences. To account for these interactions, we have introduced a sequence dependence to the nonadditive coefficients λ₂ and λ₃:

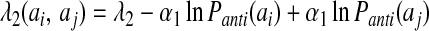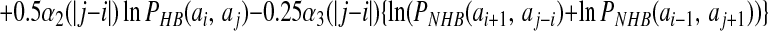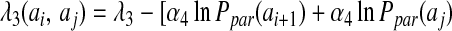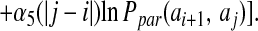The probabilities, P, for amino acids to be in particular secondary structures were computed by using a database of well-resolved x-ray structures as follows:

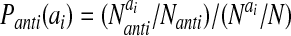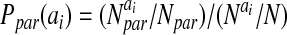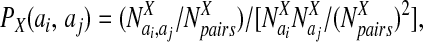where X can refer to hydrogen-bonded, nonhydrogen-bonded, or parallel pairs as defined by Regan and coworkers (17). The final values of the probabilities are in good agreement with the experimental values reported by Regan and coworkers (17) and the calculations of Wouters and Curmi (18). The coefficients, α_i, were optimized as above and are given in Table 2. The total hydrogen bond potential, V_HB, is the sum over the contribution from each pair, V(ij)_HB.

The hydrogen bond term as defined is fairly narrow; i.e., even relatively small deviations from ideal β-sheet geometry lead to a large loss of hydrogen bond energy. This is desirable from the point of view of reproducing the geometry of secondary structure elements accurately; however, it is disadvantageous in the search for a globally correct fold to have only such a strict definition of a hydrogen bond, because at temperatures where many hydrogen bonds form the barriers to breaking them will be large, leading to slow dynamics. In the spirit of making a funneled (rather than golf course-shaped) landscape, we introduce a further term to the energy function intended to encourage β strands to line up in a roughly parallel or antiparallel manner even at temperatures where the hydrogen bonding has not fully set in. This potential is based on C_α positions and gives a reduction in the total energy if when residues i and j are in contact i + 4 and j + 4 (parallel, P) or i + 4 and j − 4 (antiparallel, AP) are also in contact. The P and AP contacts are allowed different weights, and the AP term is itself split into two distance classes (AP and APH) to allow different weights for putative β-hairpins. This term is thus a sum of three parts,

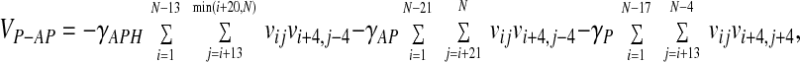where v_ij = ½(1 + tanh[7(8 − r_ij)]). The coefficients, γ, are all set to 0.4ɛ.

Finally, we have introduced two new features to the energy function that enable us to take advantage of additional information that may be available about a target sequence before predicting its structure. To the Ramachandran potential described in ref. 14, V_rama, we have added two wells centered at dihedral angels appropriate for α-helices and β-sheets, respectively. The coefficients on these wells can then be used to provide the option of biasing the protein backbone to its predicted secondary structure:

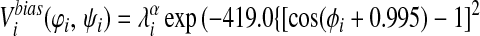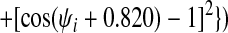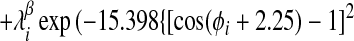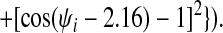For the set of test proteins discussed here the target sequence was submitted to the jpred (19) secondary structure prediction server, and λ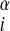 was set to 2.0ɛ for residues predicted to be helical and zero for all other residues. Similarly, λ 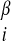was set to 2.0ɛ for those residues predicted to be β and zero otherwise. It has also been shown (9, 20) that averaging interactions over homologous sequences can improve the free energy surface of structure prediction energy functions. In several of the runs discussed below, we have done a multiple sequence alignment of top scoring hits from a psi-blast (21) search with the target sequence and computed separate potentials for each sequence (including the target) in the alignment. Molecular dynamics on the target sequence is then performed with the average force.

The total energy function also includes terms for amino acid chirality, an excluded volume term, and a combination of harmonic terms and shake (22) constraints that maintain the planarity of the peptide bond, and appropriate bond lengths, and bond angles. The coefficients for these terms are the same as used previously. The full, modified associative memory and contact (AMC) energy function, including the backbone, is:

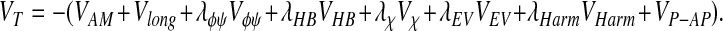We define a reduced temperature as T* = k_BT/ɛ. Here ɛ is one-quarter of the native state energy per residue averaged over the training in the following way:

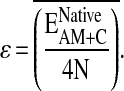With this choice of units, the folding temperature is typically near T* = 1.0.

Constrained Self-Consistent Optimization

The parameters in the AMC energy function should be chosen to give good discrimination between the native state and typical unfolded states at intermediate temperatures and to minimize the presence of local minima that can slow the search through conformational space. The minimal requirement for rapid folding of a target sequence is a sufficiently large ratio of the stability gap, δE_S, the gap in energy between the native state and the average energy of the ensemble of non-native states and the variance in energy of the unfolded states (δE_s/ΔE). The stability gap is related to the folding temperature, T_F, and the variance is related to typical depth of a local minimum, and thus to the glass transition temperature, T_G (10). Maximizing the ratio of the stability gap to the variance can be shown to be equivalent to maximizing the ratio of the folding temperature to the glass transition temperature (23).

As described, we enforce a set of constraints on the contribution to the mean energy of the globules from each proximity class, and we enforce roughly equal transition temperatures in each proximity class by constraining the variance in each class. The details of the optimization functional are contained in Hardin et al. (14).

To determine the optimal set of parameters, we choose a training set of 14 α/β proteins and generate a set of unfolded conformations via a constant temperature molecular dynamics simulation. The full set of 14 training proteins and their associated memories are discussed in the Appendix. To generate the initial set of decoys, we used an energy function that was optimized for an α-helical training set (7). Once the optimum set of parameters is chosen for a particular ensemble of unfolded states that energy function is used to generate a new set of decoys, and the procedure is iterated until self-consistency (13). The collapse temperature is related to the mean energy of the unfolded states and can vary among the members of the training set. To ensure that the globules for each training set protein come from roughly equivalent portions of phase diagram, we constrain the unfolded states to have a given degree of similarity to the native state. This is measured by the fraction of native contacts, or Q:

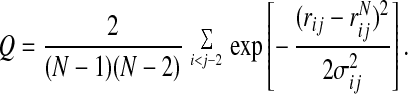The unfolded ensembles were constrained to have a Q of 0.3. The constraint procedure is described in ref. 9.

Results and Discussion

Once the optimized energy function is obtained we minimize it by using simulated annealing via molecular dynamics. Table 3 shows the results of simulations on each of the 14 training set proteins, using just the optimized energy function, i.e., without applying the bias to predicted secondary structure or the average over a multiple sequence alignment. The database of known structures from which the AMC potential is calculated was constructed by deliberately excluding any proteins with structural similarity to the corresponding training set protein. Thus scaffold proteins have global rms deviations (rmsd) that are generally >9 Å (9). There are two points about the results on the training set proteins. First, the best structure obtained in the simulation is frequently more native-like, as measured by Q, than anything in the database. This demonstrates the ability of the AMC potential to reconstruct the members of the training set by generalizing from the partial structural similarities contained in the alignments to globally unrelated structures. Finally, there is a general decline in quality of the predictions as the length of the target sequence increases. The potential is most effective for sequences <90 residues long. For most of the training proteins beyond that length, the best structure obtained is somewhat inferior to the best input structure from the point of view of the Q measure. This may indicate a generic size dependence of the potentials that is not accounted for in our model. The use of the bias to predicted secondary structure and the averaging over sequence homologs should generally improve the performance of the potential. To test this expectation, we have conducted five simulations each on proteins 2acy and 3chy with the augmented energy function. In the case of 2acy, the Q_best structure is improved compared with the previous results; however, for 3chy it is unchanged. We have used the augmented potential for all of the test set simulations, discussed below.

Table 3.

Results of simulated annealing on training set proteins

Protein	N	Q of closest scaffold	Qbest
1igd	61	0.31	0.38
2sni(i)	64	0.33	0.36
1snb	64	0.29	0.31
3il8	68	0.33	0.47
1ubi	76	0.31	0.37
1pht	83	0.25	0.31
1poh	85	0.32	0.34
1tig	88	0.32	0.36
2acy	98	0.26	0.24
1frd	98	0.30	0.27
1opc	99	0.29	0.25
1rds	105	0.26	0.29
3chy	128	0.30	0.29
5nul	138	0.35	0.31

For each protein five simulations from T* = 1.5 to T* = 0.005 were conducted. Q_best is the Q of the most native-like structure encountered in any of the runs. 

To test the optimized potential, we choose three protein domains from the critical assessment structure prediction 4 experiment. The test set proteins are domain 1C from FtsA (Protein Data Bank code 1E4F, residues 86–166), residues 200–309 of Streptococcus mutans Pyrophosphatase, and the N-terminal 115 residues of the human XRCC4 DNA repair protein. The highest Q to any member of the associative memory database used for each of these targets, Q_mem, is given in Table 4. We have also included the structural alignment from the combinatorial extension (CE) program of Shindyalov and Bourne (24). CE finds the alignment of two proteins that maximizes the structural overlap. Table 4 reports the length of the alignment, the number of residues contained in gaps in that alignment, the rmsd of the alignment, and a statistical score, Z, which is a function of the difference between the alignment score and the distribution of scores associated with random alignments. Z > 4.0 typically denotes a strong structural similarity; 3.7 ≤ Z ≤ 4.0 represents a more ambiguous structural assignment (24). The low Z values, taken together with the low Qs, demonstrate that the three test set proteins are structurally unrelated to the database proteins. Table 5 indicates that the three test set proteins are also unrelated to any of the training set proteins, and so constitute a test of the AMC potential's performance on an unknown target.

Table 4.

Structural relationship of test set proteins to database proteins

Protein	Qmem	Length of CE alignment (Naln/Ngaps)	rmsd	Z
1e4f	0.29	56/28	6.74	2.6
1i74(a)	0.27	72/62	5.4	2.3
1ful(a)	0.27	64/66	5.9	1.6

Q_mem is the best overlap to a protein in the memory database. Also shown is the result of a structural alignment of the best memory to the test protein by using CE. N_aln is the number of residues aligned, N_gap is the number of residues contained in gaps, rmsd is the rmsd of the alignment, and Z is the Z score as reported by CE. 

Table 5.

Structural relationship between test set and training set proteins

Test set protein	Closest training protein	Q	Alignment length	rmsd	CEZ score
1e4f	1tig	0.19	56/20	3.7	3.7
1i74(a)	1tig	0.22	54/5	4.2	3.7
1ful(a)	1poh	0.23	40/35	4.5	1.6

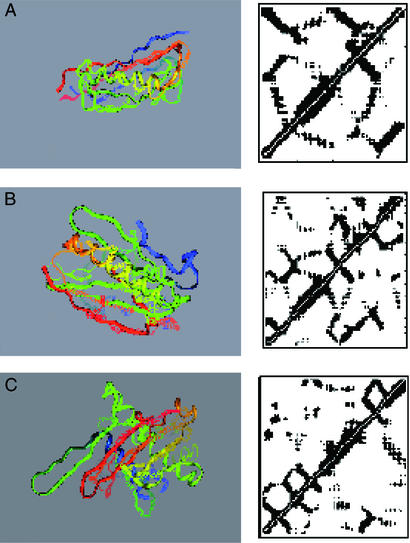
The simplest gauge of the success of a prediction is the global superposition of the predicted and correct structure. Fig. 1 illustrates such a superposition for the best Q structure (Q_best) encountered during the simulations on each of the test set proteins. Even by this very stringent evaluation criteria, the AMC potential performs rather well. It is worth noting that the distance maps look somewhat more native-like than the direct superpositions. The best structures for the test set proteins, as indicated in Table 5, have Q = 0.35, Q = 0.31, and Q = 0.28. It is possible to define a distance map overlap as:

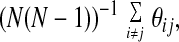where θ_ij is 1 when residues i and j have the same state (contact, no contact) in the native and predicted structure and is 0 otherwise. The corresponding distance map overlaps are 0.77 for 1e4f, 0.76 for 1i74(a), and 0.78 for 1fu1(a). It is perhaps unsurprising that the AMC potential would be more successful at predicting the set of pair distances than it is at predicting the global structure. The backbone used in the simulation is highly schematic. Given the success at predicting the inter-residue contacts, it would be interesting to see how much improvement can be achieved with a more elaborate description of the backbone or even the substitution of segments from experimental structures subject to the predicted pair constraints paralleling a fragment assembly method (25).

Figure 1.

Superpositions of Q_best structures onto the native state. The native C_α trace is shown as lines and the predicted trace as a solid ribbon. (A) Protein 1e4f. (B) Protein 1i74(a). (C) Protein 1fu1(a).

The secondary structure bias, in its present form, can sometimes lead to interesting failures. In the case of 1fu1(a), the break in the native helix at residue 60 facilitates a turn that the predicted structure lacks. The 1D prediction that enters into the bias has residue 60 as helical. In this case the rather strong bias to the predicted secondary structure that we have used (4ɛ) is a disadvantage. It is obviously possible to choose different, even optimized, weights for this term.

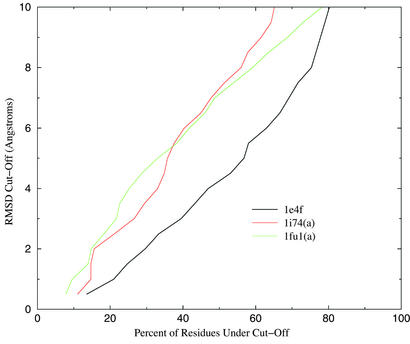
The global superposition of two structures can often fail to highlight significant segments of correct native structure. We have submitted the best Q structures to the LGA (Local-Global Alignment) server (http://PredictionCenter.llnl.gov/local/lga), and the results are given in Table 6. The predictions are evaluated according to two measures, LCS and GDT. LCS is the longest continuous (along the sequence) segment that can be superimposed on the native structure without exceeding a rmsd cutoff. The global distance test (GDT) represents the largest number of residues that lie within a distance cutoff of their correct positions. The set of residues need not be contiguous. In all three cases large portions of the prediction are correct to within the cutoff. We have also used CE to align the predicted and native structure. Note that in all three cases the predicted structure is more similar to the native than any of the database structures, thus demonstrating the ability of the potential to generalize from incorrect scaffolds. The scores of local similarity will, of course, depend on the chosen cutoff. Fig. 2 is a Hubbard plot of the percent of residues below the cutoff, as a function of the cutoff distance.

Table 6.

Results of LGA server analysis of test set predictions

Protein	N	LCS, 5 Å	Qbest	GDT, 6 Å	Alignment length	rmsd	CEZ
1e4f	81	61	0.35	51	67/12	4.4	3.7
1i74(a)	109	54	0.31	44	84/33	6.5	3.7
1ful(a)	115	45	0.28	48	72/23	7.4	3.3

Listed are the longest continuous segment of each target (LCS) that falls under a 5-Å rmsd cutoff and the sequence independent number of residues (GDT), which fall under a 6-Å distance cutoff. The LCS and GDT numbers for Q_best refer to the best Q structures encountered in any of the five runs of each target. 

Figure 2.

GDT as function of cutoff distance.

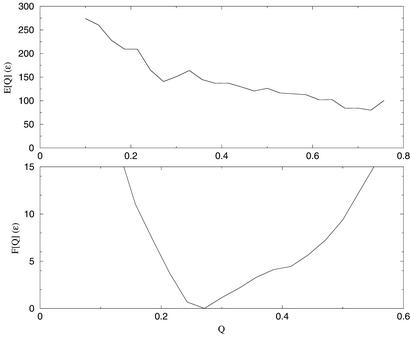
Although such successful predictions are encouraging, a more complete characterization of the AMC potential requires knowledge of the free energy as a function of similarity to the native state. We can calculate the free energy surface as a function of Q by means of the multiple histogram technique (26). The optimization procedure outlined above is expected to yield a free energy surface that is shaped like a rough funnel toward the native state. In Fig. 3 we show the energy and free energy of 1e4f. The energy declines steadily until relatively high values of Q, indicating that the free energy surface is largely funnel like, with the protein trading energy for entropy as it moves toward the native state. The energy gain is not sufficient to completely balance the loss in entropy, as indicated by the relatively low Q value at the minimum. However, structures with Q > 0.4 are certainly accessible within moderate amounts of computation time.

Figure 3.

Energy and free energy as a function of Q for protein 1e4f (CASP4 Target 0089). T* = 1.0.

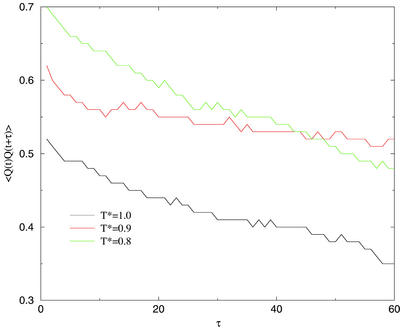
For a well-funneled landscape, it is expected that the minima will shift to higher Q as the temperature is lowered. There is a practical problem, however, with simulating at temperatures much lower than those studied here. As the temperature decreases, escape from non-native traps is slowed. At a low enough temperature, we encounter a glass transition, below which the protein is localized to a single basin. Even before that point, however, escape times can become long enough that the finite-time simulations we have performed fall out of equilibrium (27). Fig. 4 shows the Q autocorrelation functions for runs at several different temperatures. It is clear that much below T* = 1.0 the simulation is exploring an increasingly small amount of configuration space. The glass transition therefore limits the simulation to intermediate temperature even though the minima in free energy would be expected to shift to higher Q as the temperature is lowered. The energy curve shown in Fig. 4 is not monotonically decreasing in Q but is flat above Q ≈0.6. We have previously discussed the practical implications of this caldera-like shape for the sampling of predicted structures (9).

Figure 4.

Q autocorrelation functions.

Conclusion

We have described a potential energy function for the prediction of α/β protein structures without resorting to information from known, homologous structures. Using ideas from energy landscape theory, we have optimized the parameters of the potential to yield a free energy surface, which is as near to a smooth funnel as is possible given our encoding. The resulting potential performs well in tests on short- to medium-length proteins unrelated to the structures on which it was trained.

Abbreviations

AMC

associative memory and contact

CE

combinatorial extension

rmsd

rms deviation

Appendix

The α/β training set was selected to represent the various structural classes appearing in the cath database (28). The 14 training proteins ranged in length from 53 to 138 residues. The training set consisted of proteins 1igd, 2sni(i), 1snb, 3il8, 1ubi, 1pht, 1poh, 1tig, 2acy, 1frd, 1opc, 1rds, 3chy, and 5nul. The scaffolds were a subset of the α/β chains appearing in the Protein Data Bank select 2001 list (29). Structures determined by NMR, those with resolution >3.0 Å, and those with length >200 residues were removed. This process resulted in a list of 168 proteins from which the memory proteins were selected. The selection process eliminated any memory protein with structural overlap > Q > 0.4 to the training protein to which it was aligned. The final memory set consisted of the top 138 scoring alignments to unrelated scaffolds.