Computational and experimental analysis of DNA shuffling

Abstract

We describe a computational model of DNA shuffling based on the thermodynamics and kinetics of this process. The model independently tracks a representative ensemble of DNA molecules and records their states at every stage of a shuffling reaction. These data can subsequently be analyzed to yield information on any relevant metric, including reassembly efficiency, crossover number, type and distribution, and DNA sequence length distributions. The predictive ability of the model was validated by comparison to three independent sets of experimental data, and analysis of the simulation results led to several unique insights into the DNA shuffling process. We examine a tradeoff between crossover frequency and reassembly efficiency and illustrate the effects of experimental parameters on this relationship. Furthermore, we discuss conditions that promote the formation of useless “junk” DNA sequences or multimeric sequences containing multiple copies of the reassembled product. This model will therefore aid in the design of optimal shuffling reaction conditions.

Directed evolution is a strategy to improve a specific biological function through genetic diversification and selection, mimicking natural evolution but in a guided and accelerated fashion. Specifically, DNA sequences encoding a protein or set of proteins are mutagenized to generate a library of related mutant proteins from which, through careful screening, a few with improved function may be isolated. Using these as the starting material for further iterations of mutagenesis and selection can yield proteins with significantly enhanced or novel functions.

Over the past decade, directed evolution has been highly successful in improving the capabilities of proteins in a number of applications. Although most attention has been devoted to changing the activity, selectivity, and stability of enzymes important for industrial processes, the strategy has also been applied to improve viral vector stability, cytokine efficacy, and antibody fragment binding (1–3). The success of these and other studies has hinged on both the method used to create genetic diversity and the design of an effective screen or selection. In each of these cases, genetic diversity was generated by using techniques that combine DNA mutation with recombination to access relatively large regions of DNA sequence space via the combinatorial mixing of distinct genetic parents. The first and most common method to achieve in vitro DNA recombination is DNA shuffling (4), although several similar PCR-based methods have since been developed (5). In DNA shuffling, the parent sequences to be recombined, or shuffled, are randomly cut to yield fragments of a defined size, which are then reassembled by primerless PCR. This process creates a library of chimeric sequences containing crossovers between the different parent sequences.

Although DNA shuffling has been implemented successfully for many DNA sequences, the effective recovery of correctly reassembled fragments from the reaction can be difficult, and the shuffling protocol then requires optimization. However, optimization is very challenging, because the method involves highly complex reactions whose outcomes depend sensitively on a number of important parameters. These include (i) the concentration, composition, and complexity of DNA sequences to be reassembled; (ii) the fragmentation conditions and size distribution after fragmentation; and (iii) the PCR conditions for reassembly, including annealing temperature and schedule, DNA polymerase extension time, number of rounds of reassembly, salt concentration, and choice of polymerase. Any of these parameters can affect the following four outcomes, or metrics: the final length distribution of reassembled fragments, the number and location of crossovers, the fraction of reassembled fragments that are full-length sequences, and ultimately the fraction of fragments that will give rise to a protein with improved function. The first three of these considerations place an upper bound on the success of the last. That is, if no fragments reassemble into full-length sequences, or if no crossovers occur, there is little chance of recovering a mutant with improved function (using a high-fidelity polymerase).

Optimization of reaction conditions for DNA shuffling is currently conducted empirically, often with a considerable expenditure of time and effort due to the multidimensionality of the problem. The development of accurate models of shuffling would aid in the design of optimal reaction conditions for a specific DNA sequence. In fact, early work to model DNA shuffling emerged shortly after the development of the method (6). This work established that DNase I digestion yields an exponential fragment size distribution and provided a relationship between this size distribution and the efficiency of reassembling a full-length sequence, two valuable and general conclusions about DNA shuffling. Because such purely probabilistic models never considered specific nucleotide sequences, however, there were limits to their predictive capabilities (7).

More recent work made a significant advance by incorporating DNA sequence information, specifically by using DNA hybridization thermodynamics to model annealing events during the reassembly process (8). However, this model provided information only on crossover number and distribution and only for fully reassembled sequences. A further improvement to this model (9) even considered out-of-sequence reassembly of a full-length sequence. However, it did not consider the fate of all other fragments and how they affect the outcome of a shuffling reaction, especially the ease of recovering a correctly assembled fragment.

We describe here the development of a computational model based on the thermodynamics and kinetics of DNA shuffling. The model follows the state of an ensemble of DNA fragments as it proceeds through numerous rounds of shuffling and predicts how experimental parameters affect numerous metrics throughout the reassembly process. We have conducted shuffling experiments to validate model predictions of the effects of DNA fragmentation conditions and concentrations on the size distribution of fragments during reassembly. The predictive value of the model is further substantiated by comparison with recently published work in which crossover number and distribution have been analyzed experimentally (10). Therefore, this model is a potentially valuable tool for optimizing DNA shuffling results.

Experimental Methods

PCR of GFP.

DNA encoding the enhanced GFP (CLONTECH) was amplified by using the primers 5′-GCGAATTCCATCCGTACGTTGGCCGGTCGCCACCATGGTGAG-3′ and 5′-GTGAATTCCGTACGTTGGCTTGTACAGCTCGTCCATGCCTAGA-3′.

DNase I Digestion.

PCR products were fragmented as described (11). Briefly, 8 μg of DNA was incubated with 0.05 units DNase I (Roche Diagnostics) in DNase buffer (10 mM MnCl₂/25 mM Tris⋅HCl, pH 7.4), for 1, 2, and 5 min in a 60-μl reaction volume. Reactions were terminated by adding 0.5 M EDTA to a 50 mM final concentration and heat inactivating at 95°C for 10 min. Small fragments (<25 bp) were removed by gel filtration using a Centri-Sep column (Princeton Separations, Adelphia, NJ).

Reassembly.

Fragments were reassembled in a 50-μl reassembly reaction containing NEB (Beverly, MA) ThermoPol Reaction buffer [20 mM Tris⋅HCl/10 mM KCl/10 mM (NH₄)₂SO₄/2 mM MgSO₄/0.1% Triton X-100], 0.2 mM dNTPs, and 1 unit of Vent (exo-) DNA Polymerase (New England Biolabs). PCR was conducted in a Bio-Rad iCycler as follows: 1 cycle of 95°C for 1 min; 30 cycles of 95°C for 30 sec, 60°C for 30 sec, 72°C for 1 min + 2 sec per additional cycle, followed by cooling to 4°C.

Gel Imaging.

Agarose gels were imaged by using the Epi Darkroom II (Ultraviolet Products, Upland, CA), and images were analyzed by using LABWORKS 3.0 software (Ultraviolet Products).

Simulation Code.

The simulation was written in C, initially by using the freeware dev-c ide, and run on a 1.4-GHz Pentium 4 class personal computer. An updated version developed in Microsoft Visual C++ for Microsoft Windows is now available to researchers.

Model Development.

This model follows the evolution of a representative ensemble of single-stranded DNA (ssDNA) molecules as they are subjected to operations that model fragmentation and reassembly. The size of this ensemble must be large enough to adequately represent the complex mixture of sequences in a shuffling reaction, such that additional increases in the ensemble size do not affect the results. We found that this size increases with the length of the sequences being shuffled and the extent of their initial fragmentation. In all results presented, we used 100–150 full-length sequences, which were fragmented into between 1,500 and 5,000 ssDNA molecules.

Although any fragmentation algorithm can be used, we implemented a Poisson fragmentation process that yielded an exponential length distribution, typical of the DNase I digestion performed in the experiments whose results we simulated (6, 7). During the digestion step, the extent of fragmentation (digestion time) and the nature of the cutting [double-stranded cuts with the metal cofactor Mn²⁺ and single-stranded nicks with Mg²⁺ (12)] are readily controlled to yield an exponential distribution with a specific average fragment size (AFS). Digested fragments are then often subjected to a purification step, such as gel filtration or electrophoresis, to yield exponentially distributed fragment sizes within specified minimum fragment size (MFS) and maximum fragment size (XFS) bounds. Therefore, the AFS of the original fragmentation, with the MFS and XFS following purification, uniquely specify the fragment size distribution before reassembly.

These fragments are next subjected to a three-step reassembly process: (i) ssDNA molecules randomly collide; (ii) on collision, a decision is made whether the molecules will hybridize and, if so, in what arrangement; and (iii) hybridized molecules are extended in the 5′→3′ direction with a fidelity and processivity based on the polymerase used. On colliding, two ssDNA strands may hybridize to form a single double-stranded DNA (dsDNA) molecule. By estimating a molecular collision frequency, we determined that collisions are not limiting over typical experimental time scales (see Kinetics supporting information on the PNAS web site, www.pnas.org) for an annealing step (10s of seconds), and therefore collisions are allowed to proceed until the fraction of hybridized molecules remains unchanged over many collisions.

To determine whether and how annealing will occur between two colliding fragments for a given collision, all possible ways in which these two fragments could anneal with at least some minimum overlap (7 base pairs here) are analyzed to calculate a Boltzmann-weighted probability for each annealing event (see Fig. 4, which is published as supporting information on the PNAS web site). Specifically, the free energy for each annealing event is found by using the nearest-neighbor model described by SantaLucia (13), with modifications to account for the effects of sequence mismatches (14–17) and salt concentrations (18). Gapped annealing events are not considered. Fragments that do not anneal are returned to the pool of ssDNA for additional collisions.

The effect of experimental conditions on annealing probabilities is well described by the factor α, which depends only on the equilibrium constant, K (defined for ΔG_T = G_dsDNA – G_ssDNA, at temperature T), the total initial concentration of the ssDNA fragments annealing, C_T, and the identity of those fragments (b = 4 if they are distinct and b = 1 if they are self-complementary).

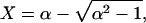1

The annealing probability decreases from 1 to 0 as α increases from ≈1 to ∞.

If two ssDNA molecules do anneal to form a hybridized pair, DNA polymerization occurs in the 5′→3′ direction off the terminal 3′ end, provided this end is stably hybridized. In all results presented, this extension was modeled as a polymerase with 100% fidelity and processivity, although the extension algorithm can be readily modified to reflect polymerase choice. Finally, dNTP monomers are always assumed to be in excess.

Once members of the ssDNA pool no longer hybridize over a large number of collisions, successfully hybridized and extended dsDNA is melted, added into the ssDNA pool, and subjected to additional rounds for progressive reassembly into longer fragments. Because the fragment sequences are independently tracked throughout this process, at the end of each round a number of shuffling metrics, length distribution, crossover number, type and distribution, and reassembly efficiency, are readily analyzed. One step of this analysis actually emulates the final step of DNA shuffling, often referred to as “PCR with primers,” where a PCR reaction using primers flanking the original parent sequence is simulated to determine what fraction of the shuffled products can serve as an effective template for the amplification of fully reassembled sequences. Finally, because this is a stochastic model, all results presented here are an average of at least five simulation runs, and error bars indicate one standard deviation from that average.

Results and Discussion

Comparison with Experiment.

Experimental validation of model.

A 769-bp DNA fragment containing the gfp gene was shuffled both in vitro and in silico. Fragmentation was performed by DNase I digestion followed by gel filtration by using the Centri-Sep (Princeton Separations) column system to remove small (<25-bp) DNA fragments. The extent of digestion was varied by changing the digestion time. The fragment lengths showed excellent agreement with an exponential distribution, consistent with earlier models of DNase I digestion as a Poisson process (7). The resulting fragment size distribution could therefore be uniquely specified by two parameters: the AFS just after digestion, and the MFS below which fragments are cleared before reassembly.

Each set of digested DNA fragments was reassembled in a primerless PCR reaction of 30 rounds. The reassembly reactions were analyzed by agarose gel electrophoresis (see Fig. 5, which is published as supporting information on the PNAS web site), and the length distributions of DNA fragments were determined from this digitized image. In parallel, simulations using the same “experimental conditions” generated length distributions for comparison. To compare experimental and simulation data directly, the simulation data were transformed to account for electrophoretic separation effects (see Length Distribution Comparisons, which is published as supporting information on the PNAS web site).

Fig. 1 directly compares experimental and transformed simulated length distributions at two digestion and two concentration conditions. The experimental results after 30 rounds of reassembly were directly comparable to 14 rounds of simulated shuffling, a difference due to experimental DNA polymerase inefficiencies to be discussed later. For heavier digestion conditions (AFS 45 bp, MFS 25 bp), a low initial fragment concentration (8 ng/μl) yielded a pronounced peak around 750 bp, the size of the reassembled gfp gene (Fig. 1a). However, increasing the initial fragment concentration 15-fold (120 ng/μl) resulted in a much broader peak and a lower percentage of reassembled products (Fig. 1b). Under heavier digestion conditions, the simulated length distributions qualitatively and quantitatively captured both the transition from a broader to sharper peak at 750 bp and the increase in the overall proportion of fragments that reassembled.

Figure 1.

Model comparison with experimental GFP shuffling. The length distribution of reassembly reactions in lanes A, C, G, and I in Fig. 2 are plotted, corresponding to four shuffling conditions: low (8 ng/μl) or high (120 ng/μl) concentrations and larger (AFS, 50 bp; MFS, 50 bp) or smaller (AFS, 45 bp; MFS, 25 bp) fragment sizes. Simulated curves based on these conditions for 14 theoretical shuffling rounds are plotted for comparison.

For milder digestion conditions (8 ng/μl), a sharp peak is observed experimentally for both high and low concentration conditions. In contrast, the simulation predicts a somewhat broader peak at 750 bp for the lower initial fragment concentration (Fig. 1c). However, the simulation accurately captures the experimentally observed distribution in the longer length region and shows that the number of fragments larger than 750 bp clearly increases at higher initial fragment concentrations (Fig. 1d).

Subtilisin E shuffling.

Zhao and Arnold (19) shuffled ≈1 kb of DNA containing wild-type subtilisin E and a mutant clone (1E2A) by reassembling fragments between 20 and 50 bp in size (19). Based on the 10 sequenced clones reported, we calculate an average of 2.3 nonsilent crossovers per reassembled gene (see Crossover Calculations from Literature, which is published as supporting information on the PNAS web site). Silent crossovers that rejoin contiguous regions from different parents with high sequence identity yield a sequence no different from either parent and therefore cannot be distinguished experimentally. The most recent DNA shuffling model overpredicts this average with a value of 3.6 nonsilent crossovers per gene (8). Our model predicts 2.7 nonsilent crossovers per gene. Furthermore, after 10 rounds of in silico shuffling, there is never a discernible peak at 1 kb in the length distribution. Most of the DNA is concentrated between 0.4–1 kb, with a smaller fraction between 1 and 2 kb. This agrees well with the electrophoretic analysis presented by Zhao and Arnold (19), which shows a bright region from 0.3 to 0.7 kb followed by a drop in intensity between 1 and 1.5 kb.

Dioxygenase shuffling.

Joern et al. (10) constructed chimeric dioxygenase libraries by family shuffling of three genes ≈2.1 kb in length, encoding the α and β subunits of toluene (tod), tetracholorobenzene (tec), and biphenyl (bph) dioxygenases. For each of the three parent sequences, probes were synthesized for each of six unique positions chosen along the dioxygenase genes. After shuffling, hybridization assays were performed on individual clones from the library by using these 18 probes to analyze crossovers within each clone. For instance, if at the first five positions only probes specific for tec hybridized, and at position 6, a probe specific to bph hybridized, there is one observed crossover from tec to bph between probe positions 5 and 6. Over 300 clones were analyzed for both the two-parent shuffling of tod and tec (84.9% identity) and the three-parent shuffling of tod, tec, and bph (tod-bph, 63.1% and tec-bph, 63.9% identity), conducted at an equimolar ratio. Because the probe hybridization assay reports observed crossovers only between the six different probe positions, Joern et al. (10) devised an algorithm to estimate the actual crossover number within each clone based on these observed crossovers.

This study was an attractive candidate for comparison with simulation, because it reports experimental data for a statistically significant number of clones. Both the two- and three-parent combinations were shuffled in silico under conditions identical to experiment. Computationally reassembled genes, selected by a simulated “PCR with primers” step, were analyzed for probe composition, observed crossovers, and actual crossovers between every probe pair. Initially, simulations were run by using an exponential fragment size distribution with an AFS of 0.5 kb within the range of 0.4–1.0 kb, consistent with the experimental conditions; however, the crossover frequency using such large fragments was much lower than what was reported. It was later determined that the fragment size distribution had a much lower bound (J. M. Joern, personal communication), and we accordingly ran simulations using a corrected exponential distribution with an AFS of 0.2 kb and a MFS of 0.1 kb.

Experimental and computational crossover results using the 0.1- to 1.0-kb distribution are compared in Table 1. Observed crossover numbers are in near-perfect agreement for both the two- and three-parent libraries. Actual crossover numbers, as calculated by Joern et al. (10), agree well with both their sequencing data and our model data in the three-parent case. In the two-parent case, however, the model predicts only 4.2 crossovers as opposed to the approximately five reported crossovers. Still, no sequencing data were reported for direct comparison.

Table 1.

Comparison of reported crossover number with model results for dioxygenase family shuffling

Crossovers	Two parent			Three parent
	Model	Reported*	Sequencing*	Model	Reported*	Sequencing*
Observed	2.11  ± 0.24	2.11  ± 0.07	—	1.81  ± 0.15	1.77  ± 0.07	—
Actual	4.2  ± 0.4	5.0  ± 0.2	ND	3.8  ± 0.4	3.7  ± 0.3	4.2  ± 0.8

ND, not determined. 

^*Ref. 10. 

In addition to counting the total number of crossovers, their positional distribution along a reassembled sequence can also be compared, because the average number of crossovers within each interprobe region was reported (10). The crossover distribution based on the simulation is presented in Fig. 2. These data agree qualitatively with the data presented in figure 6 of Joern et al. (10), but overall the average number of simulated crossovers predicted within each interprobe region is slightly lower than those reported. This can be explained by the manner in which simulation data were analyzed. Computational crossover distributions were compiled by selecting only those fully reassembled sequences that had all six probe positions completely intact. Any partial probe sequences that result from a crossover within that sequence comprised ≈12% of the total crossovers and were excluded. In contrast, when experimentally determining the crossover distribution, crossovers within the actual probe sequences may have been included if the crossover occurs at the beginning or end of a probe, because a positive probe hybridization event could potentially occur even if the entire probe sequence is not intact.

Figure 2.

Crossover distribution in dioxygenase family shuffling. Model-based prediction of average crossovers between each parent pair for each interprobe region are plotted for two-parent (a) and three-parent (b) dioxygenase family shuffling.

During the reassembly of dioxygenase sequences, the annealing temperature was stepped from 65 to 41°C in 3°C increments, with 90 sec spent at each annealing temperature. Unlike a previous model (8), this simulation does not consider annealing events between reaction steps; i.e., during reassembly it does not allow annealing to occur gradually as the temperature in the reaction ramps down from the 94°C melting temperature to the final annealing temperature. A scaling argument implies that the time for reaching equilibrium of a complex mixture of fragments at a given temperature is longer than the time a thermocycler spends at each temperature as it ramps down, an assumption that thermal melt curves support (see Estimating Collision Frequency of ssDNA in Dilute Solution, which is published as supporting information on the PNAS web site). However, with the particular annealing schedule used by Joern et al. (10), it was assumed that 90 sec was long enough to reach equilibrium, and the model was modified to consider the stepwise decrease in annealing temperature from 65°C, yielding the dioxygenase results presented. If the annealing schedule is ignored and an annealing temperature of 41°C is used, both observed and actual crossover numbers are overpredicted. If a gradual annealing is considered from 94 to 41°C, crossover numbers are underpredicted. Therefore, a careful consideration of reaction time scales is crucial in both the analysis and design of DNA shuffling reactions.

Model Insights.

The model's predictive value was validated by comparison with three independent sets of experimental data, and subsequent analysis of the simulation results leads to several insights into the DNA shuffling process. This model has the unique advantage of tracking and recording the sequences of all molecules in the ensemble throughout the shuffling reaction, thus providing a round-by-round account of the process. These data permit the analysis of any metric based on all fragments present at any step, rather than the more limited set of fully reassembled sequences at the end of the reassembly process, and thereby provide a dynamic view of how sequences evolve during reassembly. Several insights can be drawn from this type of analysis: (i) the creation of “junk” sequences, or ones that do not resemble a full-length gene; (ii) a natural tradeoff between the percent of sequences containing a fully reassembled product and the frequency of crossovers in those sequences; and (iii) the creation of multimeric reassembly peaks, in a process where fully reassembled sequences continue to assemble into larger concatemers of portions of parent gene sequences.

“Junk” Sequences and Reassembly Efficiency.

The simulation results show that during reassembly, only a fraction of fragments reassemble to contain a full-length gene, and we refer to this fraction as the reassembly efficiency.§ The remaining fragments are either on their way to becoming full-length or are “junk” sequences that do not resemble a full-length gene. The majority of annealing events occur between nearly complementary fragments that originate from contiguous sequences within their parent(s). However, simulations show that noncontiguous fragments can also anneal, and the result is often junk sequences with sections derived from disparate regions of various parents and little resemblance to the parent sequences being shuffled. Noncontiguous fragments are more likely to anneal under conditions of low hybridization stringency and/or when the parent sequences contain internal regions of high sequence identity, such as repeats.

Hybridization stringency is a function of two readily varied parameters, annealing temperature and initial fragment concentration, and is well described by the factor α in Eq. 1. The qualitative effect of varying these parameters on annealing is intuitively apparent from Le Chatelier's principle. Because annealing is an exothermic dimerization reaction, both decreasing the annealing temperature and increasing the concentration shift the equilibrium toward the dsDNA state. However, the nature of that shift is different for each parameter (see Model Development, which is published as supporting information on the PNAS web site). Temperature variation exerts very strong and sequence-dependent effects on an annealing event so that the conversion for this event varies sharply from 1 to 0 as the temperature decreases within a small range centered at its melting temperature. Therefore, decreasing the temperature progressively allows less probable mismatched annealing events to occur, but only in the precise order in which their melting temperatures are reached. In contrast, the conversion is a weaker function of concentration so that increasing the concentration only gradually increases conversion. In addition, concentration nonspecifically increases the probability for any mismatched annealing event to occur in a sequence-independent manner.

Why is this important for DNA shuffling? If one were for example shuffling two parent sequences with low sequence identity, increasing the concentration would in a nonsequence biased manner allow the shuffling reaction to gain access to low homology crossover events between correct or contiguous sequences of the parent genes, whereas reducing temperature would still bias crossovers to regions of higher sequence identity. This potentially advantageous effect of concentration variation must be finely tuned, however, because increasing concentration too high would also promote the formation of junk sequences.

Tradeoffs Between Reassembly Efficiency and Crossover Frequency.

If efficient reassembly were the sole criterion for a successful shuffling protocol, then we might always choose conditions of high stringency to minimize the formation of junk sequences. However, there is a second criterion, the genetic diversity of reassembled sequences arising from the presence of crossovers. The crossover frequency, the average number of crossovers per base pair, is a measure of this genetic diversity. A natural tradeoff between the reassembly efficiency and crossover frequency is apparent by considering how initial digestion conditions affect these metrics.

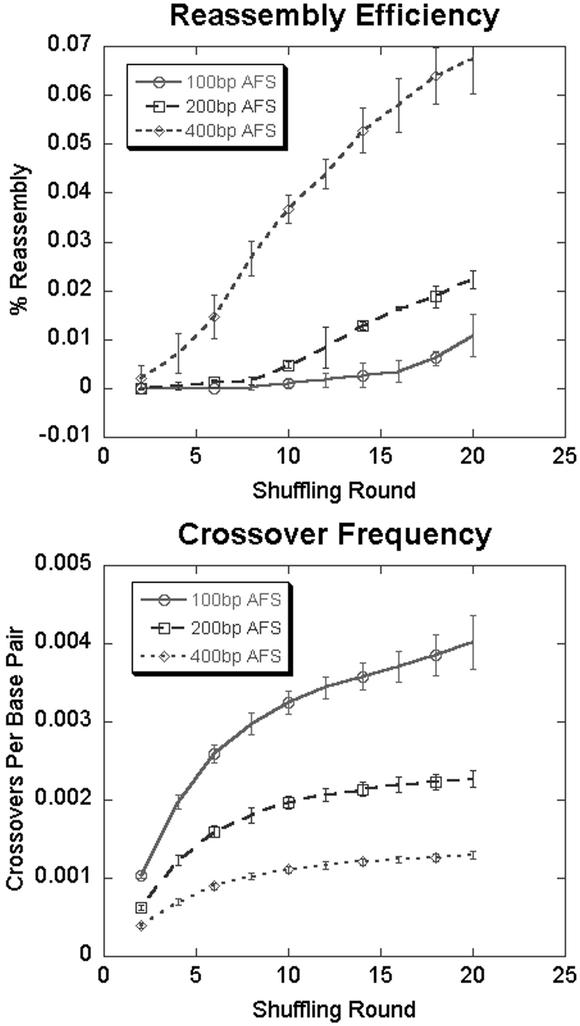
In the limit of no digestion, all initial fragments reassemble to a full-length gene, with no crossovers. As the initial fragments decrease in size, however, the fraction that reassembles decreases, but the number of crossovers among this fraction increases. To further illustrate this point, we consider the in silico family shuffling of two distinct adeno-associated viral cap genes, which encodes the viral capsid, from the AAV-1 and AAV-2 serotypes. These genes share ≈80% sequence identity and were chosen because of their large size, 2.2 kb, and a growing interest in reengineering them for gene therapy applications (20). The reassembly/crossover tradeoff for this case is illustrated in Fig. 3. The AFS was varied with a constant MFS of 50 bp. Not surprisingly, as the AFS decreases from 400 to 100 bp, there is a 4-fold increase in crossover frequency. However, there is a >6-fold drop in reassembly efficiency. Further simulations indicate that no reassembly occurs when the AFS falls below 50 bp.

Figure 3.

Tradeoffs in reassembly efficiency and crossover frequency. Plots of reassembly efficiency and crossover frequency for the in silico shuffling of the 2.1-kb cap ORF of adeno-associated virus (AAV) illustrate a tradeoff in reassembly efficiency and crossover frequency that can be selected based on digestion conditions.

For any initial fragment size distribution, moderate increases in the hybridization stringency will increase the reassembly efficiency by reducing the likelihood that mismatched sequences anneal. However, larger increases in stringency will eventually reduce the reassembly efficiency by making even correct annealing events unlikely.

These curves can be directly used to intelligently design and optimize shuffling protocols. For example, selecting the digestion conditions and/or hybridization stringency that maximize the product of reassembly efficiency and crossover frequency is an effective starting point in designing a shuffling protocol. If the initial experimental recovery of a reassembled product is successful, the benefits of repeating the experiment under conditions that promote more crossovers can be directly weighed against accompanying losses in reassembly efficiency by evaluating such curves (Fig. 3).

Multimeric Sequences.

Calculations of reassembly efficiency account for products that contain the full-length product. Once a sequence is “fully” reassembled, however, the simulation results show that it can multimerize and continue to grow indefinitely yet still serve as a template during the final “PCR with primers” step of DNA shuffling. Under high stringency conditions, sequences with no internal identity rarely grow larger than the size of the full-length product. However, sequences that contain a few internal tracts of identity tend to create multimers of the reassembled gene. As stringency conditions are lowered, these multimeric peaks in the length distribution become less prominent, as conditions favor junk DNA formation.

Although a fully reassembled sequence always remains fully reassembled as it grows (and contributes to the reassembly efficiency accordingly), multimers should be avoided because the ability of the “PCR with primers” step of shuffling to recover shuffled products is significantly reduced for any sequence much larger than the shuffled product length. This reduction occurs because primers anneal at multiple points along the template, and their extensions interfere with one another. This suggests an optimal number of rounds of shuffling for recovering the most shuffled products exists when the peak for a “monomeric” fully reassembled gene is highest within the length distribution, which the model can help locate. Moreover, decreasing the concentration could further enhance this peak because the relative annealing probabilities for “proper” reassembly versus “out of sequence” reassembly would increase, thereby reducing junk DNA formation and limiting multimer formation.

Some Limitations.

Role of polymerase.

In all comparisons of experimental data with simulation data presented here, the number of experimental rounds of shuffling is greater than the number of simulated rounds. As with conventional PCR, the reason for this difference is likely amplification inefficiencies due to the finite polymerase processivity. Table 2 compares the theoretical and actual rounds in three cases. The ratio of actual to theoretical rounds for both GFP and subtilisin E is similar but is lower for the dioxygenase family shuffling. This closer agreement for dioxygenase shuffling might be explained by the fact that the experimental annealing and extension times were three times as long in this study (10). The polymerase would have more opportunity to overcome its limited processivity during the longer extension, and possibly annealing, step.

Table 2.

Inefficiencies in reassembly

Gene	Length, bp	Actual rounds	Theoretical rounds
GFP	760	30	14
Subtilisin E	986	40	16
Dioxygenases	≈2,100	35	20

Although at present, the polymerase is modeled with perfect fidelity and processivity, future work may study the effects of polymerase choice on the shuffling outcome. For example, during the experimental GFP shuffling, the use of Vent polymerase (NEB) vs. Vent (exo-) had significant effects on reassembly efficiency (data not shown). Our simulation can be adjusted to account for effects such as error rate, finite processivity (by making longer extensions less probable), polymerase 3′ exonuclease activity (by digesting away single-stranded 3′ ends of a hybridized dsDNA molecule after annealing but before extension), or the addition of 3′ terminal adenosines, as in the case of Taq polymerase.

Annealing thermodynamics.

The calculation of annealing probabilities between two colliding DNA molecules rests on two assumptions. First, we use a two-state model of hybridization in which two ssDNA molecules transit directly between a single-stranded and double-stranded state. As fragments become larger and temperatures become lower, however, the two-state model is no longer a realistic view of the physics, because ssDNA molecules can transit through multiple states with varying degrees of secondary structure. This effect changes the associated probabilities for each state, thereby reducing the accuracy of a two-state calculation. Second, the model does not currently consider gapped annealing events. Gapped annealing occurs when multiple noncontiguous regions of the two strands of ssDNA hybridize, leaving a gap, or ssDNA loop, in one or both of the strands. The gapped portion may adopt a hairpin configuration or some other form of secondary structure to stabilize this state.

In light of the above considerations, the utility of using a two-state thermodynamic model to simulate shuffling reactions becomes increasingly limited with larger fragments (>2 kb). Although the inclusion of an exhaustive search for the equilibrium states of large fragments is too computationally intensive to be practical, limited searches might be incorporated with no change to the model framework, to improve simulations involving large fragments.

Conclusion

DNA shuffling is a powerful tool for the generation of sequence and functional diversity in the field of protein engineering and evolution. Although current techniques to create genetic diversity have traditionally been applied by using a trial-and-error approach, future approaches will likely consist of a molecular toolkit to direct classes of changes in particular locations on DNA strands with extreme precision (21), requiring an intimate understanding of the molecular processes involved. We have developed and validated a framework for modeling PCR-based in vitro genetic diversification processes that is designed to account for changes in nearly all of the experimental parameters involved. To our knowledge, this is the first model that considers the reassembly of sequences other than the full-length gene product. Our discussion of several insights gained from interpreting model results is intended to be directly useful to experimentalists and to serve as a basis for the application of this model by ourselves and others to further explore the process of DNA shuffling. Finally, the model is sufficiently flexible that only minor modifications make it directly applicable to other techniques for in vitro recombination, such as the STaggered Extension Process (22). We anticipate that this model may prove valuable in furthering our knowledge of the molecular mechanisms of DNA shuffling and for the prediction of optimal conditions for a successful shuffling reaction.

Abbreviations

AFS

average fragment size

MFS

minimum fragment size

ssDNA

single-stranded DNA

dsDNA

double-stranded DNA