Abstract
We have developed a high-throughput approach to the labor-intensive problems of DNA cyclization, which we use to characterize DNA curvature and mechanical properties. The method includes a combinatorial approach to make the DNA constructs needed and automated real-time measurement of the kinetics using fluorescence. We validated the approach and investigated the flexibility of two kinds of nicked DNA and AT dinucleotide repeats. We found that, although the nicks hardly alter the bending flexibility, they significantly increase the torsional flexibility, and that the AT repeat has 28% (±12%) lower bending rigidity than a generic DNA sequence.
Sequence-dependent DNA curvature and flexibility are important characteristics of DNA structure (1–5), which influences almost every aspect of DNA-related processes (6, 7). The idea that DNA sequence information might also be encoded through its 3D shape and mechanical properties may provide a new dimension for functional genomics (8). However, our limited power of mapping DNA tertiary structure from its sequence impedes the testing of this idea, due to lack of a reliable and convenient approach to quantify DNA bending and flexibility (9).
Among a variety of approaches that have been used to measure the global curvature and flexibility of DNA, DNA cyclization has the advantage of high sensitivity, a complete theoretical basis, and the capacity to measure almost all interesting features of global geometric and mechanical properties of DNA, including the magnitude and direction of its curvature, helical repeat, and bending and twisting flexibility (10–13). Its principle is illustrated in Fig. 7, which is published as supporting information on the PNAS web site, www.pnas.org. In this method, the J factors of a series of DNA molecules containing the same test sequence are measured and analyzed by using a model that relates them to DNA properties. The J factor is the effective concentration of one end of a DNA molecule at the other and equal to the ratio of the unimolecular ligation rate constant (k1) to the bimolecular ligation rate constant (k2) catalyzed by DNA ligase under certain conditions. Because k2 is the same for all constructs with the same cohesive ends, the main aim of DNA cyclization is to measure k1.
The traditional implementation (10, 14) of cyclization involves radioactive labeling of DNA constructs and separation of the ligation mixture by PAGE to obtain data on ligation kinetics. The data are mainly interpreted by Monte Carlo simulation to determine curvature and flexibility parameters. Several aspects limit throughput, including the time needed to prepare the ≈15 constructs required for the study of a single sequence. The need for multiple oligonucleotide syntheses, constant optimization of PCR reactions, and the limited lifetime of radioactive labeled constructs make the sample preparation extremely tedious. Second, determining ligation rates from gels is labor-intensive. Finally, data interpretation using Monte Carlo simulation is cumbersome and computationally intensive. Due to these difficulties, it is not uncommon for the analysis of a single piece of DNA to take >1 yr.
It is the main aim of this study to overcome the bottlenecks of DNA cyclization implementation and to establish a high-throughput approach suitable for extensive studies of sequence-dependent DNA curvature and flexibility. Two main improvements are presented: a combinatorial method for making DNA constructs and a fluorescence method for monitoring the kinetics of ligation. In the former, only one chemical synthesis containing the test sequence is required to make all of the needed constructs by a standard PCR protocol. In the latter, donor and acceptor fluorophores are used to label the two ends of DNA constructs during PCR. Cyclization of the construct by ligation brings the two otherwise well-separated dyes close together, leading to fluorescent resonant energy transfer between the two dyes that permits real-time measurement of the kinetics. These two improvements, coupled with a new statistical mechanical theory to replace the Monte Carlo simulation (13), significantly increase the throughput of DNA cyclization studies. Using these methods, it has been possible to obtain information about DNA bending and flexibility for many sequences within 1 wk.
In this work, we validated the new methodology, especially by checking the perturbation due to the dye-labeling, and found that its effect on the J factor is minimal and can be accounted for in cyclization modeling. We used the new approach to measure the flexibility of nicked DNA and poly(AT) dinucleotide repeat. Two different nicks in the middle of the B DNA sequence were studied: one contains a phosphate group at the 3′ end and a hydroxyl group at the 5′ end (designated as NwP), i.e., 5′-tagacctaggatgct-P OH-gactcattgtcgatt-3′, and the other lacks the phosphate group (designated as N).
The effect of breaks in the sugar–phosphate backbone on the structure and dynamics of DNA is of considerable interest due to its relevance to DNA repair. One of the main conclusions from previous investigations is that the nick barely changes the B DNA configuration and its bending flexibility, at least at high-salt conditions (15–19). We find that in addition to <7% increases in bending flexibility for both nicks, the nicks significantly enhance the torsional flexibility, with average twisting fluctuations of 30° at the nick NwP and 64° at the nick N, respectively. An 8° bending toward the opposing strand for N and 29.1° (±0.2°) unwinding for NwP was also documented.
The extent of dependence of DNA bending and torsional flexibility on sequence remains controversial. Early results from direct measurements of flexibility in solution suggested there are >40- and 3-fold variations in torsional and bending rigidities, respectively (20). Later measurements reduced the range to mainly within 2-fold (21). Numerous indirect estimations of DNA flexibility deduced from DNA crystal structure (22), protein–DNA affinity (6, 23), activities of enzymes with DNA as substrate (24), etc., have still differed significantly. In all cases, the TA step seems to be the most flexible dinucleotide step. Our cyclization experiment for the 30-bp AT repeat shows that the AT repeat has only 28% (±12%) lower bending rigidity relative to a generic B DNA control (21°C), consistent with a recent measurement of 20% from EPR at higher temperature (30°C) (25) but much less than previously thought. Similarly, we did not find significant higher torsional flexibility for the AT repeat. A slightly larger helical repeat (10.64 ± 0.04) was observed, in accordance with previous results.
Materials and Methods
Preparations of Oligonucleotides.
All oligonucleotides were synthesized by the Keck Foundation Laboratory at Yale University. Both fluorescein- and tetramethylrhodamine (TAMRA)-labeled oligonucleotides, i.e., 5′-cgccatggaatcgatgaa-(fluorescein-dt)-tcctg-3′ (L12D) and 5′-gcagatatcgatcgca-(TAMRA-dt)-cacgttg-3′, were chemically synthesized through the incorporation of fluorescein-dT and TAMRA-dT according to the manufacturer's recipe (Glen Research, Sterling, VA). The fluorescein- and TAMRA-labeled oligos were purified by 10% denaturing and nondenaturing gels, respectively. The unlabeled versions of both primers were also synthesized and gel-purified. Concentrations of all of the oligos were measured by their absorbance at 260 nm.
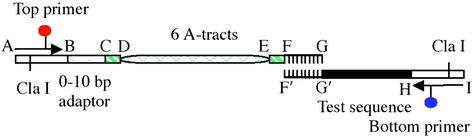
The compositions for the top and bottom templates are schematically shown in Fig. 1, with their detailed nucleotide sequences published as supporting information on the PNAS web site. The 30-bp test sequences correspond to the nucleosome positioning sequence (NPS, ref. 14), EcoRI site containing sequence, B DNA with and without nicks, and AT repeat. Nicked DNAs were made by ligation of chemically synthesized oligomers, as was the AT sequence because of insertion–deletion PCR errors (see Fig. 8, which is published as supporting information on the PNAS web site). All of the top strands were synthesized in 0.2-μmol scales, and the bottom strands in 40-nmol scales. Dilutions (104-fold) of the template strands were prepared in 10 mM Tris, pH 8.0/2 mM NaCl/0.05% Nonidet P-40/5% glycerol from ≈0.5-ml stock solutions after desalting.
Figure 1.
Diagram showing the template composition and primers of our high-throughput PCR approach to make the DNA constructs with different total lengths and phasing. The nucleotide sequences of the top and bottom strands can be found in Supporting Text, which is published as supporting information on the PNAS web site.
Preparation of DNA Constructs.
The 100-μl PCR mix containing 10 μl of 10× high-fidelity PCR buffer, 10 μl of 2 mM dNTP mix, 4 μl of 50 mM MgSO4, 2 μl of each of the primers in 50 μM, 4 μl 1:104 diluted top template strand, 2 μl of 1:104 diluted bottom template strand, 0.6–0.8 μl of 5 units/μl Platinum TaqDNA polymerase with high fidelity (Invitrogen), and sufficient H2O were split in two 0.2-ml PCR tubes and subjected to one cycle of 60 s at 94°C (to activate antibody-bound DNA polymerases) and 32 cycles of 30 s at 94, 59, and 68°C. To make radio-labeled constructs, 0.5–4 μl of 10 mCi/ml [α-33P]dATP (NEN) were added into the above mix. PCR products were purified by using a QIAquick PCR purification kit (Qiagen, Valencia, CA), digested in 60–85 μl with 0.5–5 units of ClaI for 3–12 h, and then gel purified in a dark room with 10% PAGE (40 cm long). DNA bands were cut from the gel under UV illumination after ≈15 min staining with SYBR gold gel solution (Molecular Probes) or in terms of films after 3 h exposure for the 33P labeled constructs. DNA was electroeluted from gels with a microelectroeluter (Amicon) in batches. The residual SYBR-gold was removed from the stained DNA by loading the DNA on the QIAquick spin column, washing with 2 × 0.75 ml of PE buffer, and eluting in 75 μl of 10 mM Tris, pH 7.6.
Cyclization Kinetics.
Both DNA dilution (in a fluorescence quartz cuvette with a minimum volume of 100 μl) and ligase dilution (in a 1.5-ml polypropylene tube) were prepared in 50 mM Tris⋅HCl/10 mM MgCl2/10 mM DTT/1 mM ATP/25 μg/ml BSA, pH 7.8/0.05% Nonidet P-40 and preequilibrated to 21°C before mixing. Samples were excited at 485 nm and detected at 525 nm, with both slit widths set to 20 nm, by a Cary-Eclipse fluorescence spectrometer (Varian) equipped with a Peltier containing four-cell holder. The final DNA concentrations were adjusted so that the net initial emission readings were within 10–200 arbitrary units, whereas 1 nM labeled DNA corresponds to 260 units. The maximum dead time of mixing four samples is ≈35 s. Different batches of ligase dilutions may differ in their activities up to 2-fold and should be scaled to the same activity level by doing tests on the same construct. For radioactive-based cyclization, the standard procedures were followed (11, 14).
Simulations of Cyclization Data.
Except for N, data were analyzed with the new theory (13), which assumes that the configuration fluctuations of small DNA molecules are limited to the vicinity of their mechanical configurations. For all simulations, a total of 16 J factors from both the total length assay and the phasing assay were fitted simultaneously by optimizing the indicated parameters to minimize the error between simulated and experimental values (13). The mechanical configurations for the circular DNA containing the nick N are often not available from our iterative algorithm, especially for the out-of-torsional-phase constructs, probably because the involved molecules are so floppy that the mechanical configurations belonging to different topoisomers are not well separated. Therefore, its simulation was performed by the Monte Carlo method (14, 26).
Results and Discussion
Design of DNA Constructs for Cyclization.
Two strategies have been developed to extract the curvature and mechanical properties from a set of J factor measurements: the total length assay and the phasing assay (13, 14, 27). In the first assay, the total length of the DNA construct is changed, whereas the phasing between the test sequence and the A tracts is fixed, and vice versa in the phasing assay. The former is sensitive to DNA helical repeat, bending and twisting flexibility, and the latter to DNA curvature and bending flexibility.
Our approach to making DNA constructs with different total lengths and phasing lengths is shown schematically in Fig. 1. The template consists of two oligonucleotides (e.g., strands AG and IF′) obtained by chemical syntheses, with 10 nucleotides at the 3′ ends (FG and G′F′ regions) complementary. The AG strand can vary in length from 113 to 123 nt by adjusting the adaptor BC, which is used to change the total lengths of the final DNA constructs from 150 to 160 bp, assuming a 30-bp test sequence. The A-tract region DE may shift in segment CF to change the phasing lengths (of the EG region) from 12 to 22 bp between the right end of the A-tracts and the left end of the test sequence. Once a library of top strands is synthesized, it can be used for all test sequences.
Notable features of this PCR strategy include only one synthesis needed for each new test sequence, a single pair of primers, and no purifications for the templates. Cloning and sequencing reveal that the number of mutations is less than one per construct (data not shown). In addition, shifting the A-tracts instead of the test sequence to change the phasing length (14) gives us a valuable way to detect any unwanted curvature in our construct other than that associated with the test sequence and A-tract portion, as presented below.
Naming DNA constructs starts with a character designation for the test sequence, followed in order by two numbers for the construct length and the phasing length, with L (linker) between them. For a dye-labeled construct, a suffix D is used.
Fluorescence Changes on Cyclization.
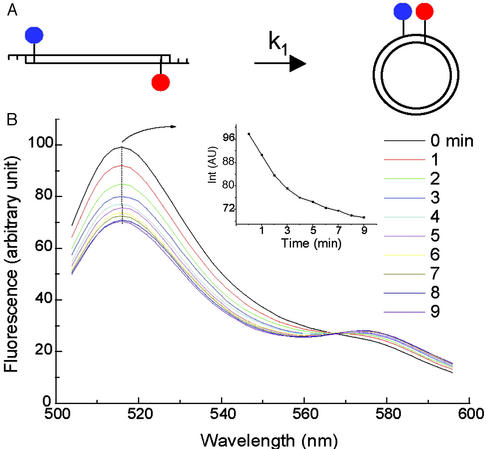
Fig. 2 exhibits the typical change in fluorescence emission spectrum on DNA cyclization. Ligation leads to an emission decrease for the fluorescein peak at 515 nm and a simultaneous increase for the TAMRA peak at 575 nm due to fluorescence resonance energy transfer, which is confirmed by the fact that no decay of fluorescein emission is observed for the construct that lacks TAMRA, as shown in Fig. 3B. Both the fluorescein and TAMRA peaks can be used to follow the cyclization kinetics directly, and they give the same cyclization rate constants within experimental error. However, because the change in amplitude of the fluorescein peak is larger, as shown in Fig. 2B Inset, it was used for all subsequent studies. The appearance of the isosbestic point at 568 nm is consistent with the existence of two fluorescent species in the ligation process: linear and ligated species.
Figure 2.
(A) Diagram showing the principle of cyclization with the fluorescence approach. (B) The emission spectra scanned every minute for ≈5 nM NPS156L16D in 50 units/ml T4 DNA ligase. The test sequence in this construct is three repeats of the 10-bp NPS, i.e., TATAAACGCC, that was recently investigated (14). Background is subtracted from the spectra. (Inset) The emission change with time at the fluorescein peak. The parameter settings for the spectrometer are: 485 nm excitation, 10 nm excitation and emission slits, 240 nm/min scan rate, and 800 V photomultiplier tube voltage.
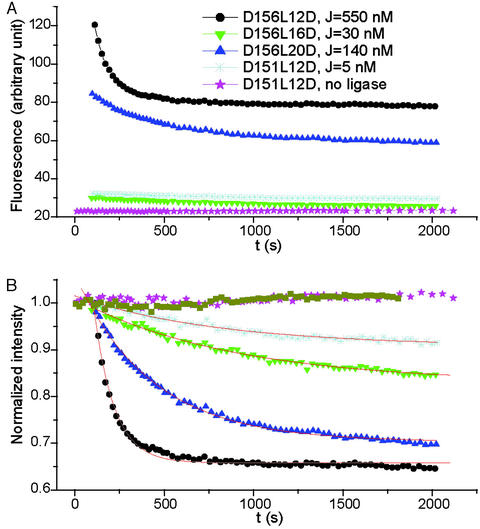
Figure 3.
(A) Fluorescein emission decay on the circularization of different DNA constructs containing the same test sequence, i.e., three repeats of CGCGAATTCG. The ligase concentration is 1,000 units/ml. All construct concentrations are estimated to be <0.5 nM. To make sure only unimolecular circularization is involved in the reactions, constructs are ligated at different concentrations, depending on their J factors. To appreciate the large span of the cyclization rates, the corresponding J factors from the radioactive approach are given (28), which follow their trace names. (B) Emission that is normalized at the first time point. The difference in the final intensities between D156L12D and D156L20D is caused by their different dead times when four cyclizations were performed in parallel, whereas the ligations for the other two have not completed yet. The same symbols as in A were used. The additional dark yellow trace represents the normalized emission of fluorescein-only labeled construct NPS156L12F in 50 units/ml ligase. The red lines are fitted curves with the formula y(t) = y0 + Ae−k1t, where k1 is the cyclization rate constant. The slight increases in emission for both the control without ligase addition and NPS156L12F were probably caused by residual bubbles during mixing, because they were not reproducible.
Fig. 3 shows the real-time emission changes for different constructs. The large span of the time scales for the circularization and the good reproducibility show that this method is highly sensitive. The decay is well fitted with a single exponential as a consequence of the unimolecular nature of the reaction.
At high DNA concentration, the observed fluorescence change may come from bimolecular ligation as well. For the dye-labeled DNA construct with CG cohesive ends, the bimolecular association can occur in three different ways: one between fluorescein- and TAMRA-labeled ends and two between ends labeled with the same dyes. The different association pathways probably have different rate constants, due to possibly different perturbations of dye-labeling for ligations, which may complicate the data interpretation. To avoid this situation, our cyclization experiments were always done at a low enough concentration so that bimolecular ligations were negligible. It can be shown that the DNA concentration should be much less than the J factor to ensure that the unimolecular reaction pathway is preferred. In this case, the measured cyclization rates are independent of the DNA concentrations (data not shown). The smallest J factor encountered in this study is ≈0.5 nM, therefore the lowest concentration should be <≈0.1 nM, which can be detected by our fluorimeter with a sensitivity of 1 pM for fluorescein.
Cyclization Rate Constant vs. Ligase Concentration.
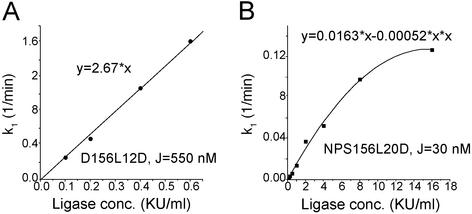
The preequilibrium requirement for DNA cyclization between the linear monomer and the circular ligatable substrate leads to a linear dependence of the ligation rate constant on the ligase concentration (see Fig. 7). To make sure the requirement is met for the dye-labeled construct, the rate constants at different ligase concentrations were measured for a good as well as a poor cyclizer, with results shown in Fig. 4. A good linear relationship was observed for the good cyclizer, where the ligase concentration changes by 6-fold. However, for the poor cyclizer, the linearity is lost at high ligase concentration in which its cyclization rate constant is still much lower than that of the good cyclizer, which probably results from failure of the preequilibrium condition. For all of the constructs to circularize in a reasonable time scale, the cyclization for poor cyclizers has to be carried out at higher ligase concentrations but still in the linear region, whereas for good cycliers, the cyclization has to be done at lower ligase concentrations. The resultant rate constants at different ligase concentrations can be normalized by taking advantage of the linear relationship.
Figure 4.
Dependence of the cyclization rate constant on ligase concentration for good (A) and poor (B) cyclizers. The equations are for the fitted curves. The indicated J factors are from refs. 14 and 28.
Unwanted Curvature in DNA Constructs.
Global curvature may exist in the B DNA part of our construct that was previously considered straight (14). We thus performed the cyclizations using constructs that lack a test sequence and are not dye labeled, using the radioactive approach. Results from the phasing assay and the total length assay are shown in Table 1 and Fig. 9A, which is published as supporting information on the PNAS web site, respectively, with the best-fit parameters given in Table 2. Due to the limited data, the bending and twisting flexibility of the B DNA and the A-tract parts was assumed to be the same. The phasing assay indicated a significant curvature in the B DNA part of these constructs. The global bending magnitude and direction could be modeled with an 8.5° roll toward the minor groove at the sixth dinucleotide step, which is exactly in the middle of an EcoRI site (gaattc). Because it has been recently shown that the EcoRI-containing sequence has a 7–8° curvature toward the minor groove (28), it is reasonable to ascribe the observed bending to the EcoRI site. However, mutation of the EcoRI site to gactac did not significantly reduce the curvature, which suggests that there is a more complex bending profile in the B DNA part.
Table 1.
Comparison of J factors from experiment and simulation in the phasing assays
| Construct name |
J factor, nM
|
|
|---|---|---|
| Experiment | Simulation | |
| V126L12 | 13.5 | 11.4 |
| V126L14 | 33.0 | 24.1 |
| V126L16 | 14.3 | 15.1 |
| V126L18 | 4.5 | 4.4 |
| V126L20 | 2.2 | 2.8 |
| B156L12 | 12.6 | 12.6 |
| B156L14 | 44.0 | 34.1 |
| B156L16 | 40.4 | 42.8 |
| B156L18 | 20.7 | 20.5 |
| B156L20 | 8.8 | 8.3 |
| B156L12D | 14.8 (±3) | 13.3 |
| B156L14D | 38.5 (±4) | 35.4 |
| B156L16D | 32.9 (±3) | 44.7 |
| B156L18D | 20.1 (±2) | 21.6 |
| B156L20D | 11.0 (±2) | 8.7 |
| NwP156L12D | 14.4 (±2) | 20.3 |
| NwP156L14D | 41.6 (±5) | 39.5 |
| NwP156L16D | 30.4 (±4) | 38.7 |
| NwP156L18D | 24.1 (±3) | 20.4 |
| NwP156L20D | 16.4 (±2) | 12.3 |
| N156L12D | 33.5 (±6) | 30.2 |
| N156L14D | 15.2 (±3) | 21.5 |
| N156L16D | 25.7 (±3) | 27.6 |
| N156L18D | 26.7 (±3) | 24.6 |
| N156L20D | 24.5 (±3) | 21.3 |
| AT156L12D | 38.1 (±4) | 37.3 |
| AT156L14D | 84.1 (±7) | 85.1 |
| AT156L16D | 74.4 (±6) | 92.3 |
| AT156L18D | 51.7 (±7) | 47.9 |
| AT156L20D | 33.9 (±4) | 27.1 |
The prefixes V, B, NwP, N, and AT denote the constructs that contain no test sequence, the non-nicked B DNA sequence, the nicked DNA with or without the phosphate with at 3′ end, and the AT repeat, respectively. The J factors for the first two sets were from the radioactive approach and the others from the fluorescent approach.
Table 2.
The best-fit parameters for the DNA in construct for cyclization
| DNA | Kink, ° | Roll and tilt fluctuations, ° | Twist fluctuations, ° | Twist, ° |
|---|---|---|---|---|
| B-DNA | −8.5 (±0.2) | 4.56 (±0.03) | 5.1 (±0.3) | 34.13 (±0.09) |
| A-tracts | * | 4.56 (±0.03) | 5.1 (±0.3) | 34.85 |
The fitting was performed by optimizing the magnitude and position of the kink for the unwanted curvature, twist of B DNA, and bending and twisting flexibilities, assuming a kink by roll and the same flexibilities for the A-tracts as those of B DNA. The bold A-tract twist is a fixed parameter for the optimization, shown here only for comparison. The base-pair fluctuations σ here are related to the persistence length P by P = 1/σ2 with the helical rise l = 3.4 Å, or base pair as unit, and the torsional force constant C by C = lkBT/σ2, respectively (13).
The parameters for the A-tract curvature are from ref. 29.
Perturbation Due to the Dye-Labeling of DNA.
Although there has been no report of dye-labeling causing a large alteration of DNA structure, a small perturbation could affect the cyclization kinetics. It was shown that TAMRA can stack at DNA ends like an additional base, and fluorescence resonance energy transfer can occur between TAMRA and G nucleotide (30, 31). Because no absolute J factors are available from direct cyclization for dye-labeled DNA molecule containing CG cohesive ends due to lack of single bimolecular association constant k2, a construct with nonpalindromic CGAT ends was designed (Fig. 8) and its J factor measured. Cyclizations of both the dye-labeled and unlabeled versions of the molecule lacking a test sequence were performed in parallel by using the radioactive approach, with results exhibited in Fig. 5. Although the dye-labeling simultaneously increases the unimolecular and bimolecular ligation rate constants by 3.8-fold, the J factor barely changes, indicating that the dye-labeling largely perturbs the two ligation processes in the same way. The increase in rates may result from the additional electrostatic and/or hydrophobic interactions between the fluorophores. Because the J factor is independent of the cohesive ends, the corresponding dye-labeled molecule with CG ends was used as a control to obtain the absolute J factors for all of the constructs with the same ends by the fluorescent approach.
Figure 5.
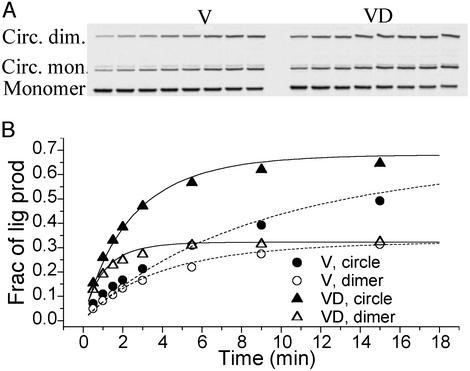
The cyclization kinetics of the 126-bp unlabeled (V) and dye-labeled (VD) DNA constructs with CGAT cohesive ends. The gel autoradiography is shown in A and the quantitative evolution of each ligation product is presented in B. Both cyclizations were carried out with the same 20 nM total DNA and 160 units/ml T4 ligase. The best-fit parameters for V are: k1 = 0.082 min−1, k2 = 0.0022 min−1⋅nM−1, J = 36.7 nM; for VD: k1 = 0.31 min−1, k2 = 0.0084 min−1⋅nM−1, J = 37.2 nM. The dashed and solid curves for V and VD, respectively, were calculated with the same formula as in ref. 11, except for the symmetric factor from the palindromic nature of the cohesive ends. The weak bands slightly above those corresponding to circular monomer barely change with time and were not identified. The ligatable fractions of both V and VD molecules were estimated to be ≈80%, and only these fractions were analyzed in B.
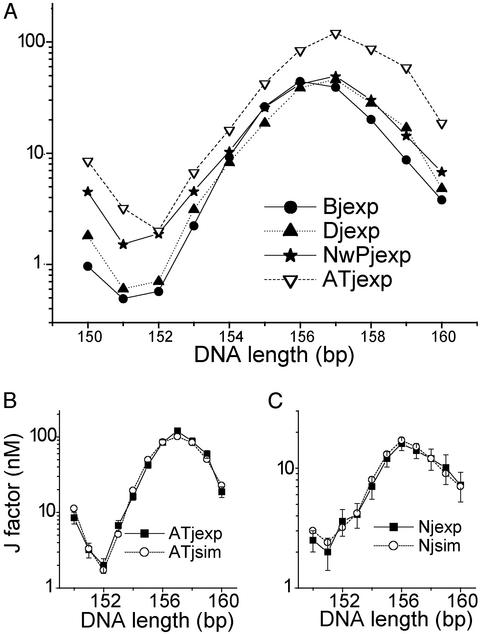
To further investigate the perturbation, cyclizations were done by using both unlabeled and labeled constructs containing a generic B DNA that has the same sequence as the nicked DNA. For the latter, the cyclizations were carried out by the fluorescent approach. The comparison of their J factors is shown in Fig. 6A and Table 1, with their individual comparisons with simulated J factors presented in Fig. 9 B and C. In general, the dye-labeling changes the J factor only slightly compared with the unlabeled one, but in the total length assay a small right shift of the peak corresponding to torsional in-phase constructs and a slight increase of the minimum ≈151 bp corresponding to torsional out-phase molecules is observed, indicating an unwinding and enhanced torsional flexibility. To quantitatively assess the effects of the dye-labeling, the parameters for the 30-bp B DNA test sequence were first obtained by fitting all of the J factors for the constructs without the presence of fluorophores, which are shown in Table 3. The 5-fold variation in J factor in the phasing assay mainly results from the unwanted curvature, instead of the 2.5° roll for the B test sequence. The perturbation of dye-labeling was then modeled with changes in twist and bending and twisting flexibilities for the first and last 15 bp, in which the fluorophores are attached, with the above parameters for the B DNA test sequence fixed. Compared with the same unlabeled region (Table 2), the two dyes cause a 7.5° (±0.9°) total unwinding and slightly enhanced bending and torsional flexibilities.
Figure 6.
Comparisons between experimental J factors for different test sequences (A) and between J factors from experiments and simulations for the AT repeat (B) and the nicked DNA without the phosphate group (C). The prefixes B and D designate the unlabeled and dye-labeled constructs containing the B DNA test sequence, respectively.
Table 3.
The best-fit parameters for the different 30-bp test sequences and the dye-labeled region
| DNA | Kink | Roll and tilt fluctuations, ° | Twist fluctuations, ° | Twist, ° |
|---|---|---|---|---|
| B test sequence | 2.5° (±1.8°) roll | 4.587 (±0.075) | 4.2 (±1.3) | 34.22 (±0.20) |
| Dye labeled region | 0 | 4.644 (±0.046) | 5.48 (±0.94) | 33.88 (±0.14) |
| NwP | 1.2° (±0.6°) tilt | 4.733 (±0.051) | 6.84 (±1.2) | 33.25 (±0.10) |
| N | 8° tilt | 4.6 | 12.4 | 34.1 |
| AT repeat | 0 | 5.388 (±0.054) | 4.58 (±0.93) | 33.83 (±0.12) |
All kinks, if present, are at the 16th dinucleotide step between ga, 1 bp toward the 3′ end from the position corresponding to the nick.
Flexibilities of Nicked DNA and AT-Repeat.
Once all of the parameters for the labeled DNA constructs, other than the test sequence, are set, the curvature and flexibility of the nicked DNA test sequence can be accurately measured from our florescent approach. Fig. 6A and Table 1 show the J factors from experiments for the nicked DNA, i.e., NwP and N, and 30-bp AT repeat, and Table 3 exhibits their best-fit parameters. Initially, when all of the parameter changes were attributed to the nicked site, the optimization was not efficient with our gradient search algorithm, probably due to the strong correlations between the parameters assigned in one site. For computational reasons, the best-fit parameters shown in Table 3 were obtained by spreading over the entire 30-bp test sequence during the optimization for the nicked DNA. Compared with the non-nicked B DNA, both nicked DNAs barely change their bending force constants. In contrast, there are decreases in twisting force constants as large as 2.7- and 8-fold for NwP and N, respectively, which were not previously observed. In addition, although a 1.2° (±0.6°) tilt toward the opposing strand is documented with its optimal position at 16th dinucleotide step for NwP, the curvature increases to 8° for N. This large change is evident from nearly complete exchange of the positions of the extreme J factors in the phasing assay, suggesting there exists a curvature comparable to the magnitude of the unwanted bending. Supposing that all of the global changes result from the nicked site, the nick renders 30° and 64° twisting fluctuations for NwP and N, respectively. As for the bending, they can be transformed to the nicked site by a combination of tilt Acosω and roll Asinω, where A is the tilt magnitude at the 16th site and ω the twist. For example, the equivalent global curvature for N can be modeled with a 6.9° tilt and a 4.1° roll at the nick.
From the global increase in the J factors of the AT repeat compared with the B DNA control, it is evident that the AT repeat has higher bending flexibility. Simulation shows that it has 28% (±12%) lower persistence length, i.e., 113.1 (±5.1) bp, than that of the control, or 156 (±26) bp. This result is consistent with the recent finding from EPR that the AT repeat has an ≈20% lower bending force constant (25). Considering the difference in the temperature at which both experiments were performed, i.e., 21°C for ours and 30°C for the EPR, and that the sequence-dependent bending force constant decreases with temperature increase (unpublished work), the consistency between both results is even better. However, although our best-fit torsional force constant of the AT repeat is 16% lower than that of B DNA, their relatively large errors weaken the conclusion. Nevertheless, it does support the early observation that there is no significant sequence-dependent torsional flexibility (32), if the AT repeat represents the most torsionally flexible sequence.
For all of the above experiments, the J factor measured by the radioactive approach has an average relative error of 20% from two independent measurements, yielding the errors shown in Tables 2 and 3. Each J factor obtained from the fluorescent approach is the average of at least three independent measurements. The error depends on the J factor: although a good cyclizer normally has a relative error <12%, a poor cyclizer has to be ligated at lower concentration, leading to an error of ≈20%. It is not clear why the fluorescence decays of the molecules containing N are abnormally fluctuating, leading to the larger errors in J factors seen in Fig. 6C, which were repeatedly observed for three batches of samples prepared. The nonspecific binding of the T4 DNA ligase to the nicks should be minimal, because the J factors do not change with total DNA concentrations (data not shown).
The small perturbation of DNA structure due to dye-labeling may result from the stacking of fluorescein or TAMRA onto the DNA duplex due to hydrophobic and electrostatic interactions (30, 31). Because of its positive charge and large aromatic ring, TAMRA might intercalate into DNA base pairs to a small extent. Previous theoretical analysis demonstrated that change in torsional flexibility mainly affects the J factors of the molecules whose ends are nearly completely out of torsional phase. Due to the small number of such constructs and the relatively larger error in determining their J factors, the measured torsional flexibilities have much greater errors than bending flexibilities. Constructs with their lengths near 162 bp should be added into our library.
Previous cyclization experiment for nicked DNA did not reveal an increase in the torsional flexibility, contrary to what is reported here (33). Two facts may explain the discrepancy. One is the relatively long DNA constructs (1,361, 250, and 247 bp) the authors used, none of them completely out-of-torsional phases. The other is their relatively large error in measuring the J factor. Our experience suggests it is very difficult to get consistent J factors with no measures to prevent ligase adsorption to polypropylene tubes: without Nonidet P-40 in the ligation buffer (12), the bulk ligase activity can reduce by half within 1 hr, as seen from Fig. 10, which is published as supporting information on the PNAS web site.
The only 27.5% higher flexibility of the AT repeat does not exclude the possibility that the local flexibility of TA dinucleotide step is much larger. Similar flexibility measurements for different dinucleotide and trinucleotide repeats should be able to resolve the local flexibility between the TA and AT steps. Finally, it must be noted that all of the apparent global flexibility parameters are abstracted from a model of isotropic flexibility.
Our approach to DNA cyclization makes possible examination of the properties of large numbers of DNA sequences. The main alternative is provided by single-molecule methods, for example the work of De Santis and colleagues (34). Because cyclization allows intense focus on small sequence elements, and single-molecule visualization provides an overall view of molecular shape, the methods should be viewed as complementary.
Supplementary Material
Acknowledgments
We thank Peter Moore, Jason Kahn, David Lilley, and Stephen Levene for helpful comments. This work was supported by National Institutes of Health Grant GM 21966 and by the National Foundation for Cancer Research.
Abbreviations
- NPS
nucleosome positioning sequence
- TAMRA
tetramethylrhodamine
References
- 1.Fratini A V, Kopka M L, Drew H R, Dickerson R E. J Biol Chem. 1982;257:4686–4707. [PubMed] [Google Scholar]
- 2.Wu H M, Crothers D M. Nature. 1984;308:509–513. doi: 10.1038/308509a0. [DOI] [PubMed] [Google Scholar]
- 3.Koo H S, Wu H M, Crothers D M. Nature. 1986;320:501–506. doi: 10.1038/320501a0. [DOI] [PubMed] [Google Scholar]
- 4.Hagerman P J. Annu Rev Biophys Biophys Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- 5.Hagerman P J. Annu Rev Biochem. 1990;59:755–781. doi: 10.1146/annurev.bi.59.070190.003543. [DOI] [PubMed] [Google Scholar]
- 6.Gartenberg M R, Crothers D M. Nature. 1988;333:824–829. doi: 10.1038/333824a0. [DOI] [PubMed] [Google Scholar]
- 7.Dickerson R E, Chiu T K. Biopolymers. 1997;44:361–403. doi: 10.1002/(SICI)1097-0282(1997)44:4<361::AID-BIP4>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 8.Pedersen A G, Jensen L J, Brunak S, Staerfeldt H H, Ussery D W. J Mol Biol. 2000;299:907–930. doi: 10.1006/jmbi.2000.3787. [DOI] [PubMed] [Google Scholar]
- 9.Crothers D M. Proc Natl Acad Sci USA. 1998;95:15163–15165. doi: 10.1073/pnas.95.26.15163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shore D, Langowski J, Baldwin R L. Proc Natl Acad Sci USA. 1981;78:4833–4837. doi: 10.1073/pnas.78.8.4833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Crothers D M, Drak J, Kahn J D, Levene S D. Methods Enzymol. 1992;212:3–29. doi: 10.1016/0076-6879(92)12003-9. [DOI] [PubMed] [Google Scholar]
- 12.Kahn J D, Crothers D M. Proc Natl Acad Sci USA. 1992;89:6343–6347. doi: 10.1073/pnas.89.14.6343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang Y, Crothers D M. Biophys J. 2003;84:136–153. doi: 10.1016/S0006-3495(03)74838-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Roychoudhury M, Sitlani A, Lapham J, Crothers D M. Proc Natl Acad Sci USA. 2000;97:13608–13613. doi: 10.1073/pnas.250476297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hays J B, Zimm B H. J Mol Biol. 1970;48:297–317. doi: 10.1016/0022-2836(70)90162-2. [DOI] [PubMed] [Google Scholar]
- 16.Pieters J M L, Mans R M W, Vandenelst H, Vandermarel G A, Vanboom J H, Altona C. Nucleic Acids Res. 1989;17:4551–4565. doi: 10.1093/nar/17.12.4551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Aymami J, Coll M, Vandermarel G A, Vanboom J H, Wang A H J, Rich A. Proc Natl Acad Sci USA. 1990;87:2526–2530. doi: 10.1073/pnas.87.7.2526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Snowdenifft E A, Wemmer D E. Biochemistry. 1990;29:6017–6025. doi: 10.1021/bi00477a020. [DOI] [PubMed] [Google Scholar]
- 19.Furrer P, Bednar J, Stasiak A Z, Katritch V, Michoud D, Stasiak A, Dubochet J. J Mol Biol. 1997;266:711–721. doi: 10.1006/jmbi.1996.0825. [DOI] [PubMed] [Google Scholar]
- 20.Hogan M, Legrange J, Austin B. Nature. 1983;304:752–754. doi: 10.1038/304752a0. [DOI] [PubMed] [Google Scholar]
- 21.Chen H H, Rau D C, Charney E. J Biomol Struct Dyn. 1985;2:709–719. doi: 10.1080/07391102.1985.10506318. [DOI] [PubMed] [Google Scholar]
- 22.Olson W K, Gorin A A, Lu X J, Hock L M, Zhurkin V B. Proc Natl Acad Sci USA. 1998;95:11163–11168. doi: 10.1073/pnas.95.19.11163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hegde R S. Annu Rev Biophys Biomol Struct. 2002;31:343–360. doi: 10.1146/annurev.biophys.31.100901.142129. [DOI] [PubMed] [Google Scholar]
- 24.Hogan M E, Roberson M W, Austin R H. Proc Natl Acad Sci USA. 1989;86:9273–9277. doi: 10.1073/pnas.86.23.9273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Okonogi T M, Alley S C, Reese A W, Hopkins P B, Robinson B H. Biophys J. 2000;78:2560–2571. doi: 10.1016/S0006-3495(00)76800-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Levene S D, Crothers D M. J Mol Biol. 1986;189:61–72. doi: 10.1016/0022-2836(86)90381-5. [DOI] [PubMed] [Google Scholar]
- 27.Sitlani A, Crothers D M. Proc Natl Acad Sci USA. 1996;93:3248–3252. doi: 10.1073/pnas.93.8.3248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nathan D, Crothers D M. J Mol Biol. 2002;316:7–17. doi: 10.1006/jmbi.2001.5247. [DOI] [PubMed] [Google Scholar]
- 29.Koo H S, Drak J, Rice J A, Crothers D M. Biochemistry. 1990;29:4227–4234. doi: 10.1021/bi00469a027. [DOI] [PubMed] [Google Scholar]
- 30.Edman L, Mets U, Rigler R. Proc Natl Acad Sci USA. 1996;93:6710–6715. doi: 10.1073/pnas.93.13.6710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Eggeling C, Fries J R, Brand L, Gunther R, Seidel C A M. Proc Natl Acad Sci USA. 1998;95:1556–1561. doi: 10.1073/pnas.95.4.1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fujimoto B S, Schurr J M. Nature. 1990;344:175–178. doi: 10.1038/344175a0. [DOI] [PubMed] [Google Scholar]
- 33.Shore D, Baldwin R L. J Mol Biol. 1983;170:957–981. doi: 10.1016/s0022-2836(83)80198-3. [DOI] [PubMed] [Google Scholar]
- 34.Zuccheri G, Scipioni A, Cavaliere V, Gargiulo G, De Santis P, Samori B. Proc Natl Acad Sci USA. 2001;98:3074–3079. doi: 10.1073/pnas.051631198. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.