Effects of Arterial Wall Stress on Vasomotion

Abstract

Smooth muscle and endothelial cells in the arterial wall are exposed to mechanical stress. Indeed blood flow induces intraluminal pressure variations and shear stress. An increase in pressure may induce a vessel contraction, a phenomenon known as the myogenic response. Many muscular vessels present vasomotion, i.e., rhythmic diameter oscillations caused by synchronous cytosolic calcium oscillations of the smooth muscle cells. Vasomotion has been shown to be modulated by pressure changes. To get a better understanding of the effect of stress and in particular pressure on vasomotion, we propose a model of a blood vessel describing the calcium dynamics in a coupled population of smooth muscle cells and endothelial cells and the consequent vessel diameter variations. We show that a rise in pressure increases the calcium concentration. This may either induce or abolish vasomotion, or increase its frequency depending on the initial conditions. In our model the myogenic response is less pronounced for large arteries than for small arteries and occurs at higher values of pressure if the wall thickness is increased. Our results are in agreement with experimental observations concerning a broad range of vessels.

INTRODUCTION

Vasomotion consists of cyclic diameter variations of muscular arteries or arterioles resulting from changes in contraction and relaxation of smooth muscle cells (SMCs) present in the vessel wall. Arterial contraction is caused by an increase in the smooth muscle cytosolic calcium concentration (1). Calcium rises may be induced by vasoconstrictors present in the vascular system. Vasomotion has been shown to result from synchronous, i.e., in-phase, calcium oscillations in SMCs (2–6). The synchronization involves cell coupling via gap junctions (4,6). Calcium increases in endothelial cells (ECs), situated at the interface between blood and muscular media, are known to induce a decrease of the calcium level in SMCs and to relax the vessel. However, the role of the endothelium for vasomotion is still controversial in the experimental literature (3–9). In a previous theoretical article we have reconciled the seemingly contradictory findings and shown that the endothelium only modulates vasomotion (10).

In vivo SMCs and ECs are exposed to various mechanical stresses. Blood pressure creates a circumferential stress in SMCs and ECs, and ECs are in addition directly subject to fluid shear stress. It has been shown that an increase in intraluminal pressure may induce a vessel constriction, a phenomenon called the myogenic response (11). Indeed, stress is known to increase the intracellular calcium level by activating cell membrane stretch-activated channels (SACs) in SMCs and ECs (12). These mechanosensitive channels are permeable to mono- and divalent cations including potassium, sodium, and calcium (13). SACs increase the cytosolic calcium level by promoting a direct influx of extracellular calcium and by depolarizing the SMCs, which leads to a calcium influx through voltage-operated calcium channels. The myogenic response occurs at higher values of pressure in hypertension (14), and it is less prevalent in large vessels than in small ones (15). Not only can intraluminal pressure modulate the amplitude and frequency of vasomotion (16–19), it can also abolish (15,16,20) or enhance vasomotion (15,20,21). Moreover, it has been observed that for a given pressure and vasoconstrictor concentration, large arteries oscillate at a lower frequency than small arteries (16). Furthermore, the vasoconstrictor concentration needed to induce vasomotion may be lower in small than in large arteries (16).

The aim of this article is to explain these experimental observations about the effects of stress on arterial vasomotion. To the best of our knowledge, there is no theoretical model linking the intracellular calcium concentration of a coupled population of SMCs and ECs to arterial diameter variations. We have previously developed a model describing the calcium dynamics of a coupled population of SMCs and ECs (10,22). This model is able to reproduce the synchronous calcium oscillations in SMCs, thus vasomotion. It is here extended to include SACs, calcium-induced active stress, and the resulting arterial diameter variations. We firstly omit the population of ECs, because the most important features of the role of stress on vasomotion can be explained by considering only the effect of stress on SMCs. We begin by analyzing the consequence of pressure variations on the calcium dynamics and the arterial radius variations. The myogenic response is reproduced. We then study how changing the arterial diameter and wall thickness affects our results. Moreover, we analyze whether active stress may have a synchronizing effect on calcium oscillations in SMCs. Finally, we show how the presence of ECs and shear stress modulate the results obtained with the population of SMCs.

MATHEMATICAL MODEL

Calcium dynamics

The equations describing the calcium dynamics in SMCs and ECs are adapted from our previous article (10). The calcium dynamics of a single SMC i is described by five variables: the calcium concentration in the cytosol c_i, the calcium concentration in the sarcoplasmic reticulum s_i, the cell membrane potential v_i, the open-state probability w_i of calcium-activated potassium channels, and the IP₃ concentration I_i. A single EC j is modeled by four variables: the cytosolic calcium concentration 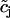, the calcium concentration in the endoplasmic reticulum , the cell membrane potential 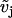, and the IP₃ concentration . Cells are connected to their nearest neighbors via gap junctional electrical, calcium, and IP₃ coupling.

The SMC model is given by

(1)

(2)

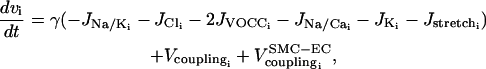(3)

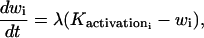(4)

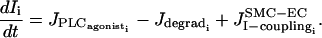(5)

The EC model reads

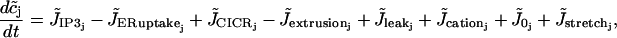(6)

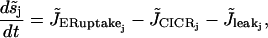(7)

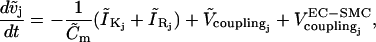(8)

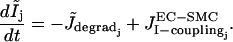(9)

The precise expressions of the various terms appearing in these two sets of nonlinear differential equations are given in the Appendix and are taken from Koenigsberger et al. (10), with the exception of and modeling the SACs. The coefficient 0.1 of in Eq. 1 takes into account that calcium is a divalent ion and carries ∼20% of the total SAC current (23). The terms and are given by

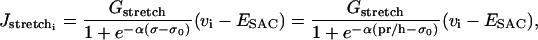(10)

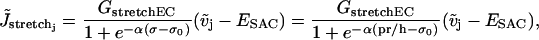(11)

where the constants E_SAC and G_stretch (or G_stretchEC) are, respectively, the reversal potential and the whole-cell conductance for SACs. The open probability of SACs is modeled by the Boltzmann equation 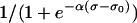, where σ is the cellular membrane tensile stress (24,25). The coefficient α has been estimated by considering the experimental fit 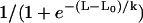relating the normalized SAC current to the length change L of the SMC (26). The constant L₀ = 0.233 is the length change for half-activation of the SAC and k = 0.018 a slope factor. Assuming a linear dependence between the length change and stress, σ = EL, with an elastic modulus E in the order of 10⁶ N/m² (27), one obtains α = (Ek)⁻¹ = 0.0074 mmHg⁻¹. The value of stress for half-activation σ₀ is set to 500 mmHg. Assuming a channel length of 100 Å (28), this value is similar to the typical tension for half-activation, which is ∼1 dyne/cm (25). The circumferential stress σ is related to the transmural pressure p by the Laplace law σ = pr/h, where r is the lumen radius and h the wall thickness.

Active stress dynamics

Calcium and force development in SMCs are related by the cross-bridge phosphorylation and latch-state model of Hai and Murphy (29). In this model, an elevated calcium level induces a contraction through the formation of cross bridges between actin and myosin filaments. There are four possible states for myosin: free nonphosphorylated cross bridges (M), free phosphorylated cross bridges (Mp), attached phosphorylated cross bridges (AMp), and attached dephosphorylated latch bridges (AM) (Fig. 1). The dynamics of the fraction of myosin in a particular state is given by

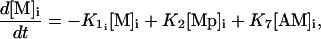(12)

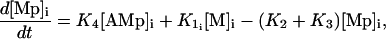(13)

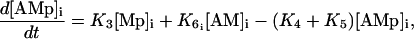(14)

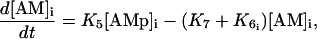(15)

where the rate constants K_n (n = 1, …, 7) regulate the phosphorylation and bridge formation. The only cell-dependent and nonconstant parameter 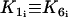is related to the cytosolic calcium concentration. Using Eqs. 12–15 and the fact that the total phosphorylation of myosin [Mp]_i + [AMp]_i is a sigmoidal function of 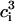(30), we may write (31)

(16)

where γ is a constant characterizing the sensitivity of the contractile apparatus to calcium. Active stress is directly proportional to the fraction of attached cross bridges [AM]_i + [AMp]_i.

FIGURE 1.

Cross-bridge phosphorylation and latch-state model of Hai and Murphy (29). A, actin; M, detached dephosphorylated cross bridge; Mp, detached phosphorylated cross bridge; AMp, attached phosphorylated cross bridge; and AM, attached dephosphorylated cross bridge (latch bridge). K_n (n = 1, …, 7) are rate constants regulating phosphorylation and bridge formation. 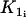and 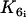depend on the cytosolic calcium concentration.

Vessel radius dynamics

The vessel radius is computed by considering the equilibrium of tangential forces in the wall (Laplace law): pr/h = σ_p + σ_a + σ_v, where σ_p is the elastic stress, σ_a the active stress, and σ_v the viscous stress. Viscous stress is given by σ_v = ηdr/dt, where η is the wall viscosity coefficient (32). The time evolution of the inner vessel radius r is then given by (32)

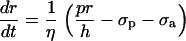(17)

Depending on the value of the radius, the expressions for σ_p are (32)

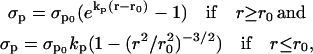(18)

where r₀ is the unstressed radius. Active stress σ_a is directly proportional to the mean fraction of attached cross bridges taken over the whole population of SMCs, < [AM]_i + [AMp]_i > _SMCs, and is dependent on the vessel external radius (32):

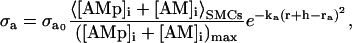(19)

where 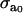is the maximal active stress and ([AMp]_i + [AM]_i)_max the maximal fraction of attached cross bridges. The expression for the wall thickness h is written by assuming that the wall is incompressible and the vessel length constant, i.e., the wall volume is assumed constant, (33):

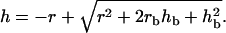(20)

Parameters

The parameter values for the SACs and the equations describing contraction are given in Table 1. Noise is added in parameter values to model stochastic opening of channels (22). In our previous study of a population of coupled SMCs we have deduced gap junctional coupling coefficients for which the solution of synchronous calcium oscillations is stable (22). In particular we have shown that calcium coupling is able to synchronize the calcium oscillations with a reasonable gap junctional permeability P (P = 0.15 μm/s). This weak gap-junctional permeability takes into account that calcium is buffered and therefore, diffuses slowly. Heterocellular coupling has been discussed in Koenigsberger et al. (10). Intracellular diffusion is neglected in our model, as the intracellular diffusion time is negligible with respect to the period of oscillation. An increase in the SMC vasoconstrictor concentration is simulated by an increase of the PLC rate . Note that here we consider receptor-ligand agonists that stimulate PLC like norepinephrine or phenylephrine, as these vasoconstrictors are commonly used experimentally to induce vasomotion (2–5).

TABLE 1.

Parameter values for SACs and contraction

Parameter	Description	Value	Source
Gstretch, GstretchEC	Whole cell conductance for SACs.	0.0061 μM mV−1 s−1	Model estimation
ESAC	Reversal potential for SACs.	−18 mV	(26)
α	Slope of stress dependence of the SAC activation sigmoidal.	0.0074 mmHg−1	Model estimation
σ0	Half-point of the SAC activation sigmoidal.	500 mmHg	Model estimation
K2	Rate constant for phosphorylation and bridge formation.	0.5	(29)
K3	Rate constant for phosphorylation and bridge formation.	0.4	(29)
K4	Rate constant for phosphorylation and bridge formation.	0.1	(29)
K5	Rate constant for phosphorylation and bridge formation.	0.5	(29)
K7	Rate constant for phosphorylation and bridge formation.	0.1	Model estimation
([AMp]i + [AM]i)max	Maximal fraction of attached cross bridges.	0.8	(29)
γ	Phosphorylation coefficient.	17 μM−3 s−1	(31)
η	Viscosity coefficient.	100 mmHg s	Model estimation
	Elastic stress.	0.0191 mmHg	(32)
kp	Elastic coefficient.	0.15 μm−1	Model estimation
r0	Unstressed radius.	50 μm	Model estimation
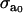	Maximal active stress.	1.8 × 105 N/m2	(32)
ka	Muscular coefficient.	0.0006 μm	Model estimation
ra	Optimal radius for active stress.	95 μm	Model estimation
rb	Basal radius.	56.3 μm	Model estimation
hb	Basal thickness.	15 μm	Model estimation

Numerical methods

The model equations were solved using a fourth-order Runge-Kutta method. The equations were integrated on a cylindrical grid of rectangular SMCs (outer layer) superposed on a cylindrical grid of rectangular ECs (inner layer), as illustrated in Fig. 2. ECs are arranged parallel and SMCs perpendicular to the vessel axis. Cell geometry is approximated by a rectangle. The width of an EC is taken as twice that of an SMC, and the length of an EC 1.3 times that of an SMC (34). The population of cells used in our numerical simulations comprise ∼80 SMCs and 30 ECs. With a single SMC size of 5 μm × 50 μm and a vessel diameter in the order of 150 μm, the vessel segment is ∼50 μm long. Each cell is connected via gap junctions with its nearest neighbors on the same layer and with the cells on the other layer directly superposed on it. Cell geometry only plays a role in determining the number of neighbors: each SMC has generally six nearest-neighboring SMCs and five-to-six nearest-neighboring ECs, and each EC has generally six nearest-neighboring ECs and ∼15 nearest-neighboring SMCs. We firstly omit the population of ECs, i.e., we set the SMC-EC coupling terms and to zero, and analyze only the effect of stress in SMCs. Indeed, we will show afterwards that ECs have only a modulating effect.

FIGURE 2.

The model equations are integrated on a cylindrical grid of SMCs (outer layer) superposed on a cylindrical grid of ECs (inner layer). ECs are arranged parallel and SMCs perpendicular to the vessel axis. Cell geometry is approximated by a rectangle. The width of an EC is taken as twice that of an SMC, and the length of an EC 1.3 times that of an SMC (34). With a size of a single SMC of 5 μm × 50 μm and a mean vessel diameter in the order of 150 μm, nine SMCs are necessary to surround the arterial lumen. Each cell is connected with its nearest neighbors on the same layer (homocellular connection, −) and with the cells on the other layer directly superposed on it (heterocellular connection, ‖).

The software AUTO, as implemented in XPPAUT by B. Ermentrout (35), was used for bifurcation diagrams. The number of equations that can be handled simultaneously with this software is limited. As even a single SMC needs 10 equations, it is difficult to treat more than one SMC with AUTO. Therefore the bifurcation diagrams present only the calcium dynamics of one uncoupled SMC or a single coupled SMC-EC pair. The vessel radius corresponds then to the one of a vessel with a mean calcium level equal to the calcium level of the uncoupled SMC. The transition from a bifurcation diagram of a single uncoupled cell to the simulation of a population of coupled cells has been studied in detail previously (10,22). We have shown that for a population of SMCs the synchronous oscillatory solution is stable for the coupling coefficients and noise level used, and a bifurcation analysis for two coupled SMCs has been presented (22). Note that the term “synchronous” is used for in-phase calcium oscillations. The bifurcation diagram of an uncoupled SMC gives, then, the solutions corresponding to a synchronous population of SMCs, as for identical cells coupling terms are zero during synchrony. All stable solutions indicated by AUTO and our numerical simulations coincide exactly.

RESULTS AND DISCUSSION

Calcium dynamics in SMCs and vessel contraction at constant pressure

Fig. 3 shows bifurcation diagrams obtained by varying the agonist-activated PLC-rate, , at a constant pressure of 80 mmHg. Fig. 3 a gives the cytosolic calcium concentration c_i of an uncoupled SMC, and Fig. 3 b the vessel radius r and the oscillation frequency f. At low values of , i.e., at low vasoconstrictor concentration, the cytosolic calcium level is in a stable steady-state (domain I). In this domain, a population of SMCs coupled through gap junctions present irregular asynchronous calcium increases arising from stochastic opening of channels (22). Increasing the vasoconstrictor concentration, the calcium concentration and the vessel contraction increase, and a Hopf bifurcation occurs: the steady state becomes unstable and the calcium level begins to oscillate (domain II). In a population of coupled SMCs, these oscillations are synchronous with our coupling coefficients (22), giving rise to an oscillating radius, thus vasomotion. The mean calcium level and the oscillation frequency essentially become higher and the mean radius smaller with increasing values of 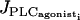. Note that for a small range of the branch of periodic orbits is unstable. This unstable part is delimited by period-doubling bifurcations, and period-doubling solutions are found for the corresponding small range of. Finally, the diagram of Fig. 3 has another Hopf bifurcation from which the steady state becomes stable again (domain III); the cytosolic calcium level is high and no longer oscillates. The radius is constant and small.

FIGURE 3.

Bifurcation diagrams obtained by varying the agonist-activated PLC-rate, , at a constant pressure of 80 mmHg (thick solid line, stable rest state; thick dashed line, unstable rest state; thin solid line, minima and maxima of stable oscillations; and thin dashed line, minima and maxima of unstable oscillations). (a) Cytosolic calcium concentration c_i of an uncoupled SMC. (b) Vessel radius r and oscillation frequency f. Two Hopf bifurcations divide the diagrams into three domains (domains I and III, steady state; and domain II, oscillations).

Time-course simulations of the calcium concentration and the vessel radius in domain II are presented in Fig. 4. The calcium concentration c_i corresponds to that of a representative SMC of a coupled population of SMCs. The vasoconstrictor concentration is higher in Fig. 4 b than in Fig. 4 a, resulting in a higher mean calcium level and oscillation frequency in Fig. 4 b. In the latter figure the radius is small and presents only very small amplitude oscillations. There are two reasons for this last observation. Firstly, at high vasoconstrictor concentration (thus high calcium concentration), there is a saturation of the fraction of attached cross bridges. Indeed, in Fig. 4 b the time-average fraction of attached cross bridges is 0.92, whereas in Fig. 4 a, this fraction amounts to 0.57. A given oscillatory calcium concentration variation changes then less the fraction of attached cross bridges (thus σ_a) in Fig. 4 b. The amplitude of the radius oscillations is therefore smaller in this figure. Secondly, for a given pressure, a high vasoconstrictor concentration induces a small radius. As the dependence of σ_a on the fraction of attached cross bridges decreases with decreasing radius (Eq. 19 with r < r_a), changes in σ_a and radius are less important for a given calcium concentration variation. Calcium oscillations that do not result in significant contraction oscillations have been observed experimentally (5).

FIGURE 4.

Time courses of the calcium concentration c_i of a representative SMC in a coupled population of ∼80 SMCs and the vessel radius r at a constant pressure of p = 80 mmHg. (a) . (b) 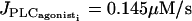. The simulation starts from the equilibrium state of the vessel in the absence of vasoconstrictor.

Role of pressure

The two-parameter bifurcation diagram of Fig. 5 shows the evolution of the two Hopf bifurcations of Fig. 3 with pressure p and rate of PLC 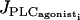. At a fixed vasoconstrictor concentration, increasing p increases the mean calcium level and shifts domains I, II, and III to the left. An increase in pressure-induced stress may then bring about a transition from domain I to domain II or from domain II to domain III. At high values of p the SMC is in domain II in the absence of vasoconstrictor, i.e., when .

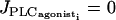FIGURE 5.

Two-parameter bifurcation diagram showing the evolution of the two Hopf bifurcations of Fig. 3 with pressure p and rate of PLC . The two Hopf bifurcations divide the diagram into three domains (domains I and III, steady state; and domain II, oscillations).

The bifurcation diagrams of Fig. 6 show the evolution of the calcium concentration of a single SMC i (Fig. 6 a) and the vessel radius (Fig. 6 b), with respect to pressure in the absence of vasoconstrictor. At low values of pressure, the radius increases with pressure. The open probability of the SAC is low and the calcium level remains constant. For 70 mmHg 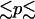140 mmHg, the radius decreases with increasing pressure, a phenomenon called the myogenic response. Experimentally the myogenic response is also observed for pressure values in this range (14). The radius decrease is due to the fact that active stress σ_a dominates the term pr/h in Eq. 17. This is caused by a significant increase in the open probability of the SAC (and thus the calcium level) after a pressure increase. In the pressure range of myogenic response, the domain shifting presented in Fig. 5 is also most significant. At a pressure >140 mmHg, the radius increases with pressure. Indeed, the open probability of the SAC is then nearly one, resulting in low calcium and σ_a variations after a pressure increase. The dominant term in Eq. 17 becomes pr/h, causing a radius increase. Note that, in Fig. 6, the pressure increase has induced a transition from domain I to domain II.

FIGURE 6.

Bifurcation diagrams for the cytosolic calcium concentration c_i of an uncoupled SMC (a) and the vessel radius r (b) with respect to pressure in the absence of vasoconstrictor (thick solid line, stable rest state; thick dashed line, unstable rest state; thin solid line, minima and maxima of stable oscillations; and thin dashed line, minima and maxima of unstable oscillations).

In Fig. 7, we consider a population of coupled SMCs stimulated by a fixed vasoconstrictor concentration. A stepwise increase in pressure induces transitions from domain I to domain II and from domain II to domain III. Indeed, the existence of these transitions is expected from Fig. 5. Within domain I near the Hopf bifurcation, we observe that the calcium transients occur essentially at the moment when the value of stress is changed. This is due to the fact that, in domain I, calcium flashes occur if the calcium level is sufficiently shifted away from its equilibrium position to reach a threshold calcium level necessary for a flash. Here a change in stress simultaneously perturbs all SMCs by moving them away from their steady state. If the system is near the first Hopf bifurcation, this global perturbation induces a simultaneous calcium flash in many SMCs. Thus a change in stress has a synchronizing effect on calcium flashes in domain I. As these calcium flashes result from a change in stress and from random noise (22), not all SMCs present a calcium flash at each stress application. These results agree with experimental observations on mouse aorta mounted on a myograph: calcium flashes in individual SMCs occurred essentially at the precise moment when a step in stretch was applied (36). Increasing p gives rise to a transition from the nonoscillatory domain I to the oscillatory domain II. The reverse transition from domain II to domain I has been observed experimentally by decreasing intraluminal pressure (16,20). In domain II, the synchronization of the calcium signals is achieved, as coupled SMCs present synchronous calcium oscillations in this domain with our coupling coefficients (22). Increasing the pressure increases the oscillation frequency, in agreement with experimental observations (16–19). Shirasawa and Benoit (37) also show that vasomotion frequency gets higher when more and more stretch is applied to the vessel. The oscillation amplitude decreases with pressure (except for a small range of pressure values near the first Hopf bifurcation), which is also reported experimentally (16–19). Increasing even more p induces a transition from domain II to domain III. Experimentally, vasomotion is abolished by increasing pressure, and it reappears after a pressure decrease (15). The transition from domain III to domain II has also been observed experimentally by decreasing the intraluminal pressure (20,21). Thus the transitions predicted by the model may explain how changes in pressure may induce or abolish vasomotion.

FIGURE 7.

Evolution of the cytosolic calcium concentration of five representative SMCs (thin curves) and of the mean calcium concentration (thick curve) of a coupled population of ∼80 SMCs. The uniform SMC vasoconstrictor stimulation begins at t = 0 s. The pressure p is increased stepwise from 40 mmHg to 140 mmHg with steps of 10 mmHg every 120 s.

Experimentally the effect of the drug thapsigargin on a mouse aorta mounted on a myograph has been studied: emptying the intracellular stores of SMCs induces an essentially sustained and nontransient calcium response at every step of stretch (36). This behavior is reproduced in our model (results not shown) when we set the contribution from the stores to zero 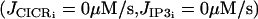. This is expected because in our model, calcium-induced calcium release (CICR) is responsible for the calcium oscillations and flashes (22).

Influence of the artery radius and thickness

As shown on Fig. 8 a, increasing the basal thickness h_b with respect to Table 1 shifts the three domains to the right with respect to Fig. 5. Indeed for the same radius and pressure the circumferential stress pr/h decreases when the thickness h increases, reducing the calcium influx through SACs. Within domain II, the oscillation frequency then decreases with increasing h/r ratio. Moreover, a higher vasoconstrictor concentration is needed to induce vasomotion in thick arteries: in a certain range of vasoconstrictor concentrations and pressure values, thick arteries may be in domain I, whereas thin ones are in domain II. The myogenic response then also occurs for higher values of pressure (compare Figs. 8 a and 6 b). In hypertensive arteries compared to normotensive ones, the sensitivity to vasoconstrictor is smaller (38) and the myogenic response is shifted to higher values of pressure (14). These observations may be related to the fact that the arterial wall is thickened in hypertension. Fig. 8 b has been obtained for a larger artery (basal radius r_b and thickness h_b are increased 1.5 times with respect to Table 1). This figure shows that the myogenic response is less pronounced for large than for small arteries, in agreement with experimental data (15). Moreover, vasomotion amplitude is smaller in large arteries (compare Figs. 8 b and 6 b), which is also observed experimentally (39).

FIGURE 8.

Bifurcation diagrams for the radius r of the vessel with respect to pressure at 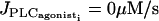(thick solid line, stable rest state; thick dashed line, unstable rest state; thin solid line, minima and maxima of stable oscillations; and thin dashed line, minima and maxima of unstable oscillations). (a) The thickness is changed and increased (h_b = 19 μm) with respect to Table 1. (b) The vessel radius and thickness are 1.5 times larger than in Table 1 (r_b = 84.45 μm, h_b = 22.5 μm, r₀ = 75 μm, and r_a = 144 μm).

Synchronizing effect of active stress

Active stress is responsible for the myogenic response and for diameter oscillations. It may therefore help to synchronize the calcium oscillations in SMCs. Indeed, the term pr/h that enters the expression modeling the SAC (Eq. 10) is the same for each SMC. This term is then a coupling term for the SMCs and may coordinate their calcium oscillations. With active stress as the only coupling, several oscillation cycles are needed to synchronize the calcium oscillations (results not shown). This synchronizing effect then seems insufficient to synchronize the calcium oscillations in the absence of gap-junctional coupling.

Modulating effect of ECs

So far our results have been obtained in the absence of ECs. Now we analyze how the presence of ECs affects our results, i.e., the coupling terms 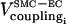and 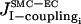are no longer set to zero. Applying circumferential and/or shear stress on ECs induces a calcium influx through SACs and increases the calcium level in ECs. The calcium response to fluid shear stress in ECs has been modeled by Wiesner et al. (40). A high calcium level leads to the hyperpolarization of the ECs and to the generation of nitric oxide. The propagation of the hyperpolarization to SMCs and the effects of nitric oxide decrease the calcium level in SMCs. This has been studied in detail in our article about the role of the endothelium on vasomotion (10). In regard to contraction, stress applied on ECs has then the opposite effect to that of stress applied on SMCs. The two-parameter bifurcation diagram of Fig. 9 gives the evolution of the three domains for a coupled SMC-EC pair with the conductance G_stretchEC of the endothelial SACs and the rate of vasoconstrictor. In this figure, the pressure is constant and we do not vary the conductance of the SAC in the SMC, since we want to analyze the effects of the SACs in ECs. Increasing the SAC conductance G_stretchEC increases the calcium level in the EC. This results in a hyperpolarization of the EC and of the SMC—which decreases the calcium level in the SMC, increases the vessel radius, and shifts the three domains to the right. Assuming that shear stress acts only on ECs, our model is in agreement with the experimentally observed vessel dilation in response to an increased flow (41,42).

FIGURE 9.

Two-parameter bifurcation diagram of a coupled SMC-EC pair showing the evolution of domains I, II, and III with the SAC conductance in EC G_stretchEC and the rate of vasoconstrictor .

Thus, there is a competition between two opposite effects: on the one hand, stress in SMCs increases the calcium level in SMCs, shifts the three domains to the left, and gives rise to the myogenic response; and on the other, stress in ECs decreases the calcium level in SMCs, shifts the three domains to the right, and attenuates the myogenic response. Experimentally, it is generally observed that an increase in pressure leads to an increased calcium level in SMCs and an augmented constriction. The effect of circumferential stress in SMCs seems to predominate its effect in ECs. This is in agreement with the work of Sun et al. (43), showing that the removal of the endothelium only slightly affects the myogenic response. In hypertensive rats, the density of pressure-activated channels has been found to be significantly higher compared with normotensive rats, which could represent a counterregulatory mechanism of ECs in hypertension (44). Indeed, the effect of stress on ECs is then increased (as the macroscopic conductivity G_stretchEC is higher in term , Eq. 11), leading to a lower calcium level in SMCs and a vessel dilation.

Importance of the mean calcium level

By showing how stress may induce and abolish vasomotion, we have illustrated the importance of the calcium level for vasomotion. Changing the calcium level may induce a transition from an nonoscillatory domain to an oscillatory domain and vice versa. We have pointed this out in our article about the role of the endothelium on vasomotion (10): depending on the initial calcium concentration (domain III or domain II) the endothelium can induce or abolish vasomotion by decreasing the calcium level.

Experimentally, no consistent way of inhibiting or promoting vasomotion has yet been found (45). This may be due to the fact that experiments using a drug that inhibits a certain cellular mechanism are generally performed at a fixed vasoconstrictor concentration. Our model suggests that if a drug abolishes vasomotion, it may not directly have abolished the mechanism necessary for oscillations. Instead, it may have affected the calcium level, and may have moved the system out of the oscillatory domain as well. In contrast, if a drug abolishes vasomotion at all vasoconstrictor concentrations, then the mechanism the drug abolishes may be necessary for vasomotion. Experiments in which drugs are applied at a fixed vasoconstrictor concentration and are found to abolish or promote vasomotion should then be interpreted with care.

Thus the vasoconstrictor concentration should always be varied to obtain vasomotion. In arterial preparations where vasomotion is not observed at any vasoconstrictor concentration (46,47), either domain II does not exist or the calcium oscillations in domain II are not able to synchronize (most probably due to an inefficient gap-junctional coupling).

Discussion of the model hypotheses

We have analyzed how changing the arterial radius and wall thickness affects our results. This discussion is simplified and limited to changes in radius and thickness for a given elasticity, viscosity, and maximal active stress of the arterial wall. However, our main conclusions (domain shifting, frequency changes) remain true independently of the precise characteristics of arteries and arterioles. Our model results can therefore be compared to different types of arteries in the experimental literature.

In our study, the effect of stress has been illustrated by analyzing how changes in pressure (thus circumferential stress) affect the calcium dynamics and diameter variations. This choice allowed us to directly compare our results to the experimental literature, as only a few studies have analyzed the role of other types of stress on vasomotion. However, our conclusions are not qualitatively dependent on the kind of stress or stretch acting on SMCs and ECs.

We have assumed that the only effect of stress is to activate SACs without considering other possible mechanosensitive pathways. It has, for example, also been suggested that stress may activate the calcium release from the intracellular stores (48). This other possible pathway can be modeled by increasing the terms 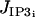or . The cytosolic calcium concentration is then also increased and the three domains are shifted to the left (results not shown).

Bifurcation diagrams have been obtained for a single SMC or SMC-EC pair, since it is difficult to treat large populations of cells with the software AUTO. All conclusions based on the bifurcation diagrams have been verified in numerical simulations of large populations of cells. The links between bifurcation diagrams of single SMCs, bifurcation diagram of two coupled SMCs, and simulation of a population of SMCs and ECs have been studied in detail previously (10,22).

CONCLUSION

We have developed a model describing the calcium dynamics of a population of SMCs coupled to a population of ECs, and the resulting arterial diameter variations. We have modeled the myogenic response and studied how pressure variations affect the intracellular calcium dynamics and vasomotion. Our study shows that an increase in stress increases the calcium concentration in SMCs and in ECs. The calcium increase in SMCs may either induce or abolish vasomotion, or increase its frequency depending on the initial conditions. The calcium increase in ECs decreases the calcium level in SMCs; thus, stress in ECs has the opposite effect on vasomotion than stress in SMCs.

APPENDIX A: DETAILS OF THE MATHEMATICAL MODEL

The various terms appearing in Eqs. 1–9 are described by the following expressions as presented previously (10,22).

The calcium fluxes

(A1)

model the calcium release from IP₃ sensitive stores.

(A2)

model the SR/ER uptake.

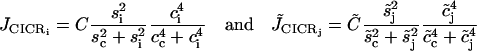(A3)

describe the calcium-induced calcium release (CICR).

(A4)

are the calcium extrusion by Ca²⁺-ATPase pumps.

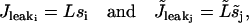(A5)

correspond to the leak from the SR/ER.

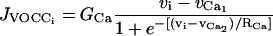(A6)

is the calcium influx through VOCCs.

(A7)

is the Na⁺/Ca²⁺ exchange.The term

(A8)

is the Na⁺-K⁺-ATPase.

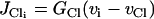(A9)

models the chloride channels.

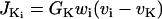(A10)

is the K⁺ efflux.

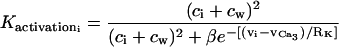(A11)

describes the calcium and voltage activation of K⁺ channels.

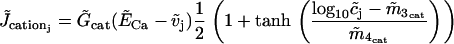(A12)

is the calcium influx through two nonselective cation channels. 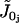regroups further calcium influx (assumed constant) to the cell.

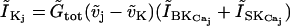(A13)

is the potassium efflux through the BK_Ca channel (a large conductance channel activated by calcium and membrane potential) and the SK_Ca channel (a small-conductance channel only activated by calcium), with

(A14)

and

(A15)

The residual current regrouping Cl⁻ and Na⁺ currents is written

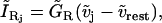(A16)

and the IP₃ fluxes

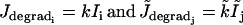(A17)

model the IP₃ degradation. The constants and 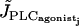are the rate of PLC activated by agonists. The term

(A18)

models the electrical coupling of SMC i with all nearest-neighboring SMCs k. The calcium coupling between SMCs describing calcium diffusion is modeled by the term

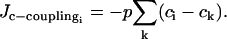(A19)

The term

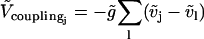(A20)

models the electrical coupling of EC j with all nearest-neighboring ECs l. Heterocellular electrical coupling is modeled by terms

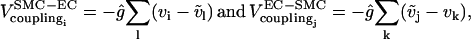(A21)

where are membrane potentials of the neighboring ECs l of SMC i, while v_k are membrane potentials of the neighboring SMCs k of EC j. Heterocellular IP₃ coupling is modeled by terms

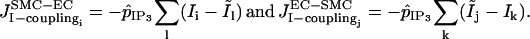(A22)

The parameter values are given in Table 2 for the SMC model and in Table 3 for the EC model. The parameters D, F_Na/K, G_Na/Ca, G_K, and have been changed with respect to Koenigsberger et al. (10), inasmuch as new terms describing SACs have been added in the equations.

TABLE 2.

Parameter values for the SMC model

Parameter	Description	Value
F	Maximal rate of activation-dependent calcium influx.	0.23 μM/s
Kr	Half-saturation constant for agonist-dependent calcium entry.	1 μM
GCa	Whole-cell conductance for VOCCs.	0.00129 μM mV−1 s−1
vCa1	Reversal potential for VOCCs.	100.0 mV
vCa2	Half-point of the VOCC activation sigmoidal.	−24.0 mV
RCa	Maximum slope of the VOCC activation sigmoidal.	8.5 mV
GNa/Ca	Whole-cell conductance for Na+/Ca2+ exchange.	0.007 μM mV−1 s−1
cNa/Ca	Half-point for activation of Na+/Ca2+ exchange by Ca2+.	0.5 μM
vNa/Ca	Reversal potential for the Na+/Ca2+ exchanger.	−30.0 mV
B	SR uptake rate constant.	2.025 μM/s
cb	Half-point of the SR ATPase activation sigmoidal.	1.0 μM
C	CICR rate constant.	55 μM/s
sc	Half-point of the CICR Ca2+ efflux sigmoidal.	2.0 μM
cc	Half-point of the CICR activation sigmoidal.	0.9 μM
D	Rate constant for Ca2+ extrusion by the ATPase pump.	0.08 s−1
vd	Intercept of voltage dependence of extrusion ATPase.	−100.0 mV
Rd	Slope of voltage dependence of extrusion ATPase.	250.0 mV
L	Leak from SR rate constant.	0.025 s−1
γ	Scaling factor relating net movement of ion fluxes to the membrane potential (inversely related to cell capacitance).	1970 mV/μM
FNa/K	Net whole cell flux via the Na+-K+-ATPase.	0.2 μM/s
GCl	Whole-cell conductance for Cl− current.	0.00134 μM mV−1 s−1
vCl	Reversal potential for Cl− channels.	−25.0 mV
GK	Whole-cell conductance for K+ efflux.	0.002 μM mV−1 s−1
vK	Reversal potential for K+.	−94.0 mV
λ	Rate constant for net KCa channel opening.	45.0
cw	Translation factor for Ca2+ dependence of KCa channel activation sigmoidal.	0 μM
β	Translation factor for membrane potential dependence of KCa channel activation sigmoidal.	0.13 μM2
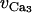	Half-point for the KCa channel activation sigmoidal.	−27.0 mV
RK	Maximum slope of the KCa activation sigmoidal.	12.0 mV
k	Rate constant of IP3 degradation.	0.1 s−1
g	Homocellular electrical coupling coefficient.	1000 s−1
p	Homocellular calcium coupling coefficient.	0.05 s−1

TABLE 3.

Parameter values for the EC model

Parameter	Description	Value
	Maximal rate of activation-dependent calcium influx.	0.23 μM/s
	Half-saturation constant for agonist-dependent calcium entry.	1 μM
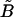	ER uptake rate constant.	0.5 μM/s
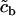	Half-point of the ER ATPase activation sigmoidal.	1.0 μM
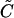	CICR rate constant.	5 μM/s
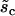	Half-point of the CICR Ca2+ efflux sigmoidal.	2.0 μM
	Half-point of the CICR activation sigmoidal.	0.9 μM
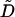	Rate constant for Ca2+ extrusion by the ATPase pump.	0.24 s−1
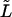	Leak from ER rate constant.	0.025 s−1
	Rate constant of IP3 degradation.	0.1 s−1
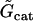	Whole-cell cation channel conductivity.	0.66 nM mV−1 s−1
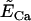	Ca2+ equilibrium potential.	50 mV
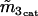		−0.18 μM
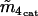		0.37 μM
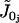	Constant calcium influx.	0 μM/s
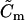	Membrane capacitance.	25.8 pF
	Total potassium channel conductivity.	6927 pS
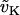	K+ equilibrium potential.	−80 mV
		53.3 μM mV
		53.3 mV/μM
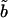		−80.8 mV
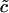		−0.4 μM
		1.32 × 10−3μM/mV
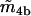		0.30 μM mV
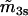		−0.28 μM
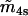		0.389 μM
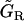	Residual current conductivity.	955 pS
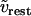	Membrane resting potential.	−31.1 mV
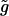	Homocellular electrical coupling coefficient.	1000 s−1
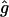	Heterocellular electrical coupling coefficient.	50 s−1
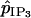	Heterocellular IP3 coupling coefficient.	0.05 s−1