Macrogeographic population structure of the tsetse fly, Glossina pallidipes (Diptera: Glossinidae)

Abstract

Tsetse flies are confined to sub-Saharan Africa where they occupy discontinuous habitats. In anticipation of area-wide control programmes, estimates of gene flow among tsetse populations are necessary. Genetic diversities were partitioned at eight microsatellite loci and five mitochondrial loci in 21 Glossina pallidipes Austin populations. At microsatellite loci, Nei’s unbiased gene diversity averaged over loci was 0.659 and the total number of alleles was 214, only four of which were shared among all populations. The mean number of alleles per locus was 26.8. Random mating was observed within but not among populations (fixation index F_ST = 0.18) and 81% of the genetic variance was within populations. Thirty-nine mitochondrial variants were detected. Mitochondrial diversities in populations varied from 0 to 0.85 and averaged 0.42, and F_ST = 0.51. High levels of genetic differentiation were characteristic, extending even to subpopulations separated by tens and hundreds of kilometres, and indicating low rates of gene flow.

Introduction

Glossina pallidipes Austin (Diptera: Glossinidae) is one of 33 species of tsetse flies. All are exclusively blood feeders. Females possess paired ovaries that consist of only four ovarioles. Fecundity is very low and a frequently fed female requires at least 15 days to produce her first offspring, a mature larva that rapidly pupariates. Further reproductive cycles each require a minimum of nine days. It is unsurprising, therefore, that compared with related Diptera such as blow flies, house flies, and Drosophila spp., tsetse fly populations are small. Despite their small populations, tsetse flies are economically highly significant, because they are the exclusive vectors of African trypanosomiasis.

Glossina pallidipes is among the most economically important tsetse flies. It is zoophagic throughout its range and although flies in some subpopulations may take human blood meals, most will not (Leak, 1999). Glossina pallidipes abundance depends critically on the availability of mammalian hosts and adequate environmental conditions (Rogers & Randolph, 1985). Its geographic distribution extends from south-western Ethiopia to Kenya, Tanzania, Mozambique, and west to the Democratic Republic of the Congo (Ford, 1971; Jordan, 1993; Rogers & Robinson, 2004). Glossina pallidipes populations are scattered and patchy, and weather patterns can explain much of their presence or absence (Robinson et al., 1997a,b). However, where appreciable human densities exist, G. pallidipes populations seem to be low or altogether absent.

Glossina pallidipes bionomics varies regionally (e.g. Langley et al., 1984), suggesting the possibility of a species complex. Because of their blood feeding requirements and low fecundity, tsetse flies are difficult and expensive to culture. Genetic work therefore lags behind that of many other economically and medically important insects (Gooding & Krafsur, 2005). Recently, however, research has begun on the population genetics of G. pallidipes. Diverse populations were sampled in East and southern Africa and allozyme, microsatellite, and mitochondrial variation assessed (Krafsur et al. 1997; Krafsur & Wohlford, 1999; Krafsur, 2002). Results suggested a high degree of population structure and lesser rates of gene flow than might be inferred from the substantial ecological literature. The picture afforded by the foregoing studies requires sharpening. How may we explain the high degree of genetic differentiation, in view of well conducted, authoritative ecological research that predicts an opposite expectation? How important is isolation by distance? Can population differentiation be simply explained by inhospitable habitats that lay between tsetse infested patches? Or by earlier bottlenecking in population densities and reduced geographic distribution? The historical record suggests large reductions in tsetse densities and distribution caused by recurring rinderpest epizootics 75 to 105 years ago that greatly reduced mammalian host populations (Ford, 1971). More intensive sampling than heretofore may help answer some of these questions.

In the present study the population genetic structure of G. pallidipes was examined at eight microsatellite loci. Only three loci were previously scored in this species (Krafsur, 2002) and intra- and inter-locus variances were substantial. Mitochondrial variation was also assessed to provide independent estimates of genetic differentiation and gene flow. Most samples were obtained from Kenya, a generally mountainous country extensively dissected by the Rift Valley. Habitats include the coastal, semi-desert, savannas and forests, some of which may act as physical barriers to gene flow. To lend broader geographic perspective, samples were included from Kenya’s northern (Ethiopia), western (Uganda), and southern neighbours (Tanzania), and also more distant populations from Zambia and Zimbabwe.

Materials and methods

Sampling procedures

Twenty-one G. pallidipes population samples from six countries in East and southern Africa (fig. 1) and totalling 720 flies were examined for genetic variation. Fourteen populations were sampled from Kenya between 2000 and 2003 (Lambwe Valley, Kodera, Busia, Kathekani, Dakabuku, Tsavo West, Shimba Hills, Oloibortoto, Sampu, Kalema, Lengongu, Shompole, Nguruman and Lengobei). One population was from Tanzania (Muvumoni, near Tanga) in 2000, one from Zambia (Kakumbi), two from Zimbabwe (Mana Angwa and Mana Pools) in 1996, and two were Ethiopian (Arba Minch and Chankar), sampled in 1996–97. The flies were caught with Epsilon or biconical traps and then preserved in 85% aqueous ethanol. Uganda flies were a laboratory culture maintained at the IAEA laboratory in Seibersdorf, Austria for c. 80 generations. Samples were grouped based on their geographic proximities: group 1, west and south-western Kenya and Uganda; group 2, southern Africa – Zimbabwe, Zambia; group 3, coastal Kenya and north-eastern Tanzania; group 4, south-western Ethiopia; and group 5, south-western Kenya.

Fig. 1.

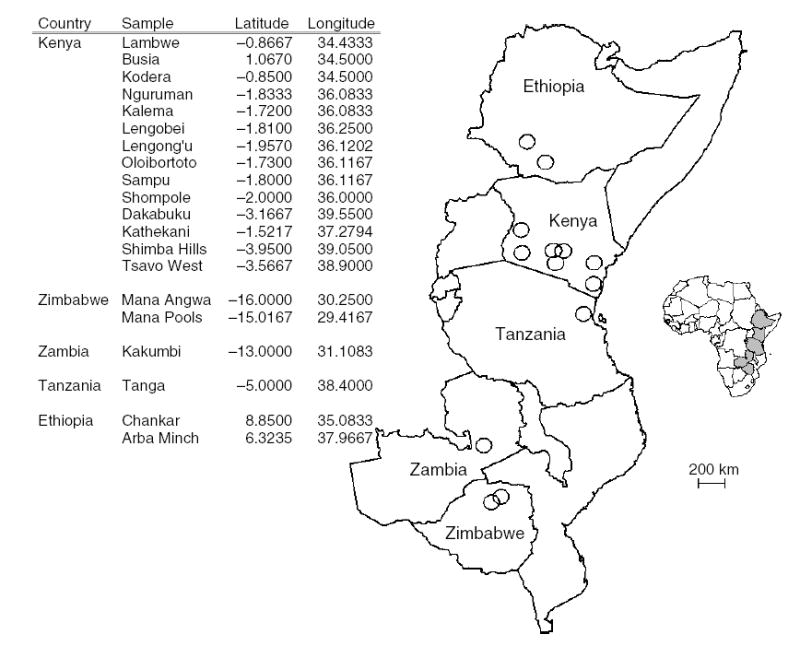
Approximate sampling locations (○) of Glossina pallidipes.

DNA extraction and microsatellite genotyping

Total genomic DNA was extracted by using the CTAB (hexadecyltrimethylammonium bromide) method as described by Krafsur & Wohlford (1999). Most flies were females. Eight polymorphic loci were examined. Primer sequences for these loci are described in Ouma et al. (2003, GenBank accession numbers AY220498–AY220504), and Baker & Krafsur (2001, GenBank accession number AY033512).

Polymerase chain reaction (PCR) amplification was performed as described in Ouma et al. (2003). One primer was end-labelled with one of two fluorescent dyes (FAM or HEX). PCR products were resolved in ABI Prism 377 automatic DNA sequencer, using Genescan^TM ver.3.1.2 and the TAMRA-350 size standard (PE Biosystems, Foster City, California). Subsequently, allele sizes were scored by using ABI Genotyper^TM software version 2.5.

Mitochondrial variation

Haplotype diversities were examined at five loci, r16SII, COI, COII, COIITLII and CyB1 by using the single strand conformation polymorphism (SSCP) technique, which allowed the identification of haplotypes, i.e. single stranded DNA conformations, based on their differential mobility when resolved through native polyacrylamide gels (Orita et al., 1989). Three major steps were involved: PCR of mitochondrial loci, SSCP electrophoresis, and visualization of variants though silver staining of SSCP gels.

PCR amplification of mitochondrial loci was accomplished using primers: N1-J-12585 and LR-N-12866 for the 16S ribosomal RNA (r16SII, 300 bp) gene; C1-J-1751 and C1-N-2191 for cytochrome oxidase I (COI, 440 bp); C2-J-3279 and C2-N-3494 for cytochrome oxidase II (COII, 214 bp) gene; TL2-J-3034 and C2-N-3389 for a fragment mapping between cytochrome oxidase II and transfer RNA leucine (COIITLII, 350 bp); CB-J-10933 and CB-N-11367 for cytochrome B1 (CyB1, 350 bp). Their sequences are set out in Simon et al. (1994). PCR and SSCP methods were as outlined in Krafsur & Wohlford (1999) and Marquez & Krafsur (2002). The SSCP gel phenotypes were visualized by silver staining as described in Black & DuTeau (1997). Haplotypes were identified based on their migration distances from the gel origin, by referencing their migration to that of the 200 bp fragment of the Øx174/HinfI size marker (Promega G1751, Madison, Wisconsin), and by comparing their migration to that of allele standards in each gel. The authenticity of SSCP gel electromorphs was checked by sequencing five to ten flies of each gel phenotype.

Data analysis

Hardy-Weinberg and linkage disequilibria analyses were performed on microsatellite loci to test the null hypotheses of their Mendelian inheritance and genotypic independence across loci. These tests were performed by using FSTAT version 2.9.1 software (Goudet, 1995).

Recently bottlenecked populations lose rare alleles via drift but heterozygosities are reduced at lesser rates (Cornuet & Luikart, 1996). Bottleneck software (Piry et al., 1999) was used to test for recent bottlenecks in population size. The two phase model was used to test for disequilibrium between heterozygosities and allele numbers in grouped populations because neither the infinite alleles model nor the stepping stone model of mutation strictly apply to micro-satellite loci.

Because of full linkage among mitochondrial loci, analysis was done on the frequencies of composite haplotypes formed by combining in each fly its haplotypes over five loci. Diversities at microsatellite and mitochondrial loci were analysed by using F statistics (Weir, 1996) and the hierarchical diversity analysis of Nei (1987). The F statistics were estimated from the analysis of variance (ANOVA) of allele frequencies as prescribed by Weir (1996) and Weir & Cockerham (1984), with a nested model of samples within groups and random effects. The ANOVA afforded a hierarchical partition of allele frequency variance into its components and the estimation of the fixation index F_ST, which is formally defined, for k loci and x alleles, as ∑^K σ_x²/∑^K[(X_T)(1 − X_T)] the standardized variance of allele frequencies among populations. F_ST also can be interpreted as the correlation of alleles among subpopulations _S with respect to the total population _T and it also estimates their degree of differentiation in terms of departures from random mating among the subpopulations. Thus, F_ST is a measure of genetic drift. F_IS is the correlation of alleles in individuals averaged over subpopulations; it measures the average departure from random mating within subpopulations. F_IT is the correlation of alleles in individuals relative to that in the entire gene pool; it measures departures from random mating thus:

$$(1–F_{\text{IT}})=(1–F_{\text{IS}})(1–F_{\text{ST}}).$$

F statistics were estimated at different hierarchies to examine the degree of population structuring.

The stepwise mutation model, via replication slippage, is thought to explain most microsatellite diversity. If so, variance in allele repeat sizes can recover more information than can variance in allele frequencies (Slatkin, 1995). The statistics R_IS, R_ST, and R_IT, analogous to the corresponding F statistics, were computed by using GENEPOP version 3.2a software (Raymond & Rousset, 1995). The R statistics are based on allele repeat numbers and F statistics on allele frequencies.

The hierarchical analysis of diversity (Nei, 1987) proceeded by estimating the unbiased population diversity as

$$h_e=2n(1–\sum X_i^2)/(2n–1)$$

with n for haploid systems, where x_i is the frequency of the ith allele or haplotype, and n is the number of individuals sampled. The average diversity over s populations was estimated as H_S = ∑h_e/s. The minimum genetic distance between two populations is

$$D_{ij}=[(J_i+J_j)/2]–J_{ij}$$

where J_i = ∑X_i² is the identity of population i, and J_ij = ∑ x_ix_j is the shared identity between populations i and j. Thus D_ij represents the unshared identity between populations. The average D_ij over s populations,

$$D_{ST}=\sum D_{ij}/s(s–1)$$

is the mean diversity among populations. The variance of D_ST was estimated according to Nei & Roychoudhury (1974). The total gene diversity, H_T, was estimated as the sum of the diversities within populations, H_S, between populations within groups, D_SG, and diversity between groups, D_GT, according to the relation,

$$H_T=H_S+D_{SG}+D_{GT}$$

Genetic differentiation between groups was estimated as G_GT = D_GT/H_T, and that among populations within groups as G_SG = D_SG/H_T. G_ST = D_ST/H_T and is analogous to Wright’s F_ST; both estimate the average degree of differentiation among populations. G_ST is a linear measure of genetic distance and F_ST is a geometric distance measure.

Assuming mutation-drift equilibrium and the infinite mutation model, the rate of gene flow can be estimated as

$$N_m~(1–G_{ST})/4G_{ST}$$

where N_m is the mean number of reproducing individuals per generation. The variance of G_ST was estimated according to Chakraborty (1974). For mitochondrial loci, the appropriate denominator is 2G_ST. An independent estimate of gene flow was obtained by Slatkin’s private allele method (Slatkin, 1985; Slatkin & Barton, 1989), which was estimated by using SAS software version 8.2 (SAS Inc., 2001). A correlation analysis between genetic and geographic distance matrices was performed according to Smouse et al. (1986) after Mantel (1967). The matrix correlation index was estimated as

$$r_{XY}=SCP(X,Y)/{[SS(X)SS(Y)]}^{-1/2}$$

where SS is the sum of squares and SCP the sum of squares and cross products of matrices X and Y. The confidence interval for the matrix correlation index was estimated by permuting the n–1 columns and rows on one matrix while holding the other constant. After each resampling, the correlation index was computed and its null distribution established. Statistical calculations were done by using SAS.

Results

Sequencing SSCP electromorphs

Nucleotide sequence analysis of SSCP electromorphs indicated that variation was underestimated (table 1). From 20 electromorphs (i.e. gel phenotypes) 33 genotypes were detected, for an overall mean detection of 61%. Only 33% of variants were detected by SSCP at COI but all were detected at COIITLII.

Table 1.

Nucleotide diversity of SSCP electromorphs at mtDNA loci in Glossina pallidipes.

	Number of
Locus	Flies	Genotypes	Electromorphs	Effective resolution %a
r16SII	19	5	4	80.0
COII	39	8	6	75.0
CyB	30	7	3	43.0
COIITLII	39	4	4	100.0
Totals	158	33	20	Mean 60.6

^aEffective resolution = 100× [no. electromorphs/no. genotypes established by sequencing]

Allele frequency distributions

No significant departures were detected from linkage equilibrium between microsatellite loci when using linkage disequilibrium tests and the sequential Bonferroni correction. All loci were polymorphic and the number of alleles per locus ranged from 11 in GpCAG133 to 42 in GpB20b, with an average of 26.75 ± 8.7. A total of 214 alleles was detected and their frequency distribution was hyperbolic showing that most microsatellite alleles were present in low copy number (fig. 2), thereby arguing against a recent bottleneck (Luikart et al., 1998). Only one allele at each of four loci was detected in all populations, 21 alleles were private (i.e. found in one sample only), and 37 (17%) were singletons (i.e. found in one fly only).

Fig. 2.

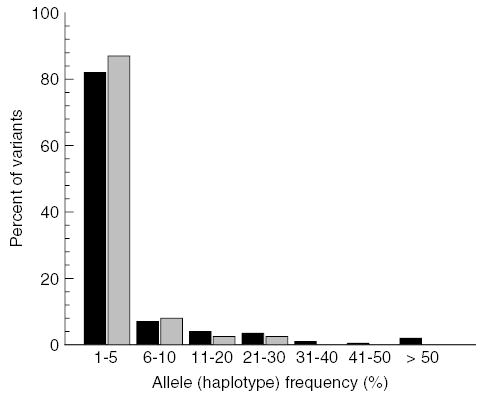
Microsatellite allele (▪) and mitochondrial haplotype (▪) frequency distribution.

Tests for recent bottlenecks indicated that allele frequency distributions in all populations were typically hyperbolic thereby showing no loss of rarer alleles. Moreover, only one of 21 populations showed a significant excess of heterozygotes, a result to be expected in c. 5% of such trials. Thus the microsatellite data provide no evidence of recent, stringent bottlenecks in G. pallidipes populations.

Among five mitochondrial loci, the number of SSCP single locus electromorphs ranged from three in COI to six in COII, and yielded a total of 39 composite haplotypes, clearly an underestimate of the underlying nucleotide variation. No haplotype was found in all populations or grouped populations. The most common composite haplotype was shared by 12 populations distributed among three population groups. Twenty-four haplotypes of 39 (62%) were confined to a single population group. Thirteen haplotypes were private (33%) and nine were singular (23%), thus most were rare at frequencies of 5% or less (fig. 2).

The number of composite haplotypes in populations varied from one in Mana Angwa (Zimbabwe) and Sampu (Kenya) to ten in Lambwe (Kenya). Southern African populations showed only four haplotypes, but 23 were recorded in south-eastern Kenya and north-eastern Tanzania. It is interesting that 50% of the haplotypes in southern Africa were private or singular.

Gene diversities

Microsatellite single locus expected diversities (heterozygosities) varied from 0.435 at GpCAG133 to 0.813 at GpB20b with an overall average of 0.659. Heterozygosities averaged over loci exceeded 50% in all populations.

The contrasts between observed and expected heterozygosities provide a measure of departures from Hardy-Weinberg equilibria, expressed by using F statistics. F_IS is a measure of departures from random mating within populations (table 2). There were no significant differences between observed and expected heterozygosities (F_IS ~ 0). Average microsatellite alleles per locus varied from 3.5 in Kalema and Lengongu to 13.9 in Tanga. Overall, grouped populations in coastal Kenya and Tanzania were the most diverse, with an average mean number of alleles per locus of 22.4 and an average heterozygosity of 0.821. The south central Kenya group was the least diverse, with mean number of alleles and heterozygosity of 9.9 and 0.619, respectively. Expected and observed heterozygosities and mean alleles per locus differed significantly among the grouped populations (table 2).

Table 2.

Gene diversity at eight microsatellite loci in Glossina pallidipes.

				Heterozygosity±SE
Group	Population	N	Avg. no. of allelesa±SE	Observedb (HO)	Expectedc (HE)	FITd
1	Lambwe	48	7.4±4.3	0.58±0.03	0.60±0.03	0.045
	Busia	48	5.8±3.0	0.62±0.03	0.57±0.03	−0.089
	Kodera	24	5.3±2.5	0.42±0.03	0.55±0.06	0.224
	Uganda lab	24	4.6±2.1	0.46±0.05	0.47±0.05	0.152
	Total and means	144	11.5±5.4	0.51±0.03	0.64±0.09	0.203
2	Mana Angwa	24	7.5±3.3	0.68±0.03	0.72±0.05	0.061
	Mana Pools	48	10.1±4.2	0.64±0.02	0.69±0.04	0.068
	Zambia	24	6.0±2.2	0.66±0.03	0.64±0.05	−0.035
	Total and means	96	12.8±5.4	0.66±0.03	0.73±0.06	0.096
3	Dakabuku	48	13.1±5.8	0.74±0.01	0.81±0.02	0.087
	Kathekani	48	13.8±6.6	0.73±0.02	0.81±0.02	0.094
	Shimba Hills	48	12.6±5.4	0.77±0.02	0.79±0.03	0.025
	Tanga	48	13.9±5.7	0.71±0.02	0.80±0.02	0.114
	Tsavo	48	13.5±6.3	0.71±0.01	0.82±0.02	0.128
	Total and means	240	22.4±8.2	0.73±0.02	0.82±0.04	0.110
4	Arba Minch	24	7.1±4.0	0.73±0.05	0.66±0.05	−0.111
	Chankar	24	8.1±3.2	0.56±0.03	0.70±0.05	0.208
	Total and means	48	10.0±4.8	0.64±0.0	0.69±0.05	0.072
5	Nguruman	48	5.6±2.0	0.55±0.04	0.57±0.04	0.019
	Kalema	14	3.5±0.8	0.55±0.07	0.63±0.06	0.136
	Lengobei	24	6.5±3.2	0.59±0.05	0.63±0.04	0.059
	Lengongu	18	3.5±0.9	0.48±0.04	0.53±0.06	0.078
	Oloibortoto	24	6.4±2.6	0.61±0.04	0.67±0.04	0.092
	Sampu	24	5.1±2.5	0.57±0.05	0.59±0.05	0.024
	Shompole	24	4.1±1.4	0.64±0.08	0.57±0.05	−0.124
	Total and means	176	9.9±4.4	0.57±0.03	0.63±0.01	0.081
Grand total and means		720	26.8±8.7	0.63±0.01	0.80±0.03	0.213

^aKruskal-Wallis test of mean alleles per locus among groups (χ²₄ = 66.1, P < 0.001)

^bKruskal-Wallis test of homogeneity of H_O among groups (χ²₄ = 19.97, P~0.005)

^cKruskal-Wallis test of homogeneity of H_E among groups (χ²₄ = 46.3, P < 0.001)

^dF_IT = 1 − (H_O/H_E)

Mitochondrial diversity is the probability that two randomly chosen flies have different composite haplotypes. Mitochondrial diversities were heterogeneous among grouped populations (χ²₄ = 10.97, P < 0.03), ranging from only 0.04 in southern Africa to 0.60 in south central and western Kenya and averaged 0.42 ± 0.02 over all samples (table 3).

Table 3.

Number of mitochondrial haplotypes and gene diversity in Glossina pallidipes.

Group	Sample	N	No. of haplotypes	HS ± SE
1	Lambwe	48	10	0.85±0.03
	Busia	48	6	0.73±0.04
	Kodera	24	3	0.41±0.10
	Uganda	40	2	0.41±0.07
	Total and mean	160	16	0.60±0.06
2	Mana Angwa	24	1	0.00±0.00
	Mana Pools	48	2	0.04±0.04
	Zambia	24	2	0.08±0.07
	Total and mean	96	4	0.04±0.03
3	Dakabuku	24	5	0.61±0.09
	Kathekani	24	4	0.43±0.12
	Shimba Hills	48	6	0.74±0.04
	Tanga	48	9	0.71±0.05
	Tsavo	24	3	0.45±0.09
	Total and mean	168	23	0.59±0.08
4	Arba Minch	24	3	0.24±0.11
	Chankar	24	5	0.63±0.10
	Total and mean	48	7	0.44±0.10
5	Nguruman	24	4	0.72±0.05
	Kalema	14	3	0.38±0.15
	Lengobei	24	2	0.29±0.10
	Lengongu	18	2	0.42±0.10
	Oloibortoto	24	5	0.31±0.12
	Sampu	24	1	0.00±0.00
	Shompole	24	4	0.31±0.12
	Total and mean	152	11	0.35±0.09
Grand total and means		624	39	0.42±0.02

Kruskal-Wallis test of homogeneity among groups (X²₄ = 10.97, P = 0.03)

Genetic differentiation

Nei’s methods were used to partition microsatellite diversity into within and between groups thereby providing estimates of the mean unshared diversity between groups, which was three-fold greater than that of populations within groups (table 4). Differentiation between groups was fourfold greater than differentiation within groups. Assuming the infinite allele model, the foregoing values would be equivalent to average exchange rates of 1.6 reproducing flies per generation among groups and 5.8 among populations within groups. The analysis of variance of allele frequencies showed that only 13% of the variance lay between groups, 5% among samples within groups, and 81% within samples. The corresponding fixation indices indicated that there was a similar degree of differentiation among groups (F_GT = 0.13) as among all populations (F_ST = 0.18; Table 4). Nei’s G_ST = 0.22 was essentially the same.

Table 4.

Gene diversity analyses of microsatellite loci of Glossina pallidipes (Nei, 1987; Weir, 1996). Populations (S) are nested in groups (G).

Index					Estimate±SE
Diversity within populations HS					0.620±0.034
Diversity between populations DST					0.175±0.0002
Diversity of populations (groups) DSG					0.071±0.003
Diversity between groups DGT					0.213±0.003
Total diversity HT					0.903±0.086
Differentiation of populations GST					0.221±0.0002
Differentiation of populations (groups) GSG					0.080±0.005
Differentiation between groups GGT					0.235±0.003
Gene flow rate of populations (groups)					5.8
Gene flow rate between groups					1.6
Source	df	Sum of squares	Expected mean squares	Percent variance	F statistics
Among groups	4	4.966	0.0041	13.2	FGT = 0.132
Among samples (groups)	16	2.137	0.0016	5.3	FSG = 0.061
Within samples	1419	35.721	0.0252	81.3	FST = 0.184
Total	1439	42.825	0.0310

The hierarchical partition of mitochondrial diversity is set forth in table 5. The amount of unshared diversity between groups, D_GT = 0.55, can also be interpreted as the mean genetic distance among groups. The corresponding distance among all populations, D_ST = 0.175. Diversity of populations within groups, G_SG = 0.21, indicates greater similarity of populations within groups than between them, G_GT = 0.45, as can be expected because of their relative geographic proximities. G_SG can also be interpreted as the probability that any two haplotypes randomly chosen from two groups are different. G_ST = 0.52, which estimates the chance that any two random flies from different populations have different haplotypes. Analysis of variance in haplotype frequencies showed that 48% of variance lay within samples, 36% in samples within groups, and only 15% among groups (table 5). The corresponding fixation indices indicated again a substantial degree of structuring (table 5).

Table 5.

Analysis of mitochondrial diversity within and among population groups of Glossina pallidipes (Nei, 1987; Weir, 1996). Populations (S) are nested in groups (G).

Index					Estimate ± SE
Diversity within populations HS					0.418 ± 0.019
Diversity between populations DST					0.454 ± 0.0006
Diversity of populations (groups) DSG					0.258 ± 0.013
Diversity between groups DGT					0.546 ± 0.008
Total diversity HT					1.222 ± 0.399
Differentiation of populations GST					0.520 ± 0.0006
Differentiation populations (groups) GSG					0.211 ± 0.035
Differentiation between groups GGT					0.446 ± 0.009
Gene flow rate of populations (groups)					1.9
Gene flow rate between groups					0.6
Source	df	Sum of squares	Expected mean squares	Percent variance	F statistics
Among groups	4	2.930	0.0037	15.4	FGT = 0.152
Among samples (groups)	16	4.198	0.0087	36.3	FSG = 0.425
Within samples	603	7.075	0.0117	48.3	FST = 0.513
Total	623	14.203	0.0240

Single locus variance estimates based on repeat size (R_ST) were greater than variances based upon allele frequencies (F_ST table 6). Both measures show substantial interlocus variance. Departures from random matings within populations (F_IS) were substantial although statistically non-significant. They are commonly observed when scoring microsatellite loci. Another method of estimating the standardized variance in allele frequencies is by converting the estimate of N_em obtained via the private allele method (Slatkin & Barton, 1989) into F_ST via the island model of migration. The mean frequency of private alleles was 0.053, thus N_em = 1.3 and the corresponding value of F_ST is 0.158. The same method applied to mitochondrial haplotype private allele frequency of 0.216 yielded N_em = 0.178 with corresponding F_ST = 0.738.

Table 6.

F-statistics (Weir & Cockerham, 1984) and R-statistics by locus (Slatkin, 1995) for 21 Glossina pallidipes samples.

Locus	FIS	FST	FIT	RIS	RST	RIT
GpA19a	0.075	0.162	0.224	0.103	0.188	0.271
GpA23b	0.095	0.171	0.250	0.164	0.194	0.326
GpB6b	0.157	0.193	0.320	0.432	0.181	0.535
GpB20b	0.128	0.094	0.210	0.137	0.174	0.288
GpC5b	0.171	0.143	0.290	0.022	0.114	0.133
GpC10b	−0.061	0.164	0.113	0.170	0.268	0.392
GpC26b	−0.031	0.121	0.093	−0.026	0.242	0.222
GpCAG133	0.041	0.293	0.322	0.058	0.279	0.321
Means	0.073	0.172	0.233	0.143	0.229	0.339
Standard errors	0.033	0.018	0.031	0.048	0.019	0.042

Comparing results in tables 7 and 8, the average pairwise genetic differentiation between groups was greater at mitochondrial (G_IJ = 0.57 ± 0.01) than at microsatellite (G_IJ = 0.25 ± 0.01) loci, as detected by Kruskal-Wallis ANOVA (χ²₄ = 13.19, P ~ 0.01). Based on mitochondrial variation, mean G = 0.73 for southern African populations compared with G ~ 0.5 for the other population groups. Within group variation at microsatellite loci varied from 0.29 among western populations to a low of 0.20 among populations near the East African coast. At microsatellite loci, genetic differentiation (G_ST) within grouped populations varied from 0.19 in western Kenya and Uganda to a low of 0.05 among the Ethiopian samples. These are substantial levels of differentiation. Mitochondrial loci indicated surprisingly high levels of differentiation in southern Africa and south central Kenya.

Table 7.

Microsatellite genetic differentiation (G_ST above diagonal), gene flow (N_em in brackets above diagonal), and numbers (below diagonal) and proportions (in brackets below diagonal) of shared alleles between population groups of Glossina pallidipes.

	Group 1	Group 2	Group 3	Group 4	Group 5
Group 1	0.19 [1.06]	0.23 [1.66]	0.24 [1.59]	0.35 [0.95]	0.35 [0.94]
Group 2	67 [0.31]	0.09 [2.53]	0.15 [2.74]	0.27 [1.32]	0.22 [1.74]
Group 3	81 [0.38]	94 [0.44]	0.10 [2.25]	0.21 [1.87]	0.21 [1.90]
Group 4	45 [0.21]	49 [0.23]	68 [0.32]	0.05 [4.75]	0.29 [1.21]
Group 5	56 [0.26]	55 [0.26]	66 [0.31]	38 [0.18]	0.08 [2.87]

Within group genetic differentiation and gene flow are shown on the diagonal in bold.

Table 8.

Mitochondrial genetic differentiation (G_ST above diagonal), gene flow (N_em in brackets above diagonal), and numbers (below diagonal) and proportions (in brackets below diagonal) of shared haplotypes between population groups of Glossina pallidipes.

	Group 1	Group 2	Group 3	Group 4	Group 5
Group 1	0.31 [1.11]	0.68 [0.23]	0.34 [0.96]	0.49 [0.63]	0.44 [0.53]
Group 2	0 [0.00]	0.91 [0.05]	0.69 [0.23]	0.75 [0.16]	0.81 [0.12]
Group 3	8 [0.21]	3 [0.08]	0.28 [1.28]	0.49 [0.51]	0.42 [0.70]
Group 4	2 [0.05]	1 [0.03]	2 [0.05]	0.08 [5.75]	0.57 [0.37]
Group 5	5 [0.13]	1 [0.03]	6 [0.15]	3 [0.08]	0.49 [0.52]

Within group genetic differentiation and gene flow are shown on the diagonal in bold.

Based on microsatellite loci, a UPGMA dendrogram of Nei’s minimum genetic distances (D_ij) among populations shows geographically close populations tend to cluster together (fig. 3). Clusters were identical to those used to assign populations to groups. The same procedure applied to mitochondrial variation was incongruent with the micro-satellite dendrogram and made no sense geographically. This could, in principle, indicate different dispersal patterns between male and female G. pallidipes. However, the Mantel test for microsatellite loci between geographic and genetic distances D_ij suggested that isolation by distance helps to explain the genetic differentiation patterns (r = 0.41, P ~ 0.001) and a similar result was obtained for mitochondrial haplotypes (r = 0.45, P ~ 0.001).

Fig. 3.

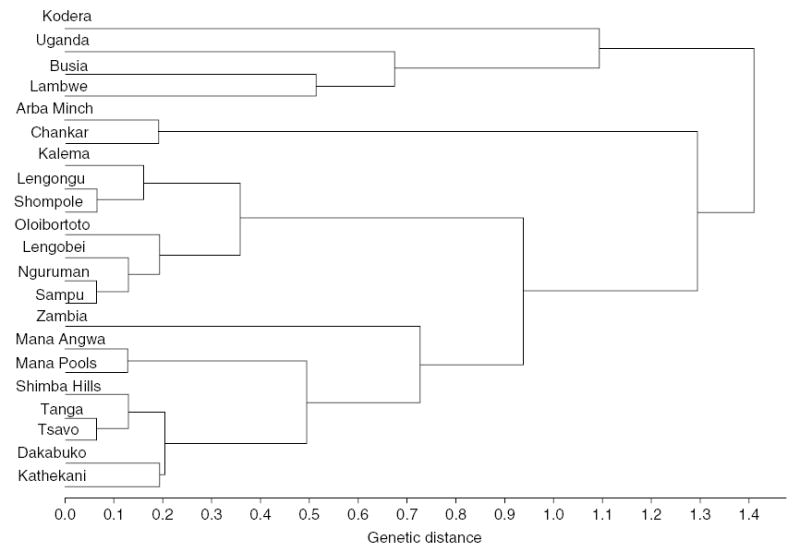
UPGMA minimum genetic distance (Nei, 1987) tree of Glossina pallidipes estimated from microsatellite loci.

Discussion

SSCPs disclosed approximately 61% of the existing mitochondrial diversity at the loci investigated, sufficiently high resolution to investigate questions relating to gene flow. The method is cost effective in that large numbers of specimens can be examined cheaply relative to the cost of nucleotide sequencing. The chief drawback is that failure to detect all the variation can allow a measure of homoplasy. Homoplasy has the effect of underestimating genetic differentiation, thereby overestimating gene flow (Balloux & Lugon-Moulin, 2002). To contrast mitochondrial with nuclear variation strengthens demographic investigations because it offers an independent view of evolutionary forces. Explicit comparisons will be discussed later, where more appropriate to do so.

We did not detect linkage between microsatellite loci. Glossina pallidipes show only two pairs of autosomes and a heteromorphic sex bivalent in addition to supernumerary chromosomes that vary from zero to at least three in number (Southern, 1980). There is no recombination in males (Gooding, 1984). The eight loci, therefore, seem to be well separated over the autosomes. The microsatellite loci used here were autosomal (Ouma et al., 2003).

The mild heterozygote deficiencies within populations (estimated by F_IS, R_IS) were not caused by inclusion of hemizygous males. Nor is it likely the deficiencies arose because some loci were located on supernumerary chromosomes, known to be highly variable in number. Heterozygote deficiencies were much more likely caused by null alleles, a common problem when using microsatellite loci.

Eighty-two percent of the microsatellite alleles and 90% of mitochondrial haplotypes occurred at frequencies ≤ 5% and may thus be considered ‘rare’. Only four of 214 microsatellite alleles were shared by all populations; the three most common mitochondrial haplotypes were shared by only three of five grouped populations. Summed over populations, the numbers of rare alleles and haplotypes are consistent with that of a mega-population near mutation-drift equilibrium. Based on microsatellites, tests for recent bottlenecks were negative in each population even though group 1, group 2 and group 5 populations had been exposed to effective tsetse control programmes in the 1980s and early 1990s (Brightwell et al., 1997; Turner & Brightwell, 1986; Hargrove, 2003). There are approximately eight generations yearly in tsetse flies, and tsetse effective population sizes are comparatively small, so four years is probably the maximum extent that detectable disequilibrium obtains between allelic diversity and heterozygosity (Cornuet & Luikart, 1996). It therefore seems reasonable to infer that populations probably recovered full allelic diversities in the intervals between population minima and the genetic sampling.

Effective tsetse management should reduce heterozygosities in the subject populations. Ethiopian and coastal East African tsetse populations have not been subjected to extensive control measures. Thus, we might expect population groups 3 and 4 to show more diversities than the others. Although microsatellite allelic, observed and expected diversities differed significantly among groups, the Ethiopian samples were not particularly diverse. Southern African mitochondrial diversities, on the other hand, were very low, such that the odds of two randomly chosen flies having different haplotypes was only 4%. Tsetse populations in Zambia and Zimbabwe, according to the historical record, suffered catastrophic declines in distribution and abundance caused by mortalities of about 90% among their chief mammalian hosts (Ford, 1971). These mortalities were caused by the rinderpest epizootic at the close of the 19th century. It is interesting that neither allozyme nor micro-satellite diversities showed detectable evidence of that bottleneck, but the mitochondrial data do provide compelling evidence that tsetse populations in southern Africa were more strongly affected than populations in East Africa. Glossina morsitans morsitans Westwood and G. m. centralis Machado showed similar patterns (Wohlford et al., 1999; Krafsur et al., 2001). Mitochondrial DNA is known to be more sensitive to population subdivision and bottlenecks than nuclear genes because of its mode of inheritance and copy number (Wilson et al., 1985).

The population grouping scheme revealed much less genetic differentiation within groups than among groups, as may be expected among closely located populations. Geographic distances within population groups were not particularly great – most pairwise distances were well under 100 km. It is therefore important that significant genetic differentiation was detected within groups, for this suggests that tsetse fly capacity for dispersal may not often be realized. Hargrove (2003) reviewed field data on dispersion of G. pallidipes and G. morsitans, concluding that mean square diffusion rates of up to 0.25 km² per day (= mean step length of 1 km) may obtain such that 30% of a standing population could disperse 10 km in a year. It would seem, therefore, that flies in the locations we sampled may not have migrated quite so far for a great many generations. The genetic data could also suggest that mark, release, recapture experiments somehow induce greater than ‘normal’ displacement rates and that recolonization of ‘eradicated’ habitats may have had significant numbers of undetected resident flies. Hargrove (2003) has suggested that as few as 16 inseminated tsetse can initiate a thriving population. Is it not fair to say that further study is necessary to resolve the issue of dispersion versus restricted gene flow?

The among-group differentiation estimates were similar when obtained by using Nei’s (1987) and Weir’s (1996) methods even though the two methods make different assumptions. Nei’s differentiation index G_ST considers populations as clades branching from a common ancestor and is based on probabilities of shared identity among grouped populations. On the other hand, Weir & Cockerham’s θ, equivalent to Wright’s coancestry coefficient F_ST, considers populations equally related to their common ancestor and is based on correlation of alleles among grouped populations relative to the overall correlation. When populations share only a small proportion of their allelic diversity, Nei’s G_ST provides better estimates than F_ST; otherwise, both indices provide good estimates of differentiation. Slatkin’s private allele method offers yet another way of examining gene flow and the results for both microsatellite loci and mitochondria were in general agreement with θ and G_ST.

R means and standard errors were greater in magnitude than the F statistics, a commonly observed phenomenon (Balloux & Lugon-Moulin, 2002). R assumes that micro-satellites obey the stepwise mutation model (SMM) but compelling evidence indicates departures from the SMM. Size homoplasy is a common problem with microsatellites and this has the effect of depressing estimates of population differentiation. High and variable mutation rates are also typical of microsatellite loci, which further depress estimates of genetic differentiation, particularly where exchange rates between populations are low. Finally, high diversities greatly depress the maximum values that F_ST can take – the theoretical maximum F_ST is one minus the mean diversity (Nagylaki, 1998; Hedrick, 1999).

Indices of genetic differentiation based on microsatellites versus those based on mitochondrial variation provide more interesting contrasts. Mitochondrial variation showed the greater degree of differentiation because it represents an effective population size of roughly one quarter that afforded by sexually reproducing, diploid variation. Mitochondrial sensitivity to demographic forces is enhanced also by its matrilineal pattern of inheritance (Avise, 2004).

Our genetic differentiation estimates indicated a rather high degree of structuring. This is surprising especially when it is considered that mark, release and recapture data and recolonization rates show G. pallidipes to be highly mobile, and can demonstrate daily mean displacement rates of 360 m to 1.1 km, depending on season (Vale et al., 1984; Brightwell et al., 1992, 1997; Hargrove, 2003). Theoretically, the exchange of approximately one reproducing fly per generation or two is sufficient to prevent the fixation of different genotypes in different populations from genetic drift (Wright, 1978). The contradiction between genetic and ecological data, therefore, is puzzling. Available maps however indicate that morsitans group tsetse taxa have a patchy distribution (Ford, 1971; Rogers & Robinson, 2004), and there seems to be little gene flow among patches and surprisingly less than we might expect within them, based on the ecological data (Krafsur, 2003). A recent trapping study at Nguruman, in southern Kenya (group 5 locations), showed that G. pallidipes tends to be highly aggregated even at geographic scales of only 4–5 km (Odulaja et al., 2001). Perhaps habitats in Nguruman include seasonally inhospitable areas between the thickets in which flies may be caught in all seasons. Earlier research at Nguruman, however, suggested seasonally extraordinary immigration rates (Brightwell et al., 1992, 1997) that should greatly overwhelm local genetic differentiation. Nevertheless, genetic data, including allozymes (Krafsur et al., 1997; Krafsur, 2002), clearly show that the forces of drift seem to be much stronger than migration in G. pallidipes throughout most of its range.