Abstract
Molecular dynamics simulations were performed to unfold a homologous pair of thermophilic and mesophilic cold shock proteins at high temperatures. The two proteins differ in just 11 of 66 residues and have very similar structures with a closed five-stranded antiparallel β-barrel. A long flexible loop connects the N-terminal side of the barrel, formed by three strands (β1–β3), with the C-terminal side, formed by two strands (β4–β5). The two proteins were found to follow the same unfolding pathway, but with the thermophilic protein showing much slower unfolding. Unfolding started with the melting of C-terminal strands, leading to exposure of the hydrophobic core. Subsequent melting of β3 and the β-hairpin formed by the first two strands then resulted in unfolding of the whole protein. The slower unfolding of the thermophilic protein could be attributed to ion pair formation of Arg-3 with Glu-46, Glu-21, and the C-terminal. These ion pairs were also found to be important for the difference in folding stability between the pair of proteins. Thus electrostatic interactions appear to play similar roles in the difference in folding stability and kinetics between the pair of proteins.
INTRODUCTION
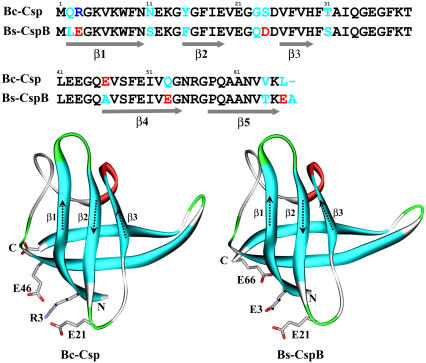
Understanding the mechanisms of protein folding and unfolding, and the structural determinants of protein stability has been the subject of intensive experimental and theoretical studies over the past several decades (1–6). Cold shock proteins have served as a good model system for such studies (7–35). The protein from the thermophile Bacillus caldolyticus (Bc-Csp) and cold shock protein B from the mesophile Bacillus subtilis (Bs-CspB) were both found to undergo reversible two-state folding, with an energetically polarized transition state according to Φ-value measurements (9,10,12,22,23,31). These two proteins differ in only 11 of 66 residues, and their three-dimensional structures show high similarity with a closed five-stranded antiparallel β-barrel capped by a long flexible loop (7,8,15,21) (Fig. 1). Yet, the thermophilic protein unfolds 20 times more slowly (10,22). There is also a significant difference in folding stability between the two proteins, with melting temperatures at 77°C and 54°C, respectively (20). Mutational studies led to the conclusion that surface charges, especially around residue 3 (occupied by Arg in Bc-Csp but Glu in Bs-CspB), play major roles in the stability difference (20). Using electrostatic calculations, we have provided quantitative rationalizations for the effects of individual and multiple substitutions and salts on the stability of the two proteins (29,34). This study aims to explain the similarity and difference in the unfolding kinetics of the two proteins, through molecular dynamics (MD) simulations at high temperatures.
FIGURE 1.
Comparison of sequence and structure between B. caldolyticus cold shock protein (Bc-Csp) and B. subtilis cold shock protein B (Bs-CspB). PDB entries for the two proteins were 1c9o (15) and 1csp (7), respectively.
MD simulations can provide a realistic view of the folding and unfolding process (36–41). High-temperature simulations have been shown to be a robust denaturing protocol for sampling conformational changes in the unfolding process (5,36,42–50). In this study, we have followed the unfolding of Bc-Csp and Bs-CspB at 500, 550, and 600 K. All three simulations showed the same sequence in the melting of the five β-strands: the two C-terminal strands (β4–β5) followed by β3 and then by the β-hairpin formed by β1 and β2. However, the unfolding of the thermophilic protein Bc-Csp was much slower. The main features of the simulations thus well reproduced the experimental results of Schmid and co-workers (22,31).
The simulations suggest that the tight turn between β1 and β2 helps stabilize these two strands and contributes to their resistance to melting. The slower unfolding of the thermophilic protein could be attributed to ion pair formation of Arg-3 with Glu-46, Glu-21, and the C-terminal, echoing the role of the ion pairs in the elevated folding stability of Bc-Csp over its mesophilic counterpart. Turn structure and tertiary contacts have been found to play prominent roles in the folding/unfolding of many β-proteins (51–60). Here the parallel study of a pair of homologous proteins provides further insight on the interplay of native architecture, turn stability, and tertiary contacts in the folding of β-proteins.
COMPUTATIONAL METHODS
All the MD simulations were performed on an IBM SP4 supercomputer by using the SANDER module of AMBER 7.0 (61). The water model was TIP3P (62,63). The lengths of bonds involving hydrogen atoms were constrained with the SHAKE program (64). The particle mesh Ewald method (65–68) was used to treat long-range electrostatic interactions. A 9-Å cutoff for nonbonded interactions was used. The nonbonded list was updated whenever any atom moved more than 1 Å (half of the default width of the nonbonded “skin” parameter) since the last list update. The weak-coupling method (69,70) was used to couple the system to a thermal bath of different temperatures (300, 500, 550, or 600 K). The system center of mass motion was repositioned at every picosecond. Simulations at 300 K were performed at constant temperature and pressure, with a time step of 2 fs. The constant temperature and pressure protocol is not feasible for the high temperatures, so simulations at 500, 550, and 600 K were carried out at constant temperature and volume, and the time step was reduced to 1 fs.
The procedures for the MD simulations were as follows. The initial structures for Bc-Csp and Bs-CspB were from Protein Data Bank (PDB) entries 1c9o (chain A) (7) and 1csp (15), respectively. Water molecules and counterions were added; the resulting system sizes are listed in Table 1. Each system was prepared by four to five cycles of energy minimization and equilibration; the minimizations were subject to successively lower constraints on the protein molecule. In the last equilibration step, the whole system targeting 300 K was gradually heated at constant temperature and pressure and equilibrated for 10 ps. The systems targeting 500, 550, or 600 K were heated at constant temperature and volume and equilibrated for 15–30 ps. Finally the MD simulations were carried out to the total times listed in Table 1. Conformations were sampled at every picosecond for later analysis. The average density in the simulation box at 300 K was 1.0 g/cm3; in comparison the average density was 0.81 and 0.83 g/cm3, respectively, for Bc-Csp and Bs-CspB in the high temperature simulations.
TABLE 1.
Setup of the MD simulations on B. caldolyticus cold shock protein (Bc-Csp) and B. subtilis cold shock protein B (Bs-CspB)
| Proteins
|
Bc-Csp
|
Bs-CspB
|
||||
|---|---|---|---|---|---|---|
| PDB
|
1c9oA
|
1csp
|
||||
| Temperature | 300 K | 500 K | 600 K | 300 K | 500 K | 600 K |
| Protein atoms | 1,020 | 1,020 | 1,020 | 1,014 | 1,014 | 1,014 |
| Counterions (Na+) | 2 | 2 | 2 | 6 | 6 | 6 |
| Water | 4,375 | 10,350 | 10,350 | 4,722 | 11,095 | 11,095 |
| Total atoms | 14,147 | 32,072 | 32,072 | 15,186 | 34,305 | 34,305 |
| Box size (Å3) | 55 × 50 × 51 | 77 × 71 × 72 | 77 × 71 × 72 | 55 × 50 × 55 | 76 × 71 × 76 | 76 × 71 × 76 |
| Ensemble | NTP | NTV | NTV | NTP | NTV | NTV |
| Total time (ns) | 12.000 | 50.699 | 6.00 | 12.00 | 20.043 | 6.00 |
For each trajectory, root mean-square deviations (RMSD) of Cα atoms from the x-ray structure were tracked. For the two 300-K trajectories, residue-based root mean-square fluctuations (RMSF) around the averaged structures and order parameters were calculated. The average structure was calculated by first removing translation and rotation through superimposing all atoms of each sampled conformation to the first conformation and then averaging the positions of the atoms. The average structure was used as the reference, and all conformations were superimposed to it. The RMSF was calculated as
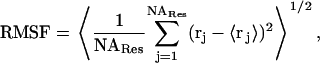 |
where 〈…〉 represents time average, rj is the position vector of atom j at different times, and NARes is the total number of atoms in a given residue. The order parameter was calculated as (71)
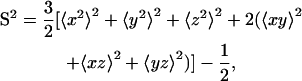 |
where x, y, and z are Cartesian components of the unit vector along the backbone N-H bond of a residue. Again, all conformations were superimposed to the average structure, but here only the backbone atoms (N, Cα, and C) were used for superposition.
For the high-temperature trajectories, the secondary structures were tracked to monitor unfolding. Secondary structures were calculated using the DSSP program (72). In the native structures of Bc-Csp and Bs-CspB, the five β-strands consist of residues 2–10, 15–19, 26–29, 46–54, and 47–65. These were labeled as β1–β5 in this work. In addition, the four residues between β1 and β2 form a tight turn. In the output of DDSP, β-structure is indicated by the letter “E”, and turn is indicated by “T”. For each sampled conformation, the unmelted fractions of the segments corresponding to the five native β-strands and the tight turn were calculated.
RESULTS
Overall conformational fluctuations and transitions
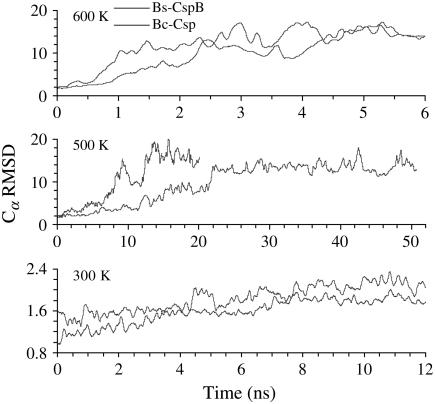
Four parallel simulations were carried out for the pair of thermophilic and mesophilic proteins at temperatures of 300, 500, 550, and 600 K in explicit water. The Cα RMSD of the two proteins along six trajectories are shown in Fig. 2. At room temperature, the two proteins showed small deviations (∼2 Å) from their x-ray structures. In contrast, the RMSD at the high temperatures reached 16 Å, indicating complete unfolding of the structures. The transition from small to large RMSD occurred much earlier at 600 K than at 500 K. Moreover, at each high temperature, the unfolding transitions of the thermophilic protein (Bc-Csp) occurred much later than the mesophilic counterpart (Bs-CspB).
FIGURE 2.
Cα RMSD Bc-Csp and Bs-CspB from their respective x-ray structures during MD simulations at 300, 500, and 600 K. Each curve represents one trajectory. In this and later figures, all time-dependent quantities are smoothed by averaging over a 100-ps interval.
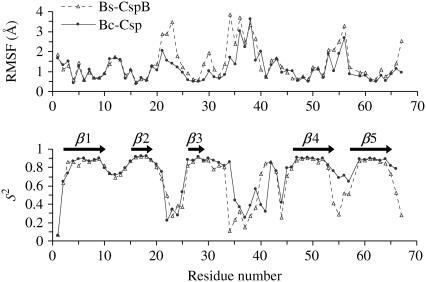
Interestingly, the RMSD of Bs-CspB showed greater fluctuations than Bc-Csp even in the 300-K simulations. In both proteins, the five β-strands were composed of residues 2–10, 15–19, 26–29, 46–54, and 57–65, respectively. RMSF revealed that the larger fluctuations of Bs-CspB occurred mostly in the loops between β2 and β3, β3 and β4, β4 and β5, and the C-terminal segment after β5 (Fig. 3). In both proteins, these regions were much more flexible than the five β-strands. The tight turn between β1 and β2 was also quite stable in both proteins, exhibiting RMSF just slightly larger than those of the β-strands. These findings are also apparent from the order parameters (S2) of individual residues calculated at 300 K (Fig. 3). A general trend of higher conformational rigidity has been observed for thermophilic proteins relative to their mesophilic counterparts (73).
FIGURE 3.
RMSF and order parameters (S2) for the residues of Bc-Csp and Bs-CspB, calculated from the simulations at 300 K.
Melting of secondary structural elements
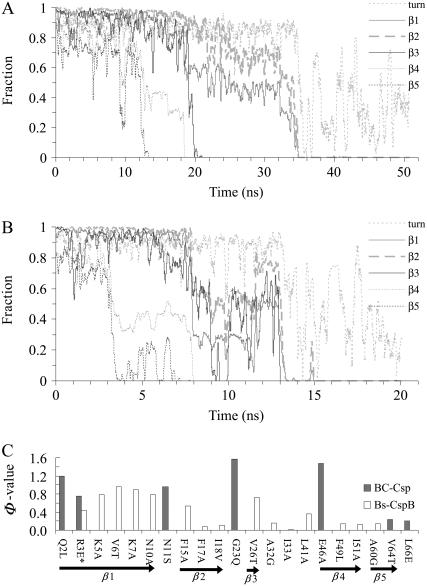
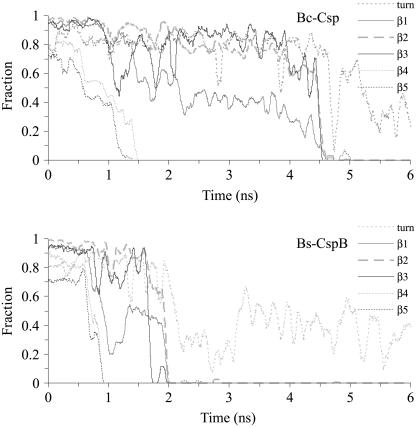
Further details of the unfolding process of the two proteins were provided by tracking the melting of the five β-strands. Fig. 4 shows the unmelted fractions of the five β-segments in Bc-Csp and Bs-CspB as a function of time at 500 K. Comparing the two proteins, the secondary structures of Bc-Csp took ∼35 ns to completely melt, whereas the secondary structures of the mesophilic counterpart took a much shorter period, ∼13 ns, to melt. On the other hand, the melting of the five β-strands occurred in the same order in the two proteins. The first strands to melt were β4 and β5, occurring at ∼12–18 ns in Bc-Csp and between 3–8 ns in Bs-CspB. This was followed by β3, with melting occurring at ∼20 ns in Bc-Csp and ∼9 ns in the mesophilic protein. Finally the two N-terminal strands appeared to melt together.
FIGURE 4.
Fraction of native secondary structure for the five β-segments and the turn between β1 and β2, as a function of simulation time at 500 K for (A) Bc-Csp and (B) Bs-CspB. The Φ-values for folding of the two proteins are shown in C, taken from Table 1 of Perl et al. (22) for Bc-Csp and Table 3 of Garcia-Mira et al. (31) for Bs-CspB. In the latter case, the reference for calculating Φ-values was the GluE3Leu mutant, and the result at position 3 is for the mutation back to the wild-type (i.e., with Glu at position 3).
That the two N-terminal strands β1 and β2 melted together prompted us to examine the status of the tight turn between them. As Fig. 4 shows, this turn was disrupted at the same time as the two β-strands in both proteins. Thus the two strands and the connecting turn existed as a cooperative unit. Some turn population even persisted after the melting of the two β-strands melted.
The melting of secondary structures at 600 K showed the same sequence of events as for 500 K, but with a much faster pace (Fig. 5). Again the melting of β4 and β5 (at ∼1.5 ns in Bc-Csp and ∼1 ns in Bs-CspB) was followed by the melting of β3 and β1-β2 (at ∼4.5 ns in Bc-Csp and ∼2 ns in Bs-CspB). The same melting sequence was also observed in parallel simulations at 550 K (data not shown). Taking all the high-temperature simulations together, it appears that the unfolding of the pair of proteins occurs in two distinct stages, the first for the melting of the two C-terminal β-strands and the second for the melting of the three N-terminal β-strands. For example, the first stage covered 0–18 ns in Fig. 4 A and 0–8 ns in Fig. 4 B, and the second stage covered 18–35 ns in Fig. 4 A and 8–13 ns in Fig. 4 B. That the N-terminal β-strands remained largely intact for an extended period of time after the melting of the two C-terminal strands suggests a transition state for folding with a partially structured N-terminal β-sheet and an unstructured C-terminal region. Such a transition state is consistent with observations of relatively high Φ-values for folding in the N-terminal β-strands and low Φ-values in the C-terminal β-strands (except for Glu-46 of Bc-Csp; Fig. 4 C) (22,31).
FIGURE 5.
Fraction of native secondary structure for the five β-segments and the turn between β1 and β2, as a function of simulation time at 600 K for Bc-Csp and Bs-CspB.
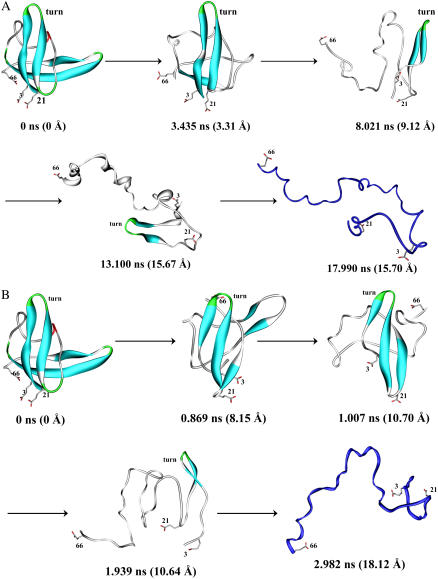
FIGURE 8.
Representative conformations of Bc-Csp during the unfolding simulations at (A) 500 K and (B) 600 K. The first step of the unfolding pathway was the buckling of strand β5. This was followed by the melting of the two strands in the C-terminal β-sheet. Subsequently β3 melted and finally the β-hairpin formed by β1 and β2 was disrupted. The time of each representative conformation and its Cα RMSD from the x-ray structure are indicated. The β1-β2 turn and ion pairing residues are labeled.
Ion pairs in the unfolding process
The unfolding of the two proteins is similar in that the same sequence of events was observed but different in that the mesophilic protein Bs-CspB showed a much higher speed of unfolding. Experimentally Bs-CspB was found to have an unfolding rate that is 20 times higher than Bc-Csp (10,22). The difference in unfolding rate must ultimately arise from the 11 substitutions between the two proteins. Since previously the difference in folding stability between the two proteins was largely attributed to differences in electrostatic interactions, especially ions pairs around Arg-3 in Bc-Csp (20,29), we wondered whether ion pairs played any role in the difference in unfolding speed observed in the simulations.
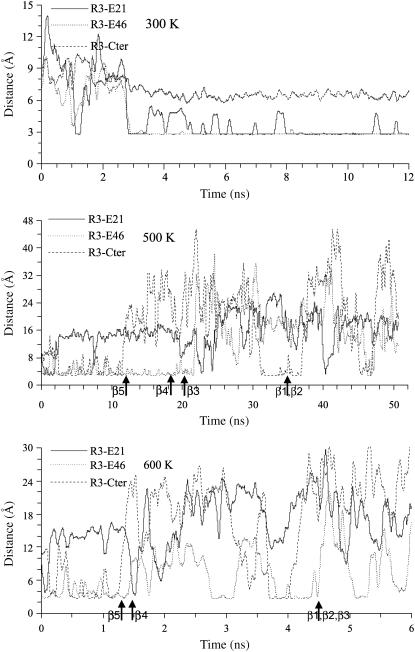
Arg-3 of Bc-Csp can potentially form ion pairs with Glu-21, Glu-46, and the C-terminal carboxyls. Fig. 6 shows the shortest distances among the positively charged atoms (NE, NH1, or NH2) on Arg-3 from negatively charged atoms on Glu-21, Glu-46, and the C-terminal (OE1 or OE2 for Glu and O and OXT for the C-terminal). In the 300-K simulation, Arg-3 was within salt-bridge distance (∼3 Å) from both Glu-21 and Glu-46 most of the time. At 500 K, Arg-3 also formed at least one salt bridge throughout most of the simulation. From 0 to 12 ns, salt bridges were formed with both Glu-46 and the C-terminal; the one with Glu-46 persisted till ∼22 ns. Thereafter Glu-21 and the C-terminal formed a salt bridge with Arg-3 intermittently. The separation of the C-terminal from Arg-3 at 12 ns coincided with the melting of the C-terminal β-sheet, at which point the C-terminal was no longer constrained by the structure of the β-sheet and thus free to move away. A similar situation of salt-bridge formation around Arg-3 was also apparent in the 600-K simulation. It appears that these salt bridges serve as a clamp which helps first the C-terminal β-sheet and then the N-terminal β-sheet resist rupture. Consequently both stages of the unfolding process for Bc-Csp took a substantially longer time than for Bs-CspB.
FIGURE 6.
Shortest distances between charged atoms of ion pair residues in Bc-Csp, calculated from MD simulations at 300, 500, and 600 K. Arrows indicate times when β-strands melted.
There is some experimental evidence for the role of the Arg-3-Glu-46 salt bridge in the unfolding process. At a high temperature of 343 K, Perl et al. (22) reported a high Φ-value (∼1.5) for the Glu-46Ala mutation (Fig. 4 C), though the effect of the mutation appears to diminish at room temperature. The stronger effect of the mutation at the higher temperature is consistent with the expected stronger electrostatic interaction between Arg-3 and Glu-46 due to the decrease in the dielectric constant of water. However, it is also possible that electrostatic interactions are overestimated in the MD simulations, which were carried out at temperatures much higher than 343 K.
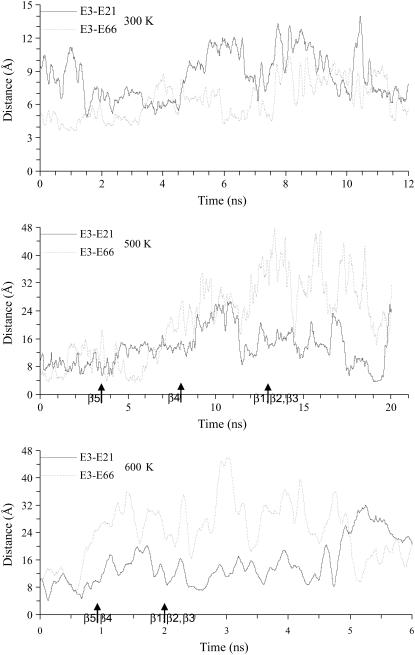
For comparison, the shortest distances in Bs-CspB between charged atoms on Glu-3 and those on Glu-21 and Glu-66 were also calculated (note that Glu-46 in Bc-Csp is substituted to Ala in Bs-CspB) (Fig. 7). Contrary to the situation in Bc-Csp, the like-charged Glu-3 and Glu-21 stayed far apart (9 Å or more) throughout the simulations, and the distance between Glu-3 and Glu-66 increased significantly as the simulations progressed. It thus appears that the repulsion between the negative charges helps to drive the structure of Bs-CspB apart during the unfolding process.
FIGURE 7.
Shortest distances between charged atoms of Glu-3 and potential charge-charge repulsion partners in Bs-CspB, calculated from MD simulations at 300, 500, and 600 K. Arrows indicate times when β-strands melted.
Unfolding pathway
By examining representative conformations along the unfolding trajectories, a more comprehensive picture of the unfolding pathway was obtained. As shown in Fig. 8 for Bc-Csp and Fig. 9 for Bs-CspB, the unfolding began with the bulging of β5, thus partially exposing the hydrophobic core. This was followed by the complete unfolding of the C-terminal β-sheet, which fully exposed the hydrophobic core and further weakened the N-terminal β-sheet. The β3 strand of the N-terminal sheet then melted away. The last two N-terminal strands, stabilized by the tight turn between them, were able to withstand unfolding for a period before capitulation.
FIGURE 9.
Representative conformations of Bs-CspB during the unfolding simulations at (A) 500 K and (B) 600 K.
This common unfolding pathway of the pair of proteins perhaps can be rationalized by the architecture of their common structure (Fig. 1). Between the two β-sheets, the C-terminal sheet is probably weaker than the N-terminal one. The latter has one additional strand and a very stable turn (see Fig. 3) between β1 and β2. Within the C-terminal sheet, β5 is probably weaker than β4, as the latter has better packing interactions with the N-terminal sheet, in particular backbone hydrogen bonds with β1. Within the N-terminal strand, β3 is probably the weakest strand as the other two strands are stabilized by the tight turn.
The unfolded state
The conformations of the proteins after all the secondary structures were melted toward the end of the MD simulations provided an opportunity to characterize the unfolded state. In particular, residual charge-charge interactions in the unfolded state have been found to be important for analyzing electrostatic effects on folding stability (29,74,75). Two extreme views of the unfolded state have been proposed. In the native-like model (74), the unfolded state is a slightly expanded version of the folded state and charged residues inherit native interactions with reduced strengths. In the Gaussian-chain model (75), charged residues lose all specific interactions and their distances are dictated by chain statistics, which results in shorter average distances for residues close along the sequence than for residues far apart along the sequence.
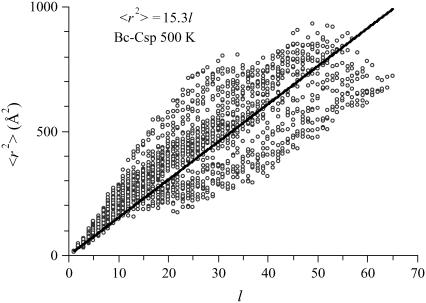
For illustration, in Fig. 10 we show the scatter plot of the mean square Cα-Cα distance 〈r2〉 versus the sequence separation l, calculated over the unfolded portion of the Bc-Csp trajectory at 500 K. For an ideal Gaussian chain, a linear relation 〈r2〉 = b2l is expected. This scatter plot and corresponding ones for the other high-temperature simulations indeed exhibited the expected trend. The fitting parameter b was 3.9 Å for Bc-Csp at 500 K. The value of b estimated from fluorescence resonance energy transfer efficiency of unfolded Thermotoga maritima cold shock protein at room temperature was ∼5.6 Å (27). The conformations right after the melting of all the secondary structures thus may still be too compact to be representative of the fully unfolded state. Toward the highest l values, the scatter of 〈r2〉 is below the linear fit (a result seen in all the unfolding simulations). This may be a consequence of excluded volume, which favors contacts between residues at the chain ends over those between inner residues (76).
FIGURE 10.
Mean square Cα-Cα distance versus the sequence separation, calculated over the unfolded portion (35.000–50.699 ns) of the MD trajectory of Bc-Csp at 500 K.
DISCUSSION
Our parallel study of a pair of homologous proteins has identified both similarity and difference in the unfolding. The two proteins were found to follow the same pathway of unfolding, with the N-terminal β-hairpin showing the greatest resistance to unfolding. On the other hand, the thermophilic protein showed much slower unfolding than its mesophilic counterpart. These major findings of this work agree well with experimental observations (22,31). We have further suggested a rationalization of the common unfolding pathway based on the architecture of the folded structure and provided an explanation for the slower unfolding of the thermophilic protein based on ion pairs formed around Arg-3.
All together we made six unfolding simulations for the two homologous proteins. Our focus was limited to the similarity and difference between the two proteins. The similarity in unfolding pathway and the difference in unfolding times were seen in the simulations at all the three high temperatures.
High temperature was used as a means for speeding up the unfolding so the simulations could be completed. However, the high temperature may alter the folding/unfolding pathway. As already noted, temperature affects the strength of electrostatic interactions. Likewise it can affect hydrophobic interactions (77). Nonetheless comparison against experimental results and other theoretical approaches continues to suggest that high temperature unfolding simulation is a useful means for elucidating the unfolding process.
Native architecture as a determinant of unfolding pathway
The two homologous cold shock proteins have very different unfolding rates and yet appear to share a common unfolding pathway in the MD simulations. A simplistic interpretation of the common pathway is that unfolding appears to follow a least-resistance path. The path is dictated by the energetics of the native architecture, i.e., the arrangement of secondary structural elements in the folded structure. The structure of the cold shock proteins is a β-barrel with a long flexible loop separating the N-terminal β-sheet from the C-terminal β-sheet. The first question faced by the protein under unfolding pressure is which β-sheet to melt first. Apparently the C-terminal sheet, with one less β-strand, is the loser. Within the C-terminal β-sheet, the next question is which of the two strands is melted first. β4, likely helped by backbone hydrogen bonds with β1, wins out. After the C-terminal β-sheet is melted, the question faced by the still intact N-terminal β-sheet is which of the three strands is melted first. Here β3 loses out as the other two strands are stabilized by a tight turn. In short, native interactions give rise to free-energy barriers to melting. Each time the part of the remaining structure experiencing the least resistance, i.e., with the lowest free-energy barrier, is melted first. Based on the argument of microscopic reversibility, the last remaining secondary structures can then be proposed to be part of the transition state for folding.
This least-resistance path model, suggested by the MD simulations of the two cold shock proteins and in apparent agreement with experimental Φ-values, also appears to be supported by the transition states of a number of other β-proteins. Like the cold shock proteins, the SH3 domain also consists of two orthogonally packed β-sheets, one with two terminal strands (β1 and β5) and the other with the three central strands (β2–β4). A tight turn (called the distal loop) connects β3 and β4. α-spectrin SH3 and src SH3 have only 33% of sequence identity, but their transition states obtained from Φ-values are remarkably similar: the two-stranded β-sheet is unstructured, but the distal β-hairpin (strands β3 and β4 connected by the distal loop) is formed. This mirrors the situation of the cold shock proteins, where the β-hairpin within the three-strand β-sheet is formed by β1 and β2. The transition state of SH3 domains has been largely reproduced in high-temperature MD simulations (44,47,49).
The Sso7d protein also consists of two orthogonally packed β-sheets, one with the first two strands (β1 and β2) and the other with the last three strands (β3–β5), plus a C-terminal α-helix. β3 and β4 are connected by a tight turn and packed against the α-helix. To construct the least-resistance path, one may argue that the two-stranded N-terminal β-sheet will be melted before the three-stranded C-terminal β-sheet, and within the C-terminal β-sheet, β5 will be melted before the β-hairpin formed by β3 and β4, which are stabilized by the tight turn between them as well as the packing against the α-helix. The remaining secondary structures are then the β-hairpin and the α-helix, which are indeed found to be formed in the transition state (56).
In these illustrations of the least-resistance path model, β-hairpins, specifically those stabilized by a tight turn, play a prominent role. This role has also been highlighted in the folding of other β-proteins (51,57–60). The least-resistance path model is similar in spirit to the method of low entropy loss routes proposed by Weikl and Dill (78), which is applied to folding instead of unfolding (more on the Weikl-Dill method later). Despite a multitude of potential routes for folding or unfolding, the protein molecule may follow only a few dominant routes with low free-energy barriers (78,79).
Polarized transition state of the cold shock proteins
There is no simple strategy for specifying the transition-state ensemble along an unfolding trajectory. We have argued that the earliest disrupted structural elements are absent in the transition state whereas the latest intact structural elements are a part of the transition state. For the cold shock proteins, the former consists of the C-terminal strands β4 and β5 and the latter consists of the N-terminal β-hairpin formed by strands β1 and β2. The absence of the former and presence of the latter result in a polarized transition state, just as shown by Φ-values.
The unfolding pathway observed in the MD simulations of the two cold shock proteins appears to be corroborated by native state hydrogen exchange studies on the homologous Escherichia coli cold shock protein A (Ec-CspA). Jaravine et al. (18) found that β5 is the least protected from hydrogen exchange among the five β-strands, suggesting that it encounters “a low free energy barrier to segmental unfolding”. In the MD simulations, melting indeed started from β5. Rodriguez et al. (26) observed relatively lower opening rates and relatively higher closing rates for residues located on β2 and β3 (but not β1), suggesting that these two strands fold first (and unfold last). This conclusion is only in partial agreement with the MD simulations. Correlation between transition-state structure and protection from native-state hydrogen exchange has been reported for other proteins, but not without exception (80).
It is of interest to compare the transition state deduced from the unfolding simulations of the cold shock proteins to other theoretical predictions. The conservatism method of Mirny et al. (81) identified V-6, I-18, V-47, and V-63, which are located on β1, β2, β4, and β5, respectively. The first two residues are thus consistent with our simulation results, but the last two are contradictory.
Alm et al. (82) developed a simplified model for protein configurations, in which each residue is either ordered or disordered and at most two contiguous stretches of ordered residues can exist. The free energy of each configuration is based on native interactions, and the transition state is identified as the highest energy state along the lowest energy path from the unfolded state to the folded state. This method predicts high Φ-values for V-6–V-28 (located on β1-β2) for Bs-CspB (their prediction is available at http://tools.bakerlab.org/∼predictions/cgi-bin/test.cgi), which are in full agreement with our simulation results. In this context we note that other simple models have also been developed to predict Φ-values (83–85).
The method of low entropy loss routes of Weikl and Dill (78) predicted two parallel routes for folding Bs-CspB. One leads to the formation of the β1-β4 contact cluster by first forming the turn between β1 and β2, or the β1-β2 or β2-β3 contact. The other leads to the formation of the β3-β5 contact cluster by first forming the β1-β2 turn, or the β3-β4 loop, or the β4-β5 contact. In reverse order, the first folding route bears resemblance to our unfolding simulations; our simulations did not show evidence for their second folding route. Their method is based on clustering native contacts according to secondary structural elements, much like our monitoring of the unfolding process by the fractions of intact secondary structures. Weikl and Dill predicted similar folding routes for Bs-CspB, Bc-Csp, and Ec-CspA.
Morra et al. (30), based on MD simulations biased toward unfolding, concluded that the two-stranded C-terminal β-sheet of Bc-Csp “forms the most stable substructure, which decomposes very late in the unfolding process”. This is just the opposite of what was found in our unfolding simulations. Possible reasons for the discrepancy include the biasing potential, which could significantly distort the free-energy landscape, and the use of implicit rather than explicit solvent in their study. MD simulations of a number of proteins with both implicit and explicit solvent have uncovered the limitations of the implicit solvent model (86–88).
Karanicolas and Brooks (89) used both a simplified model similar to that developed by Alm et al. (82) and a protein model consisting of a string of beads to study the folding mechanism of Ec-CspA. Like Alm et al., the simplified model predicted that the three-stranded N-terminal β-sheet forms first, followed by the attachment of β4 and finally β5. This is just the reverse order of our unfolding simulations. On the other hand, the bead model predicted that the two β-sheets form independently, and then coalesce to form the folded structure.
A number of simpler models as well as our explicit water simulations are thus all able to correctly predict the polarized transition state of cold shock proteins. It appears that there is robustness in the transition state, which allows the methods to transcend their limitations.
Ion pairs as modulators of unfolding rate
Despite the common unfolding pathway, the unfolding rates of Bc-Csp and Bs-CspB differ by 20 times (10,22). In the simulations Bc-Csp indeed unfolded more slowly, and we suggest ion pairs around Arg-3 as a major factor. To uncover the origin of the difference in folding stability between Bc-Csp and Bs-CspB, Perl and Schmid (20) have examined the effects of the 11 amino acid substitutions between the two proteins individually and in combination and found that the stability difference can largely be accounted for by charge substitutions at three positions: 3, 46, and 66. The effects of the substitutions were quantitatively explained by electrostatic calculations (29). Perl et al. (22) have also studied the effects of the 11 substitutions on the folding and unfolding rates kf and ku, and here again the differences seem to be concentrated on the three positions.
Our MD simulations of the two proteins elucidated the net effects of the 11 substitutions together on the unfolding process. As it is too costly to simulate all the 11 single mutants, we will now try to use the simulation results for the two proteins to rationalize experimental observations for the effects of charge substitutions at positions 3, 46, and 66 on kf and ku. Upon substitution a residue with native interactions in the transition state will have much stronger effect on kf than on ku (equivalent to a Φ ∼ 1). Perl et al. (22) found Arg-3→Glu to be such a substitution, decreasing kf of Bc-Csp by 18-fold but increasing ku by just 2.6-fold. This result can be explained by the location of Arg-3 on the intact β1-β2 hairpin in the transition state and the ion pairs formed by Arg-3 with, e.g., Glu-21 and Glu-46. In the Arg-3→Glu mutant, the Glu-3 residue will experience charge-charge repulsion with Glu-21 and Glu-46 in the transition state, thus raising its free energy and decreasing kf. In the folded state of the mutant, the repulsion with Glu-21 and Glu-46 will likely be stronger, and there is also additional repulsion with the C-terminal. The Arg-3→Glu substitution thus raises the free energy of the folded state more than that of the transition state, hence increasing ku.
The substitution of a residue without native interactions in the transition state will have a much stronger effect on ku than on kf (equivalent to a Φ ∼ 0). Leu-66→Glu was found by Perl et al. (22) to be such a substitution, increasing ku of Bc-Csp by 4.3-fold but decreasing kf by just 1.4-fold. This result can be explained by the location of Leu-66 on the melted β5 strand in the transition state. In the Leu-66→Glu mutant, the Glu-66 residue will experience charge-charge repulsion with Glu-21 and Glu-46 in the folded state. Such repulsion is much diminished in the transition state since Glu-66 along with the C-terminal is free to move away. Consequently the free-energy barrier for unfolding is lowered, resulting in an increase in ku.
Perl et al. (22) found the Glu-46→Ala substitution to decrease both kf and ku (by 43% and 17%, respectively), leading to an “abnormal” Φ-value of 1.5. The decrease in kf can be understood by the presence of the Arg-3-Glu-46 ion pair in the transition state. The favorable interaction is eliminated by the Glu-46→Ala substitution, raising the free-energy barrier for folding and decreasing kf. In the folded state, Glu-46 experiences repulsion with the C-terminal, which is diminished in the transition state. The Glu-46→Ala substitution eliminates the repulsion in the folded state, leading to a higher free-energy barrier for unfolding and a ku.
The dominant role of the substitutions at positions 3, 46, and 66 in accounting for the difference in folding and unfolding rates between Bc-Csp and Bs-CspB is demonstrated by the experimental result that the triple substitution Arg-3→Glu/Glu-46→Ala/Leu-66→Glu on Bc-Csp lowers the folding rate by 24-fold and raises the unfolding rate by 15-fold, largely closing the gap between the two proteins. Similarly, the double substitution Glu-3→Arg/Glu-66→Leu on Bs-CspB leads to folding and unfolding rates very close to those of Bc-Csp. As revealed in our MD simulations, long-range electrostatic interactions among the charged residues can significantly modulate the rate of unfolding.
Acknowledgments
We thank Robert L. Baldwin and Franz X. Schmid for reading an earlier version of the manuscript. The use of an IBM SP4 supercomputer at the School of Computational Science of Florida State University is gratefully acknowledged.
This work was supported in part by National Institutes of Health grant GM58187.
Xiaoqin Huang's present address is College of Pharmacy, University of Kentucky, Lexington, KY 40536.
References
- 1.Bryngelson, J. D., J. N. Onuchic, N. D. Socci, and P. G. Wolynes. 1995. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins. 21:167–195. [DOI] [PubMed] [Google Scholar]
- 2.Chan, H. S., and K. A. Dill. 1998. Protein folding in the landscape perspective: chevron plots and non-arrhenius kinetics. Proteins. 30:2–33. [DOI] [PubMed] [Google Scholar]
- 3.Plaxco, K. W., K. T. Simons, I. Ruczinski, and D. Baker. 2000. Topology, stability, sequence and length: defining the determinants of two-state protein folding kinetics. Biochemistry. 39:11177–11183. [DOI] [PubMed] [Google Scholar]
- 4.Baldwin, R. L. 2002. Making a network of hydrophobic clusters. Science. 295:1657–1658. [DOI] [PubMed] [Google Scholar]
- 5.Daggett, V., and A. R. Fersht. 2003. Is there a unifying mechanism for protein folding? Trends Biochem. Sci. 28:18–25. [DOI] [PubMed] [Google Scholar]
- 6.Zhou, H.-X. 2004. Polymer models of protein stability, folding, and interactions. Biochemistry. 43:2141–2154. [DOI] [PubMed] [Google Scholar]
- 7.Schindelin, H., M. A. Marahiel, and U. Helnemann. 1993. Universal nucleic acid-binding domain revealed by crystal structure of the B. subtilis major cold shock protein. Nature. 364:164–168. [DOI] [PubMed] [Google Scholar]
- 8.Schnuchel, A., R. Wiltscheck, M. Czisch, M. Herrler, G. Willimsky, P. Graumann, M. A. Marahiel, and T. A. Holak. 1993. Structure in solution of the major cold-shock protein from Bacillus subtilis. Nature. 364:169–171. [DOI] [PubMed] [Google Scholar]
- 9.Schindler, T., and F. X. Schmid. 1996. Thermodynamic properties of an extremely rapid protein folding reaction. Biochemistry. 35:16833–16842. [DOI] [PubMed] [Google Scholar]
- 10.Perl, D., C. Welker, T. Schindler, K. Schroder, M. A. Marahiel, R. Jaenicke, and F. X. Schmid. 1998. Conservation of rapid two-state folding in mesophilic, thermophilic and hyperthermophilic cold shock proteins. Nat. Struct. Biol. 5:229–235. [DOI] [PubMed] [Google Scholar]
- 11.Schindler, T., D. Perl, P. Graumann, V. Sieber, M. A. Marahiel, and F. X. Schmid. 1998. Surface-exposed phenylalanines in the RNP1/RNP2 motif stabilize the cold-shock protein CspB from Bacillus subtilis. Proteins. 30:401–406. [DOI] [PubMed] [Google Scholar]
- 12.Jacob, M., G. Holtermann, D. Perl, J. Reinstein, T. Schindler, M. A. Geeves, and F. X. Schmid. 1999. Microsecond folding of the cold shock protein measured by a pressure-jump technique. Biochemistry. 38:2882–2891. [DOI] [PubMed] [Google Scholar]
- 13.Schindler, T., P. L. Graumann, D. Perl, S. Ma, F. X. Schmid, and M. A. Marahiel. 1999. The family of cold shock proteins of Bacillus subtilis: stability and dynamics in vitro and in vivo. J. Biol. Chem. 274:3407–3413. [DOI] [PubMed] [Google Scholar]
- 14.Frankenberg, N., C. Welker, and R. Jaenicke. 1999. Does the elimination of ion pairs affect the thermal stability of cold shock protein from the hyperthermophilic bacterium Thermotoga maritime? FEBS Lett. 454:299–302. [DOI] [PubMed] [Google Scholar]
- 15.Mueller, U., D. Perl, F. X. Schmid, and U. Heinemann. 2000. Thermal stability and atomic-resolution crystal structure of the Bacillus caldolyticus cold shock protein. J. Mol. Biol. 297:975–988. [DOI] [PubMed] [Google Scholar]
- 16.Perl, D., U. Mueller, U. Heinemann, and F. X. Schmid. 2000. Two exposed amino acid residues confer thermostability on a cold shock protein. Nat. Struct. Biol. 7:380–383. [DOI] [PubMed] [Google Scholar]
- 17.Pace, C. N. 2000. Single surface stabilizer. Nat. Struct. Biol. 7:345–346. [DOI] [PubMed] [Google Scholar]
- 18.Jaravine, V. A., K. Rathgeb-Szabo, and A. T. Alexandrescu. 2000. Microscopic stability of cold shock protein A examined by NMR native state hydrogen exchange as a function of urea and trimethylamine N-oxide. Protein Sci. 9:290–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Leeson, D. T., F. Gai, H. M. Rodriguez, L. M. Gregoret, and R. B. Dyer. 2000. Protein folding and unfolding on a complex energy landscape. Proc. Natl. Acad. Sci. USA. 97:2527–2532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Perl, D., and F. X. Schmid. 2001. Electrostatic stabilization of a thermophilic cold shock protein. J. Mol. Biol. 313:343–357. [DOI] [PubMed] [Google Scholar]
- 21.Delbruck, H., U. Mueller, D. Perl, F. X. Schmid, and U. Heinemann. 2001. Crystal structures of mutant forms of the Bacillus caldolyticus cold shock protein differing in thermal stability. J. Mol. Biol. 313:359–369. [DOI] [PubMed] [Google Scholar]
- 22.Perl, D., G. Holtermann, and F. X. Schmid. 2001. Role of the chain termini for the folding transition state of the cold shock protein. Biochemistry. 40:15501–15511. [DOI] [PubMed] [Google Scholar]
- 23.Perl, D., M. Jacob, M. Bano, M. Stupak, M. Antalik, and F. X. Schmid. 2002. Thermodynamics of a diffusional protein folding reaction. Biophys. Chem. 96:173–190. [DOI] [PubMed] [Google Scholar]
- 24.Dominy, B. N., D. Perl, F. X. Schmid, and C. L. Brooks III. 2002. The effects of ionic strength on protein stability: the cold shock protein family. J. Mol. Biol. 319:541–554. [DOI] [PubMed] [Google Scholar]
- 25.Martin, A., I. Kather, and F. X. Schmid. 2002. Origins of the high stability of an in vitro-selected cold-shock protein. J. Mol. Biol. 318:1341–1349. [DOI] [PubMed] [Google Scholar]
- 26.Rodriguez, H. M., A. D. Robertson, and L. M. Gregoret. 2002. Native state EX2 and EX1 hydrogen exchange of Escherichia coli CspA, a small β-sheet protein. Biochemistry. 41:2140–2148. [DOI] [PubMed] [Google Scholar]
- 27.Schuler, B., E. A. Lipman, and W. A. Eaton. 2002. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature. 419:743–747. [DOI] [PubMed] [Google Scholar]
- 28.Schuler, B., W. Kremer, H. R. Kalbitzer, and R. Jaenicke. 2002. Role of entropy in protein thermostability: folding kinetics of a hyperthermophilic cold shock protein at high temperatures using 19F NMR. Biochemistry. 41:11670–11680. [DOI] [PubMed] [Google Scholar]
- 29.Zhou, H.-X., and F. Dong. 2003. Electrostatic contributions to the stability of a thermophilic cold shock protein. Biophys. J. 84:2216–2222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Morra, G., M. Hodoscek, and E.-W. Knapp. 2003. Unfolding of the cold shock protein studied with biased molecular dynamics. Proteins. 53:597–606. [DOI] [PubMed] [Google Scholar]
- 31.Garcia-Mira, M. M., D. Boehringer, and F. X. Schmid. 2004. The folding transition state of the cold shock protein is strongly polarized. J. Mol. Biol. 339:555–569. [DOI] [PubMed] [Google Scholar]
- 32.Rhoades, E., M. Cohen, B. Schuler, and G. Haran. 2004. Two-state folding observed in individual protein molecules. J. Am. Chem. Soc. 126:14686–14687. [DOI] [PubMed] [Google Scholar]
- 33.Jung, A., C. Bamann, W. Kremer, H. R. Kalbitzer, and E. Brunner. 2004. High-temperature solution NMR structure of TmCsp. Protein Sci. 13:342–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhou, H.-X. 2005. Interactions of macromolecules with salt ions: an electrostatic theory for the Hofmeister effect. Proteins. 61:69–78. [DOI] [PubMed] [Google Scholar]
- 35.Zeeb, M., and J. Balbach. 2005. NMR spectroscopic characterization of millisecond protein folding by transverse relaxation dispersion measurements. J. Am. Chem. Soc. 127:13207–13212. [DOI] [PubMed] [Google Scholar]
- 36.Daggett, V. 2002. Molecular dynamics simulations of the protein unfolding/folding reaction. Acc. Chem. Res. 35:422–429. [DOI] [PubMed] [Google Scholar]
- 37.Simmerling, C., B. Strockbine, and A. E. Roitberg. 2002. All-atom structure prediction and folding simulations of a stable protein. J. Am. Chem. Soc. 124:11258–11259. [DOI] [PubMed] [Google Scholar]
- 38.Garcia, A. E., and J. N. Onuchic. 2003. Folding a protein in a computer: an atomic description of the folding/unfolding of protein A. Proc. Natl. Acad. Sci. USA. 100:13898–13903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Clementi, C., A. E. Garcia, and J. N. Onuchic. 2003. Interplay among tertiary contacts, secondary structure formation and side-chain packing in the protein folding mechanism: all-atom representation study of protein L. J. Mol. Biol. 326:933–954. [DOI] [PubMed] [Google Scholar]
- 40.Cárdenas, A. E., and R. Elber. 2003. Kinetics of cytochrome C folding: atomically detailed simulations. Proteins. 51:245–257. [DOI] [PubMed] [Google Scholar]
- 41.Snow, C. D., E. J. Sorin, Y. M. Rhee, and V. S. Pande. 2005. How well can simulation predict protein folding kinetics and thermodynamics? Annu. Rev. Biophys. Biomol. Struct. 34:43–69. [DOI] [PubMed] [Google Scholar]
- 42.Lazaridis, T., I. Lee, and M. Karplus. 1997. Dynamics and unfolding pathways of a hyperthermophilic and a mesophilic rubredoxin. Protein Sci. 6:2589–2605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Li, A., and V. Daggett. 1998. Molecular dynamics simulations of the unfolding of barnase: characterization of the major intermediate. J. Mol. Biol. 275:677–694. [DOI] [PubMed] [Google Scholar]
- 44.Tsai, J., M. Levitt, and D. Baker. 1999. Hierarchy of structure loss in MD simulations of src SH3 domain unfolding. J. Mol. Biol. 291:215–225. [DOI] [PubMed] [Google Scholar]
- 45.Main, E. R. G., K. F. Fulton, and S. E. Jackson. 1999. Folding pathway of FKBP12 and characterization of the transition state. J. Mol. Biol. 291:429–444. [DOI] [PubMed] [Google Scholar]
- 46.Ferrara, P., and A. Caflisch. 2001. Native topology or specific interactions: what is more important for protein folding? J. Mol. Biol. 306:837–850. [DOI] [PubMed] [Google Scholar]
- 47.Gsponer, J., and A. Caflisch. 2001. Role of native topology investigated by multiple unfolding simulations for four SH3 domains. J. Mol. Biol. 309:285–298. [DOI] [PubMed] [Google Scholar]
- 48.Day, R., B. J. Bennion, S. Ham, and V. Daggett. 2002. Increasing temperature accelerates protein unfolding without changing the pathway of unfolding. J. Mol. Biol. 322:189–203. [DOI] [PubMed] [Google Scholar]
- 49.Guo, W., S. Lampoudi, and J.-E. Shea. 2004. Temperature dependence of the free energy landscape of the src-SH3 protein domain. Proteins. 55:395–406. [DOI] [PubMed] [Google Scholar]
- 50.Ferguson, N., R. Day, C. M. Johnson, M. D. Allen, V. Daggett, and A. R. Fersht. 2005. Simulation and experiment at high temperatures: ultrafast folding of a thermophilic protein by nucleation-condensation. J. Mol. Biol. 347:855–870. [DOI] [PubMed] [Google Scholar]
- 51.Muñoz, V., P. A. Thompson, J. Hofrichter, and W. A. Eaton. 1997. Folding dynamics and mechanism of β-hairpin formation. Nature. 390:196–199. [DOI] [PubMed] [Google Scholar]
- 52.Martinez, J. C., and L. Serrano. 1999. The folding transition state between SH3 domains is conformationally restricted and evolutionarily conserved. Nat. Struct. Biol. 6:1010–1016. [DOI] [PubMed] [Google Scholar]
- 53.Riddle, D. S., V. P. Grantcharova, J. V. Santiago, E. Alm, I. Ruczinski, and D. Baker. 1999. Experiment and theory highlight role of native state topology in SH3 folding. Nat. Struct. Biol. 6:1016–1024. [DOI] [PubMed] [Google Scholar]
- 54.Fulton, K. F., E. R. G. Main, V. Daggett, and S. E. Jackson. 1999. Mapping the interactions present in the transition state for unfolding/folding of FKBP12. J. Mol. Biol. 291:445–461. [DOI] [PubMed] [Google Scholar]
- 55.Hamill, S. J., A. Steward, and J. Clarke. 2000. The folding of an immunoglobulin-like Greek key protein is defined by a common-core nucleus and regions constrained by topology. J. Mol. Biol. 297:165–178. [DOI] [PubMed] [Google Scholar]
- 56.Guerois, R., and L. Serrano. 2000. The SH3-fold family: experimental evidence and prediction of variations in the folding pathways. J. Mol. Biol. 304:967–982. [DOI] [PubMed] [Google Scholar]
- 57.Kim, D. E., C. Fisher, and D. Baker. 2000. A breakdown of symmetry in the folding transition state of protein L. J. Mol. Biol. 298:971–984. [DOI] [PubMed] [Google Scholar]
- 58.McCallister, E. L., E. Alm, and D. Baker. 2000. Critical role of β-hairpin formation in protein G folding. Nat. Struct. Biol. 7:669–673. [DOI] [PubMed] [Google Scholar]
- 59.Jager, M., H. Nguyen, J. C. Crane, J. W. Kelly, and M. Gruebele. 2001. The folding mechanism of a β-sheet, the WW domain. J. Mol. Biol. 311:373–393. [DOI] [PubMed] [Google Scholar]
- 60.Du, D., Y. Zhu, C. Y. Huang, and F. Gai. 2004. Understanding the key factors that control the rate of β-hairpin folding. Proc. Natl. Acad. Sci. USA. 101:15915–15920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Case, D. A., D. A. Pearlman, J. W. Caldwell, T. E. Cheatham III, J. Wang, W. S. Ross, C. L. Simmerling, T. A. Darden, K. M. Merz, R. V. Stanton, A. L. Cheng, J. J. Vincent, M. Crowley, V. Tsui, H. Gohlke, R. J. Radmer, Y. Duan, J. Pitera, I. Massova, G. L. Seibel, U. C. Singh, P. K. Weiner, and P. A. Kollman. 2002. Amber Version 7.0. University of California, San Francisco, CA.
- 62.Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- 63.Neria, E., S. Fisher, and M. Karplus 1996. Simulation of activation energies in molecular systems. J. Chem. Phys. 105:1902–1921. [Google Scholar]
- 64.Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen 1977. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- 65.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: an Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 66.Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- 67.Sagui, C., and T. A. Darden. 1999. Molecular dynamics simulations of biomolecules: long-range electrostatic effects. Annu. Rev. Biophys. Biomol. Struct. 28:155–179. [DOI] [PubMed] [Google Scholar]
- 68.Toukmaji, A., C. Sagui, J. Board, and T. Darden. 2000. Efficient particle-mesh Ewald based approach to fixed and induced dipolar interactions. J. Chem. Phys. 113:10913–10927. [Google Scholar]
- 69.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- 70.Morishita, T. 2000. Fluctuation formulas in molecular-dynamics simulations with the weak coupling heat bath. J. Chem. Phys. 113:2976–2982. [Google Scholar]
- 71.Chatfield, D. C., A. Szabo, and B. R. Brooks. 1998. Molecular dynamics of staphylococcal nuclease: comparison of simulations with 15N and 13C NMR relaxation data. J. Am. Chem. Soc. 120:5301–5311. [Google Scholar]
- 72.Kabsch, W., and C. Sander. 1983. Dictionary of protein secondary structures: pattern recognition of hydrogen bonded and geometrical features. Biopolymers. 22:2577–2637. [DOI] [PubMed] [Google Scholar]
- 73.Jaenicke, R. 2000. Do ultrastable proteins from hyperthermophiles have high or low conformational rigidity? Proc. Natl. Acad. Sci. USA. 97:2962–2964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Elcock, A. H. 1999. Realistic modeling of the denatured states of proteins allows accurate calculations of the pH dependence of protein stability. J. Mol. Biol. 294:1051–1062. [DOI] [PubMed] [Google Scholar]
- 75.Zhou, H.-X. 2002. A Gaussian-chain model for treating residual charge-charge interactions in the unfolded state of proteins. Proc. Natl. Acad. Sci. USA. 99:3569–3574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Chan, H. S., and K. A. Dill. 1990. The effects of internal constraints on the configurations of chain molecules. J. Chem. Phys. 92:3118–3135. [Google Scholar]
- 77.Shimizu, S., and H. S. Chan. 2000. Temperature dependence of hydrophobic interactions: a mean force perspective, effects of water density, and nonadditivity of thermadynamic signatures. J. Chem. Phys. 113:4683–4700. [Google Scholar]
- 78.Weikl, T. R., and K. A. Dill. 2003. Folding rates and low-entropy-loss routes of two-state proteins. J. Mol. Biol. 329:585–596. [DOI] [PubMed] [Google Scholar]
- 79.Zhou, H.-X. 2005. How do biomolecular systems speed up and regulate rates? Phys. Biol. 2:R1–R25. [DOI] [PubMed] [Google Scholar]
- 80.Grantcharova, V. P., D. S. Riddle, J. V. Santiago, and D. Baker. 1998. Important role of hydrogen bonds in the structurally polarized transition state for folding of the srcSH3 domain. Nat. Struct. Biol. 5:714–720. [DOI] [PubMed] [Google Scholar]
- 81.Mirny, L. A., V. Abkevich, and E. I. Shakhnovich. 1996. Universality and diversity of the protein folding scenarios: a comprehensive analysis with the aid of a lattice model. Fold. Des. 1:103–116. [DOI] [PubMed] [Google Scholar]
- 82.Alm, E., A. V. Morozov, T. Kortemme, and D. Baker. 2002. Simple physical models connect theory and experiment in protein folding kinetics. J. Mol. Biol. 322:463–476. [DOI] [PubMed] [Google Scholar]
- 83.Galzitskaya, O. V., and A. V. Finkelstein. 1999. A theoretical search for folding/unfolding nuclei in three-dimensional protein structures. Proc. Natl. Acad. Sci. USA. 96:11299–11304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Muñoz, V., and W. A. Eaton. 1999. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. USA. 96:11311–11316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Clementi, C., H. Nymeyer, and J. N. Onuchic. 2000. Topological and energetic factors: what determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol. 298:937–953. [DOI] [PubMed] [Google Scholar]
- 86.Nymeyer, H., and A. E. Garcia. 2003. Simulation of the folding equilibrium of α-helical peptides: a comparison of the generalized Born approximation with explicit solvent. Proc. Natl. Acad. Sci. USA. 100:13934–13939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Zhou, R. 2003. Free energy landscape of protein folding in water: explicit vs. implicit solvent. Proteins. 53:148–161. [DOI] [PubMed] [Google Scholar]
- 88.Rhee, Y. M., E. J. Sorin, G. Jayachandran, E. Lindahl, and V. S. Pande. 2004. Simulations of the role of water in the protein-folding mechanism. Proc. Natl. Acad. Sci. USA. 101:6456–6461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Karanicolas, J., and C. L. Brooks III. 2003. The importance of explicit chain representation in protein folding models: an examination of Ising-like models. Proteins. 53:740–747. [DOI] [PubMed] [Google Scholar]