Complementarity of ensemble and single-molecule measures of protein motion: A relaxation dispersion NMR study of an enzyme complex

Abstract

Single-molecule fluorescence experiments have shown that the conformation of the complex between Escherichia coli general NAD(P)H:flavin oxidoreductase (FRE) and flavin adenine dinucleotide (FAD) fluctuates over a range of timescales between 10⁻⁴ and 1 s. Here we use ¹⁵N and ¹³C relaxation dispersion NMR methods to study millisecond-timescale dynamics in the complex. In this time regime, the protein is extremely flexible, with residues that undergo conformational exchange located throughout the molecule. Three distinct regions of dynamics are quantified, with two of them involving residues making contact to the donor (Tyr-35) and acceptor (FAD) sites that participate in the electron transfer reaction monitored in single-molecule experiments. Modulation of the donor–acceptor distance through these conformational exchange processes, occurring with rates of ≈400 and 1,200 s⁻¹ (22°C), affects the rate of electron transfer and partially accounts for the range of the observed dynamics monitored in the fluorescence experiments.

It is well known that biological molecules are dynamic and that these motions can be important for function (1, 2). Insight into molecular dynamics has been obtained through a large number of studies covering a wide range of systems and using a variety of methodologies (1–3). An early pioneering experiment by Wüthrich and coworkers (4) provided a glimpse of the important role that solution NMR spectroscopy would play in this area. In their study, the temperature dependence of ¹H NMR lineshapes in the basic pancreatic trypsin inhibitor was quantified, providing strong evidence for rotation about C^β–C^γ bonds in phenylalanine rings in the protein over a range of timescales (4). Such dynamics are only possible if the protein undergoes significant breathing motions. Since this work, a large number of solution-based NMR methods have emerged for quantifying site-specific protein dynamics with rates that vary by many orders of magnitude (3).

Over the past several years, single-molecule fluorescence experiments to probe dynamics of individual protein molecules have emerged, providing information about the distribution of molecular properties that cannot be obtained in ensemble-based approaches (5). In general, conformational fluctuations occurring on timescales slower than binding events or chemical reactions lead to changes in structure that result in observable modulations in binding or catalytic rates; a variety of enzymes for which this finding is the case have now been studied using single-molecule approaches (5). In addition to quantifying rate fluctuations, it is also possible to obtain information about dynamics involving specific distances. For example, Xie and coworkers (6) studied the single-molecule fluorescence properties of the enzyme Escherichia coli NAD(P)H:flavin oxidoreductase (FRE), which catalyzes the reduction of free flavins such as FAD (7–9). The fluorescence of FAD in the FRE–FAD complex is quenched by Tyr-35 in FRE. Importantly, modulations in the FRE–FAD distance over timescales varying from 0.1 ms to 1 s were quantified from fluctuations in the single-molecule fluorescence lifetime of FAD.

The study of Xie and coworkers (6) on the FRE–FAD system provides a striking demonstration of the unsynchronized, spontaneous nature of protein dynamics, as observed from studies of one molecule at a time. It also raises some interesting questions. For example, are the observed fluctuations in distance between acceptor and donor the result of processes that are spread over the entire protein, or are the fluctuations localized to a few residues near Tyr-35 of FRE? More generally, can NMR approaches that provide site-specific and ensemble-averaged dynamics information complement single-molecule studies? In this work, we present a relaxation dispersion NMR study of the FRE–FAD complex to address these issues.

Relaxation dispersion NMR spectroscopy has emerged as a powerful methodology for the study of biomolecular dynamics in the microsecond to millisecond (ms) time regime (10). Here we use Carr–Purcell–Meiboom–Gill (CPMG)-based dispersion approaches (11–13), which are sensitive to ms exchange dynamics between states, to probe motion in the FRE–FAD system. Both ¹⁵N and ¹³C methyl spin relaxation rates have been measured so that backbone and methyl side-chain fluctuations could be probed. The results demonstrate that a large fraction of FRE is dynamic on the ms timescale, with at least three distinct motional processes that can account, in part, for the observed distance fluctuations measured in single-molecule studies.

Results and Discussion

Relaxation Dispersion NMR Spectroscopy of the FRE–FAD Complex.

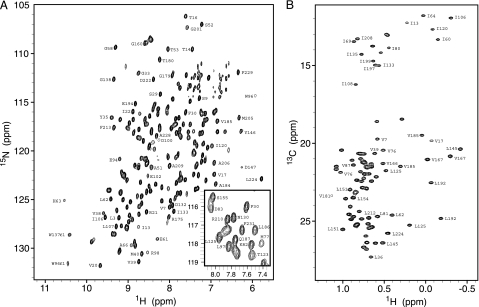
Fig. 1 shows ¹H,¹⁵N and ¹H,¹³C correlation spectra recorded on an {Ileδ1(¹³CH₃), Leu(¹³CH₃,¹³CH₃), Val(¹³CH₃,¹³CH₃)}, [U-¹⁵N,¹³C,²H] sample of FRE–FAD, prepared as described in Materials and Methods. High-quality heteronuclear single quantum coherence (HSQC) spectra are obtained with >96% of the correlations assigned to specific sites in the protein, corresponding to 90% of the residues in the molecule. The majority of the remaining 10% of residues for which assignments are not obtained are located in the ligand (FAD)-binding site and give rise to correlations that are broadened beyond detection. In this regard, it is important to note that correlations that were observed from residues in the binding region of the protein are significantly broadened as well. Close to 140 of the expected 226 peaks are well resolved in the 2D ¹H,¹⁵N transverse relaxation optimized spectroscopy (TROSY) data set at all temperatures considered and are of reasonable sensitivity, providing a large number of motional-probes throughout the protein backbone. In addition, the Ile, Leu, Val methyl correlation spectrum is well resolved with quantification possible for 51 of the 91 expected correlations, providing probes for 40 of the 54 Ile, Leu, and Val side chains. Cross-peaks derived from only a single conformer, the major state, are observed in spectra. Information about “invisible” exchanging states can be obtained, however, so long as they are populated at a level of ≈0.5% or higher, by recording CPMG relaxation dispersion data sets. In this type of experiment, a variable number of refocusing pulses (either ¹⁵N or ¹³C in the present case) is applied during a constant-time relaxation delay. This scheme leads to a (partial) attenuation of the effects of the exchange process in a manner that depends on the exchange parameters. A series of spectra in which only the number of refocusing pulses is varied can be recorded, and the intensities of peaks can be quantified. The resulting relaxation dispersion curve gives the effective relaxation rate, R_2,eff(ν_CPMG), as a function of ν_CPMG = 1/(4δ), where 2δ is the time between the equally spaced refocusing pulses. Fitting the relaxation dispersion profiles with exchange models enables rates of exchange and populations of the exchanging states to be extracted as well as structural information about the “invisible states” through measurement of chemical shift differences between them.

Fig. 1.

¹H,¹⁵N-TROSY-HSQC (A) and ¹H,¹³C-HSQC (B) spectra recorded on an {Ileδ1(¹³CH₃), Leu(¹³CH₃,¹³CH₃),Val(¹³CH₃,¹³CH₃)}, U-¹⁵N,¹³C,²H sample of FRE–FAD at 600 MHz and 27°C. Peaks are labeled according to their position in the FRE sequence. The methyl groups have not been stereospecifically assigned.

Observation of Spatially Resolved Separate Exchange Processes.

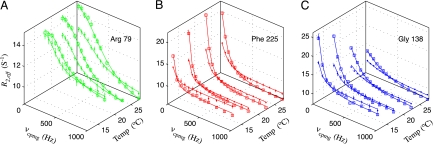
Of the 137 well resolved correlations in the ¹H,¹⁵N HSQC spectrum in the protein at 22°C, 45 showed dispersions that could be quantified [R_2,eff(50 Hz) − R_2,eff(1,000 Hz) > 1.5 s⁻¹ (at 500 MHz corresponding to 11.7 T) and 3 s⁻¹ (800 MHz, 18.8 T)]; the residues that contribute dispersions are distributed throughout the protein. Fig. 2 plots relaxation dispersion profiles as a function of temperature for Arg-79 (Fig. 2A), Phe-225 (Fig. 2B), and Gly-138 (Fig. 2C), recorded at magnetic field strengths of 11.7 (●) and 18.8 (□) T. The dispersion profiles decrease as a function of the number of refocusing pulses (proportional to ν_CPMG), indicating that the measured processes are on the ms timescale, where their effects can be attenuated by the application of radio frequency pulses. Notably, the temperature dependence of the relaxation profiles vary for the set of three residues chosen, consistent with different exchange processes at different sites in the protein (see below). Indeed, attempts to fit data from all sites together to a model of a single global two-site exchange process (i.e., same rates and populations) led to poor fits with reduced χ² values of 6 (χ_reduced² = χ²/N, where N is the number of degrees of freedom). Only when 30% of the profiles were removed, derived primarily from residues in two spatially distinct regions (referred to as Group 1 and 2 residues; see below), did χ_reduced² drop to ≈1 (14). This result confirms that the data are not reflective of a global two-state process.

Fig. 2.

¹⁵N TROSY relaxation dispersion profiles for Arg-79 (A), Phe-225 (B), and Gly-138 (C) recorded at magnetic field strengths of 11.7 (●) and 18.8 (□) T, as a function of temperature. Arg-79, Phe-225, and Gly-138 are representative residues of Groups 1, 2, and 3, respectively.

To see whether proximal residues contribute to the same dynamical process, individual residue fits using a two-state model,

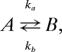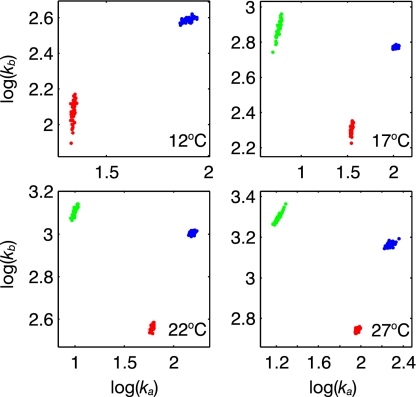
were performed, and the distribution of k_ex = k_a + k_b values was plotted on the structure. Sites close together were often found to have similar k_ex values, with three main regions of ms dynamics identified (denoted by green, red, and blue in Fig. 3), which includes 27 of the 45 residues for which amide dispersions were observed. Notably, when dispersion data from all residues within one of the three distributions were fit together, values of χ_reduced2 ∼ 1 were obtained, suggesting that proximal sites are dynamically coupled. The dynamical processes associated with each of the sites are quite distinct. Fig. 4 shows a plot of log(k_b) vs. log(k_a), obtained from fits of all residues within a given site, with each site color coded. Here a Monte Carlo procedure was performed in which 50 sets of simulated data were generated for each site, based on the experimentally derived exchange parameters and the estimated noise, and pairs of (k_a, k_b) were extracted from two-state data fits (see Materials and Methods). The variation in rates (within a given group) provides an estimate of the errors; it is clear that the difference in rates measured for each of the three distributions is significantly larger than the error limits.

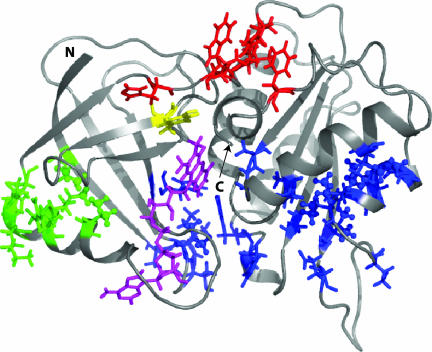
Fig. 3.

Model of the FRE–FAD complex (9, 15, 16) showing the locations of the acceptor (FAD; magenta) and donor (Tyr-35; yellow) ET partners as well as the positions of residues in Groups 1 (green), 2 (red), and 3 (blue). Side chains are only illustrated for Tyr-35 and for residues of Groups 1–3 (using a stick representation), with methyl groups indicated by balls. The positions of the N and C termini of the protein are denoted by N and C, respectively.

Fig. 4.

Residues from Groups 1 (green), 2 (red), and 3 (blue) have distinct ms timescale motions. A Monte Carlo procedure was used, as described in the text, to establish that the range of (k_a, k_b) values for each of the three exchange processes that have been quantified are well separated.

What Is the Nature of the Dynamic Processes That Have Been Characterized by the Relaxation Dispersion Data?

Some insight can be provided from the chemical-shift differences between exchanging states that are obtained from the fits. For example, the minor conformation is populated at <1% for residues in Group 1 (green in Fig. 3), with ¹⁵N chemical shifts that range from 2.4 to 7.1 ppm from the native state. These shift differences are consistent with a local unfolding process (i.e., they match differences expected based on random coil values). The temperature dependence of the exchange rates also suggests unfolding. Fig. 2A shows dispersion data for Arg-79, a Group 1 residue. The increase in the amplitude of the dispersion profiles with temperature at least in part results from the growth of the population of the minor conformation (from 0.76% to 0.83%) implying that the reaction

is endothermic, as expected for an unfolding process. The molecular nature of the exchange processes involving residues from Groups 2 (red) and 3 (blue) is more difficult to discern from the extracted chemical shift changes. For both of these exchange events, the minor states are quite populated (on the order of 15%), and only small changes in amide ¹⁵N chemical shifts between major and minor conformers are observed (between 0.4 and 1.6 ppm) that are not consistent with unfolding. In this regard, it is of interest to note that hydrogen-exchange experiments show that amides from Group 1 residues are far less protected than those from Groups 2 and 3.

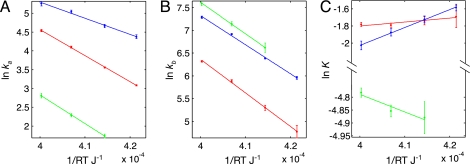
Fig. 5 and Table 1 show the temperature dependencies of k_a and k_b obtained from fits of the dispersion data for Groups 1–3; no assumption about the rate–temperature dependence has been made in extracting values of the rates. The rate profiles are linear with temperature and can be fit by using transition state theory to obtain activation and equilibrium parameters (Table 2).Of interest, the different temperature dependencies of dispersion profiles for residues of Groups 1 (representative example in Fig. 2A), 2 (Fig. 2B), and 3 (Fig. 2C) reflect the fact that ΔH is >0, ≈0, and <0, respectively, for the exchange processes that involve these sets of residues. Moreover, the differences in thermodynamic parameters that describe the transitions provide further confirmation of the distinct nature of the exchange processes that were classified on the basis of the measured exchange rates (see above). It is also possible to fit the dispersion data directly to an exchange model that assumes that the rates vary with temperature as predicted by transition-state theory [i.e., to enforce a linear relationship between ln(k/T) and 1/T from the outset]. The extracted exchange parameters obtained by using this approach are provided in Tables 3–6, which are published as supporting information on the PNAS web site.

Fig. 5.

Arrhenius (A and B) and van’t Hoff (C) plots describing the temperature dependence of the exchange processes of residues in Groups 1 (green), 2 (red), and 3 (blue). Errors in the rates are established on the basis of a Monte Carlo procedure, as described in the text.

Table 1.

Kinetic parameters for residues of Groups 1, 2, and 3

Group	χ2/N	12°C		17°C		22°C		27°C
		ka, s−1	kb, s−1	ka, s−1	kb, s−1	ka, s−1	kb, s−1	ka, s−1	kb, s−1
1	0.6	—	—	5.7 ± 0.3	751 ± 76	9.9 ± 0.4	1,267 ± 56	16.6 ± 0.9	1,983 ± 102
2	0.9	21.9 ± 0.3	119 ± 16	35.1 ± 0.6	200 ± 11	60 ± 2	361 ± 10	94 ± 3	555 ± 10
3	1.0	80 ± 4	387 ± 12	106 ± 5	592 ± 9	155 ± 7	1,008 ± 16	193 ± 12	1,460 ± 35

Group 1 consists of ¹⁵N data of amides from Val-7, Arg-79, Ile-80, Lys-82, Asp-83, and His-84 and ¹³C data of methyls from Val-7, Val-76, and Ile-80. Group 2 consists of ¹⁵N amide dispersions from His-92, Glu-94, Trp-96, Leu-97, Arg-98, Phe-225, and Nε1 from Trp-96. Group 3 includes amide dispersions from Ala-12, Ile-13, Thr-14, Val-17, His-63, Gly-138, His-144, Tyr-146, Glu-168, Thr-178, Ala-184, Ala-200, Gly-201, and Met-205 and methyl dispersions from Val-17, Val-166, Val-181, Leu-182, Val-185 (2), Leu-186, and Leu-212. None of the ¹⁵N data recorded at 12°C are used for Group 1 because the dispersions are very small. χ²/N is the reduced χ² value for the fit. (See Materials and Methods for details on fitting.)

Table 2.

Thermodynamic parameters for residues of Groups 1, 2, and 3

Group	Forward		Reverse		Equilibrium		Barrier ΔG+ at 22°C, kJ/mol
	ΔH+, kJ/mol	ΔS+, J/mol·K	ΔH+, kJ/mol	ΔS+, J/mol·K	ΔH, kJ/mol	ΔS, J/mol·K	Forward	Reverse
1	74 ± 5	24 ± 15	67 ± 7	41 ± 24	7 ± 5	−17 ± 16	66.7 ± 0.1	54.8 ± 0.1
2	67 ± 1	15 ± 4	71 ± 6	46 ± 20	−5 ± 6	−30 ± 21	62.3 ± 0.1	58.0 ± 0.1
3	41 ± 2	−66 ± 7	62 ± 2	20 ± 6	−21 ± 1	−87 ± 4	60.1 ± 0.1	55.5 ± 0.1

See the Table 1 legend for an explanation of Groups 1–3.

Merging Single-Molecule and Ensemble-Averaged Studies.

Xie and coworkers (6) have studied single-molecule conformational dynamics of the FRE–FAD complex using electron transfer (ET). A laser pulse was used to excite the isoalloxazine moiety of FAD, with fluorescence resulting from the decay back to the ground electronic state. However, the fluorescence lifetime, γ⁻¹, is mediated by Tyr-35 of FRE, which acts as a quencher by transferring an electron to FAD. Because γ⁻¹ is inversely proportional to the ET rate, k_ET = k_ET^oexp(−βR(t)), where β is 1–1.4 Å⁻¹ for proteins and R(t) is the edge-to-edge distance between electron donor and acceptor, measurement of γ⁻¹(t) provides information about those distance fluctuations that are slower than the ET time. Instead of observing a single value for γ⁻¹ [expected in the case of a constant R(t)], a distribution was observed that establishes that R(t), and hence the donor–acceptor distance in the FRE–FAD complex, fluctuates in time. The large variability in γ⁻¹ (from ≈30 ps to 3 ns) is due to motions over a range of timescales, and the fluorescence experiments are sensitive to dynamics from 0.1 to 1,000 ms. The distribution of γ⁻¹ values can, in turn, be translated into a probability density, P(R), from which a potential of mean force for the isoalloxazine–Tyr-35 pair is calculated (6). This potential, which is an effective projection of a multidimensional landscape to a single coordinate, is smooth and nearly harmonic and cannot account for the complexity of the dynamics observed in the single-molecule studies. Insight into the complex energy landscape giving rise to the single-molecule dynamics can be obtained from other approaches, however, including NMR.

In the ensemble-averaged NMR study reported here, we show that the FRE–FAD complex populates several conformations that interconvert in the ms time regime, with barrier heights on the order of 60 kJ/mol that are largely enthalpic, at 22°C (see Table 2). Three distinct distributions of residues that interconvert between states have been identified, with residues comprising Groups 2 and 3 (see above and Table 1) proximal to the donor (Tyr-35) and acceptor (FAD), respectively. Notably, a pair of hydrogen bonds is formed between His-92 (Group 2) and Tyr-35. Group 3 residues in the ligand-binding site include His-63, Tyr-146, and Gly-201, with His-63 and Tyr-146 forming hydrogen bonds with the flavin group in FAD (9, 15). Thus, the conformational changes detected by NMR involving these residues are expected to affect the donor–acceptor distance, with small changes in the edge-to-edge distance between the donor and acceptor having a significant effect on k_ET (for example, a 0.5-Å increase in distance decreases k_ET by a factor of 2, β = 1.4 Å⁻¹). Group 2 and 3 residues interconvert between conformers that have different lifetimes, τ_ex = 1/k_ex ∼ 2.4 ms (Group 2) and 0.9 ms (Group 3), at 22°C, so that donor–acceptor distance fluctuations occur at no less than two distinct rates in the ms regime. Finally, because the processes responsible for the chemical exchange detected in this study are on a much slower timescale than the rate of ET (approximately ms vs. approximately nanosecond), the conformational changes reported by NMR are partly responsible for the observed multiexponential decay of the fluorescence signal. It is also of interest that recent molecular dynamics simulations performed on this system show that even in the picosecond–nanosecond timescale, there are complex dynamics (i.e., sampling different molecular conformations) that contribute to R(t) fluctuations, although these processes are sufficiently fast that they probably do not contribute to the experimentally observed dynamics (via fluorescence) in the 0.1- to 1,000-ms timescale (16).

In summary, we used ¹⁵N and ¹³C CPMG relaxation dispersion NMR experiments to characterize ms timescale motion in the FRE–FAD complex. At least three discrete processes were observed, even in the narrow time regime that is explored here (experiments sensitive to rates of several hundred to several thousand per second). Notably, two of the processes involve sets of residues that are proximal to the donor/acceptor sites monitored in single-molecule studies. Motions of these residues certainly affect ET rates probed by fluorescence decay. The present work demonstrates the complementarity between single-molecule and NMR studies. The former are sensitive to motions over a wide range of timescales but report on modulations of only a single distance, at least in this case. The latter experiments provide information over a smaller time window, but motional properties in this time regime can be obtained for every residue in the molecule, in principle. For favorable instances, such as for Group 1 residues, it is possible to establish the nature of the exchange process as well. It is clear that a number of different methods will be needed to fully clarify the complex nature of motions that proteins undergo. The combination of single-molecule and solution NMR studies provides a powerful approach for beginning to achieve this goal.

Materials and Methods

Sample Preparation.

The DNA sequence for E. coli FRE was cloned into a pET-21b plasmid as described by Xun and Sandvik (17). BL21(DE3) cells transformed with this plasmid (pF5) were used for protein expression. Samples of FRE were prepared by growing cells in M9 minimal medium supplemented with appropriate precursors. A {Ileδ1(¹³CH₃), Leu(¹³CH₃,¹³CH₃), Val(¹³CH₃,¹³CH₃)}, [U-¹⁵N,¹³C,²H] sample of FRE–FAD was used for all of the relaxation dispersion measurements (see below), prepared following the protocol of Goto et al. (18) and purified as described (17), except for an additional unfolding/refolding step to exchange ²H with ¹H (at the amide and side-chain NH and NH₂ groups). The purified protein was denatured by dissolving in an 8 M urea solution containing 0.1 mM FAD to a final concentration of 0.5 mg/ml protein and refolded by dialyzing extensively against 20 mM potassium phosphate/100 mM NaCl/10% glycerol/0.1 mM EDTA/5 mM DTT (pH 8.0) at 4°C. The FRE–FAD complex then was concentrated and separated from any aggregates by gel filtration chromatography using a Superdex 75 column. The final sample concentration was ≈1.5 mM in protein/20 mM potassium phosphate/5 mM FAD/5 mM DTT/0.1 mM EDTA (pH 7.4) (stored under argon). A second sample of FRE–FAD that was U-¹⁵N,¹³C-labeled and fractionally deuterated was prepared by using 70% D₂O in the medium during protein overexpression. This sample, purified as described above for the perdeuterated protein and also 1.5 mM in concentration of protein, was used for all of the resonance-assignment experiments.

NMR Experiments.

Backbone assignment experiments were recorded at 27°C on a 600-MHz Varian Inova spectrometer equipped with a cold probe. All experiments made use of the TROSY principle (19) and included HNCO, HN(CA)CO, HNCA, HN(CO)CA, HN(CA)CB, and HN(COCA)CB schemes that have been described in detail (20, 21). Side-chain methyl groups were assigned by using 3D (H)C(CACO)NH total correlation spectroscopy (TOCSY) and H(CCACO)NH TOCSY experiments (22), correlating the methyl groups to previously assigned backbone amide positions.

Constant-time CPMG relaxation dispersion experiments (11, 12) were recorded at a pair of field strengths corresponding to ¹H resonance frequencies of 500 (11.7 T) and 800 (18.8 T) MHz. ¹⁵N dispersion experiments were TROSY-based (10, 23) and were performed at 12°, 17°, 22°, and 27°C, with constant-time delays, T, of 32 and 36 ms for data obtained at the two lower temperatures, respectively, and of 40 ms for the highest two temperatures. ¹³C-methyl CPMG experiments (13) were performed at 17° and 22°C with constant-time delays of 24 and 26 ms, respectively. Data were collected at no less than 12 CPMG fields, ν_CPMG = 1/(4δ), where 2δ is the time between either the ¹⁵N or ¹³C refocusing pulses applied during the constant-time element, T. Values of ν_CPMG ranged from 50 to 1,000 Hz, depending on the experiment. All NMR data were processed by using NMRPipe (24) and examined with NMRview software (25). Peak intensities were quantified by using the MUNIN approach (26).

Effective relaxation rates, R_2,eff(ν_CPMG), were extracted from experimental dispersion data by using the relation, R_2,eff(ν_CPMG) = −ln{I(ν_CPMG)/I_o}/T, where I(ν_CPMG) and I_o are intensities of correlations in the presence and absence of the constant-time relaxation element of duration T (27). Errors were estimated on the basis of repeat measurements at three CPMG fields as described (28), and a minimum error of 0.02 × R_2,eff(ν_CPMG) was used.

Data Analysis.

Relaxation dispersion data either from a single site or from groups of sites were fit to a two-state model

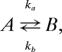where the adjustable parameters are the exchange rate constant k_ex = k_a + k_b, population (mole fraction) of the minor state p_b = k_a/(k_a + k_b), the chemical-shift difference (in ppm) between the two states Δω, and the intrinsic relaxation rates of magnetization in each of the exchanging states (assumed to be the same). Values of k_ex and p_b are fixed for all of the residues in a group at a given temperature, and when data over multiple temperatures were fit, Δω values were assumed to be temperature independent (over the narrow range examined here; see Fig. 6 and Supporting Text, which are published as supporting information on the PNAS web site). ¹⁵N relaxation data from a particular site were included in the analysis only if ΔR = R_2,eff(lowest ν_CPMG) − R_2,eff(1,000 Hz) > 1.5 and 3 s⁻¹ for dispersions recorded at field strengths of 11.7 and 18.8 T, respectively, whereas ¹³C dispersion data were analyzed only if ΔR > 2 and 4 s⁻¹ at the two fields.

Exchange parameters were estimated by minimizing the function

where R_2,eff^exp(ν_CPMG) and δR_2,eff^exp(ν_CPMG) are the measured R_2,eff(ν_CPMG) value and the corresponding error, respectively, and the summation extends over all of the experimental data. Values for R_2,eff^exp(ν_CPMG) are obtained numerically by solving the Bloch–McConnell equations (29), assuming ideal CPMG refocusing pulses. Values of k_a and k_b were calculated from the fitted values of k_ex and p_b at each temperature according to the relations, k_a = k_exp_B and k_b = k_exp_A. The equilibrium constant K [= k_a/k_b = p_b/(1 − p_b)] also was obtained at each temperature from the estimated value of the minor state population (p_b).

Errors in the extracted exchange parameters were estimated by using a Monte Carlo procedure (30). Starting from a set of fitted parameters (based on experiment) for each group that includes global (k_ex, p_b) values and (Δω,R_2,intrinsic) for each site, dispersion profiles for each residue in the group were simulated, and Gaussian noise with the same magnitude as the experimental error was added to each of the curves. The synthetic profiles were subsequently fitted in exactly the same manner as the experimental data to generate a set of exchange parameters. The process was repeated 50 times to produce a distribution of exchange parameters with the errors calculated as standard deviations in the appropriate distributions. All of the CPMG data were fit to programs written in-house by D. Korzhnev.

The rate–temperature profiles were fit to transition state theory, k = (k_BT/h)exp(−ΔG⁺/RT), where k is the rate, k_B, h, and R are Boltzmann’s, Planck’s, and the ideal gas constants, respectively, T is the temperature, and ΔG⁺ = ΔH⁺ − TΔS⁺ is the activation free energy (ΔH⁺ and ΔS⁺ are the activation enthalpy and entropy, respectively). The temperature dependence of K was used to obtain ΔS and ΔH from the relation

Abbreviations

CPMG

Carr–Purcell–Meiboom–Gill

ET

electron transfer

FRE

NAD(P)H:flavin oxidoreductase

HSQC

heteronuclear single quantum coherence

ms

millisecond

TROSY

transverse relaxation optimized spectroscopy.