Solute-induced retardation of water dynamics probed directly by terahertz spectroscopy

Abstract

The dynamics of water surrounding a solute is of fundamental importance in chemistry and biology. The properties of water molecules near the surface of a bio-molecule have been the subject of numerous, sometimes controversial experimental and theoretical studies, with some suggesting the existence of rather rigid water structures around carbohydrates and proteins [Pal, S. K., Peon, J., Bagchi, B. & Zewail A. H. (2002) J. Phys. Chem. B 106, 12376–12395]. Hydrogen bond rearrangement in water occurs on the picosecond time scale, so relevant experiments must access these times. Here, we show that terahertz spectroscopy can directly investigate hydration layers. By a precise measurement of absorption coefficients between 2.3 THz and 2.9 THz we could determine the size and the characteristics of the hydration shell. The hydration layer around a carbohydrate (lactose) is determined to extend to 5.13 ± 0.24 Å from the surface corresponding to ≈123 water molecules beyond the first solvation shell. Accompanying molecular modeling calculations support this result and provide a microscopic visualization. Terahertz spectroscopy is shown to probe the collective modes in the water network. The observed increase of the terahertz absorption of the water in the hydration layer is explained in terms of coherent oscillations of the hydration water and solute. Simulations also reveal a slowing down of the hydrogen bond rearrangement dynamics for water molecules near lactose, which occur on the picosecond time scale. The present study demonstrates that terahertz spectroscopy is a sensitive tool to detect solute-induced changes in the water network.

The many unusual properties of water combined with its importance as the solvent of life account for its continued study by numerous researchers. Indeed, the properties of water are essential in the behavior of all biological systems. For example, water plays a central role in the folding and function of proteins, and the function of carbohydrates. The dynamics of water surrounding a solute is of fundamental importance in a wide range of processes in solution. In particular, the properties of water molecules near the surface of a biomolecule have been the subject of numerous and sometimes controversial experimental and theoretical studies (1–5). The characteristics and role of this “biological” water, with properties that differ considerably from those of bulk water, are still not fully understood (6).

The importance of the hydration layer or the biological water is obvious in specific protein processes, such as opening and closing of channels, the kinetics of which has been found to be coupled with the solvent fluctuations (1). Important questions that remain so far unanswered include the following: How does solvation water differ from bulk water, and how large is the solvation layer that can be attributed to solvent water? Simulations suggest the existence of rather rigid water structures around proteins (5) and carbohydrates (7), but experimental studies that characterize the hydration layer are limited. Hydrogen bond rearrangements in water occur on the picosecond time scale (8), so that a detailed understanding of the relevant processes at a molecular level requires experimental techniques that are able to probe the hydration layers on this time scale. However, experimental investigations of fast dynamics of hydration water still remain a challenge.

A number of experimental techniques have probed properties of hydration water on the time scale between microsecond and nanosecond. These techniques include diffraction methods that map the resolved maxima in the electron density distribution. For proteins, solution x-ray and neutron scattering give information on the excess density in the hydration layer (9, 10), thereby locating hydration sites. Dynamical information has been obtained by NMR techniques, including magnetic relaxation dispersion of the quadrupolar ²H and ¹⁷O nuclei in the water molecule (11) and intermolecular nuclear Overhauser effects between the water and the solute (12). However, magnetic relaxation dispersion experiments of surface hydration are not able to detect correlation times shorter than 1 ns (4). Although NMR still gets some effective relaxation times at time scales down to 1 ps, the spectrum itself cannot be obtained, and an analysis requires the assumption of an exponential decay for orientational processes (13). Dielectric relaxation spectroscopy measures the frequency-dependent part of the relative permittivity in the frequency range from several megahertz to 20 GHz, which corresponds to time scales ranging from microseconds to 100 ps (14).

Molecular dynamics simulations show that many of the important dynamical changes of hydration lie within the picosecond and subpicosecond time range (5, 15). Therefore, experimental methods are required to directly probe the retardation of water dynamics in hydration layers on these time scales. New experimental techniques for probing dynamical solvation with femtosecond resolution have been developed and have begun to provide a clearer picture of water dynamics near the surface of proteins, including studies of the hydration dynamics at the surface of a protein in the neighborhood of an intrinsic biological fluorescent probe (16, 17). In addition, 2D IR techniques (18) monitor spectral diffusion and dephasing of a specific vibrational band (19) and have yielded new information on protein and water dynamics (20–23). Both techniques probe the changes of the solvent dynamics in the vicinity of a specific probe.

We show here that terahertz spectroscopy can be used as an approach for measuring the solute-induced subpicosecond solvent dynamics. Terahertz spectroscopy does not require labeling, provides us with complementary information, and accesses global network changes by probing the rotational and translational dynamics. The use of new terahertz sources for spectroscopy has emerged with the development of terahertz time domain spectrometers as pioneered by Fattinger and Grischkowsky (24).

In the past, studies of polar, nonpolar, and mixtures of liquids by terahertz time domain spectrometers have been reported by the group of Schmuttenmaer and Keiding (see ref. 25 and references therein), who probed low-frequency intermolecular modes.

Here, we apply terahertz absorption spectroscopy as a probe for the fast solvation dynamics around a solute. Using our unique p-Ge-laser, a powerful radiation source in the region of 1–4 THz (30–140 cm⁻¹), we were able to directly measure the absorption due to subpicosecond motions of solvated lactose. The p-Ge spectrometer was used in this study for measurements in the experimentally challenging frequency region at 2–3 THz.

As a first important solute we have chosen lactose, because it is simple enough to explore in detail and yet still of great biological significance. Oligosaccharide chains are found in glycoproteins or glycolipids. In addition, many specific cell–cell interactions and molecular recognition processes involve glycoconjugates. The glycose linkages are influenced by the solvent (26), thereby modifying their biological specificity. In some circumstances, these linkages may be stiffened by solvent-mediated hydrogen bonding, whereas in other linkages they are found to be very flexible (27, 28). The (1→4) linkage found in lactose also is present in many carbohydrate structures, including plant cell walls and insect skeletons and is a common motif in N-linked glucoproteins.

In addition to its importance as energy currency for living systems, solvated mono- and disaccharides are found to have a significant stabilization effect on proteins and membranes in a dehydrated or frozen state (29, 30). It was speculated that such slowing of the dynamics might lead to a reduced biological activity of the proteins, although the exact underlying molecular mechanism remains unclear. Recently, some indirect evidence was reported that certain trehalose motions are coupled to those of the hydration shell (31). This finding supports the idea that bioprotection of sugars is achieved via solute-induced changes in the hydration shell affecting the dynamics of water (32).

When we added lactose to water we saw changes in the structure of the surrounding water hydration shell that extended beyond the first solvation layer from the surface of the solute. We compared these experimental results with molecular dynamics simulations, which provide insight into the underlying molecular mechanism, in particular the influence of the collective dynamics of lactose and the water molecules around it on terahertz absorption and the slowing of the hydrogen bond rearrangement dynamics for water molecules near lactose. The results demonstrate the potential of terahertz spectroscopy as an experimental tool to determine the size of the hydration layer around a solute and to provide information about the dynamical nature of the hydration water.

Experimental Results

Although terahertz spectroscopy is known to probe the interesting frequency region of intermolecular interactions, applications have been limited by the lack of powerful laser sources. In recent years new sources have appeared that offer considerable promise in accessing the so-called terahertz gap.

To investigate motions on the subpicosecond time scale, we have to go beyond 1 THz. Because of the high absorption coefficient of water (increasing from approximately α = 150 cm⁻¹ at 1 THz to approximately α = 450 cm⁻¹ at 3 THz), the transmitted power decreases rapidly with increasing frequency. Using low-power radiation sources it is simply impossible to penetrate thick layers of water. As a result, studies have been mainly restricted to (bio)molecules embedded in polyethylene, which is transparent in the terahertz region (33), hydrated films of biomolecules (34), and only a few solvents (mainly water and methanol) (35, 36). Moreover, to be sure that the surface layers do not influence the results of the measurements, it is important that we probe a sufficiently large volume of the probe.

At Ruhr-Universität Bochum, we set up a p-Ge laser spectrometer that extends the application of terahertz spectroscopy to the study of solvated solutes at higher frequencies. The terahertz radiation was passed through a cell with a variable thickness containing the solvated solute.

The experimental setup is described in detail in ref. 37, which reports the measurement of the terahertz spectrum of water at ≈3 THz. For bulk water, we are able to penetrate thick layers up to 150 μm, which is of special importance for further studies because surface water may show different behavior compared with bulk water in water/biomolecule systems (38).

The transmitted intensity was measured as a function of the layer thickness d (which was varied in steps of 5 μm) and fit to an exponential function according to Beer’s law: The data were fit to the following expression: I(d) = I₀ exp(−αd) + C, where I₀, α, d, and C correspond to the intensity before the probe, the absorption coefficient of the probe, the layer thickness of the probe, and the detector offset, respectively. For the following analysis, α is the only significant parameter. I₀ and C will influence the uncertainty of the final result due to correlation.

In the terahertz region, the deviations of published absorption coefficients for water exceed that of absorption coefficients in other frequency regions (see ref. 37 and references therein). The occurrence of standing waves, which give rise to periodic power fluctuations at the detector (so-called etalon structures), is a severe problem because the optical elements have dimensions close to the used wavelengths (100 μm) or multiples thereof. The use of our high-power radiation source allows us to restrict the data analysis to larger layer sizes where absorption is the dominant effect.

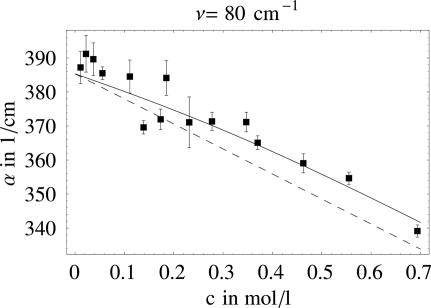
We determined the terahertz absorption coefficient as a function of increasing lactose concentration. We carried out >100 independent measurements at several lactose concentrations in the frequency range from 73 to 91 cm⁻¹. We used a statistical data analysis method that allows us to determine the absorption coefficient and its error independent of the nuisance parameters I₀ and C (see the supporting information, which is published on the PNAS web site) (39). Fig. 1 shows for each lactose concentration the averaged absorption coefficients together with their (statistical) error bars at 80 cm⁻¹.

Fig. 1.

Measured absorption coefficients of solvated lactose as a function of the lactose concentration. The dashed line shows the predictions from a two-component model (lactose plus bulk water). The solid line corresponds to the result of our fit also including hydration water.

In the combined experimental (neutron diffraction) and theoretical study of Mason et al. (40) it was found that sugars lack any tendency to preferentially interact with each other. Even at a concentration of 5 mol, which is far beyond our highest measured concentration, glucose molecules do not significantly associate (40). Therefore, we expected that the terahertz spectrum of the solvated lactose would be composed of the terahertz absorption spectrum of water and the terahertz absorption spectrum of the solute. A similar additive, two-component relation was previously found to hold for methanol–water mixtures (35).

For a two-component system we expect a linear change of terahertz absorption with the concentration of lactose. These changes account for the decrease in absorption due to the displacement of water by the presence of the lactose and the absorption of lactose itself. We have measured the change in volume by the addition of lactose. The excluded volume was determined to correspond to 11.5 water molecules at 20°C ± 1°C for each lactose, which agrees very well with previous results obtaining a volume of 12.5 water molecules at a higher temperature 35°C ± 1°C (41).

We measured the terahertz absorption of lactose powder and obtained α = 30 cm⁻¹. We compared these measurements with the values in a patent held by Albert-Ludwigs-Universität, Freiburg, Germany, which gives an absorption coefficient of α ≤ 20 cm⁻¹ for lactose (42). Because the significance of the final result increases with decreasing α_lactose, we fixed α_lactose to the highest possible value (α = 30 cm⁻¹) to obtain a conservative estimate.

Fig. 1 shows the linear curve that describes a two-component model with water and lactose. However, we found a significant systematic deviation from the linear plot, especially at high concentrations.

It is perhaps naive to expect that the terahertz spectra of this system could be analyzed in terms of a two-component model. The lactose–water system is really an effective medium, and an effective medium approach such as the Clausius–Mossotti approximation and extensions of this applied to a variety of composite media (43) including solutions (44), could potentially be applied here. However, the water layer around a biological molecule such as lactose is known to exhibit distinct dynamical properties compared with bulk water, so we continued our analysis in terms of a microscopic picture with contributions from lactose, bulk water, and the hydration water around lactose. This picture will be further justified by the molecular modeling that we carried out on this system.

Therefore, we fitted all individually determined absorption coefficients to a three-component model, which assumes a distinct absorption coefficient of the water around the sugar due to the distinct properties of the solvation water (for details, see the supporting information). When we compare the results, we see that the three-component model describes the data much better because the statistical significance of a three-component model exceeds that of a two-component model.

In our model, the total absorption coefficient of solvated lactose is described as a sum of three components. More specifically, the total absorption is assumed to consist of the volume-weighted average of the absorption of the solute, the solvation water, and the bulk water:

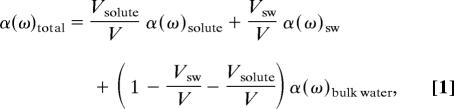where α(ω)_total, α(ω)_solute, α(ω)_sw, and α(ω)_{bulk water}, are the absorption coefficient of the solution, the absorption coefficient of the solute, the absorption coefficient of the water in the solvation layer, and the absorption coefficient of the bulk water, respectively. V, V_solute, and V_sw are the total volume probed by the terahertz beam, the volume of solute molecules, and the volume occupied by the solvation shells, respectively. We assume that we may neglect changes of the density between bulk and solvation water. The solvation shells are described by a step function. If two hydration layers overlapped, the absorption coefficient of the hydration water was assumed to be unaffected, which we confirmed by molecular modeling calculations. This assumption is further supported by Mason et al. (40), who found that the sugar molecules do preferentially interact with water. The structuring of the first hydration shell is found not to be significantly perturbed even at higher concentrations.

For very dilute solutions, an increase in the concentration of the solute will result in a linear increase of hydration water. As soon as solvation shells start to overlap, one expects a deviation from this linear behavior. The onset is especially sensitive to the size of the layer. If we further increase the concentration, the absorption of the solute will dominate the total absorption. To quantitatively describe the concentration dependence of the terahertz absorption, we performed Monte Carlo simulations by randomly inserting solute molecules into water and, thus, derived the dependence of the volume fractions of bulk water and solvation shells as a function of solute concentration and solvation layer radius. The experimentally determined total terahertz absorption coefficients were fit to a three-component model, and we fixed V, V_solute, α(ω)_{bulk water}, and α(ω)_solute and adjusted V_sw and α(ω)_sw in a nonlinear least-squares fitting routine. The result of the fit is shown in Fig. 2. By following this approach, we were able to determine the relative volume of the solvation layer and its terahertz absorption.

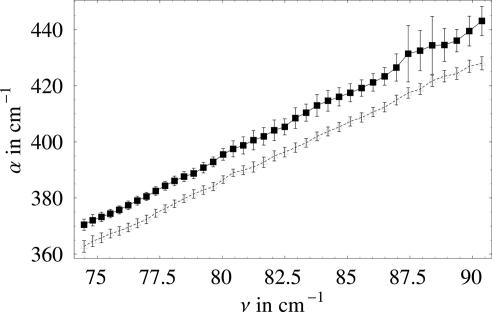
Fig. 2.

Fitted absorption coefficient of bulk water (lower curve) and hydration water (upper curve) as a function of the frequency.

The separately fitted absorption coefficients for α(ω)_{bulk water} and α(ω)_sw in the frequency range from 75 to 95 cm⁻¹ are displayed in Fig. 3. The absorption coefficient of solvation water is found to be increased by ≈10 cm⁻¹ compared with the bulk value over the whole frequency range.

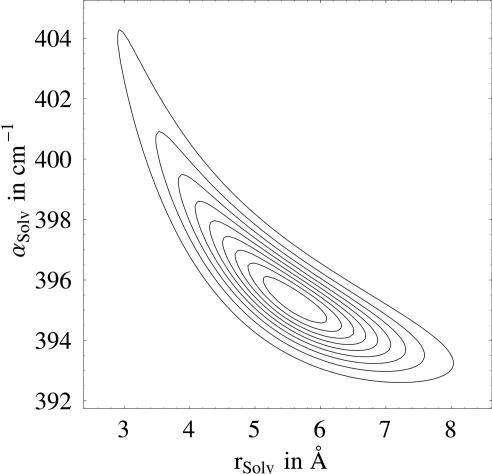
Fig. 3.

Contour plot of the normalized probability function versus solvation radius and absorption coefficient of the solvation layer. The contours are given in 10% steps.

The highest lactose concentration (0.7 mol/liter) corresponds to a relative volume of 15%, which does not contribute much to the overall absorption. The dominant contribution at the 0.7 mol/liter concentration is due to the hydration water (≈65%).

If we assume a spherical shape for the lactose and its hydration shell, the fit yields a hydration shell that extends on average to 5.24 ± 0.25 Å from the surface of the lactose molecule. In a second improved fit, we modeled the lactose as two overlapping spheres, each with a radius of 3.465 Å at a distance of 9.069 Å, which closely resembles the lactose molecule. The fit with this shape yielded a volume for the hydration shell of 3,660 Å ³, which corresponds to an extension of the hydration shell with an average distance of 5.13 ± 0.24 Å. This result agrees with the previous value. The radii of the solvation layer vary only slightly with frequency in the covered frequency range; therefore, here we give only the mean value.

Fig. 3 shows a contour plot of the normalized probability function as a function of solvation radius and α_{s w} for a fixed frequency. Whereas the solvation layer of <4 Å is unlikely within the possible ranges for α_sw, a hydration shell with an even larger radius of ≈7 Å is still quite probable.

We have shown that our experimental results reveal unambiguously a distinct solvation layer around lactose (corresponding to picosecond and subpicosecond dynamics) and allow us to determine its size and the specific terahertz absorption coefficient of this layer.

Molecular Modeling

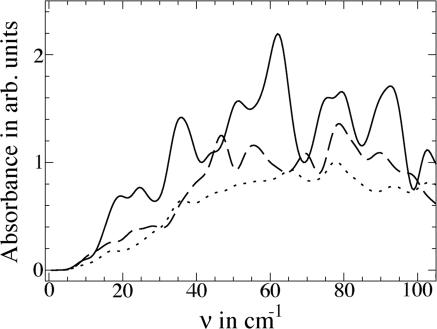
To gain insight into the observation that hydration water absorbs more strongly than bulk water, we have computed the absorption spectrum of hydrated lactose and bulk water, considering only the fundamental transitions in the terahertz region. This calculation, which is carried out in terms of the vibrational modes of solvated lactose, is similar to that of Whitmire et al. (45), who computed the low-temperature absorption spectrum of dehydrated bacteriorhodopsin in the terahertz region. In Fig. 4, we display results for lactose hydrated by 158 water molecules (corresponding to water within ≈7 Å of the solute) and the average spectrum for 158 water molecules within 10 Å of lactose (Fig. 4, dashed curve). This absorbance can be compared with the average absorbance for 158 water molecules in bulk water (Fig. 4, dotted curve). The absorbance of an isolated lactose molecule is small in the terahertz region because of the low density of vibrational modes. Absorbance is noticeably greater for the hydration water molecules than for the same number of bulk water molecules. We found that the absorbance ≈2–3 THz remains unchanged upon addition of a second lactose molecule close enough to the first so that their hydration layers overlap.

Fig. 4.

Calculated terahertz absorbance for fundamental transition of lactose hydrated by 158 water molecules (solid curve) within 7 Å of lactose and average spectrum for 158 water molecules within 10 Å of lactose (dashed curve) compared with the average absorbance of 158 bulk water molecules (dotted curve).

Analysis of the terahertz vibrations reveals that the network vibrations of water molecules near lactose oscillate more in phase with one another than do the water molecules of the hydrogen bond network. The sum of the eigenvector components contributing to 〈Ψ_α⁽⁰⁾|Q_α|Ψ_α ⁽¹⁾〉 that overlap water molecules is more than an order of magnitude larger for the water molecules in the hydration shell around lactose than for the same number of water molecules in the bulk. The lactose molecule and the water in the hydration shell oscillate coherently relative to one another, and the coherent oscillation of the water in the hydration shell in the terahertz region absorbs more strongly than does the comparatively incoherent motion of the same number of water molecules in the bulk.

Our experimental technique covers the frequency range from 75 to 95 cm⁻¹ (2.3–2.9 THz). In this spectral region we probe intermolecular collective modes of the hydrogen bond network with periods of 0.45–0.35 ps. Terahertz absorption spectroscopy is known to probe the reorientation of permanent and induced dipole moments (46). The time correlation function of the polarization of bulk water has been described by a biexponential decay with a slow and a fast component with Debye relaxation times of τ_Debye > 2 ps (attributed to structural relaxation) and τ_Debye > 50 fs, respectively (47). Whereas the first relaxation time dominates the low-frequency spectrum in the gigahertz region, the second is the major contribution ≈3 THz. The fast components are attributed to librations, intermolecular vibrations, and damped rotations, with time constant of 1 ps being determined by the individual rotational and translational motions of the molecule in the first solvation shell (48). It is thus of interest to examine the rearrangement of water molecules in the hydration layer around lactose.

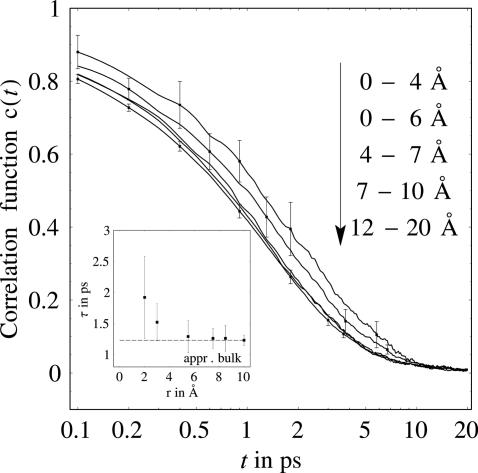
To gain insight into hydrogen bond rearrangement in the hydration layer around lactose, we computed a hydrogen bond correlation function, c(t), defined as the probability that a hydrogen bond between a random donor (D)–acceptor (A) pair at time, t = 0, is still bonded at time t regardless of whether the bond was broken at intermediate times. We computed c(t) as an average over 25 initial configurations at 300 K for solvated lactose and for water molecules lying within 0–4, 0–6, 4–7, 6–9, 7–10, and 12–20 Å of lactose. Fig. 5 shows results for c(t) in these different intervals. Differences can only be found at time scales of <10 ps. At such time scales, we observe that the hydrogen bond dynamics of 112 water molecules within 6 Å of lactose is noticeably retarded compared with that in the bulk. The hydrogen bond lifetimes, τ, computed from c(t) are plotted in Fig. 5 Inset.

Fig. 5.

Correlation function for water molecules at different solute distances versus time. (Inset) The hydrogen bond lifetime versus distance from solute molecule.

The calculations reveal an important impact of the solute on the hydrogen bond vibrations and dynamics of water. Collective oscillations between lactose and nearby water molecules are seen to enhance the absorbance of the solvation layer compared with bulk water. In addition, hydrogen bond rearrangement dynamics is slower for hydration water than for bulk water. Whereas, for bulk water, a mean value of τ = 0.9 ps can be fit with an exponential to the hydrogen bond correlation function, for the first solvation layer, a value of 1.3 ps is predicted. The results of the molecular modeling indicate significant retardation out to ≈6 Å corresponding to 112 water molecules away from the solute, because of the steric constraints on nearby waters by the solute, corresponding to a distance somewhat beyond the first solvation shell. Hydrogen bond dynamics between water molecules is particularly sluggish for the 46 water molecules within 4 Å of lactose.

In a recent study of water near glucose, sucrose, and trehalose, Lee et al. (7), computed the translational diffusion coefficient for water surrounding the solute and found a significant decrease in the diffusion coefficient for water molecules within ≈5.5 Å from the nearest solute atom. Lee et al. also computed a similarly defined c(t) for the hydrogen bonds between the hydration water and glucose and found retardation of the hydrogen bond breaking dynamics between the solute and proximal water molecules. Our study finds in additional significant slowing of hydrogen bond rearrangement between the water molecules themselves out to ≈6 Å.

Conclusion

Using terahertz spectroscopy, we are able to probe the size of the solvation layer on the femtosecond to picosecond time scale. These measurements provide us with a “snapshot” of the solvation layer. The concentration-dependent changes in the terahertz absorption spectrum are well described by a three-component model including bulk water, solvation water, and the solute itself. We assumed an averaged distinct absorption coefficient with a stepwise change from hydration water to bulk water. The size of the hydration layer was determined to extend 5.13 ± 0.24 Å from the lactose.

This layer corresponds to 123 affected water molecules per lactose molecule, which is in excellent agreement with the results of our molecular modeling calculations (where we observe a slowing of the hydrogen bond rearrangement dynamics for 112 water molecules within 6 Å). Both results clearly demonstrate a long interaction of the lactose on the water solvent beyond the first solvation shell.

A study by Magazù et al. (32) yielded hydration numbers (the number of water molecules in the hydration layer) between 7.5 and 9, which is in agreement with hydration numbers for disaccharides as evaluated from previous ultrasonic measurements (yielding 14–15). A more recent neutron diffraction study by Mason et al. (40) concluded that the long-range structure of the water is not significantly affected by the presence of the sugar solute.

However, our results are in agreement with the theoretical study of Massari et al. (31) in which they found evidence that the bioprotection of trehalose is due to its ability to immobilize the protein surface through a constrained layer of water.

This result implies that the extent to which the solute influences the solvent has been underestimated by other experimental techniques: Our results indicate the need for ultrafast techniques to investigate the influence of the solute on the solvent. When approaching 10 ps, calculated correlation functions for hydrogen bond rearrangement between water molecules at various distances from the lactose molecule approach zero and are all equal to those of bulk water. It is known that the exchange of bulk water with water in the solvation shell occurs over times between 10 and 100 ps (17), which implies that experimental techniques that average over longer time scales will not be able to see the retardation effects of the solute on the solvent dynamics, so techniques that probe the averaged dynamics have found a more restricted influence of the solute on water. In conclusion, we have to go beyond 1 THz to probe mainly the fast relaxation component in the water terahertz spectrum.

In the terahertz regime, we report an increased absorption in the hydration shell over the whole investigated frequency range, in good agreement with the modeled absorbance for the hydration layer. Previous calculations by Lee et al. (7) predicted a destructuring effect of carbohydrates on the surrounding water that mimics the effect of a temperature increase. It is interesting to note that a rise of temperature would also manifest itself in an increased terahertz absorption coefficient for water (46).

Whereas optical and IR spectroscopy techniques measure the influence of the water dynamics on a local probe, terahertz spectroscopy provides a more global picture. The technique benefits from the extreme sensitivity of the terahertz absorption of water to the water structure.

In summary, terahertz spectroscopy is introduced as a tool for providing a measure of the full layer of biological water at the surface of carbohydrates and information on the subpicosecond time scale, corresponding to hydrogen bond rearrangements. The future potential of terahertz spectroscopy for the study of hydration water is due to the fact that any changes in the water network will give rise to considerable changes in the terahertz spectrum. Therefore, terahertz spectroscopy is seen as a promising technique for studies of solvent dynamics around proteins.

Methods

Experimental.

The table-top p-Ge terahertz laser spectrometer combines high power [see ref. 49; >1 W, up to high duty cycles of 5% (50)], repetition rates of up to 45 kHz (51), laser pulse lengths of up to 32 μs (51), and broadband emission (from 1–4 THz or 30–140 cm⁻¹) (51, 52). The p-Ge laser can be tuned continuously with crossed electric and magnetic fields. In our present configuration the crystal is placed between two permanent magnets that generate a magnetic field of 1.2 tesla, emitting at ≈100 cm⁻¹. For frequency calibration, we used a blazed aluminum grating (grating constant = 0.1 mm) mounted on a rotation stage. The grating resolution limits our experimental resolution to 0.4 cm⁻¹. The terahertz radiation was passed through a cell with a variable thickness containing the solute and water. For the measurements described here, lactose (highest grade; Sigma–Aldrich, Taufkirchen, Germany) was dissolved in ultra-pure water (Baker, Deventer, The Netherlands). The solutions were filtered with 200-μm pore filters and inserted into polyethylene bags placed between two TPX (methylpentene copolymer) windows to vary the thickness of the sample layer in 5-μm steps between 25 and 350 μm. All measurements were recorded at a temperature of 20°C ± 1°C and at 8% ± 4% humidity.

The transmitted radiation was focused onto a Ge photoconductor, which was cooled to 4 K. A bias voltage of 320 mV was applied to the detector. The detected voltage drop was amplified, recorded by an oscilloscope, and averaged over 100 pulses. The mean value and its standard deviation were recorded as a function of the frequency. For each frequency ≈60–70 data points were taken.

Computational.

All molecular dynamics simulations were performed with MOIL (53), which uses a combination of AMBER, OPLS, and CHARMM force fields. The parameters for lactose were obtained from the CHARMM, Version 22, parameter set (54, 55). The lactose molecule was initially embedded in a cubic box, 40 Å on each side, that contained 1,995 TIP3 potential water molecules. Molecular dynamics simulations were performed at 300 K with volume and temperature held constant (NVT conditions). Velocities were sampled from the Maxwell distribution and scaled to reach the target temperature. A total time of 500 ps was covered in the simulation. Periodic boundary conditions were applied in all three dimensions. The Verlet integration algorithm was used, with the time step of 1 fs. The nonbonded neighbors lists were updated every 50 steps, and velocities were scaled at every step. Electrostatic interactions were evaluated using the particle-mesh Ewald method. Van de Waals interactions were truncated at 15 Å. Hydrogen bond dynamics were monitored on the 25 initial structures with 20-ps intervals.

We computed hydrogen bond dynamics for water molecules around lactose by using a geometrical criterion for the hydrogen bonds, where bonds are taken to be formed when the distance between the D and A is <3.5 Å and the angle between D, hydrogen, and A (D–H–A) is >120^o. Hydrogen bond dynamics can be quantified by the hydrogen bond correlation function similar to that in refs. 56 and 57. c(t) = 〈h(0)h(t)〉/〈h(0)〉, where h(t) is a hydrogen bond population operator, which is equal to one for a hydrogen bond between a given D–A pair at time t and is zero otherwise. The angular brackets denote an average over all D–A pairs. The function c(t) is the probability that a hydrogen bond between a random D–A pair at time, t = 0, is still bonded at time t regardless of whether the bond was broken at intermediate times. The hydrogen bond lifetime, τ, is defined as the time at which c(t) decays to 1/e.

We computed absorption spectra for solvated lactose and water in terms of normal modes. Calculations of the normal modes were carried out with MOIL (53). In terms of the normal modes, the IR absorbance for a transition in mode α, with nα vibrational quanta to n_α + 1 vibrational quanta can be estimated in terms of the mode-specific dipole derivative (45, 58). We take the charges on the atoms to be fixed. The absorbance, A_α, for a mode of frequency ν_α is then proportional to ν_α(d_x² + d_y² + d_z²), where the transition dipole moments d_x, d_y, and d_z are calculated by expansion in normal mode transition moments, 〈Ψ_α⁽⁰⁾|Q_α|Ψ_α⁽¹⁾〉 (58). The results are broadened with Gaussians that have a full-width at half maximum of 6 cm⁻¹ and yield the predicted absorption spectrum for solvated lactose.