Abstract
Biological networks have evolved through adaptation in uncertain environments. Of the different possible design paradigms, some may offer functional advantages over others. These designs can be quantified by the structure of the network resulting from molecular interactions and the parameter values. One may, therefore, like to identify the design motif present in the evolved network that makes it preferable over other alternatives. In this work, we focus on the regulatory networks characterized by serially arranged processes, which are regulated by multiple feedback loops. Specifically, we consider the tryptophan system present in Escherichia coli, which may be conceptualized as three processes in series, namely transcription, translation and tryptophan synthesis. The multiple feedback loop motif results from three distinct negative feedback loops, namely genetic repression, mRNA attenuation and enzyme inhibition. A framework is introduced to identify the key design components of this network responsible for its physiological performance. We demonstrate that the multiple feedback loop motif, as seen in the tryptophan system, enables robust performance to variations in system parameters while maintaining a rapid response to achieve homeostasis. Superior performance, if arising from a design principle, is intrinsic and, therefore, inherent to any similarly designed system, either natural or engineered. An experimental engineering implementation of the multiple feedback loop design on a two-tank system supports the generality of the robust attributes offered by the design.
Keywords: multiple feedback loops, robustness, tryptophan system, biological regulators, reverse engineering, systems biology
1. Introduction
Living systems and engineering technologies share similar goals of operating efficiently and in a stable manner in uncertain environments. Such systems must be robust and maintain an appropriate physiological response in the presence of these uncertainties (Alon et al. 1999; Goulian 2004). While engineers have relied on modelling and computational methodologies, to design robust regulatory systems, nature appears to have evolved structural motifs including cascades (Sauro & Kholodenko 2004), feedback and feedforward control (Yi et al. 2000; Shen-Orr et al. 2002; Mangan & Alon 2003; Angeli et al. 2004) and multiple feedback loops (Lauffenburger 2000), resulting in complex regulatory networks (Kitano 2001; Csete & Doyle 2002; Aldana & Cluzel 2003; Guet et al. 2003; Tyson et al. 2003). A system level analysis of these complex networks is complicated due to the numerous interactions, which results in a large number of system parameters in a model. Ultimately, the network output is a manifestation of the design principles resulting from the structural motif and system parameters (Freeman 2000). It is natural to question the relative roles of the regulatory structure and parameter space in imparting the physiological robust performance.
The network structure is defined by the interconnections between the processes, such as transcription and translation and their associated regulatory components. Knowledge of the structure and the parameter values defines a dynamic model of the network. Biological models, however, do not distinguish ‘process’ components from ‘regulatory’ components (El-Samad et al. 2002, 2005; Venkatesh et al. 2004). Such a non-discriminative approach fails to explicitly identify the role of the structure in the system-wide performance. It is, therefore, imperative to delineate the regulator from the process. For any well-characterized regulatory system, with known structure and parameter values, such delineation is usually feasible through a mathematical model, whose output represents an in vivo physiological response. Deviation in either the structure or parameters from their physiological values may lead to a different phenotypic response with implications on the overall cellular functions. An example of structural perturbation is elimination of autoregulatory loops in transcription. It has been demonstrated that such a perturbation imparts an increased variance in the in vivo protein expression resulting in phenotypic variability (Becskei & Serrano 2000). On the other hand, mutation in one copy of NF1 gene constitutes an example of parametric perturbation. Individuals with such mutations show higher incidences of benign tumours due to an increased noise-to-signal ratio caused by haploinsufficiency (Largaespada 2001; Kemkemer et al. 2002). Therefore, to quantify the impact of structural or parametric perturbations, it is imperative to identify the design components of the network that are essential for the in vivo physiological response.
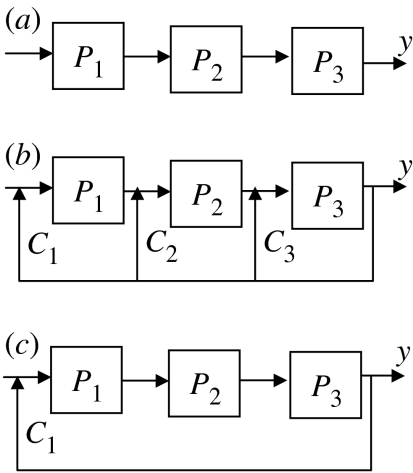
In this work, we focus on processes that are arranged serially, similar to an assembly line in a manufacturing unit. Serial processes are characterized by multiple ‘process units’, where the output of one unit influences the output of the downstream units (Faanes & Skogestad 2005). Figure 1a shows three such processes connected in series. Typically, the output of the downstream unit (P3 in figure 1a) determines the overall physiological response and is used as a feedback signal to regulate the upstream processes. This important class of serial processes is ubiquitous in biological systems including genetic networks (Ruhela et al. 2004; Venkatesh et al. 2004), signalling pathways (Freeman 2000; Sauro & Kholodenko 2004) and metabolic regulation (Hohmann 2002). It is also noted that such serial processes have evolved a regulatory strategy characterized by a multiple distribution of the output from the downstream process to regulate the upstream processes (see figure 1b) through multiple controllers in parallel. Applications of parallel control have also been reported in engineering problems (Balchen & Mummé 1988). Such distributed feedback interactions are ubiquitous in networks, across prokaryotic and higher organisms. For example, the phosphotases synthesized through high osmolarity glycerol (HOG) activation regulate multiple upstream kinases to modulate the osmotic pressure in Sacchromyces cerevisiae (Hohmann 2002). Another well-known example is the hormonal response in the insulin signalling pathway (Sedaghat et al. 2002), in which the phosphorylated Akt and Pkc interact with serially arranged upstream components, namely insulin receptor, insulin receptor substrates and upstream phosphotases to constitute multiple feedback loops. A similar multiple feedback mechanism also exists in p53 regulation of cell cycle and apoptosis (Kohn 1999), in which Cdc25 interacts at multiple points of the upstream processes arranged in series. Although, multiple feedback loops were observed in each of the above examples, one may also regulate the system by using a mere single feedback loop as shown in figure 1c to accomplish similar regulatory goals and is typically used in engineering systems. Hence, it is well motivated to analyse the role of the multiple feedback loop architecture in the overall regulation of such serial processes.
Figure 1.
(a) Schematic of three processes (Pi) in series. For the tryptophan system, P1, P2, P3, represent transcriptional ‘process’, translational ‘process’ and tryptophan synthesis, respectively. (b) Schematic of the multiple feedback loop strategy for three-processes-in-series system. For the tryptophan system, C1 represents genetic regulation, C2 represents transcriptional attenuation and C3 represents enzyme inhibition. (c) Schematic of the single feedback loop strategy. In the tryptophan system, such an architecture would arise only if the genetic regulation was operational.
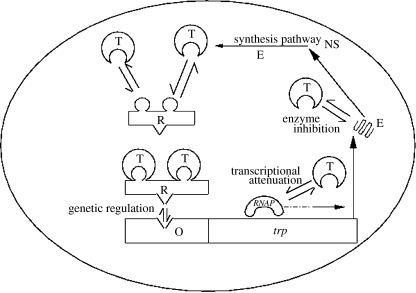
We consider the tryptophan system of Escherichia coli as a model system to quantify the relative roles of the structure and the system parameters in determining the physiological response. The key molecular mechanisms involved in the regulation of tryptophan system are illustrated in figure 2. The transcriptional process is initiated by the binding of the RNA polymerase (RNAP) to the promoter site. However, transcription is regulated by two feedback mechanisms. The activated aporepressor, which is bound by two molecules of tryptophan, interacts with the operator site, thereby, repressing transcription (Yanofsky et al. 1984). The two binding sites of the aporepressor result in an ultrasensitive genetic repression by tryptophan. Further, the process of transcription can also be attenuated by binding of the tryptophan molecule to specific mRNA sites. The transcribed mRNA encodes five polypeptides that form the subunits of the enzyme molecules, which in turn catalyse the synthesis of tryptophan from chorismic acid (Santillan & Zeron 2004). The third feedback mechanism results from the binding of the tryptophan molecule to the first enzyme in the tryptophan synthesis, namely anthranilate synthase, thereby inhibiting its activity. Binding of the tryptophan to the operator site, mRNA and the first enzyme constitutes the multiple feedback loop motif.
Figure 2.
Schematic of the tryptophan system. Binding of tryptophan molecules (T) to the aporepressor (R), mRNA and the enzyme (E) constitute the multiple feedback design. NS denotes the nitrogenous substrate in the medium.
The tryptophan system in E. coli, can also be conceptualized as a three-processes-in-series system, namely transcription, translation and tryptophan synthesis (P1, P2 and P3 in figure 1b, respectively). The regulation of tryptophan concentration is achieved by three distinct negative feedback loops, namely genetic regulation, mRNA attenuation and enzyme inhibition (C1, C2 and C3 in figure 1b, respectively). The three regulators are quantified using the Hill equation (see §5). The tryptophan system has been quantified through various mathematical models (Koh et al. 1998; Santillan & Zeron 2004; Venkatesh et al. 2004), which have been verified with experimental data. Among these, Venkatesh et al. (2004) delineated the role of regulation by explicitly modelling the multiple feedback loops resulting from repression, attenuation and inhibition. The authors showed that the multiple feedback loops enable rapid synthesis of tryptophan in a stable manner. In this work, we use the model of Venkatesh et al. (2004) to assess the role of multiple feedback loops in providing robustness to perturbations in parameter or structure, relative to a single feedback loop design.
2. Metrics to evaluate robustness
We assume that the response of the tryptophan system has evolved for efficient cellular functioning. The network model is represented by a set of physiological parameters (p*) and the regulatory structure (s*), which determine the characteristics of the in vivo physiological response O*(t, p*, s*) at time t to a given stimulus. Identification of the key parameter values and molecular interactions requires the use of a metric that quantifies performance. Thus, a metric or a key performance indicator is a measure of the functional effectiveness, and, therefore, serves to compare alternative designs. One may use a number of metrics, each quantifying a particular operational attribute of the network, and, hence, the choice of metrics is dependent on the specific network under consideration. For example, the frequency and amplitude of oscillations are appropriate metrics to evaluate the network representing circadian rhythms in Drosophila (Stelling et al. 2004a,b). Morishita et al. (2005) used the coefficient of variation in the copy number of proteins as a metric to study noise attenuation in a single gene expression system. Dekel & Alon (2005) used the difference between cost of production and maintenance of proteins and the benefits of growth in E. coli through the lac system as a metric to demonstrate optimal protein expression levels. A number of homeostatic networks have been analysed using the steady-state value as a metric (Okamoto & Hayashi 1983–1984; El-Samad et al. 2002). Walls et al. (2003) proposed five design metrics: selectivity, linear stability, parametric robustness, efficiency of input/output behaviour and temporal responsiveness for gene expression in a repressible gene circuit. All of the above performance measures characterize the dynamic output O*, as the system responds to changes in its environmental inputs (e.g. nutritional shifts) and its initial physiological state (e.g. a starved cell).
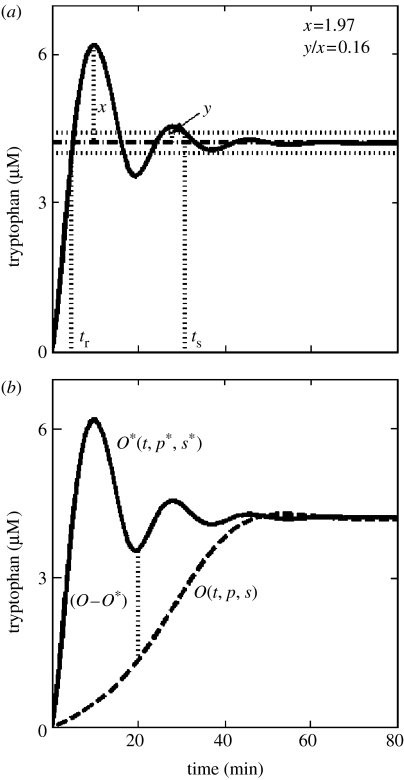
A dynamic tryptophan system represents a homeostatic network, which maintains tryptophan concentration within a narrow range. The simulated response of the tryptophan system in absence of tryptophan in the medium is shown in figure 3a. In addition to the steady-state concentration level, the performance metric must also capture the dynamic functionality of the network response. One such measure is the time required by the network to first reach its steady-state value, denoted as rise time (tr in figure 3a). Alternatively, one can quantify the time required by the network to eventually settle in the vicinity of its steady physiological state (ts in figure 3a). In engineering systems, fast rise times are associated typically with large settling times. Fast rise times also lead to a large overshoot (x in figure 3a) due to system inertia. Dissipation of the overshoot may lead to decaying oscillations, which can be quantified by the decay ratio (y/x in figure 3a).
Figure 3.
Dynamic simulation of the tryptophan system. (a) Tryptophan network response in the absence of tryptophan in the medium. tr and ts represent the rise time and the settling time, respectively, of the network response. x and y represent the amplitudes of the first and second oscillation. The tryptophan concentration rises rapidly to its in vivo steady-state value of 4.2 μM in approximately 4 min. It subsequently settles to its steady-state value in approximately 30 min. The horizontal dotted line represents the ±5% band about the target value within which the response is considered acceptable. (b) The solid curve represents the physiological response of the network indicated by O* and is reproduced from (a). The dashed curve, indicated by O, represents the response without attenuation and inhibition (i.e. single feedback loop design) and with parameters of genetic regulation altered (ηH1=0.5, Ki,1=8×10−8 μM) to yield a sub-sensitive regulator.
Perturbations in either the parameter space (p) or the regulatory structure (s) may yield a different phenotypic response, O(t, p, s), distinct from O*(t, p*, s*) as shown in figure 3b. Although, the perturbed response will lead to different values of the performance metrics described above, it may be desirable to define a single measure that reflects performance over a given duration. A simple, yet, generic measure to quantify perturbation in the network output is given by
| (2.1) |
where the limits of integration, [0,tf] represent the duration of the response. It should be noted that this performance measure depends on both system parameters (p) as well as the structure (s). The value of I(p, s) denotes an average of the temporal deviations from a given physiological performance of an evolved network, O–O* (see figure 3b). Thus, a zero value of I(p, s) indicates a dynamic response identical to that of the physiological output O*.
The magnitude of each of the above metrics emphasizes a particular aspect of the tryptophan network response. For example, it may be crucial for the survival of the cell that it responds rapidly in the absence of tryptophan, thereby, making rise time an important metric. On the other hand, in regulation of an inhibitor concentration, it must be ensured that the overshoot is small to avoid toxicity. Typically, a network may have multiple features to characterize its operation leading to use of multiple metrics. Thus, the performance metrics must be chosen judiciously depending on the application. Relative insensitivity of the selected metric to uncertainty in structure or parameter value would indicate robust behaviour of the network.
The above framework was employed to assess the role of multiple feedback loops in the tryptophan system. Perturbations in system parameters and the regulatory structure show that the tryptophan system is highly robust to parametric variations, but fragile to its structural design comprised of multiple feedback loops. Furthermore, to verify the role of the multiple feedback loops as a key design feature, we implement the regulatory architecture for level control in an experimental two-tank system, which also consists of the processes-in-series architecture. Our results suggest that robustness resulting from the multiple feedback motif is preserved across systems, natural or engineered.
3. Results
We use a model of the tryptophan system (Venkatesh et al. 2004) to evaluate the above metrics. The model equations and the parameter values have been summarized in §5 (see figure S1 in the electronic supplementary material). The model predictions for enzyme concentration match experimental data (Santillan & Mackey 2001; Bhartiya et al. 2003). In the absence of extracellular tryptophan, tryptophan synthesis exhibits a rapid surge to its steady-state level with a rise time, tr of 4 min, followed by an overshoot, x=1.97 μM, and a decay ratio, y/x=0.16 (see figure 3a). The response finally settles to its steady-state value of 4.2 μM at ts=30 min. The network output is also shown as the solid line in figure 3b and constitutes the physiological response O*(t, p*, s*) for the tryptophan regulatory network.
To evaluate, the multiple feedback loop design in the tryptophan system, we alter the feedback structure, specifically through the removal of regulation by attenuation and inhibition (C2 and C3 in figure 1b), as shown schematically in figure 1c. It should be noted that the alteration yields a new structure, s, distinct from the three feedback loop structure, s*. The response of the mutated system exhibits an extremely rapid synthesis of tryptophan with a rise time, tr=1.8 min. However, it is accompanied by a large overshoot, a subsequent long settling time, ts>600 min and a very large steady-state value of 330 μM resulting in poor overall performance indicated by I(p, s)=11 179 μM (see figure S2 in the electronic supplementary material). Such a large average deviation from the physiological response may be detrimental for the survival of the cell. Thus, I(p, s) is an important metric for evaluating network performance. To compare the performance of the single feedback loop design with the multiple feedback loop architecture, one must redesign the single feedback loop system such that the overall response resembles the physiological response as closely as possible. We, therefore, minimize the performance metric I(p, s) to obtain the altered regulator parameters of the Hill equation representing C1. The resulting perturbed network response O(t, p, s) is shown by the dashed line in figure 3b. The altered single loop system exhibits an initial sluggish dynamic behaviour with tr=ts=40 min and a minimal average deviation from the physiological response, I(p, s)=0.7 μM. From a physiological perspective, the large rise time amounts to starvation of the cell in the absence of tryptophan in the medium during the initial 40 min. We, therefore, conclude that the rise time is also a key measure of physiological performance for the tryptophan system of E. coli.
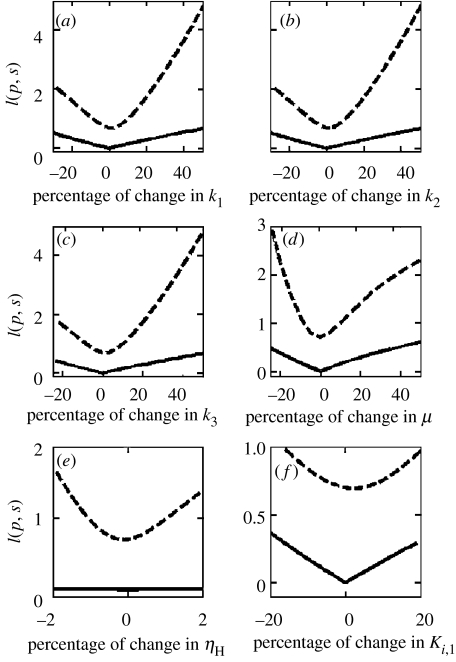
We study the robustness of the tryptophan regulatory network by evaluating the two key performance measures, namely I(p, s) and tr at different points of the parameter space p for the single and multiple feedback loop designs. Model parameters may be broadly classified into two categories: those associated with the processes, Pi, and others associated with the regulators, Ci. Figure 4 compares the metric I(p, s) for the multiple (solid line) and single (dashed line) feedback designs for variations in system parameters. It is evident from the figure that the performance of the multiple feedback loop design is relatively invariant to perturbations in process parameters as compared to the single feedback loop design (figure 4a–d). For example, a 40% deviation in either of the three rate constants leads to degradation in performance by 3 μM in the single feedback design and 0.3 μM for the multiple feedback design (see figure 4a–c). In case of a −20% deviation in the specific growth rate, the corresponding degradation in single loop and multiple loop designs are 2.2 and 0.45 μM, respectively (figure 4d). Figure 4e,f shows the variation in I(p) with respect to changes in ηH1 and Ki,1, respectively, for the genetic regulator. The results indicate that the presence of transcriptional attenuation C2(T) and enzyme inhibition C3(T) make the multiple feedback design insensitive to perturbations in genetic regulation. In summary, the lower value of the performance metric I(p, s) in case of the multiple feedback design as well as its relative insensitivity implies that the tryptophan system design not only yields a superior dynamic response, but also offers robustness to perturbations. It is noted that the regulator parameter values used in the single feedback loop design result in a minimum value of the performance metric I(p), indicating their optimality.
Figure 4.
The performance measure, I(p, s) for the multiple loop design (solid line) and the mutated single loop design (dashed line) for parametric variations in (a) rate constant of free operator formation (k1), (b) rate constant of translation (k2), (c) rate constant of tryptophan synthesis (k3) and (d) specific growth rate of E. coli (μ), (e) sensitivity of genetic regulator (ηH1) and (f) half-saturation constant of genetic regulator (Ki,1). A 0% change represents the physiological parameter values for the multiple loop design. The results show that the multiple feedback loop design yields a superior robust dynamic performance.
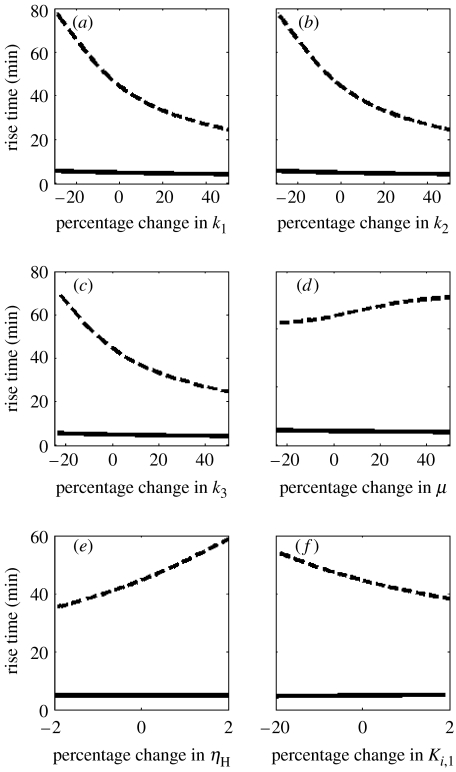
Figure 5a–d shows the rise times for step perturbations in the rate constants for transcription (k1), translation (k2), tryptophan synthesis (k3) and specific growth rate (μ) from their physiological values for the multiple (solid) and single (dashed) feedback loop architectures. The rise times of the multiple feedback loop designs are relatively invariant (about 5 min) to parametric changes. However, for the single feedback loop design, a positive change in the rate constants decreases the rise time due to faster kinetics (see figure 5a–c). Alternatively, an increase in the specific growth rate increases the dilution of the component concentration, and, therefore, slows the speed of response (figure 5d). Alterations in the tryptophan binding to the aporepressor, mRNA and protein sites are captured by variations in regulator parameters, sensitivity ηH and half-saturation constant Ki,1. Figure 5e shows that for the single feedback loop design, an increase in the Hill coefficient, ηH1, slows the system response (dashed line) due to the repressive action of the regulator. On the other hand, an increase in the half-saturation constant, Ki,1 implies that a larger amount of tryptophan is necessary to switch off the system leading to a faster response (figure 5f). One may increase the rate of transcription to achieve a rise time of 4 min as observed in the physiological system (see figure 5a). However, this will lead to a severe degradation in the overall system response indicated by the metric I(p) (see figure 4a). It is clear from the figures that the multiple feedback strategy of tryptophan system consistently synthesizes intracellular tryptophan in less than 5 min despite large variation in system parameters. Further, the rise time in the multiple feedback loop design is an order of magnitude faster than the mutated system.
Figure 5.
Rise time as a performance measure for the multiple loop design (solid line) and the mutated single loop design (dashed line) for parametric variations in (a) rate constant of free operator formation (k1), (b) rate constant of translation (k2), (c) rate constant of tryptophan synthesis (k3) and (d) specific growth rate of E. coli (μ). Variation of rise time with perturbations in genetic regulator C1 parameters (e) sensitivity (ηH1) and (f) half-saturation constant (Ki,1). A 0% change in the parameter value represents the physiological parameters for the multiple loop design. The multiple feedback design is able to provide a rapid synthesis of tryptophan in less than 5 min in the face of large deviations in parameter values. Alternatively, the single feedback loop design is sluggish and the rise time highly dependent on parameter values.
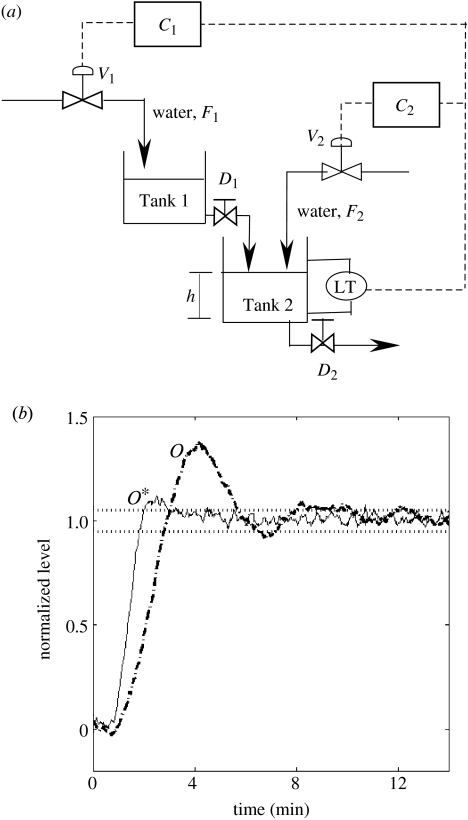
At this point, it is pertinent to ask whether the design of the tryptophan system as represented by the model is indeed the cause for robust and superior dynamic performance. To test the generality of the regulatory design, one may identify a physical system that is amenable to a similar control motif and use the same as a test bed to evaluate robust performance. A schematic of an experimental system consisting of two-tanks-in-series is shown in figure 6a. The two tanks may be considered as processes P1 and P2 as shown in figure 1a. In the single feedback loop design, water level in Tank 2 was regulated using the flow into the first tank by the regulator C1 alone. On the other hand, in the case of the multiple feedback loop paradigm akin to the tryptophan system, the measurement of water level in Tank 2 was distributed to two regulators that manipulated flows to both tanks (C1 to Tank 1 and C2 to Tank 2). The parallel between the tryptophan system and the two-tank-in-series process can be visualized by comparing figures S1 and S3 in the electronic supplementary material. While the architectures of the two systems are similar, we note that the regulators in the tryptophan system are described by Hill equations, while the two-tanks-in-series system uses PI (Proportional+Integral) controllers (Balchen & Mummé 1988). Furthermore, in the tryptophan system, the molecular bindings lead to multiplicative interactions between the controller and the process, whereas an additive interaction occurs between the controller C2 and Tank 2 in the two-tanks-in-series experimental process. Despite these minor differences, both systems distribute feedback to different points of the process, thereby establishing a similar structure with regards to information flow. The regulatory objective is to increase the water level, h, in Tank 2 from a normalized value of 0–1. The dynamic responses for the single (dash-dot) and multiple (solid) feedback loop design are shown in figure 6b. The rise times for the single and multiple feedback loop designs are noted as 3 and 2 min, respectively, whereas the corresponding settling times are 10 and 3 min, respectively. The average deviation between the single and multiple feedback strategies is noted as I(p, s)=1.5. The single feedback loop was found to be more sensitive to the controller parameters than the multiple feedback loop design. Comparisons between the multiple and single feedback loop designs for the two-tanks-in-series system are consistent with the dynamic response of the tryptophan system. Further, the robust characteristics of the multiple feedback design to process parametric changes were also evident in the two-tank system, analogous to that observed in tryptophan regulation (results not shown).
Figure 6.
(a) Schematic of a two-tank experimental set up with multiple feedback loop architecture. The water level in Tank 2 (h) constitutes the variable to be regulated. The variables F1 and F2 are flow rates of water to Tank 1 and Tank 2 through valves V1 and V2, respectively. D1 and D2 represent the drain valves at the exit of Tank 1 and Tank 2, respectively. To emulate the multiple feedback loop design of the trp system, we use the measurement of height h, to regulate the two valves by PI (Proportional+Integral) controllers, C1(h) and C2(h). In the case of the single feedback loop, only the flow rate to Tank 1, F1, is manipulated via controller C1(h) while F2 is not used for control. (b) Comparison of dynamic response from the experimental set up shown in (a) for the single feedback loop (dash-dotted line) and the multiple feedback loop (solid line) designs for control of level in the two-tank system. The PI controller parameters are as follows: C1(h): proportional gain=1.4 mA mA−1, integral time=300 s, C2(h): proportional gain=0.55 mA mA−1, integral time=500 s. Consistent with the tryptophan system, the results indicate that the multiple feedback design yields a superior robust dynamic performance relative to the single feedback design.
One may quantify the stability and performance of the two-tanks-in-series process using engineering tools such as the poles and zeros of the closed loop transfer function. The analysis of the two-tanks-in-series process using proportional (P-only) regulators C1 and C2 shows that the additional feedback loop results in addition of a system zero, indicating the direct transmission of the feedback signal to the second tank (see table S2 in the electronic supplementary material). Interestingly, a change in the proportional gain (quantifying the strength of feedback) of C2 results in the movement of both the system poles as well as zeros (see figure S4 in the electronic supplementary material). It is observed that increasing the magnitude of gain of C2 relative to C1 makes the flow rate F2 the key controlling variable in achieving the performance objective. This fact is captured through cancellation of the pole contributed by the first tank with the system zero, thereby making the dynamics of Tank 1 irrelevant (see equations S-8 and S-9 in the electronic supplementary material). The other closed loop pole becomes an increasingly large negative number with increase in the proportional gain of C2 indicating a larger stability margin. The peak value of the sensitivity transfer function above 0 dB indicates the degradation of robust performance, and, therefore, distinguishes the two alternative linear feedback designs. The variation of the peak value of the sensitivity transfer function with variation in the drain valve constants (k1 and k2 corresponding to valves D1 and D2) indicates that the multiple feedback loop design has a lower peak value relative to the single feedback loop design (see figure S5 in the electronic supplementary material). Similar results were observed for the linearized tryptophan system (results not shown). Thus, both systems appear to benefit from the multiple feedback loop design. In summary, the addition of a system zero due to the multiple feedback strategy yields smaller rise times and the proximity of the locations of one of the pole and the zero offers parametric robustness.
4. Discussion
Identification of the relationship between the network design and its function is a key step in understanding the design principles of complex regulatory networks. It is, therefore, essential to develop metrics that quantify the functional effectiveness of a specific design over alternatives. A well-designed network must continue to be functionally effective, even in presence of perturbations in parameter values and molecular interactions. Thus, for a robust system, the performance of the network must not deteriorate as measured by a performance metric. A single measure may not be sufficient to capture uniquely the dynamic performance of the network, and, thus, multiple measures may be necessary. In case of the tryptophan system, the rise time and homeostasis are motivated as the primary targets of the network. We used two performance measures, namely a temporal average of deviation from a physiological response, I(p, s) and the rise time. We demonstrated the robust attributes of the multiple feedback loop design on the homeostatic network of the tryptophan system, which is represented by a three-processes-in-series structure. Such a serial architecture is a fundamental basis in biological regulatory system design. For example, transcription of a gene to mRNA and the translation of mRNA to a protein represent a serial process. Similarly, an output of a phosphorylation cycle leads into other downstream cycles forming cascades in signalling networks that represent processes-in-series (Angeli et al. 2004). An advantage of such a design is that additional regulation is possible at multiple points in the overall process.
The analysis of multiple feedback loops regulating processes-in-series indicates that robustness is not the result of a fortuitous choice of specific parameters, but is due to the structural design resulting from molecular interactions. The structure, therefore, obviates the need for precise knowledge of system parameters. Moreover, the structure is also responsible for the fast rise time, which is a prerequisite for efficient functioning. While perturbations in parameters cause only slight degradation of regulatory performance, structural perturbations result in catastrophic failure as evidenced by the rapid degradation in system performance. In summary, robustness obtained through the structure provides insulation against catastrophic failure, while parameter magnitudes address the issue of optimal performance. These features are consistent with the concept of highly optimized tolerance (Carlson & Doyle 2002), where the regulatory structure endows the system with robustness to parametric variation, but exhibits catastrophic failure in the case of structural mutations.
From a regulatory standpoint, certain networks have evolved to achieve homeostasis, while others respond to specific changes. It has been noted that networks responding to nutritional levels are typically sensitive to specific parameters. For example, the GAL network responsible for galactose uptake by S. cerevisiae is highly sensitive to the shuttling of repressor Gal80p between the nucleus and cytoplasm, as quantified by the parameter nucleocytoplasmic distribution coefficient (Verma et al. 2003). For such networks, the design principle must be based not only on the structural motif, but also on the sensitive values of certain parameters. The use of metrics presented in this work may be easily extended to probe the design basis of such sensitive networks.
The evidence of robustness or sensitiveness on an independent system, either natural or physical, with identical structural motif corroborates the link between the network property and its structure. It is truly remarkable that the multiple feedback loop design imparts robustness for the two disparate systems, (i) naturally occurring tryptophan system and (ii) the engineered two-tank system that have completely different objectives, nonlinearities and governed by unrelated physical laws. It is, therefore, not surprising that the multiple feedback motif is a recurring theme in the spectrum of biological regulatory networks.
5. Methods
5.1 System model
The model equations describing the dynamic transcription, translation and tryptophan synthesis are as follows:
| (5.1) |
| (5.2) |
| (5.3) |
| (5.4) |
Parameters k1, k2, k3 and k4 represent kinetic rate constants for the synthesis of free operator, mRNA transcription, translation and tryptophan synthesis, respectively. Parameters Ot, μ, kd1 and kd2 refer to total operator site concentration, specific growth rate of E. coli, degradation rate constants of free operator OR and mRNA, respectively. E and T represent concentrations of enzyme anthranilate synthase and tryptophan, respectively, in the cell. Kg and g are the half-saturation constant and kinetic constant for the uptake of tryptophan for protein synthesis in the cell. Model parameter values are as follows (Santillan & Mackey 2001; Bhartiya et al. 2003): k1=50 min−1; k2=15 min−1; k3=90 min−1; k4=59 min−1; Ot=3.32 nM; kd1=0.5 min−1; kd2=15 min−1; μ=0.01 min−1; g=25 μM min−1; Kg=0.2 μM. Here, controllers C1(T), C2(T) and C3(T) represent repression, attenuation and inhibition, respectively, by tryptophan, and are modelled by Hill equations as follows:
| (5.5) |
Ki,1, Ki,2 and Ki,3 represent the half-saturation constants with values Ki,1=3.53 μM; Ki,2=0.04 μM; Ki,3=810 μM, while sensitivity of genetic regulation to tryptophan concentration, ηH=1.92. A block diagram representation of the model is shown in figure S1 (see the electronic supplementary material).
Acknowledgments
The authors are thankful to Vivek Mutalik for discussion and comments on the manuscript and M. Srinivas Rao for help in conducting experiments. K.V.V. would like to acknowledge funding from the Department of Science and Technology, India through the Swarnajayanti Fellowship. F.J.D. was supported by the Institute for Collaborative Biotechnologies through grant DAAD19-03-D-0004 from the US Army Research Office.
Supplementary Material
Block diagram of the model used for simulation of the distributed feedback structure in the trp system
References
- Aldana M, Cluzel P. A natural class of robust networks. Proc. Natl Acad. Sci. 2003;100:8710–8714. doi: 10.1073/pnas.1536783100. doi:10.1073/pnas.1536783100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alon U, Surette M.G, Barkai N, Leibler S. Robustness in bacterial chemotaxis. Nature. 1999;397:168–171. doi: 10.1038/16483. doi:10.1038/16483 [DOI] [PubMed] [Google Scholar]
- Angeli D, Ferrell J.E, Jr, Sontag E.D. Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl Acad. Sci. 2004;101:1822–1827. doi: 10.1073/pnas.0308265100. doi:10.1073/pnas.0308265100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balchen J.G, Mummé K.I. Van Nostrand Reinhold; New York: 1988. Process control structures and applications; pp. 9–35. [Google Scholar]
- Becskei A, Serrano L. Engineering stability in gene networks by autoregulation. Nature. 2000;405:590–593. doi: 10.1038/35014651. doi:10.1038/35014651 [DOI] [PubMed] [Google Scholar]
- Bhartiya S, Rawool S, Venkatesh K.V. Dynamic model of Escherichia coli tryptophan operon shows an optimal structural design. Eur. J. Biochem. 2003;270:2644–2651. doi: 10.1046/j.1432-1033.2003.03641.x. doi:10.1046/j.1432-1033.2003.03641.x [DOI] [PubMed] [Google Scholar]
- Carlson J, Doyle J.C. Complexity and robustness. Proc. Natl Acad. Sci. 2002;99:2538–2545. doi: 10.1073/pnas.012582499. doi:10.1073/pnas.012582499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csete M.E, Doyle J.C. Reverse engineering of biological complexity. Science. 2002;295:1664–1669. doi: 10.1126/science.1069981. doi:10.1126/science.1069981 [DOI] [PubMed] [Google Scholar]
- Dekel E, Alon U. Optimality and evolutionary tuning of the expression level of a protein. Nature. 2005;436:588–592. doi: 10.1038/nature03842. doi:10.1038/nature03842 [DOI] [PubMed] [Google Scholar]
- El-Samad H, Goff J.P, Khammash M. Calcium homeostasis and parturient hypocalcemia: an integral feedback perspective. J. Theor. Biol. 2002;214:17–29. doi: 10.1006/jtbi.2001.2422. doi:10.1006/jtbi.2001.2422 [DOI] [PubMed] [Google Scholar]
- El-Samad H, Kurata H, Doyle J.C, Gross C.A, Khammash M. Surviving heat shock: control strategies for robustness and performance. Proc. Natl Acad. Sci. 2005;102:2736–2741. doi: 10.1073/pnas.0403510102. doi:10.1073/pnas.0403510102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faanes A, Skogestad S. Controller design for serial processes. J. Proc. Cont. 2005;15:259–271. doi:10.1016/j.jprocont.2004.07.001 [Google Scholar]
- Freeman M. Feedback control of intercellular signalling in development. Nature. 2000;408:313–319. doi: 10.1038/35042500. doi:10.1038/35042500 [DOI] [PubMed] [Google Scholar]
- Goulian M. Robust control in bacterial regulatory circuits. Curr. Opin. Microbiol. 2004;7:198–202. doi: 10.1016/j.mib.2004.02.002. doi:10.1016/j.mib.2004.02.002 [DOI] [PubMed] [Google Scholar]
- Guet C.C, Elowitz M.B, Hsing W, Leibler S. Combinatorial synthesis of genetic networks. Science. 2003;296:1466–1470. doi: 10.1126/science.1067407. doi:10.1126/science.1067407 [DOI] [PubMed] [Google Scholar]
- Hohmann S. Osmotic stress signaling and osmoadaptation in yeasts. Microbiol. Mol. Biol. Rev. 2002;66:300–372. doi: 10.1128/MMBR.66.2.300-372.2002. doi:10.1128/MMBR.66.2.300-372.2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemkemer R, Schrank S, Vogel W, Gruller H, Kaufmann D. Increased noise as an effect of haploinsufficiency of the tumor-suppressor gene neurofibromatosis type 1 in vitro. Proc. Natl Acad. Sci. 2002;99:13 783–13 788. doi: 10.1073/pnas.212386999. doi:10.1073/pnas.212386999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitano H. MIT Press; Cambridge, MA: 2001. Foundations of systems biology; pp. 1–36. [Google Scholar]
- Koh B.T, Tan R.B.H, Yap M.G.S. Genetically structured mathematical modeling of trp attenuator mechanism. Biotechnol. Bioeng. 1998;58:502–509. doi: 10.1002/(sici)1097-0290(19980605)58:5<502::aid-bit6>3.0.co;2-h. doi:10.1002/(SICI)1097-0290(19980605)58:5<502::AID-BIT6>3.0.CO;2-H [DOI] [PubMed] [Google Scholar]
- Kohn K.W. Molecular interaction map of the mammalian cell cycle control and DNA repair systems. Mol. Biol. Cell. 1999;10:2703–2734. doi: 10.1091/mbc.10.8.2703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Largaespada D.A. Haploinsufficiency for tumor suppression: the hazards of being single and living a long time. J. Exp. Med. 2001;193:229–521. doi: 10.1084/jem.193.4.f15. doi:10.1084/jem.193.4.F15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauffenburger D.A. Cell signaling pathways as control modules: complexity for simplicity? Proc. Natl Acad. Sci. 2000;97:5031–5033. doi: 10.1073/pnas.97.10.5031. doi:10.1073/pnas.97.10.5031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangan S, Alon U. Structure and function of the feed-forward loop network motif. Proc. Natl Acad. Sci. 2003;100:11 980–11 985. doi: 10.1073/pnas.2133841100. doi:10.1073/pnas.2133841100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morishita Y, Kobayashi T.J, Aihara K. Evaluation of the performance of mechanisms for noise attenuation in a single-gene expression. J. Theor. Biol. 2005;235:241–264. doi: 10.1016/j.jtbi.2005.01.007. doi:10.1016/j.jtbi.2005.01.007 [DOI] [PubMed] [Google Scholar]
- Okamoto M, Hayashi K. Optimal control mode of a biochemical feedback system. Biosystems. 1983–1984;16:315–321. doi: 10.1016/0303-2647(83)90014-x. doi:10.1016/0303-2647(83)90014-X [DOI] [PubMed] [Google Scholar]
- Ruhela A, Verma M, Edwards J, Bhat P.J, Bhartiya S, Venkatesh K.V. Autoregulation of regulatory proteins is key for dynamic operation of GAL switch in Saccharomyces cerevisiae. FEBS Lett. 2004;576:119–126. doi: 10.1016/j.febslet.2004.09.001. doi:10.1016/j.febslet.2004.09.001 [DOI] [PubMed] [Google Scholar]
- Santillan M, Mackey M.C. Dynamic regulation of the tryptophan operon: a modeling study and comparison with experimental data. Proc. Natl Acad. Sci. 2001;98:1364–1369. doi: 10.1073/pnas.98.4.1364. doi:10.1073/pnas.98.4.1364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santillan M, Zeron E.S. Dynamic influence of feedback enzyme inhibition and transcription attenuation on the tryptophan operon response to nutritional shifts. J. Theor. Biol. 2004;231:287–298. doi: 10.1016/j.jtbi.2004.06.023. doi:10.1016/j.jtbi.2004.06.023 [DOI] [PubMed] [Google Scholar]
- Sauro H, Kholodenko B.N. Quantitative analysis of signaling networks. Prog. Biophys. Mol. Biol. 2004;86:5–43. doi: 10.1016/j.pbiomolbio.2004.03.002. doi:10.1016/j.pbiomolbio.2004.03.002 [DOI] [PubMed] [Google Scholar]
- Sedaghat A.R, Sherman A, Quon M.J. A mathematical model of metabolic insulin signaling pathways. Am. J. Physiol. Endocrinol. Metab. 2002;283:E1084–E1101. doi: 10.1152/ajpendo.00571.2001. [DOI] [PubMed] [Google Scholar]
- Shen-Orr S.S, Milo R, Mangan S, Alon U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 2002;31:64–68. doi: 10.1038/ng881. doi:10.1038/ng881 [DOI] [PubMed] [Google Scholar]
- Stelling J, Giles E.D, Doyle F.J., III Robustness properties of circadian clock architectures. Proc. Natl Acad. Sci. 2004a;101:13 210–13 215. doi: 10.1073/pnas.0401463101. doi:10.1073/pnas.0401463101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelling J, Sauer U, Szallasi Z, Doyle F.J, Doyle J.C. Robustness of cellular functions. Cell. 2004b;118:675–685. doi: 10.1016/j.cell.2004.09.008. doi:10.1016/j.cell.2004.09.008 [DOI] [PubMed] [Google Scholar]
- Tyson J.J, Chen K.C, Novak B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol. 2003;15:221–231. doi: 10.1016/s0955-0674(03)00017-6. doi:10.1016/S0955-0674(03)00017-6 [DOI] [PubMed] [Google Scholar]
- Venkatesh K.V, Bhartiya S, Ruhela A. Multiple feedback loops are key to a robust dynamic performance of tryptophan regulation in Escherichia coli. FEBS Lett. 2004;563:234–240. doi: 10.1016/S0014-5793(04)00310-2. doi:10.1016/S0014-5793(04)00310-2 [DOI] [PubMed] [Google Scholar]
- Verma M, Bhat P.J, Venkatesh K.V. Quantitative analysis of GAL genetic switch of Saccharomyces cerevisiae reveals that nucleocytoplasmic shuttling of Gal80p results in a highly sensitive response to galactose. J. Biol. Chem. 2003;278:48 764–48 769. doi: 10.1074/jbc.M303526200. doi:10.1074/jbc.M303526200 [DOI] [PubMed] [Google Scholar]
- Walls M.E, Hlavacek W.S, Savageau M.A. Design principles for regulator gene expression in a repressible gene circuit. J. Mol. Biol. 2003;332:861–876. doi: 10.1016/s0022-2836(03)00948-3. doi:10.1016/S0022-2836(03)00948-3 [DOI] [PubMed] [Google Scholar]
- Yanofsky C, Kelly R.L, Horn V. Repression is relieved before attenuation in the trp operon of Escherichia coli as tryptophan starvation becomes increasingly severe. J. Bacteriol. 1984;158:1018–1024. doi: 10.1128/jb.158.3.1018-1024.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi T.M, Huang Y, Simon M.I, Doyle J.C. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl Acad. Sci. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. doi:10.1073/pnas.97.9.4649 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Block diagram of the model used for simulation of the distributed feedback structure in the trp system