Abstract
Worldwide declines of fish stocks raise concerns about deleterious consequences of harvesting for stock abundances and individual life histories, and call for appropriate recovery strategies. Fishes in exploited stocks mature earlier at either larger or smaller sizes due to both genetic and plastic responses. The latter occur commonly when reduced competition for food leads to faster growth. Using a size-structured consumer–resource model, which accounts for both genetic and plastic responses, we show that fisheries-induced evolutionary changes in individual life history and stock properties can easily become irreversible. As a result of annual spawning, early maturation at small sizes and late maturation at large sizes can become alternative, evolutionarily and ecologically stable states under otherwise identical environmental conditions. Exploitation of late-maturing populations can then induce an evolutionary regime shift to smaller maturation sizes associated with stepwise, 1-year decreases in age at first reproduction. Complete and early fishing moratoria slowly reverse this process, but belated or partial closure of fisheries may accelerate or even instigate further evolution to smaller sizes at maturation. We suggest that stepwise decreases in maturation age can be used as early warnings of upcoming evolutionary changes, and should inspire timely restrictions of fisheries.
Keywords: complex adaptive systems, life-history evolution, ecological feedbacks, harvesting, trade-offs, reversibility
1. Introduction
Many fish stocks have been drastically depleted in recent decades, sometimes to levels of commercial extinction (Myers & Worm 2003). The depleted stocks often show little or no signs of long-term recovery in population abundance (Hutchings 2000). Moreover, mounting evidence suggests that harvesting promotes rapid life-history evolution in fishes (Reznick et al. 1990; Conover & Munch 2002; Olsen et al. 2004), which threatens the sustainability of fisheries yields over evolutionary timescales. Life-history theory predicts that size-specific or indiscriminate harvesting selects for early maturation at small size (Roff 2002; Ernande et al. 2004). Experiments with captive, marine fish populations have confirmed these predictions and revealed evolutionary effects of size-selective mortality on somatic growth, yield and population biomass (Conover & Munch 2002). However, the theory neglects that surviving fishes in exploited populations can grow faster when stock abundance declines, and the experiments were set up to exclude such density-dependent effects (Conover & Munch 2002). In general, phenotypic life-history changes in exploited fish stocks are considered to result from both genetic and plastic responses (Law 2000; Ernande et al. 2004; Hutchings 2005). The most common plastic response is the aforementioned ecological feedback: decreased competition allows surviving individuals to reach maturation sizes faster through compensatory growth (Policansky 1993) if maturation occurs at roughly fixed sizes.
Statistical analysis of maturation data for cod (Gadus morhua) in the Northwest Atlantic disentangled genetic and plastic responses and provided evidence for fisheries-induced evolution to earlier maturation at smaller sizes in this stock (Olsen et al. 2004). Mean age at first reproduction was found to have decreased almost stepwise from 6 to 5 years during the stock collapse between the mid-1980s and mid-1990s. Simultaneously, length at maturation decreased more gradually with approximately 1 cm per year. The collapse has been interpreted as a major selective episode favouring early-maturing relative to late-maturing genotypes (Hutchings 1999; Olsen et al. 2004). Similar changes in life history with larger or more abrupt decreases in age than in size at first reproduction have been reported for other cod stocks (Trippel 1995), North Sea plaice (Pleuronectes platessa; Grift et al. 2003) and American plaice (Hippoglossoides platessoides; Morgan & Colbourne 1999). Grift et al. (2003) further proved that the observed changes in North Sea plaice involve a significant genetic response. However, contrasting evidence exists for Norwegian spring-spawning herring (Clupea harengus; Engelhard & Heino 2004), Pacific halibut (Hippoglossus stenolepis; Schmitt & Skud 1978) and some commercial flatfishes in the Northwest Atlantic (Bowering & Brodie 1991), in which fisheries exploitation has led to larger sizes despite the same or earlier ages at first reproduction. Engelhard & Heino (2004) showed that the changes in Norwegian spring-spawning herring were predominantly plastic. That is, phenotypic changes associated with commercial fishing include earlier maturation at smaller, larger or unchanged sizes.
These different observations beg the question as to which harvesting conditions select for increased or decreased maturation sizes and how ecological feedback between stock abundance, competition for food and individual growth influences the selection imposed by harvesting. More importantly, fisheries-induced changes may eventually become irreversible. This fact critically determines the efficacy of management strategies (Basket et al. 2005), like fishing moratoria, which are intended to counter substantial declines in stock biomass and evolutionary changes in fish life history. In this respect, the fisheries moratorium for cod in the Northwest Atlantic inspires little hope, since the recovery of stock biomass and individual life histories appears to be slow if any (Olsen et al. 2004; Frank et al. 2005). On the other hand, the Norwegian spring-spawning herring has largely recovered in both aspects (Engelhard & Heino 2004).
To address these seemingly disparate observations on harvesting-induced changes in individual life histories and their reversibility, we studied evolutionary and ecological dynamics of an exploited fish stock using a generic, size-structured consumer–resource model (Persson et al. 1998; de Roos & Persson 2001). This is the simplest food web model that can highlight the potential role of ecological feedback in fisheries-induced life-history evolution. Size-dependent harvesting mortality, size-dependent foraging and indeterminate, size- and food-dependent growth at an individual level are modelled explicitly. The model hence accounts both for demographic, population-level responses (i.e. truncation of the age/size distribution) as well as plastic, individual life-history responses to harvesting. Reproduction is also size and food dependent and reflects the synchronized, annual spawning of most fishes in boreal and temperate regions. These life-history processes lead to a trade-off between the allocation of energy to the build-up of somatic tissue versus gonads (Kozłowski 1996), which determines the evolutionary equilibrium. We use a quantitative genetics approach as well as methods of adaptive dynamics to analyse model dynamics on evolutionary timescales, tracking the genetic response in age and size at maturation.
2. Model and methods
(a) Ecological dynamics
The model of ecological dynamics we use has been extensively studied (Persson et al. 1998; de Roos & Persson 2001). It is a generic representation of the interaction between a size-structured fish population and its shared resource base, although it is parameterized for a particular, well-studied species. All model variables and equations are summarized in tables S1–S3 of the electronic supplementary material. Tables S1 and S2 summarize the variables and individual-level model equations, while table S3 presents the equations governing the ecological dynamics at the population level. Without genetic variability between consumers, the consumer population consists of cohorts of identical individuals, fully characterized by their reversible and irreversible body mass and their maturation size. These individuals mature at body length lmat, length being allometrically related to irreversible mass (de Roos & Persson 2001). Individuals growing at different rates thus mature at different ages. The fixed maturation size for each (genetically determined) phenotype reflects a flat maturation reaction norm with respect to age, which seems plausible for various species (Grift et al. 2003; Engelhard & Heino 2004).
The unstructured resource follows semi-chemostat dynamics. Consumer's food intake rate follows a Holling type II functional response with size-dependent attack rate and handling time. Assimilated energy is first used to cover maintenance costs, which increase with body mass. The remaining net energy is used for growth and reproduction. We assume indeterminate growth; juveniles allocate net energy towards growth, while adults always split it between growth and gonad build-up. Individuals hence start allocating part of their net energy to egg production upon maturation, causing individual growth to slow down. All fishes suffer from constant background mortality, and individuals with low fat reserves experience additional starvation mortality. All mature fishes reproduce at the start of summer by releasing their entire gonad mass. Age at first reproduction hence equals the smallest integer value larger than the maturation age at which the maturation size is reached. We use parameters for roach (Rutilus rutilus) feeding on Daphnia sp.; this parameterized model has been analysed extensively (Persson et al. 1998) and it matches observed dynamics of field populations (de Roos & Persson 2001).
The original ecological model (Persson et al. 1998; de Roos & Persson 2001) predicts the occurrence of so-called single-cohort cycles, in which a single age cohort dominates the population dynamics throughout its life and adult individuals are outcompeted by their offspring right after reproduction. We analyse the evolutionary dynamics of maturation size in the original model, as well as in a slightly adapted model version, which accounts for recruitment dynamics of young-of-the-year consumers. In the latter model, individuals are not assumed to enter the population immediately. They recruit as 1 year old at 50 mm length and do not compete for resources before that. The number of recruits relates to the number of eggs spawned the previous year. It follows a Ricker stock–recruitment relationship, , where E equals the number of eggs produced the year before recruitment and hence reflects the spawning stock condition. Second, phenotypes maturing at larger sizes are assumed to have higher feeding capacities. Many physiological traits are likely to be genetically correlated with maturation size. Walsh et al. (2006) show that size-selective harvesting of large fishes selects for lower consumption rates, willingness to forage, growth efficiency, and thus lower growth rates (see also Conover & Munch 2002). Trudel et al. (2001) show explicitly that morphs with lower ingestion as well as growth rates mature earlier at smaller sizes, which is in line with the results presented by Olsen et al. (2004). Such correlations might represent countervailing selection pressures against maturation at small size. We account to a limited extent for such countervailing selection by mimicking a positive correlation between growth rate and maturation size. We assume that the maximum feeding rate (Persson et al. 1998; de Roos & Persson 2001), Amax, is related to maturation length as . In two evolutionary equilibria that we discuss below, individuals maturing at lmat=104 mm, hence, have 8% higher feeding rate than individuals with lmat=69 mm.
We model harvesting mortality as a probability function that increases sigmoidally with body size. It is characterized by the harvesting size threshold T (measured in mm), at which harvesting reaches half its maximum value, and the harvesting intensity hmax, i.e. the annual harvesting mortality for individuals well above the threshold. Once a year, prior to reproduction and recruitment, we remove a fraction of each size class l (measured in mm) of recruited fishes; additional simulations showed that the exact shape and slope of harvesting mortality leads to only quantitatively different results. To assess stock abundance and life-history characteristics, we census the population each time after harvesting but before reproduction.
(b) Evolutionary dynamics
For a limited number of harvesting intensities and size thresholds, we quantitatively studied evolutionary dynamics on ecological timescales using standard methods of quantitative genetics. With this approach we illustrate possible evolutionary trajectories in response to different harvesting strategies. In addition, we assess possible endpoints of evolution over a wider range of hmax values using an adaptive dynamics approach (Metz et al. 1996). The quantitative genetics approach assumes that maturation size is a quantitative trait controlled by a number of loci of small effect. We use a simple genetic setup, including additive genetics and normal distribution of phenotypes. The original, ecological model (Persson et al. 1998; de Roos & Persson 2001) assumes that all newborn individuals are identical and form a single cohort. To represent genetic variability in the consumer population, individuals born within the same year are assumed to group into a number of different sub-cohorts, which are identical in their size at birth, but differ in their value of the maturation size lmat (see van Kooten et al. 2004 for a comparable approach to capture spatial within-yearclass variability). Consumers within the same sub-cohort are assumed to be identical. We divide newborns into 11 such sub-cohorts, each with its own phenotype: one with the new mean lmat value, , five with lower and five with higher lmat values, equidistantly separated by a factor of with σ=0.10; other meaningful values of σ only affected the timescales. Newborn individuals are distributed over the sub-cohorts with different lmat values in such a way that their trait distribution reflects a discrete approximation to the normal distribution.
Selection differential S is calculated using standard techniques (Taylor 1996), equating individual fitness with the number of eggs spawned. In each reproductive event, S equals the difference between the mean maturation size weighed by cohort-level fecundity and the mean maturation size of all potential parents (i.e. except the 1 year olds):
The summation is over all cohorts aged more than 1 year, lmat,i indicates the maturation size of the ith cohort containing Ni individuals, and Ei is the total number of eggs it produces. The overall change in mean maturation size is set to . We assume heritability h2=0.3, which is within the range of observed values for maturation size and body weight (Policansky 1993; Law 2000). We also investigated the impact of different h2 values with larger (smaller) values of h2, which lead to increased (decreased) rates of evolution (results not shown). We restrict the change in lmat between the mean parent and offspring cohort by , as, in rare cases, cohorts of the same age but maturing at smaller sizes reproduce 1 year before similarly aged cohorts with larger maturation size. They give birth to new phenotypes that would inherit extremely low maturation sizes were it not for the constraint, which prevents such large evolutionary steps and keeps the entire phenotypic distribution approximately normal.
Selection gradients and evolutionary stable states (ESSs; figures 3 and 4) were computed as follows. Using the adaptive dynamics approach (Metz et al. 1996) we assessed, for each value of hmax and lmat characterizing the resident population, whether rare mutants with slightly smaller or larger lmat can invade the resident population. For a given combination of hmax and lmat, we first simulated the dynamics of the resident population and allowed it to settle in an ecological attractor. These attractors corresponded to fixed-point dynamics (i.e. with period n=1 year) or cyclic dynamics, mostly single-cohort cycles, with period n>1 (dynamics with a cycle length of more than 50 years were truncated). Subsequently, we introduced the mutant consumer populations. The dynamics of these mutants were governed by the environment (i.e. resource dynamics) imposed by the resident consumer, but the mutants did not affect the resource and hence resident consumer dynamics. Mutants were introduced as newborn individuals during n consecutive reproductive pulses into all possible environments generated by the resident population. Invasion success of mutants was determined by computing their long-term population growth rate using life-cycle graph analysis (Caswell 2001), in which n life stages correspond to the n environments newborn mutants can enter. In addition, we constructed pairwise invasibility plots (Dieckmann 1997) for selected harvesting intensities using the same simulation procedure with numerous mutant consumers covering a range of lmat values. From the pairwise invasibility plots, we inferred the global stability of the possible evolutionary attractors. We subsequently confirmed that successfully invading mutants always ultimately replace the resident in additional simulated competition experiments, in which feedback of mutants on resource density was accounted for.
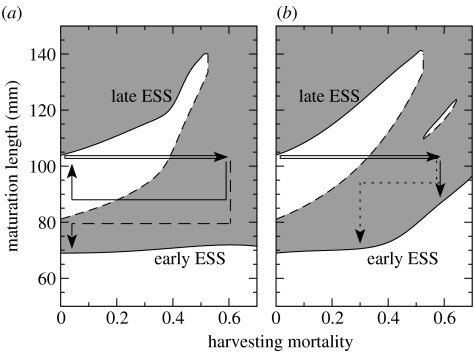
Figure 3.
Effect of harvesting intensity and size threshold on alternative evolutionary stable maturation sizes for equilibrium populations (based on adaptive dynamics approach). Harvesting size threshold equal to (a) 100 mm and (b) 80 mm. White and grey regions indicate harvesting intensities with evolution to larger and smaller maturation sizes, respectively. Solid and dashed lines: evolutionary stable states and evolutionary saddle points (repellors), respectively. Open arrows: initial increase in harvesting intensity (in year 0 in figure 1). Solid and dashed arrows in (a): consequences of imposing complete fisheries moratoria after 25 and 50 years, respectively. Solid and dotted arrows in (b): consequences of continued harvesting versus partial moratorium imposed 40 years after the onset of harvesting (see figure 1 for corresponding dynamics). Solid arrows indicate trajectories with reversible evolutionary response, while dashed and dotted arrows indicate trajectories with evolutionary regime shift.
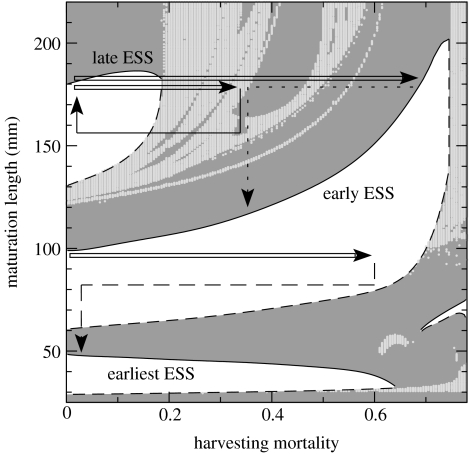
Figure 4.
Effect of harvesting intensity on alternative evolutionary stable maturation sizes for ecological dynamics involving single-cohort cycles (based on adaptive dynamics approach). Harvesting size threshold equal to 70 mm. Layout as in figure 3; paler shade of grey indicates regions of chaotic/quasiperiodic ecological dynamics and long cycles in which evolution always leads to smaller maturation size. Dynamics corresponding to the arrows (see text for details) are similar to figure 1. Several ESS phenotypes with negligible areas of attraction are omitted for clarity. Solid arrows indicate trajectories with reversible evolutionary response, while dashed and dotted arrows indicate trajectories with evolutionary regime shift.
3. Results
(a) Evolutionary dynamics in equilibrium populations
For a wide range of parameter sets that we examined, the (unharvested) population exhibits year-to-year fixed-point dynamics, in which population abundance and size distribution is the same after each spawning event. Figure 1 illustrates the general predictions of the eco-evolutionary model for this type of dynamics with a background mortality that is sufficiently low for the consumers to persist on ecological and evolutionary timescales while starting reproduction at the age of either 2 or 3 years. The figure exemplifies the evolutionary consequences of harvesting with different size thresholds and imposing harvest moratoria at different times after opening the fishery.
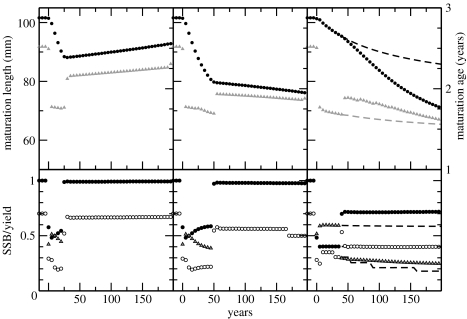
Figure 1.
Impact of harvesting and fishing moratoria on evolutionary dynamics for equilibrium populations (based on quantitative genetics approach). Consequences of a complete moratorium after 25 (left) or 50 years (middle) and halving fishing pressure after 40 years of harvesting (right). Harvesting intensity equal to 60%; size threshold equal to 100 mm (left and middle) and 80 mm (right). Dashed lines in right panel project consequences of continuing harvesting at the same intensity and size threshold. Top panels: changes in mean maturation size (black circles) and age (grey triangles); bottom panels: changes in standing stock biomass (SSB; black circles) and yearly harvesting yield (triangles). Open circles indicate total biomass of individuals larger than 110 mm. All biomass measures are expressed relative to total biomass of an unharvested population.
The model predicts that unexploited populations with phenotypes that mature mostly during their third year at lengths between 76 and 127 mm are ecologically and evolutionarily stable. Mild harvesting, in which the harvesting intensity (i.e. harvesting probability for fishes well above the size threshold) is less than roughly 40%, does not change average age at first reproduction and induces slow evolution to slightly larger maturation sizes. In contrast, exposure to 60% harvesting intensity with 100 mm size threshold leads to rapid selection toward smaller maturation sizes. Mean maturation length decreases by more than 10% within 25 years (figure 1, left column). As harvesting decreases total population biomass by 50–60%, surviving individuals exhibit compensatory growth and reach mature body sizes 1 year earlier. This advances the dominant age at first reproduction stepwise from 3 to 2 years. A complete fishing moratorium after 25 years reverses changes in stock biomass and age at first reproduction within 10 years. Selection on maturation size changes direction, but the recovery to pre-harvesting values is rather slow (figure 1, left column). A complete moratorium after 50 years comes too late to reverse the evolutionary and ecological effects, since most phenotypes in the population continue to mature during their second year (figure 1, middle column). Moreover, these phenotypes increase in frequency, as their average fitness is higher than that of the phenotypes maturing during their third year. Despite a continuing evolution to smaller maturation sizes, total population biomass recovers close to pre-harvesting levels.
With a low harvesting threshold, such that also a considerable part of juvenile individuals is targeted, we predict that a partial moratorium can be more detrimental than continued fishing at high intensity. After 40 years of harvesting at 60% intensity with 80 mm size threshold, maturation size decreases by almost 10% while stock biomass decreases by 60%. A complete moratorium slowly reverses these changes, whereas maturation size would continue to decline slowly if harvesting continued unchanged. Halving fishing pressure, however, greatly accelerates the evolution to smaller maturation sizes, even though stock biomass partly recovers (figure 1, right column).
These unexpected consequences of belated or partial fishing moratoria arise because early maturation at small sizes and late maturation at large sizes represent alternative ESSs. The changes induced by harvesting and subsequent closure of the fisheries correspond to evolutionary regime shifts (in the sense of Scheffer et al. 2001) between these alternative ESSs. These evolutionary regime shifts involve an abrupt change in the underlying ecological dynamics when most individuals can grow faster and start reproduction 1 year earlier. In turn, the ecological changes induce evolution to smaller maturation sizes. We further studied conditions required for these shifts using an adaptive dynamics approach.
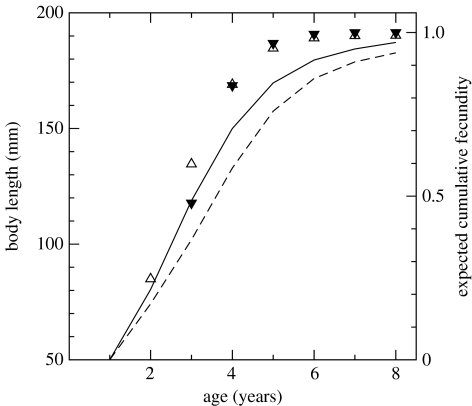
Two ESS phenotypes, ‘late’ and ‘early’, occur in the absence of harvesting in the example outlined previously. Individuals of the ‘late’ ESS phenotype mature during their third summer at 104 mm length, while individuals of the ‘early’ one mature during their second summer at only 69 mm. The ‘late’ ESS phenotype misses on the first reproductive opportunity, but benefits from a prolonged period of faster growth and concomitant higher feeding rates. Individuals hence remain consistently larger and, every year, reproduce more than the ‘early’ ESS phenotype (figure 2). Both strategies are stable against small mutations because they optimize the time before first reproduction, during which they allocate energy to the build-up of gonads (Kozłowski 1996). Phenotypes maturing earlier in the same season as the ESS at smaller sizes give up additional somatic growth and fail to benefit from increased body sizes and concomitantly higher intake rates had they matured slightly later. Phenotypes maturing later in the season at larger sizes have less time to accumulate eggs, and hence lower fitness than the ESS phenotype. Populations dominated by either the ‘late’ or the ‘early’ phenotype are evolutionarily stable even if (phenotypic) variability in maturation size is large with some individuals reproducing a year earlier or later. Moreover, both ESS phenotypes can persist on moderate timescales in environments dominated by the other one since their population growth rates differ by less than 1% (figure 2).
Figure 2.
Growth curves (lines) and expected cumulative fecundity (symbols) of ‘late’ and ‘early’ ESS phenotypes when the ‘late’ one dominates the population. Solid curve and black triangles represent the ‘late’ phenotype; dashed curve and open triangles correspond to the ‘early’ one. The pattern is nearly identical when the ‘early’ phenotype dominates.
Owing to their larger size, dominant reproductive cohorts of the ‘late’ phenotype (ages 3 and 4) are more susceptible to harvesting than those of the ‘early’ phenotype (ages 2 and 3). Harvesting with 100 mm size threshold thus significantly affects only the ‘late’ phenotype. Its maturation size increases with harvesting intensity (figure 3): the optimal within-season timing of maturation does not change significantly, but harvesting allows individuals to reach larger sizes at the same age. In contrast, the maturation size of the ‘early’ phenotype stays relatively constant with increasing harvesting intensity and a 100 mm size threshold (figure 3a). With lower harvesting size thresholds, however, the maturation size of the ‘early’ phenotype does increase with increasing harvesting intensity (figure 3b). This increase in ESS maturation size of the ‘early’ phenotype with increasing intensity is the reason why harvesting a population of the ‘late’ phenotype with an intensity of 60% leads to predominantly plastic changes (open arrow in figure 3b), with a subsequent, partial moratorium causing an evolutionary collapse to lower maturation sizes (dotted arrow in figure 3b).
In sum, populations consisting of either the ‘late’ or the ‘early’ phenotype are evolutionarily stable for considerable ranges of harvesting intensities and thresholds. However, the corresponding size ranges for which they represent the evolutionary endpoints can change considerably with harvesting intensity. Intense harvesting thus has a strong potential to cause irreversible evolutionary regime shifts from late maturation at larger size to early maturation at smaller size (figure 3).
(b) Evolutionary dynamics in fluctuating populations
A variety of freshwater and marine fish populations exhibit cyclic ecological dynamics with periods close to maturation age, e.g. the Skagerrak cod with 2–2.5-year cycles (Bjørnstad et al. 1999). These generation cycles are driven by abundant age cohorts that dominate the dynamics throughout their lifetime. For a range of parameter values, the original size-structured model (Persson et al. 1998) exhibits similar generation-type cycles in the absence of the Ricker stock–recruitment relationship. In these so-called single-cohort cycles, the population consists of a single age cohort of individuals that grow until they reach their maturation size, develop gonad mass, reproduce and subsequently starve. Length of these cycles is determined by age at maturation (Persson et al. 1998; de Roos & Persson 2001), and thus increases stepwise with maturation size but decreases with background mortality.
Despite such prominent cycles, the eco-evolutionary model leads to similar evolutionary predictions as described previously for equilibrium situations if phenotypic variability is not too high (figure 4, with no correlation between growth rate and maturation size). Unharvested populations with individual maturation sizes larger than 132 mm now exhibit 4-year single-cohort cycles. Maturation sizes between 62 and 122 mm give rise to single-cohort cycles with a 3-year period, while populations in which the maturation size is between 25 and 62 mm enter 2-year cycles, in which the differently sized cohorts born in odd and even years mature at a different date. Each of these types of cycles is associated with an ESS phenotype with maturation size within the range for which the cycle occurs. In the absence of harvesting, the ‘late’ ESS phenotype matures during its fourth summer at ca 177 mm length and the ‘early’ ESS phenotype during its third summer at 100 mm length, while the ‘earliest’ phenotype matures during the second/first year at ca 50 mm.
Maturation sizes of the ‘late’ and ‘early’ ESS phenotypes again increase with harvesting intensity. In contrast, the ESS maturation size of the ‘earliest’ phenotype slightly decreases with harvesting pressure, as only a small fraction of the population is removed and the harvesting-induced phenotypic response is low (figure 4). We also observed a concomitant decrease in age at maturation due to the accelerated growth (not shown). Hence, only for the ‘earliest’ phenotype the prediction, i.e. continuous decrease in maturation size and age, agrees with the standard theory of fisheries-induced evolution (Roff 2002).
Simulations based on the quantitative genetics approach lead to qualitatively similar results as for the equilibrium dynamics, but, frequently, the deterioration phase is even faster (not shown). If the ecological dynamics involve single-cohort cycles, phenotypes maturing 1 year earlier quickly outcompete later-maturing ones because individuals spawn only once (or only a few times), and a large cohort of developing juveniles has a strong negative impact on the fecundity and survival of currently maturing and mature fishes. The evolutionary process is therefore sensitive to phenotypic distributions spanning more than one maturation season. For example, the unharvested ‘early’ phenotype would, under moderately high phenotypic variability, quickly evolve to much smaller sizes at maturation when harvested with 60% intensity and 70 mm size threshold, although the mean maturation size is initially well within the range that leads to evolution toward larger maturation sizes for a very narrow phenotypic variability. Dashed arrow in figure 4 illustrates the effect of a complete moratorium that comes only 25 years after the onset of harvesting. As the population evolves toward early maturation at small sizes well below the harvesting threshold, harvesting yield and spawning stock biomass decrease considerably over time, and in the end no individuals ever reach the size of 70 mm (data not shown).
As in the case with equilibrium dynamics and a size threshold of 80 mm (figure 3b), the ESS maturation size of the ‘early’ phenotype increases with increasing harvesting intensity (figure 4). As a consequence, intense harvesting of the ‘late’ phenotype leads to a predominantly plastic response, because harvesting displaces the population very close to an equilibrium corresponding to the ‘early’ ESS phenotype (open arrow in figure 4). Subsequent reduction of harvesting pressure may lead to similar catastrophic consequences as outlined in the equilibrium case (dotted arrow in figure 4), since harvesting the ‘late’ ESS phenotype with 35% intensity and 70 mm size threshold leads to a rapid evolution toward small maturation sizes. Only a swift and complete fishing moratorium imposed less than 40 years after the onset of harvesting can reverse the trend (solid arrow in figure 4).
4. Discussion
We have used a simple consumer–resource model to demonstrate that life-history evolution of annually reproducing species, driven by size-selective harvesting, can lead to irreversible changes in individual properties. In addition, the results highlight the importance of population dynamic feedbacks between fish stocks and their environment. Although often neglected, the food- and density-dependent growth that may result from these feedbacks occurs even in marine stocks (Rijnsdorp 1993; Godø 2000). Tracking changes in population dynamics of commercial fish stocks becomes thereby important for successful management. As we show, upcoming evolutionary responses are signalled by stepwise decreases in age at first reproduction, which can be used for timely and appropriate management responses before irreparable damage is sustained by the exploited population.
Our model predicts that several qualitatively different responses to harvesting are possible, depending on the individual life history, genetic variance, heritability, and harvesting intensity and selectivity. Typically and in agreement with earlier studies (e.g. Law & Grey 1989; Rowell 1993; Roff 2002; Gårdmark et al. 2003; Ernande et al. 2004), harvesting leads to an evolutionary regime shift to decreased age and size at maturation. Our model yields stepwise changes in age at first reproduction and gradual changes in size at maturation as observed, for example, in the cod stocks in Northwest Atlantic (Olsen et al. 2004). This evolutionary regime shift quickly becomes irreversible. Second, harvesting may lead to increased size at maturation but the same age at first reproduction. Third, harvesting can result in a predominantly plastic response with decreased age at first reproduction and very limited evolutionary changes in maturation size. This response occurs when the maturation size of the possible ESS phenotypes increases with increasing intensity, such that harvesting induces a shift to another ESS phenotype that matures a year earlier, but at roughly the same size. Observations in the Norwegian spring-spawning herring (Engelhard & Heino 2004) might reflect the latter pattern.
Compared to other models of harvesting-driven life-history evolution (e.g. Law & Grey 1989; Rowell 1993; Roff 2002; Gårdmark et al. 2003; Ernande et al. 2004), our approach offers a fully mechanistic representation of the underlying life-history processes that ultimately drive the evolutionary dynamics. In particular, we assume seasonal reproduction, distinguish between the evolutionary and ecological response to harvesting and account for the population feedback on resources and hence on individual life history. This feedback leads to density-dependent, compensatory growth of individuals that survive harvesting. Since it arises from the interaction with the resource, we do not have to a priori include a heuristic description of density-dependent individual growth rates. In addition, the evolutionary trade-off is not a priori assumed, but results from the conflicting demands of energy allocation to growth versus reproduction. On the other hand, our predictions are based on an entirely deterministic model. We cannot rule out that strong environmental stochasticity would qualitatively change the predictions, but the deterministic skeleton does closely approximate the dynamics of models with moderately high stochasticity (van Kooten et al. 2004).
Three mechanisms are crucial for the alternative ESSs and harvesting-induced evolutionary regime shifts that we predict: (i) owing to annual spawning, reproduction can only be advanced in yearly steps, which hence show up only with large increases in harvesting; (ii) the trade-off between somatic and gonadal growth determines an optimal within-season timing to start reproductive allocation before the first reproductive pulse; (iii) given this timing, small increases in harvesting intensity expose mainly indirect effects of increased growth rates, and thus select for larger maturation sizes. Changes in model structure and parameters that leave these three mechanisms unaffected do not qualitatively change our predictions, altering at most the rates of decline and recovery and the presence of alternative ESSs. In particular, our energy allocation rule means that individuals always simultaneously allocate surplus energy to soma and gonads after maturation. Kozłowski (1996) showed that the optimal strategy might involve a shift from purely somatic to purely gonadal growth at an intermediate time during the growth season, with the shift gradually postponed towards the end of the season at higher ages. Given that the contribution to lifetime reproductive output rapidly diminishes with age due to mortality, we argue that this different energy allocation model would only lead to small quantitative differences. Also, in the model exhibiting fixed-point dynamics, we assumed a positive correlation between growth rate and maturation size, which benefits individuals maturing at larger sizes. The correlation is an example of various mechanisms (e.g. egg size, maternal effects in offspring survival) that represent countervailing selection pressure against maturation at small size. This model feature does not, however, relate to the necessary mechanisms for the alternative ESSs and only affects quantitative results. Without the assumed correlation, the model exhibiting fixed-point dynamics yields similar results for the same parameter values, except that the ‘late’ ESS phenotype is only locally stable and can be successfully invaded by the ‘early’ ESS phenotype.
Our results also suggest that species with low natural mortality and large flexibility in age at first reproduction may be especially prone to evolutionary regime shifts in maturation, because these traits allow for a larger number of alternative ESSs (figure 4). We moreover predict more rapid evolutionary changes when fish stocks exhibit population cycles, especially if phenotypic variability within the population is high. In many oceanic stocks, individual fishes of the same age cohort are indeed observed to mature over several years, which is consistent with a high degree of phenotypic plasticity. If these stocks fluctuated, they would be, according to our results, particularly vulnerable to harvesting-driven declines in age and size at maturation.
We based our model on a very simple food web, containing only the resource and consumer population. Additional research is needed to evaluate possible evolutionary responses in more complex food webs, given that their ecological dynamics can differ qualitatively. Nonetheless, we postulate that ecological and evolutionary regime shifts are likely to occur in exploited fish stocks, given that annual reproduction and food-dependent growth are characteristic for many of these populations in boreal and temperate regions. Our results show that successful management of such complex, adaptive systems is not straightforward and requires a careful unravelling of all the feedbacks in the system that influence individual life history on ecological as well as evolutionary timescales.
Acknowledgments
Our research was supported by Grant Agency of the Czech Republic, NATO Science Fellowship, FishACE European Research Training Network (D.S.B.), Netherlands Organization for Scientific Research (A.M.d.R.), the Swedish Research Council and the Swedish Research Council for Environment, Agricultural Sciences and Spatial Planning (L.P.). We thank J. Andersson, D. Claessen, U. Dieckmann, M. Heino, J. A. J. Metz, C. Parmesan, D. Reznick, A. D. Rijnsdorp, M. W. Sabelis, M. Spichtig, T. van Kooten, P. van Tienderen, N.-C. Stenseth and two anonymous referees for valuable comments and discussions.
The first two authors contributed equally to this work.
Present address: Institute of Marine Research, PO Box 1870 Nordnes, 5817 Bergen, Norway.
Supplementary Material
Tables S1–S3. Table S1: Variables and model parameters. Table S2: Individual-level equations used in the simulations. Table S3: Population-level equations used in the simulations of the ecological dynamics.
References
- Baskett M.L, Levin S.A, Gaines S.D, Dushoff J. Marine reserve design and the evolution of size at maturation in harvested fish. Ecol. Appl. 2005;15:882–901. [Google Scholar]
- Bjørnstad O.N, Fromentin J.-M, Stenseth N.Chr, Gjøsæter J. Cycles and trends in cod population. Proc. Natl Acad. Sci. USA. 1999;96:5066–5071. doi: 10.1073/pnas.96.9.5066. 10.1073/pnas.96.9.5066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowering W.R, Brodie W.B. Distribution of commercial flatfishes in the Newfoundland–Labrador region of the Canadian Northwest Atlantic and changes in certain biological parameters since exploitation. Neth. J. Sea Res. 1991;27:407–422. 10.1016/0077-7579(91)90042-Y [Google Scholar]
- Caswell H. Sinauer Associates; Sunderland, MA: 2001. Matrix population models. [Google Scholar]
- Conover D.O, Munch S.B. Sustaining fisheries yields over evolutionary time scales. Science. 2002;297:94–96. doi: 10.1126/science.1074085. 10.1126/science.1074085 [DOI] [PubMed] [Google Scholar]
- de Roos A.M, Persson L. Physiologically structured models—from versatile technique to ecological theory. Oikos. 2001;94:51–71. 10.1034/j.1600-0706.2001.11313.x [Google Scholar]
- Dieckmann U. Can adaptive dynamics invade? Trends Ecol. Evol. 1997;12:128–131. doi: 10.1016/s0169-5347(97)01004-5. 10.1016/S0169-5347(97)01004-5 [DOI] [PubMed] [Google Scholar]
- Engelhard G.H, Heino M. Maturity changes in Norwegian spring-spawning herring Clupea harrengus: compensatory or evolutionary responses? Mar. Ecol. Prog. Ser. 2004;272:245–256. [Google Scholar]
- Ernande B, Dieckmann U, Heino M. Adaptive changes in harvested populations: plasticity and evolution of age and size at maturation. Proc. R. Soc. B. 2004;271:415–423. doi: 10.1098/rspb.2003.2519. 10.1098/rspb.2003.2519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank K.T, Petrie B, Choi J.S, Leggett W.C. Trophic cascades in a formerly cod-dominated ecosystem. Science. 2005;308:1621–1623. doi: 10.1126/science.1113075. 10.1126/science.1113075 [DOI] [PubMed] [Google Scholar]
- Gårdmark A, Dieckmann U, Lundberg P. Life-history evolution in harvested populations: the role of natural predation. Evol. Ecol. Res. 2003;5:239–257. [Google Scholar]
- Godø, O. R. 2000 Maturation dynamics of Arcto-Norwegian cod. Report IR-00-024, International Institute for Applied Systems Analysis, Laxenburg, Austria, available at www.iiasa.ac.at/Research/ADN/Publications.html
- Grift R.E, Rijnsdorp A.D, Barot S, Heino M, Dieckmann U. Fisheries-induced trends in reaction norms for maturation in North Sea plaice. Mar. Ecol. Prog. Ser. 2003;257:247–257. [Google Scholar]
- Hutchings J.A. The influence of growth and survival costs of reproduction on Atlantic cod, Gadus morhua, population growth rate. Can. J. Fish. Aquat. Sci. 1999;56:1612–1623. 10.1139/cjfas-56-9-1612 [Google Scholar]
- Hutchings J.A. Collapse and recovery of marine fishes. Nature. 2000;406:882–885. doi: 10.1038/35022565. 10.1038/35022565 [DOI] [PubMed] [Google Scholar]
- Hutchings J.A. Life history consequences of overexploitation to population recovery in Northwest Atlantic cod (Gadus morhua) Can. J. Fish. Aquat. Sci. 2005;62:824–832. 10.1139/f05-081 [Google Scholar]
- Kozłowski J. Optimal allocation of resources explains interspecific life history patterns in animals with indeterminate growth. Proc. R. Soc. B. 1996;263:559–566. [Google Scholar]
- Law R. Fishing, selection, and phenotypic evolution. ICES J. Mar. Sci. 2000;57:659–668. 10.1006/jmsc.2000.0731 [Google Scholar]
- Law R, Grey D.R. Evolution of yields from population with age-specific cropping. Evol. Ecol. 1989;3:343–359. 10.1007/BF02285264 [Google Scholar]
- Metz J.A.J, Geritz S.A.H, Meszéna G, Jacobs F.J.A, Van Heerwaarden J.S. Adaptive dynamics: a geometrical study of the consequences of nearly faithful reproduction. In: van Strien S.J, Verduyn Lunel S.M, editors. Stochastic and spatial structures of dynamical systems. North Holland; Amsterdam: 1996. pp. 183–231. [Google Scholar]
- Morgan M.J, Colbourne E.B. Variation in maturity-at-age in three populations of American plaice. ICES J. Mar. Sci. 1999;56:673–688. 10.1006/jmsc.1999.0487 [Google Scholar]
- Myers R.A, Worm B. Rapid worldwide depletion of predatory fish communities. Nature. 2003;423:280–283. doi: 10.1038/nature01610. 10.1038/nature01610 [DOI] [PubMed] [Google Scholar]
- Olsen E.M, Heino M, Lilly G.R, Joanne Morgan M, Brattey J, Ernande B, Dieckmann U. Maturation trends indicative of rapid evolution preceded the collapse of northern cod. Nature. 2004;428:932–935. doi: 10.1038/nature02430. 10.1038/nature02430 [DOI] [PubMed] [Google Scholar]
- Persson L, Leonardsson K, de Roos A.M, Gyllenberg M, Christensen B. Ontogenetic scaling of foraging rates and the dynamics of a size-structured consumer–resource model. Theor. Popul. Biol. 1998;54:270–293. doi: 10.1006/tpbi.1998.1380. 10.1006/tpbi.1998.1380 [DOI] [PubMed] [Google Scholar]
- Policansky D. Fishing as a cause of evolution in fishes. In: Stokes T.K, McGlade J.M, Law R, editors. The exploitation of evolving resources. Springer; Berlin: 1993. pp. 2–18. [Google Scholar]
- Reznick D.N, Bryga H, Endler J.A. Experimentally induced life-history evolution in a natural population. Nature. 1990;346:357–359. 10.1038/346357a0 [Google Scholar]
- Rijnsdorp A.D. Fisheries as a large-scale experiment on life-history evolution: disentangling phenotypic and genetic effects in changes in maturation and reproduction of North Sea plaice, Pleuronectes platessa L. Oecologia. 1993;96:391–401. doi: 10.1007/BF00317510. 10.1007/BF00317510 [DOI] [PubMed] [Google Scholar]
- Roff D.A. Sinauer Associates; Sunderland, MA: 2002. Life history evolution. [Google Scholar]
- Rowell C.A. The effects of fishing on the timing of maturity in North Sea cod (Gadus morhua L.) In: Stokes T.K, McGlade J.M, Law R, editors. The exploitation of evolving resources. Springer; Berlin: 1993. pp. 44–61. [Google Scholar]
- Scheffer M, Carpenter S, Foley J.A, Folke C, Walker B.M. Catastrophic shifts in ecosystems. Nature. 2001;413:591–596. doi: 10.1038/35098000. 10.1038/35098000 [DOI] [PubMed] [Google Scholar]
- Schmitt, C. C. & Skud, B. E. 1978 Relation of fecundity to long-term changes in growth, abundance and recruitment. Science Report No. 66, International Pacific halibut Commission, Seattle, WA.
- Taylor P.D. The selection differential in quantitative genetics and ESS models. Evolution. 1996;50:2106–2110. doi: 10.1111/j.1558-5646.1996.tb03598.x. [DOI] [PubMed] [Google Scholar]
- Trippel E.A. Age at maturity as a stress indicator in fisheries. Bioscience. 1995;45:759–771. [Google Scholar]
- Trudel M, Tremblay A, Schetagne R, Rasmussen J.B. Why are dwarf fish so small? An energetic analysis of polymorphism in lake whitefish (Coregonus clupeaformis) Can. J. Fish. Aquat. Sci. 2001;58:394–405. 10.1139/cjfas-58-2-394 [Google Scholar]
- van Kooten T, de Roos A.M, Persson L. Local foraging and limited mobility: dynamics of a size-structured consumer population. Ecology. 2004;85:1979–1991. [Google Scholar]
- Walsh M.R, Munch S.B, Chiba S, Conover D.O. Maladaptive changes in multiple traits caused by fishing: impediments to population recovery. Ecol. Lett. 2006;9:142–148. doi: 10.1111/j.1461-0248.2005.00858.x. 10.1111/j.1461-0248.2005.00858.x [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Tables S1–S3. Table S1: Variables and model parameters. Table S2: Individual-level equations used in the simulations. Table S3: Population-level equations used in the simulations of the ecological dynamics.