Role of avidity and breadth of the CD4 T cell response in progression to AIDS

Abstract

The great variability in the time between infection with HIV and the onset of AIDS has been the object of intense study. In the current work, we examine a mathematical model that focuses on the role of immune response variability between patients. We study the effect of variation in both the avidity and the breadth of the immune response on within-patient disease dynamics, viral setpoint and time to AIDS.

We conclude that immune response variability can explain the observed variability in disease progression to a large extent. It turns out that the avidity, more than the breadth of the immune response, determines disease progression, and that the average avidity of the five best clones is a much better correlate for disease progression than the total number of clones responding. For the design of vaccines, this would suggest that, if given the choice between stimulating a broader, but average avidity response or a narrower high-avidity response, the latter option would yield better control of virus load and consequently slow down disease progression.

1. Introduction

Infection with HIV is characterized by primary infection, followed by a variable period of clinical latency and eventually AIDS. The time from infection with HIV-1 to development of AIDS varies considerably (Bacchetti & Moss 1989; Moss & Bacchetti 1989; Lemp et al. 1990; Morgan et al. 2002). Viral setpoint, i.e. the relatively stable viral load reached after primary infection—is a good correlate of disease progression (Mellors et al. 1996; Pedersen et al. 1997). It depends on the virological and immunological features of primary infection (Lifson et al. 1997; Pantaleo et al. 1997a; Staprans et al. 1999). Therefore, disease progression is in principle the result of both host and viral characteristics (Feinberg & McLean 1997). Over the course of infection, virus cytopathicity, replication rate and tropism may change; host immune response weakens through clonal exhaustion and loss of function of the cytotoxic T lymphocytes (CTL). Finally, viral escape from the immune response can also contribute to pathogenesis (Phillips et al. 1991; Borrow et al. 1997; Price et al. 1997; Evans et al. 1999).

The clinically observed relationship between breadth and magnitude of the HIV-specific T cell response and viral load, is subject to controversy. First, studies relating the breadth of the HIV-specific CD8 (and CD4) T cell response with viral load yield conflicting results (Chouquet et al. 2002; Addo et al. 2003). This might stem from the lack of standardization of methods of measuring epitope-specific response. Second, early studies reported a negative correlation between HIV-specific CTL and viral load, supporting the notion that CTL are crucial in the control of plasma viral load (Ogg et al. 1998). Later studies instead showed a positive or no correlation (Betts et al. 2001a; Frahm et al. 2004). In part, these contradicting results might be attributed to the dual role of the CD4 helper cells, both targets of infection and mediators of the CTL response. We have shown in previous work that this feature of HIV infection can explain the occurrence of both very fast and slow progression (Korthals Altes et al. 2003). Besides, theoretical insight suggests that variation in viral setpoint stems from variation in immune responsiveness, rather than in CTL abundance (Nowak & Bangham 1996). This would explain the lack of consistent correlation between viral load and CTL abundance. In this study, we focus on the effect of variation in immune responsiveness on disease progression. We simulated the process of HIV infection and progression to AIDS, incorporating two key characteristics of the immune response: the qualitative ‘immune responsiveness’, i.e. the functional avidity of the HIV-specific clones, and a more quantitative aspect of the response, i.e. the number of clones involved in the response. Our model formulation lies, in its complexity, between relatively simple earlier models of HIV pathogenesis (Fraser et al. 2001; Galvani 2005), and large computational models (Castiglione et al. 2004). Within a simple framework, it assigns different immune repertoires to the simulated patients. We assumed that progression to AIDS is driven by a process of viral escape from immune recognition. We found that individual variation in immune background, combined with the stochasticity of the escape process, are sufficient ingredients to create a realistic variation in rates of disease progression. Also, average avidity of the dominant clones and average avidity of the entire HIV-specific repertoire are good predictors of disease progression. In contrast, the breadth of the immune response at setpoint is a much poorer correlate of progression. Finally, we discuss our results in the context of vaccination strategies.

2. Model

(a) Basic model

We developed a mathematical model of HIV infection describing the dynamics of the cell populations of importance in our study, extending our previous model of HIV dynamics (Korthals Altes et al. 2003). There are three populations of cells: target cells (T) that do not participate in the immune response; HIV-specific CD4 T cells (H_i)—specific for a particular epitope i—that play a role in priming of the immune response, but that can also be infected; and infected cells (I), which are assumed to have lost their immune function. The equations describing the dynamics of these cell populations can be summarized as follows:

$$\begin{array}{c}\frac{\text{d}T}{\text{d}t}=\sigma -{\delta }_{T}T-\beta IT\\ \frac{\text{d}{H}_i}{\text{d}t}={\sigma }_H+\frac{\alpha q_{i}I{H}_i}{\gamma +q_{i}I}-ϵH_i^2-\beta I{H}_i-{\delta }_H{H}_i\\ \frac{\text{d}I}{\text{d}t}=\beta I\left(T+\sum _{i=1}^{i=n}{H}_i\right)-{\delta }_{I}I-kI\sum _{i=1}^{i=n}{q}_i{H}_i\end{array}\}.$$ 2.1

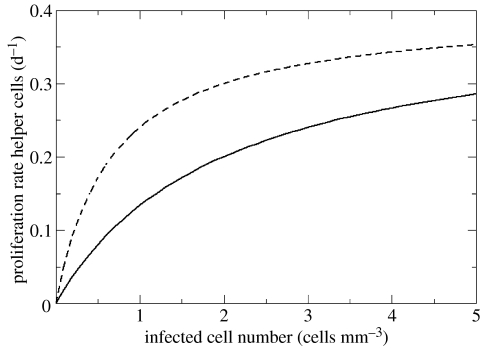
Target cells T are produced at rate σ cells per day, die at rate δ_T and are infected by virus at rate βI. HIV-specific CD4 T cells H_i are produced at rate σ_H cells per day and proliferate with a maximum rate α. The per capita proliferation rate αq_iI/(γ+q_iI) is a saturated function of antigen availability (De Boer & Perelson 1994; Fraser et al. 2001; Wodarz & Jansen 2001). This function is pictured in figure 1: more antigen is needed for equivalent proliferation rates in a low-avidity response (q_i=0.5) than in a high-avidity response (q_i=1.5). The helper cell clones H_i (throughout this paper, we use the term ‘clone’ to represent the set of CD4 helper cells recognizing epitope i) can differ in their functional avidity q_i, which implies that they need different levels of antigen to proliferate. At low cell densities, HIV-specific CD4 T helper cells have an average lifespan of 1/δ_H days; at high densities, the average lifespan is shortened due to (intra-specific) competition between helper cells and this is reflected by the ϵH_i² term (Ferguson et al. 1999; Fraser et al. 2002). Helper T cells are infected at rate βI. There are n helper cell clones H_i, each specific for a distinct viral epitope. In fact, as the results do not depend on the fact that immune cells are infected by HIV, we argue in the discussion that the population of cells H_i can be considered as CD8 T cell clones. Infected cells I appear through infection at rate $\beta \left(T+{\sum }_{i=1}^{i=n}{H}_i\right)$, die at rate δ_I and are killed by the lytic immune response, at rate $k{\sum }_{i=1}^{i=n}{q}_i{H}_i$, where we assumed an indirect link between the quality of immune recognition and lysis of infected cells. The main simplifying assumptions are detailed in the electronic supplementary material (section 1).

Figure 1.

Per capita T cell proliferation rate as a function of antigen (αq_iI/(γ+q_iI)), for immune response avidity q_i=0.5 (continuous line) and avidity q_i=1.5 (dashed line). Proliferation rate is half-maximal (α/2) for I=γ/q_i. Parameter values are α=0.4 d⁻¹ and γ=1 cell mm⁻³.

(b) Immune repertoire variation and viral escape

For simplicity, we assumed that patients have the same potential number of clones in their repertoire (n=200 in our model), but differ in their ‘immune response profile’, i.e. in the avidity of the clones. The avidities q_i of each CD4 helper clone H_i were drawn from an exponential distribution: this entails that, within each patient, only a few HIV-specific clones have high avidity. The mean avidity of this distribution was drawn randomly for each patient between 0.5 and 1.5.

The process of viral escape from the immune response was simulated by assuming an escape mutation probability, per epitope, per day. As mutations predominantly occur during reverse transcription, this probability is proportional to viral load. When such a mutation occurs, the specific response against the variant epitope becomes ineffective, and thus it will disappear (i.e. if epitope 1 mutates, q₁=0). We allowed immune escape only after 250 days, when viral load is close to its setpoint. Since many of the ‘easy’ mutations occur during primary infection (Yang et al. 2003), we only considered the slow accumulation of the more difficult mutations during the asymptomatic phase. We modelled a single monoclonal virus population, implicitly assuming rapid replacement of the wild-type population after an escape mutation, a process facilitated by the high recombination rate in HIV (Robertson et al. 1995; Salminen et al. 1997; Hoelscher et al. 2002). Furthermore, we have not assumed a fitness cost of escape mutations, but it will be considered in the discussion and in section 4 of the electronic supplementary material.

3. Results

(a) Disease progression

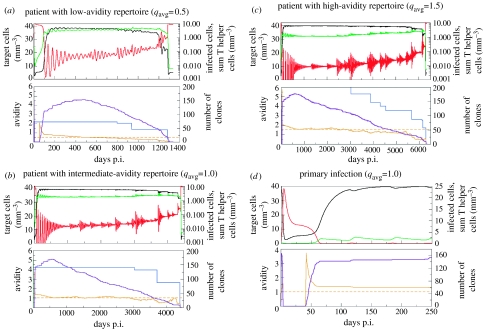
In figure 2, we represent typical disease progression in three patients with different immune backgrounds. All patients have a potential repertoire of 200 HIV-specific clones, but differ in the average avidity of their HIV-specific repertoire, with a poor avidity in figure 2a (q_avg=0.5), medium avidity in figure 2b (q_avg=1.0) and high avidity in figure 2c (q_avg=1.5). In our model, we defined the onset of AIDS as the rapid switch of infected cells to high levels (we used a criterion of more than 8 cells mm⁻³, knowing that in the steady state without immune response infected cells are at 8.75 mm⁻³). CD4 T cell counts are then drastically reduced and HIV-specific immunity disappears. The time to AIDS is strongly affected by the average avidity of the immune response, with the two extreme cases differing by a factor five in time to AIDS (around 3.5 years for q_avg=0.5 and around 18 years for q_avg=1.5). The dynamics in figure 2 correspond well to the course of HIV-infection in vivo. Virus load peaks within 50–100 days after infection. Target cells are initially massively depleted (Mattapallil et al. 2005), but then stabilize at a relatively high level during the asymptomatic phase (figure 2d). Virus load decreases several logs (about three when q_avg=1.0, see figure 2b,d) as HIV-specific T helper cells start expanding, after the peak of primary infection (figure 2d). The number of activated clones increases at the beginning of infection, even after the escape process sets in at 250 days (lower panels, figure 2a–c). The low-avidity clones take much longer to appear than the high-avidity clones. Consequently, the average avidity of the clones responding to HIV is relatively high in the initial phase (lower panels, figure 2a–c). The asymptomatic phase is characterized by a relatively stable, but slowly decreasing target cell count, and low levels of infected cells, with occasional bursts of viral load associated with escape mutations. We do not observe the more progressive CD4 decline documented in the blood: here we represent average CD4 count per volume over all body compartments, not just the blood. CD4 helper responses are also relatively stable, showing oscillations associated with viral bursts. Later in infection, total HIV-specific helper cell numbers increase slightly, in a stepwise fashion (upper panels, figure 2a–c). These increases occur when the avidity of the dominant clone decreases, after escape from the highest-avidity clone (lower panels, figure 2a–c). Clones disappear as they are gradually rendered ineffective by the viral escape process (lower panels, figure 2a–c). However, more helper cells within clones are recruited to respond, as the overall immune response is less effective at clearing infected cells.

Figure 2.

Disease progression in patients with different average avidities of their HIV-specific T cell repertoire. Parameters values: σ=2 cells mm⁻³ d⁻¹, δ_T=0.05 d⁻¹, σ_H=10⁻⁵ cells mm⁻³ d⁻¹, α=0.4 d⁻¹, β=0.04 cells⁻¹ mm³ d⁻¹, ϵ=0.1 cells⁻¹ mm³ d⁻¹, δ_H=0.01 d⁻¹, δ_I=0.2 d⁻¹, γ=1 cell mm⁻³, k=0.3 cells⁻¹ mm³ d⁻¹; the probability of escape mutations arising per day in a given epitope is p_ESC=infected cells/35. Values for the parameters and variables are based on a ‘total body model’, and rescaled to a volume of 1 mm³. q_i is dimensionless; γ/q_i represents the number of cells mm⁻³ required for half-maximal proliferation. p.i, post infection. Colour coding: target cells, black; infected cells, red; total helper cells, light green; number of clones responding, purple; average avidity immune response, orange; avidity of the best clone, blue. AIDS corresponds to the state without immune response, with high-viral load (more than 8 cells mm⁻³) and low target cell numbers. (a) Low repertoire avidity, q_avg=0.5. Fast progressor: AIDS occurs after about 3.5 years. (b) Medium repertoire avidity, q_avg=1.0. Intermediate progressor: onset of AIDS at about 12 years. (c) High-repertoire avidity, q_avg=1.5. Slow progressor: AIDS after more than 17 years. (d) Primary infection phase (first 250 days) of the individual shown in figure 2b.

The switch to AIDS is clearly related to the avidity of the HIV-specific repertoire. Before the switch, the remaining immune repertoire only just controls the virus. As a consequence of this poor control, a mutation in a high-avidity epitope will cause a large burst in viral load (e.g. in figure 2a, around t=1200 days). This viral burst in turn promotes the appearance of more escape mutants, as the probability of escape is proportional to the viral load. This positive feedback causes the accelerated loss of, among others, high-avidity clones critical in the control of virus load, leading to AIDS.

(b) Viral setpoint: relation to avidity and breadth of the immune response

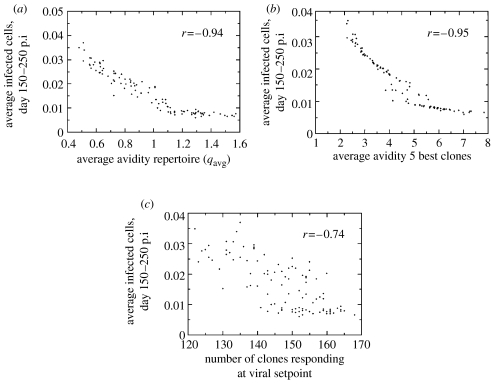
Viral setpoint is an important correlate of disease progression (Mellors et al. 1996; Pedersen et al. 1997) and varies several orders of magnitude between patients. To study whether variation in setpoint between patients can be explained by differences in the immune response, we simulated HIV-1 infection in 100 patients. We calculated viral setpoint by taking the average number of infected cells between day 150 and 250 post infection, to average out oscillations in infected cell numbers. We observed a strong negative correlation between average avidity of the immune repertoire and viral setpoint (figure 3a). In the electronic supplementary material (section 2 and fig. A1), we give an analytical approximation of the relation between infected cell numbers at setpoint and the avidity of the immune response in a single-clone model. In the high-avidity range, viral load is inversely proportional to immune response avidity. The mathematical relationship between viral load and avidity in our model is a complex function (electronic supplementary material, section 2), reminiscent of the inverse relation described by Nowak & Bangham (1996).

Figure 3.

HIV infection simulated in 100 patients with different average immune response avidities, but with the same number of HIV-specific clones. Viral setpoint was determined by averaging the number of infected cells per day, between day 150 and 250. We also monitored the breadth of the response at day 250. As a definition of a clone's activity, we used a threshold value of 10⁻³cells mm⁻³, which corresponds to values above the ‘naive state’ of a clone (the equilibrium of T helper cell clones in the absence of infection is approximately σ_H/δ_H). Correlation coefficients indicated with r. Parameters as in figure 2, with q_avg drawn randomly between 0.5 and 1.5. Initial conditions on the variables: H₀=9.9×10⁻⁴ cell mm⁻³, T₀=40 cells mm⁻³ and I₀=1 cell mm⁻³. Viral setpoint plotted against: (a) average avidity of the HIV-specific CD4 T cell repertoire. (b) average avidity of the five dominant clones. (c) breadth of the HIV-specific CD4 T cell response at viral setpoint (at 250 days). Viral setpoint is negatively correlated with the breadth of the immune response, and with the average quality of the five best clones and of the whole repertoire.

Markedly, virus load is equally strongly correlated with the average avidity of the five best clones as with the avidity of the entire repertoire (figure 3b). Considering the average avidity of the 10 best clones does not increase the correlation coefficient (r=−0.94 compared with r=−0.95). The avidity of the best clone alone is a much poorer correlate of setpoint than the average avidity of the five best clones (r=−0.84). This, together with the much poorer correlation between viral setpoint and breadth of the response (figure 3c), indicates that the quality rather than the quantity of the immune response determines viral setpoint.

To further study the role of the high-avidity clones in controlling infection, we monitored viral setpoint when only the five dominant clones of the full repertoire were allowed to expand (electronic supplementary material, fig. A2). Summarizing, in a low-avidity response, the breadth of the immune response plays a complementary role in the control of virus load, while it hardly contributes to a high-avidity response.

Essentially, the breadth of the response is set by two variables: the avidity of the immune clones and the viral load. The latter determines the breadth of the immune response by setting a lower limit to the avidity of clones that can respond. In fact, the threshold avidity for a clone to take part in the immune response increases with viral load (electronic supplementary material, section 3). This means that as the average avidity of the immune response increases, more clones will be involved in the response: the lower viral load allows for the expansion not only of more high-avidity clones, but also more low-avidity clones.

(c) Time to AIDS: relation to avidity and breadth of immune response

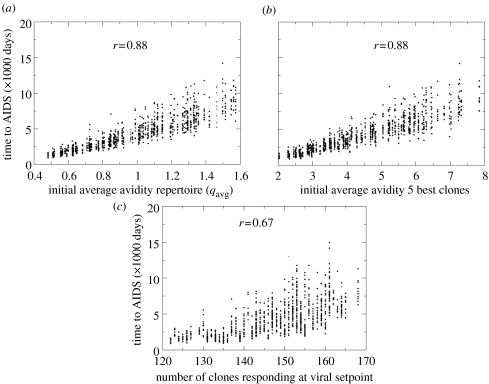
We next simulated disease progression in the above-described group of 100 (simulated) patients differing in immune background. For each patient, we generated 10 possible courses of disease by varying the seed of the random number generator for the viral escape process. This way, we obtained insight in the variability in time to AIDS stemming from the stochasticity of the escape process. The results in figure 4a show that this variability is extensive, causing up to a threefold difference in time to AIDS. This variation originates from differences in the timing of escape mutations in the epitopes associated with the best clones, and it is further amplified by the positive feedback of viral load on the mutation rate.

Figure 4.

Disease progression simulated in 100 patients, with 10 different possible courses of disease per patient (using different random seeds for the escape process, but starting with the same immune repertoire and, consequently, viral setpoint). Parameters as in figure 2. Correlation coefficients indicated with r. Time to AIDS plotted against: (a) average avidity of the HIV-specific CD4 T cell repertoire. (b) average avidity of the five dominant clones. (c) breadth of the HIV-specific CD4 T cell response at viral setpoint (at 250 days).

Average avidity of the five dominant clones is an equally good predictor of time to AIDS as average avidity of the full repertoire (figure 4a,b). As with viral setpoint, average avidity of the 10 best clones is not a better correlate (r=0.87, compared with r=0.88) and the avidity of the best clones alone a much poorer correlate (r=0.76). Time to AIDS correlates more poorly with the breadth of the response (figure 4c). Still, it takes about twice as long before AIDS occurs in patients with the full repertoire, compared to patients with only five clones responding (electronic supplementary material, fig. A3). In good responders, the subdominant clones provide substantial protection against progression, even though viral setpoint is largely determined by the five best clones.

4. Discussion

We formulated a mathematical model of HIV infection within a patient, to investigate the relationship between immune system characteristics and disease progression. The model was built on our previous model of HIV infection, in which the dual role of CD4 helper cells, being both targets of infection and mediators of the immune response, was taken into account (Korthals Altes et al. 2003). Progression to AIDS was effected through the stochastic appearance of viral escape variants. We found that for the prediction of viral setpoint and rate of progression to AIDS, the average avidity of only the five best clones involved in the response is equally informative as the average avidity of the entire HIV-specific repertoire. Both avidity measures are better correlates of progression than the breadth of the immune response at setpoint, suggesting that quality, rather than quantity of the response, determines disease progression. However, simulating progression with only the five highest avidity clones shows that the remainder of the repertoire contributes up to 50% of the protection against developing AIDS: time to AIDS is twice as long with the full repertoire. Finally, although our results do not show the same variation as the data on viral setpoint across patients (Piatak et al. 1993), our simulations confirm the trend found in the data (Staprans et al. 1999) of an inverse correlation between viral setpoint and rate of disease progression (results not shown).

In conclusion, the quality of the response (i.e. the average avidity of the five best clones) is the main determinant of viral setpoint, but the breadth of the response is equally important in setting the time to AIDS. In fact, a large part of the variation in time to AIDS is caused by the stochasticity of the escape mutation process. In our model, all epitopes have the same probability of mutating, whereas in reality epitopes at conserved functional sites in the viral genome might be harder to mutate without high fitness-cost (Wagner et al. 1999; Boaz et al. 2003). Such diversity in escape probabilities could create additional variation in time to AIDS. Robustness of our results is discussed in the electronic supplementary material (section 4 and fig. A4).

Although the purpose of this paper is not to investigate the precise causes of the transition to AIDS, we may speculate about the mechanism leading to the sudden switch to AIDS. As indicated in the results section, we think that prior to the transition to AIDS, the remaining immune repertoire only marginally controls the virus. Consequently, escape of a high-avidity clone will lead to a burst (i.e. a large oscillation) in viral load. This creates a positive feedback by increasing the mutation probability, triggering a cascade of loss of clones, including high-avidity clones critical in the control of viral load. Contrary to previous models (Korthals Altes et al. 2003), the dual role of the CD4 helper cells in the dynamics of HIV infection as targets of infection and mediators of the immune response, is not a key in the switch to high viral load at the transition to AIDS. In fact, the result that the average avidity of the five best clones is an equally good predictor of progression as average avidity of the whole repertoire still holds if CD4 helper cells simply play a role in the immune response without being infected by HIV (results not shown). In fact, in that simplified model, we could also interpret the different immune response terms H_i as different CD8 T cell clones, and ignore the HIV-specific CD4 cells. This is an important observation, as it implies that our results may apply to the CD8 T cell response as well.

A much-debated earlier theory, the antigenic diversity threshold theory (Nowak et al. 1991), proposes that increasing viral antigenic diversity ultimately causes failure of the immune system to control all viral variants. This hypothesis is driven by an asymmetry, in the sense that HIV variants can infect all CD4 cells non-specifically, while killing of infected cells by the immune system is specific. As a result, viral control decreases with the total number of HIV variants present. When diversity reaches a critical threshold, control is no longer possible. Viral diversity is absent from our model, as we modelled a uniform virus population, or, interpreted differently, a fast succession of viral variants. Therefore, we do not make any assumptions, or draw any conclusions, on the evolution of virus diversity. If anything, our results would suggest that the diversity of the immune response decreases as disease progresses, because clones are lost when escape mutants arise that render the clone ineffective. Another important difference with previous models of polyclonal immune responses against HIV, is the fact that several immune responses can coexist in our model, even in the face of a ‘homogeneous’ virus population. Previous work interpreted the pattern of shifting immunodominance over the course of infection as a succession of individual clones excluding other immune responses (Nowak et al. 1995). Here we allowed for the coexistence of different clones by including density-dependent death within clones, to match the experimental finding that many responses can be maintained at the same time (Betts et al. 2000, 2001b; Frahm et al. 2004).

Actually, our model is also applicable to theories of clonal exhaustion driving disease progression (Moskophidis et al. 1993; Pantaleo et al. 1997b; Gorochov et al. 1998; Galvani 2005), but in that case immune clones would disappear in order of decreasing avidity (references in Snyder et al. 2003). Such a scenario does not yield substantially different results, although the average quality of immune clones would then steadily decrease over time.

In conclusion, we have formulated a novel mathematical model simulating HIV disease progression in the context of a polyclonal HIV-specific immune response, gradually losing in strength as viral escape mutants appear. This alternative model of progression to AIDS helped us point at the immunologic features determining individual differences in rate of disease progression. Differences in the avidity and breadth of an individual's HIV-specific immune responses seem sufficient to explain variation in HIV disease progression. Notably, we found that the average avidity of the five dominant responses is a very good correlate of disease progression, just as the average avidity of the entire HIV-specific CD4 repertoire. The avidity of the immune response, in turn, also determines the breadth of the CD4 response mounted, which has an additional effect on setting the time to AIDS. Possible experiments to test our theoretical results include monitoring breadth and avidity of the CD4 and CD8 SIV-specific responses, as well as setpoint and rate of progression in the animal model. Also, one could compare the efficacy of a vaccine, again in the animal model, stimulating high-avidity CTL responses against five epitopes, with that of a vaccine stimulating lower-avidity responses against 10 epitopes.

The leading role of immune response avidity in determining disease progression is interesting from a clinical point of view. Our results suggest that the best approach for a vaccine is to stimulate a few high-avidity T cell responses, rather than to aim at a broad response. The high-avidity responses may in fact reduce virus load to such levels that additional, lower-avidity, autologous clones, i.e. clones not originally induced by the vaccine, may also be stimulated to respond, thus helping to control viral load even better.

Supplementary Material

Sections 1–4

Section 1, main simplifying assumptions of the model; section 2, simplified mathematical expressions for the relationship between viral setpoint and immune response avidity; section 3, threshold avidity for the establishment of an active immune response; section 4, robustness of the model results.

Sections 1–4

Section 1, main simplifying assumptions of the model; section 2, simplified mathematical expressions for the relationship between viral setpoint and immune response avidity; section 3, threshold avidity for the establishment of an active immune response; section 4, robustness of the model results